Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Retrial queues of type M/G/1//N in Kendall’s notation are queueing models with 1 server which serves N customers (clients, calls) each one producing a Poisson flow of demands. Retrial feature is characterized by the specific behaviour of the arriving customers that find the server busy. These customers join a virtual waiting room, called orbit and repeat the attempt to get service after some time. The customers in the orbit are also called retrial customers or sources of retrial calls, while the customers that are not in the orbit or under service are called sources of primary calls or customers in free state.

Retrial queues arise from various real life situations as well as telecommunication and network systems (Falin and Templeton 1997; Artalejo and Gómez-Corral 2008). For example, in a call center a customer who cannot connect with an operator tries again later (Aguir et al. 2004). Furthermore, in modeling the mobile cellular systems, retrial feature cannot be ignored (Tran-Gia and Mandjes 1997; Van Do et al. 2014). The assumption of a finite number of customers is of special interest to practice, as in real situations the number of subscribers is finite. In particular, the described finite single server retrial queues and its variants are useful in modeling magnetic disk memory systems (Ohmura and Takahashi 1985), local area networks with nonpersistent CSMA/CD protocol (Li and Yang 1995), etc. Falin and Artalejo (1998) carried out an extensive analysis of the single server finite source retrial queue, including the busy period distribution and the waiting time process. Distribution of the number of retrials, made by a retrial customer while being in orbit is investigated by Dragieva (2013). Single server finite source retrial queues with two types of breakdowns and repairs are considered by Wang et al. (2011) and by Zhang and Wang (2013).

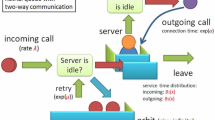
There also exist real situations, especially in service systems where customers who cannot receive service immediately upon arrival register to the system and go to other places before returning to the system after some time. On the other hand, the server once becoming idle calls for customers. The former is reflected by retrials while the latter can be modelled by outgoing calls. These real situations are the motivation for us to consider finite source retrial models with two-way communication.

Some of the first results on two-way communication retrial queues are obtained by Falin (1979), who analyzes a single server queue in which the outgoing and the incoming calls are assumed to follow the same arbitrary service time distribution. The priority retrial queues with available buffers for the outgoing calls, studied by Falin et al. (1993) and by Choi et al. (1995) could also be considered as two-way communication models. Artalejo and Phung-Duc (2012) consider single and multiple servers retrial models with two-way communication where the service times of incoming and outgoing calls follow the exponential distribution with distinct parameters. The corresponding M/G/1 queue where the service times of incoming and outgoing calls follow two distinct arbitrary distributions is investigated by the same authors Artalejo and Phung-Duc (2013). Sakurai and Phung-Duc (2015) consider two-way communication retrial queues with multiple types of outgoing calls. A two-way communication M/M/1 retrial queue with server-orbit interaction is studied by Dragieva and Phung-Duc (2016). In the model, proposed in this paper it is assumed that after some exponentially distributed idle time the server makes outgoing calls of two types. The outgoing calls of type 1 are directed to the customers in orbit, while these that are of type 2 - to the customers outside the orbit. This assumption reflects various real-life situations, like call center of a credit card company where the operator may call to customers for some advertisement, or to the customers who not yet pay the money. But, at the moment some of these customers may be in the orbit. The operator is not notified for them, so that he/she may call to a customer outside the orbit as well as to a customer in orbit. Actually, when the population of customers is considered infinite, the probability that the server, calling to an arbitrary individual from this population may choose one from the orbit, is very small. Thus, in such situations it is more appropriate to model the system by queues with finite source. This motivated us to start investigation of finite source retrial models with two-way communication.

The rest of the current paper is organized as follows. In Sect. 2 we describe the model in detail. The joint distribution of the server state and the orbit size is studied in Sect. 3.1, while Sect. 3.2 deals with the main performance macro characteristics. Section 4 is devoted to numerical examples, Sect. 5 concludes the paper and presents some possible topics for future research.

2 Model Description

As stated in the Introduction we consider a queueing model with one server which serves N customers. Each of these customers produces a Poisson flow of incoming primary calls with mean \(1/\lambda ^{\prime }\). Thus, when a source is free at time moment t (i.e. is not being served and is not waiting for service) it generates a primary call during an interval \((t,~t+dt)\) with probability \(\lambda ^{\prime }dt\). This means that if at a time moment t there are n customers in free state (sources of incoming primary calls), the arrival rate of the primary calls will be \(n\lambda ^{\prime }\) and consequently the probability of a primary call arrival during a time interval \((t,~t+dt)\) is equal to \(n\lambda ^{\prime }dt\).

If an incoming call finds the server busy upon arrival it joins the orbit of retrial customers (calls), stays in it for an exponentially distributed time with mean \(1/\mu \), and retries to get service. The incoming retrial (secondary) calls, like the incoming primary calls, are accepted if the server is idle, otherwise they enter the orbit again.

The server, in turn, after some exponentially distributed idle time makes outgoing calls of two types - to a customer in the orbit (an outgoing call of type 1) or to a customer in free state (an outgoing call of type 2). The parameters of these exponential distributions are \(\alpha \) and \(\alpha _{0}^{\prime }\), respectively. Thus, if the server is idle and there are n incoming retrial customers in the orbit, the server connects with one of them in an exponentially distributed time with parameter \(n\alpha \), and connects with one of the customers outside the orbit in an exponentially distributed time with parameter \(\left( N-n\right) \alpha _{0}^{\prime }\).

The service times of the incoming calls and the outgoing calls of both types are exponentially distributed with rate \(\nu _{1}\) and \(\nu _{2}\), respectively. When the service is over all customers go to a free state.

We assume that the arrivals of primary incoming calls, retrial intervals of secondary incoming calls, service times of incoming and outgoing calls, and the time to make outgoing calls are mutually independent.

We denote the number of customers in orbit, the server state and the number of busy servers at time t by R(t), S(t) and C(t), respectively,

$$ S(t)=\left\{ \begin{array} [c]{l} 0\text {, when the server is idle,}\\ 1,\text { when an incoming call is in service,}\\ 2,\text { when an outgoing call is in service,} \end{array} \right. $$
$$ C(t)=\left\{ \begin{array} [c]{l} 0\text {, when\ }S(t)=0,\\ 1,\text { when }S(t)=1,2. \end{array} \right. $$

Obviously, when the server is busy the number of customers in the orbit can’t be equal to N, i.e. \(R(t)<N\). As stated above after the service both incoming and outgoing customers go to a free state. This means that when the server is idle, there will be at least one customer in free state, i.e. again \(R(t)<N\). Thus, the state space of the process (S(t), R(t)) is the set \(\left\{ 0,1,2\right\} \times \) \(\left\{ 0,1,2,\ldots ,N-1\right\} \). Because of the finite state space this Markovian process is always stable.

Some particular values of the parameters in the above described model lead to other models. Namely, in the case

  • \(\alpha =\alpha _{0}^{\prime }=0\) we obtain the classical single server retrial queue, studied by a number of authors, in a number of papers, some of which are presented in the Introduction;

  • \(\alpha _{0}^{\prime }=0\) we have a single server, finite source retrial queue with search of the customers from orbit;

  • \(\mu =\lambda ^{\prime }\) we get a single server, finite source queue with losses and two-way communication.

Finally, if \(N\rightarrow \infty \), \(\lambda ^{\prime }\rightarrow 0\) and \(\alpha _{0}^{\prime }\rightarrow 0\) in such a way that \(N\lambda ^{\prime }\rightarrow \lambda \) and \(N\alpha _{0}^{\prime }\rightarrow \alpha _{0}\) our model converges to the corresponding model with infinite source, studied by Dragieva and Phung-Duc (2016).

Further in the paper we discuss some of these particular cases.

3 Stationary System State Distributions

3.1 Joint Distribution of the Server State and Orbit Size

The system of balance equations for the stationary probabilities

$$ \pi _{i,j}=\lim _{t\rightarrow \infty }P\left( S(t)=i,R(t)=j\right) ~~~i=0,1,2,~j=0,1,\ldots ,N-1 $$

is

$$\begin{aligned} \left[ (N-j)\left( \lambda ^{\prime }+\alpha _{0}^{\prime }\right) +j(\alpha +\mu )\right] \pi _{0,j}=\nu _{1}\pi _{1,j}+\nu _{2}\pi _{2,j}, \end{aligned}$$
(1)
$$\begin{aligned} \left[ (N-j-1)\lambda ^{\prime }+\nu _{1}\right] \pi _{1,j}=(N-j)\lambda ^{\prime }\pi _{0,j}+(j+1)\mu \pi _{0,j+1}+(N-j)\lambda ^{\prime }\pi _{1,j-1}, \end{aligned}$$
(2)
$$\begin{aligned} \left[ (N-j-1)\lambda ^{\prime }+\nu _{2}\right] \pi _{2,j}=(N-j)\alpha _{0}^{\prime }\pi _{0,j}+(j+1)\alpha \pi _{0,j+1}+(N-j)\lambda ^{\prime }\pi _{2,j-1}, \end{aligned}$$
(3)

with \(\pi _{0,N}=\pi _{1,-1}=\pi _{2,-1}=0\).

Because of the finite number of equations we can solve this system using general methods like Cramer’s rule. But here we present more convenient recursive schemes. Firstly, they can save a number of operations, and secondly will be useful in our future work when investigating the other descriptors of the system functioning, like the waiting time process, busy period distribution and others. We first express the probabilities \(\pi _{i,j} \) \((i=1,2)\) in terms of the probabilities \(\pi _{0,j} (j=0,1,\ldots , N-1)\). According to Eqs. (2) and (3), if denote

$$\begin{aligned} \pi _{i,j}=A_{j,0}^{(i)}\pi _{0,0}+A_{j,1}^{(i)}\pi _{0,1}+\ldots +A_{j,j+1}^{(i)} \pi _{0,j+1}, \end{aligned}$$
(4)

we have

$$\begin{aligned} \pi _{1,0}&=\frac{N\lambda ^{\prime }\pi _{0,0}}{a_{1,1}}+\frac{\mu \pi _{0,1} }{a_{1,1}},~\pi _{2,0}=\frac{N\alpha _{0}^{\prime }\pi _{0,0}}{a_{2,1}} +\frac{\alpha \pi _{0,1}}{a_{2,1}},\\ \pi _{1,j}&=\frac{(N-j)\lambda ^{\prime }}{a_{1,j+1}}\sum _{k=0}^{j}A_{j-1,k} ^{(1)}\pi _{0,k}+\frac{(N-j)\lambda ^{\prime }}{a_{1,j+1}}\pi _{0,j} +\frac{(j+1)\mu }{a_{1,j+1}}\pi _{0,j+1},\\ \pi _{2,j}&=\frac{(N-j)\lambda ^{\prime }}{a_{2,j+1}}\sum _{k=0}^{j}A_{j-1,k} ^{(2)}\pi _{0,k}+\frac{(N-j)\alpha _{0}^{\prime }}{a_{2,j+1}}\pi _{0,j} +\frac{(j+1)\alpha }{a_{2,j+1}}\pi _{0,j+1}, \end{aligned}$$

\(j=1,\ldots ,N-1\), where

$$ ~a_{i,j}=(N-j)\lambda ^{\prime }+\nu _{i},~\pi _{i,N}=0,~j=1,\ldots ,N,~i=1,2. $$

This gives the following recursive formulas for calculation of the coefficients \(A_{j,k}^{(i)}\):

$$\begin{aligned} A_{j,k}^{(1)}=\frac{(N-j)\lambda ^{\prime }}{a_{1,j+1}}\left( A_{j-1,k} ^{(1)}+\delta _{k,j}\right) , \end{aligned}$$
(5)
$$\begin{aligned} A_{j,k}^{(2)}=\frac{(N-j)}{a_{2,j+1}}\left( \lambda ^{\prime }A_{j-1,k} ^{(2)}+\delta _{k,j}\alpha _{0}^{\prime }\right) ,~k=0,\ldots ,j, \end{aligned}$$
(6)
$$\begin{aligned} A_{j,j+1}^{(1)}=\frac{\left( j+1\right) \mu }{a_{1,j+1}},~A_{j,j+1} ^{(2)}=\frac{\left( j+1\right) \alpha }{a_{2,j+1}},~j=0,1,\ldots ,N-1, \end{aligned}$$
(7)
$$ A_{-1,0}^{(1)}=A_{-1,0}^{(2)}=A_{N-1,N}^{(1)}=A_{N-1,N}^{(2)}=0. $$

Here \(\delta _{k,j}\) is the Kronecker’s symbol, which is equal to 1 if \(k=j\), and is equal to 0 if \(k\ne j\).

The explicit expressions, based on these recursive formulas are:

$$\begin{aligned} A_{j,k}^{(1)}=\frac{(N-k) \ldots (N-j)\left( \lambda ^{\prime }\right) ^{j+1-k}\left( a_{1,k}+k\mu \right) }{a_{1,k}a_{1,k+1}a_{1,k+2} \ldots a_{1,j+1} }, \end{aligned}$$
(8)
$$\begin{aligned} A_{j,k}^{(2)}=\frac{(N-k) \ldots (N-j)\left( \lambda ^{\prime }\right) ^{j-k}\left( a_{2,k}\alpha _{0}^{\prime }+k\lambda ^{\prime }\alpha \right) }{a_{2,k}a_{2,k+1}a_{2,k+2} \ldots a_{2,j+1}}, \end{aligned}$$
(9)

for \(j=0,1,\ldots ,N-1,~k=0,\ldots ,j\), \(a_{1,0}=a_{2,0}=1\). The expressions for \(A_{j,j+1}^{(i)}\) \((i=1,2)\) are given by (7).

Next, in Eq. (1) we substitute \(\pi _{i,j}\) according to formulas (4), ( \(j=0,\ldots ,N-2)\) and obtain a relation between the probabilities \(\pi _{0,j}\):

$$\begin{aligned} \begin{array}{c} \left[ \nu _{1}A_{j,j+1}^{(1)}+A_{j,j+1}^{(2)}\nu _{2}\right] \pi _{0,j+1}= \\ \left[ (N-j)\left( \lambda ^{\prime }+\alpha _{0}^{\prime }\right) +j(\alpha +\mu )-\left( \nu _{1}A_{j,j}^{(1)}+A_{j,j}^{(2)}\nu _{2}\right) \right] \pi _{0,j}- \\ \left[ \left( \nu _{1}A_{j,0}^{(1)}+A_{j,0}^{(2)}\nu _{2}\right) \pi _{0,0}+\ldots +\left( \nu _{1}A_{j,j-1}^{(1)}+A_{j,j-1}^{(2)}\nu _{2}\right) \pi _{0,j-1}\right] , \\ ~j=0,1,\ldots ,N-2,~A_{0,-1}^{(1)}=A_{0,-1}^{(2)}=0. \end{array} \end{aligned}$$
(10)

Following this scheme we can express all probabilities \(\pi _{0,j}\) \((j=1,\ldots ,N-1)\) in terms of \(\pi _{0,0}\). Then, from (4) we can express \(\pi _{i,j}\) \((i=1,2,~j=0,1,\ldots ,N-1)\) also in terms of \(\pi _{0,0}\). Finally, from the normalizing condition

$$ \sum _{i=0}^{2}\sum _{j=0}^{N-1}\pi _{ij}=1 $$

we can find \(\pi _{0,0}\). Thus, we can calculate the stationary system state distribution.

Further, having \(\pi _{0,0}\) found we can calculate the distribution \(\pi _{i,j}\) not only using formulas (10) and (4), but also by the recursive formulas, presented in the next Proposition.

Proposition 1

The stationary joint distribution \(\pi _{i,j}\) of the server state and the orbit size satisfies the following recursive formulas:

$$\begin{aligned} \pi _{0,j}=\frac{(N-j)\lambda ^{\prime }}{j\left( \mu +\alpha \right) }\left( \pi _{1,j-1}+\pi _{2,j-1}\right) ,~j=1,\ldots ,N-1, \end{aligned}$$
(11)
$$\begin{aligned} \begin{array}{c} \pi _{1,j}=\frac{(N-j)\lambda ^{\prime }}{(N-j-1)\lambda ^{\prime }\left( \mu \nu _{1}+\alpha \nu _{2}\right) +\nu _{1}\nu _{2}\left( \alpha +\mu \right) }\left\{ (N-j-1)\lambda ^{\prime }\mu \pi _{2,j-1}+\right. \\ \left[ \nu _{2}\left( \alpha +\mu \right) +(N-j-1)\mu \left( \lambda ^{\prime }+\alpha _{0}^{\prime }\right) \right] \pi _{0,j}+ \\ \left. \left[ (N-j-1)\lambda ^{\prime }\mu +\nu _{2}\left( \alpha +\mu \right) \right] \pi _{1,j-1}\right\} , \end{array} \end{aligned}$$
(12)
$$\begin{aligned} \begin{array}{c} \pi _{2,j}=\frac{(N-j)}{(N-j-1)\lambda ^{\prime }\left( \mu \nu _{1}+\alpha \nu _{2}\right) +\nu _{1}\nu _{2}\left( \alpha +\mu \right) }\{(N-j-1)\left( \lambda ^{\prime }\right) ^{2}\alpha \pi _{1,j-1}+ \\ \left[ (N-j-1)\lambda ^{\prime }\alpha \left( \lambda ^{\prime }+\alpha _{0}^{\prime }\right) +\alpha _{0}^{\prime }\nu _{1}\left( \alpha +\mu \right) \right] \pi _{0,j}+ \\ \lambda ^{\prime }\left[ (N-j-1)\lambda ^{\prime }\alpha +\nu _{1}\left( \alpha +\mu \right) \right] \pi _{2,j-1}\}. \end{array} \end{aligned}$$
(13)

Proof

We sum up Eqs. (1)–(3) for \(j=0\) and obtain formula (11) for \(j=1\),

$$\begin{aligned} (N-1)\lambda ^{\prime }\left( \pi _{1,0}+\pi _{2,0}\right) =\left( \mu +\alpha \right) \pi _{0,1}. \end{aligned}$$
(14)

Then we sum Eqs. (1)–(3) for \(j=1\),

$$\begin{aligned} \left( \mu +\alpha \right) \pi _{0,1}+(N-2)\lambda ^{\prime }\left( \pi _{1,0}+\pi _{2,0}\right) = \\ 2\left( \mu +\alpha \right) \pi _{0,2}+(N-1)\lambda ^{\prime }\left( \pi _{1,0}+\pi _{2,0}\right) , \end{aligned}$$

and add it to (14). Thus we get (11) for \(j=2\). Further, by induction it is easy to prove relations (11) for all \(j=1,\ldots ,N-1\). The rest of the recurrent formulas (11)–(13) follow from the combination of (2)–(3) with (11). Namely, substituting \(\pi _{0,j+1}\) from (11) into (2) and (3), after some transformations we get

$$\begin{aligned} \begin{array}{c} \frac{(N-j-1)\lambda ^{\prime }\alpha +\nu _{1}\left( \alpha +\mu \right) }{\mu +\alpha }\pi _{1,j}= \\ (N-j)\lambda ^{\prime }\pi _{0,j}+\frac{(N-j-1)\lambda ^{\prime }\mu }{\mu +\alpha }\pi _{2,j}+(N-j)\lambda ^{\prime }\pi _{1,j-1}, \\ \frac{(N-j-1)\lambda ^{\prime }\mu +\nu _{2}\left( \alpha +\mu \right) }{\mu +\alpha }\pi _{2,j}= \\ (N-j)\alpha _{0}^{\prime }\pi _{0,j}+\frac{(N-j-1)\lambda ^{\prime }\alpha }{\mu +\alpha }\pi _{1,j}+(N-j)\lambda ^{\prime }\pi _{2,j-1}. \end{array} \end{aligned}$$

Now we substitute \(\pi _{2,j}\) from the second into the first of these equations, and \(\pi _{1,j}\) from the first into the second,

$$\begin{aligned} \begin{array}{c} \frac{(N-j-1)\lambda ^{\prime }\alpha +\nu _{1}\left( \alpha +\mu \right) }{\mu +\alpha }\pi _{1,j}= \\ (N-j)\lambda ^{\prime }\pi _{0,j}+(N-j)\lambda ^{\prime }\pi _{1,j-1}+\frac{(N-j-1)\lambda ^{\prime }\mu }{\left[ (N-j-1)\lambda ^{\prime }\mu +\nu _{2}\left( \alpha +\mu \right) \right] }\times \\ \left[ (N-j)\alpha _{0}^{\prime }\pi _{0,j}+\frac{(N-j-1)\lambda ^{\prime }\alpha }{\mu +\alpha }\pi _{1,j}+(N-j)\lambda ^{\prime }\pi _{2,j-1}\right] , \\ \frac{(N-j-1)\lambda ^{\prime }\mu +\nu _{2}\left( \alpha +\mu \right) }{\mu +\alpha }\pi _{2,j}= \\ (N-j)\alpha _{0}^{\prime }\pi _{0,j}+(N-j)\lambda ^{\prime }\pi _{2,j-1} +\frac{(N-j-1)\lambda ^{\prime }\alpha }{(N-j-1)\lambda ^{\prime }\alpha +\nu _{1}\left( \alpha +\mu \right) }\times \\ \left[ (N-j)\lambda ^{\prime }\pi _{0,j}+\frac{(N-j-1)\lambda ^{\prime }\mu }{\mu +\alpha }\pi _{2,j}+(N-j)\lambda ^{\prime }\pi _{1,j-1}\right] . \end{array} \end{aligned}$$

Rearranging the terms, the last two equations give formulas (12) and (13).

Remark 1

If in formulas (11)–(13) we fix j and take limits as \(N\rightarrow \infty \), \(\lambda ^{\prime }\rightarrow 0\) and \(\alpha _{0} ^{\prime }\rightarrow 0\) in such a way that \(N\lambda ^{\prime }\rightarrow \lambda \), \(N\alpha _{0}^{\prime }\rightarrow \alpha _{0}\), we obtain exactly the recurrent formulas, connecting the stationary system state probabilities for the corresponding model with infinite source (Proposition 2 in Dragieva and Phung-Duc (2016)). Similarly, if take \(\alpha =\alpha _{0}^{\prime }=0\), then formulas (11)–(12) give the recursive formulas, obtained by Dragieva (2013) for the corresponding finite source retrial queue without two-way communication.

Remark 2

In fact, we do not need recursions (11)–(13) for the calculation of the system state distribution because we have the more convenient formulas (10), (5)–(7) and (4). Exactly these formulas are used in the calculation of numerical examples, presented in Sect. 4. Recursive formulas (11)–(13) may be useful in the analysis of the waiting time process, analogously to the corresponding formulas in the single server, finite source retrial queue without two-way communication (see Dragieva 2013).

Now we turn attention to the system state distribution at the moments of a primary incoming call arrival. In the models with finite source this distribution differs from the corresponding distribution at any arbitrary time moment (which is discussed in detail for example in Falin and Artalejo (1998) or in Dragieva (2013)). Thus, if we introduce the event A(t) that at time t a primary call arrives and denote by \(\overline{\pi }_{i,j}\) the stationary conditional probabilities

$$ \overline{\pi }_{i,j}=\lim _{t\rightarrow \infty }P\left\{ \left. S(t)=i,R(t)=j\right| A(t)\right\} ~~~i=0,1,2,~j=0,1,\ldots ,N-1, $$

then

$$\begin{aligned} \overline{\pi }_{i,j}=\left\{ \begin{array} [c]{c} \frac{(N-j)\lambda ^{\prime }\pi _{0,j}}{D},~\text {if }i=0,\\ \frac{(N-j-1)\lambda ^{\prime }\pi _{i,j}}{D},~\text {if }i=1,2, \end{array} \right. \end{aligned}$$
(15)
$$\begin{aligned} D=\sum _{i=1}^{2}\sum _{n=0}^{N-1}(N-n-1)\lambda ^{^{\prime }}\pi _{i,n}+\sum _{n=0}^{N-1}(N-n)\lambda ^{^{\prime }}\pi _{0,n}. \end{aligned}$$
(16)

This distribution is important in the investigation of the waiting time process.

3.2 Main Macro Characteristics of the System Performance

In the models with finite state space, if the system state distribution is obtained, then it is not difficult to calculate any of the basic macro characteristics of the system performance. Nevertheless, here we derive formulas, expressing these characteristics in terms of the server utilization (or the idle server probability).

Let’s denote

$$\begin{aligned}&P_{i}=\lim \limits _{t\rightarrow \infty }P\left\{ S(t)=i\right\} =\sum \limits _{j=0}^{N-1} \pi _{i,j}, \\&M_{i,p}=\sum \limits _{j=0}^{N-1}j^{p}\pi _{i,j},p=0,1,\ldots ,~i=0,1,2, \\&P_{i}=M_{i,0}. \end{aligned}$$

Summing all Eq. (2), then (3) over \(j=0,\ldots ,N-1\), we obtain equations for the stationary server state distribution \(P_{i} \) \((i=0,1,2)\) and the first partial moment \(M_{0,1}\),

$$\begin{aligned} \nu _{1}P_{1}=N\lambda ^{\prime }P_{0}+\left( \mu -\lambda ^{\prime }\right) M_{0,1}, \end{aligned}$$
(17)
$$\begin{aligned} \nu _{2}P_{2}=N\alpha _{0}^{\prime }P_{0}+\left( \alpha -\alpha _{0}^{\prime }\right) M_{0,1}. \end{aligned}$$
(18)

As stated in Sect. 2, if \(\mu =\lambda ^{\prime }\) we have no orbit and the model is modified to the particular case of a finite source queue with losses and two-way communication. In this case it is reasonable to take \(\alpha =\alpha _{0}^{\prime }\), but there are real situations when we can consider \(\alpha \ne \alpha _{0}^{\prime }\). For example, in a call center of some company the operator can record all unsuccessful clients and although they give up their request (\(\mu =\lambda ^{\prime }\)) he/she can call to them for advertising, reminders, or anything else, with specific intensity (\(\alpha \ne \alpha _{0}^{\prime }\)). In the case \(\mu =\lambda ^{\prime }\) and \(\alpha =\alpha _{0}^{\prime }\), from (17), (18) and the normalizing condition

$$ P_{0}+P_{1}+P_{2}=1 $$

we obtain formulas for the probabilities \(P_{i}~(i=0,1,2)\):

$$ P_{1}=\frac{N\lambda ^{\prime }}{\nu _{1}}P_{0},~P_{2}=\frac{N\alpha }{\nu _{2} }P_{0},~P_{0}=\frac{\nu _{1}\nu _{2}}{N\left( \lambda ^{\prime }\nu _{2}+\alpha \nu _{1}\right) +\nu _{1}\nu _{2}}. $$

Further we assume that either \(\mu \ne \lambda ^{\prime }\) or \(\alpha \ne \alpha _{0}^{\prime }\). Equations (17), (18) and the normalizing condition allow to express \(P_{i}\) \((i=1,2)\) and \(M_{0,1}\) in terms of \(P_{0}\):

$$\begin{aligned} P_{1}=\frac{\left( \mu -\lambda ^{\prime }\right) \nu _{2}\left( 1-P_{0} \right) +N\left( \alpha \lambda ^{\prime }-\alpha _{0}^{\prime }\mu \right) P_{0}}{\left( \alpha -\alpha _{0}^{\prime }\right) \nu _{1}+\left( \mu -\lambda ^{\prime }\right) \nu _{2}}, \end{aligned}$$
(19)
$$\begin{aligned} P_{2}=\frac{\left( \alpha -\alpha _{0}^{\prime }\right) \nu _{1}\left( 1-P_{0}\right) -N\left[ \alpha \lambda ^{\prime }-\alpha _{0}^{\prime } \mu \right] P_{0}}{\left( \alpha -\alpha _{0}^{\prime }\right) \nu _{1}+\left( \mu -\lambda ^{\prime }\right) \nu _{2}}, \end{aligned}$$
(20)
$$\begin{aligned} M_{0,1}=\frac{\nu _{1}\nu _{2}\left( 1-P_{0}\right) -N\left( \alpha _{0}^{\prime }\nu _{1}+\lambda ^{\prime }\nu _{2}\right) P_{0}}{\left( \alpha -\alpha _{0}^{\prime }\right) \nu _{1}+\left( \mu -\lambda ^{\prime }\right) \nu _{2}}. \end{aligned}$$
(21)

Further, multiplying Eq. (1) by \(j~(j=1,\ldots ,N-1)\), then (2) and (3) by \((j+1)\) \((j=0,1,\ldots ,N-1)\) and summing each of these three groups equations over j we get relations between \(M_{i,0} =P_{i},\ M_{i,1},~(i=0,1,2),~\)and \(M_{0,2}\),

$$\begin{aligned} N\left( \lambda ^{\prime }+\alpha _{0}^{\prime }\right) M_{0,1}+(\alpha +\mu -\lambda ^{\prime }-\alpha _{0}^{\prime })M_{0,2}=\nu _{1}M_{1,1}+\nu _{2}M_{2,1}, \end{aligned}$$
(22)
$$\begin{aligned} \begin{array}{c} \left( \nu _{1}+\lambda ^{\prime }\right) M_{1,1}+\left[ \nu _{1} -\lambda ^{\prime }(N-1)\right] P_{1}= \\ N\lambda ^{\prime }P_{0}+(N-1)\lambda ^{\prime }M_{0,1}+\left( \mu -\lambda ^{\prime }\right) M_{0,2}, \end{array} \end{aligned}$$
(23)
$$\begin{aligned} \begin{array}{c} \left( \nu _{2}+\lambda ^{\prime }\right) M_{2,1}+\left[ \nu _{2} -\lambda ^{\prime }(N-1)\right] P_{2}= \\ N\alpha _{0}^{\prime }P_{0}\_+(N-1)\alpha _{0}^{\prime }M_{0,1}+\left( \alpha -\alpha _{0}^{\prime }\right) M_{0,2}. \end{array} \end{aligned}$$
(24)

These equations allow to express the partial moments \(M_{0,2},M_{1,1}\) and \(M_{2,1}\) in terms of \(M_{0,0}=P_{0}\). Thus, the mean orbit size also can be expressed in terms of \(P_{0}\).

Proposition 2

The mean orbit size, \(M_{1}\) is equal to

$$\begin{aligned} \begin{array}{c} M_{1}=\lim \limits _{t\rightarrow \infty }E\left[ R(t)\right] =\sum \limits _{i=0}^{2}\sum \limits _{j=1}^{N-1}j\pi _{i,j}= \\ M_{0,1}+M_{1,1}+M_{2,1}=N-1+P_{0}+ \\ \frac{N\left[ \left( \alpha +\mu \right) \alpha _{0}^{\prime }\nu _{1} +\alpha \lambda ^{\prime }\left( \nu _{2}-\nu _{1}\right) \right] P_{0}-\left( \mu -\lambda ^{\prime }+\alpha \right) \nu _{1}\nu _{2}\left( 1-P_{0}\right) }{\lambda ^{\prime }\left[ \left( \alpha -\alpha _{0}^{\prime }\right) \nu _{1}+\left( \mu -\lambda ^{\prime }\right) \nu _{2}\right] }. \end{array} \end{aligned}$$
(25)

Proof

From Eq. (22) we express \(M_{0,2}\) in terms of \(M_{i,1} \) \((i=0,1,2)\)

$$ M_{0,2}=\frac{\nu _{1}M_{1,1}+\nu _{2}M_{2,1}-N\left( \lambda ^{\prime } +\alpha _{0}^{\prime }\right) M_{0,1}}{\alpha +\mu -\lambda ^{\prime }-\alpha _{0}^{\prime }},~\alpha +\mu \ne \lambda ^{\prime }+\alpha _{0}^{\prime }, $$

and substitute it in the Eqs. (23) and (24). After some transformations this leads to the following system for \(M_{i,1}\) \((i=1,2)\)

$$\begin{aligned} \begin{array}{c} \left( \lambda ^{\prime }+\frac{\nu _{1}\left( \alpha -\alpha _{0}^{\prime }\right) }{\alpha +\mu -\lambda ^{\prime }-\alpha _{0}^{\prime }}\right) M_{1,1}-\frac{\left( \mu -\lambda ^{\prime }\right) \nu _{2}}{\alpha +\mu -\lambda ^{\prime }-\alpha _{0}^{\prime }}M_{2,1}= \\ N\lambda ^{\prime }P_{0}-\left[ \nu _{1}-\lambda ^{\prime }(N-1)\right] P_{1}+\left( -\lambda ^{\prime }+\frac{N\left( \lambda ^{\prime }\alpha -\alpha _{0}^{\prime }\mu \right) }{\alpha +\mu -\lambda ^{\prime }-\alpha _{0}^{\prime }}\right) M_{0,1}, \\ -\frac{\left( \alpha -\alpha _{0}^{\prime }\right) \nu _{1}}{\alpha +\mu -\lambda ^{\prime }-\alpha _{0}^{\prime }}M_{1,1}+\left( \lambda ^{\prime } +\frac{\nu _{2}\left( \mu -\lambda ^{\prime }\right) }{\alpha +\mu -\lambda ^{\prime }-\alpha _{0}^{\prime }}\right) M_{2,1}= \\ N\alpha _{0}^{\prime }P_{0}-\left[ \nu _{2}-\lambda ^{\prime }(N-1)\right] P_{2}+\left[ -\alpha _{0}^{\prime }+\frac{N\left( \alpha _{0}^{\prime } \mu -\lambda ^{\prime }\alpha \right) }{\alpha +\mu -\lambda ^{\prime }-\alpha _{0}^{\prime }}\right] M_{0,1}. \end{array} \end{aligned}$$

Summing up these two equations we get

$$\begin{aligned} \begin{array}{c} \lambda ^{\prime }\left( M_{1,1}+M_{2,1}\right) =N\left( \lambda ^{\prime }+\alpha _{0}^{\prime }\right) P_{0}- \\ \left( \lambda ^{\prime }+\alpha _{0}^{\prime }\right) M_{0,1}-\left\{ \left[ \nu _{1}-\lambda ^{\prime }(N-1)\right] P_{1}+\left[ \nu _{2}-\lambda ^{\prime }(N-1)\right] P_{2}\right\} . \end{array} \end{aligned}$$

Thus, for the mean orbit size it holds

$$\begin{aligned} \begin{array}{c} M_{1}=M_{0,1}+M_{1,1}+M_{2,1}= \\ \frac{N\left( \lambda ^{\prime }+\alpha _{0}^{\prime }\right) P_{0}}{\lambda ^{\prime }}-\frac{\alpha _{0}^{\prime }}{\lambda ^{\prime }}M_{0,1}- \\ \frac{\left[ \nu _{1}-\lambda ^{\prime }(N-1)\right] P_{1}+\left[ \nu _{2}-\lambda ^{\prime }(N-1)\right] P_{2}}{\lambda ^{\prime }}. \end{array} \end{aligned}$$

Substituting here \(P_{i}~\left( i=1,2\right) \) and \(M_{0,1}\) with the expressions (19)–(21) we obtain formula (25).

Using formulas (19)–(21) and (25) we can express the other basic performance measures:

  • The blocking probability \(P_{B}\) that an arriving primary incoming call will be blocked in the orbit of retrial customers,

    $$\begin{aligned} \begin{array}{c} P_{B}=\sum \limits _{i=1}^{2}\sum \limits _{n=0}^{N-1}\overline{\pi }_{i,n}= \\ \frac{\sum _{i=1}^{2}\sum _{n=0}^{N-1}(N-n-1)\lambda ^{^{\prime }}\pi _{i,n}}{\sum _{i=1}^{2}\sum _{n=0}^{N-1}(N-n-1)\lambda ^{^{\prime }}\pi _{i,n}+\sum _{n=0}^{N-1}(N-n)\lambda ^{^{\prime }}\pi _{0,n}}= \\ \frac{(N-1)\lambda ^{^{\prime }}\left( 1-P_{0}\right) -\lambda ^{^{\prime } }\left( M_{1,1}+M_{2,1}\right) }{N\lambda ^{^{\prime }}-\lambda ^{^{\prime } }\left( 1-P_{0}+M_{1}\right) }=1+\frac{M_{0,1}-NP_{0}}{N-\left( 1-P_{0}+M_{1}\right) }; \end{array} \end{aligned}$$

  • Mean rate of generation of primary incoming calls,

    $$\begin{aligned} \varLambda =\lambda ^{\prime }\lim \limits _{t\rightarrow \infty }E\left[ N-C(t)-R(t)\right] =\lambda ^{\prime }\left[ N-(P_{1}+P_{2})-M_{1}\right] = \\ \frac{\left( \mu -\lambda ^{\prime }+\alpha \right) \nu _{1}\nu _{2}\left( 1-P_{0}\right) -N\left[ \left( \alpha +\mu \right) \alpha _{0}^{\prime } \nu _{1}+\alpha \lambda ^{\prime }\left( \nu _{2}-\nu _{1}\right) \right] P_{0} }{\left( \alpha -\alpha _{0}^{\prime }\right) \nu _{1}+\left( \mu -\lambda ^{\prime }\right) \nu _{2}}; \end{aligned}$$

  • Mean value of the waiting time W(t), that a primary incoming call, arriving at time moment t will spend in the orbit. Using Little’s formula for this mean value we have:

    $$\begin{aligned} \begin{array}{c} \lim \limits _{t\rightarrow \infty }E[W(t)]=\varLambda ^{-1}\lim \limits _{t\rightarrow \infty }E\left[ R(t)\right] =\frac{M_{1}}{\varLambda }= \\ \frac{\left( N-1+P_{0}\right) \left[ \left( \alpha -\alpha _{0}^{\prime }\right) \nu _{1}+\left( \mu -\lambda ^{\prime }\right) \nu _{2}\right] }{N\left[ \left( \alpha +\mu \right) \alpha _{0}^{\prime }\nu _{1}+\alpha \lambda ^{\prime }\left( \nu _{2}-\nu _{1}\right) \right] P_{0}-\left( \mu -\lambda ^{\prime }+\alpha \right) \nu _{1}\nu _{2}\left( 1-P_{0}\right) }-\frac{1}{\lambda ^{\prime }}; \end{array} \end{aligned}$$

  • Mean number \(E\left[ RA(t)\right] \) of retrial attempts, that a primary incoming customer, arriving at time moment t will make while being in the orbit. If the intensity of the outgoing calls to the customers in orbit is 0 (\(\alpha =0)\) then the following relation holds:

    $$ \lim _{t\rightarrow \infty }E\left[ RA(t)\right] =\mu \lim _{t\rightarrow \infty }E\left[ W(t)\right] =\mu \frac{M_{1}}{\varLambda }. $$

In the case \(\alpha >0\) if we want to calculate the mean number of retrials, we should investigate the stationary distribution of this number, which will be one of our future work.

Remark 3

For \(\alpha =\alpha _{0}^{\prime }=0\) all formulas, obtained in this Section coincide with the formulas derived by Falin and Artalejo (1998) for the corresponding model without two-way communication.

4 Numerical Examples

In this Section we present numerical examples, illustrating the influence of the system parameters on the main performance macro characteristics, considered in previous Section.

Fig. 1.
figure 1

Stationary server state distribution \(P_{i}=P(S=i)~(i=0,1,2)\) versus system parameters \(\lambda ^{\prime }\), \(\alpha _{0}^{\prime }\), \(\nu _{1}\), N. (\(\mu =0.2\), \(\nu _{2}=0.8\))

Full size image

Figure 1 shows the dependence of the stationary server state distribution \(P_{i}\) \((i=0,1,2)\) on the parameters \(\lambda ^{\prime }\) (left upper corner), \(\alpha _{0}^{\prime }\) (right upper corner), \(\nu _{1}\) (left lower corner) and N (right lower corner). We see that the behaviour of most of the presented functions is intuitively expected:

  • The proportion of time \(P_{1}\) that the server is busy with incoming calls service increases with the increase of primary intensity \(\lambda ^{\prime }\) and the mean service time of incoming calls, \(1/\nu _{1}\). \(P_{1}\) decreases with increase of the intensity \(\alpha _{0}^{\prime }\) of the outgoing calls to the customers in free state. Numerical examples, not presented here show that \(P_{1}\) increases with the increase of the secondary intensity, \(\mu \) and decreases with the increase of the mean service time of outgoing calls, \(1/\nu _{2}\) and with the increase of the intensity of outgoing calls to the orbit, \(\alpha \).

  • All presented examples show that when \(P_{1}\) increases, then the proportion of time \(P_{2}\) that the server is busy with outgoing calls decreases and vice versa.

It is interesting that for all presented values of the system parameters the server utilization, \(P_{1}+P_{2}=1-P_{0}\) is almost equal to 1. The increase of the number N of all clients of the system has little impact on the server state distribution, keeping \(P_{1}\) greater than \(P_{2}\) and \(P_{0}\), the last one almost equal to 0.

Fig. 2.
figure 2

Basic performance macro characteristics versus primary intensity \(\lambda ^{\prime }\). (\(\nu _{1}=0.1, \nu _{2}=0.8, N=10\))

Full size image
Fig. 3.
figure 3

Basic performance macro characteristics versus primary intensity \(\lambda ^{\prime }\). (\(\nu _{1}=0.1, \nu _{2}=0.8, N=10\))

Full size image

The dependence of the rest of the macro characteristics (the first partial moments, \(M_{i,1},~(i=0,1,2)\) and mean orbit size, \(M_{1}\), blocking probability, \(P_{B}\), mean waiting time, \(E[W]=\lim _{t\rightarrow \infty }E[W(t)]\) and mean rate of generation of primary incoming calls, \(\varLambda \)) on the system parameters follow intuitively expected behaviour. The only exception is the primary incoming calls intensity \(\lambda ^{\prime }\), which influence on the system performance is hard to be intuitively explained. To show this influence in more detail we present it in two figures - Figs. 2 and 3. On these figures we can see that for all presented values of the system parameters the blocking probability confirms the well known property of the finite source retrial queues to have a point of maximum as a function of \(\lambda ^{\prime }\) (Falin and Artalejo 1998; Almaási et al. 2005; Wang et al. 2011; Zhang and Wang 2013). The new comes with the behaviour of the mean waiting time, E[W] and the mean rate of generation of primary incoming calls, \(\varLambda \). We see in Fig. 2 that there exist values of the system parameters for which, like in the other finite source retrial queues (Falin and Artalejo 1998; Almaási et al. 2005; Wang et al. 2011; Zhang and Wang 2013), E[W] has a point of maximum. But, on Fig. 3 we see that for the same values of these parameters it has and a point of minimum. This property has not been observed till now in the related literature. We also see on Fig. 3 that it does not hold for all values of the system parameters. Analogously, we see that the behaviour of \(\varLambda \) as a function of \(\lambda ^{\prime }\) also depends on the values of the rest of the system parameters - for some of them it is a strictly increasing function, but for some of them it has a point of maximum. The last property has not been observed till now. For example, all numerical results, presented by Wang et al. (2011) for the single server, finite source retrial queue with server breakdowns and repairs show that \(\varLambda \) follows the intuitively expected behaviour to be strictly increasing as a function of the primary intensity \(\lambda ^{\prime }\).

It is interesting to note that for the values of the system parameters, presented on Fig. 2, the partial moment \(M_{2,1}\) is an increasing function of \(\lambda ^{\prime }\), but for the values, presented on Fig. 3 it has a point of maximum.

5 Conclusion and Future Work

In this paper we derive formulas for the joint distribution of the server state and the orbit size in a finite source retrial queue of M/M/1//N type with two-way communication. Main performance macro characteristics are expressed in terms of the server utilization. The influence of the system parameters on these macro characteristics is studied on the basis of numerical examples. Formulas, obtained in the present paper allow to extend this investigation by studying the waiting time process, the busy period distribution and other descriptors of the system performance like the number of successful and blocked events. We also plan to consider the corresponding queue of type M/G/1//N.