Adapting Side Information to Transmission Conditions in Precoding Systems

Abstract

This work proposes an hybrid precoding method in a Multiple-Input/Multiple-Output Frequency Division Duplex (MIMO FDD) system with the objective of reducing the load associated to transmit side information needed to adapt precoding matrices in both the transmitter and the receiver. The type of precoding is determined at the transmitter by using a simple rule that takes into account a receive Signal–to–Noise Ratio (SNR) estimate. The receiver computes the magnitude of the channel level fluctuations and determines the time instants when long pilot sequences are needed to estimate the precoding matrices. Using a low cost feedback channel, the receiver indicates to the transmitter both the type of precoder and transmit frames to be used.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Computational Intelligence (CI)-based approaches have been widely used to solve different problems in digital communications and networking such as call admission control, management of resources and traffic, routing, multi casting, media encoding, and synchronization [5]. CI paradigms include supervised and unsupervised learning, reinforcement learning, fuzzy logic, evolutionary computation, etc. In this paper, we propose to include a decision-based learning in precoding systems to improve the transmission rate.

Precoding is an effective strategy to equalize the channel before transmission, and is included in most of the recent wireless standards with the aim of simplifying the receiver equipment by moving the equalization task to the transmitter. Linear and nonlinear precoding techniques have been widely studied in the literature. Tomlinson-Harashima Precoding (THP) is one of the best known nonlinear precoding techniques due to its adequate compromise between performance and computational complexity. THP computational complexity is still 1.6 times higher than the linear counterpart, which will be referred to as Linear Precoding (LP), as shown in [8]. In [10] we show that the combination of both precoders, which is referred to as Hybrid Precoding (HP), allows us to improve the overall system performance.

Precoding needs Channel State Information (CSI) at the transmitter, which must be obtained at the receiver by channel estimation and sent back to the transmitter by means of a feedback channel, usually available in recent standards for Frequency Division Duplex (FDD) systems. However, this feedback channel is not necessary in Time Division Duplex (TDD) systems because the channel can be obtained by the transmitter in the uplink using reciprocity. This Partial CSI (PCSI) affects the system performance since the design of the precoding filters are based on the channel estimate and, therefore, linear and non-linear precoders will need a good channel estimate under time-varying environments [3]. Classical estimation methods are based on the sending from the transmitter of pilot symbols that are used by the receiver to obtain the channel estimate. The performance achieved with such methods, also known as supervised learning based-methods, is high, but the use of pilots affects throughput, spectral efficiency, and transmission energy consumption of the system [1, 12]. In this work, we propose to mitigate these limitations by using reinforcement learning in which the optimal policy will be determined to minimize the total pilot transmissions.

We assume that both the transmitter and the receiver are two individual entities with some capacity for decision, communication, and adaptation. The receiver is able to acquire channel information from the environment and then makes decisions as a consequence of these measurements. More specifically, this decision uses rules based on measurements of both the quality of the received signal (measured in terms of Signal–to–Noise Ratio (SNR)) and the channel fluctuations (measured according to an ad hoc metric also proposed in this work). The decisions will be communicated via the aforementioned low-cost feedback channel to the transmitter, which will send pilots symbols when a significant channel fluctuation is detected at the receiver. Then, with the information provided by the pilots, the receiver estimates the channel and sends this estimate to the transmitter. Both the transmitter and the receiver will adapt their precoding filters using the linear or the non-linear approaches as indicated by the receiver according to its receive SNR measurement. Therefore, we have an adaptive system that guarantees good performance with low complexity.

This work is organized as follows. Section 2 describes the signal and channel models, and shows the designs of the linear and non-linear precoders most commonly used in the literature. Section 3 briefly describes the supervised method for channel estimation used in this work. Section 4 explains the proposed scheme for minimizing the number of pilot symbols required by the receiver. Illustrative computer simulation results are presented in Sects. 5, and 6 contains the conclusions.

2 System Model

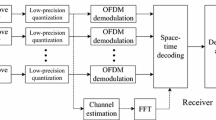
Figure 1 shows a MIMO system with $N_{\text {t}}$ TX antennas and $N_{\text {r}}$ RX antennas. In this paper we will assume $N_{\text {t}}=N_{\text {r}}=N$. We can model the received observations as

$$\begin{aligned} \varvec{y}[n] = \varvec{H}[q]\varvec{x}[n]+{\eta }[n], \end{aligned}$$

(1)

where $n=0,1,2,\ldots$ corresponds to the sample index. Given that the channel remains constant during several frames of $N_{\text {B}}$ symbols, we use $\varvec{H}[q]$ to denote the time–varying flat block fading channel.

Fig. 1.

Scheme of a MIMO system with precoding.

The equalization task can be performed at the TX and thus the channel is pre-equalized or precoded before the transmission with the goal of simplifying the requirements at the RX. Such an operation is only possible when a centralized TX is employed (e.g. the base-station of the downlink of a cellular system). We have considered the linear and non-linear precoding schemes more commonly used in the literature: Wiener LP and THP, respectively.

2.1 Linear Precoder

We assume hereinafter that the RX filter is an identity matrix (multiplied by a scalar $\beta [q]$, with $\beta [q] \in \mathbb {C})$, which allows the use of decentralized RX (see, for instance, [6]). Clearly, the restriction that all receivers apply the same scalar weight $\beta [q]$ is not necessary for decentralized receivers, but it ensures closed–form solutions for the design of the filters. The goal is to find the optimum TX filter $\varvec{F}[q] \in \mathbb {C}^{N \times N}$ and the RX filter $\varvec{G}[q]=\beta [q]\varvec{I} \in \mathbb {C}^{N \times N}$. The data symbols ${\varvec{u}}[n]$ are passed through the transmit filter ${\varvec{F}}[q]$ to form the transmitted signal ${\varvec{x}}[n]={\varvec{F}}[q]{\varvec{u}}[n] \in \mathbb {C}^{N}$. Note that the constraint for the transmitted energy must be fulfilled, $\text {E}\left[ ||{\varvec{x}}[n]||_2^2\right] \le E_{\text {tx}}$, where $E_{\text {tx}}$ is the fixed total transmitted energy. The received signal is thus given by

$$\begin{aligned} \varvec{y}[n]=\varvec{H}[q]\varvec{F}[q]\varvec{u}[n]+{\eta }[n], \end{aligned}$$

(2)

where $\varvec{y}[n] \in \mathbb {C}^{N}, {\varvec{H}}[q] \in \mathbb {C}^{N \times N}$, and ${\eta }[n] \in \mathbb {C}^{N}$ is the Additive White Gaussian Noise (AWGN). After multiplying by the receive gain $\beta [q]$, we get the estimated symbols $\varvec{\hat{u}}[n] = \beta [q]\varvec{H}[q]\varvec{F}[q]\varvec{u}[n] + g {\eta }[n]$, where $\varvec{\hat{u}}[n] \in \mathbb {C}^{N}$.

Wiener Filtering (WF) is a very powerful transmit optimization that minimizes the Mean Square Error (MSE) with a transmit energy constraint [2, 7, 11], and therefore the linear precoders of our proposal will be obtained according to that optimization.

2.2 Tomlinson-Harashima Precoder

In this subsection, we will briefly describe the Tomlinson-Harashima (TH) non-linear precoder, which will be used in this paper. This precoder employs two filters: one, denoted by ${\varvec{F}}[q]$, placed at the transmitter to suppress parts of the interference linearly, and another one, given by ${\varvec{I}}-{\varvec{B}}[q]$, inside a feedback loop and also at the transmitter to subtract the remaining interferences non-linearly, with ${\varvec{B}}$ being strictly lower triangular to ensure the causality of the feedback process. Since the order of precoding has an important effect on performance, the data signal ${\varvec{u}}[n]$ is reordered by means of the permutation filter ${\varvec{P}}[q]=\sum _{i=1}^{N}{\varvec{e}}_i{\varvec{e}}_{n_i}^{{{\mathrm{T}}}}$, where ${\varvec{e}}_i$ is the i-th column of the $N\times N$ identity matrix and $n_i$ is the index of the i-th data stream to be precoded [8]. The signal ${\varvec{P}}[q]{\varvec{u}}[n]$ is first passed through the feedback loop to get the output $\varvec{v}[n]$. The nonlinear modulo operator ${{\mathrm{M}}}(\bullet )$ of the feedback loop limits the amplitude of ${\varvec{v}}[n]$ and thus, the power of the transmit signal ${\varvec{x}}[n]$. The received signal is expressed as

$$\begin{aligned} \varvec{y}[n]={{\mathrm{M}}}\left( g[q]\varvec{H}[q]\varvec{F}[q]\varvec{v}[n]+g{\eta }[n]\right) , \end{aligned}$$

(3)

because the modulo operator is applied again at the receiver to invert its effect at the transmitter [11]. The receive weight g[q] directly follows from the transmit energy constraint. The resulting estimate of $\varvec{u}[n]$ is denoted again by $\varvec{\hat{u}}[n]$.

The Wiener THP for flat fading channels results from the minimization of the MSE and the restriction of a spatially causal feedback filtering. The filters obtained from that minimization are determined column by column [8, 9, 11], and each column requires one matrix inverse which results in a total complexity order of $O(N^4)$. With the decomposition described in [4, 13], the complexity is reduced to $O(N^3)$. In addition, some heuristic ordering strategies can be applied as described in [8].

3 Supervised Channel Estimation

Channel estimation is crucial in wireless communication systems. In this work CSI is acquired at the receiver and sent back to the transmitter via a feedback channel so that the precoding filters can be updated at both link sides. This channel estimation can be performed by means of pilot symbols, also called training sequences.

When pilots are employed, the received signal $\varvec{Y}[q]$ is a linear combination of the transmitted signals $\varvec{S}[q]$ as follows

$$\begin{aligned} \varvec{Y}[q]= & {} \varvec{S}[q]\varvec{H}[q] + {\eta }[q] \in \mathbb {C}^{K \times N}, \end{aligned}$$

(4)

where K is the length of the pilot sequence. The matrix ${\eta }[q] \in \mathbb {C}^{K \times N}$ is the AWGN with covariance matrix denoted as ${\varvec{C}}_{\eta }$. Thus, the channel estimate is obtained as

$$\begin{aligned} \varvec{\hat{H}}[q]=\varvec{W}[q] \varvec{Y}[q], \end{aligned}$$

(5)

where $\varvec{W}[q] \in \mathbb {C}^{N \times K}$ is the matrix that calculates the estimate from the observations.

The Linear Minimum Mean Square Error (LMMSE) channel estimation minimizes the average MSE between the channel and its estimate, which leads to the final expression for the MMSE linear filter

$$\begin{aligned} \varvec{W}[q]=\varvec{C}_{\varvec{HY}}\varvec{C}_{\varvec{Y}}^{-1}, \end{aligned}$$

(6)

where $\varvec{C}_{\varvec{HY}}=\varvec{C}_{\varvec{H}}\varvec{S}^{{{\mathrm{H}}}}[q]$ and $\varvec{C}_{\varvec{Y}}=\varvec{S}[q]\varvec{C}_{\varvec{H}}\varvec{S}^{{{\mathrm{H}}}}[q]+\varvec{C}_{\eta }$, being $\varvec{C}_{\varvec{H}}=N\mathbf {I}_{}$. Therefore, the channel estimate can be obtained as

$$\begin{aligned} \varvec{\hat{H}}[q]=\varvec{C}_{\varvec{H}}\varvec{S}^{{{\mathrm{H}}}}\mathbf [q](\varvec{S}[q] \varvec{C}_{\varvec{H}} \varvec{S}^{{{\mathrm{H}}}}[q]+\varvec{C}_{\eta })^{-1}\varvec{Y}[q]. \end{aligned}$$

(7)

4 Decision-Aided Precoding System

In this section we propose a MIMO system with decision-aided precoding that requires the updating of the precoding filters depending on the channel fluctuations. This system will be referred to as Decision-aided Precoding (DP) in the following. The goal of this solution is to reduce the computational complexity of the overall system without penalizing in a significant way its performance. In standard systems, the pilots are transmitted in all the frames, which produces a strong degradation of performance, spectral efficiency, and transmit energy. With our approach we will be able to minimize the loss of effective transmission rate or the channel overload produced by the sending of pilot symbols.

We will consider that the transmitter sends two types of frames: classic and user frames. The classic frames contain a long pilot sequence and user data symbols. The user frames contain a short pilot sequence and user data symbols.

For determining if the channel variations are important enough to request the sending of classic frames and the updating of the precoding filters, we propose a metric that compares the estimate of the channel matrix corresponding to the current frame, denoted by $\varvec{\hat{H}}[n]$, and that estimated in the previous frame, denoted by $\varvec{\hat{H}}[n-1]$. Both estimates are obtained by the receiver using the short pilot sequence of the user frames, which will calculate for each transmit frame the matrix $\varvec{\varGamma }[n]=(\varvec{\hat{H}}[n])^{-1}\varvec{\hat{H}}[n-1]$. In particular, we will use the error measurement, denoted as $\epsilon _{\text {CSI}}$, as follows

$$\begin{aligned} \epsilon _{\text {CSI}}=\frac{1}{N} \sum _{i=1}^{N} \sum _{j=1,j\ne i}^{N} \left( \frac{\left| \gamma _{ij}[n]\right| ^2}{\left| \gamma _{ii}[n]\right| ^2}+\frac{\left| \gamma _{ji}[n]\right| ^2}{\left| \gamma _{ii}[n]\right| ^2}\right) , \end{aligned}$$

(8)

where $\gamma _{ii}[n]$ is the i–th diagonal entry of the matrix $\varvec{\varGamma }[n]$. Thus, this value, that shows the distance between $\varvec{\varGamma }[n]$ and the identity matrix, gives us a measurement of the channel time variations. If $\epsilon _{\text {CSI}}$ is high, the channel is suffering from significant fluctuations and therefore, the receiver will request a classic frame including a long pilot sequence to the transmitter. The receiver will estimate the channel from pilots using LMMSE and the updated coefficients will be sent to the transmitter using the feedback channel. Transmit and receive precoding filters will be updated at both link sides. Otherwise, if $\epsilon _{\text {CSI}}$ is low, the precoding filters remain unchanged as had been used in the previous frame.

Moreover, in [10] we have demonstrated that LP is better than THP for low SNRs, and vice versa. Therefore, we propose to include a decision rule at the receiver to determine the action to be performed by our system, as follows

Notice that $p_{i,\text {SNR}}$ and SNR$_{l}$ are the two thresholds of our decision-aided algorithm that will be determined in a training step prior to real transmission.

5 Simulation Results

In this section we will show some results obtained from computer simulations. First, the time-varying channel will be modeled as follows

$$\begin{aligned} \varvec{H}[q]={\left\{ \begin{array}{ll} \dfrac{\left( 1-\alpha \right) \varvec{H}[q-1]+\alpha {\varvec{H_{\text {R}}}}[q]}{\sqrt{\left( 1-\alpha \right) ^2+\alpha ^2}}&{} \mathbf{if}\ q=bF,\ b=1,2,\ldots \\ \varvec{H}[q-1]&{} \mathbf{otherwise}, \end{array}\right. } \end{aligned}$$

(9)

where F is the number of frames in which the channel remains unchanged. $\varvec{H}_{\text {R}}[q]$ is randomly generated following a Rayleigh distribution. The $\alpha$ parameter determines the speed in channel variations. If $\alpha =0$ the channel is constant, whereas for $\alpha = 1$ the channel changes randomly from one block to another.

Additionally, the following simulation parameters are considered: $N=4$ transmit and receive antennas; 1000 independent experiments; 128 channel realizations in each experiment; 512 frames of 128 symbols; $F=4$ frames in which the channel remains unchanged; $P_l=12$ QPSK pilot symbols per long pilot sequence; $P_s=4$ QPSK per short pilot sequence; LMMSE channel estimation, and $\alpha =0.2$ in (9).

5.1 Training Step

In a training step prior to transmission we have evaluated the distance between the performance, evaluated in terms of Bit Error Rate (BER), obtained with both precoders, LP and THP, when the channel information is partially known at the transmitter. Classic frames are transmitted so that the long pilot sequence included in these frames are used to obtain the CSI via LMMSE estimation.

Fig. 2.

Training step: $\text {SNR}_{l}$ for using LP or THP.

Therefore, the range of application of each type of precoder is determined by using the following distance measurement

$$\begin{aligned} \epsilon _{\text {BER}}=\frac{| \text {BER}_{\text {LP}}-\text {BER}_{\text {THP}}|}{\text {BER}_{\text {LP}}}. \end{aligned}$$

(10)

Figure 2 shows this merit figure as a function of the receive SNR. Taking into account these results, we have decided to consider an SNR threshold, denoted as $\text {SNR}_{\text {l}}$, of $10\,\text {dB}$ in (4), so that LP is used for SNR values equal or less than $10\,\text {dB}$ and THP for SNR higher than that value.

Otherwise, we need to calculate the threshold values $p_{i,\text {SNR}}$ of (4) to decide if pilot symbols are required or not for channel estimation. For this purpose, for each SNR we consider only the values of $\epsilon _{\text {CSI}}[q]$ obtained every 4 frames, i.e. when the channel changes. Then, we calculate the threshold as the i–th percentile, where the $i \%$ of those values are lower than this threshold, and the $100-i \%$ are greater. Table 1 shows the threshold values $p_{i,\text {SNR}}$ as a function of receive SNR. We have selected the percentiles 1, 2, and 5 to illustrate the performance of our decision-aided system. These percentiles will be respectively denoted as $p_{1,\text {SNR}}, p_{2,\text {SNR}}$, and $p_{5,\text {SNR}}$.

Table 1. $p_{i,\text {SNR}}$ thresholds.

5.2 Transmission Step

In our experiment we will consider an $\text {SNR}_{\text {l}}=10\,\text {dB}$ and the values of $p_{i,\text {SNR}}$ in Table 1, obtained during the training step.

Fig. 3.

BER vs. SNR for LP, THP, and DP.

Figure 3 (top) shows the performance in terms of BER of the proposed DP scheme for $p_{1,\text {SNR}}, p_{2,\text {SNR}}$ and $p_{5,\text {SNR}}$. Notice that the floor effect is produced by the use of a precoder that is not adapted to the actual channel state due to the channel fluctuations not being strong enough to trigger a filter update. The curve corresponding to DP for $p_{2,\text {SNR}}$ exhibits a medium performance with a floor effect for SNRs higher than 30 dB. In Fig. 3 (bottom), we compare the results for LP, THP, and the proposed DP. As boundary cases, we have included the curves for LP and THP with Total CSI (TCSI), i.e. perfect CSI at the transmitter. The curve corresponding to DP for $p_{2,\text {SNR}}$ exhibits a medium performance, close to that achieved with LP for low SNR and to that obtained with THP for high SNR, according to the decision rule of (4).

Considering a threshold $p_{2,\text {SNR}}$, Table 2 shows the percentage of filter updates and the reduction in pilot symbols computed using the following expression

$$\begin{aligned} \epsilon _{\text {pilot}}= \left( 1 - \frac{N_u P_s + N_c P_l}{(N_u + N_c) P_l}\right) \times 100, \end{aligned}$$

(11)

where $N_u$ and $N_c$ are the number of user frames and classic frames, respectively. We can see that the reduction of pilot symbols is higher than $34\%$ for all SNRs. The reduction is considerable for SNR higher than $15\,\text {dB}$. In addition, for SNR higher than $15\,\text {dB}$, the THP filter is updated in a reduced number of times which implies a considerable improvement in terms of computational load.

Table 2. Percentage of precoder updates and pilot reduction as a function of receive SNR in dB.

6 Conclusions

In this paper a decision-aided MIMO hybrid precoding system with partial transmit CSI is proposed. The system increases the effective data rate (or spectral efficiency) by minimizing the overhead caused by the transmission of pilot symbols. This is achieved by means of limiting the number of updates of the precoding filters to the time instants in which the channel significantly varies according to a given threshold, which is fixed prior to transmission in a training step. As shown with simulation results, the loss in performance is not very significant, especially if adequate decision thresholds are selected.