The Critical Dynamics in Neural Network Improve the Computational Capability of Liquid State Machines

Abstract

In recent years, increasing studies have shown that the networks in the brain can reach a critical state where dynamics exhibit a mixture of synchronous and asynchronous firing activity. It has been hypothesized that the homeostatic level balanced between stability and plasticity of this critical state may be the optimal state for performing diverse neural computational tasks. Motivated by this, the role of critical state in neural computation based on liquid state machines (LSM), which is one of the neural network application model of liquid computing, has been investigated in this note. Different from a randomly connect structure in liquid component of LSM in most studies, the synaptic weights among neurons in proposed liquid are refined by spike-timing-dependent plasticity (STDP); meanwhile, the degrees of neurons excitability are regulated to maintain a low average activity level by Intrinsic Plasticity (IP). The results have shown that the network yield maximal computational performance when subjected to critical dynamical states.

1 Introduction

Recently, many studies have been advanced to study the critical state of the network in the brain [1,2,3]. A remarkable phenomena that critical state exhibits is power law distributions of the spontaneous neuronal avalanches sizes approximately with a slope of $-1.5$ [4]. The functional rule of this dynamical criticality can bring about optimal transmission [1], storage of information [5] and sensitivity to external stimuli [6]. The influences of network structures on critical state have been widely researched considering from the perspective of complex network, such as scale-free network [7, 8], small-world network [9, 10] and hierarchical modular network [11, 12]. However, critical dynamics are rarely used in computational neuroscience.

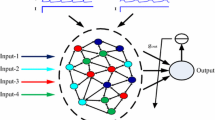
In this paper, the influences of critical state on the computational performance of LSM for real-time computing have been studied. As shown in Fig. 1(a), LSMs include three components: input component, liquid component, readout component [13]. Synaptic inputs, which are integrated from the input parts, are send to the neurons in liquid component and then it can be described in a higher dimensional state known as liquid state. As to specific assignments, the outputs of liquid component are projecting to the readout component, which plays a role as a memory-less function. In the process of computations, all the connections in the liquid component will always keep unchanged once the structure is setted up, except that readouts are trained through linear regression algorithm. As a result, many researchers are concentrating on studying the network dynamics under a predefined topological network. Considering the flexibility of neuronal connectivity in the brain, it is more reasonable to consider self-organizing neural networks based on neural plasticity.

One of the widely known forms of synaptic plasticity is the spike-timing-dependent plasticity [14]. In our previous work [15], we have given a novel liquid component of LSM refined by STDP. Compared with the LSM with tradition random liquid, LSM with new liquid has better computational performance on complex input streams. Besides, recent experimental results show that the intrinsic excitability of individual biological neurons can be adjusted to match the synaptic input by the activity of their voltage gated channels [17]. This adaption of neuronal intrinsic excitability called intrinsic plasticity (IP) has been observed in cortical areas and plays an important role on cortical functions of neural circuits [18]. It is hypothesized that IP can keep the mean firing activity of neuronal population in a homeostatic level [19], which is essential for avoiding highly intensive and synchronous firing caused by the STDP learning. Therefore, it is necessary to investigate it in combination with existing network learning algorithms to maximize the information capacity.

In this paper, we have refined the liquid component of LSM though STDP and IP learning. Therein, the synaptic weights among neurons in liquid are updated by STDP; while IP learning regulates the degrees of neurons excitability. The influence of critical dynamics on the computational performance of proposed LSM has been investigated. Results demonstrate that the network yield maximal computational performance when subjected to critical dynamical states. These results may be very significant in finding out the relationship between network learning and efficiency of information processing.

2 Network Description

2.1 Network Architecture

In this paper, as described in Fig. 1(a), we have added four different inputs to four equivalently divided groups in the liquid component. Each input is made of eight independent signal streams and generated by the Poisson process with randomly varying rates as $r_i(t)$, $\mathrm{i} = 1,...4$ (Fig. 1(b)-left), which are chosen as follows [20]. The baseline firing rates for input 1 and 2 are chosen to be 5 Hz, with randomly distributed bursts of 120 Hz for 50 ms. The rates for input 3 and 4 are periodically updated, by randomly drawn from the two values of 30 Hz and 90 Hz. The curves in Fig. 1(b)-left represents the final firing rates. Figure 1(b)-right show the responses of the neurons in liquid networks and the corresponding outputs of LSM compared with the target teaching signal $r_1 + r_3$. The results show that input signal can be expressed well as the high-dimensional liquid state, where information can be encoded into the intrinsic dynamical of neuronal population, thus the high precision of computational capability can be realized.

Fig. 1.

(a) Network structure. Neurons marked with different colors are subjected to different inputs. (b) Left: Four independent input. Right: The response of neurons in STDP+IP network(up) and the corresponding output of the readouts (bottom) according to the target signal $r_1+r_3$. (Color figure online)

2.2 Neuron Model

The network used in this article is composed of 200 Izhikevich neuron [21] described by

$$\begin{aligned} \begin{array}{lll} \dot{v_{i}}=0.04v_{i}^2+5v_{i}+140-u_{i}+I+I_{i}^{syn} \\ \dot{u_{i}}=a(bv_{i}-u_{i})+D\xi _{i} \end{array} \end{aligned}$$

(1)

$$\begin{aligned} \text{ if } v_{i}>30 \text{ mV, } \text{ then } \left\{ \begin{array}{lll} v_{i} \leftarrow c\\ u_{i} \leftarrow u_{i}+d \end{array} \right. \end{aligned}$$

(2)

where $i=1,2,...,200$. $v_{i}$ and $u_{i}$ is the membrane potential and membrane recovery variable of the neurons, respectively. The parameters a, b, c, d are constant. Choosing different values of these parameters can obtain various firing dynamic [21]. The parameter $\xi _{i}$ stand for the independent Gaussian noise with zero mean and intensity D is the noisy background. I is the external current. $I_{i}^{syn}$ is the total synaptic current through neuron i and is governed by the dynamics of the synaptic variable $s_j$:

$$\begin{aligned} \begin{array}{ll} I_{i}^{syn}=-\mathop {\sum }\nolimits _{1(j\ne i)}^N g_{ji}s_{j}(v_{i}-v_{syn})\\ \dot{s_{j}}=\alpha (v_{j})(1-s_{j})-s_{j}/\tau \\ \alpha (v_{j})=\alpha _{0}/(1+e^{-v_{j}/v_{shp}}) \end{array} \end{aligned}$$

(3)

here, $\alpha (v_{j})$ is the synaptic recovery function. If the presynaptic neuron is in the silent state $v_{j}<0$, $s_j$ reduces to $\dot{s_{j}}=-s_{j}/\tau$; if not, $s_j$ jumps quickly to 1. The excitatory synaptic reversal potential $v_{syn}$ is set to be 0. The synaptic weight $g_{ij}$ will be updated by the STDP function F:

$$\begin{aligned} \begin{array}{ll} \varDelta g_{ij}=g_{ij}F(\varDelta t)\\ F(\varDelta t)=\left\{ \begin{array}{ll} A_{+}\exp (-\varDelta t/\tau _{+})~~\mathrm {if}~\Delta t>0\\ -A_{-}\exp (\varDelta t/\tau _{-})~~\mathrm {if}~\Delta t<0 \end{array} \right. \end{array} \end{aligned}$$

(4)

where $\varDelta t=t_{j}-t_{i}$, $t_i$ and $t_j$ is the spike time of the presynaptic and postsynaptic neuron, respectively. $\tau _{+}$ and $\tau _{-}$ determine the temporal window for synaptic modification. $F(\varDelta t)=0$ when $\varDelta t=0$. $A_{+}$ and $A_{-}$ determine the maximum amount of synaptic modification. Here, $\tau _{-}=\tau _{+}=20$, $A_{+}=0.05$ and $A_{-}/A_{+}=1.05$. The synaptic weights are distribute in $[0,g_{max}]$, where $g_{max}=0.015$ is the maximum value.

Particularly, parameter b has a significant influence on the neurons excitability. To get a heterogeneous network, the initial values of b are randomly distributed in [0.12, 0.2]. The neurons with larger value b can exhibit stronger excitability, thus fire with a higher frequency. As a result we consider plastic modifications of b as a representative scheme describing IP mechanisms. The model we proposed is based on neurons’ inter-spike interval (ISI), in which a function $\phi _i$ is used to determine the amount of excitability modification:

$$\begin{aligned} \begin{array}{ll} \varDelta b_i=b_i\phi _i \\ \phi _i=\left\{ \begin{array}{ll} -\eta _{IP} \cdot exp(\frac{{T}_{min}-ISI_i}{{T}_{min}})~~\mathrm {if}~ISI_i<{T}_{min}\\ \eta _{IP}\cdot exp(\frac{ISI_i-{T}_{max}}{{T}_{max}})~~\mathrm {if}~ISI_i>{T}_{max} \\ 0,others \end{array} \right. \\ \end{array} \end{aligned}$$

(5)

where $\eta _{IP}$ is learning rate. The neuronal inter-spike interval (ISI) is $ISI^k_i=t^{k+1}_i-t^{k}_i$, where $t^{k}_i$ is the kth firing time of neuron i; ${T}_{min}$ and ${T}_{max}$ are thresholds, they determine the expected ranges of ISI. During the learning process, the most recent ISI is examined every $t_{ck}$ time and used to adjust the neuronal excitability: If $ISI_{i}$ is larger than the threshold $T_{max}$, the neuronal excitability is strengthened to make the neuron more sensitive to input stimuli; if $ISI_{i}$ is less than the threshold $T_{min}$, the neuronal excitability is weakened to make the neuron less sensitive to input stimuli. The histogram of firing rate response during IP learning for a randomly driven network is shown in Fig. 2, from which an normal distribution of firing rate is observed, and this result is consistent with the theory that the maximum-entropy distribution is Gaussian if the desired ($p(x)=\frac{ exp[{-(x-\mu )^2}/{2\sigma ^2}]}{\sigma \sqrt{2\pi }}$) variance is fixed. It indicates that our IP model is reasonable. Additionally, the values of other parameters are $\alpha _0 = 3$, $\tau =2$, $V_{shp}=5$, $a = 0.02$, $c=-65$, $d=8$, $D=0.1$, ${T}_{max}=110$, ${T}_{min}=90$.

Fig. 2.

Histogram of firing rate response by IP learning and its Gassian fit: $\mu =11.2795$, $\sigma =0.1736$.

Fig. 3.

Network structures obtained from learning rules. Left: STDP alone; Right: STDP plus IP. (a) Schematic diagram of the normalized synaptic matrix. (b) Histogram of the normalized synaptic weights. (c) Scatter plots of neurons strong synaptic weights for in-degrees and out-degrees.

At the beginning of the learning, each neuron in liquid network is bidirectionally connected to each other with the same synaptic weight of $g_{max}/2$ and the same external current of 6. After sufficient time the updated network structure by STDP alone or STDP+IP is shown in Fig. 3. Figure 3(a) indicates the active-neuron dominant structure obtained by STDP learning, where the strong connections are mainly distributed to the synapses from neurons with large values of b to inactive ones with small values of b, and most of the synapses are rewired to be either 0 or 1; while IP strengthens the competition among different neurons and makes the connectivity structure more complex and the distribution is not bimodal, but rather is skewed toward smaller values. The degree distribution for different networks are also examined, the out-degree(out) and in-degree(in) are defined as in [16]. It is demonstrated that neurons with larger values of b have larger out-degrees and smaller in-degrees in STDP condition, while only neurons with intermediate sensitivity keep this principle when IP is switched on.

3 Results

In this section, lists of real-time computational tasks were conducted to investigate the influence of critical dynamic on the computational perfromance of LSM updated by STDP+IP. To characterize and quantify the computational performance of networks systematically, we purposely tested the sensitivity of different types of LSM by varying the external current I. The results of average MSEs shown in Fig. 4(a) were obtained from 20 times independent simulations. The results of the three network are non-monotonic, which reaches the minimal value when the external stimulus current is about 5. The computational performance becomes worse when the external stimulus current I is too strong or too weak. Besides, it illustrates that LSMs refined from STDP+IP performs much better than the one with random reservoir or the one with STDP alone.

Fig. 4.

(a) Computational capability of networks with different topologies. (b) Entropy of network activity for networks with different topologies. i.e. STDP network, random network and STDP+IP network.

Fig. 5.

Firing activity of the three network with different stimulates (I = 3, 5, 8).

In order to get an insight into the potential advantages of the turning point, we have specially investigated the influence of stimulus external current on network activity. Figure 5 has shown the network activities of different network with different stimulus. It can be seen that the synchronization degree of network activity has been increased with the increase of external stimulus. Particularly, the activity exhibit a mixture of synchronous and asynchronous firing activity when the stimulus current is about 5, indicating the highly complexity of network activity. To further quantify the complexity of network activity, we have computed the information entropy of network activity, which measures the complexity of activity patterns in a neural network and defined as

$$\begin{aligned} H=-\sum _{i=1}^n p_{i}\log _2{p_i} \end{aligned}$$

(6)

where, n is the number of unique binary patterns. $p_i$ is the probability that pattern i occurs [22]. For calculation convenience, neuronal activities are measured in pattern units consisting of a certain number of neurons. In each time bin, if any neuron of the unit is firing then the event of this unit is active; otherwise it is inactive. Surprisingly, the results have shown that the maximal entropy has been reached when the current is about 5 (see Fig. 4(b)) where networks have the optimal computational performance. Therefore, these results demonstrate that the critical state with dynamics between synchronized firings and unsynchronized firings makes the system have maximal dynamical complexity and thus achieve optimal computational performance.

4 Conclusion

In this paper, the effect of critical dynamics on computational capability of liquid state machine updated by STDP+IP has been investigated. Our results have shown that the critical dynamic can remarkable improve the computation performance of liquid state machine. At the critical state, the information entropy of network activity is maximized indicating the complexity of activity patterns are maximized, which can encode the rich dynamics of different neurons. These results may be very significant in finding out the relationship between network learning and efficiency of information processing.