Keywords

3.1 Introduction

Adsorption is one of the most widely applied unit operations used to separate molecules that are present in a fluid phase (adsorbate) using a solid surface (adsorbent). In this chapter, the adsorption kinetics in liquid phase will be addressed. Adsorption kinetics is expressed as the rate of adsorbate removal from the fluid phase to the adsorbent or the time involving the mass transfer of one or more components contained in a liquid to the adsorbent (Qiu et al. 2009). When adsorption is studied, kinetic aspects should be evaluated in order to know more details about its mechanisms, characteristics, and possibilities of application. These data can determine the residence time to reach the required concentration of the adsorbate, making possible the design and operation of an adsorption equipment and defining the performance in batch and continuous systems (Ruthven 1984).

Several mathematical models have been suggested to describe adsorption operations, which are classified as diffusional models and adsorption reaction models . Both are used to describe the kinetic peculiarities of adsorption operation; however, they are completely uneven in its essence (Qiu et al. 2009). Adsorption diffusion models are constructed based on three successive steps: external mass transfer, intraparticle diffusion, and adsorption on active sites. On the other hand, adsorption reaction models, originating from chemical reaction kinetics, are based on the whole process of adsorption, without considering the adsorption diffusion steps previously mentioned. They are widely used to represent the adsorption data in the literature. The more extensively adsorption reaction models utilized are the pseudo-first-order, pseudo-second-order, and Elovich equation (Wan and Hanafiah 2008; Cadaval et al. 2013; Dotto et al. 2013).

Here, we reviewed diffusional models and adsorption reaction models to be applied in discontinuous and continuous adsorption operations. The models and its mathematical solutions are detailed.

3.2 Adsorption Kinetics in Discontinuous Batch Systems

In a discontinuous batch adsorption system, the kinetic profile is fundamental due to several reasons. The kinetic profile provides information about the adsorption rate, equilibrium time, and effectiveness of the adsorbent. Furthermore, based on the kinetic curve, it is possible to infer the mass transfer mechanisms, which are the rate-limiting steps of the adsorption process (Ruthven 1984; Suzuki 1993; Qiu et al. 2009). The kinetic profile in a discontinuous batch adsorption system is normally represented by curves of C t (adsorbate concentration in the bulk solution) versus t (contact time) or q t (amount of adsorbate adsorbed on the adsorbent) versus t. In order to obtain information about the adsorption process from these curves, several empirical, semiempirical, theoretical, and diffusion-based models are employed (Do 1998; Qiu et al. 2009; Plazinski and Rudzinski 2009; Piccin et al. 2011; Baz-Rodríguez et al. 2012; Ocampo-Pérez et al. 2012; Dotto et al. 2014, 2016). In this section, these models are divided in two main classes, which are normally employed in the majority of adsorption articles: diffusional mass transfer models and adsorption reaction models.

3.2.1 Diffusional Mass Transfer Models

Figure 3.1 shows the representation of the main mass transfer mechanisms that occur in a discontinuous batch adsorption operation . In this case, the adsorbent particle with radius R is defined as volume of control, and three consecutive steps of mass transfer are considered: external mass transfer, intraparticle diffusion, and adsorption on active sites (Ruthven 1984; Do 1998; Ocampo-Pérez et al. 2012; Dotto et al. 2016). The external mass transfer mechanism is relative to the movement of the adsorbate (molecules/ions) from the bulk solution (with concentration C t ) to the external surface of the adsorbent particle (with concentration C S (t)). This mass transfer step is governed by the external mass transfer coefficient (k f ). The intraparticle diffusion mechanism in turn is relative to the movement of the adsorbate (molecules/ions), inside the adsorbent particle. The intraparticle diffusion mechanism occurs by effective pore volume diffusion, surface diffusion, or a combination of both mechanisms. The effective pore volume diffusion describes the transport of the adsorbate (molecules/ions) in the liquid phase inside of the particle and is represented by D P , the effective pore volume diffusion coefficient. The surface diffusion is relative to the transport of the adsorbate over the surface of the adsorbent particles, from sites of higher energy to sites of lower energy. This mechanism is represented by the surface diffusion coefficient D S . Finally, the adsorption on active sites is relative to the interaction of the adsorbate with the active sites of the adsorbent. In this context, the diffusional mass transfer models are constructed on the basis in the three abovementioned consecutive steps: external mass transfer, intraparticle diffusion (effective pore volume diffusion, surface diffusion, or a combination of both mechanisms), and adsorption on an active site; and they represent realistically the adsorption kinetics (Ocampo-Pérez et al. 2012; Nieszporek 2013; Dotto et al. 2014).

Fig. 3.1
figure 1

Representation of the main mass transfer mechanisms which occur in a discontinuous batch adsorption operation

Full size image

One of the most complete diffusional models is the pore volume and surface diffusion model (PVSDM) . This model is based on the following assumptions: batch system adsorption occurs at constant temperature; the particles are spherical; the mass transport by convection within the pores is negligible; the intraparticle diffusion can occur by pore volume diffusion and surface diffusion or both; the values of effective pore volume diffusion coefficient (D p ) and effective surface diffusion coefficient (D s ) are constant; and the adsorption rate on an active site is instantaneous (Leyva-Ramos and Geankoplis 1985; Ocampo-Pérez et al. 2010). This model is defined as

$$ V\frac{dC_t}{dt}=-{mSk}_F\left({C}_t-{\left.{C}_{s(t)}\right|}_{r= R}\right) $$
(3.1)
$$ t=0,{C}_t={C}_0 $$
(3.2)
$$ {\varepsilon}_p\frac{\partial {C}_r}{\partial t}+{\rho}_p\frac{\partial q}{\partial t}=\frac{1}{r^2}\frac{\partial }{\partial r}\left[{r}^2\left({D}_p\frac{\partial {C}_r}{\partial r}+{\rho}_p{D}_s\frac{\partial q}{\partial r}\right)\right] $$
(3.3)
$$ t=0,0\le r\le R,{C}_r=0 $$
(3.4)
$$ {\left.\frac{\partial {C}_r}{\partial r}\right|}_{r=0}=0 $$
(3.5)
$$ {D}_p{\left.\frac{\partial {C}_r}{\partial r}\right|}_{r= R}+{\rho}_p{D}_s{\left.\frac{\partial q}{\partial r}\right|}_{r= R}={k}_F\left({C}_t-{\left.{C}_{s(t)}\right|}_{r= R}\right) $$
(3.6)

In Eqs. (3.1), (3.2), (3.3), (3.4), (3.5), and (3.6), V is the volume of solution, m is the amount of adsorbent, ε p is the void fraction of the adsorbent, ρ p is the apparent density of the adsorbent, S is the external surface area per mass of the adsorbent, C 0 is the initial adsorbate concentration in the bulk solution, C r is the adsorbate concentration varying with the position and time, and q is the mass of adsorbate per mass of adsorbent varying with the position and time, respectively. The other symbols were already defined.

The PVSDM model can be simplified by considering that the sole intraparticle diffusion mechanism may be either pore volume diffusion (PVDM) (D p  ≠ 0, D s  = 0) or surface diffusion (SDM) (D p  = 0, D s  ≠ 0). Furthermore, to solve this model, it is considered that there exists a local equilibrium between the adsorbate concentration of the pore solution, C r , and the mass of adsorbate adsorbed on the pore surface, q. This equilibrium relationship between C r and q is represented by the adsorption isotherm :

$$ q= f\left({C}_r\right) $$
(3.7)

The isotherm studies are detailed in Chap. 2 of this book. Also, if V is constant, it is evident that C t and q t are always related by Eq. (3.8):

$$ {q}_t=\frac{\left({C}_0-{C}_t\right) V}{m} $$
(3.8)

For illustration, the overall adsorption rate of Reactive Black 5 dye (RB5) on chitosan-based materials (powder and film) was investigated by Dotto et al. (2016) using the PVSDM model . The geometry of the adsorbents and swelling effects were evaluated. The authors found that the surface diffusion was the intraparticle diffusion mechanism that governed the adsorption, since its contribution was higher than 92% regardless the position and time. The D s values ranged from 2.85 × 10−11 to 12.1 × 10−11 cm2/s. The swelling effect was most pronounced for the chitosan films, providing an increase of about 65 times in the D s value. On the other hand, Flores-Cano et al. (2016) studied the adsorption rate of metronidazole, dimetridazole, and diatrizoate on activated carbons using the PVSDM model . The results revealed that the surface diffusion contributed >90% of the total intraparticle diffusion, confirming that surface diffusion is the mechanism that controls the intraparticle diffusion of these pollutants on activated carbons. Finally, Largitte and Laminie (2015) evaluated the concentration decay curves for the adsorption of lead on a granular activated carbon using the PVSDM model . The results showed that the PVSDM model fitted the data reasonably well and the values of D P were higher than those of D S . k L was around 10−4 cm s−1, whereas D P and D S were around 10−6 and 0 cm2/s. Therefore, the overall rate of adsorption was controlled by intraparticle diffusion, which was exclusively due to the pore volume diffusion.

Three models can be derived from the PVSDM model : external mass transfer model (EMTM), pore volume diffusion model (PVDM), and surface diffusion model (SDM) (Costa and Rodrigues 1985; Leyva-Ramos and Geankoplis 1985; Garcia-Reyes and Rangel-Mendez 2010).

The external mass transfer model (EMTM) assumes that the movement of solute from the liquid phase to the adsorbent is only due to external mass transfer. In this way, the intraparticle diffusion is instantaneous, so there is not a concentration gradient inside the particle. Therefore, the intraparticle diffusion resistance is considered to be insignificant. EMTM model is given by Eqs. (3.9), (3.10), (3.11), and (3.12) (Dotto et al. 2016):

$$ V\frac{dC_t}{dt}=-{mSk}_F\left({C}_t-{\left.{C}_{s(t)}\right|}_{r= R}\right) $$
(3.9)
$$ t=0,{C}_t={C}_0 $$
(3.10)
$$ {\left.\frac{m{\varepsilon}_p}{\rho_p}\frac{dC_r}{\partial t}\right|}_{r= R}+ m\frac{dq_t}{dt}={ m Sk}_F\left({C}_t-{\left.{C}_{s(t)}\right|}_{r= R}\right) $$
(3.11)
$$ t=0,{C}_t=0,{q}_t=0 $$
(3.12)

The pore volume diffusion model (PVDM) with external resistance is a simplification of the PVDSM model, used when the intraparticle diffusion is controlled only by effective pore diffusion (D p  ≠ 0, D s  = 0). This simplification leads to (Garcia-Reyes and Rangel-Mendez 2010)

$$ V\frac{dC_t}{dt}=-{mSk}_F\left({C}_t-{\left.{C}_{s(t)}\right|}_{r= R}\right) $$
(3.13)
$$ t=0,{C}_t={C}_0 $$
(3.14)
$$ {\varepsilon}_p\frac{\partial {C}_r}{\partial t}+{\rho}_p\frac{\partial q}{\partial t}=\frac{1}{r^2}\frac{\partial }{\partial r}\left[{r}^2\left({D}_p\frac{\partial {C}_r}{\partial r}\right)\right] $$
(3.15)
$$ t=0,0\le r\le R,{C}_r=0 $$
(3.16)
$$ {\left.\frac{\partial {C}_r}{\partial r}\right|}_{r=0}=0 $$
(3.17)
$$ {D}_p{\left.\frac{\partial {C}_r}{\partial r}\right|}_{r= R}={k}_F\left({C}_t-{\left.{C}_{s(t)}\right|}_{r= R}\right) $$
(3.18)

Based on the same analogy, the SDM model is used when the intraparticle diffusion mechanism is only controlled by surface diffusion; then the set of governing equations are given by

$$ V\frac{dC_t}{dt}=-{mSk}_F\left({C}_t-{\left.{C}_{s(t)}\right|}_{r= R}\right) $$
(3.19)
$$ t=0,{C}_t={C}_0 $$
(3.20)
$$ {\varepsilon}_p\frac{\partial {C}_r}{\partial t}+{\rho}_p\frac{\partial q}{\partial t}=\frac{1}{r^2}\frac{\partial }{\partial r}\left[{r}^2\left({\rho}_p{D}_s\frac{\partial q}{\partial r}\right)\right] $$
(3.21)
$$ t=0,0\le r\le R,{C}_r=0 $$
(3.22)
$$ {\left.\frac{\partial {C}_r}{\partial r}\right|}_{r=0}=0 $$
(3.23)
$$ {\rho}_p{D}_s{\left.\frac{\partial q}{\partial r}\right|}_{r= R}={k}_F\left({C}_t-{\left.{C}_{s(t)}\right|}_{r= R}\right) $$
(3.24)

Furthermore, if the external mass transfer is negligible, Eq. (3.18) (PVDM) and Eq. (3.24) (SDM) can be replaced by the adsorption isotherm, or by other boundary condition.

Another important model used in adsorption systems is named homogeneous surface diffusion model (HSDM) . This model considers a dual mass transport mechanism across the hydrodynamic boundary layer surrounding the adsorbent particle and intraparticle resistance within the particle in the form of surface diffusion (Leyva-Ramos and Geankoplis 1985). Mathematical equations of HSDM are

$$ m\frac{dq_t}{dt}={mAk}_F\left({C}_t-{\left.{C}_{s(t)}\right|}_{r= R}\right) $$
(3.25)
$$ t=0,{C}_t={C}_0 $$
(3.26)
$$ m\frac{dq_t}{dt}= V\frac{dC_t}{dt} $$
(3.27)
$$ {\rho}_p\frac{\partial q}{\partial t}=\frac{1}{r^2}\frac{\partial }{\partial r}\left[{r}^2\left({\rho}_p{D}_s\frac{\partial q}{\partial r}\right)\right] $$
(3.28)
$$ t=0,0\le r\le R, q=0 $$
(3.29)
$$ {\left.\frac{\partial q}{\partial r}\right|}_{r=0}=0 $$
(3.30)
$$ {\rho}_p{D}_s{\left.\frac{\partial q}{\partial r}\right|}_{r= R}={k}_F\left({C}_t-{\left.{C}_{s(t)}\right|}_{r= R}\right) $$
(3.31)

In the same way of the other models, HSDM requires a relation between the amount of adsorbate adsorbed on the adsorbent and the amount of the adsorbate in the solution, which is given by the adsorption isotherm.

3.2.2 Adsorption Reaction Models

Adsorption reaction models originating from chemical reaction kinetics are based on the adsorption as a single phenomenon, unlike diffusive model. Adsorption reaction models are widely utilized to describe the kinetic process of adsorption. In batch systems, the more applied models are the pseudo-first-order, pseudo-second-order, and Elovich equation (Qiu et al. 2009; Largitte and Pasquier 2016).

3.2.2.1 Pseudo-First-Order Model

The pseudo-first-order model presented by Lagergren is based on the solids’ capacity to adsorb and is given by Eq. (3.32) (Lagergren 1898):

$$ \frac{dq_t}{dt}={k}_1\left({q}_e-{q}_t\right) $$
(3.32)

where q e and q t (mg/g) are the adsorption capacities at equilibrium and time t (min), respectively, and k 1 (min−1) is the pseudo-first-order rate constant of the kinetic model. Integrating Eq. (3.32) using the initial conditions of q t  = 0 at t = 0 and q t  = q t at t = t leads to Eq. (3.33) (Ho 2004):

$$ \ln \left(\frac{q_e}{q_e-{q}_t}\right)={k}_1 t $$
(3.33)

which can be rewritten as

$$ {q}_t={q}_e\left(1- \exp \left({k}_1 t\right)\right) $$
(3.34)

Several scientific papers present the pseudo-first-order model as the most suitable to represent adsorption kinetics. For the adsorption of FD&C yellow 5 onto chitosan film, the pseudo-first-order model was the more satisfactory (Cadaval et al. 2015). In this study, a little effect of the stirring rate was confirmed by the little variation in the k 1 values at different stirring rates. This model is normally used when the adsorption operation is fast, attaining the equilibrium within 20–30 min.

3.2.2.2 Pseudo-Second-Order Model

Ho described a kinetic process of the adsorption of divalent metal ions onto peat (Ho and McKay 2000), in which the chemical bonding among divalent ions and functional groups on peat, were responsible for the ionic exchange. Therefore, the peat-metal interaction can be presented as Eq. (3.35), which occurs in the adsorption of Cu2+ ions onto the adsorbent (Coleman et al. 1956):

$$ {2\mathrm{P}}^{-}{+\mathrm{Cu}}^{2+}\leftrightarrow {\ \mathrm{CuP}}_2 $$
(3.35)

where P− represents the active sites on the peat surface. In the above reaction, the main assumptions were that the adsorption followed a second-order behavior and the interaction adsorbent adsorbate was chemical.

The adsorption rate described by Eq. (3.36) is dependent of divalent ion concentration on the surface of peat at time t and at equilibrium. Thus, the rate can be expressed as

$$ \frac{d{(P)}_t}{ d t}={k}_2{\left[{(P)}_0-{(P)}_t\right]}^2 $$
(3.36)

where (P)0 is the amount of equilibrium sites available on the peat, (P) t is the amount of active sites occupied on the peat at time, and k 2 (g/(mg min)) is the pseudo-second-order rate constant of adsorption .

Since the driving force (q e  − q t ) is proportional to the available fraction of active sites, then it can be written as

$$ \frac{dq_t}{dt}={k}_2{\left({q}_e-{q}_t\right)}^2 $$
(3.37)

and integrating Eq. (3.37) using the initial conditions of q t  = 0 at t = 0 and q t  = q t at t = t, yields

$$ \frac{1}{\left({q}_e-{q}_t\right)}=\frac{1}{q_e}+{k}_2 t $$
(3.38)

This equation can be rewritten as follows :

$$ {q}_t=\frac{t}{\left(\frac{1}{h_0}\right)+\left(\frac{t}{q_e}\right)} $$
(3.39)

and

$$ {h}_0={k}_2{q}_e^2 $$
(3.40)

where h 0 (mg/(g min)) is the initial adsorption rate.

The second-order rate equation has been successfully applied to the adsorption of metal ions, dyes, and organic substances from aqueous solutions. Several studies for adsorption of divalent metals reported that the majority of the sorption kinetics follows pseudo-second-order mechanism (Ho 2006; Aydin and Aksoy 2009). For instance, the adsorption of Cu (II) from copper mine water by chitosan films and the matrix effects were studied, and the pseudo-second-order model showed better fit than the other ones (Frantz et al. 2017).

3.2.2.3 Elovich Model

The Elovich equation was developed by Zeldowitsch (1934) and was used to describe the adsorption rate of carbon monoxide on manganese dioxide, which decreased exponentially with an increase of the gas adsorbed. Thus, Elovich equation is applied to determine the kinetics of chemisorption of gases onto heterogeneous surface (Rudzinski and Panczyk 2000) and was obtained from the following differential equation :

$$ \frac{dq}{dt}={ae}^{-\beta q} $$
(3.41)

where q represents the amount of gas adsorbed at time t, a is the desorption constant, and β is the initial adsorption rate. With the assumption of aβt >> 1, Eq. (3.41) was integrated with the initial conditions of q = 0 at t = 0 and q = q at t = t resulting in (Chien and Clayton 1980)

$$ {q}_t=\beta \ln \left( a\beta \right)+\beta \ln t $$
(3.42)

or

$$ {q}_t=\left(\frac{1}{a}\right) \ln \left(1+ a\beta t\right) $$
(3.43)

This equation has been applied to describe the adsorption process of different molecules from liquid medium. For example, Elovich model was the more suitable to fit the kinetic data for the adsorption of FD&C red 2 onto chitosan film (Cadaval et al. 2015) and carotenoids and chlorophylls in rice bran oil bleaching (Pohndorf et al. 2016).

3.3 Fixed-Bed Adsorption

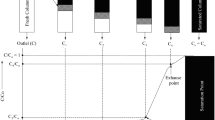
In operational level , a fixed-bed column presents a certain working time to adsorb contaminants, such that the effluent outlet can comply with allowable levels of concentration. This working time can be expressed by the so-called breakthrough curve , and this behavior is shown in Fig. 3.2.

Fig. 3.2
figure 2

(a) Progression of the mass transfer through fixed-bed column and (b) concentration profile of solute concentration at adsorbent bed outlet during the adsorption process

Full size image

Considering a vertical upward flow, initially the adsorbent is completely free of the solute, while the flow of liquid is initiated by the column. The solute is gradually transferred to the adsorbent until at a point above the bed (point I in Fig. 3.2a) . As the process progresses, the initial portions of the adsorbent are completely saturated (point III in Fig. 3.2a), and the zone where the solute is removed advances toward the final part of the column. The portion of the column in which the solute reduction occurs is called the mass transfer zone (point II in Fig. 3.2a).

When the mass transfer zone reaches the end of column, the concentration of adsorbate in the liquid gradually increases (point c in Fig. 3.2b), since not all of the solute can be removed. Then, the start of the mass transfer zone reaches the end of the column (point e in Fig. 3.2b) and the whole column is saturated, not occurring more solute removal.

The portion of the curve between the points c and e (Fig. 3.2b) of the column is called the breakthrough curve , and the point at which the concentration of adsorbate at the output of the column reaches the maximum limit is called the breakpoint .

In this way, the shape of the rupture curve provides information about the length of the mass transfer zone (point II in Fig. 3.2a), and the smaller this zone, the greater the efficiency of the column.

In general, the breakthrough curve can be affected by thermodynamic factors related to the adsorption equilibrium or isotherms, kinetic factors related to the mass transfer rate, and fluid dynamic factors related to the flow velocity (Cooney 1999).

Thus, in this session, the mass balance in fixed-bed systems will be described, showing the analytical solutions that represent the kinetics of the column adsorption and presenting the methods of analysis and scale-up for real systems.

3.3.1 Mass Balance and Modeling of the Breakthrough Curves Based on Mass Transfer Mechanism

The differential mass balances for an elementary volume of a fixed-bed column, including the fluid phase and the adsorbent within this elementary volume, are used for the development of a mathematical model, which describes the kinetic behavior of the system.

In the mathematical modeling of fixed-bed adsorption, the following considerations must be made: (i) the system is isothermal; (ii) there is only one adsorbate soluble in the liquid; (iii) the concentration of the solute in the liquid is so small that, if the whole has been adsorbed, there will be no change in the flow rate of the fluid; (iv) there is not radial velocity and; (v) from this latter consideration, it is also considered that there is not variation in adsorbate concentration in both phases in the radial directions (Cooney 1999).

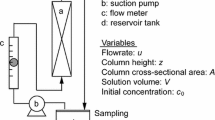
For the differential mass balance in the column, a control volume with a height Δz and a circular session identical to the column diameter (or area A) is considered. A fluid stream containing the species to be adsorbed passes through the voids of the bed (ε). Then, the volume of solid (V s ) in the volume of control is

$$ {V}_s=\left(1-\varepsilon \right) A\Delta z $$
(3.44)

Applying the mass conservation law , the mass balance of any solute i in the control volume is given by

$$ \varepsilon A\Delta z\frac{\partial {\mathrm{C}}_i}{\partial \mathrm{t}}=\varepsilon {AN}_i\mid {}_z-\varepsilon {AN}_i\mid {}_{z+\Delta z}-\left(1-\varepsilon \right) A\Delta z\frac{\partial \mathrm{q}}{\partial \mathrm{t}} $$
(3.45)

where \( \varepsilon A\Delta z\frac{\partial {\mathrm{C}}_i}{\partial \mathrm{t}} \) is the solute accumulation in the control volume, εAN i ∣ z is the mass rate of solute that enters the control volume in the z direction, εAN i ∣ z + Δz is the mass rate of solute that leaves volume control in the z direction, and \( \left(1-\varepsilon \right) A\Delta z\frac{\partial \mathrm{q}}{\partial \mathrm{t}} \) is the mass rate of solute adsorbed, respectively.

Dividing Eq. (3.45) by εAΔz and applying the limit when Δz tends to zero yields

$$ \frac{\partial {\mathrm{C}}_i}{\partial \mathrm{t}}=\frac{\partial {\mathrm{N}}_i}{\partial \mathrm{z}}-\frac{\left(1-\varepsilon \right)}{\varepsilon}\frac{\partial \mathrm{q}}{\partial \mathrm{t}} $$
(3.46)

The mass flux of solute in the fluid phase in the z direction (N iz ) is given by a convective portion, due to fluid movement, and another diffusive, due to a gradient of concentration caused by the adsorption along the column, according to the following equation:

$$ \frac{\partial {\mathrm{N}}_i}{\partial \mathrm{z}}={v}_z\frac{\partial {\mathrm{C}}_i}{\partial \mathrm{z}}-{D}_L\frac{\partial^2{\mathrm{C}}_i}{\partial {\mathrm{z}}^2} $$
(3.47)

where v z is interstitial velocity of the fluid in the z-direction and D L is the coefficient of axial dispersion or diffusion. Then, substituting in Eq. (3.46), and rearranging the equation, the mass balance in the adsorption column can be described as

$$ {v}_z\frac{\partial {\mathrm{C}}_i}{\partial \mathrm{z}}+{\left(\frac{\partial {\mathrm{C}}_i}{\partial \mathrm{t}}\right)}_{\overline{Z}}+\frac{\left(1-\varepsilon \right)}{\varepsilon}{\left(\frac{\partial \mathrm{q}}{\partial \mathrm{t}}\right)}_{\overline{Z}}={D}_L{\left(\frac{\partial^2{\mathrm{C}}_i}{\partial {\mathrm{z}}^2}\right)}_t $$
(3.48)

The adsorption rate \( {\left(\frac{\partial \mathrm{q}}{\partial \mathrm{t}}\right)}_{\overline{Z}} \) is described by the mass transfer in the particle (previous section), and then Eq. (3.48) can be solved numerically using the following initial and boundary conditions:

$$ t=0; C=0; q=0 $$
(3.49)
$$ t>0; Z=0{; C= C}_0 $$
(3.50)
$$ t\to \infty; \frac{\partial {C}_i}{\partial t}=0=\frac{\partial q}{\partial t}=0 $$
(3.51)

3.3.2 Empirical Models for Breakthrough Curves

The breakthrough curve behavior prediction is fundamental for the analysis and design of fixed-bed adsorption systems. From this curve, parameters, such as the breakthrough time and the saturation time of the column, are obtained, giving an idea of the length of the mass transfer zone. For this reason, several models were developed from analytical solutions of the differential mass balance in the fixed bed or by empirical solutions.

3.3.2.1 Bohart-Adams Model

Bohart-Adams model was developed considering the surface reaction theory which assumes that the equilibrium is not instantaneous, and the rate of adsorption is proportional to the adsorption capacity and the concentration of solute (Bohart and Adams 1920). This model is suitable for adsorption systems with high affinity equilibrium behavior (or irreversible isotherm) and is expressed as (Cooney 1999)

$$ \frac{C_t}{C_0}= \exp \left({k}_{AB}{C}_0 t-{k}_{AB}{q}_0\frac{z}{v_z}\right) $$
(3.52)

where C 0 and C t are the input and output solute concentrations, respectively, k AB is the Bohart-Adams model kinetic constant, q 0 is the stoichiometric capacity of the bed (related to the adsorption capacity predicted by the equilibrium isotherm for C e  = C 0, in units of mass per volume of adsorbent), and z is the length of bed .

3.3.2.2 Thomas Model

Thomas (1944) solved the differential mass balance for a system with adsorption isotherms of the Langmuir type, no axial dispersion, and kinetic described by pseudo-second-order model. Thomas model is one of the widely used models, and this model is based on the plug flow behavior in the bed, i.e., no axial dispersion, expressed as

$$ \frac{C_t}{C_0}=\frac{1}{1+ \exp \left(\frac{k_{Th}{q}_0 m}{Q}-{k}_{Th}{C}_0 t\right)} $$
(3.53)

where k Th is the Thomas kinetic constant, m is the mass of adsorbent, and Q is the operating flow rate. In this equation, q 0 is expressed in units of mass of solute per mass of adsorbent .

3.3.2.3 Wolborska Model

Wolborska model (1989) was based on the general equation of diffusional mass transfer for low concentration range; see Eq. (3.48). For an external diffusion with a constant coefficient, it is possible to derive

$$ \frac{\partial \mathrm{q}}{\partial \mathrm{t}}=-{v}_m\frac{\partial \mathrm{q}}{\partial \mathrm{z}}={\beta}_a\left({C}_b-{C}_i\right) $$
(3.54)

where v m is the migration rate of the solute through the fixed bed, C i is the interface solid/liquid concentration, and β a is the kinetic coefficient of external diffusion.

Using Eq. (3.54), and assuming that C i  << C b , v m  << v z , and neglecting the axial dispersion, the breakthrough curves can be described as

$$ \ln \left(\frac{C_t}{C_0}\right)=\frac{\beta_a{C}_0}{q_0} t-\frac{\beta_a z}{v_z} $$
(3.55)

3.3.2.4 Yoon-Nelson Model

Yoon-Nelson model (1984) was proposed to describe the nature of breakthrough curves of adsorbate gases on activated charcoal. This model is based on the assumption that the rate of adsorption degradation for each molecule is proportional to the adsorption rate and the yield curve of the adsorbed material, represented as

$$ \frac{C_t}{C_0}=1+ \exp \left(\tau {k}_{YN}-{k}_{YN} t\right) $$
(3.56)

where k YN is the Yoon-Nelson kinetic constant and τ is the predict time to the advance of 50% of adsorption front .

3.3.3 Design of Fixed-Bed Adsorption Systems

In fixed-bed adsorption tests (laboratory scale), the adsorption capacity of the bed is related to the area above the rupture curve, as can be seen in Fig. 3.2b. Thus, the adsorption capacity is described by

$$ q=\frac{QC_0\underset{0}{\overset{t}{\int }}\left(1-\frac{C_t}{C_0}\right) dt}{m} $$
(3.57)

The stoichiometric capacity of the bed (q eq ) can be calculated by integrating Eq. (3.57) to the point that the concentration of the effluent outlet (C t ) is identical to the inlet concentration (C 0). In this case, this adsorption capacity is associated with complete bed saturation. Theoretically, the time stoichiometric tends to infinity, and its precise location involves trial and error. The stoichiometric capacity of the column can also be obtained from equilibrium isotherm, as described in Chap. 2.

Already the column useful capacity (q b ) occurs when the concentration of effluent outlet (C t ) reaches the concentration of break of the column (C b ). Then, q b is obtained by integrating Eq. (3.57) to the breakthrough time (t b ).

For the design of fixed-bed adsorption systems, the useful length of the bed (L) can be calculated from a mass balance, considering a convex isotherm (i.e., Langmuir or Freundlich), using the mass of solute fed into the column with respect to the adsorption capacity of the adsorbent (in units of mass per volume of adsorbent, or q 0 /ρ), described by

$$ L=\frac{QC_0{t}_s}{S_0\left(1-\varepsilon \right)\raisebox{1ex}{${q}_0$}\!\left/ \!\raisebox{-1ex}{$\rho $}\right.} $$
(3.58)

In Eq. (3.58), the dividend represents the mass of solute fed in a service time (t s ) and the divisor the amount of accumulated mass per unit of bed length. Introducing the concept of hydraulic load (H), denoted by the ratio between the volumetric flow rate (Q) and the cross-sectional area (S 0) of the bed, or H = εv z  = Q/S 0, the equation can be rewritten as

$$ L=\frac{HC_0{t}_s}{\left(1-\varepsilon \right)\raisebox{1ex}{${q}_0$}\!\left/ \!\raisebox{-1ex}{$\rho $}\right.} $$
(3.59)

However, the useful length of the bed (L) considers a sharp breakthrough curve. As previously discussed, the shape of the breakthrough curve changes according to the rates of mass transfer and reaction with the adsorption sites. Thus, in order for the system to meet the design conditions, an extra length must be added to the bed.

For the calculation of the extra length of the bed, two methodologies will be presented: the length of unused bed (LUB) and the bed depth service time (BDST). These methods, performed on a laboratory scale, are intended to calculate the fraction of the column required for the reduction of the initial concentration to the acceptable design conditions and are related to the length of the mass transfer zone.

Moreover, in the scale-up of bed from laboratory data (isotherms or breakthrough curves), it is fundamental that the conditions like hydraulic load, pH, temperature, and concentration are similar.

3.3.3.1 LUB Concept

In this way, the length of unused bed (LUB) is a relation between the stoichiometric capacity (q eq ) and the useful capacity of the column (q b ). Associating the two equations, it has the following:

$$ LUB=\left(1-\frac{q_b}{q_{eq}}\right) z=\left(1-\frac{t_b}{t^{\ast }}\right) z $$
(3.60)

3.3.3.2 Bed Depth Service Time (BDST)

BDST model was used to describe the fixed-bed adsorption column operation (Hutchins 1973). This approach becomes useful if the bed depth-breakthrough time data determined from a set of curves with different bed sizes is analyzed using the irreversible isotherm model. The BDST model is expressed as

$$ \ln \left(\frac{C_0}{C_t}-1\right)=\frac{kq_0 D\left(1-\varepsilon \right)}{\varepsilon {v}_z}- kC{}_0 t $$
(3.61)

Note that q 0(1−ε) is the adsorption capacity of the bed per volumetric unit, denoted by N 0. Thus, rearranging the equation, the breakthrough time (t b ) is

$$ {t}_b=\frac{N_0}{\varepsilon {vC}_0} D-\frac{ \ln \left(\frac{C_0}{C_b}-1\right)}{k{ C}_0} $$
(3.62)

where C b is the breakthrough concentration. As can be seen, this equation suggests that the rupture time (t b ) has a linear relationship with the length of the column (D). For this case, the critical situation for operation is t b  = 0. Thus, the critical bed depth of the column (D 0) can be calculated by

$$ {D}_0=\frac{\varepsilon v}{kN_0} \ln \left(\frac{C_0}{C_b}-1\right) $$
(3.63)

or the service time (t s ) of a bed with length D can be expressed by

$$ {t}_s=\frac{N_0}{\varepsilon {vC}_0}\left( D-{D}_0\right) $$
(3.64)

3.4 Numerical Methods and Parameters Estimation

Numerical solution of diffusional mass transfer models requires the application of the numerical method of lines to solve partial differential equations (Ocampo-Pérez et al. 2010; Souza et al. 2017) which can be expressed as a system of simultaneous ordinary differential equations. For batch systems , the boundary conditions can be expressed as implicit single algebraic equations, and the Newton method can be used to solve those (Souza et al. 2017). In this case, the mass transport parameters can be either calculated, such as external mass transfer coefficient, molecular diffusivity, effective pore volume diffusion coefficient, and tortuosity factor (Leyva-Ramos et al. 2012; Ocampo-Pérez et al. 2012), or estimated by nonlinear least-square optimization , such as surface diffusion coefficient and external mass transfer coefficient (Ocampo-Pérez et al. 2010; Souza et al. 2017). For fixed bed, the mass transport parameters can also be either calculated, such as fluid interstitial velocity and voids of the bed, or estimated by nonlinear least-square optimization, such as axial dispersion or diffusion coefficient.

The prediction of adsorption reaction models and empirical models for breakthrough curves depends on parameters whose values must be estimated from available experimental (Largitte and Pasquier 2016).

3.4.1 Solving Diffusional Mass Transfer Models

The numerical method of lines utilizes ordinary differential equations for the time derivative and finite differences on the spatial derivatives (Schiesser 1991). In finite difference method , the derivatives in the partial differential equation are approximated by linear combinations of function values at the grid points. The derivatives in the partial differential equation of diffusional transfer models are discretized into N + 1 points on the spatial derivatives (radius), where N is the number of grid points.

Figure 3.3 shows the illustrative representation of discretization (grid points) of the transport of adsorbate molecules from the bulk solution to the spherical particle. In this way, it has C r in different points i where i = 0 is the grid point at r = 0 and i = N + 1 is the grid point at r = R. The grid points are spaced equally with the step size given by following equation:

$$ H=\frac{R}{N+1} $$
(3.65)
Fig. 3.3
figure 3

Discretization of the transport of the adsorbate molecules from the bulk solution to the spherical particle (illustrative representation)

Full size image

The partial differential equation of diffusional transfer models can be rewritten using the second-order central difference approximations of the first and second derivative. The second-order forward difference approximations of the first derivative can be used to solve the boundary condition at r = 0, and the second-order backward difference approximations of the first derivative can be used to solve the boundary condition at r = R (Souza et al. 2017). Useful finite approximations are shown in Table 3.1.

Table 3.1 Finite approximation functions used to solve the partial differential equations
Full size table

Implicit single algebraic equations are resulting from solving the boundary conditions with finite difference approximations. The most common method for solving nonlinear algebraic equations is the Newton method (Edgar and Himmelblau 2001). Trust-region modification of Newton method (Sorensen 1982) is the basis for the MATLAB built-in routine fsolve (Beers 2007).

Discretized partial differential equations yield ordinary differential equation systems that are very stiff; therefore, to avoid a very small time step, an implicit method can be used, as the backward difference formula (BDF) (Gear 1971). The MATLAB built-in routine ode15s is a variable order solver based on the numerical differentiation formulas (NDFs) . Optionally, it uses the backward differentiation formulas (BDF, also known as Gear method ) that are usually less efficient (Shampine and Reichelt 1997).

Nonlinear least-square optimization can be used to estimate the mass transport parameters. The nonlinear least-square objective function to be minimized is defined as the sum of the differences between the experimental data (C) and model data (Ĉ) of adsorbate concentration, given as

$$ \min \left|\kern0.2em f(p)\right|={\sum_{j=1}^{NE}\sum_{i=1}^{NY}\left[{C}_{\left( i, j\right)}-{\hat{C}}_{\left( i, j\right)}\right]}^2 $$
(3.66)

where NE is the number of experiments, NY is the number of experimental data points, and p is the mass transport parameter .

The mass transport parameter (p) can represent:

  1. (a)

    Surface diffusion coefficient : using pore volume and surface diffusion model (PVSDM), surface diffusion model (SDM), and homogeneous surface diffusion model (HSDM) for batch systems

  2. (b)

    External mass transfer coefficient : using the external mass transfer model (EMTM) for batch systems

  3. (c)

    Axial dispersion or diffusion : using the mass transfer model for fixed-bed column

The MATLAB built-in routine lsqnonlin solves nonlinear least-square (nonlinear data-fitting) problems with optional lower and upper bounds on the parameters (p). By default, lsqnonlin chooses the trust-region-reflective algorithm that is a subspace trust-region method and is based on the interior-reflective Newton method (Coleman and Yi 1994, 1996). Each iteration involves the approximate solution of a large linear system using the method of preconditioned conjugate gradients (PCG) (Barrett et al. 1994).

The mass transport parameter is estimated with intervals of 95% of confidence. Simulations are performed using the diffusional transfer models with the estimated parameter to compare to each set of experimental data and, hence, to check the fit accuracy. The Student t-test can be performed to find out if the means of the adsorbate concentration experimental curve and of the adsorbate concentration curve predicted by the model are significantly different. Further, the χ2 and the Fisher exact test are also useful to verify if variances of the experimental and model concentration data differ in any interesting way (Schwaab and Pinto 2007).

3.4.2 Solving Adsorption Reaction Models and Empirical Models for Breakthrough Curves

It is common to use linear regression (also known as linear least-square analyses ) to estimate the values of the parameters of an adsorption reaction model. However, the sorption data are better simulated when the adsorption reaction models are fitted by nonlinear regression (Largitte and Pasquier 2016).

Whereas an adsorption reaction model can be directly used in nonlinear regression, it must be linear with respect to the parameters to be used in linear regression. Very often, a linear relationship is hypothesized between a log transformed of the dependent variable and the model parameters.

The nonlinear least-square objective function to be minimized is defined as the sum of the differences between the experimental data (y) and model data (ŷ) of adsorbate adsorbed at time t, given as below:

$$ \min \left|\kern0.2em f(p)\right|={\sum_{j=1}^{NE}\sum_{i=1}^{NY}\left[{y}_{\left( i, j\right)}-{\hat{y}}_{\left( i, j\right)}\right]}^2 $$
(3.67)

In case of adsorption reaction models, y is the adsorbate adsorbed at time t. Here, p is the kinetic parameter that can represent:

  1. (a)

    Adsorption rate constant : using pseudo-first-order model and pseudo-second-order model

  2. (b)

    Desorption rate constant and initial adsorption rate : using Elovich equation

In the case of empirical models for breakthrough curves, y is the ratio of concentration of the effluent outlet (C t ) and the inlet concentration (C 0). Here, p represents the parameters set of the chosen empirical model for breakthrough curves.

The MATLAB built-in routine nlinfit solves nonlinear regression (nonlinear data-fitting). For non-robust estimation, nlinfit uses the Levenberg-Marquardt nonlinear least-square algorithm (Levenberg 1944; Marquardt 1963; Moré 1977).

The kinetic parameter can be estimated with intervals of 95% of confidence. Simulations are performed using the adsorption kinetic models with the estimated parameter to compare to each set of experimental data and, hence, to check the fit accuracy. The coefficient of determination ( R 2) and Akaike information criterion (AIC) are also calculated. The Student t-test is used to find out if the means of the experimental data and of the predicted data by the model are significantly different. Further, the χ2 and the Fisher exact test can be also performed to verify if variances of the experimental and model data differ (Schwaab and Pinto 2007).

3.5 Conclusion

This chapter presented a general description of the adsorption kinetics in liquid phase, considering batch and fixed-bed systems. For discontinuous batch adsorption systems, it was verified that the kinetic curves can be represented by diffusional mass transfer models and adsorption reaction models. Diffusional mass transfer models are based on mass transfer steps, while adsorption reaction models consider adsorption as a reaction. In this way, we believe that diffusional mass transfer models are more suitable. For the breakthrough curves obtained in fixed-bed systems, the same analogy can be made, being more useful the mass transfer-based models. Furthermore, it was reviewed that LUB and BDST concepts are adequate for design and scale-up of adsorption systems. Finally, several numerical methods and parameter estimation techniques were presented and discussed in order to better understand the treatment of the experimental adsorption data using batch and fixed-bed columns.