1 Introduction

Sir Geoffrey Ingram Taylor (1886–1975) [4] was—together with Ludwig Prandtl (1875–1953)—the probably most influential individual in the field of fluid dynamics in the central period of the last century. Among the various phenomena that today bear his name are Taylor-Couette flow, Rayleigh-Taylor instability, Taylor dispersion, and Taylor bubbles. Concerning the last topic, Taylor studied in two seminal papers the motion of large bubbles rising through tubes [9] and the displacement of liquid in a tube by a bubble [23]. An important earlier contribution on the topic originates from Dumitrescu [10], a student of Prandtl. The earliest photos of Taylor bubbles are probably due to Gibson [13], Fig. 19.1, who noted more than a century ago

… when the diameter is about 0.75 that of the tube the bubble begins to adopt a more or less cylindrical form with an ogival head and a flat stern, and the motion becomes steady. Any further increase in the volume is mainly effective in increasing the length of the cylindrical portion of the body, the form of the head remaining sensibly unchanged, and the mean diameter, although increasing with length, not altering greatly.

Taylor bubbles are encountered in various industrial applications such as aerated chemical or bio-chemical reactors and boiling of water in nuclear rod bundles, and in natural phenomena such as in volcanic eruptions [22], where they are usually called gas slugs.

Fig. 19.1
figure 1

Photos of Taylor bubbles rising in a vertical tube (diameter d). Left: d = 1. 68 cm, reprinted from [13], with permission from Taylor & Francis Ltd. Right: d = 7. 9 cm, reprinted from [9], with permission from The Royal Society

Full size image

With the significant advancement of microfabrication techniques during the last decades, gas-liquid two-phase flows in small channels came into focus in various fields like micro process engineering, lab-on-a-chip systems and material synthesis. In these applications, rather than a single bubble, a sequence of Taylor bubbles is of interest where the neighboring bubbles are separated by liquid slugs, see Fig. 19.2. This flow pattern is known as Taylor flow but is sometimes also referred to as bubble-train flow, segmented flow or capillary slug flow. The hydraulic diameter is typically below a few mm so that gravitational effects are often negligible. The flow is, therefore, usually pressure-driven and, due to the small dimensions, laminar. Taylor flow has distinct advantages especially for chemical process engineering:

  • Large interfacial area per unit volume → efficient heat and mass transfer.

  • Axial segmentation of the liquid phase → reduced axial dispersion and narrow residence time distribution.

  • Recirculation in liquid slug → good mixing and wall-normal convective transport in laminar flow.

  • Thin liquid film → short diffusion path of educts from the bubble to the catalytic wall.

Several aspects of this list will be detailed in the sequel. For a more complete discussion than is possible in this short overview, and for topics not covered here, such as pressure drop, heat transfer, etc., the interested reader is referred to recent reviews on gas-liquid Taylor flow [2, 14, 15].

Fig. 19.2
figure 2

Bubble formation for different volumetric flow rates of water (Q L) and air (Q G) in a 100 μm square channel leading to Taylor flow. In subfigures (1)–(4), Q L is decreased while Q G is increased. Reprinted figure with permission from [8] © 2005 by the American Physical Society, doi: 10.1103/PhysRevE.72.037302

Full size image

2 Hydrodynamics

The hydrodynamics of Taylor bubbles in small channels is dominated by viscous forces and surface tension forces. The capillary number Ca = μ L U B∕σ represents the ratio of both forces and is the relevant non-dimensional parameter. Here, U B is the bubble velocity, μ L the dynamic viscosity of the liquid and σ is the coefficient of surface tension. At higher velocities, inertial effects become important which can be characterized by the Reynolds number Re = ρ L d h U B∕μ L. Here, ρ L is the liquid density and d h the hydraulic diameter. The influence of gravitational forces can be estimated by the Eötvös number Eo = (ρ L −ρ G)gd h 2∕σ. Due to the proportionality Eo ∝ d h 2, the importance of gravity diminishes quickly as the channel size is reduced.

Fig. 19.3
figure 3

Sketch of Taylor flow. (a) Lateral view for Taylor flow in a circular channel. (b) Cross-sectional view in the middle of a Taylor bubble in a circular channel (d h = d). (c) Cross-sectional view in the middle of a Taylor bubble in a square channel (d h = h)

Full size image

2.1 Bubble Shape and Liquid Film Thickness

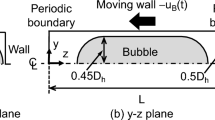
Figure 19.3a, b shows a sketch of Taylor flow in a circular channel and related geometrical dimensions. A key parameter for technical applications with Taylor flow is the thickness of the liquid film δ F. In circular channels, the liquid film is azimuthally uniform and its thickness is well described by the relation

$$\displaystyle{ \frac{\delta _{\mathrm{F}}} {d} = \frac{0.66\,Ca^{2/3}} {1 + 3.33\,Ca^{2/3}} }$$
(19.1)

This correlation is valid for capillary numbers below about 1, supposed inertia is negligible [3]. For capillary numbers smaller than 0.001, Eq. (19.1) approaches the result δ F∕d = 0. 66 Ca 2∕3 from Bretherton’s lubrication analysis for a semi-infinite bubble [6]. The effect of inertia (Re) on the film thickness is small but non-monotonic, see e.g. [2] for a detailed discussion.

The capillary number also has a large influence on the shape of the front and rear meniscus of the Taylor bubble. At very small capillary numbers, the bubble front and rear form hemispherical caps. As Ca increases, the curvature of the front meniscus increases so that the bubble nose gets more pointed while the curvature of the rear meniscus decreases (i.e., the bubble rear flattens) and may become even negative (concave shape). While inertia has a small effect on the shape of the front meniscus, the influence of Re on the rear meniscus can be quite substantial [12].

The bubble length L B and the liquid slug length L S depend both on the gas and liquid volumetric flow rates, cf. Fig. 19.2, and on the type of device used for bubble generation, see e.g. [15]. Often, T-junctions, Y-junctions or cross-junctions such as in Fig. 19.2 are used. One bubble and one liquid slug form a unit cell of the Taylor flow with length L UC.

In square channels, the liquid film thickness is azimuthally non-uniform and the situation is more complex than in circular tubes. Concerning the bubble shape, two regimes can be distinguished. When the capillary number is larger than about 0.04, the bubble is axisymmetric and its cross-sectional shape is circular. For smaller capillary numbers, the bubble is not axisymmetric. In this case there exist liquid regions in the four channel corners which are connected by thin flat films at the channel sides, see Fig. 19.3c. Correlations for the lateral and diagonal film thickness and bubble diameter are given by Kreutzer et al. [18].

The velocity U S in Fig. 19.3a denotes the mean liquid axial velocity in a cross-section within the slug, while U F denotes the mean liquid axial velocity in a cross-section within the film. By a liquid mass balance in a frame of reference moving with the bubble it follows that

$$\displaystyle{ (U_{\mathrm{S}} - U_{\mathrm{B}})A = (U_{\mathrm{F}} - U_{\mathrm{B}})A_{\mathrm{F}} }$$
(19.2)

Here, A is the area of the channel cross-section and A F is the cross-sectional area of the liquid film. Equation (19.2) is valid for circular and square channels and any other cross-sectional channel shapes as well. It reveals that the area of the liquid film and the mean velocity in the liquid film are closely related to the bubble velocity and to U S, which is in Taylor flow equal to the total superficial velocity (Q L + Q G)∕A of the two-phase flow.

2.2 Recirculation in the Liquid Slug

In his 1961 paper, Taylor [23] proposed qualitative sketches of the flow streamlines in the liquid slug ahead of the bubble. At high Ca, the bubble velocity is larger than the maximum velocity in the liquid slug on the axis of the tube (U L,max). In a reference frame co-moving with the bubble, then complete bypass flow occurs, see Fig. 19.4a. At small Ca, it is U B < U L,max and a recirculation pattern occurs in the tube center, see Fig. 19.4b. Both patterns have later been confirmed experimentally [7] and numerically [20, 25].

For a liquid slug with a fully developed laminar velocity profile it is U L,max = C × U S. The value of the constant C depends on the shape of the channel cross-section. For a circular channel it is C = 2 while for a square channel it is C = 2. 096. The condition for recirculation flow thus becomes U L,max < C × U S and occurs at Ca ≈ 0. 7 in horizontal circular tubes.

The cross-sectional regions with bypass flow close to the wall and with recirculation flow in the channel center are separated by the “dividing streamline” [24], see Fig. 19.4b. The position of the dividing streamline is obtained from the condition that the total flow rate within the recirculation area is zero in the moving frame of reference. In a cross-section of a liquid slug with fully developed velocity profile, the size of the recirculation region depends on the velocity ratio U B∕U S and C only, and increases as the velocity ratio decreases [17].

Fig. 19.4
figure 4

Sketch of possible liquid streamlines in a reference frame co-moving with the bubble. (a) Complete bypass flow, (b) recirculation flow with paths for mass transfer. Figure adapted from [18, 23]

Full size image

3 Mass Transfer and Marangoni Effects

The large interfacial area per unit volume, the thin liquid film, and the recirculation vortex in the liquid slug make Taylor flow attractive for mass transfer applications as well as for heterogeneous chemical reactions, where the channel walls are coated with a catalytic washcoat layer. A detailed review on the latter topic is given by Haase et al. [15]. The mass transfer of chemical species (educts) from the gas bubble to the solid wall takes place by two different paths, see Fig. 19.4b. The first path is given by the mass transfer from the bubble body into the liquid film and through the liquid film toward the wall. The second path is given by the mass transfer from the front and rear caps of the bubble into the liquid slug and from the liquid slug towards the wall.

In the second path, the educts need to cross the dividing streamline which is possible only by diffusion. Important in this context is the speed at which the liquid in the vortex inside the recirculation zone moves, as this will affect mixing. The intensity of this recirculation can be quantified by the dimensionless recirculation time [24]. This quantity is defined as the ratio of the time needed by a liquid fluid element to move from one end of the liquid slug to the other end, and the time needed by the liquid slug to travel a distance of its own length.

As Taylor flow is dominated by surface tension effects, even small amounts of surface-active agents (surfactants) or contaminants can have a large impact. The presence of surfactants or contaminants on the gas-liquid interface changes surface tension and, therefore, the capillary number. Gradients of the concentration of surfactants cause gradients in surface tension which induces so-called Marangoni stresses. The largest concentration gradients are found near the stagnation rings on the bubble nose where the dividing streamline reaches the interface, see Fig. 19.5. Due to these effects, surfactants and contaminants can locally modify the “boundary conditions” at the interface, which may vary between the limits free-slip and no-slip.

Fig. 19.5
figure 5

Sketch of the surface concentrations and the interaction with the fluid flow. Reprinted from [18], © (2005), with permission from Elsevier

Full size image

4 Guiding Measure Taylor Flow in the SPP 1506

For interface resolving simulations of two-phase flows, various numerical methods are available, see e.g. [26]. Among the most often used methods are the volume-of-fluid method, the level-set method and the front-tracking method. For testing the accuracy of interface resolving simulation methods, artificial test problems such as the rotation of Zalesak’s slotted disk are often used. Furthermore, two benchmark configurations which model two-dimensional bubbles rising in liquid columns have been proposed for quantitative comparison of interfacial flow codes [16]. While these test cases are certainly useful, they are essentially pure numerical exercises. For the advancement of numerical methods for interfacial flows towards valuable tools for engineering applications, however, a validation by experimental data for real physical flow problems is desirable. Clearly, there is a lack in literature as suitable local experimental data which allow for a detailed validation on practical flow problems are missing.

One goal of the guiding measure in SPP 1506 was, therefore, to undertake a step to fill this gap by providing such data for the flow of Taylor bubbles in small channels. This specific flow problem was chosen for the following reasons:

  • Taylor flow is of practical technical relevance.

  • Taylor flow is of fundamental physical interest as it constitutes a prototypical problem for the non-linear interaction between viscous, inertial and surface tension forces under geometric constraints.

  • Taylor flow allows the study of hydrodynamics and mass transfer in a relatively simple experimental set-up.

  • Taylor flow allows for an increase in the complexity of the flow and bubble shape by variation of the channel cross-section (circular and square).

  • Taylor flow hydrodynamics is controlled by one main parameter, i.e., the capillary number. For a certain liquid phase, Ca can be varied by about 1–2 orders of magnitude by variation of the bubble velocity. An even larger variation is possible by using liquids of different viscosity.

For serving as a suitable measure for validation of numerical methods and computer codes, the experiments and measurements—which will be presented in the next two chapters of this book—fulfill the following requirements:

  • Experiments are performed in circular [5] and square channels [5, 21] under well-defined and well-documented conditions which allow a detailed recalculation. This encompasses information about:

    • Thermo-physical properties of both phases.

    • Liquid and gas volumetric flow rates of both phases.

    • Geometrical flow parameters such as the volume of a single Taylor bubble and L B and L S for Taylor flow. The variation of both lengths in the experiment is sufficiently small to resemble “ideal” Taylor flow.

    • Conditions to be applied at all boundaries of the computational domain.

  • Measurements provide detailed local experimental data which allow for a quantitative validation of numerical methods and computer codes:

    • Local profiles of bubble shape (in square channel: lateral and diagonal) [5].

    • Local profiles of velocity field in liquid film and liquid slug (in square channel: lateral and diagonal) [21].

For numerical computations, there exist the following advantages (first two bullets) as well as challenges (last bullet) of Taylor flow:

  • The numerical simulations can be either 2D axisymmetric (circular channel, which limits the computational costs) or 3D (square channel with optional symmetry assumptions).

  • Both, a single Taylor bubble and Taylor flow can well be represented in numerical computations by using either inlet/outlet conditions in combination with a co-moving reference frame (single Taylor bubble) or by considering a unit cell in combination with periodic boundary conditions (ideal Taylor flow).

  • Challenging for numerical simulations are the adequate resolution of the thin liquid film and the large local interface curvature at the rear part of the liquid film as well as very thin concentration boundary layers if mass transfer is considered.

An overview of the numerical simulations [1, 11, 19] performed within the SPP 1506 concerning the guiding measure Taylor flow are presented in two subsequent chapters of this book. One chapter covers 2D planar simulations as well as axisymmetric simulations for circular pipes, while the other chapter is on 3D simulations for square channels.

5 Conclusions

The laminar flow of Taylor bubbles in small channels is of interest for various technical applications. Taylor flow in circular and square channels is also well suited to study complex interfacial hydrodynamics in confined geometry resulting from the interplay between surface tension, viscous forces and inertia in a relatively simple set-up. Carefully designed experiments on single Taylor bubbles and Taylor flow are well suited for providing local experimental data on the bubble shape and liquid velocity field which are needed for a detailed quantitative validation of numerical methods and computer codes for interface resolving simulations.

In the following chapters, the progress achieved in this context within the SPP 1506 is highlighted. The experimental data and selected numerical data gained in the course of the SPP 1506 guiding measure Taylor flow are provided online on the website of the SPP 1506, see www.dfg-spp1506.de. It is hoped that they will be useful for the entire computational multiphase fluid dynamic community.

The subject is further developed in the DFG Priority Programme SPP 1740 “Reactive Bubbly Flows” where Taylor flow serves as a guiding measure as well. Taylor flow is also attractive to investigate further interfacial phenomena not covered in both SPPs. These include the controlled coalescence of two Taylor bubbles with different volumes. The trailing smaller Taylor bubble is moving in regions with larger velocity as compared to the leading larger bubble so that the distance between both bubbles decreases and finally leads to contact and coalescence. Furthermore, thermal Marangoni effects in Taylor flow could be studied by heating one or more walls of a square channel.