Representable Hierarchical Clustering Methods for Asymmetric Networks

Abstract

This paper introduces the generative model of representability for hierarchical clustering methods in asymmetric networks, i.e., the possibility to describe a method through its action on a collection of networks called representers. We characterize the necessary and sufficient structural conditions needed on these representers in order to generate a method which is scale preserving and admissible with respect to two known axioms and, based on this result, we construct the family of cyclic clustering methods.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The relevance of clustering in modern data analysis is indubitable given its usage in multiple fields of knowledge from, e.g., medicine [22] to marketing [16]. There are literally hundreds of methods that can be applied to the determination of hierarchical [8, 11] and non-hierarchical clusters in finite metric (thus symmetric) spaces—see, e.g., [17]. Even in the case of asymmetric networks [18], multiple methods have been developed to extend the notion of clustering into this less intuitive domain [1, 7, 14, 15, 19, 20]. Although not as developed as its practice [6], the theoretical framework for clustering has been developed over the last decade for non-hierarchical [2, 3, 10, 12, 13, 21, 24] and hierarchical clustering [2, 4, 5]. Of special interest to us is this last direction, where two axioms were used to determine a bounded family of admissible clustering methods for asymmetric networks. However, we consider that admissibility is an insufficient characterization criterion to identify clustering methods of practical importance, thus, we introduce additional features with the objective to further winnow the space of admissible methods.

In the current paper, we introduce and analyze the notion of representability for hierarchical clustering methods. A representable method is one that can be specified by determining its action on a collection of networks called representers. Our main characterization result [cf. Theorem 2] states the conditions needed on these representers to obtain an associated clustering method with desirable practical properties. In Sect. 3, we present the notion of scale preservation and highlight its practical utility. In Sect. 4 we introduce the concept of representability through a reinterpretation of reciprocal clustering and build upon this to develop a more general theory. We also connect representability to the more practical concepts of scale preservation and admissibility (Sect. 4.2), and we introduce the family of cyclic clustering methods (Sect. 4.3).

Proofs, algorithmic details, and computational results are omitted due to space constraints.

2 Preliminaries

We define a network N as a pair (X, A _X ) where X is a set of n points or nodes and $A_{X}: X \times X \rightarrow \mathbb{R}_{+}$ is a dissimilarity function. Dissimilarities A _X (x, x′) from x to x′ are nonnegative, null if and only if x = x′, need not satisfy the triangle inequality and may be asymmetric, i.e., A _X (x, x′) ≠ A _X (x′, x) for some x, x′ ∈ X. We focus our study on asymmetric networks since these general structures include, as particular cases, symmetric networks and finite metric spaces.

The output of hierarchically clustering a network N = (X, A _X ) is a dendrogram D _X , i.e., a nested collection of partitions D _X (δ) indexed by a resolution parameter δ ≥ 0 [9]. Dendrograms can be represented as trees. The interpretation of a dendrogram is that of a structure which yields different clusterings at different resolutions.

Given a network (X, A _X ) and x, x′ ∈ X, a chain C(x, x′) is an ordered sequence of nodes, C(x, x′) = [x = x ₀, x ₁, …, x _l−1, x _l = x′], which starts at x and finishes at x′. The cost of chain C(x, x′) is defined as the maximum dissimilarity $\max _{i\vert x_{i}\in C(x,x')}A_{X}(x_{i},x_{i+1})$ encountered when traversing its links in order. We define the directed minimum chain cost $\tilde{u}_{X}^{{\ast}}(x,x')$ between x and x′ as the minimum cost among all the chains connecting x to x′,

$$\displaystyle{ \tilde{u}_{X}^{{\ast}}(x,x') =\min _{ C(x,x')}\,\,\max _{i\vert x_{i}\in C(x,x')}A_{X}(x_{i},x_{i+1}). }$$

(1)

An ultrametric u _X on the set X is a function $u_{X}: X \times X \rightarrow \mathbb{R}_{+}$ that satisfies symmetry u _X (x, x′) = u _X (x′, x), identity u _X (x, x′) = 0 ⇔ x = x′, and the strong triangle inequality

$$\displaystyle{ u_{X}(x,x') \leq \max \big (u_{X}(x,x''),u_{X}(x'',x')\big), }$$

(2)

for all x, x′, x″ ∈ X. It can be shown that dendrograms and finite ultrametric spaces are equivalent [2], where the ultrametric value between two points is given by the resolution at which they first merge in the dendrogram. However, ultrametrics are more convenient than dendrograms for the results developed in this paper.

Remark 1.

For the particular case when N is a finite metric space, the minimum chain cost (1) is an ultrametric and coincides with the ultrametric output of the single linkage clustering method [5].

A hierarchical clustering method is defined as a map $\mathcal{H}: \mathcal{N} \rightarrow \mathcal{D}$ from the space of networks $\mathcal{N}$ to the space of dendrograms $\mathcal{D}$, or, equivalently, as a map $\mathcal{H}: \mathcal{N} \rightarrow \mathcal{U}$ from $\mathcal{N}$ to the space $\mathcal{U}$ of networks with ultrametrics as dissimilarity functions. This loose definition permits the existence of an ample diversity of methods, many of them carrying limited practical utility. Thus, we recall an axiomatic construction formulated to determine a subclass of admissible clustering methods.

2.1 Admissible Hierarchical Clustering Methods

In [4, 5], the authors impose the two following requirements on clustering methods:

(A1) Axiom of Value

Consider a two-node network N = (X, A _X ) with X = {p, q}, A _X (p, q) = α, and A _X (q, p) = β. The ultrametric $(X,u_{X}) = \mathcal{H}(N)$ output by $\mathcal{H}$ satisfies u _X (p, q) = max(α, β).

(A2) Axiom of Transformation

Given networks N _X = (X, A _X ) and N _Y = (Y, A _Y ) and a dissimilarity reducing map ϕ: X → Y, that is a map ϕ such that for all x, x′ ∈ X it holds A _X (x, x′) ≥ A _Y (ϕ(x), ϕ(x′)), the output ultrametrics $(X,u_{X}) = \mathcal{H}(X,A_{X})$ and $(Y,u_{Y }) = \mathcal{H}(Y,A_{Y })$ satisfy u _X (x, x′) ≥ u _Y (ϕ(x), ϕ(x′)).

Axiom (A1) states that in a network with two nodes p and q, the dendrogram D _X has them merging at the maximum value of the two dissimilarities α and β. This is reasonable because at resolutions δ < max(α, β) one node can influence the other but not vice versa, which in most situations means that the nodes are not alike. Axiom (A2) states that a contraction of the dissimilarity function A _X entails a contraction of the ultrametric u _X .

A hierarchical clustering method $\mathcal{H}$ is admissible if it satisfies axioms (A1) and (A2). Two admissible methods of interest are reciprocal and nonreciprocal clustering. The reciprocal clustering method $\mathcal{H}^{\text{R}}$ with output $(X,u_{X}^{\text{R}}) = \mathcal{H}^{\text{R}}(X,A_{X})$ is the one for which the ultrametric u _X ^R(x, x′) between points x and x′ is given by

$$\displaystyle{ u_{X}^{\text{R}}(x,x') =\min _{ C(x,x')}\,\max _{i\vert x_{i}\in C(x,x')}\bar{A}_{X}(x_{i},x_{i+1}), }$$

(3)

where $\bar{A}_{X}(x,x') =\max (A_{X}(x,x'),A_{X}(x',x))$ for all x, x′ ∈ X. Intuitively, in (3) we search for chains C(x, x′) linking nodes x and x′. Then, for a given chain, walk from x to x′ and determine the maximum dissimilarity, in either the forward or backward direction, across all links in the chain. The reciprocal ultrametric u _X ^R(x, x′) is the minimum of this value across all possible chains; see Fig. 1. We define the nonreciprocal clustering method $\mathcal{H}^{\text{NR}}$ as one where the ultrametric between x and x′ is given by the maximum of the directed minimum chain costs (1) in both directions

$$\displaystyle{ u_{X}^{\text{NR}}(x,x') =\max \Big (\tilde{u}_{ X}^{{\ast}}(x,x'),\ \tilde{u}_{ X}^{{\ast}}(x',x)\Big). }$$

(4)

In (4) we implicitly consider forward chains C(x, x′) going from x to x′ and backward chains C(x′, x) from x′ to x. We then determine the respective maximum dissimilarities and search independently for the forward and backward chains that minimize the respective maximum dissimilarities. The nonreciprocal ultrametric u _X ^NR(x, x′) is the maximum of these two minimum values; see Fig. 2. Reciprocal and nonreciprocal clustering bound the range of ultrametrics generated by any other admissible method $\mathcal{H}$.

Fig. 1

Reciprocal clustering. x, x′ cluster at resolution δ if they are joined by a bidirectional chain of max. dissimilarity δ [cf. (3)]

Fig. 2

Nonreciprocal clustering. x, x′ cluster at resolution δ if they are joined in both directions by chains of max. dissimilarity δ [cf. (4)]

Theorem 1 (​​[4]).

Given any network N = (X, A _X ) and the associated reciprocal u _X ^R and nonreciprocal u _X ^NR ultrametrics as defined in  (3) and  (4). Then, for any admissible method $\mathcal{H}$ , the output ultrametric $(X,u_{X}) = \mathcal{H}(X,A_{X})$ is such that u _X ^NR(x, x′) ≤ u _X (x, x′) ≤ u _X ^R(x, x′) for all x, x′.

3 Scale Preservation

In this section we begin to explore additional conditions to winnow the space of admissible methods. One such condition is the concept of a scale preserving hierarchical clustering method.

(P1) Scale Preservation

Consider a network N _X = (X, A _X ) and a nondecreasing function $\psi: \mathbb{R}_{+} \rightarrow \mathbb{R}_{+}$ with ψ(0) = 0, ψ(z) > 0 for all z > 0 and lim _{z → ∞} ψ(z) = ∞. Define the network N _X ^ψ = (X, ψ(A _X )) with the same set of nodes and dissimilarities transformed by ψ. A hierarchical clustering method $\mathcal{H}$ is said to be scale preserving if for an arbitrary network N _X = (X, A _X ) and a function ψ satisfying the above requirements, the outputs $(X,u_{X}) = \mathcal{H}(N_{X})$ and $(X,u_{X}^{\psi }) = \mathcal{H}(N_{X}^{\psi })$ satisfy u _X ^ψ = ψ ∘ u _X .

Scale preservation entails two consequences of practical relevance. First, since ultrametric outcomes vary according to the same function that transforms the dissimilarities, scale preserving methods are invariant with respect to units. Second, in some applications we may be interested in clustering a network of which we are given a similarity function instead of dissimilarities. In such case, in order to apply a dissimilarity based method, we must apply a decreasing function to the similarity information to transform it into dissimilarities. Scale preservation ensures that the structure of the clustering hierarchy does not depend on the decreasing function used to turn similarities into dissimilarities. This property is helpful in many practical instances. In, e.g., trust networks it is more natural for subjects to express their trust of neighbors rather than their distrust. In social networks, proximity indicators—like number of exchanged messages—are more common than distance indicators.

4 Representability

We build upon the notion of representable methods—introduced for non-hierarchical clustering in [3]—to specify the hierarchical clustering of arbitrary networks through the clustering of particular examples that we call representers. To explain the concept of a representable method we first present an alternative definition for the reciprocal ultrametric (3). Start by considering a given asymmetric network N = (X, A _X ) and define ↻₂ = ({ p, q}, A _p, q ) as a two-node network with both dissimilarities equal to 1. Define the λ-multiple of the network ↻₂ as the network λ ∗ ↻₂ = ({p, q}, λA _p, q ) whose underlying set is the same and its dissimilarities are linearly scaled by a given λ > 0. Further define the Lipschitz constant of a map ϕ: { p, q} → X from ↻₂ to N as

$$\displaystyle{ L(\phi;\circlearrowright _{2},N) =\max \left (A_{X}(\phi (p),\phi (q)),A_{X}(\phi (q),\phi (p))\right ), }$$

(5)

i.e., the maximum dissimilarity into which one of the unit dissimilarities in ↻₂ is mapped. For any nodes x, x′ ∈ X we define the optimal multiple $\lambda _{X}^{\circlearrowright _{2}}(x,x')$ between x and x′ with respect to ↻₂ as

$$\displaystyle{ \lambda _{X}^{\circlearrowright _{2} }(x,x')\! =\!\big\{\! L(\phi;\circlearrowright _{2},N)\,\vert \,\phi \!:\!\{ p,q\}\! \rightarrow \! X,\,x,x'\! \in \!\text{Im}(\phi )\big\}\!. }$$

(6)

Notice that $\lambda _{X}^{\circlearrowright _{2}}(x,x')$ is the minimum multiple needed for the existence of a dissimilarity reducing map with x and x′ in its image between a multiple of ↻₂ and N.

We define the representable clustering method $\mathcal{H}^{\circlearrowright _{2}}$ associated with the representer network ↻₂ as the method with ultrametric output $(X,u_{X}^{\circlearrowright _{2}}) = \mathcal{H}^{\circlearrowright _{2}}(N)$ given by

$$\displaystyle{ u_{X}^{\circlearrowright _{2} }(x,x') =\min _{C(x,x')}\ \max _{i\vert x_{i}\in C(x,x')}\lambda _{X}^{\circlearrowright _{2} }(x_{i},x_{i+1}), }$$

(7)

for all x, x′ ∈ X. Definition (7) is illustrated in Fig. 3.

Fig. 3

Representable method $\mathcal{H}^{\circlearrowright _{2}}$ with ultrametric output as in (7). For every pair x _i , x _i+1 of consecutive nodes in the chain C(x, x′) we multiply the network ↻₂ by the minimum multiple $\lambda _{X}^{\circlearrowright _{2}}(x_{i},x_{i+1})$ that allows the existence of a dissimilarity reducing map $\phi _{x_{i},x_{i+1}}$ containing nodes x _i and x _i+1 in its image. The maximum among all these multiples determines the cost of the chain C(x, x′). The value $u_{X}^{\circlearrowright _{2}}(x,x')$ is the minimum chain cost over all possible chains linking x to x′

It is immediate that the method $\mathcal{H}^{\circlearrowright _{2}}$ with output ultrametrics as in (7) is equivalent to reciprocal clustering $\mathcal{H}^{\text{R}}$ with output ultrametrics as in (3). Indeed, given a network N = (X, A _X ) and points x, x′ ∈ X, there are only two possible maps from λ ∗ ↻₂ to N containing nodes x and x′ in their images. One map takes p to x and q to x′ and the other reverses the images and takes p to x′ and q to x. However, either maps have the same Lipschitz constant as defined in (5), ensuring that the optimal multiple in (6) is well defined. Consequently, we obtain that

$$\displaystyle{ \lambda _{X}^{\circlearrowright _{2} }(x,x') =\max \left (A_{X}(x,x'),A_{X}(x',x)\right ) =\bar{ A}_{X}(x,x'). }$$

(8)

Comparing (7) with (3) and using the observation in (8) the equivalence $\mathcal{H}^{\text{R}} \equiv \mathcal{H}^{\circlearrowright _{2}}$ follows, i.e., $\mathcal{H}^{\text{R}}(N) = \mathcal{H}^{\circlearrowright _{2}}(N)$ for all networks N. Thus, we say that the reciprocal clustering method is represented by the network ↻₂. That is, if we consider ↻₂ as an interaction modality defining a basic clustering unit, the hierarchical clustering of a generic network follows from application of (7).

The definition in (7) is certainly more cumbersome than (3). However, the former can be generalized to cases in which we consider arbitrary representers in lieu of ↻₂ as we explain next.

4.1 Representable Hierarchical Clustering Methods

Generalizing $\mathcal{H}^{\circlearrowright _{2}}$ entails redefining the Lipschitz constant of a map and the optimal multiples so that they are calculated with respect to an arbitrary representer network ω = (X _ω , A _ω ) instead of ↻₂. In representer networks ω, we allow the domain dom(A _ω ) of the dissimilarity function A _ω to be a proper subset of the product space, i.e., we may have dom(A _ω ) ≠ X _ω × X _ω . This is a technical modification that allows representer networks to have some dissimilarities that can be interpreted as arbitrarily large. Generalizing (5), given an arbitrary network N = (X, A _X ) we define the Lipschitz constant of a map ϕ: X _ω → X from ω to N as

$$\displaystyle{ L(\phi;\omega,N) =\max _{\begin{array}{c}(z,z')\in \text{dom}(A_{\omega }) \\ z\neq z' \end{array}}\frac{A_{X}(\phi (z),\phi (z'))} {A_{\omega }(z,z')}. }$$

(9)

Notice that L(ϕ; ω, N) is the minimum multiple of the network ω such that the considered map ϕ is dissimilarity reducing from L(ϕ; ω, N) ∗ω to N. Further, observe that (9) reduces to (5) when ω = ↻₂. Notice as well that the maximum in (9) is computed for pairs (z, z′) in the domain of A _ω . Pairs not belonging to the domain could be mapped to any dissimilarity without modifying the value of the Lipschitz constant. Mimicking (6), for arbitrary nodes x, x′ ∈ X we define the optimal multiple λ _X ^ω(x, x′) between x and x′ with respect to ω as

$$\displaystyle{ \lambda _{X}^{\omega }(x,x')\! =\!\min \! \left \{L(\phi;\omega,N)\,\vert \,\phi \!:\! X_{\omega } \rightarrow X,\,x,x'\! \in \!\text{Im}(\phi )\!\right \}\!\!. }$$

(10)

This means that λ _X ^ω(x, x′) is the minimum Lipschitz constant among those maps that have x and x′ in its image. Observe that (10) reduces to (6) when ω = ↻₂.

Representable methods are generalized to cases in which we are given a nonempty set Ω of representer networks ω. In such case we define the function λ _X ^Ω by considering the infimum across all representers ω ∈ Ω,

$$\displaystyle{ \lambda _{X}^{\varOmega }(x,x')\ =\ \inf _{\omega \in \varOmega }\ \lambda _{X}^{\omega }(x,x'), }$$

(11)

for all x, x′ ∈ X. The value λ _X ^Ω(x, x′) is the infimum across all multiples λ > 0 such that there exists a dissimilarity reducing map from λ ∗ω to the network containing x and x′ in its image for some representer ω ∈ Ω. For a given network N = (X, A _X ), the representable clustering method $\mathcal{H}^{\varOmega }$ associated with the collection of representers Ω is the one with outputs $(X,u_{X}^{\varOmega }) = \mathcal{H}^{\varOmega }(X,A_{X})$ such that the ultrametric u _X ^Ω is given by

$$\displaystyle{ u_{X}^{\varOmega }(x,x') =\min _{ C(x,x')}\ \max _{i\vert x_{i}\in C(x,x')}\lambda _{X}^{\varOmega }(x_{ i},x_{i+1}), }$$

(12)

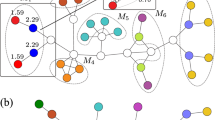
for all x, x′ ∈ X. The definition in (12) is interpreted in Fig. 4.

Fig. 4

A representable clustering method $\mathcal{H}^{\varOmega }$. The collection of representers Ω is composed by two representers ω ₁ and ω ₂ shown at the bottom of the figure. In order to compute the ultrametric value u _X ^Ω(x, x′) we link x and x′ through a chain, e.g., [x, x ₁, …, x ₆, x′] in the figure, and link pairs of consecutive nodes with multiples of the representers. We depict these multiples for pairs (x, x ₁), (x ₂, x ₃), and (x ₆, x′) and the corresponding dissimilarity reducing maps $\phi _{x,x_{1}}$, $\phi _{x_{2},x_{3}}$, $\phi _{x_{6},x'}$ from the multiple of the representers to the network, containing the corresponding pair of nodes in their images. The ultrametric value u _X ^Ω(x, x′) is given by minimizing over all chains joining x and x′ the maximum multiple of a representer used to link consecutive nodes in the chain (12)

We say that Ω is uniformly bounded if there exists a finite M such that for all ω = (X _ω , A _ω ) ∈ Ω we have that $\max _{(z,z')\in \text{dom}(A_{\omega })}A_{\omega }(z,z') \leq M$. We now formally define the notion of representability.

(P2) Representability

We say that a clustering method $\mathcal{H}$ is representable if there exists a uniformly bounded collection Ω of weakly connected representers each with finite number of nodes such that $\mathcal{H} \equiv \mathcal{H}^{\varOmega }$ where $\mathcal{H}^{\varOmega }$ has output ultrametrics as in (12). If the collection Ω is finite, we say that $\mathcal{H}$ is finitely representable.

For every collection of representers Ω satisfying the conditions in property (P2), (12) defines a valid ultrametric. Moreover, every representable clustering method abides by axiom (A2), as stated next.

Proposition 1.

Given a collection of representers Ω satisfying the conditions in (P2), the representable method $\mathcal{H}^{\varOmega }$ is valid, i.e., u _X ^Ω defined in  (12) is an ultrametric for all networks N = (X, A _X ), and satisfies the Axiom of Transformation (A2)

The condition in (P2) that a valid representable method is defined by a set of weakly connected [23] representers is necessary and sufficient. However, the condition in (P2) that Ω be uniformly bounded is sufficient but not necessary for $\mathcal{H}^{\varOmega }$ to output a valid ultrametric. Although (A2) is guaranteed for every representable method, the Axiom of Value (A1) need not be satisfied. Thus, admissibility and representability are independent properties.

Remark 2.

Representability is a mechanism for defining universal hierarchical clustering methods from given representative examples. Each representer ω ∈ Ω can be interpreted as defining a particular structure that is to be considered a cluster unit. The scaling of this unit structure [cf. (10), (11)] and its replication through the network [cf. (12)] indicate the resolution at which nodes become part of a cluster. The interest in representability is that it is easier to state desirable clustering structures for particular networks rather than for arbitrary ones. We refer the reader to Sect. 4.3 for particular examples of representer networks that give rise to intuitively appealing clustering methods.

4.2 Representability, Scale Preservation, and Admissibility

Are all representable clustering methods relevant in practice? To answer this question we seek to characterize methods that satisfy some desired properties that we deem reasonable. In particular, we consider methods that are admissible with respect to the axioms of value and transformation (A1) and (A2) as well as scale preserving in the sense of (P1).

In characterizing admissible, representable, and scale preserving methods, the concept of structure representer appears naturally. We say that a representer ω = (X _ω , A _ω ) is a structure representer if and only if | X _ω | ≥ 2 and

$$\displaystyle{ A_{\omega }(z,z') = 1,\text{ for all }z\neq z'\,\,\text{s.t.}\,\,(z,z') \in \text{dom}(A_{\omega }). }$$

(13)

The requirement in (13) implies that structure representers define the relationships that are necessary in a cluster unit but do not distinguish between different levels of influence. In the following theorem we claim that admissible, representable, and scale preserving hierarchical clustering methods are those represented by a collection Ω of strongly connected, structure representers.

Theorem 2.

A representable clustering method $\mathcal{H}$ satisfies axioms (A1)–(A2) and scale preservation (P1) if and only if $\mathcal{H} \equiv \mathcal{H}^{\varOmega }$ where Ω is a collection of strongly connected, structure representers as defined by the condition in  (13).

Recalling the interpretation of representability as the extension of clustering defined for particular cases, Theorem 2 entails that the definitions of particular cases cannot present dissimilarity degrees if we require scale preservation. That is, the dissimilarity between every pair of distinct nodes in the representers must be either 1 or undefined. The edges with value 1 imply that the corresponding influence relations are required for the formation of a cluster whereas the influence relations associated with undefined edges are not required. Conversely, Theorem 2 states that encoding different degrees of required influence for different pairs of nodes within the representers is impossible if we want the resulting clustering method to be scale preserving.

4.3 Cyclic Clustering Methods

Let ↻ _t = ({1, …, t}, A _t ) denote a cycle network with t nodes such that the domain of the dissimilarity function dom(A _t ) = {(i, i + 1)} _{i = 1} ^t−1 ∪ (t, 1) and every defined dissimilarity is equal to 1. In this section we study representable methods where the representer collections contain cycle networks. We first note that the method defined by a representer collection that contains a finite number of cycle networks is equivalent to the method represented by the longest cycle in the collection.

Proposition 2.

Given a finite collection $\varOmega =\{ \circlearrowright _{t}\vert t \in \mathcal{T}\}$ of cyclic representers, we have that $\mathcal{H}^{\varOmega } \equiv \mathcal{H}^{\circlearrowright _{t_{\max }}}$ , where $t_{\max } =\max \mathcal{T}$.

The method $\mathcal{H}^{\circlearrowright _{t}}$ is referred to as the tth cyclic method. Cyclic methods $\mathcal{H}^{\circlearrowright _{t}}$ for all t ≥ 2 are admissible and scale preserving as stated in the following corollary of Theorem 2.

Corollary 1.

Cyclic methods $\mathcal{H}^{\circlearrowright _{t}}$ satisfy axioms (A1)–(A2) and the scale preservation property (P1).

The corollary follows from the fact that networks ↻ _t are strongly connected and structure representers. The second cyclic method $\mathcal{H}^{\circlearrowright _{2}}$ was used to introduce the concept of representable clustering in (5)– (7) and shown to coincide with the reciprocal clustering method $\mathcal{H}^{\text{R}}$ in (8). Interpreting ↻₂ as a basic cluster unit we can then think of reciprocal clustering $\mathcal{H}^{\text{R}} \equiv \mathcal{H}^{\circlearrowright _{2}}$ as a method that allows propagation of influence through cycles that contain at most two nodes. Likewise, the method $\mathcal{H}^{\circlearrowright _{3}}$ can be interpreted as a method that allows propagation of influence through cycles that contain at most three nodes, and so on.

As we increase t, the output ultrametrics of methods $\mathcal{H}^{\circlearrowright _{t}}$ become smaller, in particular smaller than those output by $\mathcal{H}^{\circlearrowright _{2}} \equiv \mathcal{H}^{\text{R}}$. This is consistent with Theorem 1 and is indicative of the status of these methods as relaxations of the condition of direct mutual influence. As we increase the length of the cycles, the question arises of whether we recover nonreciprocal clustering. This is not true for any ↻ _t where t is finite. However, if we define $\mathcal{C}_{\infty } =\{ \circlearrowright _{t}\}_{t=1}^{\infty }$ the following result holds.

Proposition 3.

The clustering method $\mathcal{H}^{\mathcal{C}_{\infty }}$ represented by the family of all cycle networks $\mathcal{C}_{\infty }$ is equivalent to the nonreciprocal clustering method $\mathcal{H}^{\mathit{\text{NR}}}$ with output ultrametrics as defined in  (4).

Combining the results in Propositions 2 and 3, it follows that by considering methods $\mathcal{H}^{\circlearrowright _{t}}$ for finite t and method $\mathcal{H}^{\mathcal{C}_{\infty }}$ we are considering every method that can be represented by a countable collection of cyclic representers. The reformulation in Proposition 3 expresses nonreciprocal clustering through the consideration of particular cases, namely cycles of arbitrary length. This not only uncovers a drawback of nonreciprocal clustering—propagating influence through cycles of arbitrary length is perhaps unrealistic—but also offers alternative formulations that mitigate this limitation—restrict the propagation of influence to cycles of certain length. In that sense, cyclic methods of length t can be interpreted as a tightening of nonreciprocal clustering. This interpretation is complementary of their interpretation as relaxations of reciprocal clustering that we discussed above. Given this dual interpretation, cyclic clustering methods are of practical importance.

5 Conclusion

The notion of representability was introduced as the possibility of specifying a hierarchical clustering method through its action on a collection of representers. Moreover, the characteristics needed on the representers to obtain an admissible and scale preserving method were detailed. We then focused our attention on cyclic methods, a particular family within the representable methods.