Keywords

1 Introduction

The basic model of classical computers was initially visualized by Alan Turing, Von Neumann, and several other researchers in the 1930s and the decade after that. However the model of computers, that Turing or Neumann studied, are limited by classical physics and thus termed as classical computers. Till the end of nineteenth century, most scientists believed that Newtonian laws governing the motion of material bodies and Maxwell’s theory of electromagnetism are the fundamental areas of physics. However, the discovery of X-rays and electrons towards the end of that century finally helped the physicists to understand quantum mechanics around 1925. The limitation of classical mechanics could be understood clearly after that. In 1982, Richard Feynman presented the seminal idea of a universal quantum simulator or more informally, a quantum computer.

Informally speaking, a quantum system of more than one particles can be explained by a Hilbert space whose dimension is exponentially large in the number of particles. Thus, one naturally expects that a quantum system can efficiently solve a problem that may require exponential time on a classical computer. During the 1980s, the initial works by Deutsch-Jozsa [12] and Grover [17] could explain quantum algorithms that are exponentially faster than the classical ones. Most importantly, in 1994, Shor discovered that in quantum paradigm, factorization and discrete log problems can be efficiently solved [37]. This result had a major impact in classical cryptography. This is because, there are lot of public key cryptosystems that are based on these two tools. The internet communication as a whole, including the online banking system, depends on the security of these. Thus, in the field of public key cryptography, this warranted for cryptographic primitives that can resist attacks even with the existence of quantum computers. While commercial quantum computers are still elusive, the recent developments in the area of experimental physics are gaining huge momentum as evident from the award of Nobel prize for Physics in 2012 to Wineland and Haroche for “ground-breaking experimental methods that enable measuring and manipulation of individual quantum systems,” a study on the particle of light, the photon. The Nobel prize in Physics, 2016, is awarded to Thouless, Haldane, and Kosterlitz for “theoretical discoveries of topological phase transitions and topological phases of matter.” These results might have importance towards actual implementation of a quantum computer. Thus it shows that this domain of research is indeed one of the top priorities in international scientific community.

Data analytics is the technology of investigating raw data towards obtaining valid conclusions regarding relevant information. Such techniques are exploited by organizations to identify better business decisions towards verifying or disproving the models they study. As these algorithms, in many cases, require high complexity, it would always be interesting to investigate whether one can have more efficient solutions in the quantum domain. Consider the example of a share market. There we require huge computation in short time, need to communicate those data quickly among different parties, and at the same time the data security has to be considered with priority. While the data communication and security issues may be handled as a part where much competition might not be involved, each of the companies will be interested to have a better forecast than the other. Towards a better forecast, which is the main purpose of data analytics, one requires to have huge statistical calculations, which finally boils down to arithmetic, algebraic, combinatorial, and symbolic computations. Thus, the main question here is whether we can have better computational facilities in quantum paradigm. This is the focus of this material. At the same time, we also touch a few issues in communication and security domain that are relevant in data analytics and where the quantum paradigm has efficient tools to offer.

Before proceeding further, let us present brief introductory materials. For detailed technical understanding, one may refer to [29].

1.1 Basics of a Qubit and the Algebra

As a bit (0 or 1) is the basic element of a classical computer, the quantum bit (called the qubit) is the fundamental element in the quantum paradigm, whose physical counterpart is a photon. A qubit is represented as

$$\displaystyle{\alpha \vert 0\rangle +\beta \vert 1\rangle,}$$

where \(\alpha,\beta \in \mathbb{C}\) (i.e., complex numbers), and | α | 2 + | β | 2 = 1. If one measures the qubit in { | 0〉, | 1〉} basis, then | 0〉 is observed with probability | α | 2, and | 1〉 with | β | 2. The original state gets destroyed after the observation and collapse to the observed state.

That is, the qubits | 0〉, | 1〉 are the quantum counterparts of the classical bits 0, 1. The qubit | 0〉 can be represented as \(\left [\begin{array}{c} 1\\ 0\\ \end{array} \right ]\) and | 1〉 can be represented as \(\left [\begin{array}{c} 0\\ 1\\ \end{array} \right ]\). The superposition of | 0〉, | 1〉, i.e., α | 0〉 +β | 1〉 can be written as \(\alpha \left [\begin{array}{c} 1\\ 0\\ \end{array} \right ]+\beta \left [\begin{array}{c} 0\\ 1\\ \end{array} \right ] = \left [\begin{array}{c} \alpha \\ \beta \\ \end{array} \right ]\), where \(\alpha,\beta \in \mathbb{C}\), | α | 2 + | β | 2 = 1.

Based on this definition, one may theoretically pack infinite amount of information in a single qubit. However, it is not clear how to extract such information. Further in actual implementation of quantum circuits, it might not be possible to perfectly create a qubit for any α, β. Nevertheless, it is clear that a single qubit may contain huge information compared to a bit.

The basic algebra relating to more than one qubits can be interpreted as tensor products. Thus, consider tensor product of two qubits as

(α 1 | 0〉 +β 1 | 1〉) ⊗ (α 2 | 0〉 +β 2 | 1〉) \(= \left [\begin{array}{c} \alpha _{1}\\ \beta _{ 1}\\ \end{array} \right ]\otimes \left [\begin{array}{c} \alpha _{2}\\ \beta _{ 2}\\ \end{array} \right ]\) \(= \left [\begin{array}{c} \alpha _{1}\left [\begin{array}{c} \alpha _{2}\\ \beta _{ 2}\\ \end{array} \right ] \\ \beta _{1}\left [\begin{array}{c} \alpha _{2}\\ \beta _{ 2}\\ \end{array} \right ] \end{array}\right ] = \left [\begin{array}{c} \alpha _{1}\alpha _{2}\\ \alpha _{ 1}\beta _{2}\\ \beta _{1 } \alpha _{2} \\ \beta _{1}\beta _{2}\\ \end{array} \right ]\)

\(=\alpha _{1}\alpha _{2}\left [\begin{array}{c} 1\\ 0 \\ 0\\ 0 \end{array} \right ]+\alpha _{1}\beta _{2}\left [\begin{array}{c} 0\\ 1 \\ 0\\ 0 \end{array} \right ]+\beta _{1}\alpha _{2}\left [\begin{array}{c} 0\\ 0 \\ 1\\ 0 \end{array} \right ]+\beta _{1}\beta _{2}\left [\begin{array}{c} 0\\ 0 \\ 0\\ 1 \end{array} \right ]\)

 = α 1 α 2 | 00〉 +α 1 β 2 | 01〉 +β 1 α 2 | 10〉 +β 1 β 2 | 11〉. That is,

(α 1 | 0〉 +β 1 | 1〉) ⊗ (α 2 | 0〉 +β 2 | 1〉) = α 1 α 2 | 00〉 +α 1 β 2 | 01〉 +β 1 α 2 | 10〉+

β 1 β 2 | 11〉.

However, any 2-qubit state may not always be decomposed as above. Consider the state γ 1 | 00〉 +γ 2 | 11〉 with γ 1 ≠ 0, γ 2 ≠ 0. This can never be written as (α 1 | 0〉 +β 1 | 1〉) ⊗ (α 2 | 0〉 +β 2 | 1〉). This phenomenon is described as entanglement. An example of maximally entangled state is \(\frac{\vert 00\rangle +\vert 11\rangle } {\sqrt{2}}\), which is an example of Bell states or EPR pairs. We will later explain how to produce such entangled states and why they are important in quantum information.

Quantum input

Quantum gate

Quantum output

α | 0〉 +β | 1〉

X

β | 0〉 +α | 1〉

α | 0〉 +β | 1〉

Z

α | 0〉 −β | 1〉

α | 0〉 +β | 1〉

H

\(\alpha \frac{\vert 0\rangle +\vert 1\rangle } {\sqrt{2}} +\beta \frac{\vert 0\rangle -\vert 1\rangle } {\sqrt{2}}\)

1.2 Quantum Gates

Now let us briefly describe the quantum gates. Such gates are basic primitives in building a quantum computer. A quantum gate can be considered as a reversible circuit having n qubits as inputs and n qubits as outputs. Mathematically, they can be seen as 2n × 2n unitary matrices where the elements are complex numbers. Let us first present a few examples of single input single output quantum gates. In matrix form, the gate operations are as follows.

  • X gate: \(\left [\begin{array}{cc} 0&1\\ 1 &0\\ \end{array} \right ]\) \(\left [\begin{array}{c} \alpha \\ \beta \\ \end{array} \right ]\) \(= \left [\begin{array}{c} \beta \\ \alpha \\ \end{array} \right ]\);

  • Z gate: \(\left [\begin{array}{cc} 1& 0\\ 0 & -1\\ \end{array} \right ]\) \(\left [\begin{array}{c} \alpha \\ \beta \\ \end{array} \right ]\) \(= \left [\begin{array}{c} \alpha \\ -\beta \\ \end{array} \right ]\);

  • H gate: \(\left [\begin{array}{cr} \frac{1} {\sqrt{2}} & \frac{1} {\sqrt{2}} \\ \frac{1} {\sqrt{2}} & - \frac{1} {\sqrt{2}}\\ \end{array} \right ]\) \(\left [\begin{array}{c} \alpha \\ \beta \\ \end{array} \right ]\) \(= \left [\begin{array}{c} \frac{\alpha +\beta } {\sqrt{2}} \\ \frac{\alpha -\beta } {\sqrt{2}}\\ \end{array} \right ]\).

Note that \(\frac{\alpha +\beta } {\sqrt{2}}\vert 0\rangle + \frac{\alpha -\beta } {\sqrt{2}}\vert 1\rangle =\alpha \frac{\vert 0\rangle +\vert 1\rangle } {\sqrt{2}} +\beta \frac{\vert 0\rangle -\vert 1\rangle } {\sqrt{2}}\).

The 2-input 2-output quantum gates can be seen as 4 × 4 unitary matrices. An example is the CNOT gate which works as follows: | 00〉 → | 00〉, | 01〉 → | 01〉, | 10〉 → | 11〉, | 11〉 → | 10〉. The related matrix is \(\left [\begin{array}{cccc} 1&0&0&0\\ 0 &1 &0 &0 \\ 0&0&0&1\\ 0 &0 &1 &0\\ \end{array} \right ].\)

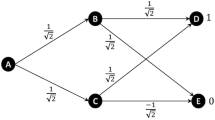
As an application of these gates, let us describe the circuit in Fig. 15.1 to create certain entangled states as follows: \(\vert \beta _{00}\rangle = \frac{\vert 00\rangle +\vert 11\rangle } {\sqrt{2}}\), \(\vert \beta _{01}\rangle = \frac{\vert 01\rangle +\vert 10\rangle } {\sqrt{2}}\), \(\vert \beta _{10}\rangle = \frac{\vert 00\rangle -\vert 11\rangle } {\sqrt{2}}\), and \(\vert \beta _{11}\rangle = \frac{\vert 01\rangle -\vert 10\rangle } {\sqrt{2}}\).

Fig. 15.1
figure 1

Quantum circuit for creating entangled state

Full size image

1.3 No Cloning

While it is very easy to copy an unknown classical bit (i.e., either 0 or 1), it is now well known that it is not possible to copy an unknown qubit. This result is known as the “no cloning theorem” and was initially noted in [13, 43]. It has a huge implications in quantum computing, quantum information, quantum cryptography, and related fields.

The basic outline of the proof is as follows. Consider a quantum slot machine with two slots labeled A and B. Here A is the data slot set in a pure unknown quantum state | ψ〉 whereas B is target slot set in a pure state | s〉 where A will be copied. Let there exist a unitary operator which does the copying procedure. Mathematically, it is written as U( | ψ〉 | s〉) = | ψ〉 | ψ〉. Note that, U being a unitary operator, UU † = I, where \((U^{\dag })_{ij} = \overline{U}_{ji}\), transpose of the matrix and scalar complex conjugate for each element. Let this copying procedure work for two particular pure states, | ψ〉 and | ϕ〉. Then we have

$$\displaystyle{U(\vert \psi \rangle \vert s\rangle ) = \vert \psi \rangle \vert \psi \rangle,U(\vert \phi \rangle \vert s\rangle ) = \vert \phi \rangle \vert \phi \rangle.}$$

From the inner product: 〈s | 〈ψ | U † U | ϕ〉 | s〉 = 〈ψ | 〈ψ | | ϕ〉 | ϕ〉. This implies 〈ψ | ϕ〉 = (〈ψ | ϕ〉)2.

Note that x = x 2 has only two solutions: x = 0 and x = 1. Thus we get either | ψ〉 = | ϕ〉 or inner product of them equals to zero, i.e., | ψ〉 and | ϕ〉 are orthogonal to each other. This implies that a cloning device can only clone orthogonal states. Therefore a general quantum cloning device is impossible. For example, given that the unknown state is one of | 0〉, \(\frac{\vert 0\rangle +\vert 1\rangle } {\sqrt{2}}\), two nonorthogonal states, it is not possible to clone the state without knowing which one it is.

This provides certain advantages as well as disadvantages. The advantages are in the domain of quantum cryptography, where by the laws of physics copying an unknown qubit is not possible. However, in terms of copying or saving unknown quantum data, this is actually a potential disadvantage. At the same time, it should be clearly explained that given a known quantum state, it is always possible to copy it. This is because, for a known quantum state, we know how to create it deterministically and thus it is possible to reproduce it with the same circuit.

For explaining with an example, one may refer to Fig. 15.2. If an unknown qubit | μ〉 is either | 0〉 or | 1〉, then it will be copied perfectly without creating any disturbance to | μ〉. However, if \(\vert \mu \rangle = \frac{\vert 0\rangle +\vert 1\rangle } {\sqrt{2}}\), say, then at the output we will get entangled state \(\frac{\vert 00\rangle +\vert 11\rangle } {\sqrt{2}}\). Thus copying is not successful here.

Fig. 15.2
figure 2

Explanation of no cloning with a simple circuit

Full size image

This concept can also be applied towards distinguishing quantum states. Given two orthogonal states { | ψ〉, | ψ  ⊥ 〉}, it is possible to distinguish them with certainty. For example, the pair of states

$$\displaystyle{\{\vert 0\rangle,\vert 1\rangle \};}$$
$$\displaystyle{\left \{ \frac{1} {\sqrt{2}}(\vert 0\rangle + \vert 1\rangle ), \frac{1} {\sqrt{2}}(\vert 0\rangle -\vert 1\rangle )\right \};}$$
$$\displaystyle{\left \{ \frac{1} {\sqrt{2}}(\vert 0\rangle + i\vert 1\rangle ), \frac{1} {\sqrt{2}}(\vert 0\rangle - i\vert 1\rangle )\right \}}$$

are orthogonal and can be certainly distinguished.

However, two non-orthogonal quantum states, this is not possible. For example, given the two states are | 0〉, \(\frac{\vert 0\rangle +\vert 1\rangle } {\sqrt{2}}\), which are nonorthogonal, it is not possible to exactly identify each one with certainty. These ideas are back-bone to the famous BB84 Quantum Key Distribution (QKD) protocol [4].

2 A Brief Overview of Advantages in Quantum Paradigm

Next we like to briefly mention a couple of areas where the frameworks based on quantum physics provide advantageous situations over the classical domain. We will consider one example each in the domain of communication as well as computation.

2.1 Teleportation

Teleportation is one of the important ideas that shows the strength of quantum model over the classical model [5]. Given a sharing of a pair of entangled states by the two parties at distant locations, one just needs to send two classical bits of information to send an unknown quantum state (this may contain information corresponding to infinitely many bits) from one side to another side (Fig. 15.3).

Fig. 15.3
figure 3

Quantum circuit for Teleporting a qubit

Full size image

As an example take | β xy 〉 = | β 00〉, G the CNOT gate, i.e., | 00〉 → | 00〉, | 01〉 → | 01〉, | 10〉 → | 11〉, | 11〉 → | 10〉. Further consider \(A = H,B = X^{M_{2}},C = Z^{M_{1}}\). This will provide the basic teleportation circuit. As a simple extension, one can use any | β xy 〉, G as CNOT and \(A = H,B = X^{M_{2}\oplus x},C = Z^{M_{1}\oplus y}\). The step by step explanation for teleportation is as follows.

  • \(\vert \psi _{0}\rangle = \vert \psi \rangle \vert \beta _{00}\rangle = (\alpha \vert 0\rangle +\beta \vert 1\rangle )\frac{(\vert 00\rangle +\vert 11\rangle )} {\sqrt{2}}\)

  • \(\vert \psi _{1}\rangle =\alpha \vert 0\rangle \frac{(\vert 00\rangle +\vert 11\rangle )} {\sqrt{2}} +\beta \vert 1\rangle \frac{(\vert 10\rangle +\vert 01\rangle )} {\sqrt{2}}\)

  • \(\vert \psi _{2}\rangle =\alpha \frac{\vert 0\rangle +\vert 1\rangle } {\sqrt{2}} \frac{(\vert 00\rangle +\vert 11\rangle )} {\sqrt{2}} +\beta \frac{\vert 0\rangle -\vert 1\rangle } {\sqrt{2}} \frac{(\vert 10\rangle +\vert 01\rangle )} {\sqrt{2}} = \frac{1} {2}(\vert 00\rangle (\alpha \vert 0\rangle +\beta \vert 1\rangle ) + \vert 01\rangle (\beta \vert 0\rangle +\alpha \vert 1\rangle )+\) | 10〉(α | 0〉 −β | 1〉) − | 11〉(β | 0〉 −α | 1〉))

  • Observe 00, nothing to do. Observe 01, apply X. Observe 10, apply Z. Observe 11, apply both X, Z.

The importance of this technique in data analytics is that if two different places may share entangled particles, then it is possible to send a huge amount of information (in fact theoretically infinite) by just communicating two classical bits. Again, one important issue to be noted is that, even if we manage to transport a qubit, in case it is unknown, it might not be possible to extract the relevant information from that.

2.2 Deutsch-Jozsa Algorithm

Deutsch-Jozsa algorithm [12] is possibly the first clear example that demonstrates quantum parallelism over the standard classical model. Take a Boolean function f: { 0, 1}n → { 0, 1}. A function f is constant if f(x) = c for all x ∈ { 0, 1}n, c ∈ { 0, 1}. Further f is called balanced if f(x) = 0 for 2n−1 inputs and f(x) = 1 for the rest of 2n−1 inputs. Given the function f as a black box, which is either constant or balanced, we need an algorithm, that can answer which one this is. It is clear that a classical algorithm needs to check the function for at least 2n−1 + 1 inputs in worst case to come to a decision. Quantum algorithm can solve this with only one input. Note that given a classical circuit f, there is a quantum circuit of comparable efficiency which computes the transformation U f that takes input like | x, y〉 and produces output like | x, y ⊕ f(x)〉 (Fig. 15.4).

Fig. 15.4
figure 4

Quantum circuit to implement Deutsch-Jozsa algorithm

Full size image

The step by step operations of the technique can be described as follows.

  •  | ψ 0〉 = | 0〉⊗n | 1〉

  • \(\vert \psi _{1}\rangle =\sum _{x\in \{0,1\}^{n}} \frac{\vert x\rangle } {\sqrt{2^{n}}}\left [\frac{\vert 0\rangle -\vert 1\rangle } {\sqrt{2}} \right ]\)

  • \(\vert \psi _{2}\rangle =\sum _{x\in \{0,1\}^{n}}\frac{(-1)^{f(x)}\vert x\rangle } {\sqrt{2^{n}}} \left [\frac{\vert 0\rangle -\vert 1\rangle } {\sqrt{2}} \right ]\)

  • \(\vert \psi _{3}\rangle =\sum _{z\in \{0,1\}^{n}}\sum _{x\in \{0,1\}^{n}}\frac{(-1)^{x\cdot z\oplus f(x)}\vert z\rangle } {2^{n}} \left [\frac{\vert 0\rangle -\vert 1\rangle } {\sqrt{2}} \right ]\)

  • Measurement: all zero state implies that the function is constant, otherwise it is balanced.

The importance of explaining this algorithm in the context of data analytics is that it is often important to distinguish between two objects very efficiently. The example of Deutsch-Jozsa algorithm [12] demonstrates that it is significantly efficient compared to the classical domain.

At this point we like to present two important aspects of Deutsch-Jozsa algorithm [12] in terms of data analytics and machine learning. First of all, one must note that we can obtain the equal superposition of all 2n many n-bit states just by using n many Hadamard gates. For this, note the first part of | ψ 1〉 which is \(\sum _{x\in \{0,1\}^{n}} \frac{\vert x\rangle } {\sqrt{2^{n}}}\). This provides an exponential advantage in quantum domain as in the classical domain we cannot access all the 2n many n-bit patterns efficiently. The second point is related to machine learning. As we have discussed, we may have the circuit of f available as a black-box and we like to learn several properties of the function efficiently. In this direction, Walsh transform is an important tool. What we obtain as the output of the Deutsch-Jozsa algorithm just before measurement is | ψ 3〉 and the first part of this is \(\sum _{z\in \{0,1\}^{n}}\sum _{x\in \{0,1\}^{n}}\frac{(-1)^{x\cdot z\oplus f(x)}\vert z\rangle } {2^{n}}\). Note that, the Walsh spectrum of the Boolean function f at a point z is defined as \(W_{f}(z) =\sum _{x\in \{0,1\}^{n}}(-1)^{x\cdot z\oplus f(x)}\). That is, \(\sum _{z\in \{0,1\}^{n}}\sum _{x\in \{0,1\}^{n}}\frac{(-1)^{x\cdot z\oplus f(x)}\vert z\rangle } {2^{n}} =\sum _{z\in \{0,1\}^{n}}\frac{W_{f}(z)} {2^{n}} \vert z\rangle\). This means that using such an algorithm, we can efficiently obtain a transform domain spectrum of the function, which is not achievable in classical domain.

Testing several properties of Boolean functions in classical as well as quantum paradigm is an interesting area of research in property testing [6], which are in turn useful in learning theory. There are several interesting properties of Boolean functions, mostly in the area of coding theory and cryptology, that need to be tested efficiently. However, in many of the cases, the efficient algorithms are elusive. The Deutsch-Jozsa Algorithm [12] is the first step in this area in quantum computational model. In a larger view, the details of various quantum algorithms can be obtained from [32].

3 Preliminaries of Quantum Cryptography

In any commercial environment, confidentiality of data is one of the most important issues. Due to Shor’s result [37] on efficient factorization as well as solving discrete logarithm in quantum domain, classical public key cryptography will be completely broken in case a quantum computer can actually be built. One must note that many of the commercial security systems, including banking, are based on algorithms whose security are promised by hardness of factorization or discrete log problems. In this regard, we present a few basic issues in classical and quantum cryptography that must be explained in any data centric environment.

The main challenge in cryptology in early seventies was how to decide on a secret information between two parties over a public channel. The solution to this has been proposed by Diffie and Hellman in 1976 [14]. The protocol is as follows.

  • In public domain, the information about a suitable group G is made available. For example, one can consider \(G = (\mathbb{Z}_{p}^{{\ast}},\cdot )\) where the elements are {1, …, p − 1} and the multiplication is modulo p. The prime p should be very large, say of the order of 1024 bits.

  • Given the generator g (which is again known in public domain) and another element h, it is hard (using a classical computer) to obtain i such that h = g i. This is well known as Discrete Logarithm Problem (DLP).

  • Thus, it is believed that in the classical paradigm, it is not easy to obtain g ab using g a, g b only (which are available to the adversary from the public channel) without any knowledge of a, b. Here g ab is used as the secret key for further secured communication. That is, this secret key is the output of the key distribution algorithm which will be secretly shared by the participating parties after communication over a public channel.

Now let us describe the famous RSA cryptosystem [35]. The RSA cryptosystem has been invented by Rivest, Shamir, and Adleman in 1977 and this is undoubtedly the most popular public key cryptosystem which is used in various electronic commerce protocols. The security of this cryptosystem relies on the difficulty of factoring a number into its two constituent primes. In practice, the prime factors of interest will be several hundred bits long. A modulus N = p × q of 1024 bits, for example, would be common. Let us now briefly describe the scheme.

Key Generation Algorithm

  • Choose primes p, q (generally same bit size, q < p < 2q)

  • Construct modulus N = pq, and ϕ(N) = (p − 1)(q − 1)

  • Set e, d such that \(d = e^{-1}\bmod \phi (N)\)

  • Public key: (N, e) and Private key: d

Encryption Algorithm: \(C = M^{e}\bmod N\)

Decryption Algorithm: \(M = C^{d}\bmod N\)

The RSA cryptosystem relies on the efficiency of the following:

  • finding two large primes p, q, and computing N = pq;

  • computing \(d = e^{-1}\bmod \phi (N)\) given N = pq and e;

  • computing modular exponentiations \(M^{e}\bmod N\) and \(C^{d}\bmod N\).

While it is very clear that if one can factor the modulus N, then RSA can be immediately broken, the other two security problems are the following.

  • To compute \(d = e^{-1}\bmod \phi (N)\) given N, e.

  • To compute \(M = C^{1/e}\bmod N\) given N, e, C [RSA Problem].

Naturally, in classical domain, there is no efficient algorithm to solve the above two problems.

Till date, there is no efficient algorithm to solve DLP or RSA in classical domain. However, in the famous work by Shor [37], it has been shown that both these problems can be solved efficiently in quantum paradigm. This opens a new area called post-quantum cryptography [31], where the cryptosystems are studied considering that the adversary can attack the systems using quantum computers. There are certain classical public key cryptosystems, for example, lattice based and code based schemes for which no efficient quantum attack is known. However, understanding these algorithms requires advanced background in mathematics and computer science. Further, the commercial implementation of these schemes is not as efficient as RSA.

On the other hand, Bennett and Brassard provided the idea of Quantum Key Distribution [4] (QKD) where the physical laws are exploited towards the security proof. This idea is quite elegant and easy to understand. More interestingly, while the commercial quantum computers are still elusive, several QKD schemes have already been implemented for commercial purposes [33, 34]. We now describe this idea in more detail.

3.1 Quantum Key Distribution and the BB84 Protocol

Based on the above discussion, it is clear that the community needs a key distribution scheme that can resist a quantum adversary. The famous BB84 [4] protocol provides a secure quantum key distribution scheme which is secure under certain assumptions. The scheme has received huge attention in the research community as evident from its citation; it has also been implemented in commercial domain as well.

Bennett and Brassard (the BB of BB84) initiated the seminal idea of QKD in 1979 based on the pioneering concept proposed by Wiesner in 1970. Both these ideas have been published much later, i.e., the idea of Wiesner in 1983 [41] and that of Bennet and Brassard in [3, 4]. The work published in 1984 [4] received more prominence and that is why the 84 of BB84 comes. Interested readers may have a look at [9] for a detailed history in this area. Informally speaking, the security of BB84 protocol comes from no-cloning theorem and indistinguishability of non-orthogonal quantum states. The basic steps of BB84 QKD may be described as follows.

  • One needs to transmit 0 or 1 securely.

  • For this, one may consider the bases

    $$\displaystyle{\{\vert 0\rangle,\vert 1\rangle \};}$$
    $$\displaystyle{\left \{ \frac{1} {\sqrt{2}}(\vert 0\rangle + \vert 1\rangle ), \frac{1} {\sqrt{2}}(\vert 0\rangle -\vert 1\rangle )\right \}.}$$

  • Choosing any one of the above bases, one may encode 0 to one qubit and 1 to the other qubit in that basis.

  • If only a single basis is used, then the attacker can measure in that basis to obtain the information and reproduce.

  • Thus Alice needs to encode randomly with more than one bases.

  • Bob will also measure in random basis.

  • Basis will match in a proportion of cases and from that the secret key will be prepared.

This is the brief idea to obtain a secret key between two parties over an insecure public channel using the BB84 [4] protocol. After obtaining the secret key, one may use a symmetric key cryptosystem (for example, a stream cipher or a block cipher, see [38] for details) for further communication in encrypted mode. One may refer to [22] for state-of-the-art results of quantum cryptanalysis on symmetric ciphers, though it is still not as havoc as it had been on classical public key schemes.

3.2 Secure Multi-Party Computation

Let us now consider another important aspect of cryptology that might be relevant in data analytics. Take the example of an Automated Teller Machine (ATM) for money transaction. This is a classic example of secure two or multi-party computation. Due to such transactions and several other application domains which are related to secure data handling, Secure Multi-Party Computation (SMC) has become a very important research topic in data intensive areas. In a standard model of SMC, n number of parties wish to compute a function f(x 1, x 2, …, x n ) of their respective inputs x 1, x 2, …, x n , keeping the inputs secret from each other. Such computations have wide applications in online auction, negotiation, electronic voting, etc. Yao’s millionaire’s problem [44] is considered as one of the initial attempts in the domain of SMC. Later, this has been studied extensively in classical domain (see [18] and the references therein). The security of classical SMC usually comes from some computational assumptions such as hardness of factorization of a large number.

In quantum domain, Lo [24] showed the impossibility for secure computation in certain two-party scenario. For example, “one out of two parties secure computation” means that only one out of two parties is allowed to know the output. As a corollary to this result [24], it had been shown that one out of two oblivious transfer is impossible in quantum paradigm. It has been claimed in [23] that given an implementation of oblivious transfer, it is possible to securely evaluate any polynomial time computable function without any additional primitive in classical domain. However, it seems that such a secure two-party computation might not work in quantum domain. Hence, in case of two-party quantum computation, some additional assumptions, such as the semi-honest third party, etc., have been introduced to obtain the secure private comparison [40].

In [45], Yao had shown that any secure quantum bit commitment scheme can be used to implement secure quantum oblivious transfer. However, Mayers [27] and Lo et al [25] independently proved the insecurity of quantum bit commitment. Very recently some relativistic protocols [26] have been proposed in the domain of quantum SMC. Unfortunately, these techniques are still not very promising for practical implementations. Thus, considering quantum adversaries, it might not be possible to achieve SMC and in turn collaborative multi-party computation in distributed environments without compromising the security.

4 Data Analytics: A Critical View of Quantum Paradigm

Given the background of certain developments in quantum paradigm over the classical world, now let us get into some specific issues of data analytics. The first point is, if we consider use of one qubit just as storing one bit of data, then that would be a significant loss in terms of exploiting the much larger (theoretically infinite) space of a qubit. On the other hand, for analysis of classical data, we may require to consider new implementation of data storage that might add additional overhead as data need to be presented in quantum platform. For example, consider the Deutsch-Jozsa [12] algorithm. To apply this algorithm, we cannot use an n-input 1-output Boolean function, but we require a form where the same function can be realized as a function with equal number of input and output bits. Further the same circuit must be implemented with quantum circuits so that the superposition of qubits can be handled. These are the overheads that need to be considered.

Next let us come to the issue of structured and unstructured data. In classical domain, if a data set with N elements are not sorted, then in worst case, we require O(N) search complexity to find a specific data. In quantum domain, the seminal Grover’s algorithm [17] shows that this is possible in only \(O(\sqrt{N})\) effort. For a huge unsorted data set, this is indeed a significant gain. However, in any efficient database, the individual data elements are stored in a well-structured manner so that one can identify a specific record in O(logN) time. This is exponentially small in comparison with both O(N) and \(O(\sqrt{N})\) and thus, in such a scenario, quantum computers may not be of significant advantage.

4.1 Related Quantum Algorithms

To achieve any kind of data analysis, we require several small primitives. Let us first consider finding minimum or maximum from an unsorted list. Similar ideas as in [17] can be applied to obtain minimum or maximum value from an unsorted list of size N in \(O(\sqrt{N})\) time as explained in [15] and [2], respectively. The work [20] considers in detail quantum searching in ordered list and sorting. However, in such a scenario where ordered lists are maintained, quantum algorithms do not provide very significant improvements. Matrix related operations are necessary elements in any kind of data analytics. Given n × n matrices, A, B, C, the matrix product verification problem is to decide whether A × B = C. While the classical domain algorithms must require Ω(n 2) time, we have \(O(n^{\frac{5} {3} })\) algorithm in quantum domain [10]. Such algorithms heavily use results related to quantum walks [39]. In a related direction, solution of a system of linear equations had naturally received serious attention in quantum domain and there are interesting speed-up in several cases. Further these results [19] have applications towards solving linear differential equations, least square techniques and in general, in the domain of machine learning. One may refer to [32] for a detailed description of quantum algorithms and then compare their complexities with the classical counterparts.

While there are certain improvements in specific areas, the situation is not always hopeful and a nice reference in this regard is [1], where Aaronson says

“Having spent half my life in quantum computing research, I still find it miraculous that the laws of quantum physics let us solve any classical problems exponentially faster than today’s computers seem able to solve them. So maybe it shouldn’t surprise us that, in machine learning like anywhere else, Nature will still make us work for those speedups.”

One may also have a look at [8, 21] for very recent state-of-the-art discussions on quantum supremacy. While most of the explanations do not provide a great recommendation towards advantages of quantum machine learning, for some initial understanding of this area from a positive viewpoint, one may refer to [42].

4.2 Database

The next relevant question is if we have significant development in the area of quantum database. In this direction there are some initial concept papers such as [36]. This work presents a novel database abstraction that allows to defer the finalization of choices in transactions until an entity forces the choices by observation in quantum terminology. Following the quantum mechanical idea, here a transaction is in a quantum state, i.e., it could be one of many possible states or might be a superposition. This is naturally undecided and unknown until observed by some kind of measurement. Such an abstraction enables late binding of values read from the database. The authors claimed that this helps in obtaining more transactions to succeed in a situation with high contention. This scenario might be useful for applications where the transactions compete for physical resources represented by data items in the database, such as booking seats in an airline or buying shares. However, these are more at the conceptual level, where actual implementation related details cannot be exactly estimated.

Let us now look at what happens when we are interested in a series of computations which are possibly the most occurring phenomenon in practice. Consider two scenarios, one from a static data set (structured) and another from a dynamic data set where arbitrary search, addition, modification, and alteration are allowed. In static case, the database is generally maintained in such a manner so that the search efforts are always logarithmic. Now consider a little more complex scenario, where the database grows or shrinks arbitrarily and the search and other write operations are allowed in arbitrary sequence. Even in case of such dynamic updations, we always try to maintain some well-known balanced tree structures. Hence, in both the scenarios, we do not have any clear advantage in quantum domain.

4.3 Text Mining

Text mining is an integral part of data analytics given the popularity of social media. Consider a scenario involving text mining problem, which uses a bag of words and unsupervised or semi-supervised clustering technique. In the simplest situation, let there be N words in a given corpus (dictionary). Say, the topics are to be extracted in an unsupervised manner from a set of n stories or documents. Each document contains a set of words. Each topic can be seen as a distribution over the set of words in the corpus and also a document can be considered to be a distribution over the set of (unknown) k topics, where the value of k is determined at the beginning depending on the granularity of the topics required. A simple (or innermost iteration) requires going through the documents one by one, allocating the words in the document to topics, while simultaneously modifying the probability distributions of topics in the documents and words in the topics. Now consider just one iteration only. There are two main steps: (1) to create the dictionary (in this case, say the dictionary is fixed, cannot be modified), and (2) we can study one document at a time. For each document, we can allocate each word to a topic and topics to stories following the distributions. It is obvious to see that in classical computation the fixed dictionary is best to be organized as a sorted array. Once this is done, the search efforts are logarithmic in classical domain and we should not get any immediate improvement in the quantum counterpart. In this regard, we also need to refer to topic modeling. Given a corpus of words, topic modeling is more static in nature. However, with time the database of the corpus has to go through changes due to both additions and deletions. The corpus size will generally increase, along with rapid increase in number of stories to be analyzed. Further, with more and more computing capabilities, finer topics and sub-topics will have to be retrieved. Here big data analysis may play an important role and related algorithms should be evaluated in quantum paradigm.

Let us now refer to certain statistical analysis [7] in this domain on a classical model. The idea of Latent Dirichlet allocation (LDA) is described here. This is based on a generative probabilistic model for collections of discrete data, for example, text. LDA is a three-level hierarchical Bayesian model. Each item of a collection is considered as a finite mixture over an underlying set of topics. These techniques can be used in text classification. However, it is not very clear how these complex ideas can be lifted in quantum domain. In a follow-up work [16], this has been extended where the authors present a Markov chain Monte Carlo algorithm for inference (for quantum speed-up for Monte Carlo methods, one may refer to [28]). This algorithm is applied to analyze abstracts from scientific journals using Bayesian model selection to identify the number of topics. Text mining is one of the most important topics in the domain of analytics and thus this kind of scenarios need to be explored in quantum domain. One may refer to [11] where several ideas of quantum Markov chains are discussed from a different information-theoretic viewpoint and it is not very clear how long it will take to connect ideas from machine learning domain and the paradigm of quantum information to obtain meaningful commercial results.

5 Conclusion: Google, PageRank, and Quantum Advantage

In this review, we have taken an approach to present certain introductory issues in quantum paradigm and then explained how they relate to basics of data analytics. We described several aspects in the domain of computation, communication, and security and pointed out why the computational part should receive prime attention. In the quantum computational model, we have enumerated several significant improvements over the classical counterpart, but the two main concerns that remain are as follows.

  • Can we fabricate a commercially viable quantum computer?

  • (Even if we have a quantum computer) Can we have significant improvements in computational complexity for algorithms related to data analytics?

Let us now conclude with a very practical and well-known problem in the domain of data analytics that received a significant attention. This should help the reader to form his/her own opinion regarding the impact of quantum computation on a significant problem. The problem is related to PageRank. PageRank is an algorithm used by Google Search to rank the websites through their search engine results. It is a method of quantifying the importance of the web pages, i.e., PageRank may be viewed as a metric proposed by Google’s owners Larry Page and Sergey Brin. According to Google:

“PageRank works by counting the number and quality of links to a page to determine a rough estimate of how important the website is. The underlying assumption is that more important websites are likely to receive more links from other websites.”

Informally speaking, the PageRank algorithm heuristically provides a probability distribution. This is used to represent the likelihood that an entity, randomly clicking on web links, will arrive at any particular page. It is very natural that this kind of technique will require huge amount of computational resources and further there will be continuous efforts in upgrading such strategies. Some parts of such effort might involve a lot of “rough” heuristics where exact quantification in such a complex environment might be very hard. In [30], it has been outlined that a quantum version of Google’s famous search algorithm may be significantly faster. However, till date it is not clearly understood how such quantum algorithms may behave on a huge network. We have to wait and watch to experience how the quantum algorithms will evolve to solve the complex problems of data analytics in the coming days.