Keywords

FormalPara Nomenclature
CNMs :

Complex non-linear modes

CxA :

Complexification-averaging technique

EEMD :

Ensemble empirical mode decomposition

EMD :

Empirical mode decomposition

FM :

Frequency modulation

HHT :

Hilbert-Huang transform

HVD :

Hilbert vibration decomposition

IA :

Instantaneous amplitude

IF :

Instantaneous frequency

IMF :

Intrinsic mode function

NNMs :

Non-linear normal modes

ROM :

Reduced order model

SDOF :

Single degree of freedom

WGC :

Weighted global criterion method

8.1 Introduction

Non-linear system identification is a challenging area with a remarkable variety of the methods that attempt to detect, characterize and quantify the non-linearity [1, 2]. While many methods exist, significant research has been recently conducted on structural dynamic testing using non-linear modal analysis. Such research efforts are partly motivated by parallel development of analytical and numerical theories for the computation of non-linear normal and complex modes [3], but also by the desire to extend the modal analysis, which has become the method of choice for dynamic testing of linear structures.

A number of viewpoints on non-linear modes exist as well as a range of methods for their numerical computation [3] and experimental investigation [2]. Non-linear normal modes (NNMs) are usually investigated using phase resonance testing [4], which eliminates the need to decompose measured signals into modes. On the other hand, multi-modal non-linear identification through the direct decomposition of experimental measurements into a set of intrinsic mono-component functions has also been presented in a number of papers [5–8]. These functions do not generally correspond to NNMs because of the absence of the superposition principle in non-linear dynamics although they constitute some approximations of them. The strength of the approaches based on the direct decomposition of measured time series is that they require no a prior characterization of the observed non-linearities, and are generally applicable to non-stationary signals.

There are two dominant decomposition methods used in structural dynamics—empirical mode decomposition (EMD) [9] (which is the first step in the Hilbert-Huang transform) and Hilbert vibration decomposition (HVD) [7]. The proposed method uses the EMD which has been previously used for linear modal analysis [10], characterization of non-linearities [6] and many other applications. Despite not having a rigorous mathematical background, physics-based foundations of the EMD were derived in [8, 11]. Specifically, it was shown how the intrinsic mode functions (IMFs), which are the outputs of the EMD, relate to the slow-flow dynamics models derived by the complexification-averaging technique (CxA).

Recently, complex non-linear modes (CNMs) were introduced in [12] and their use was extended for non-linear modal synthesis, harmonically forced and self-excited systems in [13]. The CNMs allow direct computation of amplitude-dependent frequency, damping and mode shape at the resonance in timely-fashion. Moreover, the numerical implementation of the CNMs does not require significant modifications to conventional harmonic balance solvers. In [14], the CNMs were used for the derivation of reduced order models (ROM) of slow-flow dynamics of the system. It may be therefore argued that the ROM of slow-flow dynamics might create the link between the Hilbert-Huang transform and complex non-linear modal analysis in a similar way as between the HHT and CxA.

This paper presents the method which attempts to connect the CNMs through the ROM of slow-flow dynamics with the HHT. The validity of this connection is discussed on two simple examples. The non-linear system identification method proposed is not only able to detect and characterize the non-linearity, but also quantify its coefficients in the framework of non-linear modal analysis. The method is briefly described in Sect. 8.2 and its application is shown on two numerical cases in Sect. 8.3.

8.2 Theory

The method proposed in the paper combines the HHT with the CNMs. Possible non-linearity is firstly detected and characterized using the HHT and subsequently the coefficients of the selected model are quantified by the optimization of the model in terms of the CNMs. The method can be summarized in the following steps:

  1. 1.

    Experimental measurements (substitute by simulated data in this study)

  2. 2.

    Hilbert-Huang transform

    1. (a)

      Empirical mode decomposition

    2. (b)

      Instantaneous amplitude and frequency estimation

  3. 3.

    Detection and characterization of non-linearity based on the extracted instantaneous characteristics

  4. 4.

    Optimization of the selected model based on the CNMs by a multi-objective weighted global criterion method

The outlined method works for systems with localized or geometrical non-linearities with symmetric restoring forces. It can also be used for systems with asymmetric restoring forces, but only when free non-linear modal decays are measured and processed as in [15, 16]. The method works only in presence of no mode interaction and for well separated modes (the definition of well separated modes in this context is further discussed later). Detailed description of the steps involved follows.

8.2.1 Experimental Measurement Requirements

A specific and well controlled experimental measurements must be usually used for dynamic testing based on non-linear modes. Often, free resonance decay responses are obtained for each mode of interests separately, such as in [4, 17]. It is expected that the proposed method will work for such type of excitation exceptionally well as the EMD does not have to be performed. The multi-mode free decay can be also used, because the EMD can decompose a multi-mode signal into the mono-component functions which are arguably the approximations of the CNMs. Slow sine-sweep excitation can be used as well, in which case a similar framework to forcevib [18] must be coupled with the proposed method. It might be also possible that the method may work with random excitation after the application of the phase separation technique [19]. Only the free decay cases are further discussed in this paper.

8.2.2 Hilbert-Huang Transform

The Hilbert-Huang transform (HHT) [9] is a very popular adaptive data processing method which has been successfully used in many areas of engineering, including linear and non-linear system identification. Despite not having a rigorous mathematical background, its physics-based foundation was recently explored in [8, 11]. It has been shown that the results of the HHT, termed intrinsic mode functions (IMFs), relate to the slow-flow dynamics of the system. This finding created the base of a non-linear system identification method proposed in [5], and might also link the HHT with the CNMs. The HHT has two essential parts: the empirical mode decomposition (EMD) followed by the estimation of instantaneous characteristics.

The EMD was introduced in [9] and has gained popularity over the years. The basic algorithm of the EMD iteratively extracts mono-component functions (IMFs) from a multi-component signal. The extraction is carried out through the sifting process. Many different versions and modifications of the EMD have been proposed with the goal to improve numerical or other issues of the original algorithm, for instance, ensemble empirical mode decomposition (EEMD) [20] or EMD using unconstrained optimization [21]. It was also proven that computation time complexity of the EMD is equivalent to that of the Fourier transform [22].

There are two main problems concerning the use of the EMD—mode mixing and frequency splitting. Mode mixing refers to the fact that two mono-component functions with different time scales are combined or that a part of a mono-component function is estimated in a different IMF. This problem should not usually present such an issue for non-linear system identification. The frequency splitting, however, could be an issue when connecting the HHT with the CNMs. It can be shown (using similar procedure as in [23]) that for ten iterations in sifting process two subsequent modes will be well separated if af ≥ 1 and f 2 > 1. 67f 1, with a = a 2∕a 1 and f = f 2∕f 1, where f 2 and a 2 are the frequency and amplitude of the higher frequency mode, and f 1 and a 1 are the frequency and amplitude of the lower frequency mode. The validity of this criterion may be investigated before applying the EMD by the fast Fourier or wavelet transform. Although the splitting capabilities of the EMD can be improved by increasing the number of sifting iterations or by the application of a masking signal [24], the above written relation is used as the measure of well spaced or close modes in this study.

There are a number of methods for instantaneous frequency (IF) and amplitude (IA) estimation [25, 26]. Traditionally, the Hilbert transform was used, but other methods have been developed and some of them may be used for system identification. For instance, zero-crossing [15, 17] eliminates the need for additional smoothing of results by neglecting the presence of intra-wave frequency modulation (FM). Therefore, the IF and IA obtained by the zero-crossing method correspond well with backbones estimated by analytical or numerical methods [17]. On the other hand, direct quadrature or normalized Hilbert transform [15, 25, 26] extracts intra-wave FM with great accuracy, thereby allowing characterization of non-linearities based on perturbation analysis [15, 27].

In this work, the basic algorithm of the EMD is used with no additional technique to resolve frequency splitting issue. For the estimation of the IF and IA, the zero-crossing is used for the first testing case, and normalized Hilbert transform without smoothing for the second testing case.

8.2.3 Detection and Characterization of Non-linearity

Having extracted the IF and IA, several simple visual ways of how to detect non-linearity from these characteristics can be used. These are variations of the natural frequency or damping with the amplitude of vibration, presence of intra-wave FM [15], or non-linear restoring forces which may be approximately extracted using freevib [28] or forcevib [18]. When energy operators [29] are used to estimate the instantaneous characteristics, the extracted IF does not make any sense (negative and very noisy values) when the system is non-linear.

Characterization of the non-linearity which has been previously detected in the structure can be performed based on the extracted IF and IA as well. Similarly to a typical shape of frequency response functions, the estimated backbones have also their typical shapes given by the type of non-linearity, and these shapes can serve for characterization. The backbones can be visually compared to a typical shape, or a decision making algorithm can be used (similarly to [30]). An interesting way to characterize geometrical non-linearities was presented in [27], where, based on perturbation analysis, a unique ratio of fundamental and intra-wave frequency modulation was established. The method for estimation of this ratio using a combination of zero-crossing and direct quadrature can be found in [15]. This means of characterization will be shown on an example in Sect. 8.3.

8.2.4 The Reduce Order Model (ROM) Based on Complex Non-linear Modes (CNMs)

The complex non-linear modes can be computed using complex non-linear modal analysis [12, 14] from the complex eigenproblem:

$$\displaystyle\begin{array}{rcl} & \mathrm{solve}\quad \left [(n\lambda )^{2}\mathbf{M} + n\lambda \mathbf{C} + \mathbf{K}\right ]\boldsymbol{\Psi }_{n}a +\langle \mathbf{f}(\mathbf{u}_{\mathrm{p}},\dot{\mathbf{u}}_{\mathrm{p}}),\mathrm{e}^{\mathrm{i}n\omega _{0}t}\rangle = \mathbf{0},\quad \mathrm{for}\quad n = 0,\ldots,N_{\mathrm{h}}& {}\\ & \mathrm{subject\ to}\quad \boldsymbol{\Psi }_{1}^{H}\mathbf{M}\boldsymbol{\Psi }_{1} = 1,\quad \mathfrak{R}\{\mathbf{t}^{\mathrm{H}}\boldsymbol{\Psi }_{1}\} = 0 & {}\\ & \mathrm{with\ respect\ to}\quad \lambda,\,\boldsymbol{\Psi }_{0},\,\boldsymbol{\Psi }_{1},\,\ldots,\boldsymbol{\Psi }_{N_{\mathrm{h}}} & {}\\ & \mathrm{for}\quad a \in [a_{\mathrm{min}},a_{\mathrm{max}}], & {}\\ \end{array}$$

where \(\lambda = -\delta \omega _{0} +\mathrm{ i}\omega _{0}\sqrt{1 -\delta ^{2}}\), ω 0 is the natural frequency, δ is the damping ratio, \(\boldsymbol{\Psi }_{n}\) is nth harmonic of the mode shape, N h is the total number of harmonics, and the non-linear operator 〈 , 〉 may be evaluated by the alternating frequency time procedure. The complex eigenproblem is solved using continuation on the modal amplitude a. The ROM can be derived by the CxA and the amplitude and slow phase can be computed using [14]

$$\displaystyle\begin{array}{rcl} & 2\Omega \dot{a} = -2\delta \omega _{0}\Omega a -\boldsymbol{ \Psi }_{1}^{\mathrm{H}}\mathbf{f}_{e}\sin \Theta & {}\\ & 2\Omega \dot{\Theta } =\omega _{ 0}^{2} - \Omega ^{2} -\frac{1} {a}\boldsymbol{\Psi }_{1}^{\mathrm{H}}\mathbf{f}_{ e}\cos \Theta,& {}\\ \end{array}$$

where \(\Omega\) is the angular frequency of oscillation and f e is an external excitation force. The appropriate initial conditions can be found using the optimization scheme described in [14]. The response of the ROM is then expressed as

$$\displaystyle{ \mathbf{x}(t) = a\frac{\boldsymbol{\nu }+\boldsymbol{\nu }^{{\ast}}} {2},\quad \boldsymbol{\nu } =\sum _{ n=0}^{N_{\mathrm{h}} }\boldsymbol{\Psi }_{n}\mathrm{e}^{\mathrm{i}n\left (\phi +\Theta \right )}, }$$

where ϕ is the fast phase, and asterisk marks complex conjugate. The response of the ROM and its instantaneous frequency and amplitude are compared with the results of the HHT in Sect. 8.3.

8.2.5 Quantification via Optimization

The IF and IA can be estimated and computed for all measured points and all modes of interest. If the backbone obtained for the particular mode i by the HHT is \(\hat{\omega }_{0i}(a)\) and the backbone of a selected model computed by the CNM for the same mode is ω 0i (a), a single objective function can be formulated for each measured point and the mode of interest as

$$\displaystyle{ f_{i} = \vert \vert \hat{\omega }_{0i}(a) -\omega _{0i}(a)\vert \vert _{2} }$$

A set of such single objective functions creates an optimization problem using which coefficients of a selected model can be found. This problem should not have any trade-off (the system is unique) and a multi-objective optimization might not be necessary. However, due to experimental errors it is likely that some trade-off will exist. By using the weighted global criterion method (WGC) [31] one can optimize the functions separately as well as all at once with preferences. The WGC is a scalarization method that combines all normalized objective functions to form a single objective function as

$$\displaystyle{ \min \left \{\sum _{i=1}^{k}\left [w_{ i}\left (f_{i} - f_{i}^{o}\right )\right ]^{p}\right \}^{1/p} }$$

where weights w i reflects the preferences, p governs the physical interpretation of the optimization problem, k is the total number of single objective functions, f i are normalized single objective functions and f i o are minima of these functions (also called utopia points [31]). The WGC is very flexible in terms of user preferences and any optimization engine can be used (local, global or genetic). If the utopia points f i o are the same, or lay in the range of required accuracy, for each function, the multi-objective optimization does not have to be performed. When the weight are systemically varied, a full set of Pareto front points can be obtained, while having fewer objective function evaluations compared to a genetic algorithm [31].

8.3 Results

The proposed method for detection, characterization and quantification of non-linearity is demonstrated on a two-degree-of-freedom system with a cubic non-linearity described by:

$$\displaystyle{ \mathbf{M}\ddot{\mathbf{x}} + \mathbf{C}\dot{\mathbf{x}} + \mathbf{K}\mathbf{x} + \mathbf{G}\mathbf{x}^{3} = \mathbf{0},\qquad \mathbf{x}(0) = \mathbf{x}_{ 0},\quad \dot{\mathbf{x}}(0) = \mathbf{0}, }$$

where

$$\displaystyle{ \mathbf{M} = \left [\begin{array}{*{10}c} m& 0\\ 0 &m \end{array} \right ],\quad \mathbf{C} = \left [\begin{array}{*{10}c} c&0\\ 0 & c \end{array} \right ],\quad \mathbf{K} = \left [\begin{array}{*{10}c} 2k &-k\\ -k & 2k \end{array} \right ],\quad \mathbf{G} = \left [\begin{array}{*{10}c} \alpha &0\\ 0 &0 \end{array} \right ],\quad \mathbf{x} = \left [\begin{array}{*{10}c} x_{1}(t) \\ x_{2}(t) \end{array} \right ] }$$

with parameters m = 1, k = 1, c = 0. 02, α = 0. 5. The data are simulated by the direct time integration with the sampling frequency 10 Hz. Two cases of initial conditions are investigated. In the first case, only the first mode is excited so the EMD is not necessary. This is a special case which needs to be measured, for example, by the phase separation technique [4]. In the second case, general initial conditions are used so both modes are present in the response.

8.3.1 A Special Case of Single Mode Excitation

This case tries to mimic a typical measurement which is usually made for the dynamic testing based on the NNMs. In this case, the EMD of the time series is not needed since a single mode has been isolated during the (numerical) experiment. The initial conditions corresponding to the isolated first mode chosen in this study were x 0 = [1. 1282, 1. 4285]T. The response of the system can be seen in Fig. 8.1.It can be seen that both signals decay at the same (narrow-banded) frequency and that only a single mode is present. The EMD does not have to be used as the simulated responses correspond to the IMF directly. The response computed using the ROM based on the CNMs is also shown in Fig. 8.1. It can be seen that the ROM response correspond to the response obtained by direct integration very well.

Fig. 8.1
figure 1

The response for x 0 = [1. 1282, 1. 4285]T computed via direct integration (light green thick solid line) and using the ROM based on the CNM (black dashed thin line): (a ) x 1(t), and (b ) x 2(t)

Full size image

The zero-crossing method was applied to estimate the IF and IA. No intra-wave FM is estimated using this method, so no filtering was necessary. Both instantaneous characteristics are compared with their counterparts obtained from the ROM based on the CNM in Fig. 8.2.It can be seen that the estimated and computed characteristics match very well. Figures 8.1 and 8.2 support the link between the CNMs and HHT for a SDOF system or when well controlled measurements are obtained.

Fig. 8.2
figure 2

Comparison of instantaneous characteristics obtained using the HHT and ROM: (a ) amplitude, and (b ) frequency

Full size image

The estimated characteristics can be used to detect the non-linearity, characterize its type and create the optimization problem as described previously. Only two parameters were optimized—linear stiffness k and non-linear stiffness α. When the objective functions were optimized separately, two utopia points corresponding to \([k,\alpha ]_{x_{1}} = [0.99,\,0.49]\) and \([k,\alpha ]_{x_{2}} = [0.99,\,0.51]\) were found (the subscript marks the response which instantaneous characteristics were used for the optimization). It can be seen that the estimated coefficients are practically the same so that no multi-objective optimization was needed. As expected the estimated parameters correspond very well with the original ones.

8.3.2 General Initial Conditions

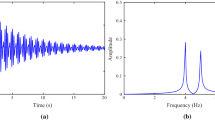
This case tries to mimic a general free decay measurement where initial conditions are not chosen specifically to isolate a single mode. In this case, the direct decomposition of the measured time series must be performed. The initial conditions chosen in this study were x 0 = [1, 0]T. The response of the system can be seen in Fig. 8.3.Unlike in the previous case, these responses decay with multiple frequencies, so both modes are present in the simulated data.

Fig. 8.3
figure 3

The response for x 0 = [1, 0]T: (a ) x 1(t), and (b ) x 2(t)

Full size image

The IMFs obtained by a basic algorithm of the EMD are shown in Fig. 8.4.It is worth noting that in order to obtain such clear results many iterations in the sifting process must be used. Generally more than 10 are needed which can lead to a loss of some information about the intra-wave modulation frequency [25]. However, from the perspective of system identification, a higher number of sifting iterations is not an issue and clearer IMFs are preferred. In total, four IMFs can be seen in Fig. 8.4. These correspond to the first and second mode of the response of the first mass (c 11 and c 12) and the response of the second mass (c 21 and c 22). All IMFs decay on a single (narrow-band) frequency, allowing the IF and IA estimation. The responses obtained using the ROM based on the CNM are also shown in Fig. 8.4. The match of the IMFs and ROM is not so good as in the previous case. It can be seen that the responses of the first mode differ in the frequencies although the amplitudes are the same.

Fig. 8.4
figure 4

Intrinsic mode functions obtained by the EMD (light green thick solid line) and corresponding responses obtained by the ROM based on the CNMs (black dashed thin line): (a ) c 11(t), (b ) c 21(t), (c ) c 12(t), and (d ) c 22(t)

Full size image

The estimated IF and IA are compared to the corresponding characteristics obtained from the ROM based on the CNMs in Fig. 8.5.The instantaneous characteristics were estimated using the normalized Hilbert transform with no smoothing, so the intra-wave frequency modulation has not been eliminated and can be used for detection and characterization of non-linearity. The ratio of intra-wave frequency modulation and fundamental frequency is approximately 2 for both modes, which indicates cubic non-linearity [6, 15].

Fig. 8.5
figure 5

Instantaneous characteristics: (a ) amplitude of the first mode, (b ) amplitude of the second mode, (c ) frequency of the first mode, and (d ) frequency of the second mode

Full size image

The instantaneous characteristics obtained using the ROM do not capture the intra-wave frequency modulation. However, it can be seen that they correspond quite well to the mean of the IF obtained by the HHT. If the smoothing were used, both frequencies would be comparable. These corresponding characteristics might justify the link between the HHT and the CNMs for a general case of initial conditions. However, in order to established the link more rigorously, more non-linear systems with different non-linearities should be investigated. In addition, it must be noted that the response of the ROM based on the CNMs do not correspond to the IMFs exactly because of the absence of the superposition principle in non-linear dynamics although they constitute some approximations of them as seen in Figs. 8.4 and 8.5.

The estimated instantaneous characteristics were used to detect the non-linearity, characterize its type and create the optimization problem. As in the previous case, only two parameters were optimized—linear and non-linear stiffness. When the objective functions were optimized separately, four utopia points corresponding to \([k,\alpha ]_{c_{11}} = [1,\,0.78]\), \([k,\alpha ]_{c_{12}} = [0.99,\,0.66]\), \([k,\alpha ]_{c_{21}} = [1,\,0.71]\), and \([k,\alpha ]_{c_{22}} = [1,\,0.49]\) were found (the subscript marks the IMF which characteristics were used for the optimization). In this case, the estimated parameters are not the same, so the multi-objective optimization was necessary. The parameters were p = 1 and w i  = 0. 25, indicating an equal weight for each objective function. The final optimized values were [k, α] = [1, 0. 65], so the linear stiffness was estimated very well, whereas the non-linear cubic stiffness coefficients was estimated with an error of 30%.

8.4 Conclusion

The objective of this paper was to discuss how the Hilbert-Huang transform (HHT) can be used for detection and characterization of non-linearity, and to present an optimization framework which combined the HHT and complex non-linear modal analysis for quantification of non-linearity. The proposed method was demonstrated on two simulated cases and led to the sufficient accuracy of optimized parameters. The method explores the connection of the HHT and CNMs through the ROM of slow-flow dynamics. Despite encouraging results, it cannot be conclusively stated that the HHT is linked, at least approximatively, to the CNMs through the ROM. In order to prove this link conclusively (at least empirically), more non-linear systems with different non-linearities and complexities should be studied in the future, and experimental demonstration conducted. The method is generally valid if all its parts fulfil their assumptions, for example the ROM can be only computed when no mode interactions exist. Overall, the proposed method may be seen as a well-suited method for complete non-linear system identification, providing information about the presence and character of non-linearity as well as an optimized model of the structure, while being partly non-parametric and applicable to a wide range of non-linear systems and excitation types.