Which Map Is Best?

Abstract

A map projection is what cartographers call the system by which the rounded surface of the Earth is transformed in order to display it on a flat surface. It is not easy. Numerous ways have been devised, but no matter how one does it, something will be wrong with the shapes and relative sizes of regions and the distances and directions among places.

This chapter is slightly modified version of the Special Publication No. 1 of the American Cartographic Association, a member organization of the American Congress on Surveying and Mapping, 210 Little Falls Street, Falls Church, VA 22046. The Special Publication No. 1, ISBN 0-9613459-1-8, has been published in 1986 by the American Congress on Surveying and Mapping.

In that time, the Committee on Map Projections consisted of the following distinguished members: James R. Carter, Marshall B. Faintich, Patricia Caldwell Lindgren, Barbara B. Petchenik, Arthur H. Robinson and John P. Snyder, Chairman. Text and design was by Arthur H. Robinson, computer plotting of projections and coastlines by Waldo R. Tobler and preparation of graphics by the University of Wisconsin Cartographic Laboratory.

Permission granted by Eric Anderson, Executive Director for CaGIS, 2011–2016

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1.1 Foreword

A map projection is what cartographers call the system by which the rounded surface of the Earth is transformed in order to display it on a flat surface. It is not easy. Numerous ways have been devised, but no matter how one does it, something will be wrong with the shapes and relative sizes of regions and the distances and directions among places.

We see a great many world maps . Many, probably most, of the projections used for them were chosen, not because they displayed geographical relationships well, but instead for “practical” reasons: already-made maps were available, a map could be easily copied, the map would fit conveniently a page format or a wall, or the map was a current fad, and so on. Equally disturbing is that most viewers seem not to care when blatantly distorted geographical shapes and sizes are displayed without reason.

1.2 Which Map Is Best?

For the least distortion the best map is one on a globe, since all the geographical relationships are correctly displayed. But globes are bulky, expensive, and do not permit the entire surface to be seen at once. Flat maps are better for most purposes.

Which projection is best for a world map? The flip answer is “none,” but that is not a good question. A better question would be: Which map projection is best for what purpose? One can narrow the options by deciding whether one wants to show shapes of features as well as possible, or correct sizes, or a good compromise between the display of shapes and sizes, or to suggest the roundness of the Earth, or to show easily how far it is from here to there, or whatever.

A poorly chosen map projection can actually be harmful. We tend to believe what we see, and when fundamental geographical relationships, such as shapes, sizes, directions, and so on, are badly distorted, we are inclined to accept them as fact if we see them that way on maps. This can lead to very wrong impressions, for example, that the route from Chicago to Rome is due east or from San Francisco to Tokyo is due west, or that North America is larger than Africa. Our mental maps , the brain’s geographical “data base,” are generated only from what we look at. Since globes are uncommon, most mental images of the Earth come from flat maps. A badly distorted map seen regularly (such as one on a television news program backdrop) will look familiar after a while and thus “look right.” This can cause one’s mental map of the world to become permanently warped.

1.3 Scale, Globe Maps and Flat Maps

A map is not a simple drawing of the Earth’s surface, but it is a model obtained on the basis of certain mathematical laws. First, we pass from the physical Earth’s surface onto a mathematical surface—rotational ellipsoid or sphere . This transfer is realised by means of orthogonal projection of physical surface points onto the mathematical surface by using a geodetic control network enabling correct geographic location and orientation of map contents within the frame of some co-ordinate network. This is followed by the transfer from the rotational ellipsoid surface or sphere onto a plane. These projections are called map projections and are the subject of the theory of map projections .

Scale is the approximate size relationship between a map and the real world. It is often expressed by a ratio, such as 1:330,000,000, that tells how many units (inches, centimeters, etc.) on the Earth surface model (a sphere or an ellipsoid of revolution) are represented by one of the same units on the map. A globe of that scale would have a diameter of 39 mm (about 1 1/2 in.).

Conceptually the projection process begins by first reducing the Earth to a globe at a chosen scale and then flattening that globe to make a flat map. But—and it is an important but—whereas the distance scale is the same everywhere on the globe, it will be the same on the flat map only at a point or along certain lines in particular directions. Everywhere else it will be larger or smaller, which is why distortion occurs in all flat maps. One can say only that the nominal scale of the flat map is that of the globe.

The several views in Fig. 1.1 are of a globe with a scale of 1:330,000,000. All the other projections illustrated in this chapter are derived from this same globe; therefore, they all have the same nominal scale .

Fig. 1.1

Orthographic projection : It is one of the oldest and still a favorite. It “looks right” because the increase in distortion toward the edges matches the normal perspective foreshortening that occurs when one observes something spherical. In visual terms, it is a realistic view of a globe

Actually the best way to appreciate the way a flat map distorts the surface of the globe is to compare it physically with a globe of the same scale. As an alternative to having one in hand, we show several views of a globe of the same scale alongside each projection so that the reader can make direct comparisons of what the map on the globe looks like and what the flattening process has done to it.

Although it can show only a hemisphere at a time, it can be considered a projection for world maps because a matched pair does display the whole Earth. Individual hemispheres are useful when interest is focused on one region. The projection can easily be made to place any region in the center where the shapes are not significantly distorted.

1.4 What Kinds of Projections for World Maps Are There?

There is a variety of map projections, and cartographers classify them in many ways. In this section we are concerned with kinds of projections distinguished by two visual characteristics: their overall shape and the arrangement on the map of the network of parallels and meridians (lines of latitude and longitude , or the graticule ).

A globe’s surface can be transformed to fit within any outline on a flat surface. As a matter of fact, such shapes as a valentine-like heart, a star, and even a stylistic butterfly have enclosed a map of the Earth. More traditionally, three simple shapes have been used: circles, ovals, and rectangles. Examples of each are included in this chapter.

Unless there is some compelling reason for not doing so, it is reasonable to assume that a general map of the whole world ought at least to suggest that we do live on a spherical Earth. Unfortunately, circular world maps have a great amount of distortion near their edges, and oval maps have been more widely used.

The meridians and parallels we use for the coordinate system define our cardinal directions, north-south and east-west. Except at the poles, they are everywhere at right angles to one another. Although this attribute of the globe can be duplicated on a flat map with curved lines, it is easier with straight lines. This forces the world into a rectangular shape, takes away the suggestion of sphericity, and no matter how it is done, much distortion is inevitable.

Because a sphere has no beginning or end it makes no difference how the transformation process is applied. But the Earth’s coordinate system , anchored to the surface by the poles, will look quite different depending upon where the transformation originates. If it is centered at the equator, the graticule will appear orderly and symmetrical around two straight lines: the equator and meridian in the center of the map. Such projections are called normal or conventional.

The equator on a projection with the same nominal scale as the globe is often the same length. That is, if the globe were 10 in. around at the equator, the equator on the map would also be 10 in. long. In cartographic terminology, a line on a projection along which the scale is constant and that is the same length on the globe is sometimes called a standard line .

1.5 What Are the Kinds of Distortions?

All projections distort the globe surface in at least two and often all three of the following ways:

• Sizes of regions appear larger or smaller than on the globe.

• Distances between points are shown as longer or shorter than on the globe.

• Direct routes between points are not shown as straight lines.

The larger the area covered by the map the larger the amount of distortion; thus, it is greatest on world maps .

To a limited degree some of these distortions can be “controlled.” For example, the correct relative sizes of regions can be maintained; such projections are called equal-area. Many other attributes of the globe surface can be retained, such as showing the direct routes from one place to all others as straight lines (such projections are called azimuthal), or showing all directions correctly arranged at each point. This last property, called conformality, is quite technical and is very useful for specific purposes, such as navigation.

The representation of sizes can be controlled. Equal-area, oval projections , such as those in Fig. 1.2, greatly deform shapes. Among such projections, in the conventional aspect, less shape distortion in equatorial sections results in more in polar regions and vice versa.

Fig. 1.2

Sinusoidal (top) and Mollweide (bottom) equal-area, oval projections . In the Sinusoidal all parallels and the central meridian are standard lines . In the Mollweide only one parallel, about 40°, is a standard line. Shapes are good in the central section of the Sinusoidal but are compressed in high latitudes . In the Mollweide, shapes are elongated in the lower latitudes but less crowded in the polar areas

There are two ways of dealing with the problem of shapes in oval, world map projections. One is to break up the smooth outline by separating it into lobes. Each lobe may be centered on a continent (or an ocean), thus lessening the crowding and shearing that occurs when all meridians converge to a single point at each pole. One example, an equal-area, interrupted projection , is shown in Fig. 1.3. Another way is to show the poles as lines instead of points, as in Fig. 1.4, thus decreasing the apparent distortion; it will still be there but in a less concentrated and noticeable form.

Fig. 1.3

Interrupted Goode Homolosine, equal-area projection . This is a combination of the better-shaped, equatorial section of the Sinusoidal projection and the less-compressed polar section of the Mollweide projection . In addition, each continental segment is centered around its own central meridian , thereby using the least distorted sections of the projections for the land areas. Ocean areas could be featured instead

Fig. 1.4

Robinson projection . A compromise projection to show the whole Earth uninterrupted with reasonable shapes. It departs somewhat from being equal-area, especially in the high latitudes , in order to provide better shapes in the mid- and low-latitude regions

An alternative to the greatly distorted displays in uninterrupted, equal-area maps are compromise projections that allow some size distortion in order to improve the general representation of shapes. Three examples are shown in Figs. 1.4, 1.5 and 1.6.

Fig. 1.5

Van der Grinten projection . A compromise projection showing the entire Earth within a circle. Shape and size distortions increase away from the central section, particularly in the high latitudes . Most of the greatly enlarged polar areas are left out when this projection is used, but then it is no more the map of the world. Four Van der Grinten projections were among the most popular new projections of the twentieth century. His first projection was adopted in 1922 for the National Geographic Society’s official new world map . In 1988, the society chose the Robinson projection to replace the Van der Grinten, and in 1998 the Winkel Tripel was introduced and retained until today (Fig. 1.6)

Fig. 1.6

Winkel Tripel projection , a modified azimuthal map projection of the world, is one of three projections proposed by Oswald Winkel in 1921. Adopetd by the National Geographic Society as the official world map in 1998

1.6 Cylindrical Projections

To force the spherical globe into a rectangle produces extreme shape distortion , but surprisingly most people do not complain.

In the normal aspect of a cylindrical projection, the meridians are equally-spaced, parallel lines. They are crossed at right angles by the parallels of latitude , just as they are on the globe. Although the orderly grid may seem right, there are some catches that make the graticule as bothersome as it is on oval maps. For example, on the globe, except at the equator, north-south lines are never parallel, and except on the equator, the shortest route to a place on the same parallel is not along that parallel. On a cylindrical projection the poles (mere points on the globe) are stretched to become lines as long as the equator, and all parallels of latitude are shown as being that same length.

Why are cylindrical projections rather common in spite of their extreme distortion of shapes, their lack of any suggestion of sphericity, and the unreality of their graticule? To a designer a rectangle is neat: It fits nicely on a rectangular page or wall, and it does not leave awkward, empty corners as oval projections do.

Probably equally, if not more important, is that they became relatively familiar because a rectangular grid has been used as the base for all nautical charts since the 15th century. Sailors try to maintain a course with a constant direction, called a rhumb or rhumb line , and for them to know where it will lead, it should plot as a straight line on their chart. Only when the meridians and parallels are spaced a certain way on a cylindrical projection can this occur. Gerardus Mercator obtained the required spacing by increasing the north-south scale poleward at the same rate that the east-west scale was increased—a result of making the meridians parallel straight lines instead of converging as they are on the globe (Fig. 1.7). Since the poles are only points, the projection extends indefinitely to the north and the south. Although he intended it to be used on sailing charts, Mercator first published the projection in 1569 as a world map to illustrate the concept.

Fig. 1.7

Mercator projection . It is conformal and has the unique attribute that any rhumb is shown as a straight line. It greatly exaggerates sizes away from the equatorial areas, as a comparison with the accompanying globes shows. It does not show true direction since all great circles , other than the meridians and the equator, plot as complex curves. It should not be used as a base for a general purpose map of the entire world

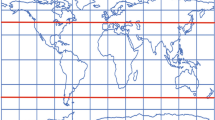
The Mercator grid became very well known, and it began to be used for general world maps even though for such a purpose the fact that rhumbs are straight lines is not at all significant. Unfortunately, it is still often chosen for such maps. It is shown in Fig. 1.7. There have been several similar-looking substitutes devised to lessen the extreme distortion in the areas near the poles. None is conformal like the Mercator. One, the Miller Cylindrical, is shown in Fig. 1.8.

Fig. 1.8

Miller Cylindrical projection . A compromise projection showing the entire Earth in a rectangle without as much size exaggeration in the high latitudes as in the Mercator projection . It is not equal-area. In contrast to the Mercator, the poles can be shown

An infinite number of cylindrical projections can be made equal-area, simply by selecting a parallel to be standard and then spacing the others appropriately. Shapes are severely distorted in all of them. One such grid, first presented by Gall in 1855 and again by Peters in 1967, has been adopted by some non-cartographers who are not troubled by the unreality of the graticule and the extreme shape distortion. It is shown in Fig. 1.9.

Fig. 1.9

Gall-Peters equal-area projection . To be equal-area within the rectangle determined by using standard parallels of 45° causes the equatorial regions to be greatly lengthened vertically and squeezed horizontally, while the higher latitudes are greatly lengthened horizontally and squeezed vertically

The name cylindrical projections comes from the fact that the image of the world in any of such projections is a rectangle, and a rectangle can be wrapped into cylindrical surface.

1.7 Direction and Distance on Map Projections

Direction on the globe is tricky. The spherical coordinate system that defines our directions is not internally consistent like the grid lines of a square, plane, Cartesian system. To appreciate how direction may or may not be shown on maps, we need to understand that the straight course, that is, the shortest route between points on a globe, is always along a line called a great circle. A complete great circle separates the globe into hemispheres . The equator is a great circle and each meridian is half a great circle. If you stretch a piece of string anywhere on a globe, it will lie on a great circle.

Any oblique great circle on the globe, that is, one that is neither along the equator nor along a meridian , that connects point A and point B will intersect the parallels and meridians at successively different angles all along its course. Consequently, the only way to designate the direction from A to B is to note the angle (direction) the great circle makes with the meridian at A. This is called the azimuth of B at A. Furthermore, except for any meridian or the equator which may be straight, most other great circles will not appear as straight lines on map projections.

The distance from A to B on the globe, along the great circle segment that connects them, is stated in any convenient unit of length, such as miles or kilometers. The scale necessarily varies from place to place on a projection. On standard lines of the graticule the unit will be true, that is, it will be the same length on a globe of the same nominal scale , but along other lines the units may be shown as equal but not true.

Several azimuthal projections show the correct course and direction from the center of the map to any other point by a straight line, but all other great circles (that is, not through the center) will be curved. The orthographic projection (Fig. 1.1) is one such projection. Only one azimuthal projection can show usefully the entire Earth within a circle, and in addition, by displaying true scale along the straight-line great circles, it is also equidistant, as shown in Fig. 1.10.

Fig. 1.10

Azimuthal-Equidistant projection centered near Chicago. Its purpose is to show all the great circle routes through the center as straight lines with correct azimuths at the center and to show the distances along the straight-line great circles with a uniform scale . It is not equal-area, and shapes in the outer half are greatly distorted. It is useful because it can be centered at any point, such as your home town

1.8 A Final Comment

A globe cannot be transformed to a flat map without distortion , but scores of systems have been devised to display various features and Earth relationships in advantageous ways. Some, like the Mercator, are excellent for a particular purpose but not for most others. A number can be used for general maps, and some for focusing attention on one region, or for making particular measurements, or for various other applications. There are many options.

Map projections should be selected and used with care.