An Object Splitting Model Using Higher-Order Active Contours for Single-Cell Segmentation

Abstract

Determining the number and morphology of individual cells on microscopy images is one of the most fundamental steps in quantitative biological image analysis. Cultured cells used in genetic perturbation and drug discovery experiments can pile up and nuclei can touch or even grow on top of each other. Similarly, in tissue sections cell nuclei can be very close and touch each other as well. This makes single cell nuclei detection extremely challenging using current segmentation methods, such as classical edge- and threshold-based methods that can only detect separate objects, and they fail to separate touching ones. The pipeline we present here can segment individual cell nuclei by splitting touching ones. The two-step approach merely based on energy minimization principles using an active contour framework. In a presegmentation phase we use a local region data term with strong edge tracking capability, while in the splitting phase we introduce a higher-order active contour model. This model prefers high curvature contour locations at the opposite side of joint objects grow “cutting arms” that evolve to one another until they split objects. Synthetic and real experiments show the strong segmentation and splitting ability of the proposed pipeline and that it outperforms currently used segmentation models.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The development of an automated, reliable segmentation method for cellular images is often challenging due to touching or overlapping cell nuclei clumps. The segmentation of the individual cells is usually performed in two phases. In the presegmentation phase, the localization of the foreground objects or the region of interest (single cells or clumps of cells) is performed followed by the identification of the individual cells in the clumps during second phase. The presegmentation methods include simple intensity thresholding [8] (e.g. Otsu segmentation) variance measures [11]. Energy minimization methods, such as graph cut [1, 20] or active contour models [2,3,4] are also used with high efficiency in this area [6]. In the second phase, cell nuclei clumps are separated into individuals. A big variety of methods were introduced to this area, usually utilizing a priori knowledge about the shape of individual objects.

A large family of such priors assume object ellipticity [9, 12, 16]. These priors are very effective for clusters of homogeneous objects, but can fail if the cluster is composed of diverse shapes. Other popular approaches prefer less specific priors and the separation of cell clusters mainly based on two underlying principles: either the localization of the individual cell centers [5, 15, 18, 19, 23] or the concavity analysis of shape boundaries [6, 8]. In the former case, once cell centers are determined, effective methods such as repulsive active contours [19], voronoi tessellation [5, 10], gradient flow back-tracking [15] or watershed [18] are used, however the accurate cell-center localization is still a challenging task. Methods based on the cluster boundary information include: the minimum model approach [22], graph cut [6, 8] and rule based segmentation [13].

In this paper we present a cell segmentation framework merely based on energy minimization principles. The main components are the following (a) image normalization, using illumination correction [21], (b) presegmentation, using anisotrop local region active contour, (c) splitting of clumped objects using a novel higher order active contour model. The structure of the paper is as follows: in Sect. 2.2 we analyze the properties of the local region based active contour model, highlighting its strong edge tracking capability, in Sect. 2.3 we introduce a higher order functional designed for cluster splitting and in Sect. 3 we present our experimental results and compare with the most frequently used method in cell segmentation.

2 The components of the cell segmentation framework

In this section we introduce the model designed to efficiently segment foreground objects (cell clumps) and split them into simple, non-further-splittable parts. The presegmentation is performed by a local-region active contour (see Sect. 2.2) which effectively tracks object boundaries even if they are slightly overlap or touch each other. After this step, remaining objects have no longer edges to be tracked. A purely geometric splitting functional (see Sect. 2.3) is designed as a second step that splits these objects further by penalizing high curvature contour regions (see Fig. 3) and moving them towards each other until they cut.

2.1 Notations

The point set of the image plane is denoted by $\varOmega$, parameterized by Cartesian image coordinates x and y, $\left[ x,y\right] \in \varOmega \subset \mathbb {R^{\mathrm {2}}}$. Contours are closed planar curves, given as vector valued function of a curve parameter t such that: $\varOmega \mathbf {\supset r}\left( t\right) =x\left( t\right) \mathbf {i}+y\left( t\right) \mathbf {j}$, where $\mathbf {i}$, $\mathbf {j}$ are the standard basis vectors and $\mathbf {k}\doteq \mathbf {i}\times \mathbf {j}$ is the unit normal vector of the image plane. The unit tangent vector of the contour is $\mathbf {t}\doteq \frac{\mathbf {\dot{r}}}{\left| \mathbf {\dot{r}}\right| }$, $\mathbf {\dot{r}}=\frac{d\mathbf {r}}{dt}$. The unit normal vector of the contour $\mathbf {n}$ is defined by the plane normal $\mathbf {k}$ as $\mathbf {n}=\mathbf {k}\times \mathbf {t}$. Note that assuming $\mathbf {i},\mathbf {\,j},\mathbf {\,k}$ are right-handed, contours that are parameterized counter-clockwise have normal vectors pointing inwards. Arclength of the curve is denoted by s. The coordinate differentials and differential operators are related with $ds=\left| \mathbf {\dot{r}}\right| dt$ and $\frac{d}{ds}=\frac{1}{\left| \mathbf {\dot{r}}\right| }\frac{d}{dt}$ respectively. The signed curvature of the contour is denoted by $\kappa$, defined with the help of the plane normal as $\frac{\mathbf {\ddot{r}}\cdot \mathbf {n}}{\left| \mathbf {\dot{r}}\right| ^{2}}$.

Fig. 1.

Local regions are defined by the local Cartesian coordinate systems with the unit tangent and normal basis vectors. The data metric used for segmentation is the difference of the mean intensities of the regions distinguished by positive/negative local ordinate values.

2.2 The Local Region Active Contour

The presegmentation is performed by using a local-region active contour discussed in details in [17]. Here we summarize the theoretical background and the properties of this method.

The local region along the contour is defined by local Cartesian coordinate system. The functional $\oint \varPhi \left( \mathbf {r},\mathbf {n}\right) ds$ contains the local coordinate system explicitly, represented by the unit normal vector of the contour. Note that the inclusion of either the unit normal or the unit tangent vector is equivalent, because in case of planar curves they are related by $\mathbf {n}=\mathbf {k}\times \mathbf {t}$. This functional was originally introduced in [7] for 3D reconstruction purpose. Applying this for image segmentation, requires the Lagrangian to be specialized. We use the difference of the mean image intensities given by local integrals

(1)

as introduced in [17], where the quantities are defined in Fig. 1. Using the local region active contour has the following advantages:

• its region-based nature does not require preliminary noise removal

• no smoothness term is required, the minimizing contour is not over-smoothed

• anisotropic: the gradient descent direction of the contour points depend on the image intensity distribution in the local regions

The last two properties explain the advantageous feature of the local-region active contours: they can track image edges even if the gaps between the foreground objects are very narrow (Fig. 2).

Fig. 2.

Comparison of isotropic/anisotropic segmentation results: original image (left), isotropic segmentation (middle) and anisotropic segmentation (right).

2.3 The Split Functional

To design the split functional we are using an analogy from electrostatics. The variational formulation of the charge density distribution $\varrho \left( \mathbf {r}\right)$ on a conductor can be characterized with the total potential energy of the system as: $\oint \oint \varrho \left( \mathbf {r}\right) \varrho \left( \mathbf {r^{\prime }}\right) l\left( d\left( \mathbf {r},\mathbf {r}^{\prime }\right) \right) d\varOmega d\varOmega ^{\prime }$, where $d\left( \mathbf {r},\mathbf {r}^{\prime }\right)$ is the Euclidean length between two points of the conductor, $l\left( d\right) =\frac{1}{\left| \mathbf {r}-\mathbf {r}^{\prime }\right| }$. The minimizer of this system¹ is the equipotential distribution of the charge on the conductor surface. We will use this analogy with the following differences: (a) the problem is applied to planar curves; (b) the force acts between the contour points is attractive and anisotropic (explained later); (c) the “attractive charges” fixed to the contour points hence the contour evolves to reach the minimal energy.

First, we assume that the set of object that compose the clump of nuclei cannot be further segmented using the local-region active contour model due to missing edge information between the parts. The splitting functional should therefore be based on purely geometric information. Second, we reduce the set of contour points to a subset satisfying certain concavity and alignment criteria. We call it “feasible subset”. The complement set of the “feasible subset” remains intact during the process. The feasible contour points are handled as weighted, oriented particle set. The associated orientation is defined by their normal vector $\mathbf {n}$, the weighs by their concavity as shown on Fig. 3. Within an energy minimization framework, the concavity is indicated by negative curvature $\kappa <0$. The aliment of two oriented points (indexed by 1, 2) is defined by the relation of their orientations and relative position such that $a_{12}\doteq \mathbf {n}_{1}\cdot \mathbf {e}_{12}+\mathbf {n}_{2}\cdot \mathbf {e}_{21}$, where $\mathbf {e}_{12}$ is the unit normal vector pointing from point 1 to 2, and $\mathbf {e}_{21}=-\mathbf {e}_{12}$. Note that this definition of the alignment is symmetric, i.e. $a_{12}=a_{21}$. Now one can define the “anisotropic energy” for a pair of points as $U_{12}\doteq f\left( \kappa _{2}\right) f\left( \kappa _{1}\right) g\left( a_{12}\right) l\left( d_{12}\right)$ with $d_{12}$ being the Euclidean distance between the points and $f,\,g,\,l$, are appropriately chosen functions discussed in the next subsection. Taking $f\left( \kappa \left( s\right) \right)$ as the density of the potential source (the “attractive² charge”) along the contour, the second-order functional:

$$\begin{aligned} -\oint \oint f\left( \kappa \left( s\right) \right) f\left( \kappa \left( s^{\prime }\right) \right) g\left( a\left( s,s^{\prime }\right) \right) l\left( d\left( s,s^{\prime }\right) \right) ds^{\prime }ds \end{aligned}$$

(2)

represents the total energy of the contour. The integral is evaluated only on the feasible subset, defined as:

$$\begin{aligned} \left[ \mathbf {r}\left( s\right) \mid \kappa \left( s\right) <-\varepsilon \wedge a\left( s,s^{\prime }\right) >\delta \right] . \end{aligned}$$

(3)

Points out of the “feasible subset” do not contribute to the total energy. Note that the minimization of the negative of the simplified functional with $g\equiv 1,\,l\equiv 1$ would result in the convex hull of the initial contour. Functional (2) represents a geometric contour, the associated Euler-Lagrange equation has component only in the normal direction (see Appendix). We solve it iteratively via gradient descent, using the Level Set method.

Fig. 3.

Illustration of the object cutting method. Contour points connected by continuous line are well aligned, whilst points connected by dashed line are not.

2.4 The Roles of the Functions

The most important part of the Lagrangian (2) is the alignment function $g\left( a\left( s,s^{\prime }\right) \right)$. The appropriately designed function keeps the correct orientation (prevents biasing from the aligned direction) between the approaching tips of the “cutting arms” during the evolution process. It also guarantees the stability of the cutting arm preventing it from unexpected bifurcation. Note that we use the smooth version of the curvature for the same reasons. (The smoothing is done by simple averaging the curvatures of a small neighborhood.) The function in Fig. 4 left acts as potential barrier with minimum at the maximal alignment. The simplest splitting functional contains only the alignment function (this special form can be derived from the general functional setting the other constituent functions ($f,\,l$) identically constant one). This however, would represent a system with energy indiscriminate w.r.t. the distance between the points of the feasible subset.

Fig. 4.

The graphs of the Aligment (left) and the Curvature (right) functions. Both can be considered potential barriers. Points outside the feasible subset marked with dashed line.

To favor point pairs otherwise appropriate, the distance function $l\left( d\left( s,s^{\prime }\right) \right)$ is introduced in the functional (2) such that closer points exhibits bigger attractive force than further ones. The distance function may have limited scope as well.

The suitable function of the curvature can provide further stability for the “cutting arms” enforcing their tips to favor certain curvature value, thus make further bifurcations unlikely. This function can be chosen to be potential barrier. Its minimum value determines the curvature of the cutting tip, hence the width of the cutting arms (Fig. 4) as well.

3 Results

To demonstrate the segmentation ability of the proposed method we present quantitative results on synthetic images and qualitative results on real images of cancer cells.

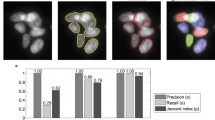
The synthetic data was created using the SIMCEP simulation tool [14] designed to test and evaluate image analysis methods for fluorescent microscopy. 60 images were generated each containing 20 nuclei of a similar size and clustering into 3–5 clusters. A slight, maximum 5%, overlap was allowed between individual cells. The method was compared to CellProfiler using its IdentifyPrimaryObjects module with intensity- and shape-based clumped object splitting options [10]. To evaluate the segmentation quality of the proposed method and compare to others we used three metrics that was proposed earlier [16]. To analyze segmentation accuracy at object level we calculated precision and recall values. Precision is the ratio of true positives (TP) to the number of detected objects (Precision = TP/(TP + FP)), while recall (or sensitivity) is the proportion of the objects of interest is found (Recall = TP/(TP + FN)). Values close to 1 represent more accurate detection. First, a matching between the ground truth and the set of segmented objects was made. TP is the number of segmented objects with matching ground truth object, while FP is the number of segmented objects that have no matching ground truth object. FN is the number of ground truth objects that have no matching segmented object. The third metric was the Jaccard-index for pixel-level accuracy, a similarity measure between sets: $\text {JI}(A,B) = |A\cap B|/|A\cup B|$, for each matched pair. Figure 5 shows sample images of CellProfiler’s intensity-based (Fig. 5 upper left) and shape-based (Fig. 5 middle) methods and results obtained using the proposed splitting model (Fig. 5 upper right).

Fig. 5.

Results on simulated data. Upper row: (left): intensity-based watershed method, (middle): shape-based watershed method; (right): result with the proposed method. Bottom plot: precision, recall and Jaccard-index statistics of the methods.

Figure 6 represents results obtained using the proposed method on real images of cancer cell cultures. The method was able to successfully identify single cells in this highly complex environment.

Fig. 6.

Sample results on real microscopic image data of cancer cells.

4 Conclusion and Future Work

We presented a novel approach that successfully separates touching cells using intensity and cell clump geometry properties. The method first performs a segmentation based on local intensity differences, than closes contour arms opposite to each other. Experimental results show that the method outperforms currently used ones and has the potential to became the de facto cell segmentation tool for certain bioimage segmentation problems. Due to the active contour framework we used, it is possible to incorporate further shape prior information into the segmentation.

In the future, we will extend the model to 3D and provide a solution for the most recent cell segmentation challenges including cancer drug discovery in 3D environment or tissue analysis using deep imaging. The model will be implemented on GPU to speed up processes.

Appendix

The derivation of the Euler-Lagrange equation associated to functional (2) is straightforward albeit long. Here we only provide the result. The notations used in the equations are the following: the point at contour parameter t is designated by position vector $\mathbf {r}\left( t\right)$. The bound variable of the integrals is denoted by $\tau$, hence the invariant arc length: $ds=\left| \dot{\mathbf {r}}\right| d\tau$ (the derivatives of the position vector w.r.t. the contour parameter are denoted by dots: $\dot{\mathbf {r}},\,\mathbf {\ddot{r}}\ldots$). The unit tangent and normal vectors of the contour are denoted by $\mathbf {e},\,\mathbf {n}$, where $\mathbf {e}=\frac{\dot{\mathbf {r}}}{\left| \dot{\mathbf {r}}\right| }$. Using right handed coordinate system, they are related with $\mathbf {n}=\mathbf {k}\times \mathbf {e}$, where $\mathbf {k}$ is the normal of the image plane, hence the contour normals point inward. The (signed) curvature of the contour is given by $\kappa =\frac{\mathbf {\ddot{r}}\cdot \mathbf {n}}{\left| \mathbf {\dot{r}}\right| ^{2}}$. The unit direction vector between points given by contour parameters t and $\tau$ is denoted by $\mathbf {e}_{t\tau }=\frac{\mathbf {r}_{\tau }-\mathbf {r}_{t}}{d_{t\tau }}$, where $d_{t\tau }=\left| \mathbf {r}_{\tau }-\mathbf {r}_{t}\right|$ is their Euclidean distance. We also use the normal to this direction vector with definition $\mathbf {n}_{t\tau }=\mathbf {k}\times \mathbf {e}_{t\tau }$. The alignment between contour points is defined by $a_{t\tau }\doteq \mathbf {n}\left( t\right) \cdot \mathbf {e}_{t\tau }+\mathbf {n}\left( \tau \right) \cdot \mathbf {e}_{\tau t}$ ($\mathbf {e}_{\tau t}=-\mathbf {e}_{t\tau }$). $f,\,g,\,l$ are the appropriately chosen functions of the curvature, alignment and distance respectively, for their derivatives we use prime mark $f^{\prime },\,f^{\prime \prime }\ldots$ The first and second derivatives of the curvature w.r.t. the arc length are denoted by $\frac{d\kappa }{ds},\,\frac{d^{2}\kappa }{ds^{2}}$. The curvature and its derivative are scalars. Note that the derivative w.r.t. the arc lenght of any scalar quantity q can be calculated on the planar grid using the formula: $\left( \nabla q\right) \cdot \mathbf {e}$, where $\nabla$ is the gradient operator with components being the partial derivatives $\left( \frac{\partial }{\partial x},\frac{\partial }{\partial y}\right)$ w.r.t. image coordinates $x,\,y$.

The formula: $A=\mathbf {e}_{t\tau }\cdot \left( \mathbf {e}\left( t\right) -\mathbf {e}\left( \tau \right) \right)$, $B=\mathbf {e}_{t\tau }\cdot \left( \mathbf {n}\left( t\right) -\mathbf {n}\left( \tau \right) \right)$,$C=\left[ \frac{l\left( d_{t\tau }\right) }{d_{t\tau }}-l^{\prime }\left( d_{t\tau }\right) \right]$, $D=\mathbf {e}_{t\tau }\cdot \mathbf {n}\left( t\right)$, $E=\mathbf {e}_{t\tau }\cdot \mathbf {e}\left( t\right)$, $F=\mathbf {n}\left( \tau \right) \cdot \mathbf {e}\left( t\right)$ are introduced to simplify the equation. The Euler-Lagrange equation associated to the half of (2) at point t has the form $\left| \dot{\mathbf {r}\left( t\right) }\right| Q\mathbf {n}\left( t\right) =\mathbf {0}$, where Q is given by the following sum:

$$\begin{aligned} -\left[ f^{\prime \prime \prime }\left( \frac{d\kappa }{ds}\right) ^{2}+f^{\prime \prime }\frac{d^{2}\kappa }{ds^{2}}\right] \oint g\left( a_{t\tau }\right) l\left( d_{t\tau }\right) f\left( \kappa \left( \tau \right) \right) ds\\ -2f^{\prime \prime }\frac{d\kappa }{ds}\oint g^{\prime }\left( a_{t\tau }\right) l\left( d_{t\tau }\right) \frac{AD}{d_{t\tau }}f\left( \kappa \left( \tau \right) \right) ds\\ +2f^{\prime \prime }\frac{d\kappa }{ds}\kappa \oint g^{\prime }\left( a_{t\tau }\right) l\left( d_{t\tau }\right) Ef\left( \kappa \left( \tau \right) \right) ds\\ +2f^{\prime \prime }\frac{d\kappa }{ds}\oint g\left( a_{t\tau }\right) l^{\prime }\left( d_{t\tau }\right) Ef\left( \kappa \left( \tau \right) \right) ds\\ -f^{\prime }\oint g^{\prime \prime }\left( a_{t\tau }\right) l\left( d_{t\tau }\right) \left[ \frac{\left( B-\kappa \left( t\right) d_{t\tau }\right) E+F}{d_{t\tau }}\right] ^{2}f\left( \kappa \left( \tau \right) \right) ds\\ +f^{\prime }\kappa \oint g^{\prime }\left( a_{t\tau }\right) l\left( d_{t\tau }\right) \frac{AE-2}{d_{t\tau }}f\left( \kappa \left( \tau \right) \right) ds\\ +f^{\prime }\kappa ^{2}\oint g^{\prime }\left( a_{t\tau }\right) l\left( d_{t\tau }\right) Df\left( \kappa \left( \tau \right) \right) ds\\ +f^{\prime }\oint g^{\prime }\left( a_{t\tau }\right) l\left( d_{t\tau }\right) \frac{BD^{2}}{d_{t\tau }^{2}}f\left( \kappa \left( \tau \right) \right) ds\\ -2f^{\prime }\oint g^{\prime }\left( a_{t\tau }\right) \frac{ACDE}{d_{t\tau }}f\left( \kappa \left( \tau \right) \right) ds\\ +2f^{\prime }\kappa \oint g^{\prime }\left( a_{t\tau }\right) CE^{2}f\left( \kappa \left( \tau \right) \right) ds\\ -f^{\prime }\kappa ^{2}\oint g\left( a_{t\tau }\right) l\left( d_{t\tau }\right) f\left( \kappa \left( \tau \right) \right) ds\\ +f^{\prime }\kappa \oint g\left( a_{t\tau }\right) l^{\prime }\left( d_{t\tau }\right) Df\left( \kappa \left( \tau \right) \right) ds\\ -f^{\prime }\oint g\left( a_{t\tau }\right) l^{\prime }\left( d_{t\tau }\right) \frac{D^{2}}{d_{t\tau }}f\left( \kappa \left( \tau \right) \right) ds\\ -f^{\prime }\oint g\left( a_{t\tau }\right) l^{\prime \prime }\left( d_{t\tau }\right) E^{2}f\left( \kappa \left( \tau \right) \right) ds\\ +f\kappa \oint g^{\prime \prime }\left( a_{t\tau }\right) l\left( d_{t\tau }\right) E^{2}f\left( \kappa \left( \tau \right) \right) ds\\ -f\oint g^{\prime \prime }\left( a_{t\tau }\right) l\left( d_{t\tau }\right) \frac{ADE}{d_{t\tau }}f\left( \kappa \left( \tau \right) \right) ds\\ -f\kappa \oint g^{\prime }\left( a_{t\tau }\right) l\left( d_{t\tau }\right) Df\left( \kappa \left( \tau \right) \right) ds\\ -f\oint g^{\prime }\left( a_{t\tau }\right) l\left( d_{t\tau }\right) \frac{D^{2}-AE}{d_{t\tau }}f\left( \kappa \left( \tau \right) \right) ds\\ +f\oint g^{\prime }\left( a_{t\tau }\right) l^{\prime }\left( d_{t\tau }\right) E^{2}f\left( \kappa \left( \tau \right) \right) ds\\ +f\oint g\left( a_{t\tau }\right) \left[ \kappa \left( t\right) l\left( d_{t\tau }\right) +l^{\prime }\left( d_{t\tau }\right) D\right] f\left( \kappa \left( \tau \right) \right) ds.\\ \end{aligned}$$

The factors outside the integrals are calculated at parameter t (i.e. independent of the bound variable). Note that any factor depending only on parameter t, could be brought before the integrals, but would lead more complicated expression.