Abstract
In this chapter strategies for controlling neuronal communication and behavior from a theoretical neuroscience perspective are discussed. The main motivation for controlling neuronal networks is to slow down, halt or reverse mental diseases like senile dementia and Alzheimer’s disease (AD (a list of acronyms most used in this chapter is provided in Table 1)), as well as other mental diseases that reduce quality of life. The concept of neuronal networks used in this chapter denotes a group of interconnected biological neurons and must be distinguished from the concepts of neural networks (group of interconnected nerves) and artificial neural networks (group of interconnected “neurons” used in computer science).
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
In this chapter strategies for controlling neuronal communication and behavior from a theoretical neuroscience perspective are discussed. The main motivation for controlling neuronal networks is to slow down, halt or reverse mental diseases like senile dementia and Alzheimer’s disease (AD (a list of acronyms most used in this chapter is provided in Table 1)), as well as other mental diseases that reduce quality of life. The concept of neuronal networks used in this chapter denotes a group of interconnected biological neurons and must be distinguished from the concepts of neural networks (group of interconnected nerves) and artificial neural networks (group of interconnected “neurons” used in computer science).
Neuronal communication can be affected by drugs, usually affecting synaptic transmission between neurons. Direct stimulation by current injection is another possibility. It is also of interest to develop non-invasive methods that can control neuronal communication from outside the body, possibly by electromagnetic—or alternating magnetic fields. Recent studies performed on gene modified AD mice showed that electromagnetic radiation (EMR) exposure at 918 MHz with 217 Hz modulation frequency with specific absorption rate (SAR) of 0.25 W/kg \(\pm 2\) dB improved the cognitive abilities of mice compared with control mice without EMR exposure [1,2,3,4]. Furthermore, it has been reported that the brain temperature decreases during exposure, eliminating the possibility that the positive effects are caused by increased temperature. Another non-invasive strategy, that has been shown to reduce symptoms in chronic pain patients, is stimulation with alternating or pulsed magnetic fields (MF) [5]. Possible explanations on why EMR or MF affect neuronal communication are that they affect ion gates or receptors embedded in the neuronal membrane and thereby the membrane conductance (see [6] Chaps. 2 and 6 with references therein). If the membrane conductance in certain synapses in the brain can be controlled, it may be possible to affect plasticity (dynamic wiring of neuron connections) in certain parts of the brain, and thereby rewire it.
An ideal invasive futuristic approach is to develop nanomachines that can deliver drugs, mimic neurotransmitters, or expose neurons to EMR/MF at very specific targets, minimizing risk of side effects. Due to all the possibilities of controlling neurons with such devices one becomes less dependent on specific physical relationships (like the EMR/MF interaction with cells).
In this chapter we summarize some of the existing theories behind EMR and MF effects, and how they are thought to interfere with neurons. We also discuss control of neuronal behavior by current injection and possible future strategies for applying nanomachines. Furthermore, existing theoretical models are summarized for neuronal signal propagation and synaptic transmission that can indicate what changes one can expect both in single neurons and networks of neurons by controlling ion gates. Any ion gate or receptor could potentially be controlled, but we emphasize on calcium here for reasons described in the following.
Calcium plays a crucial role in neuronal signal transmission and memory formation. The intracellular and extracellular calcium concentration is, among many other things, affecting how strongly two neurons are wired together through chemical synapses. It is therefore important that calcium concentration is well regulated for neuronal communication to function properly. It is believed that any disruption in the processes that regulates calcium concentration levels (referred as calcium dysregulation), will lead to dramatic changes in neuronal functioning. Studies have revealed that there is an alteration of calcium influx into neuronal cells in aging brains [7]. Recent studies have also shown that drugs blocking voltage controlled calcium ion gates (VCCG), which makes the neuron membrane permeable to calcium ions, lead to a reduction in the progression of AD [8]. Their results support the so-called calcium hypothesis, stating that transient or sustained increase in intracellular free calcium in aging brains leads to impaired functioning and eventually cell death [7,8,9]. This effect is most aggressive in brains with AD. It is also thought that amyloid-beta (A\(\beta \)) deposits, one of the most essential hallmarks of AD, lead to calcium dysregulation [10]. There is also increasing evidence that calcium dysregulation in fact leads to an increased production of A\(\beta \) [11]. The calcium hypothesis shows the importance of calcium regulation in the brain.
Some theoretical models hypothesize that calcium can be controlled by external EMR or MF, by regulating ion gates or ligand binding, although the exact mechanism is unknown. Some experiments have also shown a regulation of calcium influx and efflux under EMR exposure (see [6, 12] and references therein). Some of these results are somewhat controversial, however [6, Chap. 6].
A possible treatment in brains with calcium dysregulation is to develop strategies that re-establish proper calcium regulation, whether it is through drugs, external fields or nanomachines. The objective of this chapter is to design and develop a possible strategy of controlling calcium by deliberately affecting the neuronal electrical properties and VCCGs. We deploy the communication theory aspects integrated into neuronal biological system and re-evaluate existing mathematical models in the literature expressing important neuronal processes as function of intra—and extracellular calcium concentrations in order to link between the time-varying stimuli at targeted neuron, its response patterns, and calcium concentration. Observing the neuronal response when an alternating electric current enters a cell, we reveal the neuronal communication as frequency-dependent. Obtained results provide a strategy of manipulating the spiking frequency and thereby intracellular calcium concentrations, \([\text {Ca}^{2+}]_i\), at targeted neuron via controlled current injection. Moreover, a framework presented for synaptic transmission and modification of memory formation and storage, indicates targeted neuron being able to control the behavior of its postsynaptic neurons, as long as current is held long enough to make relevant processes reach the steady state.
The hippocampus, located in the temporal lobe of the brain, is central in the process of memory formation and consolidation from short term to long term memory. It is also one of the the areas of the brain most severely struck by senile dementia and AD. Accordingly, we emphasize on hippocampal neurons and neuronal networks.
Neuronal structure [13]
2 Neuronal Communication at Cellular Level
Neurons, whose anatomical structure is shown in Fig. 1, are specialized cells that generate electrical pulses called action potentials (APs), or spikes, via its membrane. An AP is a response to chemical inputs (usually) collected by compartments called dendrites (serve as receiver front-end), and is transmitted to presynaptic terminal down though the nerve fiber called axon (serves as communication channel connecting the neurons).
The difference in electrical potential between the interior of a neuron and the surrounding extracellular medium forms the AP pulse shape. Two processes are of special relevance here: the hyperpolarization, that makes the neuron’s membrane potential more negative due to the positively charged ions (\(\text {Na}^+\), \(\text {Ca}^{2+}\), and \(\text {K}^+\)) flowing out or negatively charged ions (\(\text {Cl}^-\)) flowing in, and depolarization, that makes the membrane less negative. Fluctuation of hyper—and depolarized electrical potential defines an AP. An electric potential difference between the cell and its surroundings additionally produce one more effect, called ephaptic coupling [14]. Since neurons are surrounded by a conducting medium, they can sense electric gradients generated during a neuronal processing and accordingly change their electrical properties. Such a way of communicating, distinct from direct point-to-point communication, can alter the functioning of neurons strongly entraining synchronization and timing of spikes [15].
A structure that further allows a neuron to pass a message generated, i.e. an electrical pulse, to another cell is called synapse (see Sect. 3.2). Synaptic transmission is based on exchange of molecular particles called neurotransmitters and corresponds to the concept of molecular communication. Regular synaptic transmission greatly depends on positively and negatively charged ions, predominately calcium ions, \(\text {Ca}^{2+}\). Synaptic transmission is closely linked to molecular biology.
The communication process between neurons can be defined as follows: (1) The postsynaptic membrane, which is a part of the neurons dendrites, can be seen as the receiver front end receiving information from another neuron (through the synaptic connection). (2) The dendrites and the soma’s (cell body) membrane can be seen as the information processing unit and transmitter. (3) The Axon as well as the synapse can be seen as the communication channel between neurons.
2.1 Calcium in Neuronal Communications
The neuron’s external and internal calcium concentration, \([\text {Ca}^{2+}]_o\) and \([\text {Ca}^{2+}]_i\), affects the neurons capability to communicate. For instance, \([\text {Ca}^{2+}]_i\) affects the probability of neurotransmitter release at the presynaptic terminal and helps modify the conductivity of the neuron membrane at the postsynaptic terminal. Both determine the synaptic strength, which again determine whether or not two neurons will be connected, and how reliably two neurons will be able to communicate.
Calcium gates are located on dendrites, soma, and axon terminal, but few (if any) are located along the axon. The magnitude of \([\text {Ca}^{2+}]_i\) is determined by calcium coming from the outside by an \(\text {Ca}^{2+}\) ion current flowing into the neuron whenever an AP arrives and opens the VCCGs, the binding of \(\text {Ca}^{2+}\) to intracellular buffers, and releases from intracellular storage facilities. We mainly consider changes in \([\text {Ca}^{2+}]_i\) due to calcium currents in this chapter.
The calcium current, \(I_{\text {Ca}}\), is mainly flowing into the neuron since \([\text {Ca}^{2+}]_o \gg [\text {Ca}^{2+}]_i\). Typical resting values are \([\text {Ca}^{2+}]_o\sim 1\) mM and \([\text {Ca}^{2+}]_i\sim 100\) nM. Since positive current direction is defined outwards from cells, the calcium current is usually negative in sign. Since dendrites are tiny with small volume, rather few ions are needed in order to raise \([\text {Ca}^{2+}]_i\) significantly. A concentration of around 10 \(\upmu \)M require about 300–400 \(\text {Ca}^{2+}\).
The \([\text {Ca}^{2+}]_i\) can be expressed by the following differential equation [16]
where \(I_{\text {Ca}}\) is the total calcium current through the membrane, \(\gamma \) is a factor that converts from [coulombs/second] to [mol/second] and \(\tau _{\text {Ca}}\) is a time constant reflecting how fast the intracellular \(\text {Ca}^{2+}\) is removed (e.g., binding to internal buffers). The solution to (1) is
The Goldman, Hodgkin and Katz equation [16] relates \(I_{\text {Ca}}\) to \([\text {Ca}^{2+}]_o\) and \([\text {Ca}^{2+}]_i\)
where \(v=2 V_m F/(R T)\), \(V_m\) is the membrane potential, R is the gas constant and T the absolute temperature. \(\mathscr {P}_{\text {Ca}}\) is the cell membranes permeability to \(\text {Ca}^{2+}\).
If the \([\text {Ca}^{2+}]_o\) is reduced, it will cause lower efficiency of the relevant synapse. An excess of \([\text {Ca}^{2+}]_o\), on the other hand, can lead to cell death due to a too high influx of \(\text {Ca}^{2+}\). In AD one observe excess \([\text {Ca}^{2+}]_o\), and thereby \([\text {Ca}^{2+}]_i\), due to loss of calcium ion-gate inhibition. This often leads to a “runaway effect” of neurotransmitter release where excess neurotransmitters will seep into extra-neuronal space making surrounding neurons overexcited, leading to more calcium influx etc. This is known as exitotoxity and leads to neuron death.
2.2 Electromagnetic Exposure on Neuronal Systems
Electrical properties of neurons, and, consequently ions’ flows, directly depends on electromagnetic fields (EMF) generated by electronic devices; therefore, the effects of EMF on human bodies are of great interest. An induced EMF has thermal and non-thermal components. The non-thermal effects are due to the extremely low frequencies, that is, modulation frequencies of the information signal. Although no definitive evidence has been found, it is generally considered that exposure to low energy EMF could be a risk to human health [17]. The non-thermal effects are still not well-known; how and why neurons and networks can function as electromagnetic receivers and demodulators for given electromagnetic transmitter characteristics have not yet been scientifically determined. It is considered that the EMF generated near the head penetrate the skull and reach neurons in the brain and that the current induced by the EMF could stimulate neurons and generate an AP. Thus, if the mechanism of the EMF effects on the neuronal network is elucidated, we could make use of the induced current to fire APs, and this could enable scientists to invent treatments of new types in the future.
There are quite a few different mathematical descriptions for neuronal behavior; e.g., models based on the integrate-and-fire model and the Hodgkin-Huxley (HH) type models. Which model to use depends on the purpose [18]. The simulation can be executed using an open-source simulator such as NEURON (www.neuron.yale.edu) and GENESIS (www.genesis-sim.org). The HH model describes the physiological process, but since it was originally developed for the axon of a squid [19], it is not necessarily the best model for simulations on humans. There are some models developed for humans [20]. In order to simulate more detailed EMF effects on a neuron or a neuronal network, it may be required to consider a mathematical model coupled with biophysical phenomena on the ribonucleic acid (RNA) level.
2.3 Possible Mechanisms Behind Neuronal Effects in Response to EMR and MF
The exact mechanism behind the effects of EMR and MF observed in neurons is unknown. There are also controversies surrounding some of the effects reported, since certain experiments have not been able to reproduce similar effects, or observe any effect at all (see [6, Chap. 6]). There are, however, lots of evidence supporting non-ionizing low intensity radiation effects on neurons, specifically related to therapeutic effects (see [6] and references therein), that does not have to do with temperature increase.
It is likely that the mechanisms explaining every aspect of EMR/MF interactions with neurons is complicated. However, there exists some simplified mathematical models in the literature able to reproduce some of the effects observed in experiments. Although there are controversies around these models, they will anyway serve as a starting point for further investigation. It is natural that models trying to describe unknown mechanisms are up for debate, and in time some of these models may turn ut to have something on them (and can be extended further), while others will have to be rejected since they are based on grounds that do not correspond with reality. This emphasizes the importance of conducting experiments in parallel with the development of theoretical models, since it will make the chances of ending up in a blind alley much smaller.
We will briefly summarize the main ideas behind some of the existing approaches of theoretical modeling here, and also mention some of the controversies surrounding these models. All models assume that the place of EMF interaction is the cell membrane where ion binding and transport is affected. It is also possible that EMF affects distribution of protein and lipids in the membrane itself by altering the kinetics of binding.
One model by Panagopoulos et al. [6, Chap. 2.2] hypothesize that ions used in the neuronal communication process (\(\text {K}^+\), \(\text {Na}^+\), \(\text {Ca}^{+2}\) etc.) experience forced vibrations in and around ion gates due to constant frequency harmonic—or pulsed EMF. Forced vibrations will affect the opening and closing of voltage controlled gates since they disrupt the electrochemical balance of the neuronal membrane. Forced vibrations are governed by the wave equation, and show that the necessary stimuli intensity needed to achieve forced vibrations, like harmonic oscillators, increases linearly with frequency. Solutions to the same equation also show that pulsed fields double the impact of the stimuli (compared to harmonic oscillators) because of transient effects. This corresponds with many experiments conducted. One of the main criticisms of this model is that fluctuations due to thermal effects are larger than the amplitudes of the forced vibrations. Panagopoulos et al. further claimed that thermal effects will average to zero over time, since they present random forces in all directions. Then, since forced vibration is a coherent motion (superimposed on the thermal motion), it will result in a net effect on average.
Another model by Liboff et al. [21], [6, Chap. 2.4] hypothesizes that MF interaction with neuronal tissue seen in experiments can be explained by ion cyclotron resonance described by the Lorentz force equation \(\mathbf {F}=q (\mathbf {v}\times \mathbf {B})\). \(\mathbf {B}\) is the magnetic field, \(\mathbf {v}\) is the particles velocity vector and q is charge (see [21] and [6, Chap. 2.4]). The Lorentz force is resulting from the acceleration a charged particle experience in a MF, where the acceleration is proportional to the charge-to-mass ratio. With an electric field, \(\mathbf {E}\), present the Lorentz force becomes
This force will in principle interfere with the ion transport through and around the membrane which further alter biological responses. It is believed that the \(\alpha \)-helical configuration of the proteins making up the ion channels places regular constraints on the ionic motion. Liboff et al. further hypothesize that if the protein channel structure forces ions to move in helical paths, then with the right direction on the magnetic (and electric) field, the Lorentz force may result in a set of gyro-frequencies (harmonics) for the channel, where each frequency corresponds to different cyclotron resonance conditions (eigenfrequencies). I.e., the channels frequency spectrum becomes quantized. The main criticism against this model is that collisions with other particles and thermal effects will eliminate the hypothesized effects [22].
Yet another model, named Electrochemical Information Transfer Model (EIT), proposed by Pilla [23], [6, Chap. 2.3] hypothesizes that low intensity EMF modulate the rate of binding of ions to receptor sites. The EIT formulates a membrane current which depends on change in membrane surface concentration of the relevant binding ion over time, the surface concentration itself, and frequency. The change in concentration is again dependent on membrane voltage and the following biochemical reactions. This model can be illustrated by an equivalent circuit diagram as that in Fig. 2. \(C_d\) is the dielectric membrane capacitance and \(R_M\) the leaky resistance (due to ions passing through ion gates under normal circumstances). The ion-binding pathway is represented by \(R_A\) and \(C_A\), and \(C_B\) and \(R_B\) represents follow-up biochemical reactions. This leads to two time constant \(R_A C_A\) and \(R_B C_B\) in addition to the (normal) leaky pathway and membrane capacitance. This model has been applied to successfully construct magnetic and electromagnetic pulses for therapeutical applications, and the resulting pulses has shown to be efficient in treating bone diseases. The model may also be applied for other cells and tissues.
Equivalent circuit diagram for (single compartment model) cell membrane exposed to EMR. The figure is based on Fig. 4 in [23]
Another relevant model that evaluate EMR effects at the cellular membrane level is given in [24]. This model is also validated with experimental data.
3 Neuron’s Message Transmission
3.1 Fundamental Neuronal Operating Principles
According to (3), \(I_{Ca}\) directly depends on the membrane potential. One possible way of controlling \([\text {Ca}^{2+}]_i\) is through change in membrane voltage, since it also drives the \([\text {Ca}^{2+}]_i\) according to (2). To change the neuronal membrane potential, it is sufficient to inject or induce a convenient current.
Referring to previous work in neuroscience, biology and chemistry, it appears to be hardly possible to determine an analytical expression for the neuron response when it is affected by specified stimulus. The reason is confined to the large trial variability directed to the biological systems even when the same stimulus is applied repeatedly [25]. In this section, we endeavour to inspect the oscillatory behavior of a biophysically realistic sample neuron, utilizing the engineering concepts integrated in a neuronal structure and keeping the analysis as simple as possible.
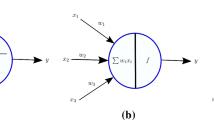
Soma is the cell body part of a neuron where summation of all the dendrite inputs takes place. It can be represented via a cascade (linear filter and static gain function), similarly to that introduced by Hunter and Korenberg in 1986 intended to general biological systems [26]. In describing neuronal processing (see Fig. 3a), we can introduce the quadratic form of gain function confined to habituation of (almost) all biological micro- and macro-systems. The nearly straight-line of preprocessing gain has been shown to correspond to the low-variance input [27]. The function, however, allows nonlinearities in the amplitude response when high-variance input is applied. Under this scenario, gain function curve exhibits reduced slope and compressive nonlinearity at hyperpolarized and depolarized potentials.
Generalized versions of deterministic IF model, GIF, formulates the membrane’s impedance (transfer function) to characterize the neuron subthreshold dynamic [28]. Since the model is capable of introducing frequency-dependent filtering of input signal, GIF model is convenient from the communication theory viewpoint. Cognizance of type-specific parameter values, such as variables characterizing the membrane dynamics, conductances, and parameters proportional to conductances, analytically define the impedance magnitude an phase as
Parameter \(\tau \) stands for time scale of the variable characterizing the membrane dynamics, C represents membrane capacitance, parameter \(\alpha \) is proportional to effective leak conductance, whereas \(\beta \) is proportional to conductance measuring the membrane potential variation [28]. Note that both the \(\alpha \) and \(\beta \) can be experimentally measured for hippocampal neurons. Since the findings presented in [27] indicate the neurons properties remains the same during stimulation, it appears that the membrane’s impedance does not differ between the low- and high-variance input. Moreover, it implies the membrane’s impedance is uniquely defined with neuron’s type and properties, which makes the analysis presented so far fully deterministic.
As stated previously, due to the many potential sources of response variability, including variable levels of arousal and attention, randomness associated with various biophysical processes that affect neuronal firing, and the effects of other cognitive processes taking place during a stimulation [25], a randomness in neuronal behavior must be accounted for in order to produce a realistic model. The neuron will typically fire, i.e., generate an action potential only when its somatic potential, v(t), reaches a threshold value of about \(-55\) to \(-50\) mV. However, this is not the only condition; neuron firing is controlled by a refractory period (RP), i.e., a time period during which a cell is incapable of or inhibited from repeating a spike generation. Two RPs are defined: the absolute refractory period (ARP), as the interval during which a new spike cannot be initiated, regardless of the intensity of stimulation, and relative refractory period (RRP), as the interval during which a new spike generation is inhibited but not impossible. The RRP follows immediately after the ARP.
One way of introducing the randomness is through the state machine mechanism that seems to be adequate for spike generation process (see Fig. 3a). A binary 1 at the input symbolizes the somatic voltage v(t) with an amplitude above the threshold, whereas 0 at the input symbolizes the voltage is beyond the threshold value. Corresponding alphabets at the output symbolize the events when spike is generated, and spike is not generated, respectively. Spontaneous generation of spikes at the time of subthreshold voltages at the input is ignored. Probabilities \(p_1\) and \(p_0\) account for randomness. The spike generation probability, denoted as \(p_1\), is set to 1 when both the ARP and RRP have expired and when somatic voltage is above the threshold. During the ARP, the probability \(p_1\) is 0, as well as when the voltage v(t) is beyond the threshold no matter what period is valid. During the RRP, the threshold is higher immediately after a spike and decays (usually exponentially) then back to its resting value. Equivalently, probability \(p_1\) increases proportionally to the time and suprathreshold amplitude of v(t) and takes the value from 0 to 1, i.e.,
where the time constant \(\tau \) follows the rule \(1/\tau \propto \text {stimuli intensity}\). Transient probability \(p_0\), in contrast, exhibits the opposite behavior relative to that of the \(p_1\), i.e., \(p_0 = 1 - p_1\). Eventually, note that not only does the suprathreshold voltage drive the probabilities \(p_1\) and \(p_0\) directly, but also indirectly, through the impact on duration of the ARP. It has been shown that the larger the suprathreshold amplitude, the smaller the ARP, or equivalently, the higher the firing rate [29]. Note, however, that the ARP has a lower bound limit because the neuron cannot fire with the rate higher than that physiologically determined.
At this point we are able to build up strategies of affecting the membrane conductances and consequently \([\text {Ca}^{2+}]_i\) via VCCGs. The analysis performed helps to eliminate signals that lead to disruption in communication, or equivalently, to select those adequate for VCCGs control. Elaboration presented so far helps not only to grasp the neuronal encoding and defines strategies of controlling the \([\text {Ca}^{2+}]_i\), but also to decently mimic the neuronal behavior while designing the information that might be followed during fabrication and assembly of nanotechnology-based neuron. Performance of introduced model, however, demand further analysis and comparison with measurements obtained in vivo.
3.1.1 Axonal Transmission
An axon is a nerve one-way channel that conducts the spikes typically in a direction outward from the soma. This propagation is called orthodromic propagation [25]. Antidromic propagation in the reverse direction is not excluded. For proper communication and functioning of the nervous system, many axons in vertebrates are wrapped with a myelin sheath that increases the speed at which impulses propagate along the fiber by hops or saltation. In order to decrease the impact of channel attenuation due to the possible significant axon length, and let the signal be amplified, electrically insulating myelin sheath is interrupted with nodes of Ranvier. There is a high density of fast voltage-dependent \(\text {Na}^{+}\) at these points making the axonal membrane uninsulated and capable of regenerating spike impulses. Axonal channel is highly reliable and adjusted to its frequency band-limited input. Owing to its properties, we refer an axonal channel as the one-way linear multi-hop amplify-and-forward channel, as shown in Fig. 3b. All relay terminals, i.e., nodes of Ranvier \(T_k\), \(k = 1, 2,\ldots , K\), are located on a straight line along the axon from the source terminal \(T_1\) to the destination terminal \(T_K\). Relaying gain of terminal \(T_k\) is denoted as \(G_k\), the channel coefficient from \(T_k\) to \(T_{k+1}\) terminal as \(H_k\), and communication noise components as \({n_a}^{(k)}\). With \({n_a}^{(k)}\) we refer to axonal noise caused by disturbances affecting the \(\text {Na}^+\) gates. Further, it is assumed that the kth terminal can only hear and amplify the signal transmitted by the \((k - 1)\)th terminal. Hence, the signal received by the presynaptic terminal can analytically be expressed as
where s(t) denotes the spike sequence entering the axon, and \(G_{K+1}=1\).
Prospective usage of nano-scale devices that interconnect with neurons and re-establish an information propagation through the network would set up a ground-breaking ICT-inspired approach in treatment of neurodegenerative diseases (see Sect. 5). Moreover, design of such nano-scale devices, i.e., synthetic neurons, can directly implement the previously defined theoretical concepts confined to soma and axon. Since myelination is thought to inhibit not only the ephaptic interactions but also other sources of disturbances making the axonal transmission very reliable, human implementation of synthetic neuron with linear multi-hop amplify-and-forward axonal channel should find out an efficient approach in reducing the noise components \({n_a}^{(k)}\).
3.2 Synaptic Transmission
Chemical synapses transfer signals from one neuron to another through neurotransmitter molecules released into the synaptic cleft. Figure 4a shows a simplified synaptic model explained in the following.
When an AP reaches the presynaptic membrane, it will depolarize, leading to opening of VCCGs and an influx of \(\text {Ca}^{2+}\) into the presynaptic terminal. This increases the probability for neurotransmitter release. There exits a myriad of neurotransmitter molecules and many postsynaptic receptors that neurotransmitters activate, making synaptic communication difficult to fully comprehend. To simplify the discussion we focus on one neurotransmitter; glutamate, one of the most important neurotransmitter for modifiable synapses. We consider only two receptors AMPA (\(\alpha \)-amino-3-hydroxy-5-methyl-4-isoxazole propionate) and NMDA (N-methyl-D-aspartate), that are crucial for memory formation and learning.
Neurotransmitters are stored in synaptic vesicles in the presynaptic terminal. We refer to the set of neurotransmitters released by one vesicle as quanta. The vesicles are transported to the synaptic terminal and attached to the presynaptic membrane at release sites. The number of quanta released per AP, \(N_q\), varies throughout the central nervous system, typically ranging from one to a few quanta per AP. This results in variations in reliability of synapses, with \(N_q=1\), the least reliable.
Synaptic strength is determined by \(N_q\), the postsynaptic conductance, and the open ion channel probability \(P_o\). \(P_o\) is the probability of finding an arbitrary gate among a large number of gates in open state. For synapses \(P_o=P_{\text {rel}} P_{\text {post}}\), where \(P_{\text {rel}}\) is the probability for neurotransmitters release when an AP is fired, and \(P_{\text {post}}\) is the open probability for postsynaptic ion gates given that neurotransmitters were released. Typically the synaptic strength/weight is proportional to the mean postsynaptic action \(N_q P_o G\), with G some postsynaptic effect, like peak conductance (or current) [16, p. 91].
3.2.1 Presynaptic Terminal and Neurotransmitter Release
A rise in \([\text {Ca}^{2+}]_i\) from its resting concentration of about \(0.1\upmu \)M increases the probability that vesicles releases neurotransmitters. Since neurotransmitters are released probabilistically, synaptic transmission is stochastic in nature.
Vesicles are usually divided into several sets named vesicle pools. Usually it is adequate to consider two pools, release ready pool and unavailable pool [30]. The ready release pool is of variable size \(N_a\), with an upper limit \(N_u\), and refers to vesicles being close to—or already docked to vesicle release sites. Unavailable pool is of size \(N_u-N_a\) and refers to vesicles that become available after a certain time. Whenever an AP leads to neurotransmitter release, the available pool may loose several vesicles. Depletion of the available pool leads to a reduction in release probability, a process called short term depression (STD), and recovers with time constant \(\tau _d\) (or refill rate \(1/\tau _d\)). Figure 4b depicts this process.
Release of a single vesicle during an AP is following a Poisson distribution with time dependent spiking rate r(t) [30]. The single vesicle release probability is \(P_v=1-e^{-\alpha _v}\), where \(e^{-\alpha _v}\) is the single vesicle failure probability, and
is named vesicle fusion rate, where \(\varDelta _t\) is the duration of the AP. With \(N_a\) vesicles in the release ready pool, and with \(N_q=1\) release sites, we get the release probability
In the hippocampus, for instance in the synapses connecting CA3 (Cornu Ammonis) pyramidal cells with CA1 neurons, \(N_q=1\), and two neurons usually form only one synapse with each other. This implies a high failure probability \(P_e=1-P_{\text {rel}}=e^{-\alpha _v N_a}\). \(P_{rel}\) can, however, increase when a high frequency spike train or a burst of spikes reach the presynaptic terminal, since \([\text {Ca}^{2+}]_i\) builds up when many AP’s are fired over a short time interval, a process named short term potentiation (STP).
3.2.1.1 Short Term Synaptic Plasticity
STP: The duration of STP increases with the frequency of AP’s, \(f_{\text {AP}}\), as well as the duration of the stimuli. Let \(P_0\) denote the baseline release probability. After a burst of high frequency APs, the release probability will be modified to \(P_p > P_0\). After this \(P_p \rightarrow P_0\) with time constant \(\tau _p\) ranging from 100ms to minutes depending on \(f_{\text {AP}}\) and stimuli duration. Since the time constant for onset \(\ll \tau _p\), we get
STD: With \(1/\tau _d\) the vacancy refill rate (\(\tau _d\) in the order of seconds), and \(P_d < P_0\), the minimal release probability after depression, then
3.2.1.2 Relation Between Release Probability and Presynaptic Calcium
The expression in (9) does not explicitly take the \([\text {Ca}^{2+}]_i\) into account, although it will indirectly affect both \(N_a\) and \(\alpha _v\). The relation between \(P_{\text {rel}}\) and \([\text {Ca}^{2+}]_i\) is complicated, and for this reason, no exact mathematical formula has been found at present (at least to our knowledge). Experiments have revealed a highly nonlinear relationship between the presynaptic \(\text {Ca}^{2+}\) current (influx) and the postsynaptic potential [31]. As mentioned by Wu and Saggau in [31], the \(\text {Ca}^{2+}\) influx caused by an AP will activate certain \(\text {Ca}^{2+}\) sensors, which further trigger the processes that cause vesicle fusion and neurotransmitter release. \(P_{\text {rel}}\) is therefore a product of two terms \(P_{\text {rel}}=P(\text {Ca}^{2+})\cdot P(\text {Ves})\), where \(P(\text {Ca}^{2+})\) is the probability reflecting the \(\text {Ca}^{2+}\) binding process (to internal buffers and sensors) and \(P(\text {Ves})\) reflects the vesicle release process (dependent on vesicle pool dynamics).
One reason that complicates the relation between \(P_{rel}\) and \([\text {Ca}^{2+}]_i\) is that the effective concentration around the vesicle release sites depends on the distance d to the VCCG [32] (see Fig. 4a). \([\text {Ca}^{2+}]_i\) needs to reach levels of about 100 \(\upmu \)M in the vicinity of a vesicle release site for neurotransmitters to be released. If \(\text {Ca}^{2+}\) enters at about \(d\approx 10\) nm, from the vesicle release site, a release of neurotransmitters usually follow, since then \([\text {Ca}^{2+}]_i\) > 100 \(\upmu \)M. If d is larger than about \(100--200\) nm, fast intracellular buffers will bind most of the calcium before \([\text {Ca}^{2+}]_i\) gets even closer to the 100 \(\upmu \)M level.
A mathematical relation between \(P_{rel}\) and \([\text {Ca}^{2+}]_i\) must take the following interrelated features into account: (1) \([\text {Ca}^{2+}]_i\) that depends on d. (2) \(\text {Ca}^{2+}\) binding through internal buffers. (3) \(\text {Ca}^{2+}\) release from endoplasmic reticulum. (4) Interaction between vesicle pools. (5) STP and STD.
3.2.2 Postsynaptic Terminal
For simplicity, it is assumed that the conductance of the postsynaptic terminal is determined by AMPA’s and that NMDA determines how conductance of AMPA gates change. This is motivated by the fact that NMDA is about 10x slower than AMPA, and so the AMPA’s are nearly closed when the NMDA’s start to conduct. In a more exact model, the NMDA’s contribution to membrane conductance should also be evaluated.
3.2.2.1 AMPA Receptors
AMPA is a fast ion conducting receptor permeable to sodium (\(\text {Na}^+\)), potassium (\(\text {K}^+\)) (and in some cases also \(\text {Ca}^{2+}\)), whenever glutamate binds to it.
The current through the AMPA’s is typically given by
where \(G_{\text {AMPA}}\) is a modifiable conductance factor, \(P_{\text {AMPA}}(t)\) is the open probability, \(V_\text {post}\) is the postsynaptic potential and \(E_x\) is the reversal potential of the relevant ion (\(\text {Na}^{+}\) or \(\text {K}^{+}\)). The rise-time in open probability is almost instantaneous compared to the decay time, \(\tau _\text {AMPA}\), and so
\(G_{\text {AMPA}}\) can be altered in two ways: (1) Modification of the conductance of AMPA receptors embedded into the postsynaptic membrane. (2) Insertion of several new AMPA receptors into the postsynaptic membrane (see Fig. 4a). In reality, both of these processes take place, referred to as AMPA receptor trafficking (a graphical explanation is given in [9, pp. 783–784]). Mathematically, these processes are modeled differently, but the end result is almost the same [33].
(1) Modification of AMPA receptor conductance: The following model was presented by Castellani et al. in [34]. The AMPA are composed of 4 protein compartments GluR1-GluR4. Different configurations of these lead to different classes of AMPA. In the hippocampus, AMPA receptors consisting of GluR1 and GluR2 are abundant. AMPAs consisting of GluR2 are impermeable to \(\text {Ca}^{2+}\). GluR1 is essential to plasticity since it can be modified depending on \([\text {Ca}^{2+}]_i\) levels. Let GluR1 be denoted by A:
(i) When \([\text {Ca}^{2+}]_i > \theta _p\) the process of protein kinase is initiated, which means that phosphate groups are added to Serine-831 and Serine-845 on the GluR1. This process is named phosphorylation. There are two kinase processes: Kinase A, denoted \(\mathscr {K}_1\), which phosphorylate Serine-845 and Kinase C, denoted, \(\mathscr {K}_2\), which phosphorylate Serine-831. Both increases the AMPA conductance. Denote the phosphate groups due to these kinase-processes \(p_1\) and \(p_2\). There are 4 possible phosphorylation processes: \(A \xrightarrow {\,\mathscr {K}_1\,}A_{p_1}\), \(A\xrightarrow {\,\mathscr {K}_2\,} A^{p_2}\), \(A^{p_2}\xrightarrow {\,\mathscr {K}_1\,}A_{p_1}^{p_2}\), \(A_{p_1}\xrightarrow {\,\mathscr {K}_2\,} A_{p_1}^{p_2}\). \(A_{p_1}^{p_2}\) is called double phosphorylation, and results in the highest conductance.
(ii) When \(\theta _d< [\text {Ca}^{2+}]_i < \theta _p\) the process of protein phosphatase is initiated, in which phosphate groups are removed from Serine-831 and Serine-845 on the GluR1 protein, denoted \(\mathscr {P}_1\) and \(\mathscr {P}_2\) respectively. This process is named dephosphorylation and decreases the AMPA conductance. There are 4 possibilities \(A \xleftarrow {\,\mathscr {P}_1\,} A_{p_1}\), \(A\xleftarrow {\,\mathscr {P}_2\,} A^{p_2}\), \(A^{p_2} \xleftarrow {\,\mathscr {P}_1\,} A_{p_1}^{p_2}\), \(A_{p_1} \xleftarrow {\,\mathscr {P}_2\,} A_{p_1}^{p_2}\).
(iii) When \( [\text {Ca}^{2+}]_i < \theta _d\), the AMPA stays unchanged.
The AMPA conductance is given by [34]
which was shown to be quite consistent with experiment. A, \({A}_{p_1}\), \({A}^{p_2}\), and \({A}_{p_1}^{p_2}\) are all functions of the kinase and phosphatase processes \(\mathscr {K}_1\), \(\mathscr {K}_2\), \(\mathscr {P}_1\) and \(\mathscr {P}_2\) given as a solution to a system of 4 differential equations [35]. \(\mathscr {K}_1,\mathscr {K}_2,\mathscr {P}_1,\mathscr {P}_2\) are all functions of \([\text {Ca}^{2+}]_i\), determined by experiment. More exact models, built on Michaelis-Menten kinetics, are derived by Castellani et al. in [35].
(2) Insertion and removal of AMPA receptors: The following model was presented by Shouval et al. in [33]. When \(\theta _d< [\text {Ca}^{2+}]_i < \theta _p\), some of the AMPAs already attached to the membrane will become detached (see Fig. 4a).
Let \(B_M\) denote the number of AMPA receptors attached to the postsynaptic membrane, and \(B_I\) denote the AMPAs available for insertion. It is assumed that \(B_M+B_I=B_T\), where \(B_T\) is a constant, corresponding to conservation of protein. Further, let \(K_I=K_I([\text {Ca}^{2+}]_i)\) and \(K_R=K_R([\text {Ca}^{2+}]_i)\) denote the kinetic constants for AMPA insertion and removal respectively. It was shown in [33] that
where \(B_M^{f_p}={B_T K_I}/({K_I+K_R})\) and \(\tau _{[\text {Ca}]_i} = {1}/({K_I+K_R})\) i.e., the steady state response and the time it takes to reach steady state. The kinetic constants \(K_I,K_R\) as functions of \([\text {Ca}^{2+}]_i\) are found by experiment [33].
3.2.2.2 NMDA Receptors
NMDA receptors differ from AMPA in several ways (in addition to being slower):
(I) When glutamate locks onto NMDA, it opens, but is still blocked by \(\text {Mg}^{2+}\) present in extracellular space (see Fig. 4a). To remove the \(\text {Mg}^{2+}\), the postsynaptic neuron must depolarize in order to “kick” the \(\text {Mg}^{2+}\) out. A current through the NMDA receptor therefore requires that glutamate is released from the presynaptic terminal and that the postsynaptic neuron subsequently depolarizes.
(II) In addition to \(\text {Na}^+\) and \(\text {K}^+\), the NMDA is permeable to \(\text {Ca}^{2+}\) (about 7\(\%\) of the NMDA current). Since AMPAs that contain GluR2 (which are the only ones considered in this chapter) are impermeable to \(\text {Ca}^{2+}\), the amount of \(\text {Ca}^{2+}\) influx through NMDA receptors signals the level of pre- and postsynaptic co-activation.
The NMDA calcium current is typically given by
\(G_{\text {NMDA}}\) is the maximal conductance and \(P_{\text {NMDA}}\) is the open probability,
The rise time, \(\tau _f\), is fast compared to the decay time \(\tau _s\), but considerably slower than the AMPA rise time. \(\mathscr {H}(V_{\text {post}})=H_{\text {NMDA}}(V_{\text {post}}) (V_{\text {post}}-E_{\text {Ca}})\), where \(E_{\text {Ca}}\) is the reversal potential for calcium and \(\mathscr {H}(V_{\text {post}})\) is a “gain” term that takes the \(\text {Mg}^{2+}\) blockage into account [36]
This implies that the higher \([\text {Mg}^{2+}]_o\) is, the higher \(V_{\text {post}}\) must be before the NMDA gate becomes conductive. Under normal conditions, typical values at temperature 37 \(^\circ \)C are \(\gamma = 0.06/\)mV, \(\eta =0.33/\)mM and \([\text {Mg}^{2+}]_e\approx 1\) mM.
A relation between the postsynaptic \([\text {Ca}^{2+}]_i\) due to the NMDA current and the frequency of a presynaptic spike train with constant frequency \(f_{\text {AP}}\) held long enough for calcium concentration to reach steady state was derived by Castellani et al. in [34]:
where \(G_\text {f}\), \(\tau _\text {f}\) and \(G_\text {s}\), \(\tau _\text {s}\) are magnitudes and time constants for fast rising- and slowly decaying conductance component respectively. This formula was found by extending the one-spike NMDA calcium current in (16) to a Poisson distributed spike train. When the current is found one can apply (2) to find the concentration. One must also determine relation between spike time and \(f_{\text {AP}}\) (see [34] for details). (19) shows that there is a linear relationship between steady state postsynaptic calcium concentration and the presynaptic spiking frequency.
Like AMPA, NMDA can be modified. A model was presented in [34], in which \(G_\text {s}\) and \(G_\text {f}\) depend on the “history” of cortical/neuronal activity.
3.2.2.3 Long Term Synaptic Modification
The more active AMPA receptors present in the postsynaptic terminal, the higher the synaptic strength becomes, and the probability that the postsynaptic neuron will fire in response to glutamate release increases. This is the process underlying Long Term Potentiation (LTP). In the opposite case, when the number of active AMPAs are reduced, a long lasting weakening of the synapse takes place, the process behind Long Term Depression (LTD). This change in conductance can last for hours, days and even weeks to years. LTP and LTD wire neurons together in a dynamical way which is essential for the brains ability to learn. It is the patterns of connections that the LTP and LTD processes create in the brains network that represent memories.
Donald Hebb’s hypothesis [37] for synaptic long term modification is: (I) synaptic connections between two neurons are strengthened when firing of the presynaptic neuron leads to immediate or slightly delayed firing of the postsynaptic neuron, i.e., when pre- and post synaptic activity are highly correlated. (II) synaptic strength is weakened when the postsynaptic neuron fires before the presynaptic neuron, or long enough after to only create moderate increase in postsynaptic potential. I.e., when the correlation between pre- and postsynaptic activity is low.
Since NMDA receptors require subsequent depolarization of pre- and postsynaptic neuron to become fully conductive, they will function as Hebbian detectors for correlated pre- and postsynaptic activity: Large influx of \(\text {Ca}^{2+}\) initiate the biochemical mechanisms behind LTP and requires strong NMDA activity. For LTD, on the other hand, the probability for finding an arbitrary NMDA gate in open state is smaller than under LTP. That is, some of the \(\text {Mg}^{2+}\) blockages are removed, but less so than under LTP. With no influx of \(\text {Ca}^{2+}\) through the NMDA, the synapse stays unchanged.
Figure 5a shows the steady state change in synaptic strength, i.e. the change in \(G_{\text {AMPA}}\), as a function of presynaptic spiking frequency, \(f_\text {AP}\). The plot was generated by (19) and (14) using results and data from Castellani et al. [34]. Observe that LTP happen at higher \(f_\text {AP}\). This is natural, since when consecutive spikes are close in time, the excitatory postsynaptic potential will accumulate more easily, and thereby it is more likely that presynaptic firing leads to postsynaptic firing, in line with Hebb’s hypothesis. Note that if the NMDA gates are modified (by changes in \(G_\text {s}\) and \(G_\text {f}\) in (19)), the frequency at which the synapse goes from LTD to LTP will be shifted up or down [34]. As stated in [34], the curve shown in Fig. 5a is also quite consistent with the experimental data in [38].
To get an idea on what stimuli frequencies lead to LTP or LTD we have plotted the spiking frequency as a function of the soma current stimuli frequency in Fig. 5b for several current amplitudes. By comparing Fig. 5a and b one can observe that for stimuli current amplitude of 100 pA, the change from LTD to LTP will happen at about 40 Hz. For stimuli current amplitude of 50 pA, this transition takes place at around 65 Hz.
4 Neuro-Spike Communications at Network Level
The anatomical configuration of brain networks can quantitatively be characterized by a graph representing either inter-neuronal- or inter-regional connectivity. If inter-neuronal connectivity is analyzed, the graph’s nodes denote neurons and the edges represent physical connections, i.e., synapses. Conversely, if inter-regional connectivity is analyzed, nodes denote brain regions and edges represents axonal projections. The former approach is subject in this section.
4.1 Graph Theoretical Modeling of Neuronal Connectivity
We analyze a graph G that consists of a set V of vertices and a set E of edges, denoted as G(V, E).
Quantitative characterization of anatomical patterns can be mathematically described through matrices, such as the adjacency (or connection) matrix (AM). An AM is with non-zero entries \(W_{ij}\) if a connection is present between neurons i and j; otherwise, \(W_{ij}\) is zero. Although we lack a formula describing \(P_{\text {rel}}\) as a function of \([\text {Ca}^{2+}]_i\), and thereby \(W_{ij}\), a formula for \(W_{ij}\) as a function of extracellular \([\text {Ca}^{2+}]_o\) has been found by Dodge and Rahminoff [39]
\(K_c\) and \(K_m\) are equilibrium constants of calcium and magnesium respectively, and a is the number of independent sites \(\text {Ca}^{2+}\) must bind to in order to release neurotransmitters. Note that synaptic connections are either excitatory or inhibitory, which corresponds to positive and negative \(W_{ij}\) values, respectively.
Anatomically, many compartments (e.g., many synapses from one axon) of single presynaptic neuron i can be connected to postsynaptic neuron j making a numerous synaptic connections. In our analysis, we assume that all such connections are superimposed, resulting in one weight value \(W_{ij}\). Furthermore, each two neurons can both be the pre- and postsynaptic ones to each other, in which case they mutually share two connections represented by usually different values of \(W_{ij}\) and \(W_{ji}\) in AM. Additionally, the graph G(V, E) representing neuronal network is directed, due to one-way axonal transmission. This ultimately makes the G(V, E) directed, weighted, and signed. Excluding the self-connections, all diagonal elements of AM are zero.
With the neuronal network mapped (usually by means of functional magnetic resonance imaging (fMRI) or electrophysiological techniques such as electroencephalography (EEG) and magnetoencephalography (MEG)), one can reveal the connectivity patterns and structure formed of densely connected clusters linked together in a small-world network [40]. Small-worldness combines high levels of local clustering among neurons, associated with high efficiency of information transfer and robustness, and short average path lengths, that link all neurons of the regional network. Small-world organization is intermediate between that of random networks, characterized with short overall path length and low level of local clustering, and that of regular networks, characterized with long path length accompanied by high level of clustering. Such a structure is essential not only for regions of specialized neurons but also for the brain in general, since it combines two fundamental functioning aspects: segregation, where the similar specialized neuronal units are organized in densely connected groups that are interconnected, and the functional integration, which allows the collaboration of a large number of neurons to build cognitive states [40].
A set of graph theory concepts of special relevance to the computational analysis of connectivity patterns and strategies of diagnosis and ICT-oriented treatment of neurodegenerative diseases will be presented later in Sect. 5.2.
4.2 Memory Networks
In memory networks so-called feed-forward (FF)- or recurrent (REC) networks are usually considered. The graph representation of a combined FF- and REC network is depicted in Fig. 6. In a FF network information coming from one stage along an information processing path (e.g., from one part of the brain to another) that has been processed by several neurons are forwarded to another set of neurons at a later stage along the processing path. A REC network refers to connections between several neurons on the same “stage” along a processing path.
Memory networks are usually modeled as a combinations of FF and REC networks, where memory is stored as connection configuration in the REC network, quantified through entries in the AM denoted M. Changes in connection patterns are governed by LTP and LTD.
A deterministic input output relation will be presented here for the network in Fig. 6, following along the lines of Dayan and Abbott in [25]. To analyze very large networks, one usually have to resort to stochastic network models (e.g., Boltzmann machines [25, pp. 273–276]).
4.2.1 Mathematical Modeling of Memory Networks
Consider Fig. 6. \(\mathbf {u}\) and \(\mathbf {v}\) denote the input and output of the network respectively. \(\mathbf {u}\) is an \(N_u\) dimensional vector with components \(u_j\) denoting presynaptic firing rate at synapse j. \(\mathbf {v}\) is an \(N_v\) dimensional vector with components \(v_j\) denoting postsynaptic firing rate at synapse j. \(\mathbf {W}\) is the connection matrix of the feed-forward stage of the network with entries \(W_{ij}\), denoting synaptic strength from input unit j to output unit i. \(\mathbf {M}\) is the connection matrix of the recurrent stage of the network with entries \(M_{ij}\), denoting the synaptic strength between output unit j and output unit i.
To model the input-output relationship, the total soma-current for neuron k, \(I_{S (k)}\), resulting from all inputs from other neurons must be found. This current will determine the output firing rate, \(v=F(I_{S (k)})\), for some nonlinear function F. Let \(\rho _j(\tau )=\sum _i \delta (\tau -t_i)\) denote the neuronal response function (a simplified expression for the spike sequence, where each AP is approximated as a Dirac-delta function) for input neuron j. For neuron k, a simplified expression for the soma current is given by [25, p. 233]
One simplification made in (21) is that the time response of each synaptic connection, \(K_s=(1/\tau _s)e^{-t/\tau _s}\), is approximately the same for all synapses. \(\tau _s\) denotes the time it takes for the soma current to reach steady state. For dendrites with AMPA receptors \(\tau _s\) is the time constant for the decay of synaptic conductance. The dynamics of the soma current is typically given by [25, p. 235] \(\tau _s \dot{I}_{S (k)}=-I_{S (k)}+\mathbf {w}\cdot \mathbf {u}\). Then the steady state firing rate at the output of neuron k becomes \(v_\infty =F(\mathbf {w}\cdot \mathbf {u})\), since \(I_{S (k)}(t)\approx \mathbf {w}\cdot \mathbf {u}\) for large t.
Under the assumption that the soma current reaches steady state long before the firing rate, \(\tau _s \ll \tau _r\), one can derive that the input output relation for the network in Fig. 6 is governed by [25, p. 260]
F makes (22) a nonlinear differential equation. One should choose F so that it corresponds well to reality. It is also important that conditions for network stability are satisfied, so that the network converges to fixed points. For instance, an F that does not allow negative firing rates and saturates at a certain (positive) firing rate leads to a stable network [25, pp. 263–264].
Let \(\mathbf {v}^m\), \(m=1,2,\ldots ,N_{\text {mem}}\) denote the set of possible memory patterns in a memory network. For exact memory retrieval, \(\mathbf {v}^m\) must be fixed points of (22), i.e., \(\mathbf {v}^m=\mathbf {F}\big (\mathbf {W}\cdot \mathbf {u}+\mathbf {M}\cdot \mathbf {v}^m\big )\). The capacity of a memory network is typically determined by the number of different \(\mathbf {v}^m\) simultaneously satisfying this fixed point condition for a conveniently chosen \(\mathbf {M}\). It is typically a tradeoff between how many memory patterns can be stored and how accurately each pattern can be represented.
One \(\mathbf {M}\) in which every \(\mathbf {v}^m\) satisfies the fixed point condition (approximately) was found in [25, Chap. 7], and the solution resembles a typical learning rule.
4.2.2 Learning Rules
A learning rule typically describes the change in synaptic strength over time as a function of pre- and postsynaptic activity. We consider a single neuron here (for simplicity) with output v receiving \(N_u\) inputs from other neurons (see [25, pp. 301–313] for an extension to several output neurons). The synaptic weight from neuron j is denoted \(W_{j}\), and all weights are gathered in the vector \(\mathbf {w}\) (w stands for “weight” here, not necessarily a FF connection. The rules described works just as well for REC connections). We also assume that stimuli is held long enough for the network to reach steady state, and so \(v=\mathbf {w}\cdot \mathbf {u}\).
Bienenstock, Cooper and Munro proposed a learning rule, named BCM rule [41]: \(\tau _w \dot{\mathbf {w}}=v \mathbf {u}(v-\theta _v)\), where \(\theta _v\) is a threshold on output firing rate above which LTD changes to LTP and \(\tau _w\) is controlling the rate at which synapses change. If \(\theta _v\) varies with synaptic strength and grow more rapidly than v as the output firing rate grows large, the BCM rule gives stable solutions for \(\mathbf {w}\). This is achieved if \(\theta _v\) is a low-pass filtered version of \(v^2\), \(\tau _\theta \dot{\theta _v}=v^2 -\theta _v\), where \(\tau _\theta \) is the time scale for threshold modification. The BCM rule incorporates competition between synapses since strengthening of some synapses leads to an increase in postsynaptic firing rate, which raises \(\theta _v\), and makes it more difficult for other synapses to be strengthened.
Shouval et. al derived a calcium based BCM-type learning rule under the assumptions that calcium entry is through NMDA receptors only, and that the presynaptic spikes are generated from a non-stationary Poisson distribution with rate, r(t), varying slowly enough to consider calcium levels at steady state [33]. Based on the AMPA insertion/removal process of Sect. 3.2.2, assuming that \(W_{j}=\beta \cdot B_M \) for some proportionality constant \(\beta \), the following rule results
where \(\varOmega _{[\text {Ca}]_i}\) is the steady state response of \(W_j\), \(\varOmega _{[\text {Ca}]_i} = \beta B_M^{f_p}\), with \(B_M^{f_p}\) as in (15). \(\tau _{[\text {Ca}]_i}\) is the convergence time to \(\varOmega \) as in (15).
Since calcium concentrations vary from synapse to synapse, a learning rule for several synapses must incorporate such variations. In a similar way as (19), Shouval et al. showed that the steady state calcium concentration as a function of the presynaptic firing rate of neuron j, \(r_j\), is given by [33]
where \(S_j(r_j)={P_{\text {inc}} \tau _N r_j}/({1+P_{\text {inc}} \tau _N r_j})\). \(\tau _N\) is the NMDA open probability decay time and \(P_{\text {inc}}\) is the increase in open probability for presynaptic AP’s leading to neurotransmitter release.
Shouval et al. [33] further claimed that an explicit expression of \(\varOmega \) and \(\tau _{[\text {Ca}]_i}\), quantitatively similar to experimental observations, is the quadratic form \(\varOmega _{\text {Ca}(j)}=[\text {Ca}^{2+}]_{i(j)}\big (([\text {Ca}^{2+}]_{i(j)}+\theta _0\big )+\varOmega _0\) with \(\varOmega _0\) is some baseline synaptic strength, \(\theta _0\) some baseline threshold (where LTD changes to LTP), and the linear relation \(\tau _{[\text {Ca}]_i}=\tau _0/[\text {Ca}^{2+}]_{i(j)}\). By inserting this and (24) into (23), a calcium based learning rule for several input synapses is achieved (see [33] for details).
To make this into a BCM rule with varying threshold, Shouval et al. [33] further defined \(\theta _M=\theta _0/(G_{\text {NMDA}}\tau _\text {Ca})\), following the differential equation \(\tau _M \dot{\theta _M}= \big (\mathscr {H}(V_m)^\upmu -\theta _M\big )\), where \(\tau _M\) must be small enough so that \(\theta _M\) grows much faster than v as v gets large. This rule works since the NMDA conductance gain increases as the firing rate increases. Note that is was assumed that \(\theta _M \sim \langle \mathscr {H}(V_m)^\upmu \rangle _{\tau _M}\), which is natural since \(\mathscr {H}(V_m)\) increases as the firing rate increases.
5 ICT-Inspired Treatment of Neurodegenerative Diseases
5.1 Complementary Techniques of Calcium Controlling
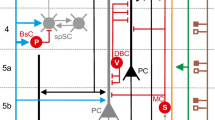
We summarize possible communication-wise contributors in the following without going into detailed biophysics (see Fig. 7).
5.1.1 Non-invasive Techniques
Human neuronal communication network is (willingly or aversely) exposed to external EMR that can be generated by several devices for many purposes. The electricity power supply and all appliances using electricity are the main sources of extremely low frequency fields that range up to 300 Hz. Other technologies are sources of intermediate frequency (IF) fields that range from 300 Hz up to 10 MHz, whereas the simple mobile phones and Wi-Fi devices produce the radio-frequency (RF) fields with frequencies from 10 MHz to 300 GHz. Depending on an electric field level, frequency and electrical properties of the human body, fields interact with the body in different ways. As a consequence, electric currents, sufficient to produce a range of effects, are induced. Apart from thermal effects, which are quantified by SAR coefficient that concern the possible alterations on cells, recent findings implies there are specific but still uncovered non-thermal interactions between RF exposure and neurons [6].
A considerable amount of research work is performed to see whether EMR can be of any damage to brain, metabolism, neuron’s membrane, DNA alterations, which further causes cancer and reduces fertility, etc. As mentioned in the introductory part, it has been even shown that neurocognitive systems affected by neurodegenerative disease can benefit from RF exposure. A framework we present considers the non-thermal effects and scenario with an EMR able to affect the neuronal communication network, i.e., to alter or even generate a certain amount of current in the brain.
To quantify the current produced by a field generated externally but induced intra-brain, natural parameters regarding the filtering features of biological tissues must be considered. The resistivity of the skull is an important physical parameter since the skeleton has a great impact on studies of bioelectricity, the biological effects of the electromagnetic field, and modeling of the electrical properties of the human head [42]. The inhomogeneity of the skull due to the variation of the structure at different positions complicates analysis. Fortunately, this issue was subject to several studies in the past [42,43,44].
The equivalent circuit models are often applied to describe the macroscopic electrical properties of biological tissues. Akhtari et al. established the three-element RC model for one- and three-layer human skulls in the 10–90 Hz frequency range [43]. Recently, Tang et al. used Cole-Cole equations to establish the three-element CPE model. The CPE is a non-intuitive circuit element that compensates for inhomogeneity in the system. The impedance and resistivity spectroscopy data of the skull samples with six types of different structures (standard tri-layer, quasi-tri-layer, standard compact, quasi-compact, dentate suture and squamous suture) are obtained from 30 Hz to 3 MHz [44]. According to the findings, real part of all impedance loci act as a low-pass filter which filters out the high frequency components of the external stimulus. Since the resistivity of the skull is much higher than that of other tissues in a human head (white and gray matter, cerebrospinal fluids, and scalp), we approximate the effects of all tissues on the pathway from outside environment to the sample hippocampal neuron as the low-pass filter, as shown in Fig. 7. Findings presented in [45] additionally support the concept since authors identified 250–300 MHz frequency band to induce the largest electric field intensity while exposing a human head to sagittal- and coronal-plane polarized waves within range of 100–1000 MHz.
Once the frequency-dependent resistivity/conductivity of the tissue is defined and the spatio-temporal electric field is evaluated inside the human head, \(E^{(e)}(x,y,z,t)\), quantification of the spatio-temporal electric current density is given [45]
Superscripts (e) tag the components resulting from externally generated field, while \(\sigma _t\) denotes the equivalent conductivity. To assess a single contribution of induced component, the total current injecting a sample neuron is derived from the current density as
where \(A_C\) denotes the total membrane area of the neuron (usually several tens of \({\upmu }\)m\(^2\)). If particular hippocampal neuron is analyzed, spatial dependency might be excluded to keep the reasoning as simple as possible.
The internally induced field may also be used in some of the models described in Sect. 2.3 in order to estimate possible change in Neuron behavior. These effects would then have to be validated by experiment in order for the model to be rendered useful.
5.1.2 Invasive Techniques
Optogenetics: Controlled pulses of light are used in neuroscience as spike triggers. Unlike inevitable ephaptic coupling and nearly inevitable EMR effects, this type of neuronal stimulation requires devoted human intervention. Among the light-oriented techniques, an optogenetics is recent neuromodulation technique that combines optics and genetics to control and monitor the activities of individual neurons [46]. Even a single cell can be targeted via genetic photo-sensitization and remote optical activation (see Fig. 7) [47]. The photo-sensitization of cells is achieved using the optogenetic actuators like protein channelrhopsin-2 (ChR2) and light-gated chloride pump halorhodopsin (NpHR), whereas the spatial selectivity can be achieved by focusing the light beam onto targeted area, e.g., soma, dendrite or axon.
Evaluation of optogenetic illumination effects can be given through definition of the ionic current that further superimposed to those invoked synaptically and ephaptically. Expression is given in [48]
Conductance of optogenetic ion channels is denoted as \(g_{OG}\). Functions \(\psi \) and f describe how the current depends on the photon flux \(\phi (t)\) and membrane voltage of targeted neuron v(t).
Direct Current Injection We present and show in Fig. 7 two approaches of direct injection of controlled current into neurons, one currently used in neuroscience, and one futuristic.
Electrodes: The “Current clamp” technique is commonly used in physiological studies deployed in neuroscience. This technique is used to study how a cell responds when electric current enters a cell by means of recording glass micro-pipettes (electrodes). Using findings presented in Sect. 3.1, an identical approach can be used in order to control \([\text {Ca}^{2+}]_i\) values as desired.
Nano-scale devices: Architecture development of nano-scale devices, which can be used intra-body to interact at cellular level, is intriguing scientific topics. Hybrid structures consisting of arrays of nano-wire field-effect transistors (FET) integrated with the individual mammalian neurons, used for stimulation, and/or inhibition of neuronal signal propagation, are tested by Patolsky and his team [49]. In terms of future-oriented works, preliminary modeling of communication between nano-scale device and sample neuron [50] encouraged the definition of conceptual nano-machine-to-neuron communication interface based on nano-scale stimulator device called synaptic nano-machine (SnM) [51]. Although there is still much to be done in this field, ranging from isolation of nano-materials to biocompatibility issues, a nano-scale device intended to either directly apply or indirectly induce a controlled amount of current will presumably be developed in this decade. According to information built into such devices, controlled alternating currents can be induced directly into neurons.
One issue to be accounted for when using any stimulation technique is the signal dependant encoding noise [52] that reflects to the input as \(i_{n}(t) = i(t) + n_e(t) = i(t) + n_{SD}(t) + n_{env}(t)\). i(t) denotes a noise-free current, \(n_{SD}(t)\) is the signal-dependent noise component derived from an auto regressive (AR) random process w(t) as \(n_{SD}(t) = i(t) * w(t)\), and \(n_{env}(t)\) is the environmental noise. Since our study accounted for ephaptic stimulation, it is reasonable to assume \(n_{env}(t)\) as zero mean Gaussian noise. Another non-trivial issue is the synchronization between stimulus sources since high levels of desynchronization can delay the generation of spikes in the targeted neuron and lead to unrestrained control.
5.2 Graph-Based Strategies of Diagnosis and Treatment of Neuronal Disorders
As previously shown in Sect. 4.1, graph interpretation of neuronal connectivity provides researchers with connectional relationships between individual neurons. Although our research is mostly confined to hippocampal neurons, without any loss of generality we use two-dimensional spatial representations of a local subnetwork of 131 neurons with 764 unidirectional connections within Caenorhabditis elegans rostral ganglia from [53] (and references therein) to show how graph theory methods can be utilized in formation of adequate strategy assisting in diagnosis and treatment of neuronal diseases. Spatial two-dimensional positions represent the position of the soma of individual neurons. It is not established which graph theory measures are most appropriate for the analysis of the brain. Nevertheless, we explore a set of those that might have relevance for neuroscience applications.
Depending on the nature of the ion flow, the synapses representing connections can have either an excitatory, depolarizing, or an inhibitory, hyperpolarizing, effect on the postsynaptic neuron. Thereby, to keep the reasoning as realistic as possible, we modify 20% of the number of synapses in AM giving them negative weights according to (20). Note that distribution of inhibitory and excitatory cells is not temporal, unlike the time-variable synaptic weight values (temporal synaptic weights form dynamic wiring of neuron connections, i.e., the plasticity).
Spatial and temporal visualization can be used in neuroscience as one possible way of diagnosis. For instance, significant reduction of clustering and loss of small-worldness might provide a clinically useful diagnostic marker indicating AD [54]. Moreover, graph theory can be used to create a certain visualization tool that might assist in neuronal treatment. As an example, we elaborate on treatment based on regulation of calcium.
Calcium signaling is crucial in neurotransmitters transmission and memory formation. The intracellular and extracellular calcium concentration level is affecting how strongly two neurons are wired together through chemical synapses. Disruption in the processes that regulates calcium concentration levels (calcium dysregulation), lead to dramatic changes in neuronal functioning and potentially weak connections between cells or clustering regions. This further lead to impaired functioning and cell death, which is the effect in brains with AD. Potential remedy of AD lies in direct regulation of calcium concentration levels or in control of amyloid-beta (A\(\beta \)) deposits, that lead to calcium dysregulation [10]. Therefore, an efficient and effective human treatment can directly explore particular graph theory measures that are able to mark critical areas and cells in network.
5.2.1 Centrality Criteria
As historically first, conceptually simplest, and very useful measure of centrality, degree is first applied here to find the neurons with most synaptic connections. Additionally, betweenness centrality is also deployed in what follows since introduced as a “measure for quantifying the control of a human on the communication between other humans in a social network” [55]. Conversely, closeness and eigenvector centrality do not qualify themselves as a usable criteria in this study due to the unmatched physical interpretations. For instance, closeness can be regarded as a measure of how long it will take to spread information from analyzed vertex to all other vertices sequentially, thereby being completely irrelevant in \([\text {Ca}^{2+}]_i\) regulation strategy.
The degree of a neuron is the sum of its indegree and outdegree values defined as the number of incoming (afferent) or outgoing (efferent) edges, respectively. We are interested in outdegrees, od(v). They are subject to constraints due to growth, tissue volume or metabolic limitations [56], but have obvious functional interpretations: high outdegree indicates a large number of potential functional targets. Outdegree criterion further qualifies an adequate neuron which \([\text {Ca}^{2+}]_i\) is to be regulated. This criterion visualizes the G(V, E) in a way shown in Fig. 8a.
Betweenness centrality measures a vertex’s or edge’s importance in network. Node betweenness quantifies the number of times a vertex participate in the shortest path between two other vertices. Analogously, the betweenness centrality of edges is calculated as the number of shortest paths among all possible vertex couples that pass through the given edge. Vertices and edges with the high centrality values are assumed to be crucial for the graph connectivity and thereby shall be monitored in potentially malfunctioning brains. Neurodegenerative disease removing important neurons and synaptic connections lead to both anatomically and functionally disconnected clusters. The most important edges, called bridges, are particularly important for decreasing the average path length among neurons in a network, and for speeding up the information transmission. Region of Caenorhabditis elegans network is visualized in Fig. 8b applying the node centrality criteria. For analyzed network consisting of 131 frontal neurons, 4 cells are identified as important for proper communication. In general, the higher the number of important neurons, the lower the network robustness.
Average path length is one of the most important measures, and can be obtained from distance matrix that is result of the Floyd-Warshall algorithm (particularly applied here to determine node betweenness). Average path length is what makes the brain efficient in information transfer from one part to the other. It is also a function of degree (e.g., for a random network \(l_{avg}\approx \log (N)/\log (<k>))\) (\(<k>\) is the average degree). In AD brains, one can typically observe an increase on average path length, as described in [54]. For network analyzed here \(l_{avg} = 3.1277\).
5.2.2 Clustering Coefficient Criterion
The cluster coefficient of a vertex, \(\gamma (v)\), is defined in [57]. As a measure of the degree to which vertices in a G(V, E) tend to cluster together, it indicates how many connections are maintained between vertex neighbors. In particular scenario with directed graph on board, neighbours are all those neurons that are connected through an incoming or an outgoing synaptic connections to the central neuron v. The ratio of actually existing connections between the neighboring neurons and the maximal number of such connections possible defines the neuron’s cluster coefficient. If neuron does not have any neighbors, then \(\gamma (v) = 0\) by convention. The average of the cluster coefficients determines the cluster coefficient of the G(V, E). Although \(\gamma (v)\) does not provide information about the number or size of clustering groups and only captures local connectivity patterns involving the direct neighbours of the central vertex [56], high values of \(\gamma (v)\) point to a neuronal region consisting of groups of units that mutually share structural connections and function in a closely related manner. Furthermore, neurons with high \(\gamma (v)\)s might serve as candidates whose control of \([\text {Ca}^{2+}]_i\) regulates the communication within the entire cluster. Visualization according to the clustering criterion produces similar result to that in Fig. 8, but with different distribution of important neurons.
6 Chapter Summary
Calcium is important in signal transmission in and between neurons. The neuron’s intracellular calcium concentration, \([\text {Ca}^{2+}]_i\), determines synaptic strength. High concentration levels usually lead to synaptic strengthening, whereas moderate levels lead to a weakening. The \([\text {Ca}^{2+}]_i\) depends on both the spike train frequency as well as stimulus frequencies. In general, higher spiking and stimulus frequencies lead to significantly increased \([\text {Ca}^{2+}]_i\) and therefore to a synapse strengthening. Lower frequencies, on the other hand, lead to a synapse weakening. If one can find means of controlling voltage controlled calcium ion-gates (VCCGs), it will be possible to regulate \([\text {Ca}^{2+}]_i\) and therefore affect the neurons ability to communicate with other neurons.
In this chapter we identified that changes in neuron’s membrane potential drive the magnitude of \([\text {Ca}^{2+}]_i\). The findings show the neuronal communication phenomena being frequency-dependent not only on the stimulus frequencies, but also on the spiking frequency. Therefore, problems in aging brains, strongly noticeable in brains with neurodegenerative diseases such as Alzheimer’s disease (AD), may be overcome via devoted human regulation of \([\text {Ca}^{2+}]_i\). From what we have presented in this chapter, it is likely that the frequency of the external stimuli is crucial in processes that may take place within the brain. The findings thus can pave the way to the definition of novel treatment tools for medical applications. Furthermore, synchronized or non-synchronized neuronal activity that underlies long term potentiation (LPT) and long term depression (LTD) processes, respectively, can be controlled at postsynaptic neurons through convenient stimulation of presynaptic neuron. Since LTP and LTD patterns are confined to memory formation and learning processes, one can exploit mapping between spiking- and stimulus frequencies presented here to drive changes in those processes. Moreover, study presented here helps in development of a graph-based strategy of neurons selection whose electrical properties should be altered in order to further evoke certain changes in \([\text {Ca}^{2+}]_i\). Obviously, it is likely that neuronal network can be described as graph, and quantitative characterization of anatomical patterns through the adjacency matrix (AM). Moreover, specified graph theory concepts have been utilized in formation of adequate strategy assisting in diagnosis and treatment of neuronal diseases. A set of graph theory measures that might have certain relevance for neuroscience applications have been stated and deployed in this study to create a visualization tool that helps in selection of targeted neurons whose \([\text {Ca}^{2+}]_i\) is to be controlled. Possible non-invasive and invasive means of controlling neuronal communications are also envisioned.
To keep the theory as realistic as possible, noise effects referred to disturbances on the stimulus currents and synchronization issues are not discussed in this chapter and are to be accounted for and thoroughly elucidated. To complete the calcium based synaptic model, it is also necessary to determine a mathematical relation between neurotransmitter release probability and the level of \([\text {Ca}^{2+}]_i\). Computationally demanding handling of huge AM describing large-scale networks, that can be recorded with functional magnetic resonance imaging, electroencephalography and magnetoencephalography, is another issue. These issues are not trivial and demand more research.
In terms of the applicability of concepts and results presented in this chapter, it is possible to make their use in communication controlling of either artificial nano-network composed of nano-devices fabricated following a design presented in Sect. 3, or neuronal biological network. Findings can also be used for implementation of novel communication technique between nano-scale devices.
An important problem to pursue through future research is to evaluate the performance of neural information processing seen from a communication perspective.
References
Arendash GW, Sanchez-Ramos J, Mori T, Mamcarz M, Lin X, Runfeldt M, Wang L, Zhang G, Sava V, Tan J, Cao C (2010) Electromagnetic field treatment protects against and reverses cognitive impairment in alzheimer’s disease mice. J Alzheimer’s Dis 19:191–210
Arendash GW (2012) Transcranial electromagnetic treatment against alzheimer’s disease: why it has the potential to trump alzheimer’s disease drug development. J Alzheimer’s Dis 32:243–266
Dragicevic N, Bradshaw PC, Mamcarz M, Lin X, Wang L, Cao C, Arendash GW (2011) Long-term electromagnetic field treatment enhances brain mitochondrial function of both alzheimer’s transgenic mice and normal mice: a mechanism for electromagnetic field-induced cognitive benefit. Neuroscience 185:135–149
Juutilainen J, Hoyto A, Kumlin T, Naarala J (2011) Review of possible modulation-dependent biological effects of radiofrequency fields. Bioelectromagnetics 32:511–534
Rosen AC, Ramkumar M, Nguyen T, Hoeft F (2009) Noninvasive transcranial brain stimulation and pain. Curr Brain Headache Rep 13(1):12–17
Stavroulakis PE (2003) Biological effects of electromagnetic fields. Springer
Disterhoft JF, Moyer JR, Thompson LT (1994) The calcium rationale in aging and Alzheimer’s disease. Annals of the New York academy of sciences—calcium hypothesis of aging and dementia, vol 747(2) pp 382–406
Goodison WV, Frisardi V, Kehoe PG (2012) Calcium channel blockers and Alzheimer’s disease: potential relevance in treatment strategies of metabolic syndrome. Annals of the New York academy of sciences—calcium hypothesis of aging and dementia 30(2):269–282
Bear MF, Connors BW, Paradiso MA (2006) Neuroscience: exploring the Brain 3rd edn. Lippincott
Green KN, LaFerla FM (2008) Linking calcium to A-beta and alzheimer’s disease. Neuron 59:190–194
Yu J, Chang RCC, Tan L (2009) Calcium dysregulation in Alzheimer’s disease: from mechanisms to therapeutic opportunities. Prog Neurobiol 89:240–255
Adey WR (1981) Tissue interactions with nonionizing electromagnetic fields. Physiol Rev 61(2):435–514
Mesiti F, Balasingham I (2011) Novel treatment strategies for neurodegenerative diseases based on RF exposure. In Proceedings of the 4th international symposium on applied sciences in biomedical and communication technologies ser, ISABEL 11, pp 100:1–100:5. http://doi.acm.org/10.1145/2093698.2093798
Buzsaki G, Anastassiou CA, Koch C (2004) The origin of extracellular fields and currents. Nat Rev Neurosci 13:407–420
Anastassiou CA, Perin R, Markram H, Koch C (2011) Ephaptic coupling of cortical neurons. Nat Neurosci 14:217–223
Koch C (1999) Biophysics of computation: information processing in single neurons. Oxford University Press, Inc
Repacholi MH (1998) Low-level exposure to radiofrequency electromagnetic fields: health effects and research needs. Bioelectromagnetics 19(1):1–19
Izhikevich EM (2004) Which model to use for cortical spiking neurons? IEEE Trans Neural Networks 15(5):1063–1070
Hodgkin AL, Huxley AF (1952) A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol 117(4):500–544
Warman EN, Durand DM, Yuen GL (1994) Reconstruction of hippocampal CA1 pyramidal cell electrophysiology by computer simulation. J Neurophysiol 71(6):2033–2045
Liboff AR, McLeod BR (1988) Kinetics of channelized membrane ions in magnetic fields. Bioelectromagnetics 9:39–51
Halle B (1988) On the cyclotron resonance mechanism for magnetic field effects on transmembrane ion conductivity. Bioelectromagnetics 9:381–385
Pilla AA (2006) Mechanisms and therapeutic applications of time-varying and static magnetic fields. In: Handbook of biological effects of electromagnetic fields. CRT Press
Appollonio F, Liberti M, d’Inzeo G, Tarricone L (2000) Integrated models for the analysis of biological effects of em fields used for mobile communications. IEEE Trans Microwave Theory Tech 48:2082–2092
Dayan P, Abbott LF (2001) Theoretical neuroscience: computational and mathematical modeling of neural systems. The MIT Press, Cambridge, Massachusets, London, England
Hunter IW, Korenberg MJ (1986) The identification of nonlinear biological systems: wiener and hammerstein cascade models. Biol Cybern 55:135–144
Cook EP, Guest JA, Liang Y, Masse NY, Colbert CM (2007) Dendrite-to-soma input/output function of continuous time-varying signals in hippocampal CA1 pyramidal neurons. J Neurophysiol 98:2943–2955
Richardson M, Brunel N, Hakim V (2003) From subthreshold to firing-rate resonance. J Neurophysiol 89:2538–2554
Mesiti F, Floor PA, Kim AN, Balasingham I (2012) On the modeling and analysis of the RF exposure on biological systems: a potential treatment strategy for neurodegenerative diseases. Elsevier Nano Commun Networks 3:103–115
Matveev V, Wang X-J (2000) Implications of all-or-none synaptic transmission and short-term depression beyond vesicle depletion: a computational study. J Neurosci 20(4):1575–1588
Wu LG, Saggau P (1997) Presynaptic inhibition of elicited neurotransmitter release. Trends Neurosci 20(5):204–212
Neher E (1998) Vesicle pools and \(\text{Ca}^{2+}\) microdomains: new tools for understanding their roles in neurotransmitter release. Neuron 20:389–399
Shouval HZ, Castellani GC, Blais BS, Yeung LC, Cooper LN (2002) Converging evidence for a simplified biophysical model of synaptic plasticity. Biol Cybern 87:383–391
Castellani GC, Quinlan EM, Cooper LN, Shouval HZ (2001) A biophysical model of bidirectional synaptic plasticity: Dependence on AMPA and NMDA receptors. PNAS 8(22):1272–12777
Castellani GC, Quinlan EM, Bersani F, Cooper LN, Shouval HZ (2005) A model of bidirectional synaptic plasticity: from signalling network to channel conductance. Learn Mem 12:423–432
Jahr CE, Stevens CF (1990) Voltage dependence of NMDA-activated macroscopic conductances predicted by single-channel kinetics. J Neurosci 10(9):3178–3182
Hebb DO (1949) The organization of behavior: a neuropsychological theory. Wiley, New York
Dudek SM, Bear MF (1992) Homosynaptic long-term depression in area CA1 of hippocampus and effects on N-methyl- D-aspartate receptor blockade. In: Proceedings of the National Academy of Sciences. USA, 89:4363–4367
Dodge FA, Rahamimoff R (1967) Cooperative action of calcium ions in transmitter release at the neuromuscular junction. J Physiol 193:419–432
Bullmore E, Sporns O (2009) Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci 10:186–198
Bienenstock EL, Cooper LN, Munro PW (1982) Theory for the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex. J Neurosci 2:32–48
Tang C, You F, Cheng G, Gao D, Fu F, Dong X (2009) Modeling the frequency dependence of the electrical properties of the live human skull. Physiol Meas 30:1293–1301
Akhtari M, Bryant HC, Emin D, Merrifield W, Mamelak AN, Flynn ER, Shih JJ, Mandelkern M, Matlachov A, Ranken DM, Best ED, DiMauro MA, Lee RR, Sutherling WW (2003) A model for frequency dependence of conductivities of the live human skull. Brain Topogr 16(1):39–55
Tang C, You F, Cheng G, Gao D, Fu F, Yang G, Dong X (2008) Correlation between structure and resistivity variations of the live human skull. IEEE Trans Biomed Eng 55:2286–2292
Khaleghi A, Eslampanah MS, Sendi, Chavez-Santiago R, Mesiti F, Balasingham I (2012) Exposure of the human brain to an electromagnetic plane wave in the 100–1000 MHz frequency range for potential treatment of neurodegenerative diseases. IET Microwaves Antennas Propag 6:1565–1572
Liu X, Ramirez S, Pang PT, Puryear CB, Govindarajan A, Deisseroth K, Tonegawa S (2012) Optogenetic stimulation of a hippocampal engram activates fear memory recall. Nature 484:381–385
Grossman N, Poher P, Grubb MS, Kennedy GT, Nikolic K, McGovern B, Palmini RB, Gong Z, Drakakis EM, Neil MA, Dawson MD, Burrone J, Degenaar P (2010) Multi-site optical excitation using Ch R2 and micro-led array. J Neural Eng 7(1):381–385
Nikolic K, Jarvis S, Grossman N, Schultz S (2013) Computational models of optogenetic tools for controlling neural circuits with light. In: Annual international conference of the IEEE, EMBS
Patolsky F, Timko BP, Yu G, Fang Y, Greytak AB, Zheng G, Lieber CM (2006) Detection, stimulation, and inhibition of neuronal signals with high-density nanowire transistor arrays. Science 313:1100–1104
Galluccio L, Palazzo S, Santagati GE (2011) Modeling signal propagation in nanomachine-to-neuron communications. Nano Commun Network 2:213–222
Mesiti F, Balasingham I. Nanomachine-to-neuron communication interfaces for neuronal stimulation at nanoscale. J Sel Areas in Commun—Special Issue on Emerging Technologies in Communications In Press
Jabbari A, Balasingham I (2013) Noise characterization in a stochastic neural communication network. Nano Commun Network 4(2):65–72
Kaiser M, Hilgetag CC (2006) Nonoptimal component placement, but short processing paths, due to long-distance projections in neural systems. PLoS Comput Biol 2(7):e95. doi:10.1371/journal.pcbi.0020095
Stam C, Jones BF, Nolte G, Breakspear M, Scheltens P (2007) Small-world networks and functional connectivity in alzheimer’s disease. Cereb Cortex 17(1):92–99
Freeman LC (1977) A set of measures of centrality based upon betweenness. Sociometry 40:35–41
Sporns O (2003) Graph Theory methods for the analysis of neural connectivity patterns. neuroscience database. Springer US, Ch
Watts D, Strogatz S (1998) Collective dynamics of ‘small-world’ networks. Nature (London) 393:440–442
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Veletić, M., Anders Floor, P., Komuro, R., Balasingham, I. (2017). On Regulation of Neuro-spike Communication for Healthy Brain. In: Suzuki, J., Nakano, T., Moore, M. (eds) Modeling, Methodologies and Tools for Molecular and Nano-scale Communications. Modeling and Optimization in Science and Technologies, vol 9. Springer, Cham. https://doi.org/10.1007/978-3-319-50688-3_9
Download citation
DOI: https://doi.org/10.1007/978-3-319-50688-3_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-50686-9
Online ISBN: 978-3-319-50688-3
eBook Packages: EngineeringEngineering (R0)