Keywords

1 Introduction

Fractional calculus deals with derivatives and integrations of arbitrary order [41, 53] and has found many applications in many fields of physics, applied mathematics and engineering. Moreover, many real-world physical systems are well characterized by fractional order differential equations, i.e., equations involving both integer and non integer order derivatives [25]. It is observed that the description of some systems is more accurate when the fractional derivative is used. For instance, electrochemical processes and flexible structures are modeled by fractional order models [38, 41]. Nowadays, many fractional-order differential systems behave chaotically, such as the fractional-order Chua system [52], the fractional-order Duffing system [2], the fractional-order Lu system, the fractional order Chen system [51].

Recently, due to its potential applications in secure communication and control processing, the study of chaos synchronization in fractional order dynamical systems and related phenomena is receiving growing attention.

The synchronization problem of fractional order chaotic systems was first investigated by Deng and Li who carried out synchronization in the case of the fractional Lü system. Afterwards, they studied chaos synchronization of the Chen system with a fractional order in a different manner [18, 19].

Fuzzy logic controllers are generally considered applicable to plants that are mathematically poorly understood and where experienced human operators are available for providing a qualitative “rule of thumb”.

Based on the universal approximation theorem [11, 60] (fuzzy logic controllers are general enough to perform any nonlinear control actions) there is rapidly growing interest in systematic design methodologies for a class of nonlinear systems using fuzzy adaptive control schemes. An adaptive fuzzy system is a fuzzy logic system equipped with a training algorithm in which an adaptive controller is synthesized from a collection of fuzzy IF–THEN rules and the parameters of the membership functions characterizing the linguistic terms in the IF–THEN rules change according to some adaptive law for the purpose of controlling a plant to track a reference trajectory.

In this work we consider Type-2 fuzzy sets which are extension of type-1 fuzzy sets introduced in the first time by Zadeh [66]. Basic concepts of type-2 fuzzy sets and systems were advanced and well established in [9, 20, 45, 54]. In 1998, Mendel and Karnik [20] introduced five different kinds of type reduction methods which are extended versions of type-1 defuzzification methods. Qilian and Mendel [54] proposed an efficient and simplified method for computing the input and antecedent operations for interval type-2 fuzzy logic controller (IT2FLC) using the concept of upper and lower Membership functions. Karnik and Mendel developed the centroid of an interval type-2 fuzzy set (IT2FS), not only for an IT2FS and IT2FLCs but also for general type-2 FSs and introduced an algorithm for its computation. Mendel [17, 44] described important advances for both general and interval type-2 fuzzy sets and systems in 2007. Because of the calculation complexity especially in the type reduction, use of IT2FLC is still controversial. Seplveda et al. showed that using adequate hardware implementation, IT2FLC can be efficiently utilized in applications that require high speed processing. Thus, the type-2 FLS has been successfully applied to several fuzzy controller designs [12, 17, 36, 42, 62].

In this paper, by incorporating the \( H^{\infty } \) tracking design technique [35, 38, 43] and Lyapunov stability criterion, a new adaptive fuzzy control algorithm is proposed so that not only the stability of the adaptive type-2 fuzzy control system is guaranteed but also the influence of the approximation error and external disturbance on the tracking error can be attenuated to an arbitrarily prescribed level via the \( {H}^\infty \) tracking design technique. The proposed design method attempts to combine the attenuation technique, type-2 fuzzy logic approximation method, and adaptive control algorithm for the robust tracking control design of the nonlinear fractional order systems with a large uncertainty or unknown variation in plant parameters and structures.

This chapter is organized as follows: Sect. 2 presents a brief review on the state of the art for the addressed problem. In Sect. 3, an introduction to fractional derivatives and its relation to the approximation solution will be addressed and the basic definition and preliminaries for fractional order systems. A description of the interval type-2 fuzzy logic is presented in Sect. 4. Section 5 and 6 generally propose adaptive type-2 fuzzy robust \( H^{\infty } \) control of uncertain fractional order systems in the presence of uncertainty and its stability analysis. In Sect. 7, application of the proposed method on fractional order expression chaotic systems (Duffing oscillator) is investigated. Finally, the simulation results and conclusion will be presented in Sect. 8.

2 Related Work: A Brief Review

Fractional adaptive control is a growing research topic gathering the interest of a great number of researchers and control engineers [32]. The main argument of this community is the significant enhancement obtained with these new real-time controllers comparatively to integer order ones [53].

Since the pioneering works of Vinagre et al. [59] and Ladaci and Charef [26, 27], an increasing number of works are published focusing on various fractional order adaptive schemes such as: fractional order model reference adaptive control [13, 27, 63], fractional order adaptive pole placement control [34], fractional high-gain adaptive control [29], fractional multi-model adaptive control [33], robust fractional adaptive control [30], fractional extremum seeking control [48], Fractional IMC-based adaptive control [31], fractional adaptive sliding mode control [15], fractional adaptive PID control [28, 47] … etc.

The study and design of fractional adaptive control laws for nonlinear systems is also an actual leading research direction [5, 6, 50, 57]. Many control strategies have been proposed in literature to deal with the control and synchronization problems of various nonlinear and chaotic fractional order systems [1, 55]. Nonlinear fractional adaptive control is wide meaning concept with many different control approaches such as: fractional order adaptive backstepping output feedback control scheme [64], adaptive feedback control scheme based on the stability results of linear fractional order systems [49], Adaptive Sliding Control [36, 65], Adaptive synchronization of fractional-order chaotic systems via a single driving variable [67], H∞ robust adaptive control [22, 37], etc. Whereas, in order to deal with nonlinear systems presenting uncertainties or unknown model parameters, many authors have used fuzzy systems [3, 7, 8, 58]. In this work, we use Type-2 Fuzzy logic systems [4, 40].

3 Basic Preliminaries for Fractional Order Systems

Fractional calculus (integration and differentiation of arbitrary ‘fractional’ order) is an old concept which dates back to Cauchy, Riemann Liouville and Leitnikov in the 19th century. It has been used in mechanics since at least the 1930s and in electrochemistry since the 1960s. In control field, several theoretical physicists and mathematicians have studied fractional differential operators and systems [14, 53].

Fractional order operator is a generalization of integration and differentiation to non integer order fundamental operators, denoted by \( _{a} D_{t}^{\alpha } \) , where a and t are the limits of the operator. This operator is a notation for taking both the fractional integral and functional derivative in a single expression defined as [22,23,24, 51]:

$$ _{a} D_{t}^{q} = \left\{ {\begin{array}{*{20}l} {\frac{{d^{q} }}{{dt^{q} }}} \hfill & {q > 0} \hfill \\ 1 \hfill & {q = 0} \hfill \\ {\int\limits_{a}^{t} {} \left( {d\tau } \right)^{ - q} } \hfill & {q < 0} \hfill \\ \end{array} } \right. $$
(1)

There are some basic definitions of the general fractional integration and differentiation. The commonly used definitions are those of Riemann–Liouville and Grünwald-Letnikov [29, 30, 56].

The Riemann-Liouville (R-L) integral of order λ > 0 is defined as:

$$ I_{RL}^{\lambda } f(t) = D^{ - \lambda } f(t)\quad = \frac{1}{{\Gamma (\lambda )}}\int\limits_{0}^{t} {(t - \tau )^{\lambda - 1} f(\tau )d\tau } $$
(2)

and the expression of the R-L fractional order derivative of order μ > 0 is:

$$ D_{RL}^{\mu } f(t) = \frac{1}{{\Gamma (n - \mu )}}\frac{{d^{n} }}{{dt^{n} }}\int\limits_{0}^{t} {(t - \tau )^{n - \mu - 1} f(\tau )d\tau } $$
(3)

with Г(.) is the Euler’s gamma function and the integer n is such that (n − 1) < μ < n. This fractional order derivative of Eq. (3) can also be defined from Eq. (2) as:

$$ D_{RL}^{\mu } f(t) = \frac{{d^{n} }}{{dt^{n} }}\left\{ {I_{RL}^{(n - \mu )} f(t)^{{}} } \right\} $$
(4)

The Grünwald–Letnikov definition of the fractional derivative, is expressed as:

$$ _{{t_{0} }}^{GL } D_{t}^{q} \,f(t) = \lim_{n \to 0} \frac{1}{{h^{n} }}\sum\limits_{j = 0}^{{\left[ {\frac{t - q}{h}} \right]}} {( - 1)^{j} } \left( {\begin{array}{*{20}c} q \\ j \\ \end{array} } \right)f(t - jh) $$
(5)

where \( \left[ {\frac{t - q}{h}} \right] \) indicates the integer part and \( ( - 1)^{j} \left( {\begin{array}{*{20}c} q \\ j \\ \end{array} } \right) \) are binomial coefficients \( c_{j}^{(q)} \left( {j = 0,1, \ldots } \right). \)

The calculation of these coefficients is done by formula of following recurrence:

$$ c_{0}^{(q)} = 1,\quad c_{j}^{(q)} = (1 - \frac{1 + q}{j})c^{(q)}_{j-1} $$

The general numerical solution of the fractional differential equation:

$$ {}_{a}^{GL} D_{t}^{q} y(t) = f(y(t),t), $$

can be expressed as follows:

$$ y\left( {t_{k} } \right) = f\left( {y\left( {t_{k} } \right),t_{k} } \right)h^{q} - \sum\limits_{j = v}^{k} {c_{j}^{\left( q \right)} } y\left( {t_{k - j} } \right). $$
(6)

The Fundamental Predictor-Corrector Algorithm

The fractional Adams-Bashforth-Moulton method used to approximate the fractional order integral operator was introduced in [14]. In fact it is more practical to use a numerical fractional integration method to compute fractional order integration or derivation as the approximating transfer functions are of relatively high orders.

Consider the differential equation

$$ D^{\alpha } y(x) = f\left( {x,y(x)} \right) $$
(7)

with initial conditions:

$$ y^{(k)} (0) = y_{0}^{(k)} ,\quad \quad k = 0,1, \ldots ,m - 1, $$
(8)

where \( m = [\alpha ] \) and the real numbers \( y^{(k)} (0) = y_{0}^{(k)} , \) \( k = 0,1, \ldots ,m - 1, \) are assumed to be given.

The basics of this technique take profit of an interesting analytical property: the initial value problem (4), (5) is equivalent to the Volterra integral equation

$$ y(x) = \sum\limits_{k = 0}^{[\alpha ] - 1} {y^{(k)} (0)\frac{{x^{k} }}{k!}} + \frac{1}{{\Gamma (\alpha )}}\int\limits_{0}^{\infty } {(x - t)^{\alpha - 1} f\left( {t,y(t)} \right)} dt $$
(9)

Introducing the equispaced nodes \( t_{j} = jh \) with some given \( h > 0 \) and by applying the trapezoidal integral technique to compute (6), the corrector formula becomes

$$ \begin{aligned} y_{h} (t_{n + 1} ) & = \sum\limits_{k = 0}^{[\alpha ] - 1} {\frac{{t_{n + 1} }}{k!}} y^{(k)} (0) + \frac{{h^{\alpha } }}{{\Gamma (\alpha + 2)}}f\left( {t_{n + 1} ,y_{h}^{P} (t_{n + 1} )} \right) \\ & \quad + \frac{{h^{\alpha } }}{{\Gamma (\alpha + 2)}}\sum\limits_{j = 0}^{n} {a_{j,n + 1} f\left( {t_{j} ,y_{h} (t_{j} )} \right)} \\ \end{aligned} $$
(10)

where

$$ \begin{aligned} a_{0,n + 1} & = n^{\alpha + 1} - (n - \alpha )(n + 1)^{\alpha } \\ a_{j,n + 1} & = (n - j + 2)^{\alpha + 1} + (n - j)^{\alpha + 1} - 2(n - j + 1)^{\alpha + 1} , \\ & \quad (1 \le j \le n) \\ \end{aligned} $$
(11)

and \( y_{h}^{P} (t_{n + 1} ) \) is given by,

$$ y_{h}^{P} (t_{n + 1} ) = \sum\limits_{k = 0}^{[\alpha ] - 1} {\frac{{t_{n + 1} }}{k!}} y^{(k)} (0) + \frac{1}{{\Gamma (\alpha )}}\sum\limits_{j = 0}^{n} {b_{j,n + 1} f\left( {t_{n} ,y_{h} (t_{j} )} \right)} $$
(12)

where now

$$ b_{j,n + 1} = \frac{{h^{\alpha } }}{\alpha }\left( {(n + 1 - j)^{\alpha } - (n - j)^{\alpha } } \right) $$
(13)

This approximation of the fractional derivative within the meaning of Grünwald-Letnikov is on the one hand equivalent to the definition of Riemann-Liouville for a broad class of functions [46], on the other hand, it is well adapted to the definition of Caputo (Adams method) because it requires only the initial conditions and has a physical direction clearly. In this work, the Grünwald–Letnikov method is used for numerical evaluation of the fractional derivative.

4 Interval Type-2 Fuzzy Systems

A brief overview of the basic concepts of Interval type-2 fuzzy systems is presented in the following [21, 37, 40]. If we consider a type-1 membership function, as in Fig. 1, then a type-2 membership function can be produced. In this case, for a specific value \( x^{{\prime }} \) the membership function \( (u^{{\prime }} ) \), takes on different values, which are not all weighted the same, so we can assign membership grades to all of those points.

Fig. 1
figure 1

Example of a type-1 membership function

Full size image

A type-2 fuzzy set in a universal set X is denoted as \( \tilde{A} \) and can be characterized in the following form:

$$ \tilde{A} = \int\limits_{x \in X} {} \mu_{{\tilde{A}}} (x,v)/x,\forall v \in J_{x} \subseteq [0,1] $$
(14)
$$ \mu_{{\tilde{A}}} (x) = \int_{{v \in J_{x} }} {} f_{x} (v)/v, $$

in which \( 0 \le \mu_{{\tilde{A}}} (x) \le 1 \).

The 2-D interval type-2 Gaussian membership function with uncertain mean \( {\text{m}} \in [{\text{m}}_{1} ,{\text{m}}_{2} ] \) and a fixed deviation \( \sigma \) is shown in Fig. 2.

Fig. 2
figure 2

Interval type-2 membership function

Full size image
$$ \upmu_{{{\tilde{\text{A}}}}} ({\text{x}}) = { \exp }\left[ { - \frac{1}{2}\left( {\frac{{{\text{x}} - {\text{m}}}}{\upsigma}} \right)^{2} } \right] $$

A fuzzy logic system (FLS) described using at least one type-2 fuzzy set is called a type-2 FLS. Type-1 FLSs are unable to directly handle rule uncertainties, because they use type-1 fuzzy sets that are certain. On the other hand, type-2 FLSs, are useful in circumstances where it is difficult to determine an exact numeric membership function, and there are measurement uncertainties [40].

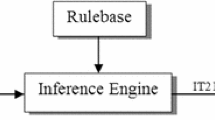
A type-2 FLS is characterized by IF–THEN rules, where their antecedent or consequent sets are now of type-2. Type-2 FLSs, can be used when the circumstances are too uncertain to determine exact membership grades such as when the training data is affected by noise. Similarly, to the type-1 FLS, a type-2 FLS includes a fuzzifier, a rule base, fuzzy inference engine, and an output processor, as we can see in Fig. 3 for a Mamdani-model.

Fig. 3
figure 3

Type-2 fuzzy logic system

Full size image

An IT2FS is described by its Lower \( \underline{\mu }_{{\tilde{A}}} (x) \) and Upper \( \bar{\mu }_{{\tilde{A}}} (x) \) membership functions. For an IT2FS, the footprint of uncertainty (FOU) is described in terms of lower and upper MFs as:

$$ FOU\left( {\tilde{A}} \right) = \mathop {\bigcup }\limits_{x \in X} \left[ {\underline{\mu }_{{\tilde{A}}} (x), \bar{\mu }_{{\tilde{A}}} (x)} \right] $$

The type-reducer generates a type-1 fuzzy set output, which is then converted in a numeric output through running the defuzzifier. This type-1 fuzzy set is also an interval set, for the case of our FLS we used center of sets type reduction, \( {\text{y}}({\text{X}}) \) which is expressed as [10] :

$$ y(X) = [y_{l} ,y_{r} ] $$

where \( y_{l} = \frac{{\mathop \sum \nolimits_{i = 1}^{M} f_{l}^{i} y_{l}^{i} }}{{\mathop \sum \nolimits_{i = 1}^{M} f_{l}^{i} }} \) and \( y_{r} = \frac{{\mathop \sum \nolimits_{i = 1}^{M} f_{r}^{i} y_{r}^{i} }}{{\mathop \sum \nolimits_{i = 1}^{M} f_{r}^{i} }} \)

The values of \( {\text{y}}_{\text{l}} \) and \( {\text{y}}_{\text{r}} \) define the output interval of the type-2 fuzzy system, which can be used to verify if training or testing data are contained in the output of the fuzzy system. This measure of covering the data is considered as one of the design criteria in finding an optimal interval type-2 fuzzy system. The other optimization criteria, is that the length of this output interval should be as small as possible.

From the type-reducer, we obtain an interval set \( {\text{y}}\left( {\text{X}} \right) \), to defuzzify it we use the average of \( {\text{y}}_{\text{l}} \) and \( {\text{y}}_{\text{r}} \), so the defuzzified output of an interval singleton type-2 FLS is [10]:

$$ y(X) = \left( {\frac{1}{2}} \right)\left( {y_{l} + y_{r} } \right) $$
(15)

where \( y_{l} \) and \( y_{r} \) are the left most and right most points of the Interval type-1 set: \( y_{l} = \sum\limits_{i = 1}^{M} {y_{l}^{i} \xi_{l}^{i} } = \underline{{\xi_{l}^{T} }} \underline{{\theta_{l} }} \) and \( y_{r} = \mathop \sum \limits_{i = 1}^{M} y_{r}^{i} \xi_{r}^{i} = \underline{{\xi_{r}^{T} }} \underline{{\theta_{r} }} \)

$$ y\left( X \right) = (y_{l} + y_{r} )/\,2 = \underline{{\xi^{T} }} \underline{\theta } $$
(16)

where \( \underline{{\xi^{T} }} = \left( {1/2} \right)[\underline{{\xi_{r}^{T} }} \underline{{\xi_{l}^{T} }} ] \) and \( \underline{\theta } = [\underline{{\theta_{r} }} \quad \underline{{\theta_{l} }} ] \)

5 \( H^{\infty } \) Adaptive Interval Type-2 Fuzzy Control Scheme

Consider an incommensurate fractional order SISO nonlinear dynamic system of the form [22, 37, 40]

$$ \left\{ {\begin{array}{*{20}l} {x_{1}^{{\left( {q_{1} } \right)}} = x_{2} } \hfill \\ \vdots \hfill \\ { x _{n - 1}^{{(q_{n - 1} )}} = x_{n} } \hfill \\ { x_{n}^{{\left( {q_{n} } \right)}} = f\left( {X,t} \right) + g\left( {X,t} \right)u + d\left( t \right) } \hfill \\ {y = x_{1 } } \hfill \\ \end{array} } \right. $$

if \( q_{1} = q_{2} = \ldots = q_{n} = q \) the above system is called a commensurate order system, then equivalent form of the above system is described as:

$$ \left\{ {\begin{array}{*{20}l} { x^{{\left( {nq} \right)}} = f\left( {X,t} \right) + g\left( {X,t} \right)u + d\left( t \right)} \hfill \\ {y = x_{1} } \hfill \\ \end{array} } \right. $$
(17)

where \( X = \left[ {x_{1} ,x_{2} , \ldots ,x_{n} } \right]^{T} = \left[ {x,x^{(q)} ,x^{(2q)} , \ldots ,x^{{(\left( {n - 1} \right)q)}} } \right]^{T} \) is the state vector, \( f\left( {X,t} \right) and g\left( {X,t} \right) \) are unknown but bounded nonlinear functions which express system dynamics, \( d(t) \) is the external bounded disturbance and \( u(t) \) is the control input. The control objective is to force the system output y to follow a given bounded reference signal \( y_{d} \), under the constraint that all signals involved must be bounded. For simplicity, in this paper adaptive IT2FLC for a commensurate order system is proposed only, since the stability condition for the incommensurate order system can be converted to that for the commensurate order system [21, 24, 40].

To begin with, the reference signal vector y d and the tracking error vector e will be defined as

$$ \begin{aligned} & \underline{y}_{d} = \left[ {y_{d} , y_{d}^{(q)} , \ldots ,y_{d}^{((n - 1)q)} } \right]^{T} \in R^{n} \\ & \underline{e} = \underline{y}_{d} - \underline{y} = \left[ {e,e^{(q)} , \ldots ,e^{{(\left( {n - 1} \right)q)}} } \right]^{T} \in R^{n} , \\ & e^{(iq)} = y_{d}^{(iq)} - y^{(iq)} . \\ \end{aligned} $$

Let \( \underline{k} = \left[ {k_{1} ,k_{2} , \ldots ,k_{n} } \right]^{T} \in R^{n} \) to be chosen such that the stable condition\( | arg(eig(A))| > q\pi /2 \) is met, where \( 0 < q < 1 \) and \( eig(A) \) represents the eigenvalues of the matrix A given in (23).

If the functions \( f\left( {X,t} \right) and g\left( {X,t} \right) \) are known and the system is free of external disturbance d, then the control law of the certainty equivalent controller is obtained as [38, 61].

$$ u_{eq} = \frac{1}{g(X,t)}\left[ { - f\left( {X,t} \right) + y_{d}^{{\left( {nq} \right)}} + \underline{k}^{T} \underline{e} } \right]. $$
(18)

Substituting (19) into (18), we have:

$$ e^{(nq)} + k_{n} e^{{\left( {n - 1} \right)q}} + \ldots + k_{1} e = 0 $$

which is the main objective of control, \( \mathop {\lim }\limits_{t \to \infty } e\left( t \right) = 0. \)

However, \( f\left( {X,t} \right)\,and\,g\left( {X,t} \right) \) are unknown and external disturbance \( d\left( t \right) \ne 0 \), the ideal control effort (18) cannot implemented. We replace \( f\left( {X,t} \right)\,and\,g\left( {X,t} \right) \) by the interval type-2 fuzzy logic system \( f\left( {\left. X \right|\underline{\theta }_{f} } \right)\,and\,g\left( {\left. X \right|\underline{\theta }_{g} } \right) \) in a specified form as (16, 17), i.e.,

$$ \begin{aligned} f\left( {\left. X \right|\underline{\theta }_{f} } \right) & = \frac{{f_{l} + f_{r} }}{2} = \frac{1}{2}\left( {\xi_{fl}^{T} \underline{\theta }_{fl} + \xi_{fr}^{T} \underline{\theta }_{fr} } \right) = \xi_{f}^{T} \underline{\theta }_{f} \\ g\left( {\left. X \right|\underline{\theta }_{g} } \right) & = \frac{{g_{l} + g_{r} }}{2} = \frac{1}{2}\left( {\xi_{gl}^{T} \underline{\theta }_{gl} + \xi_{gr}^{T} \underline{\theta }_{gr} } \right) = \xi_{g}^{T} \underline{\theta }_{g} \\ \end{aligned} $$
(19)

where \( \underline{\theta }_{f} = \left[ {\begin{array}{*{20}c} {\underline{\theta }_{fr} } & {\underline{\theta }_{fl} } \\ \end{array} } \right] \) and \( \underline{\theta }_{g} = [\begin{array}{*{20}c} {\underline{\theta }_{gr} } & {\underline{\theta }_{gl} } \\ \end{array} ] \).

Here the fuzzy basis function \( \xi \left( X \right) = \left( {\frac{1}{2}} \right)\left[ {\underline{\xi }_{r} \quad \underline{\xi }_{l} } \right] = \xi_{f} \left( X \right) = \xi_{g} \left( X \right) \) depends on the type-2 fuzzy membership functions and is supposed to be fixed, while \( \underline{\theta }_{f} \,and\,\underline{\theta }_{g} \) are adjusted by adaptive laws based on a Lyapunov stability criterion.

Therefore, the resulting control effort can be obtained as [24, 39],

$$ u = \frac{1}{{g\left( {\left. X \right|\underline{\theta }_{g} } \right)}}\left[ { - f\left( {\left. X \right|\underline{\theta }_{f} } \right) + y_{d}^{{\left( {nq} \right)}} + \underline{k}^{T} \underline{e} - u_{a} } \right] $$

so

$$ u = \frac{1}{{\frac{1}{2}\left( {\xi_{gl}^{T} \underline{\theta }_{gl} + \xi_{gr}^{T} \underline{\theta }_{gr} } \right)}}\left[ { - \frac{1}{2}\left( {\xi_{fl}^{T} \underline{\theta }_{fl} + \xi_{fr}^{T} \underline{\theta }_{fr} } \right) + y_{d}^{{\left( {nq} \right)}} + \underline{k}^{T} \underline{e} - u_{a} } \right] $$
(20)

where the robust compensator \( u_{a} \) is employed to attenuate the external disturbance and the fuzzy approximation errors.

By substituting (20) into (17), we have

$$ \begin{aligned} x^{{\left( {nq} \right)}} & = f\left( {X,t} \right) + g\left( {X,t} \right)u + d\left( t \right) + g\left( {\left. X \right|\underline{\theta }_{g} } \right)u - g\left( {\left. X \right|\underline{\theta }_{g} } \right)u \\ & = \left[ {f\left( {X,t} \right) - \frac{1}{2}\left( {\xi_{fl}^{T} \underline{\theta }_{fl} + \xi_{fr}^{T} \underline{\theta }_{fr} } \right)} \right] + y_{d}^{{\left( {nq} \right)}} + \underline{k}^{T} \underline{e} - u_{a} \\ & \quad + \left[ {g\left( {X,t} \right) - \frac{1}{2}\left( {\xi_{gl}^{T} \underline{\theta }_{gl} + \xi_{gr}^{T} \underline{\theta }_{gr} } \right)} \right]u + d(t) \\ \end{aligned} $$
(21)

then

$$ \begin{aligned} e^{{\left( {nq} \right)}} & = \left[ {f\left( {X,t} \right) - \frac{1}{2}\left( {\xi_{fl}^{T} \underline{\theta }_{fl} + \xi_{fr}^{T} \underline{\theta }_{fr} } \right)} \right] + \underline{k}^{T} \underline{e} - u_{a} + d\left( t \right) \\ & \quad + \left[ {g\left( {X,t} \right) - \frac{1}{2}\left( {\xi_{gl}^{T} \underline{\theta }_{gl} + \xi_{gr}^{T} \underline{\theta }_{gr} } \right)} \right]u = 0 \\ \end{aligned} $$
(22)

Equation (22) can be rewritten in state space representation as:

$$ \begin{aligned} \underline{e}^{(q)} & = A\underline{e} + B\left[ {\frac{1}{2}\left( {\xi_{fl}^{T} \underline{\theta }_{fl} + \xi_{fr}^{T} \underline{\theta }_{fr} } \right) - f\left( {X,t} \right) + u_{a} + \left( {\frac{1}{2}\left( {\xi_{gl}^{T} \underline{\theta }_{gl} + \xi_{gr}^{T} \underline{\theta }_{gr} } \right)} \right.} \right. \\ & \quad - \left. {\left. {g\left( {X,t} \right)u - d(t)} \right)} \right] \\ \end{aligned} $$
(23)
$$ {\text{where}}\,\,A = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & 1 & 0 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \vdots & 1 \\ { - k_{1} } & { - k_{2} } & { - k_{3} } & { - k_{4} } & \cdots & { - k_{(n - 1)} } & { - k_{n} } \\ \end{array} } \right],\quad B = \left[ \begin{aligned} 0 \hfill \\ 0 \hfill \\ \vdots \hfill \\ 0 \hfill \\ 1 \hfill \\ \end{aligned} \right] $$

The optimal parameter estimations \( \underline{\theta }_{f}^{*} \,{\text{and}}\,\underline{\theta }_{g}^{*} \) are defined:

$$ {\underline{\theta }}_{f}^{ *} = \arg \mathop {\hbox{min} }\limits_{{{\underline{\theta }}_{f} \varepsilon \varOmega_{f} }} [\mathop {\sup }\limits_{{x\epsilon \varOmega_{x} }} \left| {f\left( {\left. X \right|{\underline{\theta }}_{f} } \right) - f\left( {X,t} \right)} \right|] $$
(24)
$$ {\underline{\theta }}_{g}^{ *} = \arg \mathop {\hbox{min} }\limits_{{{\underline{\theta }}_{g} \varepsilon {\Omega }_{g} }} [\mathop {\sup }\limits_{{x\epsilon {\Omega }_{x} }} \left| {g\left( {\left. X \right|{\underline{\theta }}_{g} } \right) - g\left( {X,t} \right)} \right|] $$
(25)

where \( \Omega _{f},\,\Omega _{g} \,and\,\Omega _{{\underline{x} }} \) are constraint sets of suitable bounds on \( \underline{\theta }_{f} ,\underline{\theta }_{g} \,{\text{and}}\,x \) respectively and they are defined as \( \Omega _{f} = \left\{ {\left. {\underline{\theta }_{f} } \right|\left| {\underline{\theta }_{f} } \right| \le M_{f} } \right\} \), \( \Omega _{g} = \left\{ {\left. {\underline{\theta }_{g} } \right|\left| {\underline{\theta }_{g} } \right| \le M_{g} } \right\} \) et \( \Omega _{x} = \left\{ {\left. x \right|\left| x \right| \le M_{x} } \right\} \) where \( M_{f} \), \( M_{g} \) et \( M_{x} \) are positive constants.

By using (24)–(25), an error dynamic Eq. (23) can be expressed as:

$$ \underline{e}^{(q)} = A\underline{e} + B\left[ {f\left( {\left. X \right|\underline{\theta }_{f} } \right) - f\left( {\left. X \right|\underline{\theta }_{f}^{ *} } \right) + u_{a} + \left( {g\left( {\left. {\underline{x} } \right|\underline{\theta }_{g} } \right) - g\left( {\left. X \right|\underline{\theta }_{g}^{ *} } \right)} \right)u - d\left( t \right)} \right] $$
(26)

Also, the minimum approximation error is defined as:

$$ \omega_{1} = g\left( {\left. X \right|\underline{\theta }_{g}^{ *} } \right) - g\left( {X,t} \right) + f\left( {\left. X \right|\underline{\theta }_{f}^{ *} } \right) - f\left( {X,t} \right) - d\left( t \right) $$
(27)

If \( \underline{{\tilde{\theta }}}_{f} = \underline{\theta }_{f} - \underline{\theta }_{f}^{*} \) and \( \underline{{\tilde{\theta }}}_{g} = \underline{\theta }_{g} - \underline{\theta }_{g}^{*} \), (27) can be rewritten as:

$$ \underline{e}^{(q)} = A\underline{e} + B\left[ {\xi (X)^{T} \underline{{\tilde{\theta }}}_{f} + \xi (X)^{T} \underline{{\tilde{\theta }}}_{g} u + u_{a} + \omega_{1} } \right] $$
(28)

Following the preceding consideration, the following theorem can be obtained [35].

6 Stability Analysis

Theorem 1

Consider the commensurate fractional order SISO nonlinear dynamic system (17) with control input (20), if the robust compensator \( u_{a} \) and the type-2 fuzzy-based adaptive laws are chosen as

$$ u_{a} = - \frac{1}{r}B^{T} P\underline{e} $$
(29)
$$ \underline{\theta }_{fr}^{(q)} = - r_{1} \xi_{fr} B^{T} P\underline{e} $$
(30)
$$ \underline{\theta }_{fl}^{(q)} = - r_{2} \xi_{fl} B^{T} P\underline{e} $$
(31)
$$ \underline{\theta }_{gr}^{(q)} = - r_{3} \xi_{gr} B^{T} P\underline{e} u $$
(32)
$$ \underline{\theta }_{gl}^{(q)} = - r_{4} \xi_{gl} B^{T} P\underline{e} u $$
(33)

where \( \underline{\theta }_{f}^{(q)} = \left[ {\begin{array}{*{20}c} {\underline{\theta }_{fr}^{(q)} } & {\underline{\theta }_{fl}^{(q)} } \\ \end{array} } \right] \), \( \underline{\theta }_{g}^{(q)} = \left[ {\begin{array}{*{20}c} {\underline{\theta }_{gr}^{(q)} } & {\underline{\theta }_{gl}^{(q)} } \\ \end{array} } \right] \), \( \underline{\xi }_{f}^{T} = \left( {\frac{1}{2}} \right)\left[ {\begin{array}{*{20}c} {\underline{\xi }_{fr}^{T} } & {\underline{\xi }_{fl}^{T} } \\ \end{array} } \right] \) and \( \underline{\xi }_{g}^{T} = \left( {\frac{1}{2}} \right)\left[ {\begin{array}{*{20}c} {\underline{\xi }_{gr}^{T} } & {\underline{\xi }_{gl}^{T} } \\ \end{array} } \right] \)

where \( r > 0, r_{i} > 0, i = 1\sim 4 \) , and \( P = P^{T} > 0 \) is the solution of the following Riccati-like equation :

$$ {\text{PA}} + {\text{A}}^{\text{T}} {\text{P}} + {\text{Q}} - {\text{PB}}\left( {\frac{2}{\text{r}} - \frac{1}{{\uprho^{2} }}} \right){\text{B}}^{\text{T}} {\text{P}} = 0 $$
(34)

where \( Q = Q^{T} > 0 \) is a prescribed weighting matrix. Therefore, the \( H^{\infty } \) tracking performance can be achieved for a prescribed attenuation level ρ which satisfies \( 2\rho^{2} \ge r \) and all the variables of the closed-loop system are bounded.

In order to analyze the closed-loop stability, the Lyapunov function candidate is chosen as

$$ \begin{aligned} V(t) & = \frac{1}{2}\underline{e}^{T} \left( t \right)P\underline{e} \left( t \right) + \frac{1}{{2r_{1} }}\left( {{\tilde{\underline{\theta } }}_{fr}^{T} } \right)\left( {\tilde{\underline{\theta } }_{fr} } \right) + \frac{1}{{2r_{2} }}\left( {\tilde{\underline{\theta } }_{fl}^{T} } \right)\left( {\tilde{\underline{\theta } }_{fl} } \right) \\ & \quad + \frac{1}{{2r_{3} }}\left( {\tilde{\underline{\theta } }_{gr}^{T} } \right)\left( {\tilde{\underline{\theta } }_{gr} } \right) + \frac{1}{{2r_{4} }}\left( {\tilde{\underline{\theta } }_{gl}^{T} } \right)\left( {\tilde{\underline{\theta } }_{gl} } \right) \\ \end{aligned} $$
(35)

Taking the derivative of (36) with respect to time, we get

$$ \begin{aligned} V^{\left( q \right)} \left( t \right) & = \frac{1}{2}\left( {\underline{e}^{\left( q \right)} \left( t \right)} \right)^{T} P\underline{e} \left( t \right) + \frac{1}{2}\underline{e}^{T} \left( t \right)P\underline{e} \left( t \right) \\ & \quad + \frac{1}{{r_{1} }}\left( {\tilde{\underline{\theta} }_{fr}^{T} } \right)\left( {\tilde{\underline{\theta} }_{fr}^{(q)} } \right) + \frac{1}{{r_{3} }}\left( {\tilde{\underline{\theta} }_{gr}^{T} } \right)\left( {\tilde{\underline{\theta} }_{gr}^{(q)} } \right) + \frac{1}{{r_{2} }}\left( {\tilde{\underline{\theta} }_{fl}^{T} } \right)\left( {\tilde{\underline{\theta} }_{fl}^{(q)} } \right) + \frac{1}{{r_{4} }}\left( {\tilde{\underline{\theta} }_{gl}^{T} } \right)\left( {\tilde{\underline{\theta} }_{gl}^{(q)} } \right) \\ & = \frac{1}{2}\left\{ {A\underline{e} + B\left[ {\xi^{T} \tilde{\underline{\theta} }_{f} + \xi^{T} \tilde{\underline{\theta} }_{g} u + u_{a} + \omega_{1} } \right]} \right\}^{T} P\underline{e} + \frac{1}{2}\underline{e}^{T} \left( t \right)P\left\{ {A\underline{e} + B\left[ {\xi^{T} \tilde{\underline{\theta} }_{f} } \right.} \right. \\ & \quad \left. {\left. { + \xi^{T} \tilde{\underline{\theta} }_{g} u + u_{a} + \omega_{1} } \right]} \right\} + \frac{1}{{r_{1} }}\left( {\tilde{\underline{\theta} }_{fr}^{T} } \right)\left( {\tilde{\underline{\theta} }_{fr}^{\left( q \right)} } \right) + \frac{1}{{r_{3} }}\left( {\tilde{\underline{\theta} }_{gr}^{T} } \right)\left( {\tilde{\underline{\theta} }_{gr}^{\left( q \right)} } \right) + \frac{1}{{r_{2} }}\left( {\tilde{\underline{\theta} }_{fl}^{T} } \right)\left( {\tilde{\underline{\theta} }_{fl}^{\left( q \right)} } \right) \\ & \quad + \frac{1}{{r_{4} }}\left( {\tilde{\underline{\theta} }_{gl}^{T} } \right)\left( {\tilde{\underline{\theta} }_{gl}^{\left( q \right)} } \right) \\ \end{aligned} $$
(36)

obtained after a simple manipulation

$$ \begin{aligned} {\text{V}}^{{({\text{q}})}} ({\text{t}}) & = \frac{1}{2}\underline{\text{e}}^{\text{T}} ({\text{A}}^{\text{T}} + {\text{PA}})\underline{\text{e}} + \underline{\text{e}}^{\text{T}} {\text{PBu}}_{\text{a}} + \underline{\text{e}}^{\text{T}} {\text{PB}}\upomega_{1} + \{ \underline{{{\tilde{\uptheta }}}}_{\text{fr}}^{\text{T}} [\upxi_{\text{fr}} {\text{B}}^{\text{T}} {\text{P}}\underline{\text{e}} \\ & \quad + \frac{1}{{{\text{r}}_{1} }}(\underline{{{\tilde{\uptheta }}}}_{\text{fr}}^{{({\text{q}})}} )]\} + \left\{ {\underline{{{\tilde{\uptheta }}}}_{\text{fl}}^{\text{T}} \left[ {\upxi_{\text{fl}} {\text{B}}^{\text{T}} {\text{P}}\underline{\text{e}} + \frac{1}{{{\text{r}}_{2} }}(\underline{{{\tilde{\uptheta }}}}_{\text{fl}}^{{({\text{q}})}} )} \right]} \right\} + \{ \underline{{{\tilde{\uptheta }}}}_{\text{gr}}^{\text{T}} [\upxi_{\text{gr}} {\text{B}}^{\text{T}} {\text{P}}\underline{\text{e}} {\text{u}} \\ & \quad { + }\frac{1}{{{\text{r}}_{3} }}(\underline{{{\tilde{\uptheta }}}}_{\text{gr}}^{{({\text{q}})}} )]\} + \left\{ {\underline{{{\tilde{\uptheta }}}}_{\text{gl}}^{\text{T}} \left[ {\upxi_{\text{gl}} {\text{B}}^{\text{T}} {\text{P}}\underline{\text{e}} {\text{u}} + \frac{1}{{{\text{r}}_{4} }}(\underline{{{\tilde{\uptheta }}}}_{\text{gl}}^{{({\text{q}})}} )} \right]} \right\} \\ \end{aligned} $$
(37)

From (29) the robust compensator \( u_{a} \), and the fuzzy-based adaptive laws are given (30)–(33), \( V^{\left( q \right)} \left( t \right) \) in (37) can be rewritten as:

$$ \begin{aligned} {\text{V}}^{{\left( {\text{q}} \right)}} \left( {\text{t}} \right) & = - \frac{1}{2}\underline{\text{e}}^{\text{T}} {\text{Q}}\underline{\text{e}} - \frac{1}{{2\uprho^{2} }}\underline{\text{e}}^{\text{T}} {\text{PBB}}^{\text{T}} \underline{\text{e}} + \underline{\text{e}}^{\text{T}} {\text{PB}}\upomega_{1} \\ & = - \frac{1}{2}\underline{\text{e}}^{\text{T}} {\text{Q}}\underline{\text{e}} - \frac{1}{2}\left( {\frac{1}{\uprho}{\text{B}}^{\text{T}} {\text{P}}\underline{\text{e}} -\uprho \upomega _{1} } \right)^{\text{T}} \left( {\frac{1}{\uprho}{\text{B}}^{\text{T}} {\text{P}}\underline{\text{e}} -\uprho \upomega _{1} } \right) + \frac{1}{2}\uprho^{2}\upomega_{1}^{\text{T}}\upomega_{1} \\ & \le - \frac{1}{2}\underline{\text{e}}^{\text{T}} {\text{Q}}\underline{\text{e}} + \frac{1}{2}\uprho^{2}\upomega_{1}^{\text{T}}\upomega_{1} \\ \end{aligned} $$
(38)

Integrating (38) from t = 0 to t = T, we have

$$ V\left( T \right) - V\left( 0 \right) \le - \frac{1}{2}\mathop \smallint \limits_{0}^{T} \left( {\underline{e}^{T} Q\underline{e} dt + \frac{1}{2}\rho^{2} \omega_{1}^{T} \omega_{1} } \right)dt $$
(39)

Since \( V\left( T \right) \ge 0 \), (39) can be rewritten as follows:

$$ \begin{aligned} \mathop \smallint \limits_{0}^{T} \underline{e}^{T} Q\underline{e} dt & \le e^{T} \left( 0 \right)Pe\left( 0 \right) + \theta^{T} \left( 0 \right)\theta \left( 0 \right) \\ & \quad +\uprho^{2} \mathop \smallint \limits_{0}^{\text{T}}\upomega_{1}^{\text{T}}\upomega_{1} {\text{dt}} \\ \end{aligned} $$
(40)

Therefore, the \( H^{\infty } \) tracking performance can be achieved. The proof is completed.

7 Simulation Results

The chaotic behaviors in a fractional order modified Duffing system studied numerically by phase portraits are given by [16, 22]. In this section, we will apply our adaptive fuzzy \( H^{\infty } \) controller to synchronize two different fractional order chaotic Duffing systems.

Consider the following two fractional order chaotic Duffing systems [23]:

  • Drive system:

    $$ \left\{ {\begin{array}{*{20}l} {D^{q} y_{1} = y_{2} } \hfill \\ {D^{q} y_{2} = y_{1} - 0.25y_{2} - y_{1}^{3} + 0.3{ \cos }(t)} \hfill \\ \end{array} } \right. $$
    (41)

  • Response system:

    $$ \left\{ {\begin{array}{*{20}l} {D^{q} x_{1} = x_{2} } \hfill \\ {D^{q} x_{2} = x_{1} - 0.3x_{2} - x_{1}^{3} + 0.35\cos \left( t \right) + u\left( t \right) + d(t)} \hfill \\ \end{array} } \right. $$
    (42)

    where the external disturbance \( d(t) = 0.1sin(t). \) The main objective is to control the trajectories of the response system to track the reference trajectories obtained from the drive system. The initial conditions of the drive and response systems are chosen as:

    $$ \left[ {\begin{array}{*{20}c} {x_{1} (0)} \\ {x_{2} (0)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right]\,and\,\left[ {\begin{array}{*{20}c} {y_{1} (0)} \\ {y_{2} (0)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {0.2} \\ { - 0.2} \\ \end{array} } \right] , (\text{respectively}). $$

The simulations results for fractional order \( q = 0.98 \) are illustrated as follows:

The Fig. 4 represents the 3D phase portrait of the drive and response systems without control input. It is obvious that the synchronization performance is bad without a control effort supplied to the response system.

Fig. 4
figure 4

3D phase portrait of the drive and response systems without control input (Before the control input)

Full size image

The different values of \( 0 < q < 1 \) are considered in order to show the robustness of the proposed adaptive fuzzy \( H^{\infty } \) control with our law.

According to the two state output ranges, the membership functions of x i , for \( f\left( {\left. X \right|\underline{\theta }_{f} } \right) \) and \( g\left( {\left. X \right|\underline{\theta }_{g} } \right) \) are selected as follows:

\( \upmu_{{{\text{F}}_{\text{i}}^{\text{l}} }} ({\text{x}}_{\text{i}} ) = \exp \left[ { - 0.5\left( {\frac{{{\text{x}}_{\text{i}} - \overline{\text{x}} }}{0.8}} \right)^{2} } \right] \) \( i = 1, 2 \) and \( l = 1, \ldots ,7 \) where \( \bar{x} \) is selected from the interval \( \left[ { - 1, 2} \right]. \) (Figure 5)

Fig. 5
figure 5

Interval Type-2 Fuzzy sets Gaussian with uncertain standard deviation \( \sigma \)

Full size image

From the adaptive laws (30)–(33) and the robust compensator (29), the control law of the response system can be obtained as:

$$ u = \frac{1}{{\xi^{T} (X)\underline{\theta }_{g} }}\left[ { - \xi^{T} (X)\underline{\theta }_{f} + y_{d}^{{\left( {nq} \right)}} + \underline{k}^{T} \underline{e} - u_{a} } \right] $$
(43)

According to theorem 1, the controlled error system can be stabilized, i.e., the master system (41) can synchronize the slave system (42) with the control law (20).

The Figs. 6, 7, 8, 9, 10 represent the different simulation results of the drive and response systems with control input (43) for the fractional order q = 0.98.

Fig. 6
figure 6

3D phase portrait, synchronization performance, of the drive and response systems

Full size image
Fig. 7
figure 7

State trajectories: \( x_{1} y_{1} \)

Full size image
Fig. 8
figure 8

State trajectories: \( x_{2} y_{2} \)

Full size image
Fig. 9
figure 9

Control effort: \( u(t) \)

Full size image
Fig. 10
figure 10

Errors signals: \( e_{1} \& e_{2} \)

Full size image

It is clearly seen from Fig. 10 that the tracking errors e 1 (t) and e 2 (t) converge both to zero in less than 5 s. Synchronization is perfectly achieved as shown by the state trajectories in Figs. 7 and 8.

The control signal can be observed in the Fig. 9. It indicates that the obtained results are comparable with the solution presented in [23], but fluctuations of the control function are much smaller.

In order to have a quantitative comparison between both methods, a white Gaussian noise is applied to the measured signal with various signals to Noise and Integral of Absolute Error (IAE) is selected as the criterion.

The results in Table 1 clearly indicate that the performance of our proposed type-2 fuzzy controller surpasses the type-1fuzzy method [22]. As can be seen in high SNRs both of the methods have similar performance, however in low SNRs type-1 controller [22] has large IAEs while our proposed controller has still low IAEs. Despite the presence of additive noises in measured signals, the obtained simulation results illustrate the robustness of the proposed control strategy and the utility of introducing type-2 fuzzy modelization approach.

Table 1 IAE comparison between AT2FC and AT1FC
Full size table

8 Conclusion

In this paper a novel adaptive interval type-2 fuzzy using \( H^{\infty } \) control is proposed to deal with chaos synchronization between two different uncertain fractional order chaotic systems. The use of interval type-2 helps to minimize the added computational burden and hence renders the overall system to be more practically applicable.

Based on the Lyapunov synthesis approach, free parameters of the adaptive fuzzy controller can be tuned on line by the output feedback control law and adaptive laws. The simulation example, chaos synchronization of two fractional order Duffing systems, is given to demonstrate the effectiveness of the proposed methodology. The significance of the proposed control scheme in the simulation for different values of q is manifest. Simulation results show that a fast synchronization of drive and response can be achieved and as q is reduced the chaos is seen reduced, i.e., the synchronization error is reduced, accordingly.

Future research efforts will concern observer-based nonlinear adaptive control of uncertain or unknown fractional order systems. The problem of online identification and parameters estimation for such systems is also a good challenge. Another topic of interest is the design of new robust adaptive control laws for the class of fractional nonlinear systems based on various control configurations such as: (Internal model control) IMC, (Model reference Adaptive Systems) MRAS and the Strictly Positive realness property.