Recent Advances in Graph Partitioning

Abstract

We survey recent trends in practical algorithms for balanced graph partitioning, point to applications and discuss future research directions.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Graphs are frequently used by computer scientists as abstractions when modeling an application problem. Cutting a graph into smaller pieces is one of the fundamental algorithmic operations. Even if the final application concerns a different problem (such as traversal, finding paths, trees, and flows), partitioning large graphs is often an important subproblem for complexity reduction or parallelization. With the advent of ever larger instances in applications such as scientific simulation, social networks, or road networks, graph partitioning (GP) therefore becomes more and more important, multifaceted, and challenging. The purpose of this paper is to give a structured overview of the rich literature, with a clear emphasis on explaining key ideas and discussing recent work that is missing in other overviews. For a more detailed picture on how the field has evolved previously, we refer the interested reader to a number of surveys. Bichot and Siarry [22] cover studies on GP within the area of numerical analysis. This includes techniques for GP, hypergraph partitioning and parallel methods. The book discusses studies from a combinatorial viewpoint as well as several applications of GP such as the air traffic control problem. Schloegel et al. [191] focus on fast graph partitioning techniques for scientific simulations. In their account of the state of the art in this area around the turn of the millennium, they describe geometric, combinatorial, spectral, and multilevel methods and how to combine them for static partitioning. Load balancing of dynamic simulations, parallel aspects, and problem formulations with multiple objectives or constraints are also considered. Monien et al. [156] discuss heuristics and approximation algorithms used in the multilevel GP framework. In their description they focus mostly on coarsening by matching and local search by node-swapping heuristics. Kim et al. [119] cover genetic algorithms.

Our survey is structured as follows. First, Sect. 2 introduces the most important variants of the problem and their basic properties such as NP-hardness. Then Sect. 3 discusses exemplary applications including parallel processing, road networks, image processing, VLSI design, social networks, and bioinformatics. The core of this overview concerns the solution methods explained in Sects. 4, 5, 6 and 7. They involve a surprising variety of techniques. We begin in Sect. 4 with basic, global methods that “directly” partition the graph. This ranges from very simple algorithms based on breadth first search to sophisticated combinatorial optimization methods that find exact solutions for small instances. Also methods from computational geometry and linear algebra are being used. Solutions obtained in this or another way can be improved using a number of heuristics described in Sect. 5. Again, this ranges from simple-minded but fast heuristics for moving individual nodes to global methods, e.g., using flow or shortest path computations. The most successful approach to partitioning large graphs – the multilevel method – is presented in Sect. 6. It successively contracts the graph to a more manageable size, solves the base instance using one of the techniques from Sect. 4, and – using techniques from Sect. 5 – improves the obtained partition when uncontracting to the original input. Metaheuristics are also important. In Sect. 7 we describe evolutionary methods that can use multiple runs of other algorithms (e.g., multilevel) to obtain high quality solutions. Thus, the best GP solvers orchestrate multiple approaches into an overall system. Since all of this is very time consuming and since the partitions are often used for parallel computing, parallel aspects of GP are very important. Their discussion in Sect. 8 includes parallel solvers, mapping onto a set of parallel processors, and migration minimization when repartitioning a dynamic graph. Section 9 describes issues of implementation, benchmarking, and experimentation. Finally, Sect. 10 points to future challenges.

2 Preliminaries

Given a number $k \in \mathbb {N}_{>1}$ and an undirected graph $G=(V,E)$ with non-negative edge weights, $\omega : E \rightarrow \mathbb {R}_{>0}$, the graph partitioning problem (GPP) asks for a partition $\varPi$ of V with blocks of nodes $\varPi = (V_1,\ldots ,V_k)$:

$$\begin{aligned} 1.\,\,\,\,&V_1\cup \cdots \cup V_k = V \\ 2.\,\,\,\,&V_i\cap V_j =\emptyset \, \, \, \forall i \ne j. \end{aligned}$$

A balance constraint demands that all blocks have about equal weights. More precisely, it requires that, $\forall i\in \{1, \dots , k\}:|V_i|\le L_{\max }\text{:= } (1+\epsilon )\lceil |V|/k \rceil$ for some imbalance parameter $\epsilon \in \mathbb {R}_{\ge 0}$. In the case of $\epsilon =0$, one also uses the term perfectly balanced. Sometimes we also use weighted nodes with node weights $c:V\rightarrow \mathbb {R}_{>0}$. Weight functions on nodes and edges are extended to sets of such objects by summing their weights. A block $V_i$ is overloaded if $|V_i| > L_{\max }$. A clustering is also a partition of the nodes. However, k is usually not given in advance, and the balance constraint is removed. Note that a partition is also a clustering of a graph. In both cases, the goal is to minimize or maximize a particular objective function. We recall well-known objective functions for GPP in Sect. 2.1. A node v is a neighbor of node u if there is an edge $\{u,v\}\in E$. If a node $v \in V_i$ has a neighbor $w \in V_j$, $i\ne j$, then it is called boundary node. An edge that runs between blocks is also called cut edge. The set $E_{ij}\text{:= } \left\{ \left\{ u,v\right\} \in E:u\in V_i,v\in V_j\right\}$ is the set of cut edges between two blocks $V_i$ and $V_j$. An abstract view of the partitioned graph is the so called quotient graph or communication graph, where nodes represent blocks, and edges are induced by connectivity between blocks. There is an edge in the quotient graph between blocks $V_i$ and $V_j$ if and only if there is an edge between a node in $V_i$ and a node in $V_j$ in the original, partitioned graph. The degree d(v) of a node v is the number of its neighbors. An adjacency matrix of a graph is a $|V|\times |V|$ matrix describing node connectivity. The element $a_{u,v}$ of the matrix specifies the weight of the edge from node u to node v. It is set to zero if there is no edge between these nodes. The Laplacian matrix of a graph G is defined as $L = D-A$, where D is the diagonal matrix expressing node degrees, and A is the adjacency matrix. A cycle in a directed graph with negative weight is also called negative cycle. A matching $M\subseteq E$ is a set of edges that do not share any common nodes, i. e., the graph (V, M) has maximum degree one.

2.1 Objective Functions

In practice, one often seeks to find a partition that minimizes (or maximizes) an objective. Probably the most prominent objective function is to minimize the total cut

$$\begin{aligned} \sum _{i<j} \omega (E_{ij}). \end{aligned}$$

(1)

Other formulations of GPP exist. For instance when GP is used in parallel computing to map the graph nodes to different processors, the communication volume is often more appropriate than the cut [100]. For a block $V_i$, the communication volume is defined as comm$(V_i)\,\text{:= } \,\sum _{v \in V_i} c(v) D(v)$, where D(v) denotes the number of different blocks in which v has a neighbor node, excluding $V_i$. The maximum communication volume is then defined as $\max _i \text { comm(}V_i$), whereas the total communication volume is defined as $\sum _i \text { comm(}V_i$). The maximum communication volume was used in one subchallenge of the 10th DIMACS Challenge on Graph Partitioning and Graph Clustering [13]. Although some applications profit from other objective functions such as the communication volume or block shape (formalized by the block’s aspect ratio [56], minimizing the cut size has been adopted as a kind of standard. One reason is that cut optimization seems to be easier in practice. Another one is that for graphs with high structural locality the cut often correlates with most other formulations but other objectives make it more difficult to use a multilevel approach.

There are also GP formulations in which balance is not directly encoded in the problem description but integrated into the objective function. For example, the expansion of a non-trivial cut $(V_1, V_2)$ is defined as $\omega (E_{12})/\min ({c(V_1), c(V_2)})$. Similarly, the conductance of such a cut is defined as $\omega (E_{12})/\min (\text {vol}(V_1), \text {vol}(V_2))$, where $\text {vol}(S):= \sum _{v \in S} d(v)$ denotes the volume of the set S.

As an extension to the problem, when the application graph changes over time, repartitioning becomes necessary. Due to changes in the underlying application, a graph partition may become gradually imbalanced due to the introduction of new nodes (and edges) and the deletion of others. Once the imbalance exceeds a certain threshold, the application should call the repartitioning routine. This routine is to compute a new partition $\varPi '$ from the old one, $\varPi$. In many applications it is favorable to keep the changes between $\varPi$ and $\varPi '$ small. Minimizing these changes simultaneously to optimizing $\varPi '$ with respect to the cut (or a similar objective) leads to multiobjective optimization. To avoid the complexity of the latter, a linear combination of both objectives seems feasible in practice [193].

2.2 Hypergraph Partitioning

A hypergraph $H=(V, E)$ is a generalization of a graph in which an edge (usually called hyperedge or net) can connect any number of nodes. As with graphs, partitioning a hypergraph also means to find an assignment of nodes to different blocks of (mostly) equal size. The objective function, however, is usually expressed differently. A straightforward generalization of the edge cut to hypergraphs is the hyperedge cut. It counts the number of hyperedges that connect different blocks. In widespread use for hypergraph partitioning, however, is the so-called $(\lambda - 1)$ metric, $CV(H, \varPi ) = \sum _{e \in E} (\lambda (e, \varPi ) - 1)$, where $\lambda (e, \varPi )$ denotes the number of distinct blocks connected by the hyperedge e and $\varPi$ the partition of H’s vertex set.

One drawback of hypergraph partitioning compared to GP is the necessity of more complex algorithms—in terms of implementation and running time, not necessarily in terms of worst-case complexity. Paying this price seems only worthwhile if the underlying application profits significantly from the difference between the graph and the hypergraph model.

To limit the scope, we focus in this paper on GP and forgo a more detailed treatment of hypergraph partitioning. Many of the techniques we describe, however, can be or have been transferred to hypergraph partitioning as well [33, 34, 66, 162, 208]. One important application area of hypergraph partitioning is VLSI design (see Sect. 3.5).

2.3 Hardness Results and Approximation

Partitioning a graph into k blocks of roughly equal size such that the cut metric is minimized is NP-complete (as decision problem) [79, 106]. Andreev and Räcke [4] have shown that there is no constant-factor approximation for the perfectly balanced version ($\epsilon =0$) of this problem on general graphs. If $\epsilon \in (0, 1]$, then an $\mathrm {O}\!\left( \log ^2 n\right)$ factor approximation can be achieved. In case an even larger imbalance $\epsilon > 1$ is allowed, an approximation ratio of $\mathrm {O}\!\left( \log n\right)$ is possible [65]. The minimum weight k-cut problem asks for a partition of the nodes into k non-empty blocks without enforcing a balance constraint. Goldschmidt et al. [88] proved that, for a fixed k, this problem can be solved optimally in $\mathrm {O}(n^{k^2})$. The problem is NP-complete [88] if k is not part of the input.

For the unweighted minimum bisection problem, Feige and Krauthgamer [68] have shown that there is an $\mathrm {O}\!\left( \log ^ {1.5} n\right)$ approximation algorithm and an $\mathrm {O}\!\left( \log n\right)$ approximation for minimum bisection on planar graphs. The bisection problem is efficiently solvable if the balance constraint is dropped – in this case it is the minimum cut problem. Wagner et al. [211] have shown that the minimum bisection problem becomes harder the more the balance constraint is tightened towards the perfectly balanced case. More precisely, if the block weights are bounded from below by a constant, i. e., $|V_i| \ge C$, then the problem is solvable in polynomial time. The problem is NP-hard if the block weights are constrained by $|V_i| \ge \alpha n^\delta$ for some $\alpha , \delta > 0$ or if $|V_i| = \frac{n}{2}$. The case $|V_i| \ge \alpha \log n$ for some $\alpha > 0$ is open. Note that the case $|V_i| \ge \alpha n^\delta$ also implies that the general GPP with similar lower bounds on the block weights is NP-hard.

If the balance constraint of the problem is dropped and one uses a different objective function such as sparsest cut, then there are better approximation algorithms. The sparsest cut objective combines cut and balance into a single objective function. For general graphs and the sparsest cut metric, Arora et al. [7, 8] achieve an approximation ratio of $\mathrm {O}\!\left( \sqrt{\log n}\right)$ in $\tilde{O}({n^2})$ time.

Being of high theoretical importance, most of the approximation algorithms are not implemented, and the approaches that implement approximation algorithms are too slow to be used for large graphs or are not able to compete with state-of-the-art GP solvers. Hence, mostly heuristics are used in practice.

3 Applications of Graph Partitioning

We now describe some of the applications of GP. For brevity this list is not exhaustive.

3.1 Parallel Processing

Perhaps the canonical application of GP is the distribution of work to processors of a parallel machine. Scientific computing applications such as sparse direct and iterative solvers extensively use GP to ensure load balance and minimize communication. When the problem domain does not change as the computation proceeds, GP can be applied once in the beginning of the computation. This is known as static partitioning.

Periodic repartitioning, explained in Sect. 2.1, proved to be useful for scientific computing applications with evolving computational domains such as Adaptive Mesh Refinement (AMR) or volume rendering [11]. The graph model can be augmented with additional edges and nodes to model the migration costs, as done for parallel direct volume rendering of unstructured grids [11], an important problem in scientific visualization.

Parallel Graph Computations. GP is also used to partition graphs for parallel processing, for problems such as graph eigenvalue computations [25], breadth-first search [31], triangle listing [43], PageRank and connected components [181]. In computationally intensive graph problems, such as finding the eigenvectors and eigenvalues of graphs, multilevel methods that are tailored to the characteristics of real graphs are suitable [1].

Mesh Partitioning. A mesh or grid approximates a geometric domain by dividing it into smaller subdomains. Hendrickson defines it as “the scaffolding upon which a function is decomposed into smaller pieces” [96]. Mesh partitioning involves mapping the subdomains of the mesh to processors for parallel processing, with the objective of minimizing communication and load imbalance. A partial differential equation (PDE) that is discretized over a certain grid can be solved by numerous methods such as the finite differences method or the finite elements method. The discretization also defines a system of linear equations that can be represented by a sparse matrix. While it is always possible to use that sparse matrix to do the actual computation over the mesh or grid, sometimes this can be wasteful when the matrix need not be formed explicitly. In the absence of an explicit sparse matrix, the GP solvers first define a graph from the mesh. The right mesh entity to use as the nodes of the graph can be ambiguous and application dependent. Common choices are mesh nodes, groups of mesh nodes that need to stay together, and the dual of mesh nodes. Choosing groups of mesh nodes (such as small regular meshes [74]) with appropriate weighting as graph nodes makes GP cost effective for large problem sizes when the overhead for per-node partitioned graphs would be too big. Recent work by Zhou et al. [222] gives a thorough treatment of extreme-scale mesh partitioning and dynamic repartitioning using graph models. A variety of solution methodologies described in Sect. 6, such as the multilevel and geometric methods, has been successfully applied to mesh partitioning.

3.2 Complex Networks

In addition to the previously mentioned task of network data distribution across a cluster of machines for fast parallel computations, complex networks introduced numerous further applications of GPP. A common task in these applications is to identify groups of similar entities whose similarity and connectivity is modeled by the respective networks. The quality of the localizations is quantified with different domain-relevant objectives. Many of them are based on the principle of finding groups of entities that are weakly connected to the rest of the network. In many cases such connectivity also represents similarity. In the context of optimization problems on graphs, by complex networks we mean weighted graphs with non-trivial structural properties that were created by real-life or modelling processes [159]. Often, models and real-life network generation processes are not well understood, so designing optimization algorithms for such graphs exhibit a major bottleneck in many applications.

Power Grids. Disturbances and cascading failures are among the central problems in power grid systems that can cause catastrophic blackouts. Splitting a power network area into self-sufficient islands is an approach to prevent the propagation of cascading failures [132]. Often the cut-based objectives of the partitioning are also combined with the load shedding schemes that enhance the robustness of the system and minimize the impact of cascading events [133]. Finding vulnerabilities of power systems by GPP has an additional difficulty. In some applications, one may want to find more than one (nearly) minimum partitioning because of the structural difference between the solutions. Spectral GP (see Sect. 4.2) is also used to detect contingencies in power grid vulnerability analysis by splitting the network into regions with excess generation and excess load [60].

Geographically Embedded Networks. Recent advances of location-aware devices (such as GPS) stimulated a rapid growth of streaming spatial network data that has to be analyzed by extremely fast algorithms. These networks model entities (nodes) tied to geographic places and links that represent flows such as migrations, vehicle trajectories, and activities of people [54]. In problems related to spatial data and geographical networks, the cut-based objective of GP (and clustering) is often reinforced by the spatial contiguity constraints.

Biological Networks. Many complex biological systems can be modeled by graph-theoretic representations. Examples include protein-protein interactions, and gene co-expression networks. In these networks nodes are biological entities (such as genes and proteins) and edges correspond to their common participation in some biological process. Such processes can vary from simple straightforward interactions (such as protein-protein interaction and gene-gene co-expression) to more complex relationships in which more than two entities are involved. Partitioning and clustering of such networks may have several goals. One of them is related to data reduction given an assumption that clustered nodes behave biologically similarly to each other. Another one is the detection of some biological processes by finding clusters of involved nodes. For details see [109, 154].

Social Networks. Identification of community structure is among the most popular topics in social network science. In contrast to the traditional GPP, community detection problems rarely specify the number of clusters a priori. Notwithstanding this difference, GP methods contributed a lot of their techniques to the community detection algorithms [76]. Moreover, GP solvers are often used as first approximations for them. We refer the reader to examples of methods where GP is used for solving the community detection problem [158].

3.3 Road Networks

GP is a very useful technique to speed up route planning [48, 52, 118, 129, 138, 153]. For example, edges could be road segments and nodes intersections.¹

Lauther [129] introduced the arc-flags algorithm, which uses a geometric partitioning approach as a preprocessing step to reduce the search space of Dijkstra’s algorithm. Möhring et al. [153] improved this method in several ways. Using high quality graph partitions turns out to be one key improvement here since this reduces the preprocessing cost drastically. One reason is that road networks can be partitioned using surprisingly small cuts but these are not easy to find.

Schulz et al. [196] propose a multilevel algorithm for routing based on precomputing connections between border nodes of a graph partition. This was one of the first successful speedup technique for shortest paths. It was outclassed later by other hierarchy based methods, and, somewhat surprisingly resurfaced after Delling et al. [48, 52] did thorough algorithm engineering for this approach. Again, a key improvement was to use high quality graph partitions. Since the approach excels at fast recomputation of the preprocessing information when the edge weights change, the method is now usually called customizable route planning. Luxen and Schieferdecker [138] use GP to efficiently compute candidate sets for alternative routes in road networks and Kieritz et al. [118] parallelize shortest-path preprocessing and query algorithms. Maue et al. [141] show how to use precomputed distances between blocks of a partition to make the search goal directed. Here, block diameter seems more relevant than cut size, however.

3.4 Image Processing

Image segmentation is a fundamental task in computer vision for which GP and clustering methods have become among the most attractive solution techniques. The goal of image segmentation is to partition the pixels of an image into groups that correspond to objects. Since the computations preceding segmentation are often relatively cheap and since the computations after segmentation work on a drastically compressed representation of the image (objects rather than pixels), segmentation is often the computationally most demanding part in an image processing pipeline. The image segmentation problem is not well-posed and can usually imply more than one solution. During the last two decades, graph-based representations of an image became very popular and gave rise to many cut-based approaches for several problems including image segmentation. In this representation each image pixel (or in some cases groups of pixels) corresponds to a node in a graph. Two nodes are connected by a weighted edge if some similarity exists between them. Usually, the criteria of similarity is a small geodesic distance which can result in mesh-like graphs with four or more neighbors for each node. The edge weights represent another measure of (dis)similarity between nodes such as the difference in the intensity between the connected pixels (nodes).

GP can be formulated with different objectives that can explicitly reflect different definitions of the segmented regions depending on the applications. The classical minimum cut formulation of the GP objective (1) can lead in practice to finding too small segmented objects. One popular modification of the objective that was adopted in image segmentation, called normalized cut, is given by $\text {ncut}(A, B) = \omega (E_{AB})/ \text {vol}(A) + \omega (E_{AB}) / \text {vol}(B)$. This objective is similar to the conductance objective described in Sect. 2.1. Many efficient algorithms were proposed for solving GPP with the normalized cut objective. Among the most successful are spectral and multilevel approaches. Another relevant formulation of the partitioning objective which is useful for image segmentation is given by optimizing the isoperimetric ratio for sets [89]. For more information on graph partitioning and image segmentation see [32, 169].

3.5 VLSI Physical Design

Physical design of digital circuits for very large-scale integration (VLSI) systems has a long history of being one of the most important customers of graph and hypergraph partitioning, often reinforced by several additional domain relevant constraints. The partitioning should be accomplished in a reasonable computation time, even for circuits with millions of modules, since it is one of the bottlenecks of the design process. The goal of the partitioning is to reduce the VLSI design complexity by partitioning it into smaller components (that can range from a small set of field-programmable gate arrays to fully functional integrated circuits) as well as to keep the total length of all the wires short. The typical optimization objective (see (1)) is to minimize the total weight of connections between subcircuits (blocks), where nodes are the cells, i.e., small logical or functional units of the circuit (such as gates), and edges are the wires. Because the gates are connected with wires with more than two endpoints, hypergraphs model the circuit more accurately. Examples of additional constraints for the VLSI partitioning include information on the I/O of the circuit, sets of cells that must belong to the same blocks, and maximum cut size between two blocks. For more information about partitioning of VLSI circuits see [45, 110].

4 Global Algorithms

We begin our discussion of the wide spectrum of GP algorithms with methods that work with the entire graph and compute a solution directly. These algorithms are often used for smaller graphs or are applied as subroutines in more complex methods such as local search or multilevel algorithms. Many of these methods are restricted to bipartitioning but can be generalized to k-partitioning for example by recursion.

After discussing exact methods in Sect. 4.1 we turn to heuristic algorithms. Spectral partitioning (Sect. 4.2) uses methods from linear algebra. Graph growing (Sect. 4.3) uses breadth first search or similar ways to directly add nodes to a block. Flow computations are discussed in Sect. 4.4. Section 4.5 summarizes a wide spectrum of geometric techniques. Finally, Sect. 4.5 introduces streaming algorithms which work with a very limited memory footprint.

4.1 Exact Algorithms

There is a large amount of literature on methods that solve GPP optimally. This includes methods dedicated to the bipartitioning case [5, 6, 28, 49, 51, 69, 70, 93, 94, 111, 134, 197] and some methods that solve the general GPP [71, 198]. Most of the methods rely on the branch-and-bound framework [126].

Bounds are derived using various approaches: Karisch et al. [111] and Armbruster [5] use semi-definite programming, and Sellman et al. [197] and Sensen [198] employ multi-commodity flows. Linear programming is used by Brunetta et al. [28], Ferreira et al. [71], Lisser and Rendl [134] and by Armbruster et al. [6]. Hager et al. [93, 94] formulate GPP in form of a continuous quadratic program on which the branch and bound technique is applied. The objective of the quadratic program is decomposed into convex and concave components. The more complicated concave component is then tackled by an SDP relaxation. Felner [70] and Delling et al. [49, 51] utilize combinatorial bounds. Delling et al. [49, 51] derive the bounds by computing minimum s-t cuts between partial assignments (A, B), i. e., $A,B \subseteq V$ and $A\cap B = \emptyset$. The method can partition road networks with more than a million nodes, but its running time highly depends on the bisection width of the graph.

In general, depending on the method used, two alternatives can be observed. Either the bounds derived are very good and yield small branch-and-bound trees but are hard to compute. Or the bounds are somewhat weaker and yield larger trees but are faster to compute. The latter is the case when using combinatorial bounds. On finite connected subgraphs of the two dimensional grid without holes, the bipartitioning problem can be solved optimally in $\mathrm {O}\!\left( n^4\right)$ time [69]. Recent work by Bevern et al. [19] looks at the parameterized complexity for computing balanced partitions in graphs.

All of these methods can typically solve only very small problems while having very large running times, or if they can solve large bipartitioning instances using a moderate amount of time [49, 51], highly depend on the bisection width of the graph. Methods that solve the general GPP [71, 198] have immense running times for graphs with up to a few hundred nodes. Moreover, the experimental evaluation of these methods only considers small block numbers $k\le 4$.

4.2 Spectral Partitioning

One of the first methods to split a graph into two blocks, spectral bisection, is still in use today. Spectral techniques were first used by Donath and Hoffman [58, 59] and Fiedler [73], and have been improved subsequently by others [15, 26, 98, 172, 200]. Spectral bisection infers global information of the connectivity of a graph by computing the eigenvector corresponding to the second smallest eigenvalue of the Laplacian matrix L of the graph. This eigenvector $z_2$ is also known as Fiedler vector; it is the solution of a relaxed integer program for cut optimization. A partition is derived by determining the median value $\overline{m}$ in $z_2$ and assigning all nodes with an entry smaller or equal to $\overline{m}$ to $V_1$ and all others to $V_2$.

The second eigenvector can be computed using a modified Lanczos algorithm [125]. However, this method is expensive in terms of running time. Barnard and Simon [15] use a multilevel method to obtain a fast approximation of the Fiedler vector. The algorithmic structure is similar to the multilevel method explained in Sect. 6, but their method coarsens with independent node sets and performs local improvement with Rayleigh quotient iteration. Hendrickson and Leland [98] extend the spectral method to partition a graph into more than two blocks by using multiple eigenvectors; these eigenvectors are computationally inexpensive to obtain. The method produces better partitions than recursive bisection, but is only useful for the partitioning of a graph into four or eight blocks. The authors also extended the method to graphs with node and edge weights.

4.3 Graph Growing

A very simple approach for obtaining a bisection of a graph is called graph growing [81, 113]. Most of its variants are based on breadth-first search. Its simplest version works as follows. Starting from a random node v, the nodes are assigned to block $V_1$ using a breadth-first search (BFS) starting at v. The search is stopped after half of the original node weights are assigned to this block and $V_2$ is set to $V\backslash V_1$. This method can be combined with a local search algorithm to improve the partition. Multiple restarts of the algorithm are important to get a good solution. One can also try to find a good starting node by looking at a node that has maximal distance from a random seed node [81]. Variations of the algorithm always add the node to the block that results in the smallest increase in the cut [113]. An extension to $k > 2$ blocks and with iterative improvement is described in Sect. 5.5.

4.4 Flows

The well-known max-flow min-cut theorem [75] can be used to separate two node sets in a graph by computing a maximum flow and hence a minimum cut between them. This approach completely ignores balance, and it is not obvious how to apply it to the balanced GPP. However, at least for random regular graphs with small bisection width this can be done [29]. Maximum flows are also often used as a subroutine. Refer to Sect. 5.4 for applications to improve a partition and to Sect. 6.4 for coarsening in the context of the multilevel framework. There are also applications of flow computations when quality is measured by expansion or conductance [3, 127].

4.5 Geometric Partitioning

Partitioning can utilize the coordinates of the graph nodes in space, if available. This is especially useful in finite element models and other geometrically-defined graphs from traditional scientific computing. Here, geometrically “compact” regions often correspond to graph blocks with small cut. Partitioning using nodal coordinates comes in many flavors, such as recursive coordinate bisection (RCB) [200] and inertial partitioning [67, 221]. In each step of its recursion, RCB projects graph nodes onto the coordinate axis with the longest expansion of the domain and bisects them through the median of their projections. The bisecting plane is orthogonal to the coordinate axis, which can create partitions with large separators in case of meshes with skewed dimensions. Inertial partitioning can be interpreted as an improvement over RCB in terms of worst case performance because its bisecting plane is orthogonal to a plane L that minimizes the moments of inertia of nodes. In other words, the projection plane L is chosen such that it minimizes the sum of squared distances to all nodes.

The random spheres algorithm of Miller et al. [83, 152] generalizes the RCB algorithm by stereographically projecting the d dimensional nodes to a random $d+1$ dimensional sphere which is bisected by a plane through its center point. This method gives performance guarantees for planar graphs, k-nearest neighbor graphs, and other “well-behaved” graphs.

Other representatives of geometry-based partitioning algorithms are space-filling curves [14, 105, 171, 223] which reduce d-dimensional partitioning to the one-dimensional case. Space filling curves define a bijective mapping from V to $\{1,\dots ,|V|\}$. This mapping aims at the preservation of the nodes’ locality in space. The partitioning itself is simpler and cheaper than RCB once the bijective mapping is constructed. A generalization of space-filling curves to general graphs can be done by so-called graph-filling curves [190].

A recent work attempts to bring information on the graph structure into the geometry by embedding arbitrary graphs into the coordinate space using a multilevel graph drawing algorithm [121]. For a more detailed, albeit not very recent, treatment of geometric methods, we refer the interested reader to Schloegel et al. [191].

4.6 Streaming Graph Partitioning (SGP)

Streaming data models are among the most popular recent trends in big data processing. In these models the input arrives in a data stream and has to be processed on the fly using much less space than the overall input size. SGP algorithms are very fast. They are even faster than multilevel algorithms but give lower solution quality. Nevertheless, many applications that require extremely fast repartitioning methods (such as those that deal with dynamic networks) can still greatly benefit from the SGP algorithms when an initial solution obtained by a stronger (static data) algorithm is supplied as an initial ordering. For details on SGP we refer the reader to [160, 203, 209].

5 Iterative Improvement Heuristics

Most high quality GP solvers iteratively improve starting solutions. We outline a variety of methods for this purpose, moving from very fine-grained localized approaches to more global techniques.

5.1 Node-Swapping Local Search

Local search is a simple and widely used metaheuristic for optimization that iteratively changes a solution by choosing a new one from a neighborhood. Defining the neighborhood and the selection strategy allows a wide variety of techniques. Having the improvement of paging properties of computer programs in mind, Kernighan and Lin [117] were probably the first to define GPP and to provide a local search method for this problem. The selection strategy finds the swap of node assignments that yields the largest decrease in the total cut size. Note that this “decrease” is also allowed to be negative. A round ends when all nodes have been moved in this way. The solution is then reset to the best solution encountered in this round. The algorithm terminates when a round has not found an improvement.

A major drawback of the KL method is that it is expensive in terms of asymptotic running time. The implementation assumed in [117] takes time $\mathrm {O}\!\left( n^2 \log n\right)$ and can be improved to $\mathrm {O}\!\left( m\max ( \log n, \varDelta )\right)$ where $\varDelta$ denotes the maximum degree [64]. A major breakthrough is the modification by Fiduccia and Mattheyses [72]. Their carefully designed data structures and adaptations yield the KL/FM local search algorithm, whose asymptotic running time is $\mathrm {O}\!\left( m\right)$. Bob Darrow was the first who implemented the KL/FM algorithm [72].

Karypis and Kumar [114] further accelerated KL/FM by only allowing boundary nodes to move and by stopping a round when the edge cut does not decrease after x node moves. They improve quality by random tie breaking and by allowing additional rounds even when no improvements have been found.

A highly localized version of KL/FM is considered in [161]. Here, the search spreads from a single boundary node. The search stops when a stochastic model of the search predicts that a further improvement has become unlikely. This strategy has a better chance to climb out of local minima and yields improved cuts for the GP solvers KaSPar [161] and KaHIP [183].

Rather than swapping nodes, Holtgrewe et al. move a single node at a time allowing more flexible tradeoffs between reducing the cut or improving balance [102].

Helpful Sets by Diekmann et al. [55, 155] introduce a more general neighborhood relation in the bipartitioning case. These algorithms are inspired by a proof technique of Hromkovič and Monien [103] for proving upper bounds on the bisection width of a graph. Instead of migrating single nodes, whole sets of nodes are exchanged between the blocks to improve the cut. The running time of the algorithm is comparable to the KL/FM algorithm, while solution quality is often better than other methods [155].

5.2 Extension to k-way Local Search

It has been shown by Simon and Teng [201] that, due to the lack of global knowledge, recursive bisection can create partitions that are very far away from the optimal partition so that there is a need for k-way local search algorithms. There are multiple ways of extending the KL/FM algorithm to get a local search algorithm that can improve a k-partition.

One early extension of the KL/FM algorithm to k-way local search uses $k(k-1)$ priority queues, one for each type of move (source block, target block) [97, 182]. For a single movement one chooses the node that maximizes the gain, breaking ties by the improvement in balance.

Karypis and Kumar [114] present a k-way version of the KL/FM algorithm that runs in linear time $\mathrm {O}\!\left( m\right)$. They use a single global priority queue for all types of moves. The priority used is the maximum local gain, i. e., the maximum reduction in the cut when the node is moved to one of its neighboring blocks. The node that is selected for movement yields the maximum improvement for the objective and maintains or improves upon the balance constraint.

Most current local search algorithms exchange nodes between blocks of the partition trying to decrease the cut size while also maintaining balance. This highly restricts the set of possible improvements. Sanders and Schulz [186, 195] relax the balance constraint for node movements but globally maintain (or improve) balance by combining multiple local searches. This is done by reducing the combination problem to finding negative cycles in a graph, exploiting the existence of efficient algorithms for this problem.

5.3 Tabu Search

A more expensive k-way local search algorithm is based on tabu search [86, 87], which has been applied to GP by [16–18, 78, 175]. We briefly outline the method reported by Galinier et al. [78]. Instead of moving a node exactly once per round, as in the traditional versions of the KL/FM algorithms, specific types of moves are excluded only for a number of iterations. The number of iterations that a move (v, block) is excluded depends on an aperiodic function f and the current iteration i. The algorithm always moves a non-excluded node with the highest gain. If the node is in block A, then the move (v, A) is excluded for f(i) iterations after the node is moved to the block yielding the highest gain, i. e., the node cannot be put back to block A for f(i) iterations.

5.4 Flow Based Improvement

Sanders and Schulz [183, 185] introduce a max-flow min-cut based technique to improve the edge cut of a given bipartition (and generalize this to k-partitioning by successively looking at pairs of blocks that are adjacent in the quotient graph). The algorithm constructs an s-t flow problem by growing an area around the given boundary nodes/cut edges. The area is chosen such that each s-t cut in this area corresponds to a feasible bipartition of the original graph, i. e., a bipartition that fulfills the balance constraint. One can then apply a max-flow min-cut algorithm to obtain a min-cut in this area and hence a nondecreased cut between the blocks. There are multiple improvements to extend this method, for example, by iteratively applying the method, searching in larger areas for feasible cuts, or applying a heuristic to output better balanced minimum cuts by using the given max-flow.

5.5 Bubble Framework

Diekmann et al. [57] extend graph growing and previous ideas [216] to obtain an iterative procedure called Bubble framework, which is capable of partitioning into $k>2$ well-shaped blocks. Some applications profit from good geometric block shapes, e. g., the convergence rate of certain iterative linear solvers.

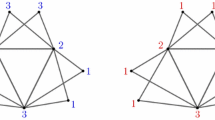
Graph growing is extended first by carefully selecting k seed nodes that are evenly distributed over the graph. The key property for obtaining a good quality, however, is an iterative improvement within the second and the third step – analogous to Lloyd’s k-means algorithm [135]. Starting from the k seed nodes, k breadth-first searches grow the blocks analogous to Sect. 4.3, only that the breadth-first searches are scheduled such that the smallest block receives the next node. Local search algorithms are further used within this step to balance the load of the blocks and to improve the cut of the resulting partition, which may result in unconnected blocks. The final step of one iteration computes new seed nodes for the next round. The new center of a block is defined as the node that minimizes the sum of the distances to all other nodes within its block. To avoid their expensive computation, approximations are used. The second and the third step of the algorithm are iterated until either the seed nodes stop changing or no improved partition was found for more than 10 iterations. Figure 1 illustrates the three steps of the algorithm. A drawback of the algorithm is its computational complexity $\mathrm {O}\!\left( km\right)$.

Fig. 1.

The three steps of the Bubble framework. Black nodes indicate the seed nodes. On the left hand side, seed nodes are found. In the middle, a partition is found by performing breadth-first searches around the seed nodes and on the right hand side new seed nodes are found.

Subsequently, this approach has been improved by using distance measures that better reflect the graph structure [144, 151, 189]. For example, Schamberger [189] introduced the usage of diffusion as a growing mechanism around the initial seeds and extended the method to weighted graphs. More sophisticated diffusion schemes, some of which have been employed within the Bubble framework, are discussed in Sect. 5.6.

5.6 Random Walks and Diffusion

A random walk on a graph starts on a node v and then chooses randomly the next node to visit from the set of neighbors (possibly including v itself) based on transition probabilities. The latter can for instance reflect the importance of an edge. This iterative process can be repeated an arbitrary number of times. It is governed by the so-called transition matrix $\mathbf {P}$, whose entries denote the edges’ transition probabilities. More details can be found in Lovasz’s random walk survey [136].

Diffusion, in turn, is a natural process describing a substance’s desire to distribute evenly in space. In a discrete setting on graphs, diffusion is an iterative process which exchanges splittable entities between neighboring nodes, usually until all nodes have the same amount. Diffusion is a special random walk; thus, both can be used to identify dense graph regions: Once a random walk reaches a dense region, it is likely to stay there for a long time, before leaving it via one of the relatively few outgoing edges. The relative size of $\mathbf {P}_{u,v}^{t}$, the probability of a random walk that starts in u to be located on v after t steps, can be exploited for assigning u and v to the same or different clusters. This fact is used by many authors for graph clustering, cf. Schaeffer’s survey [188].

Due to the difficulty of enforcing balance constraints, works employing these approaches for partitioning are less numerous. Meyerhenke et al. [148] present a similarity measure based on diffusion that is employed within the Bubble framework. This diffusive approach bears some conceptual resemblance to spectral partitioning, but with advantages in quality [150]. Balancing is enforced by two different procedures that are only loosely coupled to the actual partitioning process. The first one is an iterative procedure that tries to adapt the amount of diffusion load in each block by multiplying it with a suitable scalar. Underloaded blocks receive more load, overloaded ones less. It is then easier for underloaded blocks to “flood” other graph areas as well. In case the search for suitable scalars is unsuccessful, the authors employ a second approach that extends previous work [219]. It computes a migrating flow on the quotient graph of the partition. The flow value $f_{ij}$ between blocks i and j specifies how many nodes have to be migrated from i to j in order to balance the partition. As a key and novel property for obtaining good solutions, to determine which nodes should be migrated in which order, the diffusive similarity values computed before within the Bubble framework are used [146, 148].

Diffusion-based partitioning has been subsequently improved by Pellegrini [165], who combines KL/FM and diffusion for bipartitioning in the tool Scotch. He speeds up previous approaches by using band graphs that replace unimportant graph areas by a single node. An extension of these results to k-way partitioning with further adaptations has been realized within the tools DibaP [143] and PDibaP for repartitioning [147]. Integrated into a multilevel method, diffusive partitioning is able to compute high-quality solutions, in particular with respect to communication volume and block shape. It remains further work to devise a faster implementation of the diffusive approach without running time dependence on k.

6 Multilevel Graph Partitioning

Clearly the most successful heuristic for partitioning large graphs is the multilevel graph partitioning approach. It consists of the three main phases outlined in Fig. 2: coarsening, initial partitioning, and uncoarsening. The main goal of the coarsening (in many multilevel approaches implemented as contraction) phase is to gradually approximate the original problem and the input graph with fewer degrees of freedom. In multilevel GP solvers this is achieved by creating a hierarchy of successively coarsened graphs with decreasing sizes in such a way that cuts in the coarse graphs reflect cuts in the fine graph. There are multiple possibilities to create graph hierarchies. Most methods used today contract sets of nodes on the fine level. Contracting $U\subset V$ amounts to replacing it with a single node u with $c(u):=\sum _{w\in U} c(w)$. Contraction (and other types of coarsening) might produce parallel edges which are replaced by a single edge whose weight accumulates the weights of the parallel edges (see Fig. 3). This implies that balanced partitions on the coarse level represent balanced partitions on the fine level with the same cut value.

Fig. 2.

The multilevel approach to GP. The left figure shows a two-level contraction-based scheme. The right figure shows different chains of coarsening-uncoarsening in the multilevel frameworks.

Coarsening is usually stopped when the graph is sufficiently small to be initially partitioned using some (possibly expensive) algorithm. Any of the basic algorithms from Sect. 4 can be used for initial partitioning as long as they are able to handle general node and edge weights. The high quality of more expensive methods that can be applied at the coarsest level does not necessarily translate into quality at the finest level, and some GP multilevel solvers rather run several faster but diverse methods repeatedly with different random tie breaking instead of applying expensive global optimization techniques.

Uncoarsening consists of two stages. First, the solution obtained on the coarse level graph is mapped to the fine level graph. Then the partition is improved, typically by using some variants of the improvement methods described in Sect. 5. This process of uncoarsening and local improvement is carried on until the finest hierarchy level has been processed. One run of this simple coarsening-uncoarsening scheme is also called a V-cycle (see Fig. 2).

There are at least three intuitive reasons why the multilevel approach works so well: First, at the coarse levels we can afford to perform a lot of work per node without increasing the overall execution time by a lot. Furthermore, a single node move at a coarse level corresponds to a big change in the final solution. Hence, we might be able to find improvements easily that would be difficult to find on the finest level. Finally, fine level local improvements are expected to run fast since they already start from a good solution inherited from the coarse level. Also multilevel methods can benefit from their iterative application (such as chains of V-cycles) when the previous iteration’s solution is used to improve the quality of coarsening. Moreover, (following the analogy to multigrid schemes) the inter-hierarchical coarsening-uncoarsening iteration can also be reconstructed in such way that more work will be done at the coarser levels (see F-, and W-cycles in Fig. 2, and [183, 212]). An important technical advantage of multilevel approaches is related to parallelization. Because multilevel approaches achieve a global solution by local processing only (though applied at different levels of coarseness) they are naturally parallelization-schemes friendly.

Fig. 3.

An example matching and contraction of the matched edges.

6.1 Contracting a Single Edge

A minimalistic approach to coarsening is to contract only two nodes connected by a single edge in the graph. Since this leads to a hierarchy with (almost) n levels, this method is called n-level GP [161]. Together with a k-way variant of the highly localized local search from Sect. 5.1, this leads to a very simple way to achieve high quality partitions. Compared to other techniques, n-level partitioning has some overhead for coarsening, mainly because it needs a priority queue and a dynamic graph data structure. On the other hand, for graphs with enough locality (e.g. from scientific computing), the n-level method empirically needs only sublinear work for local improvement.

6.2 Contracting a Matching

The most widely used contraction strategy contracts (large) matchings, i. e., the contracted sets are pairs of nodes connected by edges and these edges are not allowed to be incident to each other. The idea is that this leads to a geometrically decreasing size of the graph and hence a logarithmic number of levels, while subsequent levels are “similar” so that local improvement can quickly find good solutions. Assuming linear-time algorithms on all levels, one then gets linear overall execution time. Conventional wisdom is that a good matching contains many high weight edges since this decreases the weight of the edges in the coarse graph and will eventually lead to small cuts. However, one also wants a certain uniformity in the node weights so that it is not quite clear what should be the objective of the matching algorithm. A successful recent approach is to delegate this tradeoff between edge weights and uniformity to an edge rating function [1, 102]. For example, the function $f(u,v)=\frac{\omega (\left\{ u,v\right\} )}{c(v)c(u)}$ works very well [102, 183] (also for n-level partitioning [161]). The concept of algebraic distance yields further improved edge ratings [179].

The weighted matching problem itself has attracted a lot of interest motivated to a large extent by its application for coarsening. Although the maximum weight matching problem can be solved optimally in polynomial time, optimal algorithms are too slow in practice. There are very fast heuristic algorithms like (Sorted) Heavy Edge Matching, Light Edge Matching, Random Matching, etc. [113, 191] that do not give any quality guarantees however. On the other hand, there are (near) linear time matching algorithms that are slightly more expensive but give approximation guarantees and also seem to be more robust in practice. For example, a greedy algorithm considering the edges in order of descending edge weight guarantees half of the optimal edge weight. Preis’ algorithm [173] and the Path Growing Algorithm [61] have a similar flavor but avoid sorting and thus achieve linear running time for arbitrary edge weights. The Global Path Algorithm (GPA) [140] is a synthesis of Greedy and Path Growing achieving somewhat higher quality in practice and is not a performance bottleneck in many cases. GPA is therefore used in KaHIP [183, 186, 187]. Linear time algorithms with better approximation guarantee are available [62, 63, 140, 170] and the simplest of them seem practical [140]. However, it has not been tried yet whether they are worth the additional effort for GP.

6.3 Coarsening for Scale-Free Graphs

Matching-based graph coarsening methods are well-suited for coarsening graphs arising in scientific computing. On the other hand, matching-based approaches can fail to create good hierarchies for graphs with irregular structure. Consider the extreme example that the input graph is a star. In this case, a matching algorithm can contract only one edge per level, which leads to a number of levels that is undesirable in most cases.

Abou-Rjeili and Karypis [1] modify a large set of matching algorithms such that an unmatched node can potentially be matched with one of its neighbors even if it is already matched. Informally speaking, instead of matchings, whole groups of nodes are contracted to create the graph hierarchies. These approaches significantly improve partition quality on graphs having a power-law degree distribution.

Another approach has been presented by Auer and Bisseling [10]. The authors create graph hierarchies for social networks by allowing pairwise merges of nodes that have the same neighbors and by merging multiple nodes, i. e., collapsing multiple neighbors of a high degree node with this node.

Meyerhenke et al. [145, 149] presented an approach that uses a modification of the original label propagation algorithm [174] to compute size-constrained clusterings which are then contracted to compute good multilevel hierarchies for such graphs. The same algorithm is used as a very simple greedy local search algorithm.

Glantz et al. [85] introduce an edge rating based on how often an edge appears in relatively balanced light cuts induced by spanning trees. Intriguingly, this cut-based approach yields partitions with very low communication volume for scale-free graphs.

6.4 Flow Based Coarsening

Using max-flow computations, Delling et al. [50] find “natural cuts” separating heuristically determined regions from the remainder of the graph. Components cut by none of these cuts are then contracted reducing the graph size by up to two orders of magnitude. They use this as the basis of a two-level GP solver that quickly gives very good solutions for road networks.

6.5 Coarsening with Weighted Aggregation

Aggregation-based coarsening identifies nodes on the fine level that survive in the coarsened graph. All other nodes are assigned to these coarse nodes. In the general case of weighted aggregation, nodes on a fine level belong to nodes on the coarse level with some probability. This approach is derived from a class of hierarchical linear solvers called Algebraic Multigrid (AMG) methods [41, 144]. First results on the bipartitioning problem were obtained by Ron et al. in [176]. As AMG linear solvers have shown, weighted aggregation is important in order to express the likelihood of nodes to belong together. The accumulated likelihoods “smooth the solution space” by eliminating from it local minima that will be detected instanteneously by the local processing at the uncoarsening phase. This enables a relaxed formulation of coarser levels and avoids making hardened local decisions, such as edge contractions, before accumulating relevant global information about the graph.

Weighted aggregation can lead to significantly denser coarse graphs. Hence, only the most efficient AMG approaches can be adapted to graph partitioning successfully. Furthermore one has to avoid unbalanced node weights. In [179] algebraic distance [38] is used as a measure of connectivity between nodes to obtain sparse and balanced coarse levels of high quality. These principles and their relevance to AMG are summarized in [178].

Lafon and Lee [124] present a related coarsening framework whose goal is to retain the spectral properties of the graph. They use matrix-based arguments using random walks (for partitioning methods based on random walks see Sect. 5.6) to derive approximation guarantees on the eigenvectors of the coarse graph. The disadvantage of this approach is the rather expensive computation of eigenvectors.

7 Evolutionary Methods and Further Metaheuristics

In recent years a number of metaheuristics have been applied to GPP. Some of these works use concepts that have already been very popular in other application domains such as genetic or evolutionary algorithms. For a general overview of genetic/evolutionary algorithms tackling GPP, we refer the reader to the overview paper by Kim et al. [119]. In this section we focus on the description of hybrid evolutionary approaches that combine evolutionary ideas with the multilevel GP framework [16, 17, 202]. Other well-known metaheuristics such as multi-agent and ant-colony optimization [44, 122], and simulated annealing [108] are not covered here. Neither do we discuss the recently proposed metaheuristics PROBE by Chardaire et al. [37] (a genetic algorithm without selection) and Fusion-Fission by Bichot [23] (inspired by nuclear processes) in detail. Most of these algorithms are able to produce solutions of a very high quality, but only if they are allowed to run for a very long time. Hybrid evolutionary algorithms are usually able to compute partitions with considerably better quality than those that can be found by using a single execution of a multilevel algorithm.

The first approach that combined evolutionary ideas with a multilevel GP solver was by Soper et al. [202]. The authors define two main operations, a combine and a mutation operation. Both operations modify the edge weights of the graph depending on the input partitions and then use the multilevel partitioner Jostle, which uses the modified edge weights to obtain a new partition of the original graph. The combine operation first computes node weight biases based on the two input partitions/parents of the population and then uses those to compute random perturbations of the edge weights which help to mimic the input partitions. While producing partitions of very high quality, the authors report running times of up to one week. A similar approach based on edge weight perturbations is used by Delling et al. [50].

A multilevel memetic algorithm for the perfectly balanced graph partition problem, i. e., $\epsilon =0$, was proposed by Benlic and Hao [16, 17]. The main idea of their algorithm is that among high quality solutions a large number of nodes will always be grouped together. In their work the partitions represent the individuals. We briefly sketch the combination operator for the case that two partitions are combined. First the algorithm selects two individuals/partitions from the population using a $\lambda$-tournament selection rule, i. e., choose $\lambda$ random individuals from the population and select the best among those if it has not been selected previously. Let the selected partitions be $P_1=(V_1, \ldots , V_k)$ and $P_2=(W_1, \ldots , W_k)$. Then sets of nodes that are grouped together, i. e.,

$$\begin{aligned} \mathcal {U} := \left\{ \{V_1 \cap W_{\sigma (1)}\}, \ldots , \{V_k \cap W_{\sigma (k)}\}\right\} \end{aligned}$$

are computed. This is done such that the number of nodes that are grouped together, i. e., $\sum _{j=1}^k |V_j \cap W_{\sigma (j)}|$, is maximum among all permutations $\sigma$ of $\{1, \ldots , k\}$. An offspring is created as follows. Sets of nodes in $\mathcal {U}$ will be grouped within a block of the offspring. That means if a node is in on of the sets of $\mathcal {U}$, then it is assigned to the same block to which it was assigned to in $P_1$. Otherwise, it is assigned to a random block, such that the balance constraint remains fulfilled. Local search is then used to improve the computed offspring before it is inserted into the population. Benlic and Hao [17] combine their approach with tabu search. Their algorithms produce partitions of very high quality, but cannot guarantee that the output partition fulfills the desired balance constraint.

Sanders and Schulz introduced a distributed evolutionary algorithm, KaFFPaE (KaFFPaEvolutionary) [184]. They present a general combine operator framework, which means that a partition $\mathcal {P}$ can be combined with another partition or an arbitrary clustering of the graph, as well as multiple mutation operators to ensure diversity in the population. The combine operation uses a modified version of the multilevel GP solver within KaHIP [183] that will not contract edges that are cut in one of the input partitions/clusterings. In contrast to the other approaches, the combine operation can ensure that the resulting offspring/partition is at least as good as the input partition $\mathcal {P}$. The algorithm is equipped with a scalable communication protocol similar to randomized rumor spreading and has been able to improve the best known partitions for many inputs.

8 Parallel Aspects of Graph Partitioning

In the era of stalling CPU clock speeds, exploiting parallelism is probably the most important way to accelerate computer programs from a hardware perspective. When executing parallel graph algorithms without shared memory, a good distribution of the graph onto the PEs is very important. Since parallel computing is a major purpose for GP, we discuss in this section several techniques beneficial for parallel scenarios. (i) Parallel GP algorithms are often necessary due to memory constraints: Partitioning a huge distributed graph on a single PE is often infeasible. (ii) When different PEs communicate with different speeds with each other, techniques for mapping the blocks communication-efficiently onto the PEs become important. (iii) When the graph changes over time (as in dynamic simulations), so does its partition. Once the imbalance becomes too large, one should find a new partition that unifies three criteria for this purpose: balance, low communication, and low migration.

8.1 Parallel Algorithms

Parallel GP algorithms are becoming more and more important since parallel hardware is now ubiquitous and networks grow. If the underlying application is in parallel processing, finding the partitions in parallel is even more compelling. The difficulty of parallelization very much depends on the circumstances. It is relatively easy to run sequential GP solvers multiple times with randomized tie breaking in all available decisions. Completely independent runs quickly lead to a point of diminishing return but are a useful strategy for very simple initial partitioners as the one described in Sect. 4.3. Evolutionary GP solvers are more effective (thanks to very good combination operators) and scale very well, even on loosely coupled distributed machines [184].

Most of the geometry-based algorithms from Sect. 4.5 are parallelizable and perhaps this is one of the main reasons for using them. In particular, one can use them to find an initial distribution of nodes to processors in order to improve the locality of a subsequent graph based parallel method [102]. If such a “reasonable” distribution of a large graph over the local memories is available, distributed memory multilevel partitioners using MPI can be made to scale [40, 102, 112, 213]. However, loss of quality compared to the sequential algorithms is a constant concern. A recent parallel matching algorithm allows high quality coarsening, though [24]. If k coincides with the number of processors, one can use parallel edge coloring of the quotient graph to do pairwise refinement between neighboring blocks. At least for mesh-like graphs this scales fairly well [102] and gives quality comparable to sequential solvers. This comparable solution quality also holds for parallel Jostle as described by Walshaw and Cross [214].

Parallelizing local search algorithms like KL/FM is much more difficult since local search is inherently sequential and since recent results indicate that it achieves best quality when performed in a highly localized way [161, 183]. When restricting local search to improving moves, parallelization is possible, though [2, 116, 128, 149]. In a shared memory context, one can also use speculative parallelism [205]. The diffusion-based improvement methods described in Sect. 5.6 are also parallelizable without loss of quality since they are formulated in a naturally data parallel way [147, 168].

8.2 Mapping Techniques

Fundamentals. Parallel computing on graphs is one major application area of GP, see Sect. 3.1. A partition with a small communication volume translates directly into an efficient application if the underlying hardware provides uniform communication speed between each pair of processing elements (PEs). Most of today’s leading parallel systems, however, are built as a hierarchy of PEs, memory systems, and network connections [142]. Communicating data between PEs close to each other is thus usually less expensive than between PEs with a high distance. On such architectures it is important to extend GPP by a flexible assignment of blocks to PEs [207].

Combining partitioning and mapping to PEs is often done in two different ways. In the first one, which we term architecture-aware partitioning, the cost of communicating data between a pair of PEs is directly incorporated into the objective function during the partitioning process. As an example, assuming that block (or process) i is run on PE i, the communication-aware edge cut function is $\sum _{i < j} \omega (E_{ij}) \cdot \omega _p(i, j)$, where $\omega _p(i, j)$ specifies the cost of communicating a unit item from PE i to PE j [218]. This approach uses a network cost matrix (NCM) to store the distance function $\omega _p$ [218, p. 603ff.]. Since the entries are queried frequently during partitioning, a recomputation of the matrix would be too costly. For large systems one must find a way around storing the full NCM on each PE, as the storage size scales quadratically with the number of PEs. A similar approach with emphasis on modeling heterogeneous communication costs in grid-based systems is undertaken by the software PaGrid [104]. Moulitsas and Karypis [157] perform architecture-aware partitioning in two phases. Their so-called predictor-corrector approach concentrates in the first phase only on the resources of each PE and computes an according partition. In the second phase the method corrects previous decisions by modifying the partition according to the interconnection network characteristics, including heterogeneity.

An even stronger decoupling takes place for the second problem formulation, which we refer to as the mapping problem. Let $G_c = (V_c, E_c, \omega _c)$ be the communication graph that models the application’s communication, where $(u, v) \in E_c$ denotes how much data process u sends to process v. Let furthermore $G_p = (V_p, E_p, \omega _p)$ be the processor graph, where $(i, j) \in E_p$ specifies the bandwidth (or the latency) between PE i and PE j. We now assume that a partition has already been computed, inducing a communication graph $G_c$. The task after partitioning is then to find a communication-optimal mapping $\pi : V_c \mapsto V_p$.

Different objective functions have been proposed for this mapping problem. Since it is difficult to capture the deciding hardware characteristics, most authors concentrate on simplified cost functions – similar to the simplification of the edge cut for graph partitioning. Apparently small variations in the cost functions rarely lead to drastic variations in application running time. For details we refer to Pellegrini’s survey on static mapping [167] (which we wish to update with this section, not to replace) and the references therein. Global sum type cost functions do not have the drawback of requiring global updates. Moreover, discontinuities in their search space, which may inhibit metaheuristics to be effective, are usually less pronounced than for maximum-based cost functions. Commonly used is the sum, for all edges of $G_c$, of their weight multiplied by the cost of a unit-weight communication in $G_p$ [167]: $f(G_c, G_p, \pi ) := \sum _{(u, v) \in E_c} \omega _c(u, v) \cdot \omega _p(\pi (u), \pi (v))$.

The accuracy of the distance function $\omega _p$ depends on several factors, one of them being the routing algorithm, which determines the paths a message takes. The maximum length over all these paths is called the dilation of the embedding $\pi$. One simplifying assumption can be that the routing algorithm is oblivious [101] and, for example, uses always shortest paths. When multiple messages are exchanged at the same time, the same communication link may be requested by multiple messages. This congestion of edges in $G_p$ can therefore be another important factor to consider and whose maximum (or average) over all edges should be minimized. Minimizing the maximum congestion is NP-hard, cf. Garey and Johnson [80] or more recent work [101, 120].

Algorithms. Due to the problem’s complexity, exact mapping methods are only practical in special cases. Leighton’s book [130] discusses embeddings between arrays, trees, and hypercubic topologies. One can apply a wide range of optimization techniques to the mapping problem, also multilevel algorithms. Their general structure is very similar to that described in Sect. 6. The precise differences of the single stages are beyond our scope. Instead we focus on very recent results – some of which also use hierarchical approaches. For pointers to additional methods we refer the reader to Pellegrini [167] and Aubanel’s short summary [9] on resource-aware load balancing.

Greedy approaches such as the one by Brandfass et al. [27] map the node $v_c$ of $G_c$ with the highest total communication cost w. r. t. to the already mapped nodes onto the node $v_p$ of $G_p$ with the smallest total distance w. r. t. to the already mapped nodes. Some variations exist that improve this generic approach in certain settings [84, 101].

Hoefler and Snir [101] employ the reverse Cuthill-McKee (RCM) algorithm as a mapping heuristic. Originally, RCM has been conceived for the problem of minimizing the bandwidth of a sparse matrix [81]. In case both $G_c$ and $G_p$ are sparse, the simultaneous optimization of both graph layouts can lead to reasonable mapping results, also cf. Pellegrini [166].

Many metaheuristics have been used to solve the mapping problem. Uçar et al. [210] implement a large variety of methods within a clustering approach, among them genetic algorithms, simulated annealing, tabu search, and particle swarm optimization. Brandfass et al. [27] present local search and evolutionary algorithms. Their experiments confirm that metaheuristics are significantly slower than problem-specific heuristics, but obtain high-quality solutions [27, 210].

Another common approach is to partition $G_c$ – or the application graph itself – simultaneously together with $G_p$ into the same number of blocks $k'$. This is for example done in Scotch [164]. For this approach $k'$ is chosen small enough so that it is easy to test which block in $G_c$ is mapped onto which block in $G_p$. Since this often implies $k' < k$, the partitioning is repeated recursively. When the number of nodes in each block is small enough, the mapping within each block is computed by brute force. If $k' = 2$ and the two graphs to be partitioned are the application graph and $G_p$, the method is called dual recursive bipartitioning. Recently, schemes that model the processor graph as a tree have emerged [36] in this algorithmic context and in similar ones [107].

Hoefler and Snir [101] compare the greedy, RCM, and dual recursive (bi)partitioning mapping techniques experimentally. On a 3D torus and two other real architectures, their results do not show a clear winner. However, they confirm previous studies [167] in that performing mapping at all is worthwhile. Bhatele et al. [21] discuss topology-aware mappings of different communication patterns to the physical topology in the context of MPI on emerging architectures. Better mappings avoid communication hot spots and reduce communication times significantly. Geometric information can also be helpful for finding good mappings on regular architectures such as tori [20].

8.3 Migration Minimization During Repartitioning

Repartitioning involves a tradeoff between the quality of the new partition and the migration volume. Larger changes between the old partition $\varPi$ and the new one $\varPi '$, necessary to obtain a small communication volume in $\varPi '$, result in a higher migration volume. Different strategies have been explored in the literature to address this tradeoff. Two simple ones and their limitations are described by Schloegel et al. [192]. One approach is to compute a new partition $\varPi '$ from scratch and determine a migration-minimal mapping between $\varPi$ and $\varPi '$. This approach delivers good partitions, but the migration volume is often very high. Another strategy simply migrates nodes from overloaded blocks to underloaded ones, until a new balanced partition is reached. While this leads to optimal migration costs, it often delivers poor partition quality. To improve these simple schemes, Schloegel et al. [193] combine the two and get the best of both in their tool ParMetis.

Migration minimization with virtual nodes has been used in the repartitioning case by, among others, Hendrickson et al. [99]. For each block, an additional node is added, which may not change its affiliation. It is connected to each node v of the block by an edge whose weight is proportional to the migration cost for v. Thus, one can account for migration costs and partition quality at the same time. A detailed discussion of this general technique was made by Walshaw [217]. Recently, this technique has been extended to heterogeneous architectures by Fourestier and Pellegrini [77].

Diffusion-based partitioning algorithms are particularly strong for repartitioning. PDibaP yields about 30–50% edge cut improvement compared to ParMetis and about 15% improvement on parallel Jostle with a comparable migration volume [147] (a short description of these tools can be found in Sect. 9.3). Hypergraph-based repartitioning is particularly important when the underlying problem has a rather irregular structure [34].

9 Implementation and Evaluation Aspects

The two major factors that make up successful GP algorithms are speed and quality. It depends on the application if one of them is favored over the other and what quality means. Speed requires an appropriate implementation, for which we discuss the most common graph data structures in practice first in this section. Then, we discuss GP benchmarks to assess different algorithms and implementations, some widely used, others with potential. Finally, relevant software tools for GP are presented.

9.1 Sparse Graph Data Structures

The graph data structure used by most partitioning software is the Compressed Sparse Rows (CSR) format, also known as adjacency arrays. CSR is a cache and storage efficient data structure for representing static graphs. The CSR representation of a graph can be composed of two, three, or four arrays, depending upon whether edges or nodes are weighted. The node array ($\mathsf {V}$) is of size $n+1$ and holds the node pointers. The edge array and the edge weights array, if present, are of size m each. Each entry in the edge array ($\mathsf {E}$) holds the node id of the target node, while the corresponding entry in the edge weights array ($\mathsf {W}$) holds the weight of the edge. The node array holds the offsets to the edge array, meaning that the target nodes of the outgoing edges of the ith node are accessible from $\mathsf {E}(\mathsf {V}(i))$ to $\mathsf {E}(\mathsf {V}(i+1)-1)$ and their respective weights are accessible from $\mathsf {W}(\mathsf {V}(i))$ to $\mathsf {W}(\mathsf {V}(i+1)-1)$. Both Metis and Scotch use a CSR-like data structure. Since nodes can also be weighted in graph partitioning, an additional vector of size n is often used to store node weights in that case. The CSR format can further be improved and reinforced by rearranging the nodes with one of the cache-oblivious layouts such as the minimum logarithmic arrangement [42, 180].

Among distributed-memory GP solvers, ParMetis and PT-Scotch use a 1D node distribution where each processor owns approximately n / p nodes and their corresponding edges. By contrast, Zoltan uses a 2D edge distribution that has lower communication requirements in theory.

9.2 Benchmarking

The Walshaw benchmark² was created in 2000 by Soper et al. [202]. This public domain archive, maintained by Chris Walshaw, contains 34 real-world graphs stemming from applications such as finite element computations, matrix computations, VLSI Design and shortest path computations. More importantly, it also contains for each graph the partitions with the smallest cuts found so far. Submissions are sought that achieve improved cut values for $k\in \left\{ 2, 4, 8, 16, 32, 64\right\}$ and balance parameters $\epsilon \in \left\{ 0,0.01,0.03,0.05\right\}$, while running time is not an issue. Currently, solutions of over 40 algorithms have been submitted to the archive. It is the most popular GP benchmark in the literature.

There are many other very valuable sources of graphs for experimental evaluations: the 10th DIMACS Implementation Challenge [12, 13], the Florida Sparse Matrix Collection [46], the Laboratory of Web Algorithms [220], the Koblenz Network Collection [123], and the Stanford Large Network Dataset Collection [131]. Many of the graphs are available at the website of the 10th DIMACS Implementation Challenge [12, 13] in the graph format that is used by many GP software tools.

Aubanel et al. [82] present a different kind of partitioning benchmark. Instead of measuring the edge cut of the partitions, the authors evaluate the execution time of a parallel PDE solver to benchmark the partitions produced by different GP solvers. The crucial module of the benchmark is parallel matrix-vector multiplication, which is meaningful for other numerical routines as well.

Many fast methods for GPP are based on approaches in which finding a global solution is done by local operations only. Testing if such methods are robust against falling into local optima obtained by the local processing is a very important task. In [179] a simple strategy for checking the quality of such methods was presented. To construct a potentially hard instance, one may consider a mixture of graphs with very different structures that are weakly connected with each other. For example, in multilevel algorithms these graphs can force the algorithm to contract incorrect edges that lead to uneven coarsening; also, they can attract a “too strong” refinement to reach a local optimum, which can contradict better optima at finer levels. Examples of real graphs that contain such mixtures of structures include multi-mode networks [206] and logistics multi-stage system networks [204]. Hardness of particular structures for GP solvers is confirmed by generating graphs that are similar to the given ones at both coarse and/or fine resolutions [91].

9.3 Software Tools

There are a number of software packages that implement the described algorithms. One of the first publicly available software packages called Chaco is due to Hendrickson and Leland [95]. As most of the publicly available software packages, Chaco implements the multilevel approach outlined in Sect. 6 and basic local search algorithms. Moreover, they implement spectral partitioning techniques. Probably the fastest and best known system is the Metis family by Karypis and Kumar [113, 114]. kMetis [114] is focused on partitioning speed and hMetis [115], which is a hypergraph partitioner, aims at partition quality. PaToH [35] is also a widely used hypergraph partitioner that produces high quality partitions. ParMetis is a widely used parallel implementation of the Metis GP algorithm [112]. Scotch [39, 40, 163] is a GP framework by Pellegrini. It uses recursive multilevel bisection and includes sequential as well as parallel partitioning techniques. Jostle [213, 215] is a well-known sequential and parallel GP solver developed by Chris Walshaw. The commercialised version of this partitioner is known as NetWorks. It has been able to hold most of the records in the Walshaw Benchmark for a long period of time. If a model of the communication network is available, then Jostle and Scotch are able to take this model into account for the partitioning process. Party [57, 155] implements the Bubble/shape-optimized framework and the Helpful Sets algorithm. The software packages DibaP and its MPI-parallel variant PDibaP by Meyerhenke [143, 147] implement the Bubble framework using diffusion; DibaP also uses AMG-based techniques for coarsening and solving linear systems arising in the diffusive approach. Recently, Sanders and Schulz [186, 187] released the GP package KaHIP (Karlsruhe High Quality Partitioning) which implements for example flow-based methods, more-localized local searches and several parallel and sequential meta-heuristics. KaHIP scored most of the points in the GP subchallenge of the 10th DIMACS Implementation Challenge [13] and currently holds most of the entries in the Walshaw Benchmark.

To address the load balancing problem in parallel applications, distributed versions of the established sequential partitioners Metis, Jostle and Scotch [168, 194, 215] have been developed. The tools Parkway by Trifunovic and Knottenbelt [208] as well as Zoltan by Devine et al. [53] focus on hypergraph partitioning. Recent results of the 10th DIMACS Implementation Challenge [13] suggest that scaling current hypergraph partitioners to very large systems is even more challenging than graph partitioners.

10 Future Challenges

It is an interesting question to what extent the multitude of results sketched above have reached a state of maturity where future improvements become less and less likely. On the one hand, if you consider the Walshaw benchmark with its moderately sized static graphs with mostly regular structure, the quality obtained using the best current systems is very good and unlikely to improve much in the future. One can already get very good quality with a careful application of decade old techniques like KL/FM local search and the multilevel approach. On the other hand, as soon as you widen your view in some direction, there are plenty of important open problems.

Bridging Gaps Between Theory and Practice. We are far from understanding why (or when) the heuristic methods used in practice produce solutions very close to optimal. This is particularly striking for bipartitioning, where recent exact results suggest that heuristics often find the optimal solution. In contrast, theoretical results state that we cannot even find constant-factor approximations in polynomial time. On the other hand, the sophisticated theoretical methods developed to obtain approximation guarantees are currently not used in the most successful solvers. It would be interesting to see to what extent these techniques can yield a practical contribution. There is a similar problem for exact solvers, which have made rapid progress for the case $k=2$. However, it remains unclear how to use them productively for larger graphs or in case $k>2$, for example as initial partitioners in a multilevel system or for pair-wise local improvement of subgraphs. What is surprisingly successful, is the use of solvers with performance guarantees for subproblems that are easier than partitioning. For example, KaHIP [187] uses weighted matching, spanning trees, edge coloring, BFS, shortest paths, diffusion, maximum flows, and strongly connected components. Further research into this direction looks promising.

Difficult Instances. The new “complex network” applications described in Sect. 3.2 result in graphs that are not only very large but also difficult to handle for current graph partitioners. This difficulty results from an uneven degree distribution and much less locality than observed in traditional inputs. Here, improved techniques within known frameworks (e.g., better coarsening schemes) and even entirely different approaches can give substantial improvements in speed or quality.

Another area where large significant quality improvements are possible are for large k. Already for the largest value of k considered in the Walshaw benchmark (64), the spread between different approaches is considerable. Considering graphs with billions of nodes and parallel machines reaching millions of processors, $k\le 64$ increasingly appears like a special case. The multilevel method loses some of its attractiveness for large k since even initial partitioning must solve quite large instances. Hence new ideas are required.

Multilevel Approach. While the multilevel paradigm has been extremely successful for GP, there are still many algorithmic challenges ahead. The variety of continuous systems multilevel algorithms (such as various types of multigrid) turned into a separate field of applied mathematics, and optimization. Yet, multilevel algorithms for GPP still consist in practice of a very limited number of multilevel techniques. The situation with other combinatorial optimization problems is not significantly different. One very promising direction is bridging the gaps between the theory and practice of multiscale computing and multilevel GP such as introducing nonlinear coarsening schemes. For example, a novel multilevel approach for the minimum vertex separator problem was recently proposed using the continuous bilinear quadratic program formulation [92], and a hybrid of the geometric multigrid, and full approximation scheme for continuous problem was used for graph drawing, and VLSI placement problems [45, 177]. Development of more sophisticated coarsening schemes, edge ratings, and metrics of nodes’ similarity that can be propagated throughout the hierarchies are among the future challenges for graph partitioning as well as any attempt of their rigorous analysis.

Parallelism and Other Hardware Issues. Scalable high quality GP (with quality comparable to sequential partitioners) remains an open problem. With the advent of exascale machines with millions of processors and possibly billions of threads, the situation is further aggravated. Traditional “flat” partitions of graphs for processing on such machines implies a huge number of blocks. It is unclear how even sequential partitioners perform for such instances. Resorting to recursive partitioning brings down k and also addresses the hierarchical nature of such machines. However, this means that we need parallel partitioners where the number of available processors is much bigger than k. It is unclear how to do this with high quality. Approaches like the band graphs from PT-Scotch are interesting but likely to fail for complex networks.

Efficient implementation is also a big issue since complex memory hierarchies and heterogeneity (e.g., GPUs or FPGAs) make the implementation complicated. In particular, there is a mismatch between the fine-grained discrete computations predominant in the best sequential graph partitioners and the massive data parallelism (SIMD-instructions, GPUs,...) in high performance computing which better fits highly regular numeric computations. It is therefore likely that high quality GP will only be used for the higher levels of the machine hierarchy, e.g., down to cluster nodes or CPU sockets. At lower levels of the architectural hierarchy, we may use geometric partitioning or even regular grids with dummy values for non-existing cells (e.g. [74]).

While exascale computing is a challenge for high-end applications, many more applications can profit from GP in cloud computing and using tools for high productivity such as Map/Reduce [47], Pregel [139], GraphLab [137], Combinatorial BLAS [30], or Parallel Boost Graph Library [90]. Currently, none of these systems uses sophisticated GP software.

These changes in architecture also imply that we are no longer interested in algorithms with little computations but rather in data access with high locality and good energy efficiency.

Beyond Balanced k-partitioning with Cut Minimization. We have intentionally fixed our basic model assumptions above to demonstrate that even the classical setting has a lot of open problems. However, these assumption become less and less warranted in the context of modern massively parallel hardware and huge graphs with complex structure. For example, it looks like the assumptions that low total cut is highly correlated with low bottleneck cut or communication volume (see Sect. 2.1) is less warranted for complex network [31]. Eventually, we would like a dynamic partition that adapts to the communication requirements of a computation such as PageRank or BFS with changing sets of active nodes and edges. Also, the fixed value for k becomes questionable when we want to tolerate processor failures or achieve “malleable” computations that adapt their resource usage to the overall situation, e.g., to the arrival or departure of high priority jobs. Techniques like overpartitioning, repartitioning (with changed k), and (re)mapping will therefore become more important. Even running time as the bottom-line performance goal might be replaced by energy consumption [199].