Functionals and Synthetic Indicators Over Finite Posets

Abstract

In this paper, we propose an axiomatic theory of real functionals on frequency distributions over finite posets. The theory links the properties of the functionals to the classical theory of quasi-arithmetic means. In particular, it is shown that, given the frequency distribution, the values assumed by any “well-behaved” functional on a poset π can be expressed as a quasi-arithmetic mean of the values assumed over the linear extensions of π. This result plays a central role in view of the construction of synthetic indicators for multidimensional system of ordinal indicators, as shown through an example pertaining to multidimensional bi-polarization.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In this paper, we address the problem of building real functionals on frequency distributions whose domain is a finite poset. The topic may seem very technical, but it is deeply related to relevant open problems in socio-economic statistics. Consider, for example, the measurement of inequality over multidimensional systems of ordinal indicators. This issue, fundamental in a “beyond GDP” perspective, is usually addressed by composing inequality measures over attributes into a single index, through weighted averages. The problem with this approach is that the domain of the joint frequency distribution (i.e., the collection of k-tuples of attribute scores) is considered as an unstructured set, while it is in fact a partially ordered set, whose order relation is the product order of the linear orders corresponding to ordinal attributes. Inequality is conceptually linked to the way achievements are distributed on a “low-high” axis so that the order structure, even if partial, should enter into the computations. Starting from this observation, in this paper we propose a general theory of functionals over finite posets, to provide a sound formal basis for the construction of synthetic indicators in socio-economic sciences. The basic idea of the paper can be introduced as follows. In the classical theory of statistical indices, one is primarily interested in identifying a set of properties assuring the index to capture the concept of interest and to behave in a way that is logically consistent with it. For example, in monetary inequality measurement one requires indices to increase if income is transferred from the “poor” to the “richer.” Statistical indices are then seen as functions of the frequency distribution and their properties are assessed in terms of their behavior under different distribution shapes or transformations. The order structure of the domain of the statistical variables, usually $\mathbb{R}$ or $\mathbb{N}$ with their natural total order relation, does not come into play explicitly, being trivial. But when the domain is multidimensional and different partial order relations can be imposed on it, the role of the order structure becomes essential and one must control for the way indices behave when the frequency distribution is kept fixed, but the partial order relation changes. To pursue this approach, it is natural to look at indices as scalar functions defined on the semilattice of posets sharing the same ground set. Properties of functionals may then be connected to algebraic properties of this “poset of posets,” leading to a simple and coherent axiomatic theory. The paper is organized as follows. Section 2 provides some basic definitions and sets the notation. Section 3 introduces some fundamental results in the theory of means, namely the Nagumo–Kolmogorov theorem on quasi-arithmetic means and their semigroup representation. Section 4 develops the theory of functionals on finite posets. Section 5 discusses some simple examples. Section 6 concludes.

2 Notation and Basic Definitions

A partially ordered set (or a poset) π = (X, ≤ ) is a set X (called the ground set) equipped with a partial order relation ≤ , i.e., with a binary relation satisfying the properties of reflexivity, antisymmetry, and transitivity (Davey and Priestley, 2002; Neggers and Kim, 1998; Schröder, 2002):

• 1. x ≤ x for all x ∈ X (reflexivity);

• 2. if x ≤ y and y ≤ x, then x = y, x, y ∈ X (antisymmetry);

• 3. if x ≤ y and y ≤ z, then x ≤ z, x, y, z ∈ X (transitivity).

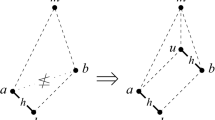
If x ≤ y or y ≤ x, then x and y are called comparable, otherwise they are said incomparable (written x  | |  y). A partial order π where any two elements¹ are comparable is called a linear order or a complete order. A subset of mutually comparable elements of a poset is called a chain. On the contrary, a subset of mutually incomparable elements of a poset is called an antichain. Given x, y ∈ π, y is said to cover x (written x ≺ y) if x ≤ y and there is no other element z ∈ π such that x ≤ z ≤ y. An element x ∈ π such that x ≤ y implies x = y is called maximal; if for each y ∈ π it is y ≤ x, then x is called (the) maximum or (the) greatest element of π. An element x ∈ π such that y ≤ x implies x = y is instead called minimal; if for each y ∈ π it is x ≤ y, then x is called (the) minimum or (the) least element of π. Given x ∈ π, the down-set of x (written ↓​ x) is the set of all the elements y ∈ π such that y ≤ x. Dually, the up-set of x (written ↑​ x) is the set of all the elements y ∈ π such that x ≤ y. Let π be a poset. If for every choice of x, y ∈ π the intersection of the down-sets of x and y has a maximum (written ∧ (x, y) and called the meet of x and y), then π is called a meet-semilattice. Given two partially ordered sets π = (X, ≤  _π ) and τ = (X, ≤  _τ ) on the same set X, we say that τ is an extension of π, if x ≤  _π y in π implies x ≤  _τ y in τ. In other terms, τ is an extension of π if it may be obtained from the latter turning some incomparabilities into comparabilities. An extension of π which is also a complete order is called a linear extension. The set of linear extensions of a poset π is denoted by $\Omega (\pi )$.

We now introduce another mathematical structure which plays a fundamental role in the following discussion. Let π ₀ be a poset on a set X and let $\Pi (\pi _{0})$ be the family of all of the posets over X that are extensions of π ₀. $\Pi (\pi _{0})$ can be turned into a poset (Brualdi et al., 1994) (here called extension poset) defining the partial order  ⊑ as

$$\displaystyle{ \pi _{1} \sqsubseteq \pi _{2} \Leftrightarrow \pi _{2}\ \text{is an extension of }\pi _{1}\text{ }(\pi _{1},\pi _{2} \in \Pi (\pi _{0})). }$$

(1)

Endowed with partial order ⊑ , the extension poset $\Pi (\pi _{0})$ is a meet-semilattice (Brualdi et al., 1994), with meet ∧ given by intersection of order relations; its minimum is π ₀ and its maximal elements are the linear extensions of π ₀.

Example.

Figure 1 depicts the Hasse diagram of a poset π ₀ ^∗ with five elements. The extension poset $\Pi (\pi _{0}^{{\ast}})$ “generated” by π ₀ ^∗ is depicted in Fig. 2. As it can be seen, the linear extensions of π ₀ ^∗ correspond to the maximal elements of $\Pi (\pi _{0}^{{\ast}})$, while its minimum is π ₀ ^∗ itself.

Fig. 1

Hasse diagram of a poset π ₀ ^∗ on five elements

Fig. 2

Extension poset $\Pi (\pi _{0}^{{\ast}})$ of the poset π ₀ ^∗ depicted in Fig. 1 (to improve readability, elements of $\Pi (\pi _{0}^{{\ast}})$ have been inserted into ellipses)

3 Quasi-Arithmetic Means

In this section, we introduce the concept of aggregation system and focus on the so-called quasi-arithmetic means, a kind of functionals² which are characterized by a set of properties crucial for indicators construction. After providing the formal definitions, we give a particular and useful representation of this class of means, drawing on the concept of semigroup. This semigroup representation is important, in view of the axiomatic theory, since it characterizes the behavior of aggregation functionals, when a sequence of nested partial aggregations is performed on their arguments.

3.1 Aggregation Systems

Let $\boldsymbol{x} = (x_{1},\ldots,x_{k})$ be a vector of k real numbers in [0, 1], $\boldsymbol{w} = (w_{1},\ldots,w_{k})$ a vector of k non-negative weights summing to 1, and g(⋅ ) a continuous and strictly monotone real function, from [0, 1] to $\mathbb{R}$, called the generating function. The weighted quasi-arithmetic mean (Beliakov et al., 2007; Grabisch et al., 2009) M _g, k (⋅ ) is defined as:

$$\displaystyle{ M_{g,k}(\boldsymbol{x};\boldsymbol{w}) = g^{-1}\left (\sum _{ i=1}^{k}w_{ i}g(x_{i})\right ) }$$

(2)

where g ⁻¹(⋅ ) is the inverse of function g(⋅ ) which exists and is well-defined from $\mathbb{R}$ to [0, 1], since g(⋅ ) is strictly monotone. Many well-known means belong to the class of quasi-arithmetic means, namely the weighted power means M _[r], k (⋅ ):

$$\displaystyle\begin{array}{rcl} M_{[r],k}(\boldsymbol{x};\boldsymbol{w})& =& \left (\sum _{i=1}^{k}w_{ i}x_{i}^{r}\right )^{1/r}\quad (g(x) = x^{r},\:r\neq 0);{}\end{array}$$

(3)

$$\displaystyle\begin{array}{rcl} M_{[0],k}(\boldsymbol{x};\boldsymbol{w})& =& \prod _{i=1}^{k}x_{ i}^{w_{i} }\quad (g(x) =\log (x)).{}\end{array}$$

(4)

When $\boldsymbol{w} = (1/k,\ldots,1/k)$, the above formulas reduce to “classical” means (called quasi-arithmetic means):

$$\displaystyle\begin{array}{rcl} M_{g,k}(\boldsymbol{x})& =& g^{-1}\left (\frac{1} {k}\sum _{i=1}^{k}g(x_{ i})\right );{}\end{array}$$

(5)

$$\displaystyle\begin{array}{rcl} M_{[r],k}(\boldsymbol{x})& =& \left (\frac{1} {k}\sum _{i=1}^{k}x_{ i}^{r}\right )^{1/r};{}\end{array}$$

(6)

$$\displaystyle\begin{array}{rcl} M_{[0],k}(\boldsymbol{x})& =& \left (\prod _{i=1}^{k}x_{ i}\right )^{\frac{1} {k} }.{}\end{array}$$

(7)

What makes quasi-arithmetic means of particular relevance for our purposes is that they contain the class of continuous, strictly monotone, and decomposable functionals. To be formal, let us call aggregation system a collection $\mathbb{F} =\{ F_{1}(\cdot ),F_{2}(\cdot ),F_{3}(\cdot )\ldots \}$ of functionals with 1, 2, 3… arguments, respectively, with F ₁(x) = x by convention. Then continuity, strict monotonicity, and decomposability for $\mathbb{F}$ are defined as follows:

• 1. Continuity. An aggregation system $\mathbb{F}$ is continuous if each of its elements $F_{k}(\cdot ) \in \mathbb{F}$ is continuous in each of its k arguments (k = 1, 2, …).

• 2. Strict monotonicity. Let $\boldsymbol{x}$ and $\boldsymbol{y}$ be two k-dimensional real vectors; a functional F _k (⋅ ) is strictly monotone if $\boldsymbol{x} <\boldsymbol{ y}$ in the product order over $\mathbb{R}^{k}$ implies $F_{k}(\boldsymbol{x}) < F_{k}(\boldsymbol{y})$. An aggregation system $\mathbb{F}$ is strictly monotone if each of its elements is strictly monotone.

• 3. Decomposability. An aggregation system $\mathbb{F}$ is decomposable if and only if for all m, n = 1, 2, … and for all $\boldsymbol{x} \in [0,1]^{m}$ and $\boldsymbol{y} \in [0,1]^{n}$:

  $$\displaystyle{ F_{m+n}(\boldsymbol{x},\boldsymbol{y}) = F_{m+n}(\mathop{\underbrace{F_{m}(\boldsymbol{x}_{m}),\ldots,F_{m}(\boldsymbol{x}_{m})}}\limits _{m\:\text{times}},\boldsymbol{y}). }$$

  (8)

The last formula requires the value of functional F _m+n (⋅ ) to be obtained substituting to the first m arguments their aggregated value F _m (⋅ ), replicated m times. The statement becomes clearer when specialized to arithmetic means. In this case, it simply states that one can compute the average of m + n numbers substituting to each of the first m the average of the first m numbers themselves.

According to the Nagumo–Kolmogorov theorem (Beliakov et al., 2007), an aggregation system $\mathbb{F} =\{ F_{k}(\cdot )\}$ (k = 1, 2, 3, …) is continuous, strictly monotone, and decomposable if and only if there exists a monotone bijective function g(⋅ ): [0, 1] → [0, 1] such that for k > 1, F _k (⋅ ) is a quasi-arithmetic mean M _g, k (⋅ ). A functional F is homogeneous if, for every real number c ∈ [0, 1], it is $F(c \cdot \boldsymbol{ x}) = c \cdot F(\boldsymbol{x})$; it can be proved that the only homogeneous quasi-arithmetic means are the power means M _[r], k (⋅ ) (see again Beliakov et al. 2007). Finally, notice that quasi-arithmetic means are symmetric, i.e., they are invariant under permutations of their arguments. As a consequence, they satisfy the property of strong decomposability (Grabisch et al., 2009), i.e., they are invariant under the aggregation of any subset of (and not just of consecutive) arguments.

3.2 Semigroup Representation of Quasi-Arithmetic Means

In this paragraph, we show that quasi-arithmetic means can be computed by the repeated application of a binary associative and commutative operation. This will be useful when connecting the properties of functionals to the structure of the extension poset. The presentation follows quite closely (Pursiainen, 2005).

Let $\mathbb{F}$ be an aggregation system. Assume its elements are symmetric (as defined above) and suppose that, if vector $\boldsymbol{x} = (x_{1},\ldots,x_{m})$ is partitioned into k subvectors $\boldsymbol{x}_{(1)},\ldots,\boldsymbol{x}_{(k)}$, of length n ₁, …, n _k , respectively, it holds:

$$\displaystyle{ F_{m}(\boldsymbol{x}) = F_{k}\left (F_{n_{1}}(\boldsymbol{x}_{(1)}),\ldots,F_{n_{k}}(\boldsymbol{x}_{(k)})\right ) }$$

(9)

(i.e., suppose that aggregation can be performed “aggregating partial aggregations”). An aggregation system satisfying (9) will be called consistent in aggregation. An important special case of the above formula is the following:

$$\displaystyle{ F_{m}(x_{1},\ldots,x_{m}) = F_{2}\left (F_{m-1}(x_{1},\ldots,x_{m-1}),x_{m}\right ), }$$

(10)

which means that vector $\boldsymbol{x}$ can be aggregated in “two steps,” the first of which aggregates m − 1 components. Using this formula repeatedly, one can reduce F _m (⋅ ) to a nested sequence of applications of F ₂(⋅ ); for example:

$$\displaystyle{ F_{4}(x_{1},x_{2},x_{3},x_{4}) = F_{2}\left (F_{3}(x_{1},x_{2},x_{3}),x_{4}\right ) = F_{2}\left (F_{2}(F_{2}(x_{1},x_{2}),x_{3}),x_{4}\right ). }$$

(11)

One thus sees that F ₂(⋅ , ⋅ ) determines the entire aggregation system $\mathbb{F}$. Thanks to symmetry, F ₂(x ₁, x ₂) = F(x ₂, x ₁) and also $F_{2}\left (F_{2}(x_{1},x_{2}),x_{3}\right ) = F_{2}\left (x_{1},F_{2}(x_{2},x_{3})\right )$, i.e., F ₂(⋅ , ⋅ ) is commutative and associative. Thus F ₂(⋅ , ⋅ ) is a commutative semigroup operation and $\mathbb{F}$ is a commutative semigroup, generated by F ₂(⋅ , ⋅ ). Denoting F ₂(⋅ , ⋅ ) as ∘_​F , we can write formula (11) in the following clearer way:

$$\displaystyle{ F_{4}(x_{1},x_{2},x_{3},x_{4}) = (x_{1} \circ _{\!F}^{}x_{2}) \circ _{\!F}^{}x_{3}) \circ _{\!F}^{}x_{4} = x_{1} \circ _{\!F}^{}x_{2} \circ _{\!F}^{}x_{3} \circ _{\!F}^{}x_{4}, }$$

(12)

where the second equality comes from associativity of ∘_​F .

For our purposes, what is interesting is that weighted quasi-arithmetic means, and power means in particular, are consistent in aggregation and are generated by a suitable choice of F ₂(⋅ , ⋅ ). To show this, some notation must be introduced first. Let x ₁ and x ₂ be the numbers we want to aggregate, using a weighted quasi-arithmetic mean with weights w ₁ and w ₂. Put $\boldsymbol{x_{1}} = (x_{1},w_{1})$ and $\boldsymbol{x_{2}} = (x_{2},w_{2})$; then the following binary operation ∘_​g generates M _g, k (⋅ ):

$$\displaystyle{ \boldsymbol{x}_{1} \circ _{\!g}^{}\boldsymbol{x}_{2} = \left (g^{-1}\left (\frac{w_{1}g(x_{1}) + w_{2}g(x_{2})} {w_{1} + w_{2}} \right );w_{1} + w_{2}\right ) }$$

(13)

Specializing this formula to g(⋅ ) = id(⋅ ) (identity function) we get the generating operator for the weighted arithmetic mean:

$$\displaystyle{ \boldsymbol{x}_{1} \circ _{\!id}^{}\boldsymbol{x}_{2} = \left (\frac{w_{1}x_{1} + w_{2}x_{2}} {w_{1} + w_{2}};w_{1} + w_{2}\right ). }$$

(14)

Applying recursively this formula to a set of numbers x ₁, …, x _m , starting with w ₁ = w ₂ = 1, gives the simple arithmetic mean (Pursiainen, 2005).

Remark.

Notice that to represent weighted and unweighted quasi-arithmetic means in semigroup terms, it has been necessary to jointly state the update formula for both the values and the weights, so as that each step of the recursion carries over all of the information needed for the next nested application of the semigroup operation.

4 Building Functionals Over Finite Posets

Let us consider a finite poset π ₀ and a distribution $\boldsymbol{p}$ of relative frequencies defined on it. Let $\Pi (\pi _{0})$ be the extension poset generated by π ₀, let $\pi \in \Pi (\pi _{0})$ be an extension of π ₀, and let $F(\pi,\boldsymbol{p})$ be a functional evaluated on the distribution $\boldsymbol{p}$ over π. From a statistical point of view, when π is a linear order λ, $F(\lambda,\boldsymbol{p})$ can be interpreted as a unidimensional index, in that F(⋅ ) applies on a unidimensional poset, which can be seen simply as an ordinal attribute. Properties of $F(\lambda,\boldsymbol{p})$, as the distribution $\boldsymbol{p}$ changes, determine the nature of the functional. We do not address these aspects here, since they pertain to the proper field of the axiomatic theory of univariate statistical indexes. Instead, we focus on the properties of $F(\pi,\boldsymbol{p})$ as the poset π changes in $\Pi (\pi _{0})$, while the distribution $\boldsymbol{p}$ is kept fixed. More specifically, we ask ourselves whether $F(\cdot,\boldsymbol{p})$ can be assigned to elements of $\Pi (\pi _{0})$ “freely,” or whether the algebraic structure of the poset of posets imposes consistency constraints on such assignments. This question has two main motivations. The first is of a formal and technical nature. In order to develop a satisfactory theory of functionals, we need to link their properties to those of the “context” they act upon. Given that here we are dealing with the poset of posets, the only properties that can be considered pertain to extensions and, as it will be seen below, intersections of posets. The second motivation is of an applied nature. In the social sciences, posets may arise from evaluation and comparison processes and may reflect different systems of social values, against which social facts are assessed through some indicators (see, for example, Fattore 2016). In this respect, poset structure is an input to the evaluation process and the behavior of a statistical index as such a structure changes must be taken into account, to assess its effectiveness as a measurement tool. To work out the consistency constraints to be imposed on functionals, some preliminary definitions and technical results must be discussed. They are of a poset theoretical nature and pertain to the properties and the structure of particular subfamilies of elements of the extension poset. The role of the frequency distribution is left aside, until it comes back into play when defining specific statistical indicators, as we do in Sect. 5, in connection to social polarization.

4.1 Non-overlapping Generating Families of Posets

We begin introducing useful ways to represent posets as the intersection of other posets.

Definition.

A collection of posets $\pi _{1},\ldots,\pi _{k} \in \Pi (\pi _{0})$ will be called a generating family for π ₀, if π ₀ = ∧(π ₁, …, π _k ), i.e., if π ₀ = π ₁ ∩ … ∩π _k .

Examples of generating families for poset π ₀ ^∗ of Fig. 1 are reported in Fig. 3.

Fig. 3

Examples of generating families for poset π ₀ ^∗ of Fig. 1

A generating family {π ₁, …, π _k } for π ₀ is called non-overlapping if the sets $\Omega (\pi _{i})$ of linear extensions of its elements are disjoint, i.e., if

$$\displaystyle{ \bigcap _{i=1}^{k}\Omega (\pi _{ i}) =\emptyset }$$

(15)

(for the sake of clarity, we stress that in the above formula, we are not taking the intersection of different linear extensions, but of different families of linear extensions, i.e., we are imposing to these families to have no linear extension in common). A generating family is called complete if the union of the sets of linear extensions of its elements equals the set of linear extensions of π ₀, i.e., if:

$$\displaystyle{ \bigcup _{i=1}^{k}\Omega (\pi _{ i}) = \Omega (\pi _{0}). }$$

(16)

Definition.

A generating family which satisfies both condition (15) and condition (16) is called a non-overlapping complete (NOC) generating family for π ₀.

Given a poset π ₀, at least one NOC generating family exists, namely the set $\Omega (\pi _{0}^{})$ of its linear extensions. Other examples of NOC generating families for poset π ₀ ^∗ of Fig. 1 are reported in Fig. 3 (panels A, B and C). NOC generating families have some simple but relevant properties, summarized in the following proposition:

Proposition.

Let G = {π ₁, …, π _k } be an NOC generating family for π ₀. (A) Sets $\Omega (\pi _{1}),\ldots,\Omega (\pi _{k})$ provide a partition of $\Omega (\pi _{0}^{})$. (B) For a fixed index h (1 ≤ h ≤ k), let $G_{h}^{} =\{\pi _{ h_{1}}^{},\ldots,\pi _{h_{s}}^{}\}$ be an NOC generating family for π _h ; then G∖{π _h } ∪ G _h is an NOC generating family for π ₀.

Proof.

(A) This is just a restatement of (15) and (16). (B) That G∖{π _h } ∪ G _h is a generating family for π ₀ is evident. Since G and G _h are NOC families, the collection $\{\Omega (\pi _{i}^{})\}$ (π _i  ∈ G) is a partition of $\Omega$ and $\{\Omega (\pi _{j}^{})\}$ (π _j  ∈ G _h ) is a partition of $\Omega (\pi _{h}^{})$. Consequently, $\bigcup _{\pi \in G\setminus \pi _{h}\cup G_{h}}\Omega (\pi )$ is a partition of $\Omega (\pi _{0}^{})$. Thus G∖{π _h } ∪ G _h is an NOC generating family for π ₀.

q.e.d.

In practice, property (B) states that if an element of an NOC generating family for π ₀ is substituted by one among its own NOC generating families, the resulting collection of posets is again an NOC generating family for π ₀.

4.2 Axiomatic Properties of Functionals on $\Pi (\pi _{0})$

In this paragraph, we specify the properties we want functionals on posets to satisfy, in order to provide useful aggregation tools for statistical indicator construction. At the heart of the axiomatic system, there is the consistency between the behavior of functionals and the nested structure of NOC generating families, that will lead to quasi-arithmetic means.

Let $\varphi (\pi _{0}^{},\boldsymbol{p})$ be a functional (e.g., a statistical index) over a distribution $\boldsymbol{p}$ of relative frequencies defined on a poset π ₀ (since here we are interested in the behavior of $\varphi (\pi _{0}^{},\boldsymbol{p})$ as the poset changes, $\boldsymbol{p}$ being fixed, we drop the second argument and write simply φ(π ₀); this should not produce any confusion). Since π ₀ may be reconstructed from its generating families, it is natural to assume φ(π ₀) to be expressible as a function of the values of φ(⋅ ) on the elements of such families. In other words, once φ(⋅ ) is assigned on a generating family for π ₀, its value on π ₀ itself should be univocally given. Formulated this way, however, this statement is not really useful. To see why, consider again Fig. 2 and notice that {π ₉ ^∗, π ₁₃ ^∗}, {π ₁₀ ^∗. π ₁₂ ^∗}, and {π ₉ ^∗, π ₁₀ ^∗, π ₁₂ ^∗. π ₁₃ ^∗} are generating families for π ₀ ^∗; thus, two functions F ₂(⋅ ) and F ₄(⋅ ) (subscripts stand for the number of arguments) should exist such that one could equivalently write:

$$\displaystyle\begin{array}{rcl} \varphi (\pi _{0}^{{\ast}})& =& F_{ 2}(\varphi (\pi _{9}^{{\ast}}),\varphi (\pi _{ 13}^{{\ast}})) \\ \varphi (\pi _{0}^{{\ast}})& =& F_{ 4}(\varphi (\pi _{9}^{{\ast}}),\varphi (\pi _{ 10}^{{\ast}}),\varphi (\pi _{ 12}^{{\ast}}),\varphi (\pi _{ 13}^{{\ast}})) \\ \varphi (\pi _{0}^{{\ast}})& =& F_{ 2}(\varphi (\pi _{10}^{{\ast}}),\varphi (\pi _{ 12}^{{\ast}})). {}\end{array}$$

(17)

As a consequence

$$\displaystyle{ F_{2}(\varphi (\pi _{9}^{{\ast}}),\varphi (\pi _{ 13}^{{\ast}})) = F_{ 4}(\varphi (\pi _{9}^{{\ast}}),\varphi (\pi _{ 10}^{{\ast}}),\varphi (\pi _{ 12}^{{\ast}}),\varphi (\pi _{ 13}^{{\ast}})) = F_{ 2}(\varphi (\pi _{10}^{{\ast}}),\varphi (\pi _{ 12}^{{\ast}})) }$$

(18)

so that, on the one hand, F ₄(⋅ ) should be independent of φ(π ₁₀ ^∗) and φ(π ₁₂ ^∗) (first equality) and, on the other hand, it should be independent of φ(π ₉ ^∗) and φ(π ₁₃ ^∗) (second equality). In practice, F ₄(⋅ ) and F ₂(⋅ ) should be constant functions, leading to a trivial theory. These problems arise since any subset of $\Pi (\pi _{0})$ comprising a generating family is a generating family itself. To overcome them, we still require φ(π ₀) to be a function of the values of φ(⋅ ) on other posets, but restricting them to elements of NOC generating families for π ₀. Formally, given two NOC families {π ₁, …, π _k } and {τ ₁, …, τ _m }, we require that an aggregation family $\mathbb{F}$ exists such that:

$$\displaystyle{ \varphi (\pi _{0}^{}) = F_{k}(\varphi (\pi _{1}),\ldots,\varphi (\pi _{k})) = F_{m}(\varphi (\tau _{1}),\ldots,\varphi (\tau _{m})) }$$

(19)

where $F_{k}(\cdot ),F_{m}(\cdot ) \in \mathbb{F}$. This invariance property has two main consequences:

• 1. φ(π ₀) can be computed as a function of the values of φ(⋅ ) on the linear extensions of π ₀. In fact, $\Omega (\pi _{0}^{})$ is an NOC family and thus one can set:

  $$\displaystyle{ \varphi (\pi _{0}^{}) = F_{\omega }(\varphi (\lambda _{1}),\ldots,\varphi (\lambda _{\omega })) }$$

  (20)

  where λ ₁, …, λ _ω are the linear extensions of π ₀.

• 2. F _k (⋅ ) behaves in a consistent way, when an element of an NOC family is replaced by one of its NOC families. To see this, suppose {π ₁, π ₂} is an NOC family for π ₀ and let {τ ₁, …, τ _m } be an NOC family for π ₁. Since then {τ ₁, …, τ _m , π ₂} is an NOC family for π ₀, the “invariance” principle requires that:

  $$\displaystyle{ \varphi (\pi _{0}^{}) = F_{2}(\varphi (\pi _{1}),\varphi (\pi _{2})) = F_{m+1}(\varphi (\tau _{1}),\ldots,\varphi (\tau _{m}),\varphi (\pi _{2})). }$$

  (21)

  Similarly, it must be

  $$\displaystyle{ \varphi (\pi _{1}) = F_{m}(\varphi (\tau _{1}),\ldots,\varphi (\tau _{m})) }$$

  (22)

  so that

  $$\displaystyle{ \varphi (\pi _{0}) = F_{2}(F_{m}(\varphi (\tau _{1}),\ldots,\varphi (\tau _{m})),\varphi (\pi _{2})). }$$

  (23)

  The above equalities lead to

  $$\displaystyle{ F_{2}(F_{m}(\varphi (\tau _{1}),\ldots,\varphi (\tau _{s})),\varphi (\pi _{2})) = F_{m+1}(\varphi (\tau _{1}),\ldots,\varphi (\tau _{s}),\varphi (\pi _{2})) }$$

  (24)

  which is essentially a “consistency in aggregation” requirement on nested NOC generating families.

The first property links functionals over general finite posets to functionals over the simplest kind of posets, i.e., linear orders [so justifying the use of the concept of linear extensions in many theoretical and applied studies (see, for example, Bruggemann and Annoni 2014 and Fattore 2016)]. The second property resembles formula (10), which expresses the semigroup nature of consistent-in-aggregation functionals.

In addition to the above properties, we require the aggregation system $\mathbb{F}$ to be continuous and monotone (see Sect. 3). The first is a technical, but natural, requirement; the second is a natural condition too, in view of application to statistical indicator construction: suppose that the value of the statistical indicator of interest grows on each linear extension of π ₀ (for example, since the underlying frequency distribution changes in a specific way), then we want it to increase on π ₀ as well. According to the discussion of Sect. 3, the most natural candidate aggregation system for frequency distributions on finite posets is thus the class of quasi-arithmetic means. Since in applications to statistical indicators it is also customary to impose homogeneity to aggregation functions, we finally restrict the class of functionals to power means.

According to the semigroup representation of quasi-arithmetic means (and hence of power means), it is easy to state how to compute F(π ₀), given an NOC generating family. To be simple, let {π ₁, π ₂} be an NOC family and let $\Omega _{1} = \Omega (\pi _{1})$ and $\Omega _{2} = \Omega (\pi _{2})$ be the corresponding sets of linear extensions. Since {π ₁, π ₂} is an NOC family, it is $\Omega _{1} \cap \Omega _{2} =\emptyset$ and $\Omega = \Omega (\pi _{0}^{}) = \Omega _{1} \cup \Omega _{2}$. Then φ(π ₀) is simply the power mean of φ(π ₁) and φ(π ₂), with weights given by the relative cardinality of $\Omega _{1}$ and $\Omega _{2}$:

$$\displaystyle{ \varphi (\pi _{0}) = M_{[2];w}\left (\varphi (\pi _{1}),\varphi (\pi _{2});\left (\frac{\vert \Omega _{1}\vert } {\vert \Omega \vert }, \frac{\vert \Omega _{2}\vert } {\vert \Omega \vert }\right )\right ). }$$

(25)

This formula can be directly extended to NOC families with more than two elements. In particular, for the NOC family composed of the linear extensions of π ₀, it reduces to a non-weighted power mean of the values of the functional φ(⋅ ) on the linear extensions themselves.

Final remark.

The above discussion may be informally summarized as follows: to be consistent with the meet-semilattice structure of the extension poset, functionals over $\Pi (\pi _{0})$ are required to be invariant and consistent in aggregation with respect to NOC families. As a consequence, once functionals are assigned to maximal elements of $\Pi (\pi _{0})$ (i.e., to the linear extensions of π ₀), they can be extended to any poset in $\Pi (\pi _{0})$, through a power mean M _[k], w (⋅ ). The axiomatic theory cannot impose any constraint on the properties of functionals on linear extensions (in view of statistical indicators construction, these “intrinsic” properties depend upon the nature of the univariate index corresponding to the functional and upon the way it “reacts” to changes in the frequency distribution). It can only give prescriptions on the “structural” properties of the aggregation system $\mathbb{F}$, for the extension process to be consistent with the algebraic structure of $\Pi (\pi _{0})$.³

5 Application to Synthetic Index Construction: An Example

For exemplificative purposes, in this section, we apply the extension procedure to the construction of bi-polarization⁴ indices (Wolfson, 1994) on $\Pi (\pi _{0}^{{\ast}})$ (see Fig. 2) for different frequency distributions. We must first introduce a univariate bi-polarization index, to “start” the process. Let $\boldsymbol{p} = (p_{a_{1}}^{},\ldots,p_{a_{m}}^{})$ be a distribution of relative frequencies on a linear order a ₁ < a ₂ < ⋯ < a _m . The following functional (Berry and Mielke, 1992):

$$\displaystyle{ L(\boldsymbol{p}_{i}^{}) = \frac{2} {m - 1}\sum _{i=1}^{m}\sum _{ j=1}^{m}p_{ a_{i}}^{}p_{a_{j}}^{}\vert r(a_{i}) - r(a_{j})\vert }$$

(26)

(where r(x) stands for the rank⁵ of x) is called the Leti index (Leti, 1983) and can be interpreted as a normalized measure of bi-polarization on ordinal attributes. We consider six different frequency distributions on π ₀ ^∗, to analyze the behavior of the functionals in different cases. As often in statistics, here we aggregate through arithmetic means. Frequency distributions are reported in Table 1. We denote by $L(\pi _{j}^{{\ast}},\boldsymbol{p^{}}_{i})$, where i = 1, …, 6, j = 0, …, 13, the Leti functional “extended” to poset π _j ^∗ and computed on the frequency distribution $\boldsymbol{p}_{i}$, i.e., the functional on poset π _j ^∗ derived by $L(\boldsymbol{p^{}}_{i})$. Formally:

$$\displaystyle{ L(\pi _{j}^{{\ast}},\boldsymbol{p^{}}_{ i}) = \frac{1} {\vert \Omega (\pi _{j}^{{\ast}})\vert }\sum _{\lambda \in \Omega (\pi _{j}^{{\ast}})}L(\lambda,\boldsymbol{p^{}}_{i}) }$$

(27)

where $L(\lambda,\boldsymbol{p^{}}_{i})$ is the unidimensional Leti index defined in (26), specialized to the linear order corresponding to linear extension λ. Table 2 reports the values of the extended Leti functionals in the various cases. Reading the table by rows, one can see how inequality changes as poset structure changes, while the frequency distribution is kept fixed; reading it by columns, one sees how the index changes when the frequency distribution changes on the same poset. Values associated with the various posets satisfy the consistency-in-aggregation constraint. To help grasping this, Figs. 4 and 5 report “symbolically” the computation of the extended Leti index on π ₀ ^∗, for different NOC families (shaded Hasse diagrams stand for the evaluation of the Leti index on the corresponding poset, i.e., they represent scalars).

Fig. 4

Evaluation of the extended Leti index, for a generic frequency distribution, based on the NOC family of the linear extensions

Fig. 5

Evaluation of the extended Leti index, for a generic frequency distribution, based on the NOC families reported in Fig. 3

Table 1 Frequency distributions over the poset π ₀ ^∗ depicted in Fig. 1

Table 2 Extended Leti functionals over $\Pi (\pi _{0}^{{\ast}})$ for the six distributions of Table 1

6 Conclusion

In this paper, we have developed an axiomatic theory of continuous, monotone, and consistent-in-aggregation functionals on frequency distributions defined on finite posets, as a step towards a general theory for the construction of synthetic indicators over multidimensional systems of ordinal attributes. In concrete applications to socio-economic measurement, the formal setting outlined before must be integrated with the axiomatics of specific classes of indicators, since what specifies a particular functional as an inequality, a polarization, or a variability index (to make a few examples) lays outside the general theory here proposed. This, in fact, may be seen as a “trick” to extend to partially ordered sets univariate indicators, i.e., indicators defined on linear orders. This “device” has been exemplified in the case of the Leti bi-polarization index, but it may be applied to any kind of indicator and may be seen as a general procedure to produce well-behaved “multidimensional versions” of univariate indices. The advantage of this approach over classical attempts to get multidimensional generalizations of univariate measures is that the axiomatic setting is neat and general and does not involve any attempt to generalize “core” axioms, which are “context specific.” A prototypical example of this situation concerns again the measurement of bi-polarization. While it is clear how to (partially) order univariate distributions in terms of bi-polarization (Allison-Foster criterion), it is not clear how to do this neatly in the multidimensional case. Correspondingly, while an axiom of “monotonicity” can be easily and unambiguously stated for univariate polarization indices, the same is not true for the corresponding multidimensional versions. These problems are circumvented when one imposes the index to behave consistently under changes in the order structure of the domain of the frequency distributions. The resulting multidimensional index is coherent as a bi-polarization index since (1) on linear orders it behaves as expected and (2) on multidimensional posets it behaves consistently with changes of the partial order structure. As usual when dealing with finite posets, computations may be difficult due to the huge number of linear extensions. The problem is well known and can be addressed using sampling procedures (Bubley and Dyer, 1999) to estimate the values of statistical indicators, rather than to compute them exactly. However, the primary interest of the paper is of a theoretical kind, so we have not considered this issue here.