Abstract
We prove the Garden of Eden theorem for cellular automata with finite set of states and finite neighbourhood on right amenable left homogeneous spaces with finite stabilisers. It states that the global transition function of such an automaton is surjective if and only if it is pre-injective. Pre-Injectivity means that two global configurations that differ at most on a finite subset and have the same image under the global transition function must be identical.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
The notion of amenability for groups was introduced by John von Neumann in 1929. It generalises the notion of finiteness. A group G is left or right amenable if there is a finitely additive probability measure on \(\mathcal {P}(G)\) that is invariant under left and right multiplication respectively. Groups are left amenable if and only if they are right amenable. A group is amenable if it is left or right amenable.
The definitions of left and right amenability generalise to left and right group sets respectively. A left group set \({(M, G, \triangleright )}\) is left amenable if there is a finitely additive probability measure on \(\mathcal {P}(M)\) that is invariant under \(\triangleright \). There is in general no natural action on the right that is to a left group action what right multiplication is to left group multiplication. Therefore, for a left group set there is no natural notion of right amenability.
A transitive left group action \(\triangleright \) of G on M induces, for each element \(m_0 \in M\) and each family \(\{g_{m_0, m}\}_{m \in M}\) of elements in G such that, for each point \(m \in M\), we have \(g_{m_0, m} \triangleright m_0 = m\), a right quotient set semi-action  of \(G \slash G_0\) on M with defect \(G_0\) given by
of \(G \slash G_0\) on M with defect \(G_0\) given by  , where \(G_0\) is the stabiliser of \(m_0\) under \(\triangleright \). Each of these right semi-actions is to the left group action what right multiplication is to left group multiplication. They occur in the definition of global transition functions of cellular automata over left homogeneous spaces as defined in [5]. A cell space is a left group set together with choices of \(m_0\) and \(\{g_{m_0, m}\}_{m \in M}\).
, where \(G_0\) is the stabiliser of \(m_0\) under \(\triangleright \). Each of these right semi-actions is to the left group action what right multiplication is to left group multiplication. They occur in the definition of global transition functions of cellular automata over left homogeneous spaces as defined in [5]. A cell space is a left group set together with choices of \(m_0\) and \(\{g_{m_0, m}\}_{m \in M}\).
A cell space \(\mathcal {R}\) is right amenable if there is a finitely additive probability measure on \(\mathcal {P}(M)\) that is semi-invariant under  . For example cell spaces with finite sets of cells, abelian groups, and finitely right generated cell spaces of sub-exponential growth are right amenable, in particular, quotients of finitely generated groups of sub-exponential growth by finite subgroups acted on by left multiplication. A net of non-empty and finite subsets of M is a right Følner net if, broadly speaking, these subsets are asymptotically invariant under
. For example cell spaces with finite sets of cells, abelian groups, and finitely right generated cell spaces of sub-exponential growth are right amenable, in particular, quotients of finitely generated groups of sub-exponential growth by finite subgroups acted on by left multiplication. A net of non-empty and finite subsets of M is a right Følner net if, broadly speaking, these subsets are asymptotically invariant under  . A finite subset E of \(G \slash G_0\) and two partitions \(\{A_e\}_{e \in E}\) and \(\{B_e\}_{e \in E}\) of M constitute a right paradoxical decomposition if the map
. A finite subset E of \(G \slash G_0\) and two partitions \(\{A_e\}_{e \in E}\) and \(\{B_e\}_{e \in E}\) of M constitute a right paradoxical decomposition if the map  is injective on \(A_e\) and \(B_e\), and the family
is injective on \(A_e\) and \(B_e\), and the family  is a partition of M. The Tarski-Følner theorem states that right amenability, the existence of right Følner nets, and the non-existence of right paradoxical decompositions are equivalent. We prove it in [6] for cell spaces with finite stabilisers.
is a partition of M. The Tarski-Følner theorem states that right amenability, the existence of right Følner nets, and the non-existence of right paradoxical decompositions are equivalent. We prove it in [6] for cell spaces with finite stabilisers.
For a right amenable cell space with finite stabilisers we may choose a right Følner net \(\mathcal {F} = \{F_i\}_{i \in I}\). The entropy of a subset X of \(Q^M\) with respect to \(\mathcal {F}\), where Q is a finite set, is, broadly speaking, the asymptotic growth rate of the number of finite patterns with domain \(F_i\) that occur in X. For subsets E and \(E'\) of \(G \slash G_0\), an \((E, E')\)-tiling is a subset T of M such that  is pairwise disjoint and
is pairwise disjoint and  is a cover of M. If for each point \(t \in T\) not all patterns with domain
is a cover of M. If for each point \(t \in T\) not all patterns with domain  occur in a subset of \(Q^M\), then that subset does not have maximal entropy.
occur in a subset of \(Q^M\), then that subset does not have maximal entropy.
The global transition function of a cellular automaton with finite set of states and finite neighbourhood over a right amenable cell space with finite stabilisers, as introduced in [5], is surjective if and only if its image has maximal entropy and it is pre-injective if and only if its image has maximal entropy. This establishes the Garden of Eden theorem, which states that a global transition function as above is surjective if and only if it is pre-injective. This answers a question posed by Sébastien Moriceau at the end of his paper ‘Cellular Automata on a G-Set’ [4].
The Garden of Eden theorem for cellular automata over \({\mathbb {Z}}^2\) is a famous theorem by Edward Forrest Moore and John R. Myhill from 1962 and 1963, see the papers ‘Machine models of self-reproduction’ [2] and ‘The converse of Moore’s Garden-of-Eden theorem’ [3]. This paper is greatly inspired by the monograph ‘Cellular Automata and Groups’ [1] by Tullio Ceccherini-Silberstein and Michel Coornaert.
In Sect. 1 we introduce E-interiors, E-closures, and E-boundaries of subsets of M. In Sect. 2 we introduce \((E, E')\)-tilings of cell spaces. In Sect. 3 we introduce entropies of subsets of \(Q^M\). And in Sect. 4 we prove the Garden of Eden theorem.
Preliminary Notions. A left group set is a triple \((M, G, \triangleright )\), where M is a set, G is a group, and \(\triangleright \) is a map from \(G \times M\) to M, called left group action of G on M, such that \(G \rightarrow \mathrm{Sym}(M)\), \(g \mapsto [g \triangleright \mathord {\_}]\), is a group homomorphism. The action \(\triangleright \) is transitive if M is non-empty and for each \(m \in M\) the map \(\mathord {\_}\triangleright m\) is surjective; and free if for each \(m \in M\) the map \(\mathord {\_}\triangleright m\) is injective. For each \(m \in M\), the set \(G \triangleright m\) is the orbit of m, the set \(G_m = (\mathord {\_}\triangleright m)^{-1}(m)\) is the stabiliser of m, and, for each \(m' \in M\), the set \(G_{m, m'} = (\mathord {\_}\triangleright m)^{-1}(m')\) is the transporter of m to \(m'\).
A left homogeneous space is a left group set \(\mathcal {M} = (M, G, \triangleright )\) such that \(\triangleright \) is transitive. A coordinate system for \(\mathcal {M}\) is a tuple \(\mathcal {K} = (m_0, \{g_{m_0, m}\}_{m \in M})\), where \(m_0 \in M\) and for each \(m \in M\) we have \(g_{m_0, m} \triangleright m_0 = m\). The stabiliser \(G_{m_0}\) is denoted by \(G_0\). The tuple \(\mathcal {R} = (\mathcal {M}, \mathcal {K})\) is a cell space. The set \(\{g G_0 \mid g \in G\}\) of left cosets of \(G_0\) in G is denoted by \(G \slash G_0\). The map  , \((m, g G_0) \mapsto g_{m_0, m} g g_{m_0, m}^{-1} \triangleright m\ (= g_{m_0, m} g \triangleright m_0)\) is a right semi-action of \(G \slash G_0\) on M with defect \(G_0\), which means that
, \((m, g G_0) \mapsto g_{m_0, m} g g_{m_0, m}^{-1} \triangleright m\ (= g_{m_0, m} g \triangleright m_0)\) is a right semi-action of \(G \slash G_0\) on M with defect \(G_0\), which means that

It is transitive, which means that the set M is non-empty and for each \(m \in M\) the map  is surjective; and free, which means that for each \(m \in M\) the map
is surjective; and free, which means that for each \(m \in M\) the map  is injective; and semi-commutes with \(\triangleright \), which means that
is injective; and semi-commutes with \(\triangleright \), which means that

The maps \(\iota :M \rightarrow G \slash G_0\), \(m \mapsto G_{m_0, m}\), and  are inverse to each other. Under the identification of M with \(G \slash G_0\) by either of these maps, we have
are inverse to each other. Under the identification of M with \(G \slash G_0\) by either of these maps, we have  .
.
A left homogeneous space \(\mathcal {M}\) is right amenable if there is coordinate system \(\mathcal {K}\) for \(\mathcal {M}\) and there is a finitely additive probability measure \(\mu \) on M such that

in which case the cell space \(\mathcal {R} = (\mathcal {M}, \mathcal {K})\) is called right amenable. When the stabiliser \(G_0\) is finite, that is the case if and only if there is a right Følner net in \(\mathcal {R}\) indexed by \((I, \le )\), which is a net \(\{F_i\}_{i \in I}\) in \(\{F \subseteq M \mid F \ne \emptyset , F \text { finite}\}\) such that

A semi-cellular automaton is a quadruple \(\mathcal {C} = (\mathcal {R}, Q, N, \delta )\), where \(\mathcal {R}\) is a cell space; Q, called set of states, is a set; N, called neighbourhood, is a subset of \(G \slash G_0\) such that \(G_0 \cdot N \subseteq N\); and \(\delta \), called local transition function, is a map from \(Q^N\) to Q. A local configuration is a map \(\ell \in Q^N\), a global configuration is a map \(c \in Q^M\), and a pattern is a map \(p \in Q^A\), where A is a subset of M. The stabiliser \(G_0\) acts on \(Q^N\) on the left by \(\bullet :G_0 \times Q^N \rightarrow Q^N\), \((g_0, \ell ) \mapsto [n \mapsto \ell (g_0^{-1} \cdot n)]\), and the group G acts on the set of patterns on the left by

The global transition function of \(\mathcal {C}\) is the map \(\varDelta :Q^M \rightarrow Q^M\),  .
.
A cellular automaton is a semi-cellular automaton \(\mathcal {C} = (\mathcal {R}, Q, N, \delta )\) such that \(\delta \) is \(\bullet \) -invariant, which means that, for each \(g_0 \in G_0\), we have \(\delta (g_0 \bullet \mathord {\_}) = \delta (\mathord {\_})\). Its global transition function is  -equivariant, which means that, for each \(g \in G\), we have
-equivariant, which means that, for each \(g \in G\), we have  .
.
For each \(A \subseteq M\), let \(\pi _A :Q^M \rightarrow Q^A\),  .
.
1 Interiors, Closures, and Boundaries
In this section, let \(\mathcal {R} = ((M, G, \triangleright ), (m_0, \{g_{m_0, m}\}_{m \in M}))\) be a cell space.
In Definition 1 we introduce E-interiors, E-closures, and E-boundaries of subsets of M. In Lemma 3 we define surjective restrictions \(\varDelta _{X, A}^-\) of global transition functions to patterns. And in Theorem 1 we show that right Følner nets are those nets whose components are asymptotically invariant under taking finite boundaries.
Definition 1
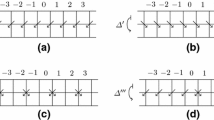
Let A be a subset of M and let E be a subset of \(G \slash G_0\).
-
1.
The set
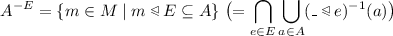
is called E -interior of A.
-
2.
The set
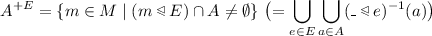
is called E -closure of A.
-
3.
The set
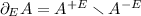 is called E -boundary of A.
is called E -boundary of A.
Remark 1
Let \(\mathcal {R}\) be the cell space \(((G, G, \cdot ), (e_G, \{g\}_{g \in G}))\), where G is a group and \(e_G\) is its neutral element. Then, \(G_0 = \{e_G\}\) and  . Hence, the notions of E-interior, E-closure, and E-boundary are the same as the ones defined in [1, Sect. 5.4, Paragraph 2].
. Hence, the notions of E-interior, E-closure, and E-boundary are the same as the ones defined in [1, Sect. 5.4, Paragraph 2].
Example 1
Let M be the Euclidean unit 2-sphere, that is, the surface of the ball of radius 1 in 3-dimensional Euclidean space, and let G be the rotation group. The group G acts transitively but not freely on M on the left by \(\triangleright \) by function application, that is, by rotation about the origin. For each point \(m \in M\), its orbit is M and its stabiliser is the group of rotations about the line through the origin and itself.
Furthermore, let \(m_0\) be the north pole \((0,0,1)^\intercal \) of M and, for each point \(m \in M\), let \(g_{m_0, m}\) be a rotation about an axis in the (x, y)-plane that rotates \(m_0\) to m. The stabiliser \(G_0\) of the north pole \(m_0\) under \(\triangleright \) is the group of rotations about the z-axis. An element \(g G_0 \in G \slash G_0\) semi-acts on a point m on the right by the induced semi-action  by first changing the rotation axis of g such that the new axis stands to the line through the origin and m as the old one stood to the line through the origin and \(m_0\), \(g_{m_0, m} g g_{m_0, m}^{-1}\), and secondly rotating m as prescribed by this new rotation.
by first changing the rotation axis of g such that the new axis stands to the line through the origin and m as the old one stood to the line through the origin and \(m_0\), \(g_{m_0, m} g g_{m_0, m}^{-1}\), and secondly rotating m as prescribed by this new rotation.
Moreover, let A be a curved circular disk of radius \(3 \rho \) with the north pole \(m_0\) at its centre, let g be the rotation about an axis a in the (x, y)-plane by \(\rho \) radians, let E be the set \(\{g_0 g G_0 \mid g_0 \in G_0\}\), and, for each point \(m \in M\), let \(E_m\) be the set  . Because \(G_0\) is the set of rotations about the z-axis and
. Because \(G_0\) is the set of rotations about the z-axis and  , the set \(E_{m_0}\) is the boundary of a curved circular disk of radius \(\rho \) with the north pole \(m_0\) at its centre. And, for each point \(m \in M\), because
, the set \(E_{m_0}\) is the boundary of a curved circular disk of radius \(\rho \) with the north pole \(m_0\) at its centre. And, for each point \(m \in M\), because  , the set \(E_m\) is the boundary of a curved circular disk of radius \(\rho \) with m at its centre.
, the set \(E_m\) is the boundary of a curved circular disk of radius \(\rho \) with m at its centre.
The E-interior of A is the curved circular disk of radius \(2 \rho \) with the north pole \(m_0\) at its centre. The E-closure of A is the curved circular disk of radius \(4 \rho \) with the north pole \(m_0\) at its centre. And the E-boundary of A is the annulus bounded by the boundaries of the E-interior and the E-closure of A.
Essential properties of and relations between interiors, closures, and boundaries are given in the next lemma. The upper bound given in its corollary follows from the last part of Item 7.
Lemma 1
Let A be a subset of M, let \(\{A_i\}_{i \in I}\) be a family of subsets of M, let e be an element of \(G \slash G_0\), and let E and \(E'\) be two subsets of \(G \slash G_0\).
-
1.
\(A^{-\{G_0\}} = A\), \(A^{+\{G_0\}} = A\), and \(\partial _{\{G_0\}} A = \emptyset \).
-
2.
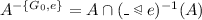 ,
, 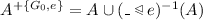 , and
, and  .
. -
3.
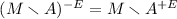 and
and 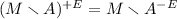 .
. -
4.
Let \(E \subseteq E'\). Then, \(A^{-E} \supseteq A^{-E'}\), \(A^{+E} \subseteq A^{+E'}\), and \(\partial _E A \subseteq \partial _{E'} A\).
-
5.
Let \(G_0 \in E\). Then, \(A^{-E} \subseteq A \subseteq A^{+E}\).
-
6.
Let \(G_0 \in E\) and let A be finite. Then, \(A^{-E}\) is finite.
-
7.
Let \(G_0\), A, and E be finite. Then, \(A^{+E}\) and \(\partial _E A\) are finite. More precisely, \(\vert A^{+E}\vert \le \vert G_0\vert \cdot \vert A\vert \cdot \vert E\vert \).
-
8.
Let \(g \in G\) and let \(G_0 \cdot E \subseteq E\). Then, \(g \triangleright A^{-E} = (g \triangleright A)^{-E}\), \(g \triangleright A^{+E} = (g \triangleright A)^{+E}\), and \(g \triangleright \partial _E A = \partial _E (g \triangleright A)\).
-
9.
Let \(m \in M\), let \(G_0 \cdot E \subseteq E\), and let \(\iota :M \rightarrow G \slash G_0\), \(m \mapsto G_{m_0, m}\). Then,
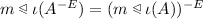 ,
, 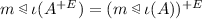 , and
, and 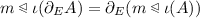 .
.
Corollary 1
Let \(G_0\) be finite, let A be a finite subset of M, and let \(\mathfrak {g}\) be an element of \(G \slash G_0\). Then,  .
.
The restriction \(\varDelta _{X, A}^-\) of \(\varDelta \) given in Lemma 3 is well-defined according to the next lemma, which itself holds due to the locality of \(\varDelta \).
Lemma 2
Let \(\mathcal {C} = (\mathcal {R}, Q, N, \delta )\) be a semi-cellular automaton, let \(\varDelta \) be the global transition function of \(\mathcal {C}\), let c and \(c'\) be two global configurations of \(\mathcal {C}\), and let A be a subset of M. If  , then
, then  .
.
Lemma 3
Let \(\mathcal {C} = (\mathcal {R}, Q, N, \delta )\) be a semi-cellular automaton, let \(\varDelta \) be the global transition function of \(\mathcal {C}\), let X be a subset of \(Q^M\), and let A be a subset of M. The map

is surjective. The map \(\varDelta _{Q^M, A}^-\) is denoted by \(\varDelta _A^-\).
In the proof of Theorem 1, the upper bound given in Lemma 6 is essential, which itself follows from the upper bound given in Corollary 1 and the inclusion given in Lemma 5, which in turn follows from the equality given in Lemma 4.
Lemma 4
Let m be an element of M, and let \(\mathfrak {g}\) be an element of \(G \slash G_0\). There is an element \(g \in \mathfrak {g}\) such that

in particular, for said \(g \in \mathfrak {g}\), we have  .
.
Lemma 5
Let A and \(A'\) be two subsets of M, and let \(\mathfrak {g}\) and \(\mathfrak {g}'\) be two elements of \(G \slash G_0\). Then, for each element  ,
,

Lemma 6
Let \(G_0\) be finite, let F and \(F'\) be two finite subsets of M, and let \(\mathfrak {g}\) and \(\mathfrak {g}'\) be two elements of \(G \slash G_0\). Then,

Theorem 1
Let \(G_0\) be finite and let \(\{F_i\}_{i \in I}\) be a net in \(\{F \subseteq M \mid F \ne \emptyset , F \,{ finite}\}\) indexed by \((I, \le )\). The net \(\{F_i\}_{i \in I}\) is a right Følner net in \(\mathcal {R}\) if and only if
Proof
First, let \(\{F_i\}_{i \in I}\) be a right Følner net in \(\mathcal {R}\). Furthermore, let \(E \subseteq G \slash G_0\) be finite. Moreover, let \(i \in I\). For each \(e \in E\) and each \(e' \in E\), put  . For each \(\mathfrak {g} \in G \slash G_0\), put
. For each \(\mathfrak {g} \in G \slash G_0\), put  . According to Definition 1,
. According to Definition 1,

Hence, \(\vert \partial _E F_i\vert \le \sum _{e, e' \in E} \vert A_{i,e,e'}\vert \).
According to Lemma 6, we have \(\vert A_{i,e,e'}\vert \le \vert G_0\vert ^2 \cdot \max _{g \in e} B_{i, g^{-1} \cdot e'}\). Put \(E' = \{g^{-1} \cdot e' \mid e, e' \in E, g \in e\}\). Because E is finite, \(G_0\) is finite, and, for each \(e \in E\), we have \(\vert e\vert = \vert G_0\vert \), the set \(E'\) is finite. Therefore,

In conclusion, \(\lim _{i \in I} \frac{\vert \partial _E F_i\vert }{\vert F_i\vert } = 0\).
Secondly, for each finite \(E \subseteq G \slash G_0\), let \(\lim _{i \in I} \frac{\vert \partial _E F_i\vert }{\vert F_i\vert } = 0\). Furthermore, let \(i \in I\), let \(e \in G \slash G_0\), and put \(E = \{G_0, e\}\). According to Item 2 of Lemma 1, we have  . Therefore,
. Therefore,

In conclusion, \(\{F_i\}_{i \in I}\) is a right Følner net in \(\mathcal {R}\). \(\square \)
2 Tilings
In this section, let \(\mathcal {R} = ((M, G, \triangleright ), (m_0, \{g_{m_0, m}\}_{m \in M}))\) be a cell space.
In Definition 2 we introduce the notion of \((E,E')\)-tilings. In Theorem 2 we show using Zorn’s lemma that, for each subset E of \(G \slash G_0\), there is an \((E,E')\)-tiling. And in Lemma 7 we show that, for each \((E,E')\)-tiling with finite sets E and \(E'\), the net \(\{\vert T \cap F_i^{-E}\vert \}_{i \in I}\) is asymptotic not less than \(\{\vert F_i\vert \}_{i \in I}\).
Definition 2
Let T be a subset of M, and let E and \(E'\) be two subsets of \(G \slash G_0\). The set T is called \((E, E')\)-tiling of \(\mathcal {R}\) if and only if the family  is pairwise disjoint and the family
is pairwise disjoint and the family  is a cover of M.
is a cover of M.
Remark 2
Let T be an \((E, E')\)-tiling of \(\mathcal {R}\). For each subset F of E and each superset \(F'\) of \(E'\) with \(F' \subseteq G \slash G_0\), the set T is an \((F, F')\)-tiling of \(\mathcal {R}\). In particular, the set T is an \((E, E \cup E')\)-tiling of \(\mathcal {R}\).
Remark 3
In the situation of Remark 1, the notion of \((E, E')\)-tiling is the same as the one defined in [1, Sect. 5.6, Paragraph 2].
Example 2
In the situation of Example 1, let \(E'\) be the set \(\{g (g')^{-1} G_0 \mid e, e' \in E, g \in e, g' \in e'\}\ (= \{g_0 g g_0' g^{-1} G_0 \mid g_0, g_0' \in G_0\})\) and, for each point \(m \in M\), let  . Because \(g^{-1}\) is the rotation about the axis a by \(-\rho \) radians, the set \(G_0 g^{-1} \triangleright m_0\) is equal to \(E_{m_0}\) and the set \(g G_0 g^{-1} \triangleright m_0\) is equal to \(E_{g \triangleright m_0}\). Because
. Because \(g^{-1}\) is the rotation about the axis a by \(-\rho \) radians, the set \(G_0 g^{-1} \triangleright m_0\) is equal to \(E_{m_0}\) and the set \(g G_0 g^{-1} \triangleright m_0\) is equal to \(E_{g \triangleright m_0}\). Because  , the set \(E'_{m_0}\) is the curved circular disk of radius \(2 \rho \) with the north pole \(m_0\) at its centre. And, for each point \(m \in M\), because
, the set \(E'_{m_0}\) is the curved circular disk of radius \(2 \rho \) with the north pole \(m_0\) at its centre. And, for each point \(m \in M\), because  , the set \(E'_m\) is the curved circular disk of radius \(2 \rho \) with m at its centre.
, the set \(E'_m\) is the curved circular disk of radius \(2 \rho \) with m at its centre.
If the radius \(\rho = \pi / 2\), then the circle \(E_{m_0}\) is the equator and the curved circular disk \(E'_{m_0}\) has radius \(\pi \) and is thus the sphere M, and hence the set \(T = \{m_0\}\) is an \((E, E')\)-tiling of \(\mathcal {R}\); if the radius \(\rho = \pi / 4\), then the curved circular disks \(E'_{m_0}\) and \(E'_{S}\), where S is the south pole, have radii \(\pi / 2\), thus they are hemispheres, and hence the set \(T = \{m_0, S\}\) is an \((E, E')\)-tiling of \(\mathcal {R}\); if the radius \(\rho = \pi / 8\), then the curved circular disks \(E'_{m_0}\) and \(E'_{S}\) have radii \(\pi / 4\), and it can be shown with spherical geometry that the set T consisting of the north pole \(m_0\), the south pole S, four equidistant points \(m_1\), \(m_2\), \(m_3\), and \(m_4\) on the equator, and the circumcentres \(c_1\), \(c_2\), \(\cdots \), \(c_8\) of the 8 smallest spherical triangles with one vertex from \(\{m_0, S\}\) and two vertices from \(\{m_1, m_2, m_3, m_4\}\) (see Fig. 1).
The points \(m_0, S\), \(m_1, m_2, m_3, m_4\), \(c_1, c_2, \cdots , c_8\) constitute an \((E, E')\)-tiling of the sphere; the circles \(E_m\) about these points are drawn solid; the boundaries of the curved circular disks \(E'_m\) about these points are drawn dotted; the inclined circle about \(g \triangleright m_0\) is the rotation \(E_{g \triangleright m_0}\) of \(E_{m_0}\) by \(\pi / 8\) about the axis a; and the other inclined circles are rotations \(g_0 \triangleright (E_{g \triangleright m_0})\) of \(E_{g \triangleright m_0}\) about the z-axis, for a few \(g_0 \in G_0\).
Theorem 2
Let E be a non-empty subset of \(G \slash G_0\). There is an \((E, E')\)-tiling of \(\mathcal {R}\), where \(E' = \{g (g')^{-1} G_0 \mid e, e' \in E, g \in e, g' \in e'\}\).
Proof
Let  . Because \(\{m_0\} \in \mathcal {S}\), the set \(\mathcal {S}\) is non-empty. Moreover, it is preordered by inclusion.
. Because \(\{m_0\} \in \mathcal {S}\), the set \(\mathcal {S}\) is non-empty. Moreover, it is preordered by inclusion.
Let \(\mathcal {C}\) be a chain in \((\mathcal {S}, \subseteq )\). Then, \(\bigcup _{S \in \mathcal {C}} S\) is an element of \(\mathcal {S}\) and an upper bound of \(\mathcal {C}\). According to Zorn’s lemma, there is a maximal element T in \(\mathcal {S}\). By definition of \(\mathcal {S}\), the family  is pairwise disjoint.
is pairwise disjoint.
Let \(m \in M\). Because T is maximal and  is non-empty, there is a \(t \in T\) such that
is non-empty, there is a \(t \in T\) such that  . Hence, there are e, \(e' \in E\) such that
. Hence, there are e, \(e' \in E\) such that  . According to Lemma 4, there is a \(g' \in e'\) such that
. According to Lemma 4, there is a \(g' \in e'\) such that  , and there is a \(g \in e\) such that
, and there is a \(g \in e\) such that  . Therefore,
. Therefore,  . Because \(g (g')^{-1} G_0 \in E'\), we have
. Because \(g (g')^{-1} G_0 \in E'\), we have  . Thus,
. Thus,  is a cover of M.
is a cover of M.
In conclusion, T is an \((E, E')\)-tiling of \(\mathcal {R}\). \(\square \)
Lemma 7
Let \(G_0\) be finite, let \(\{F_i\}_{i \in I}\) be a right Følner net in \(\mathcal {R}\) indexed by \((I, \le )\), let E and \(E'\) be two finite subsets of \(G \slash G_0\), and let T be an \((E, E')\)-tiling of \(\mathcal {R}\). There is a positive real number \(\varepsilon \in \mathbb {R}_{> 0}\) and there is an index \(i_0 \in I\) such that, for each index \(i \in I\) with \(i \ge i_0\), we have \(\vert T \cap F_i^{-E}\vert \ge \varepsilon \vert F_i\vert \).
3 Entropies
In this section, let \(\mathcal {R} = ((M, G, \triangleright ), (m_0, \{g_{m_0, m}\}_{m \in M}))\) be a right amenable cell space, let \(\mathcal {C} = (\mathcal {R}, Q, N, \delta )\) be a semi-cellular automaton, and let \(\varDelta \) be the global transition function of \(\mathcal {C}\) such that the stabiliser \(G_0\) of \(m_0\) under \(\triangleright \), the set Q of states, and the neighbourhood N are finite, and the set Q is non-empty.
In Definition 3 we introduce the entropy of a subset X of \(Q^M\) with respect to a net \(\{F_i\}_{i \in I}\) of non-empty and finite subsets of M, which is the asymptotic growth rate of the number of finite patterns with domain \(F_i\) that occur in X. In Lemma 8 we show that \(Q^M\) has entropy \(\log \vert Q\vert \) and that entropy is non-decreasing. In Theorem 3 we show that applications of global transition functions of cellular automata on subsets of \(Q^M\) do not increase their entropy. And in Lemma 9 we show that if for each point t of an \((E,E')\)-tiling not all patterns with domain  occur in a subset of \(Q^M\), then that subset has less entropy than \(Q^M\).
occur in a subset of \(Q^M\), then that subset has less entropy than \(Q^M\).
Definition 3
Let X be a subset of \(Q^M\) and let \(\mathcal {F} = \{F_i\}_{i \in I}\) be a net in \(\{F \subseteq M \mid F \ne \emptyset , F \,{ finite}\}\). The non-negative real number
is called entropy of X with respect to \(\mathcal {F}\).
Remark 4
In the situation of Remark 1, the notion of entropy is the same as the one defined in [1, Definition 5.7.1].
Lemma 8
Let \(\mathcal {F} = \{F_i\}_{i \in I}\) be a net in \(\{F \subseteq M \mid F \ne \emptyset , F \,{ finite}\}\). Then,
-
1.
\(\mathrm{ent}_{\mathcal {F}}(Q^M) = \log \vert Q\vert \);
-
2.
 ;
; -
3.
\(\forall X \subseteq Q^M :\mathrm{ent}_{\mathcal {F}}(X) \le \log \vert Q\vert \).
In the remainder of this section, let \(\mathcal {F} = \{F_i\}_{i \in I}\) be a right Følner net in \(\mathcal {R}\) indexed by \((I, \le )\).
Theorem 3
Let X be a subset of \(Q^M\). Then, \(\mathrm{ent}_{\mathcal {F}}(\varDelta (X)) \le \mathrm{ent}_{\mathcal {F}}(X)\).
Proof
Suppose, without loss of generality, that \(G_0 \in N\). Let \(i \in I\). According to Lemma 3, the map \(\varDelta _{X, F_i}^- :\pi _{F_i}(X) \rightarrow \pi _{F_i^{-N}}(\varDelta (X))\) is surjective. Therefore, \(\vert \pi _{F_i^{-N}}(\varDelta (X))\vert \le \vert \pi _{F_i}(X)\vert \). Because \(G_0 \in N\), according to Item 5 of Lemma 1, we have \(F_i^{-N} \subseteq F_i\). Thus,  . Hence,
. Hence,

Because \(G_0 \in N\), according to Item 5 of Lemma 1, we have \(F_i \subseteq F_i^{+N}\). Therefore,  . Because \(G_0\), \(F_i\), and N are finite, according to Item 7 of Lemma 1, the boundary \(\partial _N F_i\) is finite. Hence,
. Because \(G_0\), \(F_i\), and N are finite, according to Item 7 of Lemma 1, the boundary \(\partial _N F_i\) is finite. Hence,
Therefore, because N is finite, according to Theorem 1,

Lemma 9
Let Q contain at least two elements, let X be a subset of \(Q^M\), let E and \(E'\) be two non-empty and finite subsets of \(G \slash G_0\), and let T be an \((E, E')\)-tiling of \(\mathcal {R}\), such that, for each cell \(t \in T\), we have  . Then, \(\mathrm{ent}_{\mathcal {F}}(X) < \log \vert Q\vert \).
. Then, \(\mathrm{ent}_{\mathcal {F}}(X) < \log \vert Q\vert \).
Corollary 2
Let Q contain at least two elements, let X be a  -invariant subset of \(Q^M\), and let E be a non-empty and finite subset of \(G \slash G_0\), such that
-invariant subset of \(Q^M\), and let E be a non-empty and finite subset of \(G \slash G_0\), such that  . Then, \(\mathrm{ent}_{\mathcal {F}}(X) < \log \vert Q\vert \).
. Then, \(\mathrm{ent}_{\mathcal {F}}(X) < \log \vert Q\vert \).
4 Gardens of Eden
In this section, let \(\mathcal {R} = ((M, G, \triangleright ), (m_0, \{g_{m_0, m}\}_{m \in M}))\) be a right amenable cell space and let \(\mathcal {C} = (\mathcal {R}, Q, N, \delta )\) be a semi-cellular automaton such that the stabiliser \(G_0\) of \(m_0\) under \(\triangleright \), the set Q of states, and the neighbourhood N are finite, and the set Q is non-empty. Furthermore, let \(\varDelta \) be the global transition function of \(\mathcal {C}\), and let \(\mathcal {F} = \{F_i\}_{i \in I}\) be a right Følner net in \(\mathcal {R}\) indexed by \((I, \le )\).
In Theorem 4 we show that if \(\varDelta \) is not surjective, then the entropy of its image is less than the entropy of \(Q^M\). And the converse of that statement obviously holds. In Theorem 5 we show that if the entropy of the image of \(\varDelta \) is less than the entropy of \(Q^M\), then \(\varDelta \) is not pre-injective. And in Theorem 6 we show the converse of that statement. These four statements establish the Garden of Eden theorem, see Main Theorem 1.
Definition 4
Let c and \(c'\) be two maps from M to Q. The set \(\mathrm{diff}(c, c') = \{m \in M \mid c(m) \ne c'(m)\}\) is called difference of c and \(c'\).
Definition 5
The map \(\varDelta \) is called pre-injective if and only if, for each tuple \((c, c') \in Q^M \times Q^M\) such that \(\mathrm{diff}(c, c')\) is finite and \(\varDelta (c) = \varDelta (c')\), we have \(c = c'\).
In the proof of Theorem 4, the existence of a Garden of Eden pattern, as stated in Lemma 10, is essential, which itself follows from the existence of a Garden of Eden configuration, the compactness of \(Q^M\), and the continuity of \(\varDelta \).
Definition 6
-
1.
Let \(c :M \rightarrow Q\) be a global configuration. It is called Garden of Eden configuration if and only if it is not contained in \(\varDelta (Q^M)\).
-
2.
Let \(p :A \rightarrow Q\) be a pattern. It is called Garden of Eden pattern if and only if, for each global configuration \(c \in Q^M\), we have
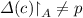 .
.
Remark 5
-
1.
The global transition function \(\varDelta \) is surjective if and only if there is no Garden of Eden configuration.
-
2.
If \(p :A \rightarrow Q\) is a Garden of Eden pattern, then each global configuration \(c \in Q^M\) with
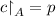 is a Garden of Eden configuration.
is a Garden of Eden configuration. -
3.
If there is a Garden of Eden pattern, then \(\varDelta \) is not surjective.
Lemma 10
Let \(\varDelta \) not be surjective. There is a Garden of Eden pattern with non-empty and finite domain.
Theorem 4
Let \(\delta \) be \(\bullet \)-invariant, let Q contain at least two elements, and let \(\varDelta \) not be surjective. Then, \(\mathrm{ent}_{\mathcal {F}}(\varDelta (Q^M)) < \log \vert Q\vert \).
Proof
According to Lemma 10, there is a Garden of Eden pattern \(p :F \rightarrow Q\) with non-empty and finite domain. Let  . Then,
. Then,  and, because
and, because  is free, \(\vert E\vert = \vert F\vert < \infty \). Because p is a Garden of Eden pattern,
is free, \(\vert E\vert = \vert F\vert < \infty \). Because p is a Garden of Eden pattern,  . Hence,
. Hence,  . Moreover, according to [5, Item 1 of Theorem 2], the map \(\varDelta \) is
. Moreover, according to [5, Item 1 of Theorem 2], the map \(\varDelta \) is  -equivariant. Hence, for each \(g \in G\), we have
-equivariant. Hence, for each \(g \in G\), we have  . In other words, \(\varDelta (Q^M)\) is
. In other words, \(\varDelta (Q^M)\) is  -invariant. Thus, according to Corollary 2, we have \(\mathrm{ent}_{\mathcal {F}}(\varDelta (Q^M)) < \log \vert Q\vert \). \(\square \)
-invariant. Thus, according to Corollary 2, we have \(\mathrm{ent}_{\mathcal {F}}(\varDelta (Q^M)) < \log \vert Q\vert \). \(\square \)
In the proof of Theorem 5, the fact that enlarging each element of \(\mathcal {F}\) does not increase entropy, as stated in the next lemma, is essential.
Lemma 11
Let X be a subset of \(Q^M\) and let E be a finite subset of \(G \slash G_0\) such that \(G_0 \in E\). Then, \(\mathrm{ent}_{\{F_i^{+E}\}_{i \in I}}(X) \le \mathrm{ent}_{\mathcal {F}}(X)\).
Theorem 5
Let \(\mathrm{ent}_{\mathcal {F}}(\varDelta (Q^M)) < \log \vert Q\vert \). Then, \(\varDelta \) is not pre-injective.
Proof
Suppose, without loss of generality, that \(G_0 \in N\). Let \(X = \varDelta (Q^M)\). According to Lemma 11, we have \(\mathrm{ent}_{\{F_i^{+N}\}_{i \in I}}(X) \le \mathrm{ent}_{\mathcal {F}}(X) < \log \vert Q\vert \). Hence, there is an \(i \in I\) such that
Thus, \(\vert \pi _{F_i^{+N}}(X)\vert < \vert Q\vert ^{\vert F_i\vert }\). Furthermore, let \(q \in Q\) and let  . Then, \(\vert Q\vert ^{\vert F_i\vert } = \vert X'\vert \). Hence, \(\vert \pi _{F_i^{+N}}(X)\vert < \vert X'\vert \). Moreover, according to Item 3 of Lemma 1, we have
. Then, \(\vert Q\vert ^{\vert F_i\vert } = \vert X'\vert \). Hence, \(\vert \pi _{F_i^{+N}}(X)\vert < \vert X'\vert \). Moreover, according to Item 3 of Lemma 1, we have  . Hence, for each \((c, c') \in X' \times X'\), according to Lemma 2, we have
. Hence, for each \((c, c') \in X' \times X'\), according to Lemma 2, we have  . Therefore,
. Therefore,
Hence, there are c, \(c' \in X'\) such that \(c \ne c'\) and \(\varDelta (c) = \varDelta (c')\). Thus, because \(\mathrm{diff}(c, c') \subseteq F_i\) is finite, the map \(\varDelta \) is not pre-injective. \(\square \)
In the proof of Theorem 6, the statement of Lemma 12 is essential, which says that if two distinct patterns have the same image and we replace each occurrence of the first by the second in a configuration, we get a new configuration in which the first pattern does not occur and that has the same image as the original one.
Definition 7
Identify M with \(G \slash G_0\) by \(\iota :m \mapsto G_{m_0, m}\). Let

Remark 6
Let A be a subset of M, let p be map from A to Q, and let m be an element of M. Then,  .
.
Definition 8
Identify M with \(G \slash G_0\) by \(\iota :m \mapsto G_{m_0, m}\), let A be a subset of M, let p be map from A to Q, let c be map from M to Q, let m be an element of M. The pattern p is said to occur at m in c and we write \(p \sqsubseteq _m c\) if and only if  .
.
Lemma 12
Identify M with \(G \slash G_0\) by \(\iota :m \mapsto G_{m_0, m}\), let A be a subset of M, let \(N'\) be the subset \(\{g^{-1} \cdot n' \mid n, n' \in N, g \in n\}\) of \(G \slash G_0\), and let p and \(p'\) be two maps from \(A^{+N'}\) to Q such that  and \(\varDelta _{A^{+N'}}^-(p) = \varDelta _{A^{+N'}}^-(p')\). Furthermore, let c be a map from M to Q and let S be a subset of M, such that the family
and \(\varDelta _{A^{+N'}}^-(p) = \varDelta _{A^{+N'}}^-(p')\). Furthermore, let c be a map from M to Q and let S be a subset of M, such that the family  is pairwise disjoint and, for each cell \(s \in S\), we have \(p \sqsubseteq _s c\). Put
is pairwise disjoint and, for each cell \(s \in S\), we have \(p \sqsubseteq _s c\). Put

Then, for each cell \(s \in S\), we have \(p' \sqsubseteq _s c'\), and \(\varDelta (c) = \varDelta (c')\). In particular, if \(p \ne p'\), then, for each cell \(s \in S\), we have \(p \not \sqsubseteq _s c'\).
Theorem 6
Let \(\delta \) be \(\bullet \)-invariant, let Q contain at least two elements, and let \(\varDelta \) not be pre-injective. Then, \(\mathrm{ent}_{\mathcal {F}}(\varDelta (Q^M)) < \log \vert Q\vert \).
Proof
Suppose, without loss of generality, that \(G_0 \in N\). Identify M with \(G \slash G_0\) by \(\iota :m \mapsto G_{m_0, m}\). Because \(\varDelta \) is not pre-injective, there are c, \(c' \in Q^M\) such that \(\mathrm{diff}(c, c')\) is finite, \(\varDelta (c) = \varDelta (c')\), and \(c \ne c'\). Put \(A = \mathrm{diff}(c, c')\), put \(N' = \{g^{-1} \cdot n' \mid n, n' \in N, g \in n\}\), put \(E = A^{+N'}\), and put  and
and  . Because \(\varDelta (c) = \varDelta (c')\), we have \(\varDelta _{A^{+N'}}^-(p) = \varDelta _{A^{+N'}}^-(p')\).
. Because \(\varDelta (c) = \varDelta (c')\), we have \(\varDelta _{A^{+N'}}^-(p) = \varDelta _{A^{+N'}}^-(p')\).
Because N is finite and, for each \(n \in N\), we have \(\vert n\vert = \vert G_0\vert < \infty \), the set \(N'\) is finite. Moreover, \(G_0 \cdot N' \subseteq N'\). According to Item 5 of Lemma 1, because \(G_0 \in N'\) and \(A \ne \emptyset \), we have \(E \supseteq A\) and hence E is non-empty. According to Item 7 of Lemma 1, because \(G_0\), A, and \(N'\) are finite, so is E. Because E is non-empty, according to Theorem 2, there is a subset \(E'\) of \(G \slash G_0\) and an \((E, E')\)-tiling T of \(\mathcal {R}\). Because \(G_0\) and E are non-empty and finite, so is \(E'\).
Let \(Y = \{y \in Q^M \mid \forall t \in T :p \not \sqsubseteq _t y\}\). For each \(t \in T\), we have  and therefore
and therefore  . According to Lemma 9, we have \(\mathrm{ent}_{\mathcal {F}}(Y) < \log \vert Q\vert \). Hence, according to Theorem 3, we have \(\mathrm{ent}_{\mathcal {F}}(\varDelta (Y)) < \log \vert Q\vert \).
. According to Lemma 9, we have \(\mathrm{ent}_{\mathcal {F}}(Y) < \log \vert Q\vert \). Hence, according to Theorem 3, we have \(\mathrm{ent}_{\mathcal {F}}(\varDelta (Y)) < \log \vert Q\vert \).
Let \(x \in Q^M\). Put \(S = \{t \in T \mid p \sqsubseteq _t x\}\). According to Lemma 12, there is an \(x' \in Q^M\) such that \(x' \in Y\) and \(\varDelta (x) = \varDelta (x')\). Therefore, \(\varDelta (Q^M) = \varDelta (Y)\). In conclusion, \(\mathrm{ent}_{\mathcal {F}}(Q^M) < \log \vert Q\vert \). \(\square \)
Main Theorem 1
(Garden of Eden theorem; Edward Forrest Moore, 1962; John R. Myhill, 1963). Let \(\mathcal {M} = (M, G, \triangleright )\) be a right amenable left homogeneous space with finite stabilisers and let \(\varDelta \) be the global transition function of a cellular automaton over \(\mathcal {M}\) with finite set of states and finite neighbourhood. The map \(\varDelta \) is surjective if and only if it is pre-injective.
Proof
There is a coordinate system \(\mathcal {K} = (m_0, \{g_{m_0, m}\}_{m \in M})\) such that the cell space \(\mathcal {R} = (\mathcal {M}, \mathcal {K})\) is right amenable. Moreover, according to [5, Theorem 1], there is a cellular automaton \(\mathcal {C} = (\mathcal {R}, Q, N, \delta )\) such that Q and N are finite and \(\varDelta \) is its global transition function.
In the case that \(\vert Q\vert \le 1\), the proof is trivial. Let it be the case that \(\vert Q\vert > 1\). According to Theorem 4 and Item 1 of Lemma 8, the map \(\varDelta \) is not surjective if and only if \(\mathrm{ent}_{\mathcal {F}}(\varDelta (Q^M)) < \log \vert Q\vert \). And, according to Theorems 5 and 6, we have \(\mathrm{ent}_{\mathcal {F}}(\varDelta (Q^M)) < \log \vert Q\vert \) if and only if \(\varDelta \) is not pre-injective. Hence, \(\varDelta \) is not surjective if and only if it is not pre-injective. In conclusion, \(\varDelta \) is surjective if and only if it is pre-injective. \(\square \)
Remark 7
In the situation of Remark 1, Main Theorem 1 is [1, Theorem 5.3.1].
References
Ceccherini-Silberstein, T., Coornaert, M.: Cellular Automata and Groups. Springer Monographs in Mathematics. Springer, Heidelberg (2010)
Moore, E.F.: Machine models of self-reproduction. In: Proceedings of Symposia in Applied Mathematics, vol. 14, pp. 17–33 (1962)
Myhill, J.R.: The converse of Moore’s Garden-of-Eden theorem. Proc. Am. Math. Soc. 14, 685–686 (1963)
Moriceau, S.: Cellular automata on a \(G\)-Set. Journal Cellular Automata 6(6), 461–486 (2011)
Wacker, S.: Cellular automata on group sets and the uniform Curtis-Hedlund-Lyndon theorem. In: Cook, M., Neary, T. (eds.) AUTOMATA 2016. LNCS, vol. 9664, pp. 185–198. Springer, Heidelberg (2016). doi:10.1007/978-3-319-39300-1_15
Wacker, S.: Right Amenable Left Group Sets and the Tarski-Følner Theorem [math.GR]. arXiv:1603.06460
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Wacker, S. (2016). The Garden of Eden Theorem for Cellular Automata on Group Sets. In: El Yacoubi, S., Wąs, J., Bandini, S. (eds) Cellular Automata. ACRI 2016. Lecture Notes in Computer Science(), vol 9863. Springer, Cham. https://doi.org/10.1007/978-3-319-44365-2_7
Download citation
DOI: https://doi.org/10.1007/978-3-319-44365-2_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-44364-5
Online ISBN: 978-3-319-44365-2
eBook Packages: Computer ScienceComputer Science (R0)




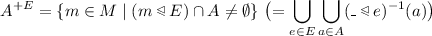
 is called E -boundary of A.
is called E -boundary of A.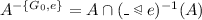 ,
, 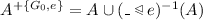 , and
, and  .
.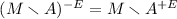 and
and 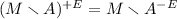 .
.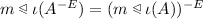 ,
, 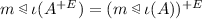 , and
, and 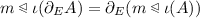 .
.
 ;
;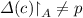 .
.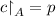 is a Garden of Eden configuration.
is a Garden of Eden configuration.