Reduced Order Analyses of Multi-stage Coupled Structures with Main Focus on Disk-Dominated Modes

Abstract

Rotors manufactured as blisk (Blade Integrated Disk) has become state-of-the-art in turbomachinery. This integral design saves a lot of mass and enables higher rotational speeds allowing for higher pressure ratios and hence an increased efficiency. The advantage comes along with the drawback that the structural damping level is extremely low. Nowadays, the dynamics of single-stage rotors is well-investigated, as dynamical analysis of cyclic structures is one of the most important subjects in applied research in turbomachinery. However, the stage-to-stage coupling effect is neglected in most cases. The importance of proper interstage treatment is obvious for adequate multi-stage analyses. Hence the structural dynamics of a multi-stage assembly has recently become an important area of research. In this paper, some multi-stage effects are discussed and three different reduced order techniques are summarized and demonstrated on a multi-stage assembly of academic blisks. The findings are compared to a FE-solution. Particular attention must be paid to disk-dominated modes, which are highly affected by multi-stage behavior. Mistuning modeling is not considered, because it mainly influences blade-dominated vibrations.

1 Introduction

In turbomachinery, rotating structures are assessed by dynamic analyses of their operating behavior. Dynamic analyses of high pressure compressors assume some simplifications. First of all, it is common to fulfill stage by stage analyses. It is then possible to investigate the complete cyclic structure by analyzing an elementary sector using cyclic symmetry boundary conditions [1]. However, due to manufacturing or material tolerances, there are no identical blades. In order to consider small mistuning and to estimate resulting amplification factors, various reduced order models (ROMs) are invented [2, 3], adapted and advanced.

Since stage methods will not predict dynamic behavior of the assembled compressor with adequate accuracy. Stage-to-stage coupling effects may significantly impact eigenfrequencies and modes. A priori, disk-dominated modes are highly affected whereas blade-dominated modes hardly contribute to interstage coupling [4].

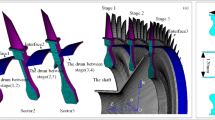
This paper summarizes different methods [2, 5, 6] to calculate Multi-stage modes at moderate costs. Aiming at a drastic reduction of the DOF-number, different reduced order models are applied. These techniques are demonstrated by means of academic sample rotors, shown in Fig. 1. Since every ROM implies errors compared to a full FE-model, results from a full analysis are used as reference.

Fig. 1

Elementary sectors (rotor 1 and 2) and multi-stage assembly

First, the dynamic of the assembly is characterized and interesting modes, which demonstrate the need of a Multi-Stage analysis, are identified. Since the main focus of this paper is on disk-dominated Multi-Stage modes and blade individual mistuning particularly modify blade-dominated modes, mistuning is neglected here. However, there are ways to consider small deviations (e.g. material property), if the interaction between blade induced mistuning and stage-to-stage coupling were discussed.

2 Dynamics of the Multi-stage Assembly

Figure 1 depicts a two staged academic compressor, which is evaluated in this paper. The geometry is quite simple; however basic characteristics (e.g. blade-dominated, disk-dominated modes and interactions) appear.

Although Rotor 1 consists of 9 blades and Rotor 2 is composed of 13 blades, the assembled mesh is compatible. Thus, FE-meshes of both rotors are matching along the interstage boundary. If the meshes are incompatible, multipoint constraints are used to ensure interstage coupling.

The dynamics of the assembled structure is determinate by a modal analysis. Furthermore, single stage modal analyses with cyclic symmetry boundaries of both rotors are performed. Figure 2a shows the eigenfrequencies versus the corresponding periodic parameter (cyclic symmetry mode). Even though single stage modal analyses yield passable results in blade-dominated mode families, there are critical inaccuracies in disk-dominated regions (e.g. green mark in Fig. 2a).

Fig. 2

Influence of interstage coupling: a eigenfrequency versus periodic index map b relative stage participation (Color figure online)

Figure 2b reflects the relative participation of stage 1. The Participation Factor R ^(s)_k [4] expresses the portion of elastic strain energy for the kth mode of stage (s). Values around 1.0 indicate that main fraction of elastic energy is concentrated on stage 1. Values near 0.0 imply stage 2 dominated modes. Obviously, there are mode families localized on a single stage, but there are mixed modes as well. One can find that mixed modes tend to be badly predicted in single stage analyses (e.g. Modes 29–33 are non-represented in the single stage cyclic symmetry analyses of Fig. 2a).

3 Reduced Order Model of Multi-stage Structures

Every ROM presented subsequently uses the mass and stiffness information from one elementary sector of each stage to build a reduced equation of motion of the unreduced assembly. The damped equation of motion (EOM) can be written as

$$ {\mathbf{M}}{{\ddot{\mathbf{x}}}} + {\mathbf{C}}{{\dot{\mathbf{x}}}} + {\mathbf{Kx}} = {\mathbf{f}}_{{\mathbf{e}}}. $$

(1)

The coupling of both stages is the cornerstone. It can be achieved by introducing geometrical constrain ${\mathbf{A}}$ between interstage degrees of freedom (DOF)

$$ \Delta {}^{\Gamma }{\mathbf{x}} = {\mathbf{A}} \, \cdot {}^{\Gamma }{\mathbf{x}}^{(1)} - {}^{\Gamma }{\mathbf{x}}^{(2)} = 0. $$

(2)

3.1 Multi-stage Multi-level Craig-Bampton Approach

Basically, this ROM (msmlcb) [2] differentiates between inner ${}^{i}{\mathbf{x}}$ and outer ${}^{b}{\mathbf{x}}$ DOF. Here, the outer DOF contain left and right boundary DOF as well as interstage DOF. The EOM of an elementary sector is rearranged as

$$ \left( {\begin{array}{*{20}c} {{}^{ii}{\mathbf{m}}} & {{}^{ib}{\mathbf{m}}} \\ {{}^{bi}{\mathbf{m}}} & {{}^{bb}{\mathbf{m}}} \\ \end{array} } \right) \cdot \left( {\begin{array}{*{20}c} {{}^{i}{\ddot{\mathbf{x}}}} \\ {{}^{b}{\ddot{\mathbf{x}}}} \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {{}^{ii}{\mathbf{k}}} & {{}^{ib}{\mathbf{k}}} \\ {{}^{bi}{\mathbf{k}}} & {{}^{bb}{\mathbf{k}}} \\ \end{array} } \right) \cdot \left( {\begin{array}{*{20}c} {{}^{i}{\mathbf{x}}} \\ {{}^{b}{\mathbf{x}}} \\ \end{array} } \right) = 0. $$

(3)

The inner DOF can be expressed by eigenmodes ${\varvec{\Phi}}$. Constraint modes ${\varvec{\Psi}}$ are introduced to ensure the static solution. The reduction is executed as

$$ \left\langle {{\mathbf{M}},{\mathbf{K}}} \right\rangle_{CB} = {\mathbf{T}}_{CB}^{T} \cdot \left\langle {{\mathbf{M}},{\mathbf{K}}} \right\rangle \cdot T_{CB} $$

(4)

with

$$ {\mathbf{T}}_{CB} = \left( {\begin{array}{*{20}c} {\varvec{\Phi}} & {\varvec{\Psi}} \\ 0 & {\mathbf{I}} \\ \end{array} } \right)\quad {\text{while}}\quad \begin{array}{*{20}l} {{\varvec{\upomega}}^{2} \cdot {}^{ii}{\mathbf{m}} \cdot {\varvec{\Phi}} = {}^{ii}{\mathbf{k}} \cdot {\varvec{\Phi}}} \hfill \\ {{}^{i}{\mathbf{x}} = - {}^{ii}{\mathbf{k}}^{ - 1} \cdot {}^{ib}{\mathbf{k}} \cdot {}^{b}{\mathbf{x}} = {\varvec{\Psi}} \cdot {}^{b}{\mathbf{x}}} \hfill \\ \end{array} $$

(5)

Once the reduction step is completed, the single stage system can be synthesized with another Boolean that connects adjoining sectors [2]. Both stages are reduced, but still uncoupled. However, there is a huge amount of DOF in ${}^{b}{\mathbf{x}}^{(s)}$, which are useless from now on. Therefore a second Craig-Banpton reduction can be performed. Thereby only the interstage boundary DOF are obtained physically. Equation 2 yields a constraint to the multi-stage system Eq. 6.

$$ \, \left\langle {{\mathbf{M}},{\mathbf{K}}} \right\rangle = \left( {\begin{array}{*{20}c} {\mathbf{I}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{I}} & {\mathbf{0}} & {{\mathbf{A}}^{T} } \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{I}} & {\mathbf{0}} \\ \end{array} } \right) \cdot \left( {\begin{array}{*{20}c} {\left\langle {{\mathbf{M}},{\mathbf{K}}} \right\rangle_{CB}^{(1)} } & {\mathbf{0}} \\ {\mathbf{0}} & {\left\langle {{\mathbf{M}},{\mathbf{K}}} \right\rangle_{CB}^{(2)} } \\ \end{array} } \right) \cdot \left( {\begin{array}{*{20}c} {\mathbf{I}}{\mathbf{0}}{\mathbf{0}} \\ {\mathbf{0}}{\mathbf{I}}{\mathbf{0}} \\ {\mathbf{0}}{\mathbf{0}}{\mathbf{I}} \\ {\mathbf{0}}{\mathbf{A}}{\mathbf{0}} \\ \end{array} } \right) $$

(6)

On that account the DOF in Eq. 1 are sorted as

$$ {\mathbf{x}} = \left( {\begin{array}{*{20}c} {{\mathbf{q}}^{(1)} } & {{}^{\Gamma }{\mathbf{x}}} & {{\mathbf{q}}^{(2)} } \\ \end{array} } \right)^{\text{T}} . $$

(7)

3.2 Multi-stage Cyclic Symmetry Method

This method (called mscsm) [5] forgoes physical DOF and transforms Eq. 2 in cyclic symmetry modes [1]. Prior to this, left intersector DOF of each sector ${}^{l}{\mathbf{x}}$ are eliminated with respect to the corresponding nodal diameter n

$$ {}^{l}{\mathbf{x}} = {\text{e}}^{{{\text{j}}2\pi n/N}} \cdot {}^{r}{\mathbf{x}}. $$

(8)

The matrices are reduced in an equal way. The physical coordinates of the complete blisks are obtained by

$$ {\mathbf{x}} = {\mathbf{e}}_{n} \otimes {\tilde{\mathbf{x}}}_{n} \;{\text{with}}\;{\mathbf{e}}_{n} = \left( {\begin{array}{*{20}l} 1 \hfill & {{\text{e}}^{{{\text{j}}2\pi /N}} } \hfill & \ldots \hfill & {{\text{e}}^{{{\text{j}}(N - 1)2\pi n/N}} } \hfill \\ \end{array} } \right)^{\text{T}} . $$

(9)

Assuming different numbers of sector N⁽¹⁾ and N⁽²⁾, one find corresponding equivalent nodal diameters $n(p)$ [5]. Considering Eq. 2, the dynamics of the multi-stage structure of one nodal diameter $p$ can be expressed as

$$ {\mathbf{T}}_{p}^{*} \cdot \left( {\begin{array}{*{20}c} {{\mathbf{M}}_{n(p)}^{(1)} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{M}}_{p}^{(2)} } \\ \end{array} } \right) \cdot {\mathbf{T}}_{p} \cdot {\ddot{\tilde{\mathbf{x}}}}_{p} + {\mathbf{T}}_{p}^{*} \cdot \left( {\begin{array}{*{20}c} {{\mathbf{K}}_{n(p)}^{(1)} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{K}}_{p}^{(2)} } \\ \end{array} } \right) \cdot {\mathbf{T}}_{p} \cdot {\tilde{\mathbf{x}}}_{p} . $$

(10)

The transformation matrix ${\mathbf{T}}_{p}$ is defined by

$$ {\mathbf{T}}_{p} = \left( {\begin{array}{*{20}c} {\mathbf{I}}&{\mathbf{0}}&{\mathbf{0}} \\ {\mathbf{0}}&{\mathbf{I}}&{\mathbf{0}} \\ {\mathbf{0}}&{\mathbf{0}}&{\mathbf{I}} \\ {\mathbf{0}}&{{\mathbf{B}}_{p} }&{\mathbf{0}} \\ \end{array} } \right)\;\;{\text{with}}\;\;\begin{array}{*{20}l} {{\mathbf{B}}_{p} = \left( {{\mathbf{e}}_{{N^{(2)} ,p}}^{{^{*} }} \otimes {\mathbf{I}}} \right) \cdot {\mathbf{A}} \cdot \left( {{\mathbf{e}}_{{N^{(1)} ,n(p)}} \otimes {\mathbf{I}}} \right)} \hfill \\ {{\tilde{\mathbf{x}}}_{p} = \left( {\begin{array}{*{20}c} {{}^{i}{\tilde{\mathbf{x}}}_{n(p)}^{(1)} } & {{}^{\Gamma }{\tilde{\mathbf{x}}}_{n(p)} } & {{}^{i}{\tilde{\mathbf{x}}}_{p}^{(2)} } \\ \end{array} } \right)^{T} } \hfill \\ \end{array} $$

(11)

3.3 Multi-stage Modified Modal Domain Analysis

This analysis (msmmda) starts straightly in Eq. 1 by reading all information of mass, damping and stiffness from the Multi-Stage FE-model. Nevertheless, solving the problem itself is still too expensive. Rather, DOF are reduced with eigenmodes, calculated with elementary sector models extended with an additional connecting ring [6], which automatically guarantees mesh compatibility.

$$ {\mathbf{y}} = {\varvec{\Phi}} \cdot {\mathbf{x}} = \left( {\begin{array}{*{20}c} {{\varvec{\Phi}}^{(1)} } & {{\varvec{\Phi}}_{f}^{(1)} } & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {{\varvec{\Phi}}^{(2)} } & {{\varvec{\Phi}}_{f}^{(2)} } \\ \end{array} } \right) \cdot \left( {\begin{array}{*{20}c} {{\mathbf{x}}^{(1)} } \\ {{\mathbf{x}}^{(2)} } \\ \end{array} } \right) . $$

(12)

${\varvec{\Phi}}^{(s)}$ denote eigenmodes of the stage (s) with the connecting ring having free end and ${\varvec{\Phi}}_{f}^{(1)}$ are eigenmodes with the connecting ring having fixed end [6]. Equation 1 is written as

$$ {\varvec{\Phi}}^{*} \cdot {\mathbf{M}} \cdot {\varvec{\Phi}} \cdot {\ddot{\mathbf{y}}} + {\varvec{\Phi}}^{*} \cdot {\mathbf{C}} \cdot {\varvec{\Phi}} \cdot {\dot{\mathbf{y}}} + {\varvec{\Phi}}^{*} \cdot {\mathbf{K}} \cdot {\varvec{\Phi}} \cdot {\mathbf{y}} = {\varvec{\Phi}}^{*} \cdot {\mathbf{f}}_{{\mathbf{e}}}. $$

(13)

4 Conclusions

Three different ROM are presented in this paper. Figure 3a shows the eigenfrequencies from every ROM and full FE-solution. There are—even not in evidence—minute deviations. Figure 3b summarizes the relative error in eigenfrequency. As shown, the ROM implied error is extremely small. Depending on the individual task, one of the presented methods satisfies the requirements best. The msmlcb yields the best results, but is due to the constraint modes the most expensive one. The mscsm works quite fast and affords acceptable quality, but is limited to one-to-one nodal diameter modes. The msmmda represent a comfortable ROM, because all modes are implied and commercial FE-tools are intensively used. Moreover even geometric mistuning is conceivable.

Fig. 3

Comparison between full 360° FE versus msmlcb (red), mscsm (blue) and msmmda (green) eigenfrequency and relative error in eigenfrequency versus full 360° FE-solution (Color figure online)