Keywords

1 Introduction

The use of numerical, mainly finite elements and experimental approaches to characterize weld residual stresses is fairly widespread, but limitations to these methods are not fully known and they need to be recognized. However, when the two approaches are combined, and the results corroborate each other sufficiently well, the resulting residual stress distribution can be confidently used for assessment.

The use of numerical techniques to simulate the welding process is not new and the increase in computing power has seen the size and complexity of the models increase.

Simulation of the welding process, considering the moving electrode, is actually a three-dimensional problem requiring a lot of computer time and effort. Alternative two-dimensional, quasi-steady state models based on simple transformations are widely used instead of the three-dimensional unsteady welding process. The two-dimensional problem involves the analysis of the thermal and stress distributions in the normal plane to the weld direction in the case of thick plate components and on the surface for thin plate configurations. The accuracy of the two-dimensional cross-sectional model increases as the weld speed increases, which corresponds to simulating the condition of a negligible temperature gradient in the direction of the weld [1, 2].

An algorithm for the analysis of non-linear heat transfer was presented by Bathe and Khosgoftaar [3] with an iterative solution procedure for time integration for a general three-dimensional configuration. This has been used by researchers for obtaining transient temperature distributions during a welding process by modeling heat input due to a weld torch as an internal heat generation or as a surface boundary condition. Goldak [4] demonstrated the application of elliptical power density distribution of heat flux input with reference to two-dimensional in-plane, cross-sectional and three-dimensional geometric configurations. This concept of weld heat input has been used by many researchers [5, 6].

This paper describes a finite element analysis of the repair threads in a hole in the cover of a pressure vessel by welding using the commercial finite element packages SYSWELD [7]. The geometry of the symmetry part of the cover of pressure vessels has been modeled in 3D. The heat source is defined by the Goldak model [2]. Some results from this analysis are presented in this paper

2 Heat Transfer Analysis

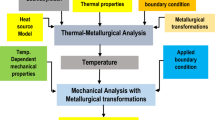
The use of analytical, mainly finite elements and experimental approaches to characterize weld residual stresses is fairly widespread, but limitations to these methods are not fully known and they need to be recognized. However, when the two approaches are combined, and the results corroborate each other sufficiently well, the resulting residual stress distribution can be confidently used for assessment. To determine the thermal field during the welding process, two different analyses are required, namely heat conduction and phase transformation analyses. The most significant factors affecting both analyses are the heat input rate, the moving speed of the heat source and the thickness of the base material.

The fundamental behavior of heat conduction is that a flux [8]. \( {\text{Q}}^{{\prime \prime }} \) (W/m2), of energy flows from a hot region to cooler regions, linearly dependent on the temperature gradient, \( \nabla {\text{T}} \):

$$ {\text{Q}}^{{\prime \prime }} = k\nabla {\text{T}} $$
(1)

where k is the thermal conductivity of the material. The energy required to change the temperature of the material is defined by specific heat c or enthalpy H. The conservation of energy is expressed in differential form having the terms for specific heat, thermal flux and a distributed volume heat-source term \( {\text{Q}}^{{{\prime \prime \prime }}} \)(W/m3) and it is given as

$$ \uprho{\text{c}} \dot{\text{T}} - \nabla \text{(}k\nabla {\text{T}}\text{)} - {\text{Q}}^{{\prime \prime }} = 0 $$
(2)

where \( {\dot{\text{T}}} = \partial {\text{T}}/\partial {\text{t}} \) with t being the time parameter and ρ the density of the materials.

3 Finite Element Analysis and Model

In the FEM analysis, the boundary conditions are applied to the model by specifying the value of the heat transfer coefficient and the surrounding temperatures at the elements and nodes, respectively, of the “skin elements” by creating a mesh at the boundaries of the domain studies.

When applied to the heat Eq. (2), the finite element method involves the solution of a system of differential equations [8]:

$$ {\text{C}}\dot{\text{T}} + {\text{KT}} = {\text{Q}} $$
(3)

The above Eq. (3) can be written as

$$ {\text{R}} = {\text{Q}} - {\text{C}} \dot{\text{T}} - {\text{KT}} = 0 $$
(4)

where R is a vector containing all the residual nodal forces (temperature). For non-linear analysis, Eq. (4) is to be solved by an iterative method at each time step. \( {\text{T}} \) is the nodal temperature vector, \( {\dot{\text{T}}} \) is the time derivative of the temperature, \( {\text{C}} \) is the specific heat matrix, \( {\text{K}} \) is the conductivity matrix and \( {\text{Q}} \) is the vector of nodal power equivalent to an internal heat source and boundary conditions.

A 3D model for transient analysis is shown in Fig. 1. This model contained 120356 linear elements.

Fig. 1
figure 1

3D model for finite element analysis

Full size image

3.1 Material Properties

The temperature dependent value of thermal conductivity, specified heat capacity, thermal expansion coefficient and Young’s modulus can be found in Table 1. Density was assumed to be 7700 kg m−3 and Poisson’s ratio to be 0.3, both independent of temperature. Other material properties are in [9].

Table 1 Thermo-mechanical properties
Full size table

3.2 Heat Source Model

In this model the heat source distribution is comprised of two different ellipses in Fig. 2, i.e. one is in the front quadrant of the heat source and the other is in the rear quadrant. The power densities of the double-ellipsoidal heat source, qf (x, y, z) and qr (x, y, z) describe the Goldak heat flux distribution inside the front and rear quadrant of the heat source and can be expressed as [2]:

Fig. 2
figure 2

Goldak model of heat source

Full size image
$$ {\text{q}}_{\text{f}} \text{(}{\text{x}},{\text{y}},{\text{z}}\text{)} = \frac{{6\sqrt 3 \,{\text{f}}_{\text{f}} \text{Q}}}{{{\text{abc}}_{\text{f}}\uppi\sqrt\uppi }}{\text{e}}^{{ - \tfrac{{3{\text{x}}^{2} }}{{{\text{a}}^{2} }}}} {\text{e}}^{{ - \tfrac{{3{\text{y}}^{2} }}{{{\text{b}}^{2} }}}} {\text{e}}^{{ - \tfrac{{3\text{(}{\text{z}} - {\text{v}}(\uptau - {\text{t}}\text{))}^{2} }}{{{\text{c}}_{\text{f}}^{2} }}}} $$
(5)
$$ {\text{q}}_{\text{r}} \text{(}{\text{x}},{\text{y}},{\text{z}}\text{)} = \frac{{6\sqrt 3 \,{\text{f}}_{\text{r}} {\text{Q}}}}{{{\text{abc}}_{\text{r}}\uppi\sqrt\uppi }}{\text{e}}^{{ - \tfrac{{3{\text{x}}^{2} }}{{{\text{a}}^{2} }}}} {\text{e}}^{{ - \tfrac{{3{\text{y}}^{2} }}{{{\text{b}}^{2} }}}} {\text{e}}^{{ - \tfrac{{3\text{(}{\text{z}} - {\text{v}}{(\tau } - {\text{t}}\text{))}^{2} }}{{{\text{c}}_{\text{r}}^{2} }}}} $$
(6)

where \( {\text{Q}} \) is the energy input rate, ff and fr are the fractional factor of the heat deposit in the front and rear quadrant, a, b, cf and cr are heat source parameters, v is welding rate and τ is total time of welding. Parameters of heat source are in [9].

4 Results

In the numerical simulation the Goldak heat source moves along the helical with 91 screw-threads. Total time of transient thermal and mechanical analysis for one-layer welding is 21160 s. Results from thermal analysis are the thermal fields in Figs. 3 and 4, and phase distributions in Figs. 6, 7 and 8. In Fig. 5 the temperature change is along the depth of the neighbor hole and a selected point in the outside surface of numerical model (top and lateral surface).

Fig. 3
figure 3

Temperature field in time 16090 s of welding

Full size image
Fig. 4
figure 4

Temperature field in time 1000 s of welding

Full size image
Fig. 5
figure 5

Change of temperature along the length of the repair hole with cooling phase of solution

Full size image

In Fig. 8 the result for mechanical analysis with consideration of thermal field and metallurgical phase fractions from thermal analysis is presented. In the mechanical solution the isotropic hardening model for plastic deformations was considered.

Fig. 6
figure 6

Distribution of sorbite phase after welding of first layer

Full size image
Fig. 7
figure 7

Distribution of tempered martensite phase after welding of first layer

Full size image
Fig. 8
figure 8

Von Mises stress after welding of first layer

Full size image

5 Conclusions

Parameters of the Goldak model of heat source were determined from experimental measurements in selected points using thermocouples. Good agreement was obtained between the measurement and numerically calculated value in thermal and mechanical results. In this paper one of the methods of repair is presented for a hole with an incorrect screw-thread by using welding. After creating welding layers in the repair hole in the cover of pressure vessels we cut a new screw-thread. An isotropic hardening model was used for the solution of mechanical stress, which leads to an over-conservative estimate of stress.