Keywords

1 Introduction

With the merits of large actuation force, high positioning resolution and quick response time, piezoelectric actuators (PEAs) have been extensively applied in various nanopositioning equipments, such as scanning probe microscopes [1], micro-/nano-manipulators [2], and nano-manufacturing devices [3]. However, the intrinsic hysteresis nonlinearity of the PEAs can seriously damage the positioning/tracking accuracy of these nanopositioning equipments [4]. In the nanopositioning stages driven by PEAs, the hysteresis effect can induce positioning/tracking errors up to \(15\,\% \) of the travel range [4].

To deal with the hysteresis of the PEAs, a number of control methods have been developed [5–7]. Among the existing methods, feedforward control is most commonly used, which is on the basis of a mathematical model that can accurately characterize the hysteresis nonlinearity. A lot of such mathematical models have been developed in the literature, such as the Dahl model [2], the Preisach model [8], the Prandtl-Ishlinskii model [7], and the Bouc-Wen (BW) model [9]. In these models, the BW model owns the benefit of simplicity for computing, as it only requires one differential equation with a few parameters [9]. In addition, it is capable of describing many categories of hysteresis nonlinearity [9]. However, the classical Bouc-Wen (CBW) model is limited to the symmetric hysteresis description [10]. Moreover, the hysteresis curve generated by the CBW model does not change with the input frequencies [11], which makes it impossible for the CBW model to characterize the rate-dependent behavior of the hysteresis. Hence, when the CBW model is utilized to represent the hysteresis effect of the PEAs which exhibits asymmetric and rate-dependent characteristics, large modeling errors would occur [11]. To describe the asymmetric hysteresis, investigations have been performed to modify the CBW model by introducing a non-odd input function [12] or an asymmetric term into the differential equation [10]. To represent the rate-dependent characteristic, various efforts have also been made in the literature. In [13], experimental data in a certain range are utilized to identify the CBW model. In [11], a factor in the frequency domain is introduced to characterize the rate-dependent behavior. In [14], a Hammerstein structure with CBW model is developed to describe the hysteresis effect with rate-dependent behavior. It can be found that, nowadays, design of BW models to describe the hysteresis effect of PEAs still attracts attention. However, the existing hysteresis descriptions with BW models are not completely satisfactory. For instance, the modeling errors in [13] are still large and the model in [14] cannot describe the asymmetric hysteresis behavior. Hence, there is a necessity to further research on how to model the hysteresis with asymmetric and rate-dependent characteristics using the BW model.

In this work, a modified Bouc-Wen (MBW) model with a third-order input function is introduced to characterize the hysteresis nonlinearity in PEAs with asymmetric behavior. Then, considering that the rate-dependent characteristic of the hysteresis can be treated as the coupled effect of the rate-independent hysteresis and the linear dynamics [15], the proposed MBW model is cascaded with the linear dynamics model of the PEA-actuated stage as a Hammerstein-like structure to characterize the rate-dependent hysteresis effect. The parameters of the hysteresis model, linear dynamics model and delay time are derived with three identification steps using the specific inputs and the corresponding system outputs. Experiments are conducted on a PEA-actuated nanopositioning stage to validate the effectiveness and feasibility of the proposed model structure. The experimental results validate that the predicted responses with the identified model well match the system responses.

The rest of this paper is organized as follows. Section 2 presents the model description of the PEA-actuated nanopositioning stage. Section 3 presents the experimental platform and the model identification. Experimental results are presented in Sect. 4, and Sect. 5 draws the conclusion.

2 Model Description

The BW model was firstly proposed by Bouc [16] and modified by Wen [17]. It is capable of describing many categories of hysteresis and it also owns the benefit of simplicity in computing. The CBW model can be expressed in the form of

$$\begin{aligned} \mathrm{{w}}(t) = pv(t) + h(t) \end{aligned}$$
(1)
$$\begin{aligned} \dot{h} = A\dot{v} - \beta \left| {\dot{v}} \right| \, \left| h \right| ^{n - 1} h - \gamma \dot{v}\left| h \right| ^n \end{aligned}$$
(2)

where w(t) is the hysteresis output, v(t) is the input voltage to the PEAs, h(t) is a variable about the hysteresis, \(\dot{h}\) and \(\dot{v}\) are the first derivative of h and v with respect to time, respectively, A, \(\beta \), \(\gamma \) and n are the shape parameters of hysteresis curves. Due to the properties and characteristics of the component material in the PEAs, \(n=1\) is generally utilized to characterize the hysteresis of the PEA-actuated nanopositioning stages [9].

Fig. 1.
figure 1

Comparison of hysteresis curves generated by the CBW model and MBW model.

Full size image

The hysteresis generated by the CBW model exhibits symmetrical characteristic about the center point [10], as can be observed from Fig. 1. Thus, it cannot accurately characterize the asymmetric hysteresis in PEAs. In this work, a MBW model will be developed to describe the hysteresis effect in PEAs with asymmetric characteristic.

2.1 MBW Model

Inspired by our previous work [7], to describe the hysteresis in PEAs which exhibits asymmetric characteristic, a third-order input function is utilized to develop the MBW model by modifying (1) as follows:

$$\begin{aligned} w(t) = p_1 v(t)^3 + p_2 v(t) + h(t) \end{aligned}$$
(3)

It can be found that, when \(p_1=0\), the proposed MBW model is simplified as the CBW model. Hence, the CBW model can be regarded as a special case of the MBW model. To test the ability of the proposed MBW model to characterize the hysteresis effect with asymmetric feature, the output of MBW model under sinusoidal input signal is shown in Fig. 1. The parameters of the MBW model are \(A=-0.7\), \(\beta =3\), \(\gamma =-1\), \(n=1\), \(p_1=-0.1\), and \(p_2=1\). As a comparison, the output of the CBW model with \(p=1\) is also shown in Fig. 1. The other parameters of the CBW model are the same with those of the MBW model. It can be found that the hysteresis curve of the CBW model is symmetrical about the center point, while the hysteresis curve generated with the MBW model exhibits asymmetric characteristic.

It should be mentioned that, in this work the input voltage is always positive value. Hence, the introduction of the third-order polynomial term of input function can result in the asymmetric characteristic of the MBW model. When the input voltage is symmetrical about the origin, non-odd polynomial term can be added to the model to produce the asymmetric characteristic [12].

Fig. 2.
figure 2

The cascaded model (Hammerstein-like structure) of the PEA-actuated nanopositioning systems.

Full size image

2.2 Hammerstein-Like Model Structure

The rate-dependent hysteresis can be treated as the coupled effect of the rate-independent hysteresis and the linear dynamics of the PEA-actuated nanopositioning stage [15]. Hence, for the purpose of characterizing the rate-dependent behavior of the hysteresis effect, the dynamics model of the PEA-actuated nanopositioning stage is described as a cascaded model of the hysteresis nonlinearity and the linear dynamics model, as shown in Fig. 2, which is actually a Hammerstein-like model structure. In this work, the hysteresis effect \(H( \cdot )\) is represented by the proposed MBW model in Sect. 2.1. The linear dynamics model G(z) can be written as

$$\begin{aligned} G(z) = \frac{{B(z)}}{{A(z)}}z^{ - d} \end{aligned}$$
(4)

with

$$\begin{aligned} A(z)= & {} 1 + a_1 z^{ - 1} + a_2 z^{ - 2} + \cdots + a_{na} z^{ - na} \nonumber \\ B(z)= & {} b_1 + b_2 z^{ - 1} + \cdots + b_{nb} z^{ - nb + 1} \end{aligned}$$
(5)

where \(z^{-1}\) represents the one step time delay, \(z^{-d}\) is the delay steps of the nanopositioning stage with d being a positive integer, and A(z) and B(z) are denominator and numerator of G(z), respectively. The degrees of A(z) and B(z) are na and \(nb-1\), respectively.

It should be mentioned that in [14] a BW model based Hammerstein model is also used for the description of the hysteresis nonlinearity in PEAs with rate-dependent behavior. The differences between this work and [14] lie in that: (i) the MBW model in this work is modified to be capable of describing the asymmetric characteristic of the hysteresis; (ii) the delay time is considered in this work, which is not considered in [14]; and (iii) the identification procedure in this work is quite different from that in [14] where the hysteresis nonlinearity is identified first by regarding w\((t)=y(t)\). Our identification steps will be presented in the next section.

Fig. 3.
figure 3

The experimental setup. (a) The experimental platform. (b) Block diagram of the experimental platform.

Full size image

3 Model Identification

There are three types of parameters in the system model to be identified, i.e. the parameters of the MBW model, the coefficients \(a_i\) and \(b_i\) of the linear dynamics model, and the delay steps d of the nanopositioning stage. The delay time of the PEA-actuated nanopositioning stage can be derived directly by comparing the input signal and output signal in the time domain. Besides, when the input with low amplitude is used to drive the PEA-actuated nanopositioning stage, the influence of the hysteresis can be neglected [15], which makes it possible to identify the linear dynamics model. After identifying the delay steps and the coefficients of A(z) and B(z), the hysteresis output w(t) can be determined when the system output y(t) under low-frequency input is measured. Then, the parameters of the MBW model can be optimized with the low-frequency input data and the hysteresis output data. This three-step identification procedure is similar to that in our previous work [15].

3.1 Experimental Setup

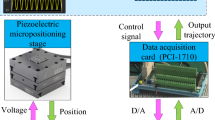
A PEA-actuated XY nanopositioning stage developed in our previous paper [18] is adopted to evaluate the proposed model structure in this work. Figure 3(a) shows the experimental platform. A dSPACE-DS1103 board is used to transmit the control voltage signal and the displacement signal between the software and the experimental devices. The 16-bit DACs of the dSPACE interface provide the control voltage which is calculated in the software of the computer to the high-voltage amplifier (HVA). Then, the HVA amplifies the control voltage with a gain of 20 and provides it to the PEAs. Capacitive sensors (Probe 2823 and Gauging Module 8810 from MicroSense) are utilized to measure the displacements of the end-effector of the nanopositioning stage. The 16-bit ADCs of the dSPACE interface acquire the sensor output signal and then transmit it to the computer for the control signal calculation. In this work, the sample time is set as 0.00002 s. The block diagram of the experimental setup is shown in Fig. 3(b).

Fig. 4.
figure 4

Experimental results of the step response.

Full size image

3.2 Identification of the Delay Time

The step signal input and the corresponding system output is used to identify the delay time of the nanopositioning system. The experimental results of the step response of the nanopositioning stage are shown in Fig. 4. By comparing the system response with the input signal, it is found that the delay time between the output signal and input signal is 0.00006 s. It should be noted that several experiments under step signal inputs are conducted with different sample times. All the experimental results show the same delay time, i.e. 0.00006 s. As the sample time in this work is 0.00002 s, the time delay term \(d = 3\) is derived.

Fig. 5.
figure 5

The frequency responses of the experimental data and the identified model.

Full size image

3.3 Identification of the Linear Dynamics

To identify the linear dynamics model of the nanopositioning stage, a band-limited white noise signal with low amplitude is utilized to excite the system. The input voltage and output signal are simultaneously acquired by the dSPACE. Then, they are used to identify the coefficients of \(a_i\) and \(b_i\) of the linear dynamics model with the System Identification Toolbox of Matlab. ARX algorithm is employed for the identification and the Least squares method is adopted for the parameter optimization. It should be mentioned that, the higher order of na and nb, the more accuracy of the identified linear dynamics model, but the more computational complexity. Hence, the tradeoff of the identification accuracy and the computational complexity should be made during the identification. In this work, na and nb are both chosen as 8. The coefficients of A(z) and B(z) are finally identified as \(a_1=-0.05847\), \(a_2=0.2423\), \(a_3=-0.05833\), \(a_4=-0.4917\), \(a_5=0.4170\), \(a_6=-0.1945\), \(a_7=0.07748\), \(a_8=-0.01198\), \(b_1=0.004481\), \(b_2=0.04629\), \(b_3=0.1320\), \(b_4=0.1154 \), \(b_5=-0.02198\), \(b_6=-0.06236\), \(b_7=-0.0007691\), and \(b_8=0.01408\). The prediction error of the identified model is 2.534e-09. Besides, the frequency responses of the identified model and the experimental results are shown in Fig. 5, which also verifies the accuracy of the identified linear dynamics model.

Fig. 6.
figure 6

Comparison of the hysteresis nonlinearity of the experimental results and the predicted response with the identified MBW model.

Full size image

3.4 Identification of the MBW Model

To obtain the parameters of the MBW model, a triangular signal with multiple amplitudes is utilized as the input to the nanopositioning stage. The fundamental frequency of the triangular signal is 1 Hz. With this frequency, the linear dynamics of the nanopositioning stage can be treated as a dc gain with a fixed time delay. As \(G(j2\pi ) = 0.2464\), the hysteresis output \(\mathrm{{w}}(t)\) as shown in Fig. 2 can be derived as \(\mathrm{{w}}(i) = y(i + 3)/0.2464\). Then, the parameters of the MBW model can be identified using the input data v(t) and hysteresis output data \(\mathrm{{w}}(t)\). For convenience, both of the input voltage and the system output are normalized. A discrete form of the MBW model is used for the parameters identification, which can be expressed as

$$\begin{aligned} \mathrm{{w}}_\mathrm{{i}} = p_1 v_i^3 + p_2 v_i + h_i \end{aligned}$$
(6)
$$\begin{aligned} h_i = h_{i - 1} + A\Delta v_i \mathrm{{ - }}\beta \left| {\Delta v_i } \right| h_{i - 1} - \gamma \Delta v_i \left| {h_{i - 1} } \right| \end{aligned}$$
(7)

with \(\Delta v_i = v_i - v_{i - 1}\). In this work, the nonlinear least squares method is adopted to optimize the parameters of the MBW model. The identified parameters of the MBW model is \(A =-0.7691\), \({\beta }=4.6075\), \({\gamma } = - 0.8725\), \(p_1 = -0.1085\), and \(p_2 = 2.1925\). Figure 6 shows the simulated results with the identified MBW model in comparison with the experimental results. It can be seen that the hysteresis curves generated by the identified MBW model well match the experimental response of the PEA-actuated nanopositioning stage. The RMS prediction error is \(0.73\,\% \), which also validates the accuracy of the identified MBW model.

Fig. 7.
figure 7

The experimental results of the PEA-actuated nanopositioning stage and the prediction results of the dynamic model (Hammerstein-like structure) and MBW model under sinusoidal reference input with frequencies of (a) 1 Hz; (b) 50 Hz; (c) 100 Hz; (d) 200 Hz; (e) 300 Hz and (f) 400 Hz.

Full size image
Table 1. The RMS prediction errors of the dynamic model (Hammerstein-like structure) and the MBW model under sinusoidal reference input with various frequencies.
Full size table

4 Experimental Evaluation

To evaluate the effectiveness of the MBW model based Hammerstein-like structure to represent the hysteresis in PEAs with rate-dependent characteristic, experiments are performed with sinusoidal signals and triangular signals with different frequencies.

Fig. 8.
figure 8

The prediction errors of the dynamic model (Hammerstein-like structure) and the MBW model under sinusoidal reference with frequencies of (a) 1 Hz; (b) 50 Hz; (c) 100 Hz; (d) 200 Hz; (e) 300 Hz; and (f) 400 Hz.

Full size image

Firstly, the input signals are chosen as \(v(t)=3.5+2.5sin(2{\pi }ft)\) (V) with frequencies of \(f=\)1, 50, 100, 200, 300, and 400 Hz. Figure 7 shows the comparison of the experimental results and the predicted results with the dynamic model (Hammerstein-like model structure) and the MBW model. Figure 8 shows the comparison of the predicted errors of these two models. It can be observed from Fig. 7 that the predicted results with MBW model exhibit the rate-independent characteristic and it can only characterize the hysteresis effect of the PEA-actuated nanopositioning stage with the input frequency below 100 Hz. This is why we propose the dynamic model which cascades the MBW model with the linear dynamics of the nanopositioning stage. From Fig. 7, it can be observed that the dynamic model accurately describes the rate-dependent hysteresis nonlinearity under different input frequencies. To quantize the comparison, Table 1 lists the RMS prediction errors of the Hammerstein-like model structure and the MBW model, which also demonstrates the advantage of the proposed dynamic model structure. Hence, the effectiveness of the proposed Hammerstein-like structure with the MBW model to represent the rate-dependent hysteresis nonlinearity in PEAs is validated.

To further demonstrate the feasibility of the proposed model structure under multiple harmonics inputs, the comparisons of experimental responses and model prediction results under triangular signal input with the fundamental frequency of 100 Hz are illustrated in Fig. 9. It can be observed that the results with dynamic model structure match the experimental responses more accurately, which also validates the effectiveness of the Hammerstein-like structure with the MBW model.

Fig. 9.
figure 9

The experimental responses of the PEA-actuated nanopositioning stage and the simulated results of (a) MBW model and (b) dynamic model under triangular signal input with fundamental frequency of 100 Hz. (c) is the comparison of prediction errors with MBW model and the dynamic model.

Full size image

5 Conclusions

This paper proposes a MBW model with a third-order input function to describe the asymmetric hysteresis effect in the PEAs. Then, the MBW model is cascaded with a linear dynamics model as a Hammerstein-like structure to represent the hysteresis nonlinearity in PEAs with rate-dependent characteristic. The proposed Hammerstein-like model is identified with three steps using the specific input signals and the corresponding output responses of the nanopositioning stage. Experimental results on a PEA-actuated nanopositioning stage demonstrate that the proposed model can well predict the rate-dependent hysteresis nonlinearity. This work lays a foundation for the design of controllers that require system models.