Keywords

1 Introduction

Since its invention, the atomic force microscope (AFM) has emerged as the workhorse tool for studying, interrogating, and manipulating objects and matter at the nanoscale [1–4]. In AFMs, parallel piezo-actuated flexure-based nanopositioning stages are commonly used for positioning optics and many other micro and nanoscale systems [5–7]. However, piezo-actuated stages themselves suffer from the inherent drawbacks produced by the inherent creep and hysteresis nonlinearities [8, 9]. On the other hand, the raster scan trajectory is conventionally used in AFMs, The triangular signal excites the mechanical resonance modes of the PTS. This limits the positioning accuracy of PTSs for high speed surface imaging [10]. On top of that, the signal applied to the X-axis will corrugate the traced trajectory in the X-Y plane due to the presence of the cross-coupling effect in high frequency raster scanning [11, 12].

Various control approaches have been proposed to improve the performance of the AFM at high scanning rates. In high-speed and short distance AFM scanning, the creep and hysteresis nonlinearities are not the prime concern. Therefore, the following review focus on vibration damping and cross-coupling effect reduction. These works can be divided into feedforward and feedback categories [1, 5, 7, 10]. Feedforward control techniques [13, 14] are popular because of their noise efficiency, packageability, and low cost [15]. Model inversion methods are applied for vibration compensation in [16, 17]. However, the dynamics of nanopositioners change with the sample weight, ageing, and temperature [18]. Iterative learning control (ILC) [19–21] technique provides good tracking performance, but the performance of ILC is sample dependent [18].

There are also feedback control methods taking vibration damping and cross-coupling reduction into consideration. Some fix-structure damping controllers have been proposed, such as positive position feedback (PPF) [22], polynomial-based pole placement [23], positive velocity and position feedback (PVPF) controller [24], resonant control (RC) [25], and integral resonant control (IRC) [26]. Such controllers are effective to handle with vibration damping in single input single output (SISO) systems. For parallel MIMO systems, cross coupling effect at high scanning speed cannot be ignored. A high bandwidth MIMO H∞ controller is designed, regarding the cross coupling effect as external disturbance to improve tracking performance [11]. But the order of H∞ controllers depend on the order of systems. This will increase the complexity in the design process for high-order systems. The implementation of high-order controllers requires advanced DSP systems [15]. The MIMO damping controllers using reference model matching approach [18, 27] and mixed negative-imaginary approach [28] have been proposed to damp the first resonant mode as well as minimize cross-coupling effect simultaneously. However, the reference model matching approach relies on the optimal searching process. The initial values of parameters in order matrices are not easy to determine.

The motivation of this paper is to eliminate vibration and cross coupling effect in parallel nanopositioners. For vibration elimination, the double resonant controllers (IRC and RC) in [27] are adopted as their low orders and simple structure. Being different form the reference model matching approach for MIMO systems in [27], the effect of cross coupling is reduced through model-free decoupling filters (MFDF) applied to each axis. The advantages of this combination are the simplicity of controller design and the ease of implementation. Our contribution lies in improving the double resonant controllers for coupled parallel nanopositioners by introducing the MFDFs into the control loop of each axis.

The reminder of this paper is organized as follows. The system description of a parallel nanopositioner is given in Sect. 2. Section 3 discusses the model-free decoupling filter and double resonant controllers design. The simulation results with the analysis are presented in Sect. 4. Finally, the paper is concluded in Sect. 5.

2 System Description

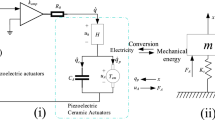
A 2-DOF parallel piezo-actuated nanopositioning stage was used as the controlled objective shown in Fig. 1. Each of the x- and y-axes is actuated by a PZT with a stroke of 100 μm. The displacement of each axis is detected by a capacitive sensor with the close loop resolution of 10 nm. The normalized transfer function of the MIMO system from the identification process is obtained using sinusoidal sweep response method as shown in Eq. (1).

$$ \left\{ \begin{aligned} G_{xx} = \frac{{146.6s^{5} + 7.9 \times 10^{5} s^{4} + 9.8 \times 10^{8} s^{3} + 2.1 \times 10^{12} s^{2} + 7.3 \times 10^{14} s + 9.4 \times 10^{17} }}{{s^{6} + 1009s^{5} + 3.8 \times 10^{6} s^{4} + 1.8 \times 10^{9} s^{3} + 3.5 \times 10^{12} s^{2} + 7.1 \times 10^{14} s + 9.4 \times 10^{17} }} \hfill \\ G_{xy} = \frac{{104.1s^{5} - 3.6 \times 10^{4} s^{4} + 8.9 \times 10^{7} s^{3} - 1.7 \times 10^{11} s^{2} + 8.2 \times 10^{13} s - 1.6 \times 10^{4} }}{{s^{6} + 1009s^{5} + 3.8 \times 10^{6} s^{4} + 1.8 \times 10^{9} s^{3} + 3.5 \times 10^{12} s^{2} + 7.1 \times 10^{14} s + 9.4 \times 10^{17} }} \hfill \\ G_{yx} = \frac{{104.1s^{5} - 3.6 \times 10^{4} s^{4} + 8.9 \times 10^{7} s^{3} - 1.7 \times 10^{11} s^{2} + 8.2 \times 10^{13} s - 1.6 \times 10^{4} }}{{s^{6} + 1009s^{5} + 3.8 \times 10^{6} s^{4} + 1.8 \times 10^{9} s^{3} + 3.5 \times 10^{12} s^{2} + 7.1 \times 10^{14} s + 9.4 \times 10^{17} }} \hfill \\ G_{yy} = \frac{{146.6s^{5} + 7.9 \times 10^{5} s^{4} + 9.8 \times 10^{8} s^{3} + 2.1 \times 10^{12} s^{2} + 7.3 \times 10^{14} s + 9.4 \times 10^{17} }}{{s^{6} + 1009s^{5} + 3.8 \times 10^{6} s^{4} + 1.8 \times 10^{9} s^{3} + 3.5 \times 10^{12} s^{2} + 7.1 \times 10^{14} s + 9.4 \times 10^{17} }} \hfill \\ \end{aligned} \right. $$
(1)
Fig. 1.
figure 1

A 2-DOF parallel nanopositioning stage

Full size image

Vibration Problem.

The frequency response of the system was obtained as displayed in Fig. 2. It can be seen that the first order of mechanical resonance mode occurs at the frequency of 123 Hz. For AFMs, a raster scan trajectory is the most widely used as scan trajectory because of the simplicity of the image reconstruction [18]. However, with increasing scan speeds, the high-frequency components of the trajectory reference signals will excite the mechanical resonant modes of the nanopositioner and introduce unwanted residual vibrations and tracking errors [7]. Therefore, vibration damping is important for high speed raster scan in AFMs.

Fig. 2.
figure 2

Frequency response of the MIMO system. The resonant peak is 15.8 dB at 123 Hz for diagonal frequency responses and 12.3 dB at 123 Hz for non-diagonal frequency responses.

Full size image

Cross Coupling Effect.

As is known, the cross coupling in parallel structures between the x- and y-axes can be more difficult to deal with compared to serial mechanisms [5]. Therefore, like the existing works in [12, 29, 30], the stage in Fig. 1 was designed to be decoupled with cross coupling as low as possible. As depicted in Fig. 2, the cross coupling in non-diagonal plots are achieved as −65 dB to −20 dB at low frequency (from 1 Hz to 70 Hz). However, the magnitude tends to be positive with the increase of scan speed, which results in strong cross coupling effect on imaging. This limits the positioning accuracy of the stage.

3 Controller Design

As analyzed in Sect. 2, the main control objectives of this paper are vibration damping and cross coupling reduction. In order to achieve these goals, a combination of double resonant controller and decoupling finite impulse response (FIR) filter is designed in this section.

3.1 Design of Double Resonant Controller

The double resonant control is firstly proposed in [18] and discussed deeply in [15, 27]. This method contains an IRC controller to damp the first resonant mode and a RC controller to broaden the close loop bandwidth.

Integral Resonant Controller.

IRC is a feedback control technique suitable for damping highly resonant structures [26]. It is a combination of integral controller and a feed through term with its simplified structure given in Fig. 3. The integral controller is wrapped around the controlled objective to achieve damped close loop system. The feed through term d is selected to achieve a zero-pole interlacing property instead of pole-zero interlacing property for the system [27]. To build an IRC, the controlled system needs to be reduced into a second-order system [26] with the dynamics displayed as

$$ G\left( s \right) = \frac{\Upgamma}{{s^{2} + 2\xi_{p} \omega_{p} s + \omega_{p}^{2}}} $$
(2)

where \( \Upgamma > 0 \) is the low frequency gain, \( \omega_{p} \) denotes the natural frequency, and \( \xi_{p} \) is the damping coefficient.

Fig. 3.
figure 3

Double resonant controller. \( K_{r} ,\;\xi_{r} \;\text{and}\;\omega_{r} \) are the static gain, damping constant and resonant frequency of R, respectively [18].

Full size image

The feed through term d can be achieved through Eq. (3) and the integral gain K can be obtained by Eq. (4).

$$ d = - \frac{4\Upgamma }{{3\omega_{p}^{2} }} $$
(3)
$$ K = \frac{{\sqrt {2\omega_{p} } }}{d} $$
(4)

Resonant Controller.

The introducing of integral component of IRC leads to a decreased bandwidth of the closed-loop system. Therefore, a high-pass resonant controller R needs to be added into the control system given in Fig. 3. The combined closed-loop transfer function can be expressed as

$$ T_{cl} \left( s \right) = \frac{{G\left( s \right)\left( {C\left( s \right) + R\left( s \right)} \right)}}{{1 + G\left( s \right)\left( {C\left( s \right) + R\left( s \right)} \right)}}. $$
(5)

In this paper, the MIMO system in (1) is regarded as two SISO systems. A double resonant controller described in Fig. 3 is applied to each SISO loop for vibration damping. The cross coupling effect is reduced by a decoupling controller discussed in Sect. 3.2. There are five parameters in the double resonant controller with the initial values of C(s) chosen according to Eq. (3). With respect to the chosen of parameter values in the high-pass resonant controller R(s), the resonant frequency \( \omega_{r} = 2\pi \omega_{d} \) can be estimated according to the ideal close-loop transfer function set as

$$ T\left( s \right) = \frac{1}{{\frac{1}{2\pi \omega }s + 1}} $$
(6)

where \( \omega \) is the ideal close-loop bandwidth in Hz. Here, \( \omega \) was chosen as 120 Hz based in the frequency response shown as Fig. 2.

Some trials need to be conducted to determine the static gain and the damping constant, making sure that the close-loop (5) is stable.

Optimization Process.

Following the initial selection of controllers is the parameter optimization process. The optimization was carried out by using the simulated annealing algorithm from the MATLAB optimization toolbox [18]. The fminsearch command was adopted for optimization. The objective function is

$$ \left\| {E\left( s \right)} \right\|_{\infty } = \left\| {T\left( s \right) - T_{cl} \left( s \right)} \right\|_{\infty } $$
(7)

where \( E\left( s \right) \) denotes for the error function, \( \left\| \cdot \right\|_{\infty } \) represents the infinity norm of a transfer function.

The optimized results are \( K = - 314,\;d = - 2,\;K_{r} = 0.1,\;\xi_{r} = 0.6,\;\omega_{r} = 753.6 \) for each axis control loop as the x- and y-axes are designed symmetry. Taking x-axis as the example, the closed-loop and open-loop bode plots are shown in Fig. 4. The Fig. 4a describes the step response. Figure 4b is the bode diagram, which tells that the designed closed-loop bandwidth is close to the first resonant peak as shown in Fig. 2.

Fig. 4.
figure 4

Designed results of double resonant controller for x-axis.

Full size image

3.2 Design of Model-Free Decoupling Controller

In general, the model-based decouplers are infinite impulse response (IIR) model with the need for accurate identified model and model structure. For instance, the model-based decoupler for x-axis can be derived as

$$ D_{x} \left( s \right) = \frac{{G_{xy} \left( s \right)}}{{G_{xx} \left( s \right)}} $$
(8)

However, the non-minimum phase zeros can be an obstacle to solve the decouplers via IIR model. Another method is to use a finite impulse response (FIR) filter with the advantage of no model structure to be chosen, i.e. modeling-free approach. In this paper, the FIR Model-free Decoupling Controller (MFDF) design can be treated as (1) nonparametric frequency-domain system estimation and (2) IDFT transformation. It should be mentioned that Step (1) is conducted based on [31], and Step (2) is our contribution to introduce the method into decoupling controller design.

Nonparametric Frequency-Domain System Estimation.

The synthesis of MFDF is based on empirical transfer-function estimate (ETFE) [31] of the plant. A two-run method for the plant is adopted. Here, we use the pseudo-random binary signal (PRBS) that is deterministic and spectrally white as the input to excite system. The x-axis input is PRBS and y-axis has no input for the first run. The second run is reverse. Then, two sets of data can be obtained as describe in Fig. 5.

Fig. 5.
figure 5

The two-run block diagram for ETFE.

Full size image

In the frequency samples \( k \in \left[ {0,\;M - 1} \right] \), the ETFT plants from x- to x-axis and y- to x-axis (see Fig. 2) are denoted \( \hat{G}_{xx} \left( k \right),\;\hat{G}_{xy} \left( k \right) \) respectively,

$$ \hat{G}_{xx} \left( k \right) = \frac{{x_{out}^{1} \left( k \right)}}{{x_{in}^{1} \left( k \right)}} $$
(9)
$$ \hat{G}_{yx} \left( k \right) = \frac{{x_{out}^{2} \left( k \right)}}{{y_{in}^{2} \left( k \right)}} $$
(10)

where \( x_{out}^{1} \left( k \right),\;y_{in}^{1} \left( k \right),\;x_{out}^{2} \left( k \right),\;y_{in}^{2} \left( k \right) \) are the discrete Fourier transforms (DFT) with the superscript denoting experiment number and the subscript denoting data flow. Hereto, the ETFT of decoupler for x-axis can be expressed as

$$ \hat{D}_{x} \left( k \right) = \frac{{x_{out}^{2} \left( k \right)}}{{x_{out}^{1} \left( k \right)}}, $$
(11)
$$ \left\{ \begin{aligned} x_{out}^{1} \left( k \right) = \sum\limits_{n = 0}^{M - 1} {x_{out}^{1} \left( n \right)\;\text{e}^{ - j2\pi kn/M} } \hfill \\ x_{out}^{2} \left( k \right) = \sum\limits_{n = 0}^{M - 1} {x_{out}^{2} \left( n \right)\;\text{e}^{ - j2\pi kn/M} } \hfill \\ \end{aligned} \right., $$
(12)

and n stands for the time samples.

IDFT Transformation.

To obtain the FIR decoupler, the inverse discrete Fourier transform (IDFT) is implemented for the unit impulse response \( d_{x} \left( n \right) \)

$$ d_{x} \left( n \right) = \frac{1}{M}\sum\limits_{k = 0}^{M - 1} {\hat{D}_{x} \left( k \right)\;\text{e}^{j2\pi kn/M} ,}^{{}} $$
(13)

and the FIR filter then expressed in the z-domain as

$$ D_{xfir} \left( {z^{ - 1} } \right) = \sum\limits_{n = 0}^{M - 1} {d_{x} \left( n \right)z^{ - n} .} $$
(14)

In this paper, the decoupler design was implemented through the MATLAB. The etfe command was used for frequency-domain system estimation, and the impulseest command was used for IDFT transformation. The designed result of MFDF is shown in Fig. 6 comparing with derived results using model information through Eq. (8). It can be observed that the designed MFDF is anastomotic to the model-based decoupler, especially in high-frequency domain.

Fig. 6.
figure 6

Comparisons of model-based decoupler and the designed MFDF for x-axis. The solid dark line (–) is model-based decoupler and the blue dash line (–) is the MFDF. (Color figure online)

Full size image

3.3 Overall Design Procedure

Hereto, we propose the following design procedure.

  1. 1.

    Use the two-run method in Fig. 5 to collect two set of the experiment data, and design MFDF for x- and y-axes.

  2. 2.

    Design the double resonant controller for each axis independently. Select the initial values for the IRC and RC according to Eqs. (3), (4) and (6). Perform the optimization process to achieve the final controller.

Compared with design methods in [18, 27], we decreased the number of parameters in the MIMO double resonant controller from 13 to 5 for 2-DOF motion systems through adding the MFDF to reduce cross coupling effect instead of the order matrices (8 parameters). Finally, the control scheme can be depicted as Fig. 7.

Fig. 7.
figure 7

Combined MFDF and double resonant controller scheme.

Full size image

4 Evaluation

4.1 Cross Coupling Reduction by Adding MFDF

Before raster scan simulations, the cross coupling reduction was analyzed through one-channel input. Results are shown in Fig. 8. It can be seen that the slightest cross coupling effect is achieved by the combination of IRC&RC&MFDF.

Fig. 8.
figure 8

Cross coupling outputs of y-axis by inputting triangular signals to the x-axis at 5 Hz (Fig. 9a), 15 Hz (Fig. 9b) and 25 Hz (Fig. 9c) with a distance of 4 μm under open-loop, IRC&RC and IRC&RC&MFDF, respectively.

Full size image

4.2 Raster Scan Results Under the Combination

Raster scan simulations were conducted to evaluate the proposed combination of IRC&RC&MFDF. Triangular signals under 5 Hz, 10 Hz and 20 Hz with the amplitude of 4 μm were inputted into x-axis, and the synchronized staircase waves with the stair step of 0.05 μm were inputted into y-axis. Figure 9 shows the close look of the scan results at 20 Hz case. It can be seen that both the vibration (see Fig. 9b) and the cross coupling (see Fig. 9c) are reduced to the least under IRC&RC&MFDF control.

Fig. 9.
figure 9

Raster scan results. (a) X-axis tracking versus time. (b) Y-axis tracking versus time. (c) XY-plane tracking

Full size image

The root mean square (RMS) errors of raster signal corresponding to the two sets of controllers for 75 % of the x-axis scanning range (i.e., 3 μm along the x-axis) are documented in Table 1. It can be observed that all the RMS errors under IRC&RC&MFDF scan remain below 7 nm, which is smaller than that under IRC&RC alone control. For the 20 Hz scan, the proposed control strategy reduces the RMS error by 78 % (from 30.5 to 6.8 nm).

Table 1. RMS errors of the raster tracking performance.
Full size table

5 Conclusions

The main goal of this paper was to damp vibration and reduce cross coupling simultaneously for high-speed raster scan in nanopositioners. This was done by: (1) applying an IRC to damp the first mechanical resonant of the structure and a RC to broaden the closed-loop system bandwidth and (2) adding a MFDF designed through nonparametric frequency-domain system estimation and inversed DFT transformation, which was our contribution in this work. Comparisons between double resonant controller alone with IRC&RC&MFDF control were made through simulations to evaluate the proposed method. Results proved that the proposed IRC&RC&MFDF achieved a 78 % RMS error improvement under 20 Hz raster scan from IRC&RC alone control, i.e., the better tracking performance for high-speed rater scanning.

The ongoing work involves the consideration of external disturbance as well as noise, and the implementation of experiments.