Keywords

1 Introduction

Supply Chain Management, in particular production and inventory management, is a classical scientific research area in Operations Research. The desire to organize the resource usage and material flow through the value chain in the most efficient way has inspired the development of suitable mathematical models and analytic as well as computational solution techniques for over a century. Many cornerstones of inventory theory are now an integral part of every Operations Research textbook, providing essential insights into the fundamental trade-offs between resource cost and service level and how to optimally parameterize and control inventory systems, even under uncertainty.

Yet, many traditional approaches and tools cannot readily cope with the growing complexity and size of today’s supply and production networks, and results that hold for simple systems (such as single warehouse or serial systems) do not extend to general networks. In fact, except for a few special cases, inventory network control problems are usually intractable, and a common approach is to resort to simple heuristics that are known to work well in simpler situations.

Another way to deal with complex problems is by approximation, that is, to solve a problem approximately with less effort, but ideally with some performance guarantees. This paper explores the question whether a recently developed type of approximate dynamic programming, based on piece-wise linear convex value function approximations, is useful approximation technique for typical supply chain control problems. The next section motivates and describes the technique, which is then applied to the well-known problems of multiple sourcing (Sect. 3) and dynamic inventory allocation (Sect. 4), respectively.

1.1 Monotone Approximate Relative Value Iteration

Using appropriate definitions of state and action spaces, multi-echelon supply chain control problems can conveniently be formulated as Markov decision processes (MDPs). However, as solving an MDP explicitly requires to store values for all states, the curse of dimensionality usually makes it impossible to solve such models for supply chain control problems of realistic size.

One way to cope with the curse of dimensionality is to look for an approximate solution for the MDP, for instance using Approximate Dynamic Programming (ADP). ADP is an active research area with a variety of literature. Standard textbooks include, e.g., Bertsekas and Tsitsiklis (1996) or Powell (2007).

A typical approach in ADP is to approximate the optimal value function using a linear combination of a fixed set of functions on the state space, called basis functions. Such approaches were shown to work well for some applications (see e.g. Schweitzer and Seidmann 1985 or Farias and Van Roy et al. 2006). However, determining a good set of basis functions is often very difficult and very problem-specific.

In this section, we propose a generic approach for supply chains by exploiting the fact that many supply chain control problems can be described as controlled linear systems in discrete time with the following features:

  • The state space is given by a polyhedral set \( {\text{S}}\,{:=}\, \{{\text{x}} \in {\text{R}}^{\text{n}} |{\text{Qx}} \le \beta \} \).

  • The set of feasible actions U(x) for a given state x ∈ S is defined as \( {\text{U(x)}}\,{:=}\, \{ {\text{u }} \in {\text{ R}}^{\text{m}}|{\text{Ru}} + {\text{Vx}} \le \delta \} , \) that is, a polytope for each state x.

  • The dynamics are linear so that for any state-action pair (x, u), the random successor state x is given by \( {\text{x}}^{\prime}\,{:=}\,{\text{Ax}} + {\text{Bu}} + {\text{C}} \) where (A, B, C) is a multidimensional random variable that takes values in Rn×n × Rn×m × Rn. We assume there are J ∈ N different possible realizations for (A, B, C), denoted by (Aj, Bj, Cj) with probabilities pj ∈ [0, 1].

  • The immediate costs r: S × U → R are assumed to be piecewise linear and convex.

As shown in Woerner et al. (2015), there exists a convex solution for the discounted cost as well as for the average cost optimality equation for SLCPs. This motivates the use of piece-wise linear convex approximations of the value function (instead of a linear combination of basis functions as in usual ADP approaches). Therefore we use a specialized algorithm called MARVI (Monotone Approximate Relative Value Iteration, see Woerner et al. 2015), to obtain a piece-wise linear convex value function approximation for it.

Any such value function approximation h: S → R defines a corresponding policy as

$$ \pi_{h} (x) = \mathop {\arg \hbox{min} }\limits_{u \in U(x)} \left\{ {r(x,u) + \sum\limits_{j = 1}^{J} {p_{j} h\left( {A_{j} x + B_{j} u + C_{j} } \right)} } \right\} $$

Thus, instead of fixing a set of basis functions as in standard ADP approaches, we take the maximum of a set of hyperplanes, which will be adaptively generated during the run of the algorithm.

2 Application for Multiple Sourcing

The multiple sourcing problem is a well-studied problem in inventory control (Minner 2003). The goal is to optimally control a single stock by continuously ordering from a given set of potential suppliers. In this setup, each supplier represents a different combination of ordering cost and lead time.

Figure 1 gives a schematic view of the multiple sourcing problem for the case of two suppliers. Supplier S1 has a longer delivery lead-time, in this case three time steps, which is indicated by its order queue the ordered items have to pass until they reach the inventory node. In contrast, the orders of the faster supplier S2 are available already in the next time step after an order is placed. Using the notation of the previous section, x represents the state (the inventory level and the open orders) and u represents the action (the ordering decisions at the two suppliers).

Fig. 1
figure 1

Schematic view of the multiple sourcing problem for two suppliers

Full size image

The multiple sourcing problem is a well-studied hard problem. The goal is to find an optimal policy (a mapping from states to actions) that minimizes the infinite horizon average cost, which consists of ordering cost, inventory holding cost and backlog cost for unmet demand.

Since nothing is known about an optimal policy, different heuristics have been developed and are commonly used in practice:

  • The Fixed Order Ratio Policy simply allocates a fixed ratio of the order quantity to each supplier in each time step.

  • The Constant Order Policy orders a constant amount at one supplier (usually the slower one) and reacts to variability via optimally ordering from the other supplier. The problem is thereby reduced to a standard one-warehouse inventory control problem, which can be solved efficiently.

  • The Single Index Policy uses the inventory position (inventory level plus unfilled orders) as an index to be compared to a threshold to determine how much to order at each of the suppliers.

  • The Dual Index Policy uses the inventory position as well as the expedited inventory position (inventory level plus unfilled orders that will arrive within the lead time of the fast supplier) to determine how much to order at the slow and the fast supplier, respectively.

The Dual Index Policy has been shown to perform very well compared to the optimal policy on a set of small instances where the optimal policy could be computed by numerically solving the corresponding MDP (Veeraraghavan and Scheller-Wolf 2008).

We now compare the Dual Index Policy with the policy found by applying the MARVI algorithm as described in the previous section. The following problem parameters are chosen:

  • Holding cost: 1$ per time step,

  • Backlog cost: 5$ per time step,

  • Ordering cost: 1$ per unit for the slow supplier S1 and 2$ per unit for the fast supplier S2.

The delivery lead time of the fast supplier is fixed at zero, while we consider different problem instances where the lead time of the slow supplier varies from 1 to 6 time steps.

Figure 2 displays the resulting total costs as a function of the lead-time of the slow supplier, for both the optimal Dual-Index Policy and a MARVI policy. The results show that the MARVI policy obtains lower total costs than the Dual Index Policy, and that this gap tends to increase with increasing lead-time difference between the suppliers. Furthermore, a lower bound is shown, which is also computed by the MARVI algorithm as a by-product and allows us to give an instance-specific performance guarantee.

Fig. 2
figure 2

Total costs for the dual sourcing problem as a function of the lead-time of the slow supplier

Full size image

Another advantage of the MARVI policy is that it reduces the order variance for the suppliers, as shown in Fig. 3.

Fig. 3
figure 3

Average order quantities and standard deviation (per time step) of the Dual Index Policy and the MARVI policy

Full size image

3 Application for Dynamic Inventory Allocation

Dynamic inventory allocation is the process of allocating inventory (from a potentially large set of alternative stocking locations) to incoming orders. This task is typically faced in operations of large, spatially distributed inventory networks, such as spare part networks (Tiemessen et al. 2013) or in order fulfillment of large e-commerce retailers.

The key decision in dynamic inventory allocation is therefore the decision from which stocking point a given order should be satisfied. This decision should optimally balance the (immediate) fulfillment cost (which mainly consists of transportation and handling costs) with the expected future opportunity cost of decreasing the inventory at the stocking point chosen for fulfillment. This opportunity cost is mainly related to the loss of serviceability in case of future orders (for example lost sales in an e-commerce environment or contract penalties for spare part operations).

The decision situation faced by the dispatcher is schematically represented in Fig. 4 for the example of a spare part request of a customer with contractually guaranteed delivery time of 8 h. The score card lists the different delivery options for the current order, together with the respective delivery costs, and estimation of the expected future opportunity costs and the resulting total cost. The graph below depicts the decision situation geographically.

Fig. 4
figure 4

Decision situation for dynamic inventory allocation

Full size image

Besides the customer of the current order and the different delivery options, Fig. 4 also indicates the location of another potential customer. In case the first customer order is satisfied from Warehouse 1, a potential future demand by the second customer might lead to a stock-out situation at Warehouse 1, and consequently, if no other delivery options are available, to a violation of the service level agreement and hence a penalty payment. This risk is captured in the expected future costs.

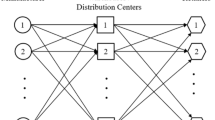
The main question is how to compute the expected future cost. If this value was known, the optimal policy would be to allocate the order to the delivery option with lowest total costs. As in the previous sections, the problem can be formulated as a Markov decision process with the inventory levels at the different warehouses, the open replenishment orders (due to the replenishment lead-times), and the open customer demand as the state variables and the allocation as well as replenishment decisions as control actions. Figure 5 shows such a network with a central hub (top), two stocking locations (center), and two customers (bottom), as well as all possible delivery options.

Fig. 5
figure 5

Simplified state space representation of the dynamic inventory allocation problem

Full size image

Again, solving the MDP model for an inventory allocation network of realistic size is prohibitive and thus heuristic or approximate techniques are needed.

In a case study with approximately 40 warehouses and 150 customers the MARVI algorithm was applied to approximate optimal inventory allocation policies. Policies were computed separately for 18 different products. Compared to a greedy heuristic that simply allocates based on lowest immediate delivery cost, the study has shown that, depending on the instance, a total cost reduction of 1 % to 10 % was achievable. Besides optimizing the fulfillment decisions, a further advantage of applying MARVI is that it also yields an estimation of the expected future cost, which is very useful information for the dispatcher, as it gives a clear quantitative rationale why the suggested fulfillment option is optimal.

4 Conclusions

Two typical problems in multi-echelon supply chain management have been discussed in this paper, one regarding the supply side (multiple sourcing) and another one regarding the demand side (dynamic inventory allocation) of the supply network. Both problems are hard, so that a direct solution by solving the corresponding Markov decision process is usually impossible due to the size of the state space. Nevertheless, both problems are widely encountered in practice and need to be dealt with somehow, usually by simple heuristics.

This paper has discussed the application of a new approximation technique—Monotonous Approximate Relative Value Iteration—that exploits the structural properties that these problems (and many other supply chain control problem) have, specifically their linear dynamics and piece-wise linear convex cost structure. The main advantages of this approach are: (i) it handles high-dimensional state spaces, (ii) it provides a policy on any approximation it builds (even on a coarse approximation) and (iii) it provides lower bounds. The main disadvantages are: (i) the approach is algorithmically more difficult to implement than a standard dynamic programming approach and (ii) the policy as well as the bounds might be weak if the approximation is not good enough. A limitation is given by the assumption of piece-wise linear and convex costs, so the approach is not able to handle fixed costs.

Whether the mentioned disadvantages and limitations prevent the approach to yield meaningful results is case specific. On the examples considered in this chapter, the approximation technique achieves a noticeable (up to 10 %) cost reduction compared to the best-know heuristics while at the same time giving valid lower bounds on the total cost. In future work, the applicability of the technique to other problems in supply chain management should be considered and its scalability to larger state space dimensions should be explored. One goal of further investigation would be to analyze whether certain problem properties, such as the mixing properties of the underlying Markov chain or the number of different realizations of the random variables, are indicative of the complexity of the optimal value function, its approximability, and thus the quality and performance of our approximation approach.