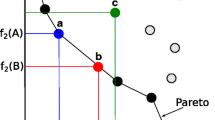
Abstract
This paper proposes and develops a novel multi-objective optimization scheme called MORSGO based on iterative adaptation of plant root growth behaviors. In MORSGO, the basic local and global search operators are designed deliberately based on auxin-regulated tropism of the natural root system, including branching, regrowing of different types of roots. The fast non-dominated sorting approach is employed to get priority of non-dominated solutions obtained during the search process, and the diversity over archived individuals is maintained by using dynamical crowded distance estimation strategy. Accordingly, Pareto-optimal solutions obtained by MORSGO have merits of better diversity and lower computation cost. The proposed MORSGO is evaluated on a set of bio-objective and tri-objective test functions taken from the ZDT benchmarks in terms of two commonly used metrics IGD and SPREAD, and it is compared with NSGA-II and MOEA/D. Test results verify the superiority and effectiveness of the proposed algorithm.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Many real-world optimization problems often involve simultaneously optimizing over two or more mutually conflicting objective functions with some uncertain constrains instead of transforming them into a single objective, and accordingly they are generally named as multi-objective optimization problems (MOPs) [1, 2]. These MOPs are more difficult to be handled than the single-objective issues due to the fact that decision makers would find a set of Pareto-optimal solutions (PS) or non-dominated solutions with a trade-off among objectives [3]. Inspired by different backgrounds, an increasing number of multi-objective evolutionary algorithms (EAs) or swarm intelligence (SI) algorithms have been proposed and extended to tackle the MOPs, prominent examples being non-dominated sorting genetic algorithm II (NSGA-II) [2], multi-objective evolutionary algorithm based on decomposition (MOEA/D) [3], strength Pareto evolutionary algorithm (SPEA2) [4], and multi-objective particle swarm optimization (MOPSO) [5]. However, how to improve the diversity of population or overcome the local convergence of algorithms is still a challenging issue in MO optimization [6, 7]. In this paper a new multi-objective bionic algorithm is proposed derived from plant root growth behaviors and optimal foraging, namely multi-objective root system growth optimizer (MORSGO), which adopts the branching, regrowing, mortality and tropism operations of the root system. Intuitively, the basic search technique of MORSGO can acquire appropriate balance of local search and global search and dynamical variance of population size [6, 7]. Generally, this elite retention strategy can effectively eliminate the infeasible individuals and keep feasible individuals throughout the search process [2]. Accordingly, Pareto-optimal solutions obtained by MORSGO have better diversity and lower computation cost.
2 Multi-objective Root System Growth Optimizer
2.1 Root System Growth Model (RSGO)
2.1.1 Auxin Information
Assume that the total sum of auxin concentration F i is defined as 1 in the root system, and each root’s F i value can be calculated as:
Assume that the total sum of auxin concentration F i is defined as 1 in the root system, and each root’s F i value can be calculated as:
where i is the position of the growing point, \( \upxi \) is a uniform random quantity, N is the total number of the points, fit (.) is the fitness value of the point and f worst and f best are the maximum and minimum of the current points, respectively. Nutrition i is the current nutrient concentration of individual i and it can be expressed as:
In each growing cycle, all individuals are sorted by their auxin concentrations in descending order [7, 8]. That is, the strong individuals with higher auxin concentrations can be selected as main roots to branch. In our model, half of current sorted roots are selected as main roots:
where \( S_{m}^{t} \) is the number of selected main roots, P t is the size of current population.
2.1.2 Mainroots Growth Operations
-
Regrowing
-
Step 1. In each cycle, the group of main roots is constructed by selecting half population sorted according to auxin concentration.
-
Step 2. Considering effect of hydrotropism, select half of current main roots to search towards the optimal position of individuals, given by:
$$ x_{i}^{t + 1} = x_{i}^{t} + R_{3} (x_{best}^{t} - x_{i}^{t} ) $$(6)where \( i \subseteq [1,\,S_{m}^{t} /2] \), R 3 is random value in the range (0, 1), and \( x_{best}^{t} \) is the best position in the root tip group.
-
Step 3. Considering gravitropism, the rest of main roots will grow along their original directions as:
$$ x_{i}^{t + 1} = x_{i}^{t} + R_{4} I_{\hbox{max} } (\phi_{i}^{t} ) \, if \, x_{i}^{t} > x_{i}^{t - 1} $$(7)where \( i \subseteq [{{S_{m}^{t} } \mathord{\left/ {\vphantom {{S_{m}^{t} } 2}} \right. \kern-0pt} 2},\,\,S_{m}^{t} ],\,\,l_{\hbox{max} } \) is the maximum of root elongation length, R 4 is a normally distributed random number with mean 0 and standard deviation 1; \( H(\phi_{i}^{t} ) \) is a D-dimensional growth direction of the main root \( i;\,\,\phi_{i}^{t} = (\phi_{i1}^{t} ,\,\phi_{i2}^{t} , \ldots ,\phi_{i(D - 1)}^{t} ) \in R^{D - 1} \) is a D-1-dimensional growth angle, given by:
$$ \phi_{i}^{t + 1} = \phi_{i}^{t} + R_{5} *\omega_{\hbox{max} } ,\,\,\text{0 < }\omega_{\hbox{max} } < \pi $$(8)where \( R_{5} \in R^{D - 1} \) is a uniformly distributed random sequence in the range (0, 1); \( \omega_{\hbox{max} } \) is the maximum of growing angle, which is limited to \( \pi \).
-
-
Branching
-
Step 1. The nutrient concentration (Nutrition i ) of mainroot i is compared with BranchG (0 < BranchG < 1) to determine whether it performs branching operator:
-
$$ \left\{ {\begin{array}{*{20}c} {branching} & {if \, Nutition_{i} > BranchG} \\ {nobranching} & {otherelse} \\ \end{array} } \right. $$(9)
-
Step 2. Calculated the new branching points as:
-
$$ X_{i}^{t + 1} = X_{i}^{t} + R_{1} *D_{i} {(\varphi }_{i} \text{)}, $$(10)
-
where \( X_{i}^{t + 1} \) is the new growing point from \( X_{i}^{t} ,\,R_{ 1} \), is the elongate-length unit, which is a random varying from 0 to 1, φ i is the growth angle \( (\varphi_{i1} ,\,\varphi_{i2} \ldots \varphi_{i(D - 1)} ) \).
-
The growth angle \( {\varphi }_{i} \) is calculated as follows:
-
$$ {\varphi }^{t + 1} = {\varphi }^{t} + R_{2}\upalpha_{init} + K*\beta \hbox{max} /S_{\hbox{max} } , $$(11)
-
where R 2 is a random coefficient varying from 0 to 1, αinit is original growth angle of the initial mainroot as zero degree, K is randomly parameter selecting the subzone, S max is subzones number, and βmax is the maximum growing turning angle. Empirically, βmax is limited to \( \pi \).
-
2.1.3 Lateral Roots Growth Operation
At the t th iteration, each lateral root tip generates a random head angle and a random elongation length, given by:
where \( i \subseteq [0,S_{l}^{t} ] \), R 5 and R 6 are random values in the range (0, 1), \( \phi_{\hbox{max} } \) is the maximum growing turning angle, and \( l_{\hbox{max} } \) is the maximum of root elongation length.
2.1.4 Dead-Roots Elimination
In the proposed root foraging model, it is assumed that \( N_{i} \) is the current population size, \( N_{i} \) will increase by one if a root tip splits and reduce by one if a root dies determined by auxin distribution, and it will vary in the searching process [9, 10].
2.2 The MORSGO Algorithm
2.2.1 Fast Non-dominated Sorting
In each computational iteration, two significant operations need to be calculated, namely domination count D x , and the set of solutions S x dominated by solution x. D x donates the number of solutions dominated by x from current population P. Detailed procedures of this process is given in Algorithm 1.

2.2.2 The Dynamical Crowded Distance Estimation Method
In order to pick out the redundant PS archive and maintain a certain number of solutions, the crowding-distance estimation method [2] is usually used to calculate the average distance of two points on either side of this point along each of the objectives, and it can be formulated as follows:
where C i is the crowding distance of individual i, M is the number of objective functions, f i,j is the j-th objective function value of individual i.
Then, an improved selection method, namely the dynamical crowded distance estimation method is adopted instead of the traditional crowded distance method [2]. Detailed procedures of this method are given in Algorithm 2.

Finally, based on above mechanisms and strategies, the main procedures of MORSGO are listed in Table 1.
3 Benchmark Test
3.1 Test Problems and Performance Measures
Five representative benchmarks, including bio-objective ZDT1, ZDT2, and ZDT6, and tri-objective DTLZ1 and DTLZ6, are selected to evaluate the performance of the proposed algorithm [9]. Detailed formulas of these test instances are referred in [9].
Two performance measures are considered: (1) convergence metric \( \varUpsilon \) based on IGD-metric [10], (2) spread metric \( \Delta \) proposed in [2]. Accordingly the detailed information about the two metrics can refer to [2, 10] respectively.
3.2 Experimental Setup
Experiments are conducted with MORSGO, NSGA-II [2], and MOEA/D [3]. The common parameters for all algorithms are set as following: the population size is 100, the maximum iteration number is set to 1000, and the number of independent algorithmic runs is 20. For other parameters in MOEA/D and NSGA-II, they keep the same with their original Refs. [2, 3].
3.3 Results and Analysis
Tables 2 and 3 give computational results obtained by MORSGO, NSGA-II and MOEA/D in 20 runs on bi-objective and tri-objective ZDTs. It is seen from Table 2 that MORGO is able to find better mean, best and standard deviation values of the IGD metric in all bio-objective test functions except ZDT2. MOEA/D and NSGA-II obtain a little better performance than MORSGO on ZDT2 only in terms of best and median values of IGD-metric. For the \( \Delta \)-metric, in all cases with MORGO, the standard deviation and mean values are significantly satisfactory, except in NSGA-II with ZDT2 and in MOEA/D with ZDT6. This means that MORGO can get a better spread of non-dominated solutions than other algorithms. From Table 2, it is clearly seen that MORSGO yields similar performance in terms of diversity and convergence to the bio-objective test case. Specially, MORSGO is able to obtain the best spread of solutions on DTLZ1 and DTLZ6. For the IGD metric, on DTLZ1, MORGA obtains the best mean and standard deviation values, but NSGA-II also obtains the best mean values. On DTLZ2, MORGA obtain better performance in terms of mean, best and median values than the others, but MOEA/D obtains the best standard deviation.
4 Conclusions
In this paper, a new plant-inspired algorithm called MORSGO is designed to handle multi-objective optimization problems. In MORSGO, several basic search operators are designed and developed inspired from the plant root growth behaviors. To effectively handle non-dominated solutions, the fast non-dominated sorting approach is employed to get priority of non-dominated solutions obtained during the search process, and the dynamical crowded distance estimation strategy is used to maintain diversity of Pareto optimal solution.
A set of test functions including bio-objective and tri-objective instances have been employed to evaluate the computational performance of the proposed algorithm. Experimental results show that MORSGO has a promising ability of maintaining better population diversity and accordingly obtains better convergence, which indicates that MORSGO has potential ability of effectively tackling real-world problems in the near future.
References
Yi, X., Zhou, Y.: A dynamic multi-colony artificial bee colony algorithm for multi-objective optimization. Appl. Soft Comput. 35, 766–785 (2015)
Deb, K., Pratap, A., Agarwal, S., Meyarivan, T.: A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 6(2), 182–197 (2002)
Zhang, Q., Liu, W., Li, H.: The performance of a new version of MOEA/D on CEC09 unconstrained MOP test instances. In: Proceedings of Congress on Evolutionary Computation (CEC 2009), Norway, pp. 203–208 (2009)
Zitzler, E., Laumanns, M., Thiele, L.: SPEA2: improving the strength pareto evolutionary algorithm. In: Proceedings of EUROGEN 2001: Evolutionary Methods Design Optimization Control with Applications to Industrial Problems, Athens, Greece, pp. 95–100 (2002)
Coello Coello, C.A., Pulido, G.T., Lechuga, M.S.: Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 8(3), 256–279 (2004)
Ma, L., Hu, K., Zhu, Y., Chen, H.: A hybrid artificial bee colony optimizer by combining with life-cycle. Powell’s Search Crossover Appl. Math. Comput. 252, 133–154 (2015)
Hodge, A., Berta, G., Doussan, C., Merchan, F., Crespi, M.: Plant root growth, architecture and function. Plant Soil 321(1–2), 153–187 (2009)
Ma, L., Zhu, Y., Liu, Y., Tian, L.: A novel bionic algorithm inspired by plant root foraging behaviors. Appl. Soft Comput. 37, 95–113 (2015)
Deb, K., Thiele, L., Laumanns, M., Zitzler, E.: Scalable multi-objective optimization test problems. In: Proceedings of Congress on Evolutionary Computation, pp. 825–830 (2002)
Zhou, A.M., Jin, Y.C., Zhang, Q.F., Sendhoff, B., Tsang, E.: Combining model-based and genetics-based offspring generation for multi-objective optimization using a convergence criterion. In: Proceedings of Congress on Evolutionary Computation, pp. 3234–3241 (2001)
Acknowledgements
This work is supported by National Natural Science Foundation of China under Grant No. 61503373; Natural Science Foundation of Liaoning Province under Grand 2015020002.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Ma, L., Li, X., Liu, J., Gao, Y. (2016). A Novel Multi-objective Bionic Algorithm Based on Plant Root System Growth Mechanism. In: Huang, DS., Han, K., Hussain, A. (eds) Intelligent Computing Methodologies. ICIC 2016. Lecture Notes in Computer Science(), vol 9773. Springer, Cham. https://doi.org/10.1007/978-3-319-42297-8_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-42297-8_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-42296-1
Online ISBN: 978-3-319-42297-8
eBook Packages: Computer ScienceComputer Science (R0)