Keywords

1 Introduction

Mutualism is a positive relationship between two or more species in a community that benefits all individuals of those species. It drives evolution and most organisms are mutualistic in some way. These interactions are essential for life. One well known example of a mutualistic relationship is oxpecker and zebra. Oxpeckers land on zebras and eat ticks and other parasites that live on their skin. The oxpeckers get food and the beasts get pest control. Also, when there is danger, the oxpeckers fly upward and scream a warning, which helps the symbiont. Another one is bacteria and the human. A certain kind of bacteria lives in the intestines of humans and many other animals. The human cannot digest all of the food that it eats. The bacteria eats the food that the human cannot digest and partially digest it, allowing the human to finish the job. The bacteria benefit by getting food, and the human benefits by being able to digest the food it eats.

The members of many species cooperate; they get help for hunting or deceiving predators. They come together to survive negative conditions or in other way to find sexual reproduction. When there are a few individuals, it looks like they will take advantage of more welding, however, they will also suffer from a lack of conspecific. The balance changes if this negativity has more power, that is, population may extinct at low reproduction. Their fitness will be less when the population size is getting smaller. This is, in essence, Allee effect.

There are several mechanisms for Allee effects. Well-known mechanisms include fertilization efficiency in sessile organisms, mate finding in mobile organisms and cooperative breeding. In our model we study the mate limitation factor which is the situation that harder to find a (compatible and receptive) mate at low population size or density. For example; cod, gypsy moth, Glanville fritillary butterfly, alpine marmot.

The most popular one for mutualism is the interaction between flowering plants and their pollinators or between fruit-producing plants and seed dispersers. Amarasekare [1] studied both obligatory and facultative mutualisms in which one of the mutualists was non-mobile (such as a plant) and the other mobile (such as a pollinator or seed disperser), using a metacommunity framework (a set of local communities connected by dispersal). If obligate mutualisms and only one local community are considered, both species go extinct from any initial conditions if the colonization rate of the mobile mutualist is low, and a strong Allee effect arises if it is high. For facultative mutualisms, a strong Allee effect arises if the fitness reduction in absence of the mutualist drops below a critical value, otherwise both species coexist from any initial conditions. In a metacommunity composed of two or more local communities, dispersal of the mobile mutualist from source communities can rescue sink communities from extinction and thus maintain regional persistence of both species [8].

Among obligate mutualists, system bistability arises as a direct consequence of the mutualistic interaction; that is, we have an emergent Allee effect, simply because neither species can live without the other. Among facultative mutualists, however, the Allee effect is not emergent, because the decline in fitness when the second species is absent is incorporated explicitly into the model. Sexual reproduction can also be considered a sort of (within-species) obligate mutualism.

A coupled discrete logistic model is used in [2] by R. Lpez-Ruz and D. Fourner-Prunaret:

$$ \left. \begin{array}{lcl} x_{n+1}&{} =&{}\mu (y_{n})x_n(1-x_n) \\ y_{n+1}&{} =&{}\mu (x_{n})y_n(1-y_n)\end{array} \right. $$

which is symbiotic interaction between both species provokes that the growth rate \(\mu (z)\) is varying with time and must be positive.

In [3] W. Krawcewicz, T.D. Rogers and in [4] H.L. Smith studied a dynamical model for cooperation between two species, each of which benefits in a symmetric manner from the other. Such an idealized relationship is expressed through the family of two-dimensional recursions

$$ \left. \begin{array}{lcl} x_{n+1}&{} =&{}x_{n}exp[r(1-x_n)+sy_n] \\ y_{n+1}&{} =&{}y_{n}exp[r(1-y_n)+sx_n]\end{array} \right. $$

where the parameters r and s are nonnegative.

A simple, autonomous cooperative system is discussed in [5] by K. Yang, X. Xie and F. Chen,

$$ \left. \begin{array}{lcl} x_{n+1}&{} =&{}x_{n}exp [r_{1}\left( \frac{K_{1}+a_{1}y_{n}}{ 1+y_{n}}\right) -x_n] \\ y_{n+1}&{} =&{}y_{n}exp [r_{2}\left( \frac{K_{2}+a_{2}x_{n}}{ 1+x_{n}}\right) -y_n]\end{array} \right. $$

where \(r_{i}\), \(K_{i}\), i = 1, 2 are all positive constants.

In [6] by Cruz Vargas-De-Len, the global stability in continuous time cooperative models is studied to describe facultative mutualism. He subjected to the Lotka-Volterra mutualism model with proportional harvesting

$$ \left. \begin{array}{lcl} \frac{d x}{d t}&{} =&{}r_{1} x [1-\frac{x}{K_{1}}+b_{12}\frac{y}{K_{1}}] -e_{1} x\\ \frac{d y}{d t}&{} =&{}r_{2} y [1-\frac{y}{K_{2}}+b_{21}\frac{x}{K_{2}}] -e_{2} y\end{array} \right. $$

where constants \(e_{1}\) and \(e_{2}\) are harvesting efforts on respective populations, \(r_{i}\), \(K_{i}\), \(b_{12}\) and \(b_{21}\) (i = 1, 2) are all positive constants, \(r_{i}\) are the linear birth rates, \(K_{i}\) are the carrying capacities, \(b_{12}\) and \(b_{21} \) measure the cooperative effect of \(x_{1}\) and \(x_{2}\).

M.R.S. Kulenovic and M. Nurkanovic studied the global asymptotic behaviour of the following system [7]:

$$\begin{aligned} \left. \begin{array}{lcl} x_{n+1}&{} =&{}A x_{n} \frac{y_n}{1+y_n} \\ y_{n+1}&{} =&{}B y_{n} \frac{x_n}{1+x_n} \end{array} \right. \end{aligned}$$
(1)

with parameters A, B > 0 and initial values \(x_{0},y_{0}> 0\).

In a modeling setting, the system (1) of nonlinear difference equations represents the rule by which two discrete, cooperating populations reproduce from one generation to the next. The phase variables \(x_n\) and \(y_n\) denote population sizes during the n-th generation and the sequence or orbit (\(x_n\),\(y_n\)) , n = 0,1,2,... depicts how the populations evolve over time. Cooperation between two populations is reflected by the fact that the transition function for each population is an increasing function of the other population size.

In this study we add Allee effect to the first component in model (1) and get a new one:

$$\begin{aligned} \left. \begin{array}{lcl} x_{n+1}&{} =&{}A x_{n} \frac{y_n}{1+y_n} \frac{x_n}{u+x_{n}} \\ y_{n+1}&{} =&{}B y_{n} \frac{x_n}{1+x_n} \end{array} \right. \end{aligned}$$
(2)

where \(u>0\) denotes the Allee effect constant that determines the strength of Allee effect.

2 Analysis of Model (1)

2.1 Fixed Points and Their Stability

The system

$$ \left. \begin{array}{lcl} x_{n+1}&{} =&{}A x_{n} \frac{y_n}{1+y_n} \\ y_{n+1}&{} =&{}B y_{n} \frac{x_n}{1+x_n} \end{array} \right. $$

has two fixed points (0, 0) and \((\frac{1}{B-1},\frac{1}{A-1})\) that is positive when \(A>1\) and \(B>1\).

The positive fixed point \((\frac{1}{B-1},\frac{1}{A-1})\) is always saddle (Fig. 3). The other fixed point (0, 0) is always locally asymptotically stable because

$$ J(0, 0)= \left( \begin{array}{cc} 0 &{} 0 \\ 0 &{} 0 \\ \end{array} \right) $$

Since both eigenvalues are zero (Fig. 1, Fig. 2 and Fig. 3).

2.2 Stability via Lyapunov Function

In order to check the global stability, we use a Lyapunov function of the map

$$\begin{aligned} F\left( \begin{array}{c} x \\ y\\ \end{array} \right) = \left( \begin{array}{c} A x \frac{y}{1+y} \\ B y \frac{x}{1+x}\\ \end{array} \right) \end{aligned}$$

Let \(V(x, y)=xy\) is the corresponding positive definite Lyapunov function (Fig. 6). Then

$$\begin{aligned} \varDelta V\left( \begin{array}{c} x \\ y\\ \end{array} \right)= & {} V ( F\left( \begin{array}{c} x \\ y\\ \end{array} \right) ) - V(x, y)\\ \varDelta V(x,y)= & {} (A x \frac{y}{1+y}) ( B y \frac{x}{1+x})-xy < 0 \end{aligned}$$

Since \(x,y>0\) and if \(AB\le 1\) then

$$\begin{aligned} \varDelta V(x,y)=AB \frac{(xy)^2}{(1+x)(1+y)}-xy =\frac{xy(ABxy-1-x-y-xy)}{(1+x)(1+y)}< 0 \end{aligned}$$
Fig. 1.
figure 1

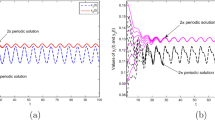
Phase Plane Diagrams: the first one is the phase diagram with initial point (0.1,0.1) where A = 0.7, B = 0.4 for which there is no positive fixed point and (0,0) is globally stable. For the second one, the initial point is (0.1,0.1), A = 3, B = 5, there are two fixed points: (0,0) and (0.25,0.5), which are stable and saddle respectively

Full size image

Since \(|X|\rightarrow \infty \), \(V(X)\rightarrow \infty \), then (0, 0) is globally asymptotically stable.

3 Numerical Simulations of Model (1)

3.1 Phase Plane Diagrams

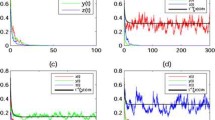
3.2 Time Series Diagrams

Fig. 2.
figure 2

Time Series Diagrams: the first one is the time series diagram with initial point (0.1,0.1) where A = 0.7, B=0.4. For the second one, the initial point is (0.1,0.1) again with A = 3, B=5. In both cases the population go to extinction in time.

Full size image

3.3 Basin of Attraction

Fig. 3.
figure 3

Basin of Attraction: for the first one A=0.2, B=0.3 and there is no positive fixed point. For the second one, A=1.5, B=1.5, the positive fixed point is (2,2).

Full size image

4 Analysis of Model (2)

4.1 Fixed Points and Their Stability

We get the following system by adding the mate limitation Allee effect:

$$ \left. \begin{array}{lcl} x_{n+1}&{} =&{}A x_{n} \frac{y_n}{1+y_n} \frac{x_n}{u+x_{n}} \\ y_{n+1}&{} =&{}B y_{n} \frac{x_n}{1+x_n} \end{array} \right. $$

Fixed points of this system are (0,0) and \((\frac{1}{B-1},\frac{1-u+B u}{-1+A+u-B u})\).

The second fixed point is positive when \(B>1\) and \(A>1+u(B-1)\) or equally \(B>1\), \(A>1\) and \(0<u<\frac{A-1}{B-1}\).

(0, 0) is again always locally asymptotically stable because

$$ J(0, 0)= \left( \begin{array}{cc} 0 &{} 0 \\ 0 &{} 0 \\ \end{array} \right) $$

So both eigenvalues are zero again.

For positive fixed point \((\frac{1}{B-1}, \frac{1-u+B u}{-1+A+u-B u})\) Jacobian matrix is,

\( J= \left( \begin{array}{cc} 2+\frac{1}{-1+u-B u} &{} \frac{(-1+A+u-B u)^2}{A (-1+B) (1+(-1+B) u)} \\ -\frac{(-1+B)^2 (1+(-1+B) u)}{B (1-A+(-1+B) u)} &{} 1 \\ \end{array} \right) \)

and corresponding eigenvalues are,

\(\lambda _{1}=\frac{\sqrt{A} \sqrt{B} (2+3 (-1+B) u)+\sqrt{-1+B} \sqrt{-4 (1+(-1+B) u)^3+A (4+(-1+B) u (8-4 u+5 B u))}}{2 \sqrt{A} \sqrt{B} (1+(-1+B) u)}\)

\(\lambda _{2}=\frac{\sqrt{A} \sqrt{B} (2+3 (-1+B) u)-\sqrt{-1+B} \sqrt{-4 (1+(-1+B) u)^3+A (4+(-1+B) u (8-4 u+5 B u))}}{2 \sqrt{A} \sqrt{B} (1+(-1+B) u)}\).

Solving inequalities together with \(B>1\), \(A>1\) and \(0<u<\frac{A-1}{B-1}\), \(|\lambda _{1}|\le 1\) has infeasible solution while \(|\lambda _{2}|\le 1\) holds true everywhere in the domain. That means the positive fixed point is saddle point again (Fig. 4, Fig. 5 and Fig. 6).

4.2 Stability via Lyapunov Function

In order to check the global stability of (0,0), we use a Lyapunov function of the map. Let \(V(x, y)=xy\) be the corresponding positive definite Lyapunov function. If \(AB<1\), \(A>1\) and \(1<u\) then

\(\varDelta \) V\(\left( \begin{array}{c} x \\ y\\ \end{array} \right) \) = V ( F\(\left( \begin{array}{c} x \\ y\\ \end{array} \right) \)) - V(x, y)

\(\varDelta V(x,y)=(\frac{A x^{2}y}{(1+y)(u+x)}) (\frac{ Bxy}{1+x})-xy < 0\)

So (0,0) is globally asymptotically stable.

5 Numerical Simulations of Model (2)

In this section we provide some numerical evidences for the qualitative dynamic of the Model 2, the phase portraits, time series diagrams, and basin of attractions by using the codes of [9];

5.1 Phase Plane Diagrams

Fig. 4.
figure 4

Phase Plane Diagrams: the first one is the phase diagram with initial point (0.1,0.1) where A = 0.7, B = 0.4 and u = 0.25 for which there is no positive fixed point and (0,0) is globally stable. For the second one, the initial point is (0.1,0.1), A = 3, B = 5 and u = 0.1 there are two fixed points: (0,0) and (0.25,0.875), which are stable and saddle respectively.

Full size image

5.2 Time Series Diagrams

Fig. 5.
figure 5

Time Series Diagrams: the first one is the time series diagram with initial point (0.1,0.1) where A = 0.7, B = 0.4, u = 0.25. For the second one, the initial point is (0.1,0.1) again with A = 3, B = 5, u = 0.1. In both cases the population go to extinction in time.

Full size image

5.3 Basin of Attraction

Fig. 6.
figure 6

Basin of Attraction: for the first one A = 0.2, B = 0.3, u = 0.5. For the second one, A = 1.5, B = 1.5, u = 0.6 with positive fixed point (2,6.5).

Full size image

6 Conclusion

In this paper, chaotic dynamic and the stability of the fixed points of a nonlinear discrete-time cooperation model with Allee Effect have been investigated. Global stability of the fixed point is investigated by a Lyapunov function. Nevertheless, identifying complicated, possibly chaotic dynamics in population data, stability region of the positive fiexed point, and bifurcation of the system have remained.