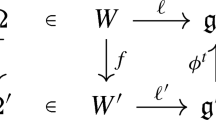On Deformations of n-Lie Algebras

Abstract

The aim of this paper is to review the deformation theory of n-Lie algebras. We summarize the 1-parameter formal deformation theory and provide a generalized approach using any unital commutative associative algebra as a deformation base. Moreover, we discuss degenerations and quantization of n-Lie algebras.

1 Introduction

The purpose of this paper is to provide a survey on deformations of n-Lie algebras. Deformation is one of the oldest techniques used by mathematicians and physicists. The first instances of the so-called deformation theory were given by Kodaira and Spencer for complex structures and by Gerstenhaber for associative algebras. Abstract deformation theory and deformation functors in algebraic geometry were inspired and developed in the works of André, Deligne, Goldman, Grothendick, Illusie, Laudal, Lichtenbaum, Milson, Quillen, Schlessinger, and Stasheff. Among concrete deformation theory developed by Gerstenhaber for associative algebras and later with Schack for bialgebras, the Lie algebras case was studied by Nijenhuis and Richardson and then by Fialowski and her collaborators in a more general framework. Deformations of n-ary algebras were considered in several papers. Deformation theory is the study of a family in the neighborhood of a given element. Intuitively, a deformation of a mathematical object is a family of the same kind of objects depending on some parameters. The main and popular tool is the power series ring or more generally any commutative algebras. By standard facts of deformation theory, the infinitesimal deformations of an algebra of a given type are parametrized by a second cohomology of the algebra. More generally, it is stated that deformations are controlled by a suitable cohomology. Deformations help to construct new objects starting from a given object and to infer some of its properties. They can also be useful for classification problems. A modern approach, essentially due to Quillen, Deligne, Drinfeld, and Kontsevich, is that, in characteristic zero, every deformation problem is controlled by a differential graded Lie algebra, via solutions of Maurer-Cartan equation modulo gauge equivalence. Some mathematical formulations of quantization are based on the algebra of observables and consist in replacing the classical algebra of observables (typically complex-valued smooth functions on a Poisson manifold) by a noncommutative one constructed by means of an algebraic formal deformations of the classical algebra. In 1997, Kontsevich solved a longstanding problem in mathematical physics, that is every Poisson manifold admits formal quantization which is canonical up to a certain equivalence. Deformation theory has been applied as a useful tool in the study of many other mathematical structures in Lie theory, quantum groups, operads, and so on. Even today it plays an important role in many developments of contemporary mathematics, especially in representation theory.

The n-ary algebraic structures, which are natural generalizations of binary operations, appeared naturally in various domains of theoretical and mathematical physics. Indeed, theoretical physics progress of quantum mechanics and the discovery of the Nambu mechanics (1973) see [82], as well as a work of Okubo [85] on Yang-Baxter equation gave impulse to a significant development on n-ary algebras. The n-ary operations appeared first through cubic matrices which were introduced in the nineteenth century by Cayley. The cubic matrices were considered again and generalized by Kapranov et al. in 1994 see [60] and Sokolov in 1972 see [89]. Another recent motivation to study n-ary operation comes for string theory and M-Branes where appeared naturally a so called Bagger-Lambert algebra involving a ternary operation [10]. Hundred of papers are dedicated to Bagger-Lambert algebra. For other applications in Physics and Mathematical Physics see [1, 12, 14, 22, 24–27, 29, 50, 51, 57, 63–69, 87].

The first conceptual generalization of binary algebras was the ternary algebras introduced by Jacobson [59] in connection with problems from Jordan theory and quantum mechanics, he defined the Lie triple systems. A Lie triple system consists of a space of linear operators on vector space V that is closed under the ternary bracket [x, y, z] _T  = [[x, y], z], where [x, y] = xy − yx. Equivalently, the Lie triple system may be viewed as a subspace of the Lie algebra closed relative to the ternary product. A Lie triple system arose also in the study of symmetric spaces [74]. More generally, we distinguish two kinds of generalization of binary Lie algebras. Firstly, n-ary Lie algebras in which the Jacobi identity is generalized by considering a cyclic summation over $\mathcal{S}_{2n-1}$ instead of $\mathcal{S}_{3}$, see [53, 80] and secondly n-ary Nambu algebras in which the fundamental identity generalizes the fact that the adjoint maps are derivations. The corresponding identity is called fundamental identity and it appeared first in Nambu mechanics [82], the abstract definition of n-ary Nambu algebras or n-Lie algebras (when the bracket is skew symmetric) was given by Fillipov in 1985, see [38, 90, 91] for the algebraic formulation of the Nambu mechanics. The Leibniz n-ary algebras were introduced and studied in [19].

This article is organized as follows. In Sect. 4.2 we summarize the definitions of n-ary algebras of Lie type and associative type, and provide some classical examples. Moreover, we discuss the representations of n-Lie algebras. In Sect. 4.3, we review homological algebra tools and define the cohomology for n-Lie algebra that suits with deformation theory. Section 4.4 is dedicated to one-parameter formal deformations based on formal power series. We also describe the case where the parameter no longer commutes with the original algebra. In Sect. 4.5, we present a more general approach based on any commutative associative algebra, generalizing to n-Lie algebras, the approach developed by Fialowski and her collaborators for Lie algebras. Section 4.6 deals with algebraic varieties of n-Lie algebras and degenerations. In Sect. 4.7, we discuss n-Lie-Poisson algebras and quantization.

2 Definitions and Examples of n-Lie Algebras and Other Types of n-ary Algebras

Throughout this paper, $\mathbb{K}$ is a field of characteristic zero and $\mathcal{N}$ is a $\mathbb{K}$-vector space.

2.1 n-Lie Algebras

In this section, we provide basics on n-Lie algebras which are also called Filippov n-ary algebras or Nambu-Lie algebras. See [2, 3, 15, 28, 38, 47, 49, 54, 61, 79, 90, 93]

Definition 4.1.

An n-Lie algebra is a pair $(\mathcal{N},[\cdot,\ldots,\cdot ])$, consisting of a vector space $\mathcal{N}$ and an n-linear map $[\,\cdots \,,\ ]: \mathcal{N}^{\times n} \rightarrow \mathcal{N}$ satisfying

$$\displaystyle{ [x_{1},\ldots,x_{n-1},[x_{n},\ldots,x_{2n-1}]] =\sum _{ i=n}^{2n-1}[x_{ n},\ldots,x_{i-1},[x_{1},\cdots \,,x_{n-1},x_{i}],x_{i+1},\ldots,x_{2n-1}], }$$

(4.1)

and

$$\displaystyle{ [x_{\sigma (1)},\cdots \,,x_{\sigma (n)}] = Sgn(\sigma )[x_{1},\cdots \,,x_{n}],\quad \forall \sigma \in \mathcal{S}_{n}\text{ and }\forall x_{1},\cdots \,,x_{n} \in \mathcal{N} }$$

(4.2)

where $\mathcal{S}_{n}$ stands for the permutation group on n elements and sgn(σ) denotes the signature of σ.

We call condition (4.1) Nambu identity, it is also called fundamental identity or Filippov identity.

Remark 4.1.

Let $(\mathcal{N},[\cdot,\ldots,\cdot ])$ be an n-Lie algebra. Let $x = (x_{1},\ldots,x_{n-1}) \in \mathcal{N}^{n-1}$ and $y \in \mathcal{N}$. Let L _x be a linear map on $\mathcal{N}$, defined by

$$\displaystyle{ L_{x}(y) = [x_{1},\cdots \,,x_{n-1},y]. }$$

(4.3)

Then the Nambu identity maybe written

$$\displaystyle{ L_{x}([x_{n},\ldots,x_{2n-1}]) =\sum _{ i=n}^{2n-1}[x_{ n},\ldots,x_{i-1},L_{x}(x_{i}),x_{i+1}\ldots,x_{2n-1}]. }$$

Morphisms of n-Lie algebras are defined as follows.

Definition 4.2.

Let $(\mathcal{N},[\cdot,\ldots,\cdot ])$ and $(\mathcal{N}',[\cdot,\ldots,\cdot ]')$ be two n-Lie algebras. A linear map $\rho: \mathcal{N} \rightarrow \mathcal{N}'$ is an n-Lie algebras morphism if it satisfies

$$\displaystyle{ \rho ([x_{1},\cdots \,,x_{2n-1}]) = [\rho (x_{1}),\cdots \,,\rho (x_{2n-1})]'. }$$

Example 4.1.

The polynomial algebra of three variables x ₁, x ₂, x ₃, with the bracket defined by the functional jacobian:

$$\displaystyle{ [f_{1},f_{2},f_{3}] = \left \vert \begin{array}{ccc} \frac{\delta f_{1}} {\delta x_{1}} & \frac{\delta f_{1}} {\delta x_{2}} & \frac{\delta f_{1}} {\delta x_{3}} \\ \frac{\delta f_{2}} {\delta x_{1}} & \frac{\delta f_{2}} {\delta x_{2}} & \frac{\delta f_{2}} {\delta x_{3}} \\ \frac{\delta f_{3}} {\delta x_{1}} & \frac{\delta f_{3}} {\delta x_{2}} & \frac{\delta f_{3}} {\delta x_{3}} \end{array} \right \vert, }$$

(4.4)

is a 3-Lie algebra.

We have also this fundamental example:

Example 4.2.

Let $V = \mathbb{R}^{4}$ be the 4-dimensional oriented euclidian space over $\mathbb{R}$. The bracket of 3 vectors $\mathop{x_{1}}\limits^{ \rightarrow },\mathop{x_{2}}\limits^{ \rightarrow },\mathop{x_{3}}\limits^{ \rightarrow }$ is given by:

$$\displaystyle{ [\mathop{x_{1}}\limits^{ \rightarrow },\mathop{x_{2}}\limits^{ \rightarrow },\mathop{x_{3}}\limits^{ \rightarrow }] =\mathop{ x_{1}}\limits^{ \rightarrow }\times \mathop{x_{2}}\limits^{ \rightarrow }\times \mathop{x_{3}}\limits^{ \rightarrow }= \left \vert \begin{array}{c} \begin{array}{cccc} x_{11}&x_{12}&x_{13}&\mathop{e_{1}}\limits^{ \rightarrow }\\ x_{ 21}&x_{22}&x_{23}&\mathop{e_{2}}\limits^{ \rightarrow } \end{array}\\ \begin{array}{cccc} x_{ 31}&x_{32}&x_{33}&\mathop{e_{3}}\limits^{ \rightarrow } \end{array}\\ \begin{array}{cccc} x_{ 41}&x_{42}&x_{43}&\mathop{e_{4}}\limits^{ \rightarrow } \end{array} \end{array} \right \vert }$$

where (x _1r , …, x _4r ) _{r = 1, 2, 3} are the coordinates of $\mathop{x_{r}}\limits^{ \rightarrow }$ with respect to orthonormal basis {e _r }. Then, (V, [. , . , . ]) is a 3-Lie algebra.

Remark 4.2.

Every 3-Lie algebra on $\mathbb{R}^{4}$ could be deduced from the previous example (see [39]).

2.2 n-ary Algebras of Associative Type

There are several possible generalizations of binary associative algebras. A typical example is the ternary product of rectangular matrices introduced by Hestenes [55] defined for $A,B,C \in \mathcal{M}_{n,m}$ by AB ^∗ C where B ^∗ is the conjugate transpose.

Consider an n-ary operation $m: \mathcal{N}\otimes \cdots \otimes \mathcal{N} \rightarrow \mathcal{N}$ or $m: \mathcal{N}\times \cdots \times \mathcal{N}\longrightarrow \mathcal{N}$. The n-ary operation is said to be symmetric (resp. skew-symmetric) if

$$\displaystyle{ m(x_{\sigma (1)} \otimes \cdots \otimes x_{\sigma (n)}) = m(x_{1}\cdots \otimes x_{n}),\quad \forall \sigma \in \mathcal{S}_{n}\text{ and }\forall x_{1},\cdots \,,x_{n} \in \mathcal{N}, }$$

(4.5)

resp.

$$\displaystyle{ m(x_{\sigma (1)} \otimes \cdots \otimes x_{\sigma (n)}) = Sgn(\sigma )m(x_{1} \otimes \cdots \otimes x_{n}),\quad \forall \sigma \in \mathcal{S}_{n}\text{ and }\forall x_{1},\cdots \,,x_{n} \in \mathcal{N}, }$$

(4.6)

where Sgn(σ) denotes the signature of the permutation $\sigma \in \mathcal{S}_{n}$.

It is said to be commutative if

$$\displaystyle{ \sum _{\sigma \in \mathit{S}_{n}}\ Sgn(\sigma )m(x_{\sigma (1)} \otimes \cdots \otimes x_{\sigma (n)}) = 0,\ \quad \forall x_{1},\cdots \,,x_{n} \in \mathcal{N}. }$$

(4.7)

Remark 4.3.

A symmetric ternary operation is commutative.

We have the following type of “associative” ternary operations.

Definition 4.3.

A totally associative n-ary algebra is given by a $\mathbb{K}$-vector space $\mathcal{N}$ and an n-ary operation m satisfying, for all $x_{1},\cdots \,,x_{2n-1} \in \mathcal{N}$,

$$\displaystyle{ m(m(x_{1}\otimes \cdots \otimes x_{n})\otimes \cdots \otimes x_{2n-1}) = m(x_{1}\otimes \cdots \otimes x_{i}\otimes m(x_{i+1}\otimes \cdots \otimes x_{i+n})\otimes \cdots x_{2n-1})\ \forall i. }$$

Example 4.3.

Let {e ₁, e ₂} be a basis of a 2-dimensional space $\mathcal{N} = \mathbb{K}^{2}$, the ternary operation on $\mathcal{N}$ given by

$$\displaystyle{ \begin{array}{ll} \begin{array}{lll} m(e_{1} \otimes e_{1} \otimes e_{1})& =&e_{1} \\ m(e_{1} \otimes e_{1} \otimes e_{2})& =&e_{2} \\ m(e_{1} \otimes e_{2} \otimes e_{2})& =&e_{1} + e_{2} \\ m(e_{2} \otimes e_{1} \otimes e_{1})& =&e_{2} \end{array} & \begin{array}{lll} m(e_{2} \otimes e_{2} \otimes e_{1})& =&e_{1} + e_{2} \\ m(e_{2} \otimes e_{2} \otimes e_{2})& =&e_{1} + 2e_{2} \\ m(e_{1} \otimes e_{2} \otimes e_{1})& =&e_{2} \\ m(e_{2} \otimes e_{1} \otimes e_{2})& =&e_{1} + e_{2} \end{array} \end{array} }$$

defines a totally associative ternary algebra.

Definition 4.4.

A weak totally associative n-ary algebra is given by a $\mathbb{K}$-vector space $\mathcal{N}$ and a ternary operation m, satisfying for all $x_{1},\cdots \,,x_{2n-1} \in \mathcal{N}$,

$$\displaystyle\begin{array}{rcl} m(m(x_{1} \otimes \cdots \otimes x_{n}) \otimes \cdots \otimes x_{2n-1}) = m(x_{1} \otimes \cdots \otimes m(x_{n} \otimes \cdots \otimes x_{2n-1})).& & {}\\ \end{array}$$

Naturally, any totally associative n-ary algebra is a weak totally associative n-ary algebra.

Definition 4.5.

A partially associative n-ary algebra is given by a $\mathbb{K}$-vector space $\mathcal{N}$ and an n-ary operation m satisfying, for all $x_{1},\cdots \,,x_{2n-1} \in \mathcal{N}$,

$$\displaystyle\begin{array}{rcl} \sum _{i=0}^{n-1}m(x_{ 1} \otimes \cdots \otimes x_{i} \otimes m(x_{i+1} \otimes \cdots \otimes x_{i+n}) \otimes \cdots x_{2n-1}) = 0.& & {}\\ \end{array}$$

Example 4.4.

Let {e ₁, e ₂} be a basis of a 2-dimensional space $\mathcal{N} = \mathbb{K}^{2}$, the ternary operation on $\mathcal{N}$ given by m(e ₁ ⊗ e ₁ ⊗ e ₁) = e ₂ defines a partially associative ternary algebra.

Remark 4.4.

Let $(\mathcal{N},\cdot )$ be a bilinear associative algebra. Then, the n-ary operation, defined by m(x ₁ ⊗⋯ ⊗ x _n ) = x ₁ ⋅ … ⋅ x _n determines on the vector space $\mathcal{N}$ a structure of totally associative n-ary algebra which is not partially associative See the following references for further results [7, 62, 70, 72, 75].

The category of totally (resp. partially) n-ary algebras is encoded by non-symmetric operad denoted tAs ⁽ⁿ⁾ (resp. pAs ⁽ⁿ⁾). The space on p-ary non-symmetric operations of tAs ⁽ⁿ⁾ is given by $tAs_{in-i-1}^{(n)} = \mathbb{K}$, tAs _p ⁽ⁿ⁾ = 0 otherwise. If we put the degree k − 2 on the generating operation of pAs ⁽ⁿ⁾, then the non-symmetric operads tAs ⁽ⁿ⁾ and pAs ⁽ⁿ⁾ are Koszul dual to each other. Moreover, the Koszulity can be proved by the rewriting method [73].

There is another generalization of Jacobi condition that leads to another type of n-ary Lie algebra.

Definition 4.6.

An n-ary Lie algebra is a skew-symmetric n-ary operation [ , ⋯ ,  ] on a $\mathbb{K}$-vector space $\mathcal{N}$ satisfying $\forall x_{1},\cdots \,,x_{2n-1} \in \mathcal{N}$ the following generalized Jacobi condition

$$\displaystyle{ \sum _{\sigma \in \mathit{S}_{2n-1}}\ Sgn(\sigma )[[x_{\sigma (x_{1})},\cdots \,,x_{\sigma (x_{n-1})}],x_{\sigma (x_{n})},\cdots \,,x_{\sigma (x_{2n-1})}] = 0. }$$

As in the binary case, there is a functor which makes correspondence to any partially associative n-ary algebra an n-ary Lie algebra (see [45, 46]).

Proposition 4.1.

To any partially associative n-ary algebra on a vector space $\mathcal{N}$ with n-ary operation m, one associates an n-ary Lie algebra on $\mathcal{N}$ defined $\forall x_{1},\cdots \,,x_{n} \in \mathcal{N}$ by the bracket

$$\displaystyle{ [x_{1},\cdots \,,x_{n}] =\mathop{\sum Sgn(}\limits_{\sigma \in \mathit{S}_{n}}\sigma )m(x_{\sigma (1)} \otimes \cdots \otimes x_{\sigma (n)}). }$$

(4.8)

2.3 Representations of n-Lie Algebras

In this section we consider adjoint representations of n-Lie algebras and show that any n-Lie algebra can be represented by a Leibniz algebra.

Definition 4.7.

A representation of an n-Lie algebra $(\mathcal{N},[\cdot,\ldots,\cdot ])$ on a vector space $\mathcal{N}$ is a skew-symmetric multilinear map $\rho: \mathcal{N}^{n-1}\longrightarrow End(\mathcal{N})$, satisfying for $x,y \in \mathcal{N}^{n-1}$ the identity

$$\displaystyle{ \rho (x) \circ \rho (y) -\rho (y) \circ \rho (x) =\sum _{ i=1}^{n-1}\rho (x_{ 1},\ldots,ad_{y}(x_{i}),\ldots,x_{n-1}), }$$

(4.9)

where ad _y (x _i ) = [y ₁, ⋯ , y _n−1, x _i ] is an endomorphism of $\mathcal{N}$.

Two representations ρ and ρ′ on $\mathcal{N}$ are equivalent if there exists $f: \mathcal{N} \rightarrow \mathcal{N}$ an isomorphism of vector space such that f(x ⋅ y) = x ⋅ ′f(y) where x ⋅ y = ρ(x)(y) and x ⋅ ′y = ρ′(x)(y) for $x \in \mathcal{N}^{n-1}$ and $y \in \mathcal{N}.$

Example 4.5.

Let $(\mathcal{N},[\cdot,\ldots,\cdot ])$ be an n-Lie algebra. The map ad defined in (4.3) is a representation. The identity (4.9) is equivalent to Nambu identity. It is called adjoint representation.

Leibniz algebras were introduced by Loday. A Leibniz algebra is a pair (A, [⋅ , ⋅ ]) consisting of a vector space A, a bilinear map [⋅ , ⋅ ]: A × A → A satisfying, for x, y, z ∈ A,

$$\displaystyle{ [x,[y,z]] = [[x,y],z] + [y,[x,z]]. }$$

(4.10)

Let $(\mathcal{N},[\cdot,\ldots,\cdot ])$ be an n-Lie algebras and $\wedge ^{n-1}\mathcal{N}$ be the set of elements x ₁ ∧ … ∧ x _n−1 that are skew-symmetric in their arguments. We denote by $\mathcal{L}(\mathcal{N})$ the space $\wedge ^{n-1}\mathcal{N}$ and call it the fundamental set. Let $x = x_{1} \wedge \ldots \wedge x_{n-1} \in \wedge ^{n-1}\mathcal{N},\ y = y_{1} \wedge \ldots \wedge y_{n-1} \in \wedge ^{n-1}\mathcal{N},\ z \in \mathcal{N}$. Let $L: \wedge ^{n-1}\mathcal{N}\longrightarrow End(\mathcal{N})$ be a linear map defined as

$$\displaystyle{ L(x) \cdot z = [x_{1},\ldots,x_{n-1},z], }$$

(4.11)

and extending it linearly to all elements of $\wedge ^{n-1}\mathcal{N}$. Notice that L(x) ⋅ z = ad _x (z). We define a bilinear map $[\,\ ]: \wedge ^{n-1}\mathcal{N}\times \wedge ^{n-1}\mathcal{N}\longrightarrow \wedge ^{n-1}\mathcal{N}$ by

$$\displaystyle{ [x,y] = L(x)\bullet y =\sum _{ i=1}^{n-1}\big(y_{ 1},\ldots,L(x) \cdot y_{i},\ldots,y_{n-1}\big). }$$

(4.12)

Lemma 4.1.

The map L satisfies

$$\displaystyle{ L([x,y]) \cdot z = L(x) \cdot \big (L(y) \cdot z\big) - L(y) \cdot \big (L(x) \cdot z\big), }$$

(4.13)

for all $x,\ y \in \mathcal{L}(\mathcal{N}),\ z \in \mathcal{N}$.

Proposition 4.2.

The pair $\big(\mathcal{L}(\mathcal{N}),\ [\,\ ]\big)$ is a Leibniz algebra.

Proof.

Straightforward verification, see [23].

We obtain a similar result if we consider the space $T\mathcal{N} = \otimes ^{n-1}\mathcal{N}$ instead of $\mathcal{L}(\mathcal{N})$.

2.4 Central Extensions

We recall some basics about extensions of n-Lie algebras.

Definition 4.8.

Let A, B, C be three n-Lie algebras (n ≥ 2). An extension of B by A is a short sequence:

$$\displaystyle{A\mathop{ \rightarrow }\limits^{\lambda } C\mathop{ \rightarrow }\limits^{\mu } B,}$$

such that λ is an injective homomorphism, μ is a surjective homomorphism, and $\mathop{\mathrm{Im}}\nolimits \lambda \subset \ker \mu$. We say also that C is an extension of B by A.

Definition 4.9.

Let A, B be two n-Lie algebras, and $A\mathop{ \rightarrow }\limits^{\lambda } C\mathop{ \rightarrow }\limits^{\mu } B$ be an extension of B by A.

• The extension is said to be trivial if there exists an ideal I of C such that

  C = kerμ ⊕ I.

• It is said to be central if kerμ ⊂ Z(C).

We may equivalently define central extensions by a 1-dimensional algebra (we will simply call it central extension) this way:

Definition 4.10.

Let $\mathcal{N}$ be an n-Lie algebra. We call central extension of $\mathcal{N}$ the space $\bar{\mathcal{N}} = \mathcal{N}\oplus \mathbb{K}c$ equipped with the bracket:

$$\displaystyle\begin{array}{rcl} & & \left [x_{1},\ldots,x_{n}\right ]_{c} = \left [x_{1},\ldots,x_{n}\right ] +\omega \left (x_{1},\ldots,x_{n}\right )c\text{ and }\left [x_{1},\ldots,x_{n-1},c\right ]_{c} = 0, {}\\ & & \quad \forall x_{1},\ldots,x_{n} \in \mathcal{N}, {}\\ \end{array}$$

where ω is a skew-symmetric n-linear form such that $\left [\cdot,\ldots,\cdot \right ]_{c}$ satisfies the Nambu identity (or Jacobi identity for n = 2).

Proposition 4.3 ([23]).

• 1. The bracket of a central extension satisfies the Nambu identity if and only if ω is a 2-cocycle for the scalar cohomology of n-Lie algebras.

• 2. Two central extensions of an n-Lie algebra A given by two maps ω ₁ and ω ₂ are isomorphic if and only if ω ₂ −ω ₁ is a 2-coboundary for the scalar cohomology of n-Lie algebras.

3 Deformation Cohomology of n-Lie Algebras

The basic concepts of homological algebra are those of a complex and homomorphisms of complexes, defining the category of complexes, see for example [92]. A chain complex $\mathcal{C}_{.}$ is a sequence $\mathcal{C} =\{ \mathcal{C}_{p}\}_{p}$ of abelian groups or more generally objects of an abelian category and an indexed set δ = {δ _p } _p of homomorphisms $\delta _{p}: \mathcal{C}_{p} \rightarrow \mathcal{C}_{p-1}$ such that δ _p−1 ∘δ _p  = 0 for all p. A chain complex can be considered as a cochain complex by reversing the enumeration $\mathcal{C}^{p} = \mathcal{C}_{-p}$ and δ ^p = δ _−p . A cochain complex $\mathcal{C}$ is a sequence of abelian groups and homomorphisms $\cdots \mathop{\longrightarrow }\limits^{\delta ^{p-1}}\mathcal{C}^{p}\mathop{\longrightarrow }\limits^{\delta ^{p}}\mathcal{C}^{p+1}\mathop{\longrightarrow }\limits^{\delta ^{p+1}}\cdots$ with the property δ ^p+1 ∘δ ^p = 0 for all p. The homomorphisms δ ^p are called coboundary operators or codifferentials. A cohomology of a cochain complex $\mathcal{C}$ is given by the groups $H^{p}(\mathcal{C}) = Ker\delta ^{p}/Im\delta ^{p-1}$.

The elements of $\mathcal{C}^{p}$ are p-cochains, the elements of Z ^p: = Kerδ ^p are p-cocycles, the elements of B ^p: = Imδ ^p−1 are p-coboundaries. Because δ ^p+1 ∘δ ^p = 0 for all p, we have $0 \subseteq B^{p} \subseteq Z^{p} \subseteq \mathcal{C}^{p}$ for all p. The pth cohomology group is the quotient H ^p = Z ^p∕B ^p.

The cohomology of n-Lie algebras is induced by the cohomology of Leibniz algebras. Let $(\mathcal{N},[\cdot,\ldots,\cdot ])$ be an n-Lie algebra and the pair $(\mathcal{L}(\mathcal{N}) = \mathcal{N}^{\otimes n-1},[\cdot,\cdot ])$ be the Leibniz algebra associated to $\mathcal{N}$ where the bracket is defined in (4.12).

Theorem 4.1.

Let $(\mathcal{N},[\cdot,\ldots,\cdot ])$ be an n-Lie algebra.

Let $\mathcal{C}^{p}(\mathcal{N},\mathcal{N}) = Hom(\otimes ^{p}\mathcal{L}(\mathcal{N}) \otimes \mathcal{N},\mathcal{N})$ for p ≥ 1 be the cochains set and $\varDelta: \mathcal{C}^{p}(\mathcal{N},\mathcal{N}) \rightarrow C^{p}(\mathcal{L}(\mathcal{N}),\mathcal{L}(\mathcal{N}))$ be the linear map defined for p = 0 by

$$\displaystyle\begin{array}{rcl} \varDelta \varphi (x_{1} \otimes \cdots \otimes x_{n-1})& =& \sum _{i=1}^{n-1}x_{ 1} \otimes \cdots \otimes \varphi (x_{i}) \otimes \cdots \otimes x_{n-1} {}\\ \end{array}$$

and for p > 0 by

$$\displaystyle\begin{array}{rcl} & & (\varDelta \varphi )(a_{1},\cdots \,,a_{p+1}) =\sum _{ i=1}^{n-1}x_{ p+1}^{1} \otimes \cdots \otimes \varphi (a_{ 1},\cdots \,,a_{n-1} \otimes x_{p+1}^{i}) \otimes \cdots \otimes x_{ p+1}^{n-1}, {}\\ \end{array}$$

where a _j = x _j ¹ ⊗⋯ ⊗ x _j ⁿ⁻¹ . Then there exists a cohomology complex $(\mathcal{C}^{\bullet }(\mathcal{N},\mathcal{N}),\delta )$ for n-Lie algebras such that d ∘Δ = Δ ∘δ.

The coboundary map $\delta: \mathcal{C}^{p}(\mathcal{N},\mathcal{N}) \rightarrow \mathcal{C}^{p+1}(\mathcal{N},\mathcal{N})$ is defined for $\varphi \in \mathcal{C}^{p}(\mathcal{N},\mathcal{N})$  by

$$\displaystyle\begin{array}{rcl} \delta ^{p+1}\psi (a_{ 1},\ldots,a_{p},a_{p+1},z)& =& \sum _{1\leq i<j}^{p+1}(-1)^{i}\psi \big(a_{ 1},\ldots,\widehat{a_{i}},\ldots,a_{j-1},[a_{i},a_{j}],\ldots,a_{p+1},z\big) {}\\ & & +\sum _{i=1}^{p+1}(-1)^{i}\psi \big(a_{ 1},\ldots,\widehat{a_{i}},\ldots,a_{p+1},L(a_{i}) \cdot z\big) {}\\ & & +\sum _{i=1}^{p+1}(-1)^{i+1}L(a_{ i}) \cdot \psi \big (a_{1},\ldots,\widehat{a_{i}},\ldots,a_{p+1},z\big) {}\\ & & +(-1)^{p}\big(\psi (a_{ 1},\ldots,a_{p},\ ) \cdot a_{p+1}\big)\bullet z, {}\\ \end{array}$$

where

$$\displaystyle{\big(\psi (a_{1},\ldots,a_{p},\ ) \cdot a_{p+1}\big)\bullet z =\sum _{ i=1}^{n-1}[x_{ p+1}^{1},\ldots,\psi (a_{ 1},\ldots,a_{p},x_{p+1}^{i}),\ldots,x_{ p+1}^{n-1},z],}$$

for element $a_{i} \in \mathcal{L}(\mathcal{N})$ , $z \in \mathcal{N}$.

In particular, for p = 1, we get the set of 2-cocycles

$$\displaystyle{Z^{2}(\mathcal{N},\mathcal{N}) =\{\psi: \mathcal{N}^{n} \rightarrow \mathcal{N}\text{ satisfying }\delta ^{2}\psi = 0\},}$$

where for a ₁ = x ₁ ¹ ⊗⋯ ⊗ x ₁ ⁿ⁻¹ and a ₂ = x ₂ ¹ ⊗⋯ ⊗ x ₂ ⁿ⁻¹

$$\displaystyle\begin{array}{rcl} & & \delta ^{2}(a_{ 1},a_{2},z) ={}\end{array}$$

(4.14)

$$\displaystyle\begin{array}{rcl} & & -\sum _{i=1}^{n-1}\psi (x_{ 2}^{1},\cdots \,,[x_{ 1}^{1},\cdots x_{ 1}^{n-1},x_{ 2}^{i}],\cdots x_{ 2}^{n-1},z) -\psi (x_{ 2}^{1},\cdots \,,x_{ 2}^{n-1},[x_{ 1}^{1},\cdots \,,x_{ 1}^{n-1},z]) \\ & & +\psi (x_{1}^{1},\cdots \,,x_{ 1}^{n-1},[x_{ 2}^{1},\cdots \,,x_{ 2}^{n-1},z]) + [x_{ 1}^{1},\cdots \,,x_{ 1}^{n-1},\psi (x_{ 2}^{1},\cdots \,,x_{ 2}^{n-1},z)] \\ & & -[x_{2}^{1},\cdots \,,x_{ 2}^{n-1},\psi (x_{ 1}^{1},\cdots \,,x_{ 1}^{n-1},z)] -\sum _{ i=1}^{n-1}[x_{ 2}^{1},\cdots \,,\psi (x_{ 1}^{1},\cdots x_{ 1}^{n-1},x_{ 2}^{i}),\cdots x_{ 2}^{n-1},z].{}\end{array}$$

(4.15)

For p = 0, $\psi: \mathcal{N} \rightarrow \mathcal{N}$ and $(x_{1},\cdots \,,x_{n}) \in \mathcal{N}^{n}$, we have

$$\displaystyle{ \delta ^{1}\psi (x_{ 1},\cdots \,,x_{n}) = -\psi ([x_{1},\cdots \,,x_{n}]) +\sum _{ i=1}^{n}[x_{ 1},\cdots \,,\psi (x_{i})\cdots x_{n}] }$$

(4.16)

Notice that a linear map $\psi: \mathcal{N} \rightarrow \mathcal{N}$ such that δ ¹ ψ = 0 is a 1-cocycle and it corresponds to a derivation of the n-Lie algebra. The set of 2-coboundaries is defined as

$$\displaystyle{B^{2}(\mathcal{N},\mathcal{N}) =\{\psi: \mathcal{N}^{n} \rightarrow \mathcal{N}:\exists \varphi: \mathcal{N} \rightarrow \mathcal{N}\text{ such that }\psi =\delta ^{1}\varphi \}.}$$

Hence, the second cohomology group, which plays an important role in deformation theory, is defined as

$$\displaystyle{H^{2}(\mathcal{N},\mathcal{N}) = Z^{2}(\mathcal{N},\mathcal{N})/B^{2}(\mathcal{N},\mathcal{N}).}$$

4 Formal Deformation of n-Lie Algebras

In this section we study one parameter formal deformations of n-Lie algebras. This approach were introduced by Gerstenhaber for associative [41] and by Nijenhuis and Richardson for Lie [84]. Since then the approach was extended to many other algebraic structures. The main results connect formal deformation to cohomology groups. The noncommutative case was studied by Pincson [86]. See the following references for further results about deformations [16, 17, 31, 32, 40, 42–44, 54, 78, 83, 93].

4.1 One-Parameter Formal Deformation of n-Lie Algebras

Let $\mathbb{K}[[t]]$ be the power series ring in one variable t and coefficients in $\mathbb{K}$ and $\mathcal{N}[[t]]$ be the set of formal series whose coefficients are elements of the vector space $\mathcal{N}$, ($\mathcal{N}[[t]]$ is obtained by extending the coefficients domain of $\mathcal{N}$ from $\mathbb{K}$ to $\mathbb{K}[[t]]$). Given a $\mathbb{K}$-n-linear map $\varphi: \mathcal{N}\times \ldots \times \mathcal{N} \rightarrow \mathcal{N}$, it admits naturally an extension to a $\mathbb{K}[[t]]$-n-linear map $\varphi: \mathcal{N}[[t]] \times \ldots \times \mathcal{N}[[t]] \rightarrow \mathcal{N}[[t]]$, that is, if $x_{i} =\sum _{j\geq 0}a_{i}^{j}t^{j}$, 1 ≤ i ≤ n then $\varphi (x_{1},\ldots,x_{n}) =\sum _{j_{1},\ldots,j_{n}\geq 0}t^{j_{1}+\ldots +j_{n} }\varphi (a_{1}^{j_{1} },\ldots,a_{n}^{j_{n} })$.

Definition 4.11.

Let $(\mathcal{N},[\cdot,\ldots,\cdot ])$ be an n-Lie algebra. A one-parameter formal deformation of the n-Lie algebra $\mathcal{N}$ is given by a $\mathbb{K}[[t]]$-n-linear map

$$\displaystyle{[\cdot,\ldots,\cdot ]_{t}: \mathcal{N}[[t]] \times \ldots \times \mathcal{N}[[t]] \rightarrow \mathcal{N}[[t]]}$$

of the form $[\cdot,\ldots,\cdot ]_{t} =\sum _{i\geq 0}t^{i}[\cdot,\ldots,\cdot ]_{ i}$ where each [⋅ , …, ⋅ ] _i is a skew-symmetric $\mathbb{K}[[t]]$-n-linear map $[\cdot,\ldots,\cdot ]_{i}: \mathcal{N}\times \ldots \times \mathcal{N} \rightarrow \mathcal{N}$ (extended to a $\mathbb{K}[[t]]$-n-linear map), and [⋅ , …, ⋅ ]₀ = [⋅ , …, ⋅ ] such that for (x _i )_{1 ≤ i ≤ 2n−1}

$$\displaystyle\begin{array}{rcl} & [x_{1},\ldots,x_{n-1},[x_{n},\ldots,x_{2n-1}]_{t}]_{t} =\sum _{ i=n}^{2n-1}[x_{n},\ldots,x_{i-1},[x_{1},\cdots \,,x_{n-1},x_{i}]_{t},& \\ & \quad x_{i+1},\ldots,x_{2n-1}]_{t}. &{}\end{array}$$

(4.17)

The deformation is said to be of order k if $[\cdot,\ldots,\cdot ]_{t} =\sum _{ i=0}^{k}t^{i}[\cdot,\ldots,\cdot ]_{ i}$ and infinitesimal if t ² = 0.

The condition (4.17) may be written for $x = (x_{i})_{1\leq i\leq n-1},\ y = (x_{i})_{n\leq i\leq 2n-2} \in \mathcal{L}(\mathcal{N})$ and by setting z = x _2n−1

$$\displaystyle{ L_{t}([x,y]) \cdot (z) = L_{t}(x) \cdot \big (L_{t}(y) \cdot z\big) - L_{t}(y) \cdot \big (L_{t}(x) \cdot z\big), }$$

(4.18)

where L _t (x) ⋅ z = [x ₁, …, x _n−1, z] _t .

Assume that the deformation is infinitesimal and set ψ = [⋅ , ⋯ , ⋅ ]₁. Then Eq. (4.18) is equivalent to

$$\displaystyle\begin{array}{rcl} & & \big[x_{1},\ldots.,x_{n-1},\psi (y_{1},\ldots.,y_{n})\big] +\psi \big (x_{1},\ldots.,x_{n-1},[y_{1},\ldots.,y_{n}]\big) {}\\ & & =\sum _{ i=1}^{n}\big[y_{ 1},\ldots.,y_{i-1},\psi (x_{1},\ldots.,x_{n-1},y_{i}),y_{i+1},\ldots,y_{n}\big] {}\\ & & +\sum _{i=1}^{n}\psi \big(y_{ 1},\ldots.,y_{i-1},[x_{1},\ldots.,x_{n-1},y_{i}],y_{i+1},\ldots,y_{n}\big). {}\\ \end{array}$$

This identity may be viewed as the 2-cocycle condition δ ²[⋅ , …. , ⋅ ]₁ = 0 defined in (4.15).

More generally, let $(\mathcal{N},\mu )$ and $(\mathcal{N},\nu )$ be two n-ary operations, $\mu,\nu: \mathcal{N}^{n} \rightarrow \mathcal{N}$. We define a (2n − 1)-ary operation μ ∘ν by

$$\displaystyle\begin{array}{rcl} \mu \circ \nu (x_{1},\ldots,x_{n-1},x_{n},\ldots,x_{2n-1}) =\mu (x_{1},\ldots,x_{n-1},\nu (x_{n},\ldots,x_{2n-1}))& & \\ -\sum _{i=n}^{2n-1}\mu (x_{ n},\ldots,x_{i-1},\nu (x_{1},\cdots \,,x_{n-1},x_{i}),x_{i+1},\ldots,x_{2n-1}).& &{}\end{array}$$

(4.19)

Then, an n-ary operation μ on a vector space $\mathcal{N}$ satisfies Nambu identity if and only if μ ∘μ = 0.

Therefore, the Nambu identity (4.17) is equivalent to an infinite system, called deformation equation,

$$\displaystyle{ \left \{\sum _{i=0}^{k}[\cdot,\ldots,\cdot ]_{ i} \circ [\cdot,\ldots,\cdot ]_{k-i} = 0\qquad k = 0,1,2,\cdots \,\right. }$$

(4.20)

For an arbitrary k > 1, the kth equation of the previous system may be written

$$\displaystyle{\delta ^{2}[\cdot,\ldots,\cdot ]_{ k} =\sum _{ i=1}^{k-1}[\cdot,\ldots,\cdot ]_{ i} \circ [\cdot,\ldots,\cdot ]_{k-i}.}$$

Assume that a deformation of order m satisfies the deformation equation. The truncated deformation is extended to a deformation of order m + 1 if

$$\displaystyle{\delta ^{2}[\cdot,\ldots,\cdot ]_{ m} =\sum _{ i=1}^{m-1}[\cdot,\ldots,\cdot ]_{ i} \circ [\cdot,\ldots,\cdot ]_{m-i}.}$$

The right-hand side of this equation is called the obstruction to find [⋅ , …, ⋅ ] _m extending the deformation.

It turns out that the obstruction is a 3-cocycle. Then, if $H^{3}\left (\mathcal{N},\mathcal{N}\right ) = 0$, it follows that all obstructions vanish and every $[\cdot,\ldots,\cdot ]_{m} \in Z^{2}\left (\mathcal{N},\mathcal{N}\right )$ defines a deformation of order m + 1.

In the following, we characterize equivalent and trivial deformations.

Definition 4.12.

Let $(\mathcal{N},[\cdot,\ldots,\cdot ])$ be an n-Lie algebra. Given two deformations $\mathcal{N}_{t} = (\mathcal{N}[[t]],[\cdot,\ldots,\cdot ]_{t})$ and $\mathcal{N}_{t}^{'} = (\mathcal{N}[[t]],[\cdot,\ldots,\cdot ]_{t}^{'})$ of $\mathcal{N}$ where $[\cdot,\ldots,\cdot ]_{t} =\sum \limits _{ i\geq 0}^{k}t^{i}[\cdot,\ldots,\cdot ]_{i}$ and $[\cdot,\ldots,\cdot ]_{t}^{'} =\sum \limits _{ i\geq 0}^{k}t^{i}[\cdot,\ldots,\cdot ]_{i}^{'}$ with [⋅ , …, ⋅ ]₀ = [⋅ , …, ⋅ ]₀ ^′ = [⋅ , …, ⋅ ]. We say that $\mathcal{N}_{t}$ and $\mathcal{N}_{t}^{'}$ are equivalent if there exists a formal automorphism $\phi _{t}: \mathcal{N}[[t]]\longrightarrow \mathcal{N}[[t]]$ that may be written in the form $\phi _{t} =\sum \limits _{i\geq 0}\phi _{i}t^{i}$, where $\phi _{i} \in End(\mathcal{N})$ and ϕ ₀ = Id such that

$$\displaystyle\begin{array}{rcl} \phi _{t}([x_{1},\cdots \,,x_{n}]_{t})& =& [\phi _{t}(x_{1}),\cdots \,,\phi _{t}(x_{n})]_{t}^{'}.{}\end{array}$$

(4.21)

A deformation $\mathcal{N}_{t}$ of $\mathcal{N}$ is said to be trivial if $\mathcal{N}_{t}$ is equivalent to $\mathcal{N}$, viewed as an n-ary algebra on $\mathcal{N}[[t]]$.

Let $(\mathcal{N},[\cdot,\ldots,\cdot ])$ be an n-Lie algebra and $[\cdot,\ldots,\cdot ]_{1} \in Z^{2}(\mathcal{N},\mathcal{N})$.

The 2-cocycle [⋅ , …, ⋅ ]₁ is said to be integrable if there exists a family ([⋅ , …, ⋅ ] _i ) _i ≥ 0 such that $[\cdot,\ldots,\cdot ]_{t} =\sum \limits _{i\geq 0}t^{i}[.,.]_{i}$ defines a formal deformation $\mathcal{N}_{t} = (\mathcal{N},[\cdot,\ldots,\cdot ]_{t})$ of $\mathcal{N}$.

Theorem 4.2.

Let $(\mathcal{N},[\cdot,\ldots,\cdot ])$ be an n-Lie algebra and $(\mathcal{N}[[t]],[\cdot,\ldots,\cdot ]_{t})$ , where $[\cdot,\ldots,\cdot ]_{t} =\sum _{i\geq 0}t^{i}[\cdot,\ldots,\cdot ]_{ i}$ , be a one-parameter formal deformation.

• 1. The first term [⋅,….,⋅] ₁ is a 2-cocycle, that is $[\cdot,\ldots.,\cdot ]_{1} \in Z^{2}(\mathcal{N},\mathcal{N})$.

• 2. There exists an equivalent deformation $\mathcal{N}_{t}^{\prime} = (\mathcal{N}, [\cdot,\ldots,\cdot ]_{t}^{\prime} )$ , where $[\cdot,\ldots,\cdot ]_{t}^{'} =\sum \limits _{i\geq 0}t^{i}[\cdot,\ldots,\cdot ]_{i}^{'}$ such that $[\cdot,\ldots,\cdot ]_{1}^{'} \in Z^{2}(\mathcal{N},\mathcal{N})$ and $[\cdot,\ldots,\cdot ]_{1}^{'}\not\in B^{2}(\mathcal{N},\mathcal{N})$.

Moreover, if $H^{2}(\mathcal{N},\mathcal{N}) = 0$ , then every one-parameter formal deformation is trivial.

The proof is similar to the case n = 2.

4.2 Noncommutative One-Parameter Formal Deformations

In previous formal deformation theory, the parameter commutes with the original algebra. Motivated by some nonclassical deformation appearing in quantization of Nambu mechanics, Pinczon introduced a deformation called noncommutative deformation where the parameter no longer commutes with the original algebra. He developed also the associated cohomology [86].

Let $\mathcal{N}$ be a $\mathbb{K}$-vector space and σ be an endomorphism of $\mathcal{N}$. We give $\mathcal{N}[[t]]$ a $\mathbb{K}[[t]]$-bimodule structure defined for every $a_{p} \in \mathcal{A},\lambda _{q} \in \mathbb{K}$ by:

$$\displaystyle\begin{array}{rcl} \sum _{p\geq 0}a_{p}t^{p} \cdot \sum _{ q\geq 0}\lambda _{q}t^{q}& =& \sum _{ p,q\geq 0}\lambda _{q}a_{p}t^{p+q}, {}\\ \sum _{q\geq 0}\lambda _{q}t^{q} \cdot \sum _{ p\geq 0}a_{p}t^{p}& =& \sum _{ p,q\geq 0}\lambda _{q}\sigma ^{q}(a_{ p})t^{p+q}. {}\\ \end{array}$$

Definition 4.13.

A σ-deformation of an n-ary algebra $\mathcal{N}$ is a $\mathbb{K}[[t]]$-algebra structure on $\mathcal{N}[[t]]$ which is compatible with the previous $\mathbb{K}[[t]]$-bimodule structure and such that

$$\displaystyle{\mathcal{N}[[t]]/(\mathcal{N}[[t]]t)\cong \mathcal{A}.}$$

A generalization of these deformations was proposed by Nadaud [81] where he considered deformations based on two commuting endomorphisms σ and τ. The $\mathbb{K}[[t]]$-bimodule structure on $\mathcal{N}[[t]]$ is defined for $a \in \mathcal{N}$ by the formulas t ⋅ a = σ(a)t and a ⋅ t = τ(a)t, (a ⋅ t being the right action of t on a).

The remarkable difference with commutative deformation is that the Weyl algebra of differential operators with polynomial coefficients over $\mathbb{R}$ is rigid for commutative deformations but has a nontrivial noncommutative deformation; it is given by the enveloping algebra of the Lie algebra osp(1, 2).

5 Global Deformations

This approach follows from a general fact in Schlessinger’s works [88] and was developed by A. Fialowski and her collaborators for different kind of algebras (Lie algebra, Leibniz algebras ….[32, 34–37]). In the sequel we extend this approach to n-Lie algebras. Let B be a commutative algebra over a field $\mathbb{K}$ of characteristic 0 and an augmentation morphism $\varepsilon: \mathcal{A}\rightarrow \mathbb{K}$ (a $\mathbb{K}$-algebra homomorphism, ɛ(1 _B ) = 1). We set m _ɛ  = Ker(ɛ); m _ɛ is a maximal ideal of B. A maximal ideal m of B such that $\mathcal{A}/m\cong \mathbb{K}$, defines naturally an augmentation. We call (B, m) base of deformation.

Definition 4.14.

A global deformation of base (B, m) of an n-Lie algebra $(\mathcal{N},[\cdot,\ldots,\cdot ])$ is a structure of B-algebra on the tensor product $B \otimes _{\mathbb{K}}\mathcal{N}^{n}$ with a bracket [⋅ , …, ⋅ ] _B such that $\varepsilon \otimes id: B \otimes \mathcal{N} \rightarrow \mathbb{K} \otimes \mathcal{N} = \mathcal{N}$ is an n-ary algebra homomorphism. i.e. $\forall a,b \in B$ and $\forall x_{1},\cdots \,,x_{n} \in \mathcal{N}$:

• 1. [a ₁ ⊗ x ₁, ⋯ , a _n ⊗ x _n ] _B  = (a ₁ … a _n ⊗ id)[1 ⊗ x ₁, ⋯ , 1 ⊗ x _n ] _B (B−linearity)

• 2. The bracket [⋅ , …, ⋅ ] _B satisfies Nambu identity.

• 3. $\varepsilon \otimes id\left ([1 \otimes x_{1},\cdots \,,1 \otimes x_{n}]_{B}\right ) = 1 \otimes [x_{1},\ldots,x_{n}]$

Every formal deformation of an n-Lie algebra $\mathcal{N}$, in Gerstenhaber sense, is a global deformation with a basis $\left (B,m\right )$ where $B = \mathbb{K}[[t]]$ and $m = t\mathbb{K}[[t]]$.

Remark 4.5.

Condition 1 shows that to describe a global deformation it is enough to know the brackets [1 ⊗ x ₁, …, 1 ⊗ x _n ] _B , where $x_{1},\cdots \,,x_{n} \in \mathcal{N}.$ The conditions 1 and 2 show that we have an n-Lie algebra and the last condition insures the compatibility with the augmentation. We deduce

$$\displaystyle{[1 \otimes x_{1},\cdots \,,1 \otimes x_{n}]_{B} = 1 \otimes [x_{1},\ldots,x_{n}] +\sum _{i}\alpha _{i} \otimes z_{i}\quad \text{with }\alpha _{i} \in m,\ z_{i} \in \mathcal{N}.}$$

• A global deformation is called trivial if the structure of n-ary B-algebra on $B \otimes _{\mathbb{K}}\mathcal{N}$ satisfies [1 ⊗ x ₁, …, 1 ⊗ x _n ] _B  = 1 ⊗ [x ₁, …, x _n ]. 

• Two deformations of an n-Lie algebra with the same base are called equivalent (or isomorphic) if there exists an algebra isomorphism between the two copies of $B \otimes _{\mathbb{K}}\mathcal{N}^{\setminus }$, compatible with ɛ ⊗ id. 

• A global deformation with base (B, m) is called local if B is a local $\mathbb{K}$-algebra with a unique maximal ideal m _B . If, in addition m ² = 0, the deformation is called infinitesimal.

• Let B ^′ be another commutative algebra over $\mathbb{K}$ with augmentation $\varepsilon ^{{\prime}}: B^{{\prime}}\rightarrow \mathbb{K}$ and Φ: B → B ^′ an algebra homomorphism such that $\varPhi (1_{B}) = 1_{B^{{\prime}}}$ and ɛ ^′∘Φ = ɛ. If a deformation μ _B with a base (B, Ker(ɛ)) of $\mathcal{A}$ is given we call push-out $[\cdot,\ldots,\cdot ]_{B^{{\prime}}} =\varPhi _{{\ast}}[\cdot,\ldots,\cdot ]_{B}$ a deformation of $\mathcal{A}$ with a base (B ^′, Ker(ɛ ^′)) with the following algebra structure on $B^{{\prime}}\otimes \mathcal{A} = \left (B^{{\prime}}\otimes _{B}B\right ) \otimes \mathcal{A} = B^{{\prime}}\otimes _{B}\left (B \otimes \mathcal{A}\right )$

  $$\displaystyle{[a_{1}^{{\prime}}\otimes _{ B}\left (a_{1} \otimes x_{1}\right ),\cdots \,,a_{n}^{{\prime}}\otimes _{ B}\left (a_{n} \otimes x_{n}\right )]_{B^{{\prime}}}:= a_{1}^{{\prime}}\ldots.a_{ n}^{{\prime}}\otimes _{ B}[a_{1} \otimes x_{1},\cdots \,,a_{n} \otimes x_{n}]_{B},}$$

  with $a_{1}^{{\prime}},a_{2}^{{\prime}}\in B^{{\prime}},a_{1},a_{2} \in B,x_{1},x_{2} \in \mathcal{A}$. The algebra B ^′ is viewed as a B-module with the structure $aa^{{\prime}} = a^{{\prime}}\varPhi \left (a\right )$. Suppose that

  $$\displaystyle{[1 \otimes x_{1},\cdots \,,1 \otimes x_{n}]_{B} = 1 \otimes [x_{1},\cdots \,,x_{n}] +\sum _{i}\alpha _{i} \otimes z_{i}\quad }$$

  with $\alpha _{i} \in m,\ z_{i} \in \mathcal{N}$. Then

  $$\displaystyle{[1 \otimes x_{1},\cdots \,,1 \otimes x_{n}]_{B^{{\prime}}} = 1 \otimes \mu [x_{1},\cdots \,,x_{n}] +\sum _{i}\varPhi (\alpha _{i}) \otimes z_{i}\quad }$$

  with $\alpha _{i} \in m,\ z_{i} \in \mathcal{N}$.

One may address the problem of finding, for a fixed algebra, particular deformations which induces all the others in the space of all deformations (moduli space) or in a fixed category of deformations. The problem of constructing universal or versal deformations of Lie algebras was considered for the categories of deformations over infinitesimal local algebras and complete local algebras (see [32, 35, 36]). They show that if we consider the infinitesimal deformations, i.e. the deformations over local algebras B such that m _B ² = 0 where m _B is the maximal ideal, then there exists a universal deformation (the morphism between base algebras is unique). If we consider the category of complete local rings, then there does not exist a universal deformation but only versal deformation (there is no unicity for the morphism).

Let B be a complete local algebra over $\mathbb{K}$, so B = $\overleftarrow{\lim }_{n\rightarrow \infty }(B/m^{n})$ (inductive limit), where m is the maximal ideal of B and we assume that $B/m\cong \mathbb{K}$.

A formal global deformation of $\mathcal{N}$ with base $\left (B,m\right )$ is an algebra structure on the completed tensor product $B\stackrel{\wedge }{\otimes }\mathcal{N} =\overleftarrow{ \lim }_{n\rightarrow \infty }((B/m^{n}) \otimes \mathcal{N})$ such that $\varepsilon \stackrel{\wedge }{\otimes }id: B\stackrel{\wedge }{\otimes }\mathcal{N} \rightarrow K \otimes \mathcal{N} = \mathcal{N}$ is an algebra homomorphism.

The formal global deformation of $\mathcal{N}$ with base $\left (\mathbb{K}[[t]],t\mathbb{K}[[t]]\right )$ are the same as formal one parameter deformation of Gerstenhaber.

6 The Algebraic Varieties $\mathcal{L}ie_{m}^{n}$ and Degenerations

Let $\mathcal{N}$ be an m-dimensional vector space over $\mathbb{K}$ and {e ₁, ⋯ , e _m } be a basis of $\mathcal{N}$. An n-linear bracket [⋅ , …, ⋅ ] can be defined by specifying the m ⁿ⁺¹ structure constants $C_{i_{1},\cdots \,,i_{n}}^{k} \in \mathbb{K}$ where

$$\displaystyle{[e_{i_{1}},\ldots,e_{i_{m}}] =\sum _{ k=1}^{m}C_{ i_{1},\cdots \,,i_{n}}^{k}e_{ k}.}$$

The Nambu identity and skew-symmetry limits the sets of structure constants $C_{i_{1},\cdots \,,i_{n}}^{k}$ to a subvariety of $\mathbb{K}^{m^{2}(m-1)\cdots (m-n+1) }$ which we denote by $\mathcal{L}ie_{m}^{n}$. It is generated by the polynomial relations

$$\displaystyle\begin{array}{rcl} \sum _{k=1}^{m}C_{ j_{1},\cdots \,,j_{n}}^{k}C_{ i_{1},\cdots \,,i_{n-1},k}^{s} -\sum _{ r=1}^{n}\sum _{ k=1}^{m}C_{ i_{1},\cdots \,,i_{n-1},j_{r}}^{k}C_{ j_{1},\cdots \,,j_{r-1},k,j_{r+1},\cdots j_{n}}^{s} = 0,& & \\ \quad 1 \leq i_{1}\cdots \,,i_{n-1},j_{1},\cdots \,,j_{n},s \leq m.& &{}\end{array}$$

(4.22)

Therefore, $\mathcal{L}ie_{m}^{n}$ carries a structure of algebraic variety which is quadratic, non regular and in general non-reduced. The natural action of the group $GL_{m}(\mathbb{K})$ corresponds to the change of basis: two n-Lie algebras $(\mathcal{N},[\cdot,\ldots,\cdot ]_{1})$ and $(\mathcal{N},[\cdot,\ldots,\cdot ]_{2})$ are isomorphic if there exists f in $GL_{m}(\mathbb{K})$ such that $\mathcal{N}_{2} = f \cdot \mathcal{N}_{1}$, that is:

$$\displaystyle{\forall x_{1},\cdots \,,x_{n} \in \mathcal{N}\quad [x_{1},\ldots,x_{n}]_{2} = f^{-1}([f(x_{ 1}),\ldots,f(x_{n})]_{1}.}$$

The orbit of an n-Lie algebra $\mathcal{N}_{0} = (\mathcal{N},[\cdot,\ldots,\cdot ]_{0})$, denoted by $\vartheta \left (\mathcal{N}_{0}\right )$, is the set of all its isomorphic n-Lie algebras.

A point in $\mathcal{L}ie_{m}^{n}$ is defined by m ²(m − 1)⋯(m − n + 1) parameters, which are the structure constants $C_{i_{1},\cdots \,,i_{n}}^{k}$ satisfying (4.22). The orbits are in 1-1-correspondence with the isomorphism classes of m-dimensional n-Lie algebras. The stabilizer subgroup of $\mathcal{N}_{0}$

$$\displaystyle{stab\left (\mathcal{N}_{0}\right ) = \left \{f \in GL_{m}\left (\mathbb{K}\right ): \mathcal{N}_{0} = f \cdot \mathcal{N}_{0}\right \}}$$

is $Aut\left (\mathcal{N}_{0}\right )$, the automorphism group of $\mathcal{N}_{0}$. The orbit $\vartheta \left (\mathcal{N}_{0}\right )$ is identified with the homogeneous space $GL_{m}\left (\mathbb{K}\right )/Aut\left (\mathcal{N}_{0}\right )$. Then

$$\displaystyle{\dim \vartheta \left (\mathcal{N}_{0}\right ) = m^{2} -\dim Aut\left (\mathcal{N}_{ 0}\right ).}$$

The orbit $\vartheta \left (\mathcal{N}_{0}\right )$ is provided, when $\mathbb{K} = \mathbb{C}$ (a complex field), with the structure of a differentiable manifold. In fact, $\vartheta \left (\mathcal{N}_{0}\right )$ is the image through the action of the Lie group $GL_{m}\left (\mathbb{K}\right )$ of the point $\mathcal{N}_{0}$, considered as a point of $Hom\left (\mathcal{N}^{\otimes n},\mathcal{N}\right )$. The Zariski tangent space to $\mathcal{L}ie_{m}^{n}$ at the point $\mathcal{N}_{0}$ corresponds to $Z^{2}(\mathcal{N},\mathcal{N})$ and the tangent space to the orbit corresponds to $B^{2}(\mathcal{N},\mathcal{N})$.

The first approach to study varieties $\mathcal{L}ie_{m}^{n}$ is to establish classifications of n-Lie algebras up to isomorphisms for a fixed dimension. Classification of n-Lie algebras of dimension less than or equal to n + 2 is known, see [11, 38]. We have the following results.

Theorem 4.3 ([38]).

Any n-Lie algebra $\mathcal{N}$ of dimension less than or equal to n + 1 is isomorphic to one of the following n-ary algebras: (omitted brackets are either obtained by skew-symmetry or 0)

• 1. If $dim\mathcal{N} <n$ then A is abelian.

• 2. If $dim\mathcal{N} = n$ , then we have 2 cases:

  • a. A is abelian.

  • b. $\left [e_{1},\ldots,e_{n}\right ] = e_{1}.$

• 3. if $dim\mathcal{N} = n + 1$ then we have the following cases:

  • a. A is abelian.

  • b. $\left [e_{2},\ldots,e_{n+1}\right ] = e_{1}$.

  • c. $\left [e_{1},\ldots,e_{n}\right ] = e_{1}$.

  • d. $\left [e_{1},\ldots,e_{n-1},e_{n+1}\right ] = ae_{n} + be_{n+1};\left [e_{1},\ldots,e_{n}\right ] = ce_{n} + de_{n+1}$ , with $C = \left (\begin{array}{*{10}c} a&b\\ c &d\end{array} \right )$ an invertible matrix. Two such algebras, defined by matrices C ₁ and C ₂ , are isomorphic if and only if there exists a scalar α and an invertible matrix B such that C ₂ = αBC ₁ B ⁻¹.

  • e. $\left [e_{1},\ldots,\widehat{e_{i}},\ldots,e_{n}\right ] = a_{i}e_{i}$ for 1 ≤ i ≤ r, $2 <r =\mathop{ \mathrm{dim}}\nolimits D^{1}(A) \leq n$ , a _i ≠ 0

  • f. $\left [e_{1},\ldots,\widehat{e_{i}},\ldots,e_{n}\right ] = a_{i}e_{i}$ for 1 ≤ i ≤ n + 1 which is simple.

Theorem 4.4 ([11]).

Let $\mathbb{K}$ be an algebraically closed field. Any (n + 2)-dimensional n-Lie algebra $\mathcal{N}$ is isomorphic to one of the n-ary algebras listed below, where $\mathcal{N}^{1}$ denotes $\left [\mathcal{N},\ldots,\mathcal{N}\right ]$ :

• 1. If $dim\mathcal{N}^{1} = 0$ then $\mathcal{N}$ is abelian.

• 2. If $dim\mathcal{N}^{1} = 1$ , let $\mathcal{N}^{1} =\langle e_{1}\rangle$ , then we have

  • a. $\mathcal{N}^{1} \subseteq Z(\mathcal{N})$ : $\left [e_{2},\ldots,e_{n+1}\right ] = e_{1}$.

  • b. $\mathcal{N}^{1} \not\subseteq Z(\mathcal{N})$ : $\left [e_{1},\ldots,e_{n}\right ] = e_{1}$.

• 3. If $dim\mathcal{N}^{1} = 2$ , let $\mathcal{N}^{1} =\langle e_{1},e_{2}\rangle$ , then we have

  • a. $\left [e_{2},\ldots,e_{n+1}\right ] = e_{1};\left [e_{3},\ldots,e_{n+2}\right ] = e_{2}$.

  • b. $\left [e_{2},\ldots,e_{n+1}\right ] = e_{1};\left [e_{2},e_{4},\ldots,e_{n+2}\right ] = e_{2};\left [e_{1},e_{4},\ldots,e_{n+2}\right ] = e_{1}$.

  • c. $\left [e_{2},\ldots,e_{n+1}\right ] = e_{1};\left [e_{1},e_{3},\ldots,e_{n+1}\right ] = e_{2}$.

  • d. $\left [e_{2},\ldots,e_{n+1}\right ] = e_{1};\left [e_{1},e_{3},\ldots,e_{n+1}\right ] = e_{2};\left [e_{2},e_{4},\ldots,e_{n+2}\right ] = e_{2};\left [e_{1},e_{4},\ldots,e_{n+2}\right ] = e_{1}$.

  • e. $\left [e_{2},\ldots,e_{n+1}\right ] =\alpha e_{1} + e_{2};\left [e_{1},e_{3},\ldots,e_{n+1}\right ] = e_{2}$.

  • f. $\left [e_{2},\ldots,e_{n+1}\right ] =\alpha e_{1} + e_{2};\left [e_{1},e_{3},\ldots,e_{n+1}\right ] = e_{2};\left [e_{2},e_{4},\ldots,e_{n+2}\right ] = e_{2};\left [e_{1},e_{4},\ldots,e_{n+2}\right ] = e_{1}$.

  • g. $\left [e_{1},e_{3},\ldots,e_{n+1}\right ] = e_{1};\left [e_{2},e_{3},\ldots,e_{n+1}\right ] = e_{2}$.

  where $\alpha \in \mathbb{K}\setminus \left \{0\right \}$

• 4. If $dim\mathcal{N}^{1} = 3$ , let $\mathcal{N}^{1} =\langle e_{1},e_{2},e_{3}\rangle$ , then we have

  • a. $\left [e_{2},\ldots,e_{n+1}\right ] = e_{1};\left [e_{2},e_{4},\ldots,e_{n+2}\right ] = -e_{2};\left [e_{3},\ldots,e_{n+2}\right ] = e_{3}$.

  • b. $\left [e_{2},\ldots,e_{n+1}\right ] = e_{1};\left [e_{3},\ldots,e_{n+2}\right ] = e_{3} +\alpha e_{2};\left [e_{2},e_{4},\ldots,e_{n+2}\right ] = e_{3};\left [e_{1},e_{4},\ldots,e_{n+2}\right ] = e_{1}$.

  • c. $\left [e_{2},\ldots,e_{n+1}\right ] = e_{1};\left [e_{3},\ldots,\right.$ $\left.e_{n+2}\right ] = e_{3};\left [e_{2},e_{4},\ldots,e_{n+2}\right ] = e_{2};\left [e_{1},e_{4},\ldots \right.$ , $\left.e_{n+2}\right ] = 2e_{1}$.

  • d. $\left [e_{2},\ldots,e_{n+1}\right ] = e_{1};\left [e_{1},e_{3},\ldots,e_{n+1}\right ] = e_{2};\left [e_{1},e_{2},e_{4},\ldots,e_{n+1}\right ] = e_{3}$.

  • e. $\left [e_{1},e_{4},\ldots,e_{n+2}\right ] = e_{1};\left [e_{2},e_{4},\ldots,e_{n+2}\right ] = e_{3};\left [e_{3},\ldots,e_{n+2}\right ] =\beta e_{2} + (1+\beta )e_{3}$ , $\beta \in \mathbb{K}\setminus \left \{0,1\right \}$.

  • f. $\left [e_{1},e_{4},\ldots,e_{n+2}\right ] = e_{1};\left [e_{2},e_{4},\ldots,e_{n+2}\right ] = e_{2};\left [e_{3},\ldots,e_{n+2}\right ] = e_{3}$.

  • g. $\left [e_{1},e_{4},\ldots,e_{n+2}\right ] = e_{2};\left [e_{2},e_{4},\ldots,e_{n+2}\right ] = e_{3};\left [e_{3},\ldots,e_{n+2}\right ] = se_{1} + te_{2} + ue_{3}$ . And n-Lie algebras corresponding to this case with coefficients s,t,u and s′,t′,u′ are isomorphic if and only if there exists a non-zero element $r \in \mathbb{K}$ such that

    $$\displaystyle{s = r^{3}s';t = r^{2}t';u = ru'.}$$

• 5. If $dim\mathcal{N}^{1} = r$ with 4 ≤ r ≤ n + 1, let A ¹ = 〈 e ₁ ,e ₂ ,…,e _r〉 , then we have

  • a. $\left [e_{2},\ldots,e_{n+1}\right ] = e_{1};\left [e_{3},\ldots,e_{n+2}\right ] = e_{2};\ldots;\left [e_{2},\ldots,e_{i-1},e_{i+1},\ldots,e_{n+2}\right ] = e_{i};\left [e_{2},\ldots,e_{r-1},e_{r+1},\ldots,e_{n+2}\right ] = e_{r}$.

  • b. $\left [e_{2},\ldots,e_{n+1}\right ] = e_{1};\ldots;\left [e_{1},\ldots,e_{i-1},e_{i+1},e_{n+1}\right ] = e_{i};\ldots$ ; $\left [e_{1},\ldots,e_{r-1}\right.$ , $\left.e_{r+1},e_{n+1}\right ] = e_{r}$.

The second approach to study the algebraic variety $\mathcal{L}ie_{m}^{n}$ is to describe its irreducible components. This problem was considered for binary Lie algebras of small dimensions but it is still open for n-Lie algebras. The main approach uses formal deformations and degenerations. A degeneration notion is a sort of dual notion of a deformation. It appeared first in physics literature [58]. Degeneration is also called specialisation or contraction. We provide first the geometric definition of a degeneration, using Zariski topology.

Definition 4.15.

Let $\mathcal{N}_{0} = (\mathcal{N},[\cdot,\ldots,\cdot ]_{0})$ and $\mathcal{N}_{1} = (\mathcal{N},[\cdot,\ldots,\cdot ]_{1})$ be two m-dimensional n-Lie algebras. We said that $\mathcal{N}_{0}$ is a degeneration of $\mathcal{N}_{1}$ if $\mathcal{N}_{0}$ belongs to the closure of the orbit of $\mathcal{N}_{1}$ in $\mathcal{L}ie_{m}^{n}$ ($\mathcal{N}_{0} \in \overline{\vartheta \left (\mathcal{N}_{1}\right )}$).

Therefore, $\mathcal{N}_{0}$ and $\mathcal{N}_{1}$ are in the same irreducible component.

A characterization of degeneration for Lie algebras, in the global deformations viewpoint, was given by Grunewald and O’Halloran in [52]. It generalizes naturally to n-Lie as follows.

Theorem 4.5.

Let $\mathcal{N}_{0}$ and $\mathcal{N}_{1}$ be two m-dimensional n-Lie algebras over $\mathbb{K}$ with brackets [⋅,…,⋅] ₀ and [⋅,…,⋅] ₁ . The n-Lie algebra $\mathcal{N}_{0}$ is a degeneration of $\mathcal{N}_{1}$ if and only if there is a discrete valuation $\mathbb{K}$ -algebra B with residue field $\mathbb{K}$ whose quotient field $\mathcal{K}$ is finitely generated over $\mathbb{K}$ of transcendence degree one (one parameter), and there is an m-dimensional n-Lie algebra [⋅,…,⋅] _B over B such that $[\cdot,\ldots,\cdot ]_{B} \otimes \mathcal{K}\cong [\cdot,\ldots,\cdot ]_{1} \otimes \mathcal{K}$ and $[\cdot,\ldots,\cdot ]_{B} \otimes \mathbb{K}\cong [\cdot,\ldots,\cdot ]_{0}$.

We call such a degeneration, a global degeneration. A formal degeneration is defined as follows.

Definition 4.16.

Let $\mathcal{N}_{1} = (\mathcal{N},[\cdot,\ldots,\cdot ]_{1})$ be an m-dimensional n-Lie algebra. Let t be a parameter in $\mathbb{K}$ and {f _t } _{t ≠ 0} be a continuous family of invertible linear maps on $\mathcal{N}$ over $\mathbb{K}$.

The limit (when it exists) of a sequence $f_{t} \cdot \mathcal{N}_{1}$ , $\mathcal{N}_{0} =\lim _{t\rightarrow 0}f_{t} \cdot \mathcal{N}_{1}$, is a formal degeneration of $\mathcal{N}_{1}$ in the sense that $\mathcal{N}_{0}$ is in the Zariski closure of the set $\left \{f_{t} \cdot \mathcal{N}_{1}\right \}_{t\neq 0}.$

The bracket [⋅ , …, ⋅ ]₀ is given by

$$\displaystyle{\forall x_{1},\cdots \,,x_{n} \in \mathcal{N}\quad [x_{1},\ldots,x_{n}]_{0} =\lim _{t\rightarrow 0}f_{t}^{-1}([f_{ t}(x_{1}),\ldots,f_{t}(x_{n})]_{1}.}$$

We have the following observations.

• 1. The bracket [⋅ , …, ⋅ ] _t  = f _t ⁻¹ ∘ [⋅ , …, ⋅ ]₁ ∘ f _t × f _t satisfies Nambu identity. Thus, when t tends to 0 the condition remains satisfied.

• 2. The linear map f _t  is invertible when t ≠ 0  and may be singular when t = 0. Then, we may obtain by degeneration a new n-Lie algebra.

• 3. The definition of formal degeneration may be extended naturally to infinite dimensional case.

• 4. When $\mathbb{K}$ is the complex field, the multiplication given by the limit, follows from a limit of the structure constants, using the metric topology. In fact, f _t ⋅ [⋅ , …, ⋅ ]₁ corresponds to a change of basis when t ≠ 0. When t = 0, they give eventually a new point in $\mathcal{L}ie_{m}^{n}$.

• 5. If f _t is defined by a power series, the images of $f_{t} \cdot \mathcal{N}$ are in general in the Laurent power series ring $\mathcal{N}\left [\left [t,t^{-1}\right ]\right ]$. But when the degeneration exists, it lies in the power series ring $\mathcal{N}\left [\left [t\right ]\right ]$.

• 6. Every formal degeneration is a global degeneration.

Remark 4.6.

Rigid n-Lie algebras will have a special interest, an open orbit of a given n-Lie algebra is dense in the irreducible component in which it lies. Then, its Zariski closure determines an irreducible component of $\mathcal{L}ie_{m}^{n}$, i.e. all n-Lie algebras in this irreducible component are degenerations of the rigid n-Lie algebra and there is no n-Lie algebra which degenerates to the rigid n-Lie algebra. Two non-isomorphic rigid n-Lie algebras correspond to different irreducible components. So the number of rigid n-Lie algebra classes gives a lower bound of the number of irreducible components of $\mathcal{L}ie_{m}^{n}$. Note that not all irreducible components are Zariski closure of open orbits.

7 n-Lie-Poisson Algebras and Quantization

7.1 n-Lie-Poisson Algebras

We introduce the notion of n-Lie-Poisson algebra.

Definition 4.17.

An n -Lie-Poisson algebra is a triple $(\mathcal{N},\mu,\{.,.,.\})$ consisting of a $\mathbb{K}$-vector space N, a bilinear map $\mu: \mathcal{N}\times \mathcal{N} \rightarrow \mathcal{N}$ and an n-ary bracket {⋅ , …, ⋅ } such that

• 1. $(\mathcal{N},\mu )$ is a binary commutative associative algebra,

• 2. $(\mathcal{N},\{\cdot,\ldots,\cdot \})$ is a n-Lie algebra,

• 3. the following Leibniz rule

  $$\displaystyle{ \{x_{1},\ldots.,x_{n-1},\mu (x_{n},x_{n+1})\} =\mu (x_{n},\{x_{1},\ldots,x_{n-1},x_{n+1}\}) +\mu (\{x_{1},\ldots.,x_{n}\},x_{n+1}) }$$

holds for all $x_{1},\ldots,x_{n+1} \in \mathcal{N}$.

A morphism of n-Lie-Poisson algebras is a linear map that is a morphism of the underlying n-Lie algebras and associative algebras.

Example 4.6.

Let $C^{\infty }(\mathbb{R}^{3})$ be the algebra of C ^∞ functions on $\mathbb{R}^{3}$ and x ₁, x ₂, x ₃ the coordinates on $\mathbb{R}^{3}$. We define the ternary brackets as in (4.4), then $(C^{\infty }(\mathbb{R}^{3}),\{.,.,.\})$ is a ternary 3-Lie algebra. In addition the bracket satisfies the Leibniz rule: {f g, f ₂, f ₃} = f{g, f ₂, f ₃} +{ f, f ₂, f ₃}g where $f,g,f_{2},f_{3} \in C^{\infty }(\mathbb{R}^{3})$ and the multiplication being the pointwise multiplication that is f g(x) = f(x)g(x). Therefore, the algebra is a 3-Lie-Poisson algebra.

This algebra was considered already in 1973 by Nambu [82] as a possibility of extending the Poisson bracket of standard hamiltonian mechanics to bracket of three functions defined by the Jacobian. Clearly, the Nambu bracket may be generalized further to an n-Lie-Poisson allowing for an arbitrary number of entries.

7.2 Quantization of Nambu Mechanics

The quantization problem of Nambu Mechanics was investigated by Dito et al. [29, 30], see also [20, 21, 94]. Let M be an m-dimensional $\mathbb{C}^{\infty }$-manifold and $\mathcal{A}$ be the algebra of smooth real-valued functions on M.

Assume that $\mathcal{A}$ carries a structure of n-Lie-Poisson structure, where the commutative associative multiplication is the pointwise multiplication. The skew-symmetry of the Nambu bracket and the Leibniz identity imply that there exists an n-vector field η on M such that

$$\displaystyle{ \{f_{1},\ldots.,f_{n}\} =\eta (df_{1},\ldots,df_{n}),\quad \forall f_{1},\ldots.,f_{n} \in \mathcal{A}. }$$

(4.23)

An n-vector field is called a Nambu tensor if its associated Nambu bracket defined by (4.23) satisfies the Nambu identity (4.1).

Definition 4.18.

A Nambu-Poisson manifold (M, η) is a manifold M on which is defined a Nambu tensor η. Then M is said to be endowed with a Nambu-Poisson structure.

The dynamics associated with a Nambu bracket on M is specified by n − 1 Hamiltonians $H_{1},\ldots,H_{n-1} \in \mathcal{A}$ and the time evolution of $f \in \mathcal{A}$ is given by

$$\displaystyle{ \frac{df} {dt} =\{ H_{1},\ldots,H_{n-1},f\}. }$$

(4.24)

Then $f \in \mathcal{A}$ is called an integral of motion for the system defined by (4.24) if it satisfies {H ₁, …, H _n−1, f} = 0.

It follows from the Nambu identity that a Poisson-like theorem exists for Nambu-Poisson manifolds:

Theorem 4.6.

The Nambu bracket of n integrals of motion is also an integral of motion.

It turns out that a direct application of deformation quantization to Nambu- Poisson structures is not possible, a solution to the quantization problem was presented in the approach of Zariski quantization of fields (observables, functions, in this case polynomials). Instead of looking at the deformed Nambu bracket as some skew-symmetrized form of an n-linear product, the Nambu bracket is deformed directly.

In the case of previous example, the usual Jacobian bracket is replaced by any n-ary bracket having the preceding properties, we get a “modified Jacobian” which is still a Nambu bracket. That is to say, the “modified Jacobian” is skew- symmetric, it satisfies the Leibniz rule with respect to the new bracket and the Nambu identity is verified.

The deformed bracket is given by

$$\displaystyle{ [f_{1},f_{2},f_{3}] =\mathop{\sum \varepsilon (}\limits_{\sigma \in \textit{ S}_{3}}\sigma )\frac{\partial f_{1}} {\partial x_{\sigma _{1}}} \times \frac{\partial f_{2}} {\partial x_{\sigma _{2}}} \times \frac{\partial f_{3}} {\partial x_{\sigma _{3}}}, }$$

where S ₃ is the permutation group of {1, 2, 3} and ɛ(σ) is the signature. In this approach the whole problem of quantizing Nambu-Poisson structure reduces to the construction of the deformed product ×. A non-trivial abelian deformation of the algebra of polynomials on $\mathbb{R}^{m}$ doesn’t exist because of the vanishing of the second Harrison cohomology group. Nevertheless, it is possible to construct an abelian associative deformation of the usual pointwise product of the following form

$$\displaystyle{ f \times _{\beta }g = T(\beta (f) \otimes \beta (g)), }$$

(4.25)

where β maps a real polynomial on $\mathbb{R}^{3}$ to the symmetric algebra constructed over the polynomials on $\mathbb{R}^{3}\ (\beta: \mathcal{A}\rightarrow Symm(\mathcal{A}))$. T is an “evaluation map” which allows to go back to (deformed) polynomials $(T: Symm(\mathcal{A})\longrightarrow \mathcal{A})$.

It replaces the (symmetric) tensor product by a symmetrized form of a “partial” Moyal product on $\mathbb{R}^{3}$ (Moyal product on a hyperplane in $\mathbb{R}^{3}$ with deformation parameter t). The extension of the map β to deformed polynomials by requiring that it annihilates (non-zero) powers of t, will give rise to an Abelian deformation of the usual product (T restores a t-dependence). In general (4.25) does not define an associative product and we look for a β which makes the product × _β associative.

7.3 Ternary Virasoro-Witt Algebras

Curtright, Fairlie and Zachos provided the following ternary q-Virasoro-Witt algebras constructed through the use of s u(1, 1) enveloping algebra techniques.

Definition 4.19.

The ternary algebras defined on the linear space V W generated by $\{Q_{n},R_{n}\}_{n\in \mathbb{Z}}$ and the skewsymmetric ternary brackets:

$$\displaystyle\begin{array}{rcl} [Q_{k},Q_{m},Q_{n}]& =& (k - m)(m - n)(k - n)R_{k+m+n}{}\end{array}$$

(4.26)

$$\displaystyle\begin{array}{rcl} [Q_{k},Q_{m},R_{n}]& =& (k - m)(Q_{k+m+n} + znR_{k+m+n}){}\end{array}$$

(4.27)

$$\displaystyle\begin{array}{rcl} [Q_{k},R_{m},R_{n}]& =& (n - m)R_{k+m+n}{}\end{array}$$

(4.28)

$$\displaystyle\begin{array}{rcl} [R_{k},R_{m},R_{n}]& =& 0{}\end{array}$$

(4.29)

is called ternary Virasoro-Witt algebras.

Actually the previous ternary algebra is a ternary Nambu-Lie algebra only in the cases z = ±2ı.

Larsson showed in [71] that the above ternary Virasoro-Witt algebras can be constructed by applying, to the Virasoro representation acting scalar densities (i.e. primary fields), the ternary commutator bracket

$$\displaystyle\begin{array}{rcl} [x,y,z]& =& x \cdot [y,z] + y \cdot [z,x] + z \cdot [x,y] \\ \ & =& x \cdot (y \cdot z) - x \cdot (z \cdot y) + y \cdot (z \cdot x) - y \cdot (x \cdot z) + z \cdot (x \cdot y) - z \cdot (y \cdot x){}\end{array}$$

(4.30)

where the dot denotes the associative multiplication and [⋅ , ⋅ ] the binary commutator bracket of its corresponding Lie algebra. He considered the operators

$$\displaystyle\begin{array}{rcl} E_{m}& =& e^{\imath mx} {}\\ L_{m}& =& e^{\imath mx}(-\imath \frac{d} {dx} +\lambda m) {}\\ S_{m}& =& e^{\imath mx}(-\imath \frac{d} {dx} +\lambda m)^{2} {}\\ \end{array}$$

which lead to the binary commutators

$$\displaystyle{[L_{m},L_{n}] = (n - m)L_{m+n},\quad [E_{m},E_{n}] = nE_{m+n},\quad [L_{m},E_{n}] = 0.}$$

Therefore, one obtains the ternary brackets

$$\displaystyle\begin{array}{rcl} [L_{k},L_{m},L_{n}]& =& (\lambda -\lambda ^{2})(k - m)(m - n)(n - k)E_{ k+m+n}{}\end{array}$$

(4.31)

$$\displaystyle\begin{array}{rcl} \ [L_{k},L_{m},E_{n}]& =& (m - k)(L_{k+m+n} + (1 - 2\lambda )nE_{k+m+n}){}\end{array}$$

(4.32)

$$\displaystyle\begin{array}{rcl} \ [L_{k},E_{m},E_{n}]& =& (m - n)E_{k+m+n}{}\end{array}$$

(4.33)

$$\displaystyle\begin{array}{rcl} \ [E_{k},E_{m},E_{n}]& =& 0{}\end{array}$$

(4.34)

The brackets involving S’s are not needed to recover the ternary Virasoro-Witt algebras. The brackets (4.26)–(4.29) are obtained by taking

$$\displaystyle{L_{m} = -\root{4}\of{\lambda (1-\lambda )}Q_{k},\quad E_{m} = (\root{4}\of{\lambda (1-\lambda )})^{-1}R_{ k},\quad z = \frac{1 - 2\lambda } {\sqrt{\lambda (1-\lambda )}}.}$$

Naturally, these ternary algebras are 3-Lie algebras only for λ = ±2ı.

Remark 4.7.

One may notice that the ternary commutator (4.30) does not lead automatically to ternary Nambu-Lie algebra when starting from an associative algebra and the corresponding Lie algebra given by the binary commutators. See [4, 9] for triple commutator leading to 3-Lie algebras and ternary Hom-Nambu-Lie algebras [8]. More general construction of (n + 1)-Lie algebras induced by n-Lie algebras was studied in [5].