Keywords

1 Introduction

At present, human-like biped robot locomotion becomes scientific and technical challenge, targeting to provide similar to human gait features of multi-functionality, energy efficiency and flexibility. Over the last few decades, a number of approaches for stable robot walking has been developed [1].

Most of modern bipeds use analytical or controller-based methods to ensure locomotion stability. The analytical approaches are based on physics with consideration of multi-body dynamics, pre-calculated joint trajectories, zero-moment point (ZMP), and trajectory optimization methods. Alternatively, controller-based approaches are able to provide stable biped locomotion by using feedback strategies, continually adapting robot forward dynamics to the stability criteria. However, beside their considerable achievements both analytical and controller-based methods demonstrate serious disadvantages like strong model dependency, high energetic and computational costs, and susceptibility to different disturbances. Therefore, locomotion of biped robots is still far from achieving a human level of anthropomorphism, energy efficiency, stability and robustness.

To reduce cost and time of software development with a real robot while providing system debugging on early stages of algorithm formation, it is crucial to build a relevant simulation model which would take into account robot physical properties and its interaction with the environment. Among other positive effects of simulation prior to experimentation, such simulations help to develop and test balance-based biped locomotion algorithms before experiencing potentially destructive failures with real robots—and these simulations could provide extremely valuable clues on dynamical and static stability behavior and potential issues of robot gaits.

Our long-term research goal targets to develop dynamically stable walking for Russian biped robot AR-601M. This paper presents one particular approach of generating walking primitives of biped robot locomotion in Simulink. We consider two robot models which differ with their legs modelling: a simple initial model with 6-DoF legs (3 DoFs per each leg) and a realistic model with 12-DoF legs (6 DoFs per each leg), while we use the same walking strategies for both models. In such strategy a robot makes a step and then joins another leg with a pause between the steps in order to damp the robot body inertia. The 6 DoFs simulation is the earlier model which was previously presented in [2]; the robot model was constrained to sagittal plane motions only and had four input angles for hip and knee joints and two input of torques which actively stabilize the robot at the end of each step. In this paper we introduce the current stage of our study and, in addition to the simple model, present the extended 12 DoFs simulation model of the biped robot in Simulink/SimMechanics. This advanced 3D model precisely reflects the kinematic structure and the hardware of AR-601M robot legs and implies no artificial restrictions on the motion directions and planes. To calculate joint angles with inverse kinematics in Simulink the model requires three input parameters: step length, step time, and sine feet trajectories. The further goal of our research is to apply 3D model of AR-601M biped robot to the robust and high graphical quality robot simulator GazeboFootnote 1 and to perform evaluative testing of our locomotion algorithms under ROS frameworkFootnote 2 [3].

The rest of the paper is organized as follows. Section 2 introduces Russian humanoid robot AR-601M. Section 3 considers the theoretical background of a biped robot locomotion methods. Section 4 describes the simple (6 DoFs per legs) and the extended (12 DoFs per legs) biped robot models which were designed in Simulink environment. The simulation results and their discussion appear in Sect. 5. Finally, Sect. 6 is used to familiarize the reader with our future research plans and to conclude.

2 System Setup

The biped robot AR-601M (Fig. 1) is being developed by a Russian company Android Technics.Footnote 3 It is a human-like biped robot with the height of 144 cm and weight of 65 kg, having 57 DoFs (41 active DoFs, including 12 DoFs in robot legs) [2]. Nowadays, the robot comes with a software that allows it to walk at a low-speed gait with position control when its center of mass (CoM) trajectory is constrained to stay inside the support polygon of a supporting leg footprint during each step.

Fig. 1
figure 1

Android Technics AR-601M robot

Full size image

3 Biped Robot Locomotion Modelling

This section familiarizes the reader with popular models of biped robot locomotion and methods for robot motion control.

Inverted pendulum models are widely used approaches for building biped robot models. When the robot is approximated with inverted pendulum, the biped robot locomotion is considered as motion of an inverted pendulum. During a step of the biped robot, its swinging leg is similar to an inverted pendulum with a massless rod, which connects the foot and robot’s CoM [4]. The linear inverted pendulum model is employed widely as a useful model which simplifies trajectory generation task [5]. There are various modifications of the inverted pendulum: virtual height inverted pendulum model, multiple masses inverted pendulum model, gravity compensated inverted pendulum model, etc. [6]. Among these models, we emphasize a spring loaded inverted pendulum model, which describes the spring-like leg behavior of human and animal walking or running [7]. The model is also used to approximate bipedal robot locomotion with a human gait [8].

Our research is aimed to achieve energy efficient locomotion with an acceptable walking speed while maintaining the dynamically-stable robot motion. Below we briefly describe methods, which are applied for biped robot locomotion control by various research teams.

Passive walking control is based on the body’s momentum. Passive walking on a slope is known as the most efficient and natural walking style because there is no extra power without potential energy, and the motion occurs inherently according to its mechanical property [9]. It creates movements in a similar way as a human does, but due to low stability for disturbances, this approach is not broadly used [10].

Zero Moment Point (ZMP) defines a special point on the surface where the sum of horizontal inertial and gravitational forces equals to zero [11]. Vukobratovic in his work [12] proposed to use ZMP as a criteria for dynamic stability for biped locomotion. It says that to keep dynamic balance robot’s ZMP should lie within the boundaries of a stability area. This approach plays a role of a criterion in the stability analysis of biped robot locomotion and could be considered as a dynamic analogue of CoM or center of gravity (CoG) criterion for static stability analysis [13]. ZMP approach causes poor energy efficiency of the locomotion, because it defines trajectory of robot bodies without considering the load of each particular joint.

Walking primitives approach generates trajectories for the joints. Moreover, each walking primitive is calculated off-line, whereas during the locomotion a planning algorithm can generate motions as a sequence of predefined walking primitives [14] in order to move a robot from the current posture and location to the goal location. Each primitive implies the following restrictions: at the beginning and at the end of each primitive the accelerations and velocities of all joints are equal to zero, and, therefore, ZMP always stays inside a support polygon [15]. In order to combine two walking primitives together, the initial state of the second primitive should be the end state of the previous one. Combining together a set of walking primitives is used to obtain a stable locomotion of the robot.

Artificial neural network approach uses a neuroadaptive control algorithm to learn the biped robot locomotion, based on the dynamic balance optimization criterion, such as ZMP. This strategy does not use analytical approach, and there is no need to describe all details of robot motion. This approach is used by Boston Dynamics for locomotion control of Atlas robot [16]. Major drawback of neural networks is in its practical use for real-time control applications—as far as a system becomes more complicated it has the exponential growth of the number of parameters and the computational cost becomes too high for real-time usage.

Central Pattern Generator (CPG) approach is borrowed from animal locomotion. CPG is capable of producing the rhythms which are associated with each gait. CPG is commonly modeled as a network of identical differential equation systems [17]. Instead of prescribing a trajectory and playing it back on the robot, these approaches focus on the limit cycle behavior of legged locomotion. It is shown that limit-cycle motion control could have better energy efficiency than the trajectory-based control [18]. CPG is a network of neuron oscillators coupled by mutual inhibition, which can be used to control the robot’s limb motion, and displays characteristics close to natural ones [19, 20].

Full-body posture goal strategy for path planning performs a search through all achievable robot states with a goal to find a collision-free path to the goal posture while keeping dynamic balance. This approach is divided into two phases: the first phase computes a statically-stable, collision-free path, and the second phase smoothens and transforms this path into a dynamically stable trajectory for the entire body [21].

4 3D Modelling of Biped Robot in Simulink

Robotics simulators significantly accelerate robotic research, promote advanced designs, help to test new control algorithm and solve tasks for complex problems. We model and simulate robot mechanical systems in Matlab/Simulink environment using SimMechanics toolFootnote 4 as the mechanical developer module. SimMechanics simulates 3D translational and rotational motion by predicting the system’s future from the current state through differential equations of Newtonian dynamics. SimMechanics allows quite simple 3D modelling of a biped robot as a multibody system using blocks which represent bodies, joints, constraints, and force elements; it supports such features as mass distribution and inertia assignments, external forces, trajectory generation etc. Moreover, SimMechanics automatically generates 3D animation which helps to visualize system dynamics.

Fig. 2
figure 2

6 DoFs (left) and 12 DoFs (right) robot models in Matlab/Simulink environment

Full size image

In this paper we present two simplified models of AR-601M robot: with 6 DoFs and 12 DoFs per legs (Fig. 2, 3DoF and 6DoF per each leg respectively). The model concentrates only on leg’s kinematics and dynamics, anchoring all other joints for upper body of the human-like robot model. We use crude approximation of the robot body based on simplified geometrical shapes and mass distribution. However, all main parameters of the models that influence walking dynamics of the robot (such as foot area, leg length, CoM position) precisely correspond to AR-601M kinematical structure and hardware properties.

Fig. 3
figure 3

SimMechanics block diagram of a biped robot: top level of abstraction

Full size image

The following steps were performed in SimMechanics environment:

  • Specification of robot’s rigid parts geometry and their inertial properties (bodies and links).

  • Connecting the robot bodies and links with rotational joints.

  • Setting up the ground reaction forces.

  • Assigning the reference signals at each joint position.

  • Running Simulink solver.

  • Performing the simulation visualization.

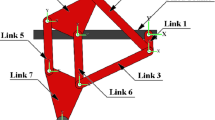
Our current robot model consists of 12 rigid bodies (see, Fig. 2) which are connected to each other with revolute joints for knees, ankles, hips and anchored joints for a neck, elbows and shoulders. We use the geometric primitives for robot bodies simulation such as (1) parallelepipeds for a torso and feet, (2) a sphere as a head, (3) cylinders for all other bodies. Figure 3 shows top level abstraction block diagram of the whole biped robot in SimMechanics, and Table 1 describes all the parameters in details. The next two subsections present the walking primitives approach for a simple 6-DoF legs robot model (3 DoFs per leg) which moves only in sagittal plane and for a 12-DoF legs model (6 DoFs per leg) which can locomote both in sagittal and frontal planes.

Table 1 The robot bodies parameters
Full size table

4.1 The 6 DoFs Robot Model

The simple 6 DoFs robot model (3 DoFs per leg) allows the motion in sagittal plane only. It has single revolutionary joints with one rotational DoF in ankles, knees and hips (Fig. 4). The torso has 3 DoFs in sagittal plane with regard to the global (ground-fixed) coordinate system: 2 translational DoFs in vertical and horizontal directions and 1 rotational DoF.

Fig. 4
figure 4

SimMechanics block diagram for a leg in the 6 DoFs robot model

Full size image

In [2] we considered the 6 DoFs robot locomotion based on walking primitives, i.e. on the gait parts with identical time periods, at the beginning and at the end of which the robot returned to the same positions. The leg motion pattern is the same in each primitive and consists of four phases: (1) raising the left foot; (2) performing the inverted pendulum motion until the left foot touches the ground; (3) moving the right foot forward to make the knee and hip joint’s angles equal to zero; (4) damping forward motion by applying torque in the ankles. In the next step, the same phases are repeated for the right leg. Thus, we realized the robot locomotion by setting four angles for hip and knee joints as inputs and two torques on the ankle joints, damping the robot inertia at the end of each step. The input angles of knee and thigh joints were found empirically and are shown in Figs. 5 and 6 respectively.

Fig. 5
figure 5

The input angle for the left knee (on the left) and the right knee (on the right)

Full size image
Fig. 6
figure 6

The input angle for the left hip (on the left) and the right hip (on the right)

Full size image

4.2 The 12 DoFs Robot Model

As a step forward from the presented above simple model towards a complete 41 active DoFs AR-601M robot model, we created a newer model with 12 DoFs by adding one rotational DoF in ankle and two rotational DoFs in hip joints (Fig. 2, on the right). This advanced 12 DoFs legs model with 6 DoFs per leg precisely reflects the kinematic structure and the hardware of AR-601M robot legs and implies no artificial restrictions on the motion directions and planes. The top abstraction level SimMechanics block diagram of the robot remains the same as shown in Fig. 3, whereas the leg diagram implies significant changes which are depicted in Fig. 7.

Fig. 7
figure 7

SimMechanics block diagram for a 6DoF leg within the 12 DoFs robot model

Full size image

The robot starts the motion from the initial position when the feet are located next to each other. Similar to the simple 6FoFs model we divide each walking primitive into four phases: (1) forward movement of the left foot (from the initial position); (2) waiting until oscillations are damped (the opposite to the 6 DoFs model where no pause before the next motion is required); (3) joining the right leg to the left leg with its forward movement (this way the robot returns into the state which is identical to its initial state, but has its global position incremented for one step); (4) waiting until oscillations are damped.

For the 12 DoFs robot model we cannot build walking primitive pattern based on empirical values of joint angles because of motion complexity. Therefore, at first we define trajectory in Cartesian space and then find joint angle functions, solving the inverse kinematics task. To solve inverse kinematics of 12 joint angles, it is necessary to define 12 Cartesian coordinates: 6 coordinates for a torso and 6 coordinates for a moving foot—3 rotational and 3 translational coordinates for each. We assume that rotational angles of the torso and a swinging foot are always zero, i.e. the foot is parallel to the ground and the torso is always kept vertical, and there are no torso motion and foot swinging in frontal plane which allows to keep the torso at the constant height. This way, foot swinging and the torso trajectories in sagittal plane could be calculated from trigonometric functions. We set the reference frame center in the middle of supporting foot and summarize Cartesian coordinates functions for a moving foot and the torso as follows:

$$\begin{aligned} x_{foot}=x_{0}; \quad y_{foot}=\frac{1}{2} a (1-\cos (\frac{\pi t}{T})); \quad z_{foot}=\frac{1}{2} h (1-\cos (\frac{2\pi t}{T})); \end{aligned}$$
(1)
$$\begin{aligned} x_{torso}=0.5x_{0}; \quad y_{torso}=\frac{1}{4} a (1-\cos (\frac{\pi t}{T})); \quad z_{foot}=z_{0}; \end{aligned}$$
(2)

where \(x_{0}\) is the distance between feet centers, a is the step length, h is the maximum height of the moving foot, T is the step period, \(z_{0}\) is the height of torso movement.

These trajectories are applied in the first phase of the walking primitive pattern, where the left foot moves forward. For the third phase, where the right foot returns to the initial position, we use similar equations with reference frame center in the middle of left foot. Notice that to solve inverse kinematics we anchor supporting foot to the ground. It means that if we apply calculated angle functions to move the robot, its trajectory will be different due to supporting foot lifting. In order to damp oscillations, occurring after each step, we fix angle values at the end of the first and third phases for certain amount of time \(\triangle t\).

4.3 Contact Force Modelling in SimMechanics

The foot-ground interaction is a very important issue in biped robot simulation and should be carefully modeled. Generally, the contact force, which takes place when robot’s feet touch the ground, can be studied in terms of normal and tangential (friction) forces.

Normal Force. Two compliant contact models for normal force were considered in our work. The first one is the Linear Spring-Damper model. Then the normal force is given as:

$$\begin{aligned} F_n=k_n z+b_n \dot{z} \end{aligned}$$
(3)

where z is the coordinate of the leg tip (\(y=0\) corresponds to ground surface), \(k_n\) and \(b_n\) are elastic constant and damping coefficient respectively. The normal force is applied only when \(z\le 0\), i.e. when the leg touches the ground. Being computationally simple, this approach has some drawbacks: (1) the contact force is not continuous at the beginning of impact due to the damping term character; (2) there is a sticking effect, which holds feet at the lifting moment. The second issue can be solved by limiting \(F_n\) to positive values only, while the first issue can not be solved using linear model. Furthermore, the equivalent coefficient of restitution, which shows the relation of body velocity before and after collision, in linear model depends on body mass and does not depend on body velocity, which is contrary to empirical results presented in [22]. The optimal solution to these problems, proposed in [23], is to replace the Linear Spring-Damper parallel combination with a nonlinear one, changing the contact normal force equation as follows:

$$\begin{aligned} F_n=k_n z^{n}+b_n z^{n}\dot{z} \end{aligned}$$
(4)

where the power n is close to one and depends on the surface geometry of the impact. The advantage of this model is that while the computational time is similar, the contact force increases continuously with the impact and coefficient of restitution depends on impact velocity. In our work we used nonlinear model with the power n equal to one.

Friction Force. In our work tangential forces (friction) were modeled similar to viscous forces and given as:

$$\begin{aligned} F_t=b_t z \dot{x} \end{aligned}$$
(5)

where \(b_t\) is tangential damping coefficient. Firstly, notice that force is nonzero only when a motion in tangential direction exists. It means that we do not have sticking, where body is fully at rest. However this motion is negligible, if we take large values for coefficient \(b_t\). Secondly, tangential force is proportional to penetration depth, which again increases the force with the continuous impact. Equation 5 works perfect at leg landing, whereas at leg raising we cannot provide strict vertical movement and have a horizontal component of velocity, which results in large tangential force. To avoid this effect, the absolute value of tangential force should be limited to \( \mu F_n\), where \(\mu \) is a friction coefficient. At leg landing \(F_n\) value is large, so the tangential force will be large enough to prevent the robot from sliding. At leg raising \(F_n\) is small enough to avoid sticking. Similarly to normal force, tangential force is applied only when \(z\le 0\). The ground coefficients \(k_n,b_n,b_t\) should be large (see Table 2) to minimize penetrations of feet below ground level (\(k_n\)) and provide fast damping of contact velocity (\(b_n,b_t\)).

Fig. 8
figure 8

Nonlinear spring-damper model between a foot and ground

Full size image
Table 2 The ground parameters for the foot-ground interaction model
Full size table

The contact between a supporting foot and ground was modeled by four contact points shown in Fig. 8. The number of contact points can be increased, but it will increase computational cost. We performed simulations with four and eight contact points for each foot but did not detect any significant differences. Therefore, for flat surfaces and rectangular foot shape we used four contact points at the foot’s corners that should be enough for suitable foot-ground interaction modelling of a biped robot locomotion.

5 Simulation Results

Fig. 9
figure 9

A single step of the biped robot. The robot moves from right to left as the time passes

Full size image
Fig. 10
figure 10

Robot torso velocity in sagittal plane

Full size image
Fig. 11
figure 11

Torques in the left (on the left) and the right (on the right) knee

Full size image
Fig. 12
figure 12

Torques in the left (on the left) and the right (on the right) hip

Full size image
Fig. 13
figure 13

Torques in the left (on the left) and the right (on the right) ankle

Full size image
Fig. 14
figure 14

Angle functions for knee (left), hip (center), and ankle (right) joints

Full size image

Results for the 6 DoFs Model. To solve differential equations described above we used Simulink solver method “ODE 23t”. Figure 9 shows a sequence of the biped robot frames at different time during a single step. The smooth walking of the simulated model illustrates reasonable settings of the angle values for the joints and contact forces within the model. Robot torso center velocity of 0.3–0.4 m/s in sagittal plane is shown in Fig. 10, demonstrating the periodical body movement with the 3 s time period. At the beginning of each period the body velocity is zero. Torque values in the hip and knee joints from the simulation are shown in Figs. 11 and 12, which can help to estimate motor characteristics. The simulation shows that maximum torque should be approximately 1500 N*m in the thigh joints and the knee joints. At the same time discontinuous peaks in calculated torque values were detected, which are caused by foot-ground collisions. Torque values in ankles are shown in Fig. 13. As we expected, the torque was applied to damp robot’s inertia only in the last step phase. In our work the duration of one walking primitive is 3 s, the time between stepping phases \(\triangle t=1.3\) s.

Results for the 12 DoFs Model. At first, angle functions for each joint were obtained by solving inverse kinematics equations. Figure 14 shows angle functions for a knee, a hip and an ankle joints for their rotations around X axis. The step parameters were defined as step length \(a=0.1\) m, the maximum height of the moving foot \(h=0.1\) m, the step period \(T=0.5\) s. The time between stepping phases \(\triangle t\) was chosen equal to 1 s.

Fig. 15
figure 15

Frontal and side view of robot stepping

Full size image
Fig. 16
figure 16

Robot falling down in the frontal plane with the step period of 1 s

Full size image

Figure 15 shows frontal and side views of the robot stepping. The supporting foot rotates around its inner edge because robot’s CoM leaves supporting foot’s area. Therefore, at the end of step we have impact of stepping foot with ground. The same happens at the third phase, when the other foot moves forward to its initial position. Notice that if we set larger values for step period T and height of torso movement \(z_{0}\), the robot falls down (Fig. 16). Therefore, robot should make steps reasonably fast. From AR-601M robot motor characteristics (see Table 3 for maximum rotation acceleration and torques for leg joint motors) we can estimate if walking primitive pattern would guarantee the real AR-601M locomotion stability or not. For this reason, we simulated the 12 DoFs robot model locomotion with different step parameters, presenting the simulation results in Table 4: stable robot gait or falling. Table 4 shows that the robot walking can be stable at the maximum step period \(T=0.7\) s with step length \(a=0.15\) m, whereas the maximum height of stepping foot h is achieved at 0.1 m with the height of torso movement \(z_{0}=0.85\) m.

Table 3 Maximum motor characteristics for AR-601M robot leg joints
Full size table

For the robot stable locomotion case (the first row in Table 4) the maximum torque values are applied to ankle and knee joints of the supporting leg (Fig. 17). However, for the case of fast walking the robot needs maximum torque of nearly 90 N*m in ankle joint, which is much higher than the motor can provide.

Thus, the simulation results with 12 DoFs robot model clearly demonstrated that walking primitive approach could not support fast biped locomotion of the real AR-601M robot due to leg’s motor torque limitations.

Table 4 Influence of walking primitive pattern parameters on the AR-601M robot model locomotion stability
Full size table
Fig. 17
figure 17

Torques in ankle (on the left) and knee (on the right) joints of the supporting leg

Full size image

6 Conclusions and Future Work

In this paper we presented Russian biped robot AR-601M and its locomotion modelling in Simulink environment using walking primitives approach. We considered two robot models: with 6 and 12 Degrees of Freedom (DoFs) per legs, using the same walking strategies with robot inertia damping and a pause between the steps. While the simplified 6 DoFs model is constrained to sagittal plane motions, the 12 DoFs model precisely reflects the hardware of AR-601M robot legs. The locomotion algorithm utilizes position control and involves inverse kinematics computations for the joints. The resulting biped robot locomotion was dynamically stable for both models at the step length up to 0.15 m and the step time of 0.7 s with relatively long damping pauses between the steps.

The simulation allowed us to adjust the models with proper parameters’ selection which then have demonstrated good results of the walking primitives approach. However, this approach could not be further applied for the real AR-601M robot as AR-601M cannot provide sufficient actuator torques for such fast steps. This points at a non one-to-one correspondence of successful simulations and reality, emphasizing crucial necessity of adequate simulations prior to real world experimentation. Our further research aims to complete a 41 DoFs precise model of AR-601M robot in Simulink and Gazebo environments with preview control methods and genetic algorithms techniques, and to perform exhaustive testing under ROS framework. Next, the successful solutions will be transferred onto a real robot hardware in order to verify their performance in the real world.