Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Dilaton and Axion Fields

1.1 Scalar Fields

The Jordan-BransFootnote 1-Dicke scalar, the dilaton, the axion, the inflaton—scalar fields everywhere—and eventually even one, the scalar, that is, the spinless Higgs boson \( {H}^{ {0}}\), which has been found experimentally as heavy as some 134 protons. These different scalar fieldsFootnote 2 are not necessarily independent from each other, it could be, for example, that the JBD-scalar can be identified with the dilaton (see [30]) or the Higgs boson with the inflaton (see [6, 7]). Thus, the list of potentially existing universally coupled scalar fields could be somewhat smaller. For the history of the JBD-scalar, one can compare Brans [11] and Goenner [32] and, for the role of the inflaton in different models, Vennin et al. [97].

1.2 Einstein Gravity and the Energy-Momentum Current

As remarked by Brans [10] in the quotation above, if universally coupled, the scalar fields are intrinsically related to the gravitational field. In Einstein’s theory of gravity, general relativity (GR), the gravitational potential is the metric \(g_{ij}\), with \(i,j =0,1,2,3\) as (holonomic) coordinate indices. As its source acts the symmetric energy-momentum tensor \(T_{ij}\) of matter. This is a second rank tensor, which is generated already in special relativity (SR) with the help of the group T(4) of translations in space and in time. Together with the Lorentz transformations SO(1, 3), the translations T(4) build up the Poincaré group P(1, 3) as a semi-direct product: \(P(1,3)=T(4)\rtimes \textit{SO}(1,3)\). This is the group of motion in the Minkowski space of special relativity, see [31].

Accordingly, if one desires to understand gravity from the point of view of the gauge principle, the T(4) is an indispensable part of these considerations. However, being only one piece of the P(1, 3), it is suggestive to gauge the complete P(1, 3). This is exactly what Sciama and Kibble did during the beginning 1960s, see [73], [9, Chap. 4], and [16].

1.3 Einstein-Cartan Gravity: The Additional Spin Current

This gauging of the P(1, 3) extends the geometrical framework of gravity. The 4 translational potentials \(e_i{}^ \alpha \) and the 6 Lorentz potentials \(\varGamma _i{}^{\alpha \beta }=-\varGamma _i{}^{\beta \alpha } \) span a Riemann-Cartan spacetime, enriching the Riemannian spacetime of GR by the presence of Cartan’s torsion; here \(\alpha ,\beta =0,1,2,3\) are (anholonomic) frame indices. Whereas the translational potentials couple to the canonical energy-momentum tensor of matter \(\varSigma _\alpha {}^i\), the Lorentz potentials couple to the canonical spin current of matter \(\tau _{\alpha \beta }{}^i=-\tau _{\beta \alpha }{}^i\).

The simplest version of the emerging Poincaré gauge models is the Einstein-Cartan theory (EC), a viable gravitational theory competing with GR if highest matter densities are involved. If \(l_{\text {Planck}}\) denotes the Planck length and \(\lambda _{\text {Compton}}\) the Compton wave length of a particle, then deviations of the Einstein-Cartan from Einstein’s theory are expected at length scales of below \({\sim }\!(l_{\text {Planck}}^2\,\lambda _{\text {Compton}})^{1/3}\); for protons, prevalent in the early cosmos, it is about \(10^{-29}\,\text {m}\). According to Mukhanov [65], it is exactly this order of magnitude down to which, according to recent cosmological data, GR is known to be valid.

From a gauge theoretical point of view, the EC-theory looks more reasonable than GR since the Einsteinian principles of how to heuristically derive a gravitational theory were followed closely: they were just applied to fermionic matter instead of to macroscopic point particles or Euler fluids or to classical electromagnetism, as Einstein did.

Incidentally, in the EC-theory and, more generally, in the Poincaré gauge theory, the Poincaré and, in particular, the Lorentz covariance are valid locally by construction, similar as in a \(\textit{SU}(2)\) Yang-Mills theory, we have local \(\textit{SU}(2)\) covariant. Kostelecký (priv. comm., Jan. 2016) agrees that the “Einstein-Cartan theory maintains local Lorentz invariance.” Then the same is true for a Poincaré gauge theory, which acts likewise in a Riemann-Cartan spacetime with torsion and curvature. However, in an experimental set-up, according to Kostelecký [48], torsion must be considered as an external field and, according to the “standard lore for backgrounds,” local Lorentz invariance is broken. By the same token, an external magnetic field in electrodynamics breaks local Lorentz invariance. This is, in my opinion, an abuse of language, which conveys the wrong message that the existence of a torsion field violates local Lorentz invariance.

If, for theoretical reasons, one wants to evade the emergence of the Riemann-Cartan spacetime, then one can manipulate, in the underlying Minkowski space, the intrinsic or spin part of the total angular momentum of matter in such a way that it vanishes on the cost of increasing the orbital part of it by the corresponding amount, see [63]. This procedure is called Belinfante-Rosenfeld symmetrization of the canonical energy-momentum current, which, in general, is defined as an asymmetric tensor by the Noether procedure. Accordingly, by symmetrization the energy-momentum current is made fit to act as a source of the Einstein field equation. In this way, one can effectively sweep the spin and the torsion under the rug and can live happily forever in the paradise of the Riemannian spacetime of GR.

Of course, in the end observations and/or experiments will decide which of the two theories, GR or EC, will survive. We opt for the latter.

1.4 Dilaton Field and Dilation Current

The dilaton field \(\phi \) entered life as a Nambu-Goldstone boson of broken scale invariance, see Fujii in [30]. Thus, \(\phi \) is related to dilat[at]ions or scale transformations in space and time. But the dilaton also occurs in theories of gravity (JBD) and in string theory, see Di Vecchia et al. [21]. The P(1, 3), if multiplied (semi-directly) with the scale group, becomes the Weyl group W(1, 3). This 11-parameter group is an invariance group for massless particles in special relativity. The translations, via Noether’s theorem, generate the conserved energy-momentum tensor \(\varSigma _{ij}\), the Lorentz transformations the conserved total angular momentum tensor \(J_{ij}{}^k:=\tau _{ijk}+x_{[i}\varSigma _{j]}{}^k=-J_{ji}{}^k\), and the dilation the conserved total dilation current \(\varUpsilon ^k:=\varDelta ^k+x^l\varSigma _l{}^k\),

$$\begin{aligned} \partial _k\varSigma _i{}^k= & {} 0\,,\end{aligned}$$
(4.1)
$$\begin{aligned} \partial _kJ_{ij}{}^k= & {} \partial _k\tau _{ij}{}^k-\varSigma _{[ij]}=0\,,\end{aligned}$$
(4.2)
$$\begin{aligned} \partial _k\varUpsilon ^k= & {} \,\,\,\partial _k\varDelta ^k+\varSigma _k{}^k=0\,, \end{aligned}$$
(4.3)

see [47, 59] particularly for \(\varUpsilon ^k\). Thus, if a universal coupling is assumed, then \(\phi \) should have the intrinsic dilation current \(\varDelta ^k\) as its source; for theories in Weyl spaces in which \(\varDelta ^k\) does not play a role, see Scholz [86, 87].

There are numerous field theoretical models under way which, if scale or dilation invariance is implemented, have conformal invariance as a consequence; for a more recent review see Nakayama [66]. Hence, jumping to conformal invariance, before one understood scale invariance, is probably not a very good strategy. For this reason we confine ourselves here to scale invariance, to the dilaton, and to the 11-parametric Weyl group. But it should be understood that the light cone is also invariant under the 15-parametric conformal group, see Barut and Ra̧czka [5] and Blagojević [8] and, for a historical account, Kastrup [45].

Both currents, the intrinsic dilation current \(\varDelta ^k\) and the energy-momentum current \(\varSigma _i{}^k\) are related to external groups, to the dilation (scale) and to the translation groups, respectively. This is the reason for their universality.

1.5 The Weyl-Cartan Spacetime as a Natural Habitat of the Dilaton Field

We only tried to make a strong case in favor of the EC-theory in order to repeat the corresponding arguments for the dilation group. Gauging the Weyl group yields a Weyl-Cartan spacetime. The classical paper in that respect is the one of Charap and Tait, see [9, Chap. 8]. A universally coupled massless scalar field induces a Weyl covector \(Q_i\) as the corresponding dilation potential willy nilly. This is the type of spacetime Weyl used (with vanishing torsion) for his failed unified theory of 1918. Here the Weyl space with the connection \( ^{\text {W}}\varGamma \) is resurrected for the dilation current, instead of for the electric current, see [8]:

$$\begin{aligned} \mathop {\mathop {\nabla }\limits ^\mathrm{W}}\nolimits _ig_{jk}=-Q_ig_{jk}\,,\quad \, ^{\text {W}}\varGamma _{ijk}=\,^{\text {RC}}\varGamma _{ijk}+\frac{1}{2}(Q_ig_{jk} +Q_jg_{ki}-Q_kg_{ij})\,; \end{aligned}$$
(4.4)

\(^{\text {RC}}\varGamma \) is the connection of the Riemann-Cartan space. Again, as in the case of the Lorentz group, one can manipulate the total dilation current \(\varUpsilon ^k\) and can transform its intrinsic part into an orbital part by modifying in this case the trace \(\varSigma _k{}^k\) of the energy-momentum current. Then, again, one can stay within the realm of the Riemannian space of GR, see Callan et al. [13].

As we mentioned already, the gauge theoretical answer was given by Charap and Tait [15]. Again, which approach will succeed is eventually a question to experimental verification.

We see, if the JBD-scalar is interpreted as a dilaton, then we would expect that the Weyl-Cartan spacetime is its arena. Clearly this does only provide the kinematics of the theory. The dynamics would depend on the exact choice of the dilaton Lagrangian.

Recently, Lasenby and Hobson [53] wrote an in-depth review of gauging the Weyl group and, moreover, formulated an “extended Weyl gauge theory.” Also within their framework, the Weyl-Cartan space, and a straightforward extension of it, play an important role, see also Haghani et al. [33]. Definite progress has also been achieved in the study of equations of motion within the scalar tensor theories of gravity, see Obukhov and Puetzfeld [76, 81, 82]. The breaking of scale invariance in the more general approach of metric-affine gravity was studied in [34], for example; for somewhat analogous breaking mechanisms, see [60–62].

1.6 Axion Field

Dicke did not only introduce in 1961, together with Brans [12], a scalar field into gravity, but he also discussed, in 1964, and pseudoscalar or axial scalar field \(\varphi ^2\) in the context of gravitational theory, see [20, Appendix 4, p. 51, Eq. (7)].

Subsequently, in the early 1970s, Ni [67] investigated matter coupled to the gravitational field and to electromagnetism and looked for consistency with the equivalence principle. He found it possible to introduce in this context a new neutral pseudoscalar field accompanying the metric field, see also [4, 68–70]. Later, in the context of the vacuum structure of quantum chromodynamics, a light neutral pseudoscalar, subsequently dubbed “axion” was hypothesized, see Weinberg [98, pp. 458–461]. Similar as Ni’s field, the axion couples also to the electromagnetic field, see Wilczek’s paper [99] on “axion electrodynamics”.

The axion field is of a similar universality as the gravitational field. In other words, the axion belongs to the universally coupled scalar fields. Let in electrodynamics, \(\mathcal{H}^{ij}=(\mathbf {D},\mathbf {H})=-\mathcal{H}^{ji}\) and \(F_{ij}=(\mathbf {E},\mathbf {B})=-F_{ji}\) denote the excitation and the field strength, respectively. The constitutive relation characterizing the axion field \(\alpha (x)\) (in elementary particle terminology it is called \(A^0\)) reads [35],

$$\begin{aligned} \mathcal {H}^{ij}=\frac{1}{2}\alpha \epsilon ^{ijkl} F_{kl}\quad \text {or}\quad {\left\{ \begin{array}{ll} D^a=\;\;\,\alpha B^a\,,\\ H_a=-\alpha E_a\,, \end{array}\right. } \end{aligned}$$
(4.5)

see also [37] for the corresponding formalism; here \(\epsilon \) is the totally antisymmetric Levi-Civita symbol with \(\epsilon ^{ijkl}=\pm 1\), moreover, \(a=1,2,3\). Clearly, the axion embodies the magnetoelectric effect par excellence. It is a pseudoscalar under 4-dimensional diffeomorphisms.

In electrotechnical terms, the axion behaves like the (nonreciprocal Tellegen) gyrator of network analysis, see [49, 100]; also the perfect electromagnetic conductor (PEMC) of Lindell and Sihvola [58, 93] represents an analogous structure. Metaphorically speaking, as we see from (4.5), the axion “rotates” the voltages \((\mathbf {B},\mathbf {E})\) into the currents \((\mathbf {D},\mathbf {H})\). In SI, we have the units \([B]=\mathrm{{V}}\mathrm{{s}} /\mathrm{{m}^2}, [E]=\mathrm{V}/\mathrm {m};\,\; [D]=As/\mathrm{{m}^2}, [H]=\mathrm{A}/\mathrm {m}\). Thus, \([\alpha ]=1/\text {ohm}=1/\varOmega \) carries the physical dimension of an admittance. Now, in the Maxwell Lagrangian, we find an additional piece \(\sim \alpha (x) \epsilon ^{ijkl} F_{ij}F_{kl}\sim \alpha (x)\mathbf {E}\cdot \mathbf {B}\), a term, which was perhaps first discussed by Schrödinger [89, pp. 25–26]. If \(\alpha \) were a constant, the field equations would not change.

As we already remarked, \(\alpha \) is a 4-dimensional pseudoscalar. The same is true for the von Klitzing constant \(R_{\text {K}}\approx 25\,813\,\varOmega \). And this covariance is a prerequisite for its universal meaning. Phenomenologically, the quantum Hall effect (QHE) can also be described by a constitutive law of the type (4.5), see [35, Eq. (B.4.60)].

It is possible to apply the constitutive relation (4.5) directly to a solid, too. By the evaluation of experiments we have shown [37] that in the multiferroic Cr\(_2\)O\(_3\) (chromium sesquioxide) we have a nonvanishing axion piece of up to \(\sim \)10\(^{-3}\lambda _0\), where \(\lambda _0\) is the vacuum admittance of about \(1/377 \,\varOmega \). This fact demonstrates that there exist materials with a nonvanishing, if small, (pseudoscalar) axion piece. This may be considered as a plausibility argument in favor of a similar structure emerging in fundamental physics. If the \(A^0\) were found, it would not be an unprecedented structure, see in this context also Ni et al. [72].

In matter-coupled \(\mathcal{N}=2\) supergravity models, there are examples in which a dilaton and an axion are contained simultaneously in the allowed particle spectrum, see Freeman and Van Proeyen [29, p. 451]. However, in the next section we will demonstrate that in a fairly simple classical model of an electromagnetic universe, the axion can emerge jointly with a dilaton and the metric.

More recently, there have been attempts to relate the axion field to the torsion of spacetime, see, for example Mielke et al. [64] and Castillo-Felisola et al. [14]. To us, this assumed link between the internal symmetry U(1) of the axion with the external translation symmetry T(4) related to the torsion appears to be artificial and not supported by physical arguments.

2 An Electromagnetic Model Universe

2.1 The Premetric Maxwell Equations

We consider a 4-dimensional differentiable manifold. The electromagnetic field is specified by its excitation \(\mathcal {H}^{ij}\), a 2nd rank antisymmetric contravariant tensor density, and by its field strength \(F_{ij}\), a 2nd rank antisymmetric covariant tensor; the electric current \(\mathcal {J}^k\) is a contravariant vector density, see Post [80]. On this manifold, the Maxwell equations read

$$\begin{aligned} \partial _k\mathcal {H}^{ik}=\mathcal {J}^k\,,\qquad \partial _{[i} F_{jk]}=0\,; \end{aligned}$$
(4.6)

the brackets \(_{[\;]}\) denote antisymmetrization of the corresponding indices with 1/3! as a factor, see [88]; for the Tonti-diagram of (4.6), compare [95, p. 315].

In none of these equations the metric tensor \(g_{ij}\) nor the connection \(\varGamma _{ij}{}^k\) are involved. Still, these equations are valid and are generally covariant in the Minkowski space of special relativity, in the Riemann space of general relativity, and in the Riemann-Cartan or Weyl-Cartan space of gravitational gauge theories. The Maxwell equations (4.6) as such, apart from a historical episode up to 1916, see [22, 23], have no specific relation to the Poincaré or the Lorentz group.

Perlick [78] has shown that the initial value problem in electrodynamics can be particularly conveniently implemented by means of the premetric form of the Maxwell equations.

In contrast to most textbook representations, no “comma goes to semicolon rule” is required. The Maxwell equations (4.6) are just universally valid for all forms of electrically charged matter. Incidentally, this represents also a simplifying feature for numerical implementations. The price one has to pay is to introduce, as Maxwell did, the excitation \(\mathcal {H}^{ij}\), besides \(F_{ij}\), as an independent field quantity and to note that it is a tensor density. From a phenomenological point of view, this is desirable anyway, since the excitation has an operational definition of its own, namely as charge/length\(^2\) (\(\mathbf {D}\)) and current/length (\(\mathbf {H}\)), respectively, which is independent from the definition of the field strength as force/charge (\(\mathbf {E}\)) and force/current (\(\mathbf {B}\)). For a rendition in the calculus of exterior differentiable forms, one can compare with the axiomatic scheme in [18, 35], see also [19].

Let us stress additionally that \(\mathcal {H}^{ij}\), \(F_{ij}\), and \(\mathcal {J}^k\) can be defined in a background independent way.

The Maxwell equations (4.6) are based on the conservation laws of electric charge \(Q:=\int d\sigma ^{ijk}\varepsilon _{ijkl}\,\mathcal {J}^l\) (unit in SI “coulomb”) and magnetic flux \(\varPhi :=\int d\sigma ^{ij}F_{ij}\) (unit in SI “weber”). Charge Q and flux \(\varPhi \) are 4-dimensional scalars. They induce the structure of the excitation \(\mathcal {H}_{ij}\) and the field strength \(F_{ij}\). In this context, the field strength is operationally defined via the Lorentz force density \(\mathfrak {f}_i=F_{ij}\mathcal {J}^j\), the current being directly observable and the force and its measurement known from mechanics.

The charge and its conservation is the anchor of electrodynamics. Its current \(\mathcal {J}^k\) defines, by means of the Lorentz force density \(\mathfrak {f}_i\), the field strength \(F_{ij}\), which allows to define the magnetic flux \(\varPhi \). Faraday’s induction law is an incarnation of magnetic flux conservation.

Some people have no intuition about the conservation of a quantity that is defined in 3 dimensions by integration over a 2-dimensional area \({\sim }\int d\sigma ^a B_a\), since we usually associate conservation with a quantity won by 3-dimensional volume integration, namely \({\sim }\int dV\rho \). Some mathematics education about dimensions will enable us to understand the induction law as a “continuity equation.”

Summing up: the premetric Maxwell equations are a close-knit structure, the 4-dimensional diffeomorphisms covariance holds it all together. Clearly, a metric as well as a connection are alien to the Maxwell equations.

2.2 A Local and Linear Electromagnetic Response

In order to fill the Maxwell equations with life, one has to relate \(F_{ij}\) to \(\mathcal {H}^{ij}\):

$$\begin{aligned} \mathcal {H}^{ij}= \mathcal {H}^{ij}(F_{kl}) \end{aligned}$$
(4.7)

If we assume this functional to be local, that is, \(\mathcal {H}^{ij}(x)\) depends only on \(F_{kl}(x)\), and linear homogeneously, then we find

$$\begin{aligned} \mathcal {H}^{ij}=\frac{1}{2}\,\chi ^{ijkl}F_{kl}\qquad \text {with}\qquad \chi ^{ijkl}=-\chi ^{ijlk}= -\chi ^{jikl}\,; \end{aligned}$$
(4.8)

here the field \(\chi ^{ijkl}(x)\) represents the electromagnetic response tensor density of rank 4 and weight \(+1\), with the physical dimension \([\chi ]=1/\text {resistance}\). An antisymmetric pair of indices corresponds, in 4 dimensions, to 6 independent components. Thus, \(\chi ^{ijkl}\) can be understood as a \(6\times 6\) matrix with 36 independent components.

We want to characterize the electromagnetic model spacetime by this response tensor field \(\chi ^{ijkl}(x)\) with 36 independent components.Footnote 3 This is the tensor density defining the structure of spacetime. It transcends the metric and/or the connection.

We decompose the \(6\times 6\) matrix into its 3 irreducible pieces. On the level of \(\chi ^{ijkl}\), this induces [17, 35]

$$\begin{aligned} \chi ^{ijkl}= & {} \,^{(1)}\chi ^{ijkl}+ \,^{(2)}\chi ^{ijkl}+ \,^{(3)}\chi ^{ijkl}\,.\\ \nonumber 36= & {} 20\oplus 15 \oplus 1\,. \end{aligned}$$
(4.9)

The third part, the axion part, is totally antisymmetric \(^{(3)} \chi ^{ijkl}:= \chi ^{[ijkl]} ={\alpha }\,{\epsilon }^{ijkl}\), with the pseudoscalar \({\alpha }\), see also [83]. The skewon part is defined according to \( ^{(2)}\chi ^{ijkl}:=\frac{1}{2}(\chi ^{ijkl}- \chi ^{kl ij})\). Under reversible conditions, (4.8) can be derived from a Lagrangian, then \(^{(2)}\chi ^{ijkl}=0\). The principal part \(^{(1)}\chi ^{ijkl}\) fulfills the symmetries \( ^{(1)}\chi ^{ijkl}= {}^{(1)}\chi ^{klij}\) and \(^{(1)}\chi ^{[ijkl]}=0\).

The local and linear response relation now reads

$$\begin{aligned} { \mathcal {H}^{ij}=\frac{1}{2}\left( {}^{(1)}{\chi }^{ijkl}+ {}^{(2)}{\chi }^{ijkl} +{\alpha }\, {\epsilon }^{ijkl}\right) F_{kl}\,,} \end{aligned}$$
(4.10)

and, split in space and time [35, 37],

$$\begin{aligned} {D}^a&=( \varepsilon ^{ab} - \, \epsilon ^{abc}\,n_c )E_b\,+( \gamma ^a{}_b + s_b{}^a - \delta _b^a s_c{}^c) {B}^b + {\alpha }\,B^a \,, \end{aligned}$$
(4.11)
$$\begin{aligned} {H}_a&= \>( \mu _{ab}^{-1} - {\epsilon }_{abc}m^c ) {B}^b +(- \gamma ^b{}_a + s_a{}^b - \delta _a^b s_c{}^c)E_b - {\alpha }\,E_a\,; \end{aligned}$$
(4.12)

here \(\epsilon ^{abc}= {\epsilon }_{abc}=\pm 1,0\) are the 3-dimensional Levi-Civita symbols. The 6 permittivities \(\varepsilon ^{ab}= \varepsilon ^{ba}\), the 6 permeabilities \(\mu _{ab}=\mu _{ba}\) were already known to Maxwell. The 8 magnetoelectric pieces \(\gamma ^a{}_b\) (its trace vanishes, \(\gamma ^c{}_c=0\)) were found since 1961, see Astrov [2]. Eventually, the hypothetical skewon piece [35] carries 3 permittivities \(n_a\), the 3 permeabilities \(m^a\), and the 9 magnetoelectric pieces \(s_a{}^b\). Equivalent response relations were formulated by Serdyukov et al. [91, p. 86] and studied in quite some detail, see also de Lange and Raab [52].

Suppose we have as special case a vacuum spacetime described by a Riemannian metric \(g_{ij}\). Then the response tensor turns out to be

$$\begin{aligned} \chi ^{ijkl}=\,^{(1)}\chi ^{ijkl}=2\lambda _0\sqrt{-g}g^{i[k}g^{l]j}\qquad \text {and} \qquad \mathcal {H}^{ij}= \lambda _0\sqrt{-g}F^{ij}\,, \end{aligned}$$
(4.13)

with the vacuum admittance \(\lambda _0\approx 1/377\, \varOmega \). Thus, we recover known structures, and we recognize that the relation (4.8) represents a natural generalization of the vacuum case. The metric \(g^{ij}\) can be considered as some kind of a square root of the electromagnetic response tensor \(\chi ^{ijkl}\).

We should keep in mind that a local and homogeneous electromagnetic response like (4.8) can be, if the circumstances require it, generalized to nonlocal and/or to nonlinear laws. Examples of nonlocal laws have been proposed by Bopp and PodolskyFootnote 4 and by Mashhoon.Footnote 5 Nonlinear laws are due to Heisenberg and Euler,Footnote 6 Born and Infeld,Footnote 7 and Plebański.Footnote 8 Fresnel surfaces for the nonlinear case were found by Obukhov and Rubilar [77], for example. More recently, Lämmerzahl et al. [51] and Itin et al. [44] investigated electrodynamics in Finsler spacetimes. In the premetric framework, this corresponds to a nonlocal constitutive law, see [44, Eq. (3.29)], somewhat reminiscent of the Bopp-Podolsky scheme.

2.3 Propagation of Electromagnetic Disturbances

The obvious next step in evaluating the physics of our model of spacetime is to look how electromagnetic disturbances propagate in this spacetime. One can either consider the short wave-length limit of the electromagnetic theory, the WKB-approximation, or one can study, as we will do here, the propagation of electromagnetic disturbances with a technique developed by Hadamard; for a general outline, see [96, Chap. C].

Hadamard describes an elementary wave as a process that forms a wave surface. Across this surface, the electromagnetic field is continuous, but the derivative of the field has a jump. The direction of a jump is given by the wave covector. The subsequent integration produces the rays, with the wave vectors as tangents to rays, see for our case [35, 40, 46, 74]. In the meantime, our methods have been improved, see [3, 24, 27].

Out of the electromagnetic response tensor density we can define, with the help of the covariant Levi-Civita symbol \(\epsilon _{ijkl}=\pm 1,0\), the premetric “diamond” (single) dual and the diamond double dual, respectively:

$$\begin{aligned} \chi ^{\diamond \, ij}{}_{kl}:=\frac{1}{2} \chi ^{ijcd}\epsilon _{cdkl}\,,\qquad {^\diamond }\chi ^{\,\diamond }_{ijkl}:=\frac{1}{2} \epsilon _{ijab} \chi ^{\diamond \, ab}{}_{kl} =\frac{1}{4} \epsilon _{ijab}\chi ^{abcd} \epsilon _{cdkl}\,. \end{aligned}$$
(4.14)

The covariant Levi-Civita symbol carries weight \(-1\) and \(\chi ^{abcd}\) weight \(+1\). Thus, the double dual has weight \(+1\), too. Performing the double dual apparently corresponds to a lowering of all four indices of \(\chi ^{abcd}\)—and this is achieved without having access to a metric of spacetime.

After this preparation, it is straightforward to define the (premetric) 4th rank Kummer tensor density, which is cubic in \(\chi \), as [3]

$$\begin{aligned} {\mathcal{K}^{ijkl}[\chi ]}:= \chi ^{ai bj}{}\, {^\diamond }\chi ^\diamond _{acbd}\chi ^{ckdl}\,. \end{aligned}$$
(4.15)

It has weight \(+1\) and obeys the symmetry \({{\mathcal{K}^{ijkl}}=\;{\mathcal{K}^{klij} \,.}}\)

At each point in spacetime, the wave covectors \(q_i=(\omega ,\mathbf {k})\) of the electromagnetic waves span the Fresnel wave surfaces, which are quartic in the wave covectors according to

$$\begin{aligned} \mathcal{K}^{ijkl}[\chi ]\,q_iq_jq_kq_l =\mathcal{K}^{(ijkl)}[\chi ]\,q_iq_jq_kq_l =0\,. \end{aligned}$$
(4.16)

The Tamm-Rubilar (TR) tensor density [35, 84], with the conventional factor 1 / 6, is defined by

$$\begin{aligned} \mathcal{G}^{ijkl}\,[\chi ]:=\frac{1}{6}\,\mathcal{K}^{(ijkl)}[\chi ] =\frac{1}{6} \chi ^{a(i j|b}{}\, {^\diamond }\chi ^\diamond _{acbd}\chi ^{c|kl)d}\,. \end{aligned}$$
(4.17)

It is totally symmetric and carries 35 independent components. By straightforward algebra it can be shown that the axion field drops out from the TR-tensor:

$$\begin{aligned} \mathcal{G}^{ijkl}\,[\chi ]= \mathcal{G}^{ijkl}\,[\,^{(1)}\!\chi +{}^{(2)}\!\chi ]\,; \end{aligned}$$
(4.18)

see in this connection also [39] and the references given there. The effect of the skewon piece on light propagation has been studied in [75]. Ni [68] was the first to understand that the axion field doesn’t influence the light propagation in the geometrical optics limit. Note that \(^{(1)}\!\chi +{}^{(2)}\!\chi \) has \(20+15\) independent components, exactly as \(\mathcal G\)—probably not by chance.

Accordingly, the totally symmetric TR-tensor \(\mathcal{G}^{ijkl}[\chi ]\), with its 35 independent components, can, up to a factor, be observed by optical means, that is, the TR-tensor—in contrast to the Kummer tensor, as far as we know—has a direct operational interpretation.

2.4 Fresnel Wave Surface

The (generalized) Fresnel equation

$$\begin{aligned} \mathcal{G}^{ijkl}[\chi ]\,q_iq_jq_kq_l=0\,, \end{aligned}$$
(4.19)

determines a Fresnel wave surface. A trivial test for checking the correctness of (4.19) is to substitute the response tensor for the Maxwell-Lorentz vacuum electrodynamics (4.13)\(_{1}\) into the TR-tensor of (4.19). One finds straightforwardly \((g^{ij}q_iq_j)^2=0\), that is, two light cones that collapse onto each other. The decomposition of (4.19) into space and time can be found in [35, (D.2.44)].

For illustration, following [3, 85], see also [41], we will display a classical example of such a surface. In Eqs. (4.11) and (4.12), we choose an anisotropic permittivity tensor with three different principal values and assume trivial vacuum permeability, whereas all magnetoelectric moduli—with the possible exception of the axion \(\alpha \)—vanish,

$$\begin{aligned} (\varepsilon ^{ab})=\left( \begin{matrix}\varepsilon ^{1}&{}0&{}0\\ 0&{}\varepsilon ^{2}&{}0\\ 0&{}0&{}\varepsilon ^{3}\end{matrix}\right) \quad \text {and}\quad (\mu ^{-1}_{ab})=\mu ^{-1}_0\left( \begin{matrix}1\;&{}0&{}0 \\ 0&{} 1 \;&{}0\\ 0&{}0&{}1\;\end{matrix}\right) . \end{aligned}$$
(4.20)

Substitution into the Fresnel equation yield the quartic polynomial

$$\begin{aligned}&(\alpha ^2x^2+\beta ^2y^2+\gamma ^2z^2)(x^2+y^2+z^2) \nonumber \\&-\left[ \alpha ^2(\beta ^2+\gamma ^2)x^2+\beta ^2(\gamma ^2+\alpha ^2)y^2+\gamma ^2(\alpha ^2+\beta ^2)z^2 \right] +\alpha ^2\beta ^2\gamma ^2=0\,,\quad \end{aligned}$$
(4.21)

with the 3 parametersFootnote 9 \(\alpha :=c/\sqrt{\varepsilon _{1}},\;\beta :=c/\sqrt{\varepsilon _{2}},\;\gamma :=c/\sqrt{\varepsilon _{3}}\), and with \(c=1/\sqrt{\varepsilon _0\mu _0}\) as the vacuum speed of light.

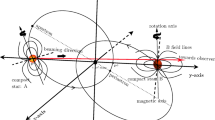
The corresponding surface is drawn in Fig. 4.1. As an example of a Fresnel surface for a more exotic material, we provide one for the so-called PQ-medium of Lindell [56]. It may turn out that this response tensor can only be realized with the help of a suitable metamaterial, see [92]. Corresponding investigations are underway by Favaro [25].

Let us shortly look back on what we have achieved so far: We have formulated the Maxwell equation in a premetric way. For the response tensor only local and linear notions are used, no distances or angles were mentioned nor implemented. Under such circumstances, electromagnetic disturbances propagate in a birefringent way in accordance with the Fresnel wave surfaces, such as presented in Figs. 4.1 and 4.2.

How can we now bring in distances and angles, which are concepts omnipresent in everyday life? The answer is obvious, we have to suppress birefringence.

Fig. 4.1
figure 1

Fresnel wave surface for the permittivities and the permeabilities of Eq. (4.20). It had been drawn by Jaumann for an optically biaxial crystal, see Schaefer [85, p. 485]. This crystal has the property of birefringence (or double refraction). The origin at \(x=y=z=0\) is the point in 3-dimensional space from where the wave covectors \(\mathbf {k}\) originate. They end on the Fresnel wave surface. Their modulus is proportional to the reciprocal of the phase velocity \(\omega /k\). In other words, up to a sign, we have usually in one direction two different phase velocities. This is an expression of the birefringence. Only along the optical axes I and II, we have only one wave covector. The upper half depicts the exterior shell with the funnel shaped singularities, the lower half the inner shell. The two shells cross each other at four points forming cusps

Full size image
Fig. 4.2
figure 2

Fresnel wave surface for a PQ-medium of Lindell [56, 57]. Using Lindell’s dyadic version of the Fresnel equation [54, 55], Sihvola [94] drew the Fresnel wave surface by using Mathematica. Our image was later created by Favaro [25] in a similar way, again with Mathematica. For the wave covector, we have \(q_i=(\omega ,k_1,k_2,k_3)\)

Full size image

2.5 Suppression of Birefringence: The Light Cone

Looking at the figures, it is clear that we have to take care that both shells in each Fresnel wave surface become identical spheres. Then light propagates like in vacuum. For this purpose, we can solve the quartic Fresnel equation (4.19) with respect to the frequency \(q_0\), keeping the 3-covector \(q_a\) fixed. One finds four solutions, for the details please compare [38, 50]. To suppress birefringence, one has to demand two conditions. In turn, the quartic equation splits into a product of two quadratic equations proportional to each other. Thus, we find a light cone \(g^{ij}(x)\,q_iq_j=0\) at each point of spacetime.

Perhaps surprisingly, we derived also the Lorentz signature, see [35, 42, 43]. This can be traced back to the Lenz rule, which determines the relative sign of the two terms in the induction law, as compared to the relative sign in the Ampère-Maxwell law. The Lorentz signature can be understood on the level of classical electrodynamics, no appeal to quantum field theory, which is widespread in the literature, is necessary.

Globally in the cosmos, birefringence is excluded with high accuracy, see the observations of Polarbear [1] and the discussion of Ni [71].

2.6 Axion, Dilaton, Metric

At the premetric level of our framework, besides the principal piece, first the skewon and the axion fields emerged. Only subsequently the light cone was brought up. The skewon field was phased out by our insistence of the vanishing birefringence in the vacuum. Accordingly, the axion field and the light cone survived the suppression of the birefringence.

The light cone does not define the metric uniquely. Rather an arbitrary function \(\lambda (x)\) is left over:

$$\begin{aligned} {\lambda }(x)\,g^{ij}(x)\,q_iq_j=0\,. \end{aligned}$$
(4.22)

The light cone is invariant under the 15-parametric conformal group. The 4 proper conformal transformation correspond to a reflection at the unit circle and, as such, are of a nonlocal nature. As a consequence, if two frames are related to each other by a proper conformal transformation and one frame is inertial, the other one is accelerated with respect to the former one. Accordingly, there is an operational distinction possible between a proper conformal and a dilation or scale transformation. Thus, only the 11 parameter Weyl subgroup of the 15 parameter conformal group is based on local transformations.

If we compare our result in (4.22) with vacuum response in (4.13), we recognize, not forgetting the axion field, that we find the following response equation for vanishing birefringence:

(4.23)

Because of the presence of the dilation within the Weyl group, it is natural to identify the function \(\lambda (x)\) with the dilaton field.Footnote 10

In the calculus of exterior differential forms, see [35], the twisted excitation 2-form \(H=\frac{1}{2} \epsilon _{ijkl}{\mathcal H}^{kl}dx^i\wedge dx^j\) and the untwisted field strength 2-form \(F=\frac{1}{2} F_{ij} dx^i\wedge dx^j\), together with the twisted current 3-form \(J=\frac{1}{3!}\epsilon _{ijkl}\mathcal {J}^ldx^i\wedge dx^j \wedge dx^k\), obey the Maxwell equations \(dH=J\) and \(dF=0\). By means of the metric, we can introduce the Hodge star \({}^\star \) operator. Then the response relation (4.23) becomes even more compact [26, 36]:

$$\begin{aligned} {H}=\varvec{[}\lambda (x)\,^{\varvec{\star }} + \alpha (x)\varvec{]}F\,. \end{aligned}$$
(4.24)

Equations (4.23) and (4.24) represent the end result of investigating an electromagnetic spacetime model with local and linear response and without birefringence. The three fields \(\lambda (x)\), \(g^{ij}(x)\), and \(\alpha (x)\) come up together with a reasonable interpretation. At least in the way we defined them here, \(\lambda (x)\), \(g^{ij}(x)\), and \(\alpha (x)\) are all three descendants of electromagnetism.

As we have argued in Sect. 1.5, the dilaton seems to be at home in the Weyl-Cartan spacetime. Our results (4.23) or (4.24) are consistent with this expectation, that is, we believe that these equations are valid in a Weyl-Cartan spacetime.

What are we told by experiments and observations? The axion \(A^0\) has not been found so far, so we can provisionally put \(\alpha =0\). Moreover, under normal circumstances, the dilaton seems to be a constant field and thereby sets a certain scale, that is, \(\lambda (x)= \lambda _{0}=\text {const}\), where \(\lambda _{0}\) is the admittance of free space, the value of which is, in SI-units, \(\approx \!\! 1/(377\;\varOmega )\). Under these conditions, we are left with the response relation of conventional Maxwell-Lorentz electrodynamics,

$$\begin{aligned} \mathcal {H}^{ij} = \lambda _0\sqrt{-g}\,F^{ij}\qquad \hbox {or}\qquad H=\lambda _0\,^\star F\,. \end{aligned}$$
(4.25)

The possible generalizations are apparent.

3 Discussion

Gravity, coupling to all objects carrying energy-momentum, is a truly universal interaction. Electromagnetism is only involved in electrically charged matter. What is curious and what we still do not understand is that the gravitational potential \(g^{ij}\) emerges in an electromagnetic context, that is, in studying electromagnetic disturbances, we can suppress birefringence, and then the light cone emerges. And the light cone is essentially involved in general relativity. In other words, we cannot formulate a general-relativistic theory of gravity unless some electric charge is around: electromagnetic waves are a necessary tool for constructing general relativity.

Perlick is not concerned about it. He observes that [79] “...the vacuum Maxwell equations are but one example that have the light cones of the spacetime metric for their characteristics. The same is true of the Dirac equation, the Klein-Gordon equation and others....” Yes, this is true. However, if a metric is not prescribed, we cannot even formulate Dirac’s theory. In contrast, in premetric electrodynamics, if a local and linear response tensor density is assumed, we can derive the metric, as we discussed above. In this sense, electrodynamics is distinguished from Dirac’s theory—and in this, and only in this sense, the premetric Maxwell equations are more fundamental than the Dirac equation.

Accordingly, there seems to be a deep connection between electromagnetism and gravity, even though gravity is truly universal, in contrast to electrodynamics.