Keywords

1 Introduction

The recent diffusion of on-line trading platforms gave virtually anyone the possibility of investing in any stock exchange market, starting from any amount of money. The ever-growing number of small investors wishes to find the optimal strategies to manage their portfolio, that is, to select the best investment policy in term of minimum risk and maximum return, given their collection of investment tools, income, budget, and convenient time frame.

Portfolio management can be defined as the art of establishing the optimal composition of the investor’s portfolio at each instant of time in an ever-changing scenario. Managing a portfolio can be expressed as a list of decisions: for each tradable, determine the amount to be bought or sold. The motivations behind each operation can be simplified as: buy/sell now the amount A of tradable T because in a limited time period its price will rise/fall. We call the expected return of such operation \(R^{+}\), while the maximum loss caused by it is \(R^{-}\).

The risk profile is a measure of how much an investor is afraid to lose money, or, conversely, is willing to take risks hoping for a higher return. The risk profile limits the set of financial instruments that can be used, since highly volatile instruments are considered riskier, and could be incompatible with the investor’s preferences.

Generally speaking, the world of finance is extremely complex (for an introduction, see [1–3]). Over time, many types of tradable have been created, the most common of which are: stocks, fixed income bonds, zero-coupon bonds, futures, options, export trading companies (ETCs), exchange-traded funds (ETFs), currency crosses, contract for difference (CFD). For each type there are further differentiations, and while this proliferation can seem baffling, it is needed to meet different stakeholders’ needs. For example, stockholders could secure the company’s stock price at a fixed cost using options; or big farmers could exploit grain futures in margination as insurance for price variations. Such margination, a service offered by brokers, is the possibility to control capital C keeping only \(\frac{C}{L}\) invested, where L is called the leverage. Indeed, leverage could be highly beneficial for the farmers in the example, because they would be required to immobilize a much smaller capital. Finally, investors trading such a wide assortment of instruments are necessary for the market liquidity: to be successful, a trade requires both the offer and the demand.

Commonly, investors wish to maximize the return on their portfolio, while minimizing the risks – however, a high return is frequently accompanied by a higher risk. In 1952, Markowitz started the so-called “modern portfolio theory”, describing in a quantitative way how the diversification of assets could be used to minimize, but not eliminate, the overall risk without changing the portfolio expected return [4]. In Markowitz’s original view, choosing an optimal portfolio is a mean-variance optimization problem, where the objective is to minimize the variance for a given mean. Despite its past popularity, the model is known to be based upon assumptions that do not hold in practice: investors are considered flawlessly risk-averse; and either the distribution of the rate of return is assumed multivariate normal, or the utility of the investor a quadratic function of the rate of return. It is now widely recognized that real-world portfolios do not follow a multivariate normal distribution.

More recently, researchers proposed different portfolio theories. The very same Markowitz improved his mean-variance idea in 1968 [5]; other improvements include post-modern portfolio [6]; and behavioral portfolio [7], that, differently from other approaches, takes into consideration investors who are not completely risk-adverse.

In this work, we study a decision-support tool for management strategies of small portfolios. The tool takes in input market data and, after a training phase, starts an investing simulation. During training, the performance expectation of each tradable over three days will be modeled by a separate neural network. Afterwards, for each day, the simulation uses the neural networks as oracles to optimize the portfolio management strategy, resorting to a multi-objective evolutionary algorithm.

The rest of the paper is organized as follows. Section 2 illustrates the financial real-world dataset used during the experience; the choice of architecture for the ANNs is discussed in Sect. 3; the proposed approach is presented in Sect. 4; while Sect. 5 shows the obtained results and concludes the paper.

2 Data

In this study, we consider end-of-day (EoD) data for about one hundred stocks from Borsa Italiana (Milan stock exchange), 40 % of them from medium-to-large companies and 60 % from small companies. Data are taken from Yahoo! finance Footnote 1, starting from January, 3rd 2000 to August, 2rd 2011. In the EoD data, open and close represent, respectively, the opening and closing price for a share, the prices traded in the opening and closing auction; min and max are, respectively, the minimum and the maximum price for that share traded during the day; while vol is the number of shares traded. To compare stocks performances from different companies, we choose to normalize EoD data resorting to the following formulas:

$$\begin{aligned} open'_{i}=\frac{open_{i}-close_{i-1}}{close_{i-1}} \end{aligned}$$
(1)
$$\begin{aligned} close'_{i}=\frac{close_{i}-open_{i}}{open_{i}} \end{aligned}$$
(2)
$$\begin{aligned} min'_{i}=\frac{min_{i}-open_{i}}{open_{i}} \end{aligned}$$
(3)
$$\begin{aligned} max'_{i}=\frac{max_{i}-open_{i}}{open_{i}} \end{aligned}$$
(4)
$$\begin{aligned} vol'_{i}=\frac{w_{i}-w_{i-1}}{w_{i-1}} \end{aligned}$$
(5)
$$\begin{aligned} w_{k}=vol'_{k} \cdot \frac{max'_{k}-min'_{k}}{2} \end{aligned}$$
(6)

The dataset is divided in two contiguous blocks: the beggining 90 % of the original data, 03/01/2000-01/06/2010; and the ending 10 %, 03/06/2010-02/08/2011. The first block is used for the neural networks, and it is further divided into the canonical: training, validation and testing sets; while the second block is used in the performances simulation, see Sect. 4.3.

3 Forecasting: Architecture Selection

As common sense suggests, it is impossible to forecast rare, abrupt events which lead to sudden collapses of quotations, such as terrorist attacks, or sensational news on companies. This is a part of inherent market risk that cannot be avoided: however, that does not mean that profiting from trading is an unattainable goal.

In trading, there are different techniques that are widely used to forecast stock performances [8]. In summary, fundamental analysis studies company reports and macroeconomical data, and estimates future earnings, which also define the fair stock price [1, 9, 10]. It’s a time-consuming activity that needs experience, better suited for long-term trading: widely used stocks comparison metrics for this approach are \(\frac{price}{earnings}\), \(\frac{price}{book value}\), \(\frac{price}{cash flow}\), \(\frac{dividend}{price}\) (also known as dividend yield).

Technical analysis, also known as chart trading [11, 12], studies prices charts, and gives buy and sell signals through combinations of indicators and oscillators. The most known methodologies of this kind are RSI (relative strength index), BB (Bollinger bands), moving averages (SMA, EMA, WMA), resistance, supports, and trends. Modeling financial time series is an intense research field for computer science as well, and applications are range from agent-based systems [13], to classifiers (EDDIE and \(cAnt-miner_{PB}\) [14]), to genetic algorithms, and, more generally, evolutionary computation [15–23].

We are modeling how the investor’s rate of return expectation (RRe) changes in the various market conditions, we test the multi-layer perceptron (MLP) prediction capability. MLP is a feed-forward artificial neural network (ANN) consisting of a layer of inputs, one or more hidden layers and one output layer. Every layer has a set of nodes, each one fully connected to the nodes on the next layer, forming a directed graph. MLPs are trained using the backpropagation algorithm, a supervised learning algorithm that map examples, each one being a pair of input and output features. MLP can be used for function approximation or as a classifier [24]. Briefly, for our purposes, the difference is in the meaning of the output: when MLP is used as function approximation, the output is the RRe codomain; when MLP is used as classifier, the output is a discretized RRe codomain, each output node represents a class, and the connected value is a belief measure. Higher values are linked to a higher confidence for the sample belonging to that class. Our choice of this machine learning paradigm is motivated by the good results obtained with MLP for financial forecasting in [25].

Table 1. Training parameters, common to all tests.
Full size table

The Eni price is a common benchmark for financial forecasting in Italy, and here it is used to compare the performance of different MLP architectures and configurations. For each architecture we applied different input-output configurations, see Table 2 for a summary. The benchmark data comes from the dataset presented in Sect. 2, and it is composed by Eni and all companies in the oil and natural gas index. This dataset is divided in three parts: training, validation and testing (60 %, 20 %, 20 % of the original data, respectively).

Table 2. Input/output configurations (conf); the EoD input data is for Eni, oil and natural gas share index, output is for Eni only.
Full size table
Table 3. Learning algorithms compared during the trials, all from the gradient descent family.
Full size table

3.1 MLP as a Classifier

From start it is apparent that a MLP classifier has a more complex architecture than a MLP used for function approximation. The output classes are chosen clustering the close performance using k-means algorithm [27] over all the shares in the benchmark. The aim is to select the more realistic performance classes. After clustering trials from 20 to 60 clusters, we choose as reference 60 classes, because this configuration has a better resolution over the central and most frequently matched intervals. Table 2 reports the configurations and Table 3 the training functions, using 100-epoch and 500-epoch training. However, the correct class is rarely chosen first, mean errors are far from being acceptable and the solution scalability is minimal, due to the high training time needed. This architecture is thus abandoned, as the MLP function approximation yields better results in less time.

3.2 MLP for Function Approximation

The I/O configuration used is reported in Table 2, the neuron activation function is a hyperbolic tangent, and learning algorithms are reported in Table 3. The initialization algorithm that chooses initial weights and bias is Nguyen-Widrow (NW) [28]; for the first and third hidden layers we also use a random generator in the (0, 1) interval. All training parameters are reported in Table 1.

Results are strongly dependent from initial weights and the network tends to fall into local minima, but, we noticed that a necessary condition for accepting the trained network is to test if the error distribution in the output layer belongs to a normal distribution family as in Fig. 1. Operatively, we can require that in all the three output nodes the error mean and variance should be lesser than e and e*10 respectively, where e starts from 0.1 and it is incremented by 30 % every 10 refusals.

Fig. 1.
figure 1

An example of a fitting curve for error distribution of an acceptable NN.

Full size image
Table 4. Best results for MLP as function approximation, configuration 1, mean(\(\mu _{i}\)) and variance( \(\sigma _{i}\)) of error; randomly initialized NN have performed worst then NW. 1h, 2h, 3h are the number of hidden layer, number of neurons for each layer: ff1h(201), ff2h(200,100), ff3h(100,50,25). 100 input features, 3 output features.
Full size table
Table 5. Best results for MLP as function approximation, configuration 2, number of neurons for each layer: ff1h(81), ff2h(80,40), ff3h(80,40,20). 40 input features, 3 output features.
Full size table
Table 6. Best results for MLP as function approximation, configuration 3, number of neurons for each layer: ff1h(41), ff2h(40,20), ff3h(40,20,10). 20 input features, 3 output features.
Full size table

Tables 4, 5, 6 show the best results among our tests: for our purposes, gradient descent back-propagation with adaptive learning performs generally better than the other techniques. Configurations 2 and 3 perform much better than configuration 1, both in final results and in training time, as they have less input features and hidden layers with less neurons. The result suggests that, for this ANN architecture, using the complete EoD data for each input day does not improve forecast capability.

4 Proposed Approach

We propose a decision-support tool, a portfolio optimizer with a simulator, whose optimization process is divided into two phases. The first step is devoted to building, for each stock, a MLP that models the performance expectation for the next three days. Being the core of the fitness function that will later be used, this phase is crucial, as a good approximation will lead to good decisions. The second step consists of searching for a performing stock combination, a Pareto set of portfolios able to satisfy our model constraints. Finally, the simulator is used to measure the strategy performance in simplified market conditions. It must be noted that the simulator can also be used in real conditions as, for each simulated day and for each stock, it provides the quantity and the book price to sell and buy. The three phases are summarized in Fig. 2.

Fig. 2.
figure 2

High-level scheme of the proposed approach. Training data, properly clustered, is used to train the MLP oracles that will try to predict the performance of company shares. The optimizer uses a MOEA to obtain a trade-off between (predicted) risk and reward. Finally, the simulator computes the effective reward obtained, exploiting unseen validation data.

Full size image

4.1 Phase I: Building the MLP Oracle

In the first phase, we build the MLP oracle, a procedure that is time consuming and requires a considerable amount of data, for which we use the base dataset, described in Sect. 2. From the considerations and the preliminary experiments reported in Sect. 3, the better solution is MLP with data configuration 3, and 2 hidden layers with 35 and 20 nodes, respectively. This combination in empirical tests provided the best results in terms of mean error and variance, with less trials. The chosen training algorithm is the gradient descent backpropagation with adaptive learning rate, while for the initialization, we use Nguyen-Widrow. Data configuration 3 includes the last 10 days input of a target stock’s close performance with 10 days input of the related stocks. In the experiments reported in Sect. 3, the related stocks were chosen by hand, but here we resort to an automatic selection. To us, related stocks are stocks whose behavior patterns, the sequence of closing performances in a 10-day range, are similar to the target stock. Fu, in [29], has shown how Self Organizing Maps (SOMs) are particularly apt at discovering shape patterns, and thus we exploit this methodology to define stock clusters.

Briefly, a SOM is an ANN with an input layer and a node matrix as output layer. The learning algorithm is unsupervised and defines in the output layer the concept of neighborhood: given a node, his neighborhood is composed by the near nodes, constrained by the layer topology and the distance measure. Learning means increasing the weight of a node and distance inverse-proportionally increase the weights of the nodes in the neighborhood, the neighborhood shrinks with time [24].

Our SOM configuration has 10 input nodes and a layer of 100 nodes in output, 100 training epochs, initial neighborhood distance 3, and a hexagonal layer topology. The base set defined in Sect. 2 is divided into blocks of 10 consecutive daily-close. Each block has every stock and it is used to train a SOM. It is natural that stocks in block x, which are classified in class y, can be assigned to a different class or to different neighbor classes, in block \(x+1\). To bypass this problem we use an a-priori algorithm [30–32] and mine frequent item-sets from the dataset of classes for every block without empty rows, where each row is a cluster. As each stock in a block can fall into a single class, the min-support used is lesser than 1 % and min-confidence used is greater than 95 %. Association rules discovered here define the related classes of stocks.

4.2 Phase II: MOEA Optimization

For the optimization step, we assume that the investor has a small budget, arbitrarily set to B €. Such an amount is small enough not to influence the overall market behavior, but still permits diversification with marginal transaction costs in the real world. No margination and no short selling are allowed. The investor does not want to lose more then L% budget daily.

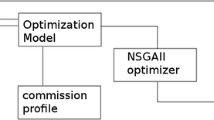
The resulting model, an adaptation of Markowitz mean-variance model discussed in [33], is shown in Fig. 3. The model chooses portfolios composed by stocks whose most expected performance was uncorrelated in the last 30 days.

We optimize the following equations:

Equation 8 is the global correlation minimization between portfolio stocks. \(\sigma _{i,j}\) is the covariance between performance of stock i and j in past 30 days — it does not make sense to consider a longer interval, given our short investing horizon: decisions can be changed daily, and we assume there are no liquidity problems. The equation must be minimized to penalize portfolios composed by highly correlated stocks.

Equation 7 is the expected return: \(q_i\) is an unknown model, and it represents the number of stocks i that will be bought tomorrow, where n is the stock number. Equation 11 is the third-day total expected return; Eq. 12 is the expected price for the buy, the average between the price for today, and tomorrow’s expected price. It must be maximized.

Equation 10 expresses the constraint of maintaining the portfolio value to (at least) 95 % of the budget, preventing compositions that are expected to lose money. Equation 13 is the price that is expected after two days, which is the first possible day for eventually freeing the position; \(e_i\) is the mean error that the considered MLP has produced in past 30 days. Equation 9 is the budget constraint, where \(pv_i(t+k)\), with \(k=1,2,3\) is the stock i performance, the output node k of our MLP oracle.

Fig. 3.
figure 3

Equations composing the model for portfolio optimization. \(l=\frac{L}{100}\)

Full size image

This mixed-integer problem is non-linear and features several conflicting objectives. Multi-objective evolutionary algorithms (MOEA) [34, 35] has been shown effective in finding a good approximation for the Pareto-front in such cases. We use NSGA-II [36], as it was already successfully exploited in [37], where it was demonstrated scalable and able to efficiently find solutions.

4.3 Phase III: Simulation

Our artificial investor builds its strategies for the next day after market closure. It is very disciplined and the following day, whatever happens, it will strictly follow the planned strategy. It desires a differentiated portfolio, it does not want to lose more then 5 %, and it wishes to maximize its returns. If the conditions aren’t met, it can also stay out of the market, meaning that it will not hold any share. It is forbidden from taking short positions or borrowing money. Its budget for strategy optimization is defined as the remaining cash available for the current day, added to the money expected from the following day’s liquidation of its actual portfolio. After the optimization, the artificial investor will have a set of Pareto optimal portfolios; it will chose the one that generate the least number of transactions, in order to minimize the transactions’ cost, and execute the related strategy.

The market used in the simulations is a simplified version of a real market: there are no intra-day operation, no issues linked to partial order executionsFootnote 2, no taxation, no issues related to sell-buy order synchronizationsFootnote 3 as sell operations are executed before the buy operations, and no negotiation suspensionFootnote 4.

When a sell operation is executed: if the open price is greater than the target price, the stock is sold at an open price; else, if the target price is between min e max, then the stock is sold at target price; otherwise, the sell operation is not executed. The quantity is the difference between the old portfolio and the new. When a buy operation is executed: if the open price is less than the target price, the operation is completed at open price; if the target price is between min e max, then the stuck is bought at target price; otherwise, the operation is not executed. The quantity depends on available cash, if the artificial investor does not possess enough resources, the quantity will be zero.

Fig. 4.
figure 4

The proposed approach portfolio’s daily rate of return in a 300-day simulation. Despite considerable fluctuations, the approach is able to obtain a 0.445 % average daily rate of return.

Full size image

5 Preliminary Results and Conclusions

In a first experimental evaluation, starting from a budget of 20,000 €, after 300 trading days simulated using the simulation data in Sect. 2, the results are quite interesting, see Figs. 4 and 5. The proposed approach is able to multiply its initial budget 3.788 times. Such a result might look astonishing, but we have to take into account the simplifications in the simulation (such as the absence of taxation), the market conditionsFootnote 5, and the dataset composition. Still, it is important to notice that, even when the proposed portfolio choice is wrong, losses are contained (see Fig. 6).

Fig. 5.
figure 5

Portfolio budget cumulative rate of return for each Euro invested.

Full size image
Fig. 6.
figure 6

Histogram of performances, bar steps are 0.002 wide.

Full size image

It’s not trivial to obtain a fair comparison of the proposed approach, given both the limited initial investment, that makes it impossible to weight it against large hedge funds, and the assumptions used in the simulation, that prevent our tool from performing several potentially rewarding intra-day operations, but also disregard taxation and costs for performing the transactions. Taking into account these real-world elements would cut the return rate of the approach approximately by 30 %, reducing it to a still considerable 194.6 % total performance.

In order to present at least an estimate for the goodness of the methodology, we use the Hall of Fame of ITCUPFootnote 6, a competition for Italian traders with starting budgets ranging from 2,000 to 50,000 €. The objective of the competition is to obtain the highest possible performance, expressed as a percentage of the initial investment, in a single month of trading. Data is available for years 2007-2015: for year 2011, our considered time frame, in one month (April) the champion obtained a performance of 123.54 % (investing 5,000 € and earning 11,176.96), second place a performance of 18.27 % and third place had 6.17 %. Our algorithm, even with the corrections to take into account taxation and costs, had a performance of 14.35 % for the same month, outperforming third place, and coming a little short of the second position. Thus, the final result obtained through the proposed approach seems realistic and consistent with this real-world data.

The proposed approach is easily scalable, because it does not require a real-time response: after the negotiation market closes, more then 15 hours are available for calculations, before the opening of the following day. The training part is computationally heavy, and on a normal notebook computer takes at least 2 calculation days, but a cluster would reduce the time to a fraction, and the training could be done once completely, and then upgraded monthly. Still, a complete run of the algorithm on the 300-day test set requires more than one day. We are currently running further experiments, to obtain a more reliable assessment of the algorithm’s capabilities. Future works will focus on including all real-world conditions disregarded in the simulation, in order to obtain a better assessment of the proposed approach. Further studies must be performed on the stock performance forecasting, as this is the core of the problem, in particular the forecasting of inversion points as they are crucial to maximize returns.