Real-Time Estimation of the Interference in Random Waypoint Mobile Networks

Abstract

It is well known that the stochastic nature of the interference deeply impacts on the performance of emerging and future wireless communication systems. In this work we consider an ad hoc network where the mobile nodes adopt the Random Waypoint mobility model. Assuming a time-varying wireless channel due to slow and fast fading and, considering the dynamic path loss caused by the node’s mobility, we start by characterizing the interference caused to a receiver by the moving nodes positioned in a ring. Based on the interference distribution, we evaluate two different methodologies to estimate the interference in real-time. The accuracy of the results achieved with the proposed methodologies in several simulations show that they may be used as an effective tool of interference estimation in future wireless communication systems, being the main contribution of this work.

1 Introduction

Interference is an important metric in the future generation of wireless communication systems because the traditional single transmitter and receiver model is being progressively replaced by a different approach, where multiple nodes may transmit simultaneously for a single or even multiple receivers.

The interference in wireless mobile networks, and particularly its characterization, is important for many applications. In most wireless mobile scenarios the characterization of the interference is a non-trivial task. While several authors model the interference in non-mobile networks [1], the assumption nodes’ mobility introduces a novel degree related with the time-varying nature of nodes’ positions. The works already published approaching a formal description of the interference in mobile networks are mainly focused on modeling. The use of statistics describing the level of mobility of the interferers in the modeling process was considered in [2–4]. [2] models the aggregate interference caused by static interferers, being considered that the nodes’ mobility only causes a time-varying displacement with respect to the different non-mobile cells. [3] admits a mobile scenario where the nodes adopt the Random Direction mobility model. [4] considers that the mobile nodes adopt the Random Waypoint mobility model (RWP), but only the interference power from the nearest interferer to the receiver is considered. [5] proposes an interference model for ad hoc mobile networks where the nodes move in accordance with the RWP and all the contributions of the nodes located within a defined region are considered.

This work starts by characterizing the distribution of the interference caused to a receiver by multiple moving nodes located in a ring, considering path loss and slow and fast fading. Based on the interference distribution, we evaluate two different methodologies to estimate the interference in real-time. The major contribution of this work is the identification of a method to estimate the aggregate interference in random waypoint mobility networks, leading to accurate results when used in real-time.

The next section describes the main contributions of this work. Section 3 presents the general assumptions. In Sect. 4 the distribution of the interference values obtained through simulation is approximated by known distributions in order to identify possible approximations. Section 5 describes two estimation methodologies as well as the real-time estimates obtained through simulation and finally the conclusions are present in Sect. 6.

2 Relationship to Cyber-Physical Systems

Recently, Cyber-physical Systems have attracted much attention from the academic community. These systems are mainly focused on the link between computation and physical processes in terms of their reciprocal interaction. Instead of considering standalone physical devices, Cyber-Physical Systems adopt an integrated network of multiple physical devices to enrich the interactions and cooperation between the devices and the virtual worlds available through computation.

Recent advances in wireless communications systems and distributed wireless networks have supported a plethora of innovation in Cyber-Physical Systems. Significant progresses have been observed in mobile ad hoc networks and wireless sensor networks. Examples of Cyber-Physical Systems include mobile robotics and mobile sensors or actuators.

Our work contributes to the development of mobile Cyber-Physical Systems, by studying interference phenomena in mobile wireless networks formed without a central coordinator. By characterizing the interference caused by multiple mobile nodes, the wireless communication process can be improved. Consequently, mobile Cyber-Physical Systems may benefit when higher throughput or reliability is needed.

Basically, we show the impact of the mobility, in terms of average velocity of the cyber-physical devices, in the interference caused to a central receiver. We characterize the interference power at the receiver taking into account the specifics associated with the propagation and mobility scenario. In this way, we contribute to the advance of Cyber-Physical Systems, by proposing an effective solution to estimate the interference, which may be used for different purposes ranging from wireless energy harvesting to the improvement of the wireless communication system.

3 System Description

3.1 Mobility Assumptions

This work considers that the nodes move in accordance with the RWP mobility model [6]. In a RWP model all nodes are firstly placed in a random position ($x, y$). ($x, y$) is sampled from an uniform distribution denoted by $x \in [0, X_{max} ]$ and $y \in [0, Y_{max} ]$. ($x, y$) denotes the starting point, and the following procedure is the definition of the ending point ($x^{'} ,y^{'}$), which is uniformly selected as the starting point (i.e. $x^{'} \in [0, X_{max} ]$ and $y^{'} \in [0, Y_{max} ]$). Afterwards a node samples the velocity $v \in [V_{min} ,V_{max} ]$ from an uniform distribution, which is adopted to travel from the starting point to the ending point.

After arriving at the ending point ($x^{'} ,y^{'}$), a node selects the duration of a pause ($T_{p}$) during which it remains stopped at the ending point. After the time $T_{p}$, a node selects another value for the velocity to travel to a different ending point. After arriving at the ending point, a node repeats the same procedure as many times as parameterized in the mobility simulations.

Considering that ${\text{E}}[L]$ represents the expected distance between two random points and ${\text{E}}[V_{wp} ]$ represents the expected velocity of the nodes without considering pause, the expected velocity of the nodes considering pause is given by

$$ {\text{E}}\left[ V \right] = \left( {\frac{{{\text{E}}[L]}}{{{\text{E}}\left[ {V_{wp} } \right]^{ - 1} {\text{E}}\left[ L \right] + {\text{E}}[T_{p} ]}}} \right) , $$

(1)

where ${\text{E}}[V_{wp} ]$ and ${\text{E}}[L]$ are defined in [7] as ${\text{E}}\left[ {V_{wp} } \right] = \left( {\frac{{V_{max} - V_{min} }}{{\ln (V_{max} /V_{min} )}}} \right)$, ${\text{E}}\left[ L \right] \approx 521.405$ m, and ${\text{E}}[T_{p} ]$ represents the expected value of the pause duration.

3.2 Network Scenario

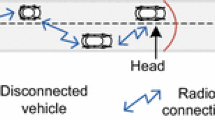
The network scenario considered in this work assumes a RWP scenario where $n$ nodes travel in a rectangular region with area $X_{max} \times Y_{max}$. The network model considered in this work assumes that a static node $N_{c}$ is placed in the center of the considered scenario (located at ($X_{max} /2, Y_{max} /2$)). $N_{c}$ is a receiver of the mobile transmitters. The objective of this paper is the study (in terms of statistics and estimation) of the interference caused to $N_{c}$ by the transmitting nodes $\left\{ {N_{1} , N_{2} , \ldots ,N_{k} } \right\}$ positioned within the interference region, i.e. the mobile transmitters located within the ring bounded by the smaller circle of radius $R_{i}$ and the larger circle of radius $R_{o}$, represented in Fig. 1. Knowing that the interference depends on the distance between the transmitter and receiver, a circular model was chosen. The parameters describing the network and the mobility conditions are described in Table 1.

Fig. 1.

Interference sensed by $N_{c}$ due to the mobile interferers located in the annulus area $\pi \left( {R_{o}^{2} - R_{i}^{2} } \right)$.

Table 1. Parameters adopted in the simulations.

3.3 Radio Propagation Assumptions

This subsection describes the radio propagation scenario considered in this work.

The aggregate interference power received by the node $N_{c}$ located in the centre is expressed by

$$ I_{agg} = \mathop \sum \limits_{i = 1}^{{n_{{AR_{i} R_{o} }} }} I_{i} , $$

(2)

where $I_{i}$ is the interference caused by the node $i$, and $n_{{AR_{i} R_{o} }}$ is the number of transmitters positioned in the interference area $\pi \left( {R_{o}^{2} - R_{i}^{2} } \right)$. The interference power $I_{i}$ is given by

$$ I_{i} = P_{Tx} \psi_{i} r_{i}^{ - \alpha } , $$

(3)

where $P_{Tx}$ is the transmitted power of the node $i$ ($P_{Tx} = 10^{3}$ mW). $\psi_{i}$ denotes the fading occurring in the channel between the node $N_{c}$ and a transmitter $i$ and $r_{i}$ is the distance between the transmitter $i$ and the receiver. Finally, $\alpha$ denotes the path-loss coefficient. In this works we consider that the transmitters do not adjust its transmitting power (i.e. no power control is considered).

The fading $\psi_{i}$ includes the small-scale fading and shadowing effects. The small-scale fading effect is assumed to be distributed in accordance with a Rayleigh distribution, which is represented by

$$ f_{\zeta } \left( x \right) = \frac{x}{{\sigma_{\zeta }^{2} }} e^{{\frac{{ - x^{2} }}{{2\sigma_{\zeta }^{2} }}}} , $$

(4)

where $x$ is the envelope amplitude of the received signal, and $2\sigma_{\zeta }^{2}$ is the mean power of the multipath received signal. $\sigma_{\zeta } = 1$ is adopted in this work.

Regarding the fading effect, we have assumed that it follows a Lognormal distribution

$$ f_{\xi } \left( x \right) = \frac{1}{{\sqrt {2\pi } \sigma_{\xi } x}} e^{{\frac{{ - (\ln \left( x \right) - \mu )^{2} }}{{2\sigma_{\xi }^{2} }}}} , $$

(5)

where $\sigma_{\xi }$ is the shadow standard deviation when $\mu = 0$. The standard deviation is usually expressed in decibels and is given by $\sigma_{\xi dB} = 10\sigma_{\xi } /\ln (10)$. For $\sigma_{\xi } \to 0$, no shadowing results. Although (5) appears to be a simple expression, it is often inconvenient when further analyses are required. Consequently, [8] has shown that the log-normal distribution can be accurately approximated by a gamma distribution, defined by

$$ f_{\xi } \left( x \right) = \frac{1}{{\Gamma (\vartheta )}} \left( {\frac{\vartheta }{{\omega_{s} }}} \right)^{\vartheta } x^{\vartheta - 1} e^{{ - x \frac{\vartheta }{{\omega_{s} }}}} , $$

(6)

where $\vartheta$ is equal to $1/\left( {e^{{\sigma_{\xi }^{2} }} - 1} \right)$ and $\omega_{s}$ is equal to $e^{\mu } \sqrt {\left( {\vartheta + 1} \right)/\vartheta }$. $\Gamma \left( . \right)$ represents the Gamma function. The probability distribution function of the fading $\psi$ is thus represented by

$$ f_{\psi } \left( x \right) = \frac{2}{{\Gamma (\vartheta )}} \left( {\frac{\vartheta }{{\omega_{s} }}} \right)^{{\frac{\vartheta + 1}{2}}} x^{{\frac{\vartheta - 1}{2}}} K_{\vartheta - 1} \left( {\sqrt {\frac{4 \vartheta x}{{\omega_{s} }}} } \right) , $$

(7)

which is the Generalized-K distribution, where $K_{\vartheta - 1} (.)$ is the modified Bessel function of the second kind.

4 Characterization of the Interference Distribution

Following the assumptions considered in the previous section, several simulations were performed considering two different mobility scenarios:

• Mobility scenario 1 - $V_{min} = 5$ m/s, $V_{max} = 20$ m/s, and $T_{p} = 0$ s, representing an average node’s velocity ${\text{E}}\left[ V \right] = 10.82$ m/s;

• Mobility scenario 2 - $V_{min} = 5$ m/s, $V_{max} = 20$ m/s, and $T_{p} = 300$ s, representing an average node’s velocity ${\text{E}}\left[ V \right] = 1.50$ m/s.

Regarding the propagation conditions, we have considered the following scenario:

• Radio scenario – $\alpha = 2$ and $\sigma_{\xi dB} = 3$ dB.

During the simulations, the interference power sensed by the node $N_{c}$ was sampled every second in order to compute its Cumulative Distribution Function (CDF). The samples acquired in $1000$ different simulations, totaling a sample set of $l = 3 \times 10^{6}$ samples, were also used to determine the parameters of a set of different probability density functions (PDFs) using a maximum-likelihood (ML) fitting methodology. For each one of the considered PDF $f$, an average logarithm likelihood was defined as follows

$$ \hat{g} = \frac{1}{l} \mathop \sum \limits_{k = 1}^{l} \ln f(x_{k} |\Theta ) , $$

(8)

where $\Theta$ represents the parameters of the PDF and $x_{k}$ represents each individual sample. ML was used to maximize the likelihood in order to determine $\Theta$, which is described as follows

$$ {\hat{\varTheta }}_{MLE} = \mathop {\text{argmax}}\limits_{\Theta } \hat{g}(\Theta ;x_{1} , \ldots ,x_{l} ) . $$

(9)

Figure 2 represents the CDFs computed with the parameters obtained in (9) for the Generalized Extreme Value (GEV) and Gamma distributions. As illustrated, the fitting obtained with the GEV distribution presents a better approximation for the two mobility scenarios. Because of this observation, the estimation methods proposed in the next section assume that the interference distribution follows a GEV distribution.

Fig. 2.

Interference CDF.

5 Interference Estimation

This section assumes that the aggregate interference can be approximated by a GEV (Generalized Extreme Value) distribution, being its PDF represented by

$$ f\left( {x;\sigma ,\gamma ,\mu } \right) = \frac{1}{\sigma } t(x)^{\gamma + 1} e^{ - t(x)} , $$

(10)

where

$$ t\left( x \right) = \left\{ {\begin{array}{*{20}l} {{{{\left( {1 + \gamma {{x - \mu } \over \sigma }}\right)}^{{{ -1}\big/ \gamma}}}, \gamma \ne 0} } \\ {{e^{ - \left( {x - \mu } \right)/\sigma }}, \quad\quad \gamma = 0 } \\ \end{array} }\right.\!\!\!\!. $$

(11)

A Maximum Log-likelihood estimator (MLE) and a Probability Weighted Moments (PWM) estimator are introduced in the next subsections, in order to be used in real-time to estimate the aggregate interference. Hereafter, we denote the elements of an interference sample set by $\chi = X_{1} , X_{2} , \ldots ,X_{m}$. We also consider the ordered sample set, which is denoted by $X_{1,m} \le \ldots \le X_{m,m}$.

5.1 Log-Likelihood Estimator

The log-likelihood function for a sample set $\chi = \left\{ {X_{1} , \ldots ,X_{m} } \right\}$ of i.i.d GEV random variables is given by

$$ \begin{aligned}{\log L \left( {\sigma ,\gamma ,\mu } \right)} =& {- m\;\log\sigma - \left( {{1 \over \gamma } + 1} \right)\Sigma_{i = 1}^m \log \left( {1 + \gamma {{{X_i} - \mu } \over \sigma }} \right)} \\ & {- \Sigma_{i = 1}^m \log{{\left({1 + \gamma {{{X_i} - \mu } \over \sigma }} \right)}^{{-1}\big/\gamma}}}\\ \end{aligned},$$

(12)

under the condition $1 + \gamma \frac{{X_{i} - \mu }}{\sigma } > 0$. The MLE estimator $(\hat{\sigma },\hat{\gamma },\hat{\mu })$ for $(\sigma ,\gamma ,\mu )$ is obtained by maximizing (12).

5.2 PWM Estimator

As described in [9], the PWM of a random variable $X$ with distribution function $F\left( X \right) = P(X \le x)$ are the quantities

$$ M_{p,r,s} = {\text{E}}\left[ {X^{p} \left( {F\left( {\text{X}} \right)} \right)^{r} \left( {1 - F\left( {\text{X}} \right)} \right)^{s} } \right]\!, $$

(13)

for real $p$, $r$ and $s$ values. For the GEV distribution, [10] shows that ${\text{E}}\left[ {X \left( {F\left( {\text{X}} \right)} \right)^{r} } \right]$ can be written as

$$ M_{1,r,0} = \frac{1}{r + 1} \left\{ {\mu - \frac{\sigma }{\gamma } \left[ {1 - \left( {r + 1} \right)^{\gamma } \Gamma \left( {1 - \gamma } \right)} \right]} \right\}\!, $$

(14)

with $\gamma < 1$ and $\gamma \ne 0$. The PMW estimators $(\hat{\sigma },\hat{\gamma },\hat{\mu })$ of the Generalized Extreme Value distribution parameters $(\sigma ,\gamma ,\mu )$ may be computed through the following system of equations

$$ \left\{ {\begin{array}{*{20}c} {M_{1,0,0} = \mu - \frac{\sigma }{\gamma } (1 -\Gamma (1 - \gamma ))} \\ {2M_{1,1,0} - M_{1,0,0} = \frac{\sigma }{\gamma }\Gamma \left( {1 - \gamma } \right) (2^{\gamma } - 1)} \\ {\frac{{3M_{1,2,0} - M_{1,0,0} }}{{2M_{1,1,0} - M_{1,0,0} }} = \frac{{3^{\gamma } - 1}}{{2^{\gamma } - 1}}} \\ \end{array} } \right.\!\!\!, $$

(15)

in which $M_{1,r,0}$ is replaced by the unbiased estimator proposed in [11]

$$ \hat{M}_{1,r,0} = \frac{1}{m} \mathop \sum \limits_{j = 1}^{m} \left( {\mathop \prod \limits_{l = 1}^{r} \frac{j - l}{m - l}} \right) X_{j,m} . $$

(16)

5.3 Simulation Results

Figure 3 presents the simulation results obtained for the same scenario adopted in Fig. 2. The “Simulation” curve represents the CDF obtained with the entire set of samples ($3 \times 10^{6}$ samples). To apply the MLE and the PWM estimators in real-time we have considered a sample set $\chi$ of length $m = 100$ samples. The estimators were computed for 20 different sets of samples, thus 20 different CDFs were computed (one per set). The CDF presented in Fig. 3 is the average of the 20 CDFs computed for each sample set. All of the algorithms to find the estimators were solved by using the MATLAB.

Fig. 3.

Simulation results obtained with the MLE and PWM estimators.

Regarding the accuracy of the proposed estimators, both MLE and PWM present high accuracy. As a final remark, the results presented in Fig. 3 validate the proposed estimation methodologies, being the PWM estimator more adequate for the real-time estimation due to its higher accuracy. Finally, we highlight that approximate results were observed for smaller sample set sizes using the PWM estimator, and similar results may be achieved using only $m = 10$ samples per sample set, which is a remarkable low number of samples. The results are not show in the paper due to lack of space.

6 Conclusions

In this work we consider an ad hoc mobile network where the nodes move in accordance with the Random Waypoint mobility model. Assuming a time-varying wireless channel due to slow and fast fading and, considering the dynamic path loss due to the mobility of the nodes, we start by characterizing the interference distribution caused to a receiver by the mobile interferers located in a ring. The simulation results confirmed that the distribution of the aggregated interference may be accurately approximated by a Generalized Extreme Value distribution. Based on the interference distribution, two different methodologies (MLE and PWM) were assessed to estimate the interference in real-time. The accuracy of the results achieved with the proposed methodologies show that they may used as an effective tool of interference estimation in future wireless communication systems. Moreover, the low number of required samples constitutes one of the advantages of the proposed PWM estimator, even when the samples are highly correlated.