Keywords

1 Introduction

The Virtual Reference Feedback Tuning (VRFT) technique for data-driven controllers has been proposed and applied in [1] to Single Input-Single Output (SISO) systems, in [2] to Multi Input-Multi Output (MIMO) systems, and next extended in [3, 4] to nonlinear systems. The main feature of VRFT, as that of all data-driven controller tuning techniques, consists in collecting the input/output (I/O) data of an unknown open-loop process to compute the controller parameters. A shortcoming of this technique is that it does not guarantee the control system (CS) stability.

The main features of Model-Free Adaptive Control (MFAC) algorithms are [5, 6]: only the online I/O data of the process is used, and the CS stability is guaranteed through reset conditions imposed to the Pseudo-Partial-Derivatives (PPD) matrix. As pointed out in [7], the MFAC algorithm applied to TRAS acts as a pure integrator when the PPD matrix is almost constant during adaptation revealing an insufficient parameterization of the controller.

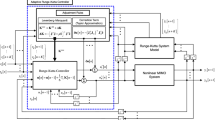
Given that the MFAC and VRFT have complementary features, this paper proposes a new data-driven control approach that combines these data-driven techniques resulting in new mixed data-driven algorithms. The mixed VRFT-MFAC algorithm has been applied to a class of nonlinear SISO systems in [7]. The mixed approach aims to control the azimuth and pitch motions of a Cyber-Physical System (CPS) represented by Twin Rotor Aerodynamic System (TRAS) system. Our mixed data-driven algorithm is efficient versus the current specialized literature [1–6] in finding the optimal parameters of MFAC algorithms as it has only eight parameters in the MIMO setting.

The paper is organized as follows: the relation to CPSs is submitted in the next section, the mixed MFAC-VFRT approach and algorithm are presented in Sect. 3, the 4th section offers the experimental validation on the TRAS laboratory equipment, and the conclusions are drawn in Sect. 5.

2 Relation to Cyber-Physical Systems

The nonlinear state-space model that describes the MIMO TRAS process is specified as follows in [8], and the variables are defined in [9]:

$$ \begin{aligned} & \dot{\varOmega }_{h} = [l{}_{t}F_{h} (\omega_{t} )\cos \alpha_{v} + \varOmega_{h} f_{h} + u_{2} k_{vh} ]/J_{h} , \\ & \dot{\varOmega }_{v} = \{ l_{m} F_{v} (\omega_{m} ) + \varOmega_{v} f_{v} + g[(A - B)\cos \alpha_{v} - C\sin \alpha_{v} ] \\ & \qquad\; - (\varOmega_{h}^{2} /2)(A + B + C)\sin 2\alpha_{v} \} /J_{v} , \\ & \dot{\alpha }_{h} = \varOmega_{h} ,\,\,\dot{\alpha }_{v} = \varOmega_{v} ,\,\,\dot{\omega }_{h} = (u_{1} - \omega_{h} /k_{Hh} )/I_{h} ,\,\,\dot{\omega }_{v} = (u_{2} - \omega_{v} /k_{Hv} )/I_{v} , \\ & y_{1} = \alpha_{h} ,\,y_{2} = \alpha_{v} . \\ \end{aligned} $$
(1)

The relation to CPSs is threefold from both the process and the controller points of view. First, Eq. (1) shows that TRAS is a nonlinear MIMO mechatronics process, its complexity associated with the inclusion of communication, electronics, hardware and software makes it a representative example of CPS. Second, the digital control algorithms are offered for this process, the controllers are implemented on a PC which communicates with the process by means of an adequate interface. Third, the mix of two data-driven approaches (namely, MFAC and VRFT) is advantageous as the process model is not needed in the controller tuning. This is especially important in case of CPSs as our approach outperforms the traditional model-based approaches that are strongly dependent on the process model, and accurate models are extremely difficult to obtain for CPSs.

3 Mixed MFAC-VRFT Control Approach

The control law and estimation mechanism specific to MFAC algorithms are expressed in the state-space form

$$ {{\begin{aligned} & {\mathbf{u}}(k) = {\mathbf{u}}(k - 1) + \frac{{\uprho {\hat{\mathbf{\varPhi }}}^{T} (k)[{\mathbf{y}}^{*} (k + 1) - {\mathbf{y}}(k)]}}{{\uplambda + ||{\hat{\mathbf{\varPhi }}}({\boldsymbol{k}})||^{2} }}, \\ & {\hat{\mathbf{\varPhi }}}({\boldsymbol{k}}) = {\hat{\mathbf{\varPhi }}}(k - 1) + \frac{{\upeta[\Delta {\mathbf{y}}(k) - {\hat{\mathbf{\Phi }}}(k - 1)({\mathbf{u}}(k - 1) - {\mathbf{u}}(k - 2))]({\mathbf{u}}^{T} (k - 1) - {\mathbf{u}}^{T} (k - 2))}}{{\upmu + ||{\mathbf{u}}(k - 1) - {\mathbf{u}}(k - 2)||^{2} }}, \\ \end{aligned}}} $$
(2)

where \( {\mathbf{y}}^{ * } (k + 1) = [\begin{array}{*{20}c} {y_{1}^{*} (k + 1)} & {y_{2}^{*} (k + 1)} \\ \end{array} ]^{T} \) is the tracking reference input vector, \( {\mathbf{y}}(k) = [\begin{array}{*{20}c} {y_{1} (k)} & {y_{2} (k)} \\ \end{array} ]^{T} \in {\mathbf{R}}^{2 \times 1} \) is the controlled output vector, \( {\mathbf{u}}(k) = [\begin{array}{*{20}c} {u_{1} (k)} & {u_{2} (k)} \\ \end{array} ]^{T} \in {\mathbf{R}}^{2 \times 1} \) is the control signal vector, \( T \) indicates matrix transposition, \( {\hat{\mathbf{\varPhi }}}(k) \) is the estimated PPD matrix, \( 0 < \upeta < 1 \) is the first step size constant, \( \upmu > 0 \) is a weighting factor parameter, \( \uprho > 0 \) is the second step size constant. \( \lambda \ge 0 \) in (2) is a weighting parameter that appears in the following optimization problem whose solving is the objective of MFAC:

$$ \begin{aligned} & {\mathbf{u}}^{ * } (k) = \arg \mathop {\hbox{min} }\limits_{{{\mathbf{u}}(k)}} J_{MFAC} ({\mathbf{u}}(k)), \\ & J_{MFAC} ({\mathbf{u}}(k)) = ||{\mathbf{y}}^{ * } (k + 1) - {\mathbf{y}}(k + 1)||^{2} + \lambda ||\varDelta {\mathbf{u}}(k)||^{2} . \\ \end{aligned} $$
(3)

An equivalent model to (2) is

$$ \begin{aligned} & {\mathbf{u}}(k) = {\mathbf{g}}({\hat{\mathbf{\varPhi }}}(k),{\mathbf{u}}(k - 1),{\mathbf{y}}^{*} (k + 1),{\mathbf{y}}(k),{\varvec{\uptheta}}), \\ & {\hat{\mathbf{\varPhi }}}({\boldsymbol{k}}) = {\mathbf{h}}({\hat{\mathbf{\varPhi }}}(k - 1),{\mathbf{u}}(k - 1),{\mathbf{u}}(k - 2),{\mathbf{y}}(k),{\mathbf{y}}(k - 1),{\varvec{\uptheta}}), \\ \end{aligned} $$
(4)

where \( {\mathbf{g}},{\mathbf{h}} \in {\mathbf{R}}^{2 \times 1} \) are nonlinear functions of their arguments, \( {\varvec{\uptheta}} = [\uprho \,\,\,\upeta \,\,\,\uplambda \,\,\,\upmu ]^{T} \) is the parameter vector. Introducing the additional state vector \( {\mathbf{z}}(k) = {\mathbf{u}}(k - 1) \) and replacing \( {\hat{\mathbf{\varPhi }}}({\boldsymbol{k}}) \) from the second equation in (4) in the first equation in (4), the state-space model (4) is transformed into

$$ {\varvec{\upchi}}(k) = {\mathbf{F}}({\varvec{\upchi}}(k - 1)\,,\,{\mathbf{U}}(k),\,{\varvec{\uptheta}}), $$
(5)

with the extended state vector \( {\varvec{\upchi}}(k) = [{\mathbf{u}}(k)\,\,\,{\mathbf{z}}(k)\,\,\,{\hat{\mathbf{\varPhi }}}(k)]^{T} \), the extended control signal vector \( {\mathbf{U}}(k) = [{\mathbf{y}}^{*} (k + 1)\,\,\,{\mathbf{y}}(k)\,\,\,{\mathbf{y}}(k - 1)]^{T} \), and

$$ {{{\mathbf{F}}({\varvec{\upchi}}(k - 1)\,,\,{\mathbf{U}}(k),\,{\varvec{\uptheta}}) = \left[ {\begin{array}{*{20}c} {{\mathbf{g}}({\hat{\mathbf{\varPhi }}}({\boldsymbol{k}} - 1),{\mathbf{u}}(k - 1),{\mathbf{z}}(k - 1),{\mathbf{y}}(k),{\mathbf{y}}(k - 1),{\mathbf{y}}^{*} (k + 1),{\varvec{\uptheta}})} \\ {{\mathbf{u}}(k - 1)} \\ {{\mathbf{h}}({\hat{\mathbf{\varPhi }}}({\boldsymbol{k}} - 1),{\mathbf{z}}(k),{\mathbf{z}}(k - 1),{\mathbf{y}}(k),{\mathbf{y}}(k - 1),{\varvec{\uptheta}})} \\ \end{array} } \right].}} $$
(6)

Starting with the initial conditions \( {\hat{\mathbf{\varPhi }}}(1),{\mathbf{u}}(1),{\mathbf{z}}(1) = {\mathbf{u}}(0) \), \( {\mathbf{u}}(k) \) is expressed recurrently as

$$ {\begin{aligned} {\hat{\mathbf{\varPhi }}}(2) & = {\mathbf{h}}({\hat{\mathbf{\varPhi }}}(1),{\mathbf{u}}(1),{\mathbf{u}}(0),{\mathbf{y}}(2),{\mathbf{y}}(1),{\varvec{\uptheta}}), \\ {\mathbf{u}}(2) & = {\mathbf{g}}({\hat{\mathbf{\varPhi }}}(1),{\mathbf{u}}(1),{\mathbf{u}}(0),{\mathbf{y}}(2),{\mathbf{y}}(1),{\mathbf{y}}^{*} (3),{\varvec{\uptheta}}), \\ {\mathbf{u}}(3) & = {\mathbf{g}}({\hat{\mathbf{\varPhi }}}(2),{\mathbf{u}}(2),{\mathbf{u}}(1),{\mathbf{y}}(3),{\mathbf{y}}(2),{\mathbf{y}}^{*} (4),{\varvec{\uptheta}}) \\ & = {\mathbf{g}}({\mathbf{h}}({\hat{\mathbf{\varPhi }}}(1),{\mathbf{u}}(1),{\mathbf{u}}(0),{\mathbf{y}}(2),{\mathbf{y}}(1),{\varvec{\uptheta}}),{\mathbf{g}}({\hat{\mathbf{\varPhi }}}(1),{\mathbf{u}}(1),{\mathbf{u}}(0),{\mathbf{y}}(2),{\mathbf{y}}(1),{\mathbf{y}}^{*} (3),{\varvec{\uptheta}}), \\ & \qquad\; {\mathbf{u}}(1),{\mathbf{y}}(3),{\mathbf{y}}(2),{\mathbf{y}}^{*} (4),{\varvec{\uptheta}}) \\ & = {\mathbf{g}}({\hat{\mathbf{\varPhi }}}(1),{\mathbf{u}}(1),{\mathbf{u}}(0),{\mathbf{y}}(3),{\mathbf{y}}(2),{\mathbf{y}}(1),{\mathbf{y}}^{*} (3),{\mathbf{y}}^{*} (4),{\varvec{\uptheta}}), \\ \ldots \\ {\mathbf{u}}(k) & = {\mathbf{g}}({\hat{\mathbf{\varPhi }}}(1),{\mathbf{u}}(1),{\mathbf{u}}(0),{\mathbf{y}}(k),{\mathbf{y}}(k - 1), \ldots ,{\mathbf{y}}(2),{\mathbf{y}}(1){\mathbf{,y}}^{*} (k + 1),{\mathbf{y}}^{*} (k), \ldots ,{\mathbf{y}}^{*} (4), \\ & \qquad\; {\mathbf{y}}^{*} (3),{\varvec{\uptheta}}) \\ & = {\mathbf{g}}({\hat{\mathbf{\varPhi }}}(1),{\mathbf{u}}(1),{\mathbf{u}}(0),{\mathbf{y}}^{*} (k + 1) - {\mathbf{y}}(k),{\mathbf{y}}^{*} (k) - {\mathbf{y}}(k - 1), \ldots ,{\mathbf{y}}^{*} (3) - {\mathbf{y}}(2),{\mathbf{y}}(1),{\varvec{\uptheta}}). \\ \end{aligned}} $$
(7)

Using the notation \( {\mathbf{e}}(k) = {\mathbf{y}}^{*} (k + 1) - {\mathbf{y}}(k) \) for the tracking error, \( {\mathbf{u}}(k) \) in (7) can be considered to emerge from the I/O nonlinear recurrent controller

$$ {\mathbf{u}}_{{{\varvec{\uptheta}}_{e} }} (k) = C_{{{\varvec{\uptheta}}_{e} }} ({\varvec{\uptheta}}_{e} ,{\mathbf{u}}(k - 1), \ldots ,{\mathbf{u}}(k - n_{uc} ),{\mathbf{e}}(k), \ldots ,{\mathbf{e}}(k - n_{ec} )), $$
(8)

with \( {\varvec{\uptheta}}_{e} = \{ {\hat{\mathbf{\varPhi }}}(1),\;{\varvec{\uptheta}}^{T} \} \). Using the controller model (8), the model reference objective function (o.f.) specific to nonlinear VRFT is [10].

$$ J_{MR} ({\varvec{\uptheta}}) = \sum\limits_{k = 1}^{N} {\left\| {{\mathbf{y}}_{{\varvec{\uptheta}}} (k) - {\mathbf{y}}^{d} (k)} \right\|^{2} } , $$
(9)

where \( {\mathbf{y}}_{{\varvec{\uptheta}}} (k + 1) = {\mathbf{f}}({\mathbf{y}}(k), \ldots ,{\mathbf{y}}(k - n_{y} ),{\mathbf{u}}_{{\varvec{\uptheta}}} (k), \ldots ,{\mathbf{u}}_{{\varvec{\uptheta}}} (k - n_{u} )) \) is the nonlinear process model (with \( {\mathbf{y}}_{{\varvec{\uptheta}}} (k + 1) \) – the process output), \( uc \) and \( ec \) are the known orders of the fixed structure controller parameterized by the vector \( {\varvec{\uptheta}} \), \( {\mathbf{r}}(k) \) is the reference input to the closed-loop CS, \( {\mathbf{y}}^{d} (k) = {\mathbf{m}}({\mathbf{y}}^{d} (k - 1), \ldots ,{\mathbf{y}}^{d} (k - n_{{{\mathbf{y}}m}} ),{\mathbf{r}}(k - 1), \ldots ,{\mathbf{r}}(k - n_{{{\mathbf{r}}m}} )) \) is the output of the user-selected nonlinear reference model \( {\mathbf{m}} \) of orders \( {\mathbf{y}}m \) and \( {\mathbf{r}}m \) if the input is set as \( {\mathbf{r}}(k) \). Herein, \( {\mathbf{m}} \) is assumed to be invertible.

Assuming that an I/O data pair \( \{ {\mathbf{u}}(k),{\mathbf{y}}(k)\} \), \( k = 0 \ldots N \), is available form an open loop experiment on the stable process. Then a virtual reference input \( {\bar{\mathbf{r}}}(k) \) is calculated as \( {\bar{\mathbf{r}}}(k) = {\mathbf{m}}^{ - 1} ({\mathbf{y}}(k)) \) such that the reference model output and the closed-loop CS output have similar trajectories. By abuse of notation, \( {\mathbf{m}}^{ - 1} ({\mathbf{y}}(k)) \) results in \( {\bar{\mathbf{r}}}(k) \), which, set as input to \( {\mathbf{m}} \), gives \( {\mathbf{y}}(k) \). The virtual reference tracking error is calculated as \( {\bar{\mathbf{e}}}(k) = {\bar{\mathbf{r}}}(k) - {\mathbf{y}}(k) \). The controller that achieves \( {\mathbf{u}}(k) \) caused by \( {\bar{\mathbf{e}}}(k) \) is the one that carries out reference model tracking, and the parameters of this controller are calculated by minimizing the o.f. [10]

$$ J_{VRFT} ({\varvec{\uptheta}}) = \frac{1}{N}\sum\limits_{t = 1}^{N} {\left\| {{\mathbf{C}}_{{\varvec{\uptheta}}} ({\varvec{\uptheta}},{\bar{\mathbf{e}}}(k)) - {\mathbf{u}}(k)} \right\|^{2} } . $$
(10)

As shown in [10], MIMO VRFT does not require any time-varying filter to make \( J_{MR} ({\varvec{\uptheta}}) \) and \( J_{VRFT} ({\varvec{\uptheta}}) \) approximately equal, as is usually the case in classical VRFT. The two o.f.s in (9) and (10) can be made approximately equal for a rich parameterization of the controller which can be, for example, a neural network [10, 11].

Our mixed data-driven control approach is based on considering that \( {\mathbf{r}}(k) \) specific to VRFT equals \( {\mathbf{y}}^{*} (k + 1) \) specific to MFAC:

$$ {\mathbf{r}}(k) = {\mathbf{y}}^{*} (k + 1). $$
(11)

Therefore, the MFAC algorithm structure is included in a closed-loop CS. Figure 1 shows the feedback control structure with the MFAC algorithm tuned by VRFT.

Fig. 1.
figure 1figure 1

Structure of mixed MFAC-VRFT CS

Full size image

4 Experimental Results

Two tuning approaches are proposed to highlight the performance of the mixed VRFT-MFAC control approach, an indirect one in which the VRFT framework is used and the o.f. in (10) is minimized, and a direct one in which a process model is used and a metaheuristic Gravitational Search Algorithm (GSA) optimizer [12–15] minimizes the following o.f. in the MIMO setting:

$$ {\varvec{\uptau}}^{*} = \arg \;\mathop {\hbox{min} }\limits_{{\varvec{\uptau}}} J({\varvec{\upupsilon}}),\,\,\,J_{\varepsilon } ({\varvec{\uptau}}) = \frac{1}{N}\sum\limits_{k = 1}^{N} {(({\mathbf{y}}_{1}^{*} (k,{\varvec{\uptau}}) - {\mathbf{y}}_{1} (k,{\varvec{\uptau}}))^{2} + ({\mathbf{y}}_{2}^{*} (k,{\varvec{\uptau}}) - {\mathbf{y}}_{2} (k,{\varvec{\uptau}}))^{2} )} , $$
(12)

where \( {\varvec{\uptau}} = [\hat{\varPhi }_{11} (1)\,\,\,\hat{\varPhi }_{12} (1)\,\,\,\hat{\varPhi }_{21} (1)\,\,\,\hat{\varPhi }_{22} (1) \, \rho \, \eta \, \lambda \, \mu ]^{T} \) is the parameter vector of VRFT-MFAC and MFAC algorithms and \( {\varvec{\uptau}}^{*} \) is the optimal value of \( {\varvec{\uptau}} \).

The MFAC objective [5] is to solve the optimization problem in (3).

Use is made in MFAC of the PPD matrix \( {\varvec{\Phi}}(k) = [\phi_{ij} (k)]_{{i,j \in \{ 1,2\} }} \), \( ||{\varvec{\Phi}}(k)|| \le b \), which appears in the compact form dynamic linearization (CFDL) MFAC process model [5]

$$ \varDelta {\mathbf{y}}(k + 1) = {\varvec{\Phi}}(k)\varDelta {\mathbf{u}}(k), $$
(13)

this matrix should be diagonally dominant and fulfill

$$ |\phi_{ij} (k)| \le b_{1} , \, b_{2} \le |\phi_{ii} (k)| \le a \, b_{2} , \, i,j \in \{ 1,2\} , \, i \ne j, \, a \ge 1, \, b_{2} > b_{1} (2a + 1), $$
(14)

The digital reference model is

$$ {\mathbf{m}}(z) = \left( {\begin{array}{*{20}c} {\frac{{0.00115z^{ - 1} + 0.00115z^{ - 2} }}{{1 - 1.997z^{ - 1} + 0.999z^{ - 2} }}} & 0 \\ 0 & {\frac{{0.00092z^{ - 1} + 0.00091z^{ - 2} }}{{1 - 1.947z^{ - 1} + 0.949z^{ - 2} }}} \\ \end{array} } \right), $$
(15)

which is the discretized version of a diagonal transfer matrix of second-order normalized t.f.s.

The values of the initial parameters of the mixed VRFT-MFAC algorithm obtained by a GSA that minimizes the o.f. given in (10) are

$$ {\varvec{\uptau}} = [746.99\,\,\,0.064\,\,\,0.048\,\,\,1757\, \, 4 6. 4 2 { }\,0. 1 0 1 { }\, \, 7 0. 4 6\, \, \,9 0 7. 6]^{T} , $$
(16)

where, according to (14), the lower and the upper bounds of the PPD matrix were set as \( \left( {\begin{array}{*{20}c} {373.49} & 0 \\ 0 & {878.5} \\ \end{array} } \right) \) and \( \left( {\begin{array}{*{20}c} {1120.49} & {0.129} \\ {0.097} & {2635.51} \\ \end{array} } \right) \). The initial parameters of the MFAC algorithm were also obtained by a GSA that minimizes the o.f. given in (12):

$$ {\varvec{\uptau}} = [835\,\,\,0.1\,\,\,0.1\,\,\,1838\, \, 4 9. 3 4 { }\,0. 7 { }\,{ 6} . 5 4 4\, \, \,0. 874]^{T} , $$
(17)

where the lower and the upper bounds of the PPD matrix were set as \( \left( {\begin{array}{*{20}c} {417.5} & 0 \\ 0 & {919} \\ \end{array} } \right) \) and \( \left( {\begin{array}{*{20}c} {1252.5} & {0.2} \\ {0.2} & {2757} \\ \end{array} } \right) \). Different bounds were imposed to the PPD matrices specific to the two algorithms such the matrix elements can vary according to [5, 6] and the stability is fulfilled.

One of the aims of this paper is to analyze if the performance indices of the CS with mixed VRFT-MFAC algorithm is similar to that of the with MFAC algorithm. The CS performance is assessed through ten experimental trials concerning \( J_{\varepsilon } \). The averages and variances of these o.f.s are next computed in order to highlight more accurately the algorithms and CS performance.

The values of \( J_{\varepsilon } \) obtained by the application of both data-driven algorithms are presented in Table 1. A sample of experimental results is exemplified in Fig. 2.

Table 1. The values of the o.f. in the MIMO experimental scenario
Full size table
Fig. 2.
figure 2figure 2

Experimental results expressed as CS responses in the MIMO scenario: control signals \( u_{1} \) and \( u_{2} \), process outputs \( y_{1} \) and \( y_{2} \) and references trajectories \( y_{1}^{*} \) and \( y_{2}^{*} \)

Full size image

5 Conclusions

This paper has given a new MIMO model-free data-driven controller tuning approach, referred as mixed VRFT-MFAC approach, which optimally tunes all parameters of MFAC algorithms by VRFT. The mixed VRFT-MFAC algorithm that results from this approach has been implemented on the nonlinear TRAS laboratory equipment.

The comparison with the classical MFAC algorithm (Table 1 and Fig. 2) shows, in correlation with [16, 17], the small differences between what VRFT-MFAC and MFAC exhibit. Therefore, the mixed VRFT-MFAC approach is a time-saving controller tuning solution with similar performance to MFAC.

The proposed approach is useful when controlling processes whose identification is difficult or impossible, and such processes are specific to CPSs. Further research will be focused on the constraints concerning the reference model choice. The constraints related to the optimization problems come from the special features of CPS processes.