Keywords

1 Introduction

Developing telecommunication services are successfully provided via IP-based Multimedia Subsystem (IMS), where Session Initiation Protocol (SIP) is the main signaling protocol [1]. Signaling traffic load is auxiliary for communication nodes and is used for providing communications services to users. Signaling messages have so-called life time. When life time is over, information becomes not actual, signaling messages are retransmitted and overload the SIP server that processes them. Among the other problems with Session Initiation Protocol the overloading problem was stated by IETF in [2], and solution requirements that address the problems were formulated in [3]. Providing telecommunication services of required quality results in necessity of detailed research of communication system structure, statistic data analysis, implementation of processing algorithm for different types of signaling messages in order to increase number of successfully initiated sessions and decrease of service and sojourn time at a SIP server [6]. Many papers from the IETF documents [3–5] to a number of scientific papers [11–16, 18–24] were devoted to developing and investigating mechanisms of SIP-server overload control. For example, signaling messages service process was presented as asymmetric polling system [9], as queueing model with threshold control [10]. Sometimes you can see research even with unreliable servers [17].

In this paper were chosen the following parameters for the investigation: average queue length and average waiting time. The first one enables estimation of SIP server’s buffer capacity during the busy hour, the second when summed with service time enables estimation of SIP server sojourn time and is comparable to the message life time.

Process of signaling messages arrival and processing at a SIP server is performed via a single-server queue with batch arrivals and vacations. The vacation models the time interval when server processes messages that differ from signaling ones. In a model the batch arrival of customers corresponds to the simultaneous requests of the group of online subscribers.

In [6–8] there is an estimation of average value of queue length and average waiting time for general distribution of batch size. In [8] the analysis for the four batch size distribution functions has been done: Zipf, geometric, logarithmic and uniform distribution. In [8] a statistical dependence of investigating parameters on batch size distribution in case of Poisson process has been analyzed. In contrast with the papers where an investigation was performed only for geometrical distribution, in [8] it is recommended to use a uniform distribution of batch size that essentially simplifies formulas for calculations. In this paper an approach to performance measures analysis is proposed, sensitivity of model parameters to batch size distribution was estimated.

Distribution function variation was evaluated in [8] under different norms. Those with highest reliability of estimated statistical dependence were chosen. It turned out that analysis of numeric evaluation of SIP server performance parameters sensitivity to batch size distribution variation can be carried out with high reliability (0.99).

Since only sampling distribution functions of parameters are available for preliminary analysis, so we want to evaluate model parameters with statistical fluctuation of sampling distribution function when the distribution is not converge to any general population because of non-stationary behavior. We denote, that the batch size is a measured on practice, whereas average waiting time and average queue length depend on messages service time and processor vacation time. Distribution functions of the last two parameters are assumed to be known, because they depend on the SIP server hardware implementation. However, confidence interval for average queue length may not be got from corresponding empirical distribution, because we do not know this distribution function. We can evaluate these parameters by means of the simplified models only. In [8] the sensitivity analysis for one of models was carried out. Analysis was later applied to empirical distribution function of batch size.

2 SIP Server Model as a Queue with Batch Arrivals and Vacations

A mathematical model of signaling messages processing at a SIP server is investigated as a queuing system with batch arrivals and vacations. According to Basharin-Kendall notation this system is denoted as . Let suppose that a batch of customers arrives according to Poisson process with rate \(\lambda \). Customer service time is a random variable with a distribution function B(t), where \(b_{1} \) is the mean value and \(b_{2} \) is the finite second moment. If there are no customers in the queue, the server goes for a vacation. The vacation time is a random variable with a distribution function V(t) with finite first and second moments \(v_{1} \) and \(v_{2} \).

Let f(k) be probability that batch size is equal to \(k\ge 1\). We denote the corresponding distribution function F(k). For the queuing system with vacations we can find average queue length and average waiting time depending on offered load \(\rho \) which is estimated as follows:

$$\begin{aligned} \rho =\lambda b_{1} l^{(1)} , \end{aligned}$$
(1)

where \(l^{(1)}\) is average batch size with distribution function F(k).

In [6] a generating function was obtained for the queue length distribution for a single server model with vacations. The result is expressed as follows:

$$\begin{aligned} P(z)=\frac{1-\rho }{\lambda v_{1} } \cdot \frac{1-z}{1-L(z)} \cdot \frac{1-\phi (\lambda ,z)}{\beta (\lambda ,z)-z} , \end{aligned}$$
(2)

where L(z) is a generating function for batch size with the distribution function F(k): \(L(z)=\sum \limits _{k=0}^{\infty }f(k)z^{k} \). Other functions mentioned in (2) are expressed with the following equations: \(v_{1} =\int \limits _{0}^{\infty }t\,dV(t) \, \), \(\phi (\lambda ,z)=\int \limits _{0}^{\infty }e^{-\lambda t\left( 1-L(z)\right) } \, dV(t) \, \), and \(\beta (\lambda ,z)=\int \limits _{0}^{\infty }e^{-\lambda t\left( 1-L(z)\right) } \, dB(t) \). According to [8] average queue length depending on load \(\rho \) is obtained by the generating function (2) as follows:

$$\begin{aligned} N=\mathop {\lim }\limits _{z\rightarrow 1} P'(z)=\frac{v_{2} }{2v_{1} b_{1} } \rho +\frac{l^{(2)} -l^{(1)} }{2l^{(1)} } \frac{\rho }{1-\rho } +\frac{b_{2} }{2b_{1}^{2} } \frac{\rho ^{2} }{1-\rho } . \end{aligned}$$
(3)

Taking into account the notation \(v_{s} =\int \limits _{0}^{\infty }t^{s} dV(t) \), \(b_{s} =\int \limits _{0}^{\infty }t^{s} dB(t)\) and

\(l^{(s)} =\sum \limits _{k}k^{s} f(k) \), \(s=1;\, 2\), the average waiting time is obtained as follows:

$$\begin{aligned} \tau =\frac{Nb_{1} }{\rho } =\frac{v_{2} }{2v_{1} } +\frac{l^{(2)} -l^{(1)} }{2l^{(1)} } \frac{b_{1} }{1-\rho } +\frac{b_{2} }{2b_{1} } \frac{\rho }{1-\rho } . \end{aligned}$$
(4)
Fig. 1.
figure 1

Average queue length depending on load.

Full size image
Fig. 2.
figure 2

Average waiting time depending on load.

Full size image

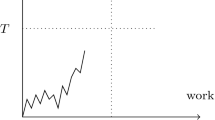
You can see the average queue length (Fig. 1) and average waiting time (Fig. 2) for 4 batch size distributions for exponential service time and vacation time with the following initial data \( b_{1}= 15\) ms – average service time, \( v_{1}= 15l_{1}\) ms – average vacation time, \(l_{1}=3\) – average batch size. This is the starting point of the reseaches. The plots (Figs. 1 and 2) have similar behavior. We investigate the sensitivity of the model parameters to probability variation of batch size.

3 Sensitivity of the Model Parameters to Probability Variation

As a base of our analysis we use 4 batch size distributions with following distribution functions (Table 1), where \(f_{i} (k)\) is the probability, that batch size is equal k. We assume, that maximum batch size is equal to 8. The distribution functions can be found by formula \(F_{i} (n)=\sum _{k=1}^{n}f_{i} (k)\).

Table 1. Distribution functions
Full size table

We consider 5 types of norms and define the distance between two DFs by the formulas from the Table 2, where the distance from i to j distribution functions is \(\rho _{ij}^{norm}\). The first step of our investigation was to compare distances between DFs in several norms.

Table 2. Definition of distance in norms
Full size table
Table 3. Distances between batch size distributions
Full size table

Table 3 shows the distances between batch size DFs in considered norms. For example, the first row shows the distance between Logarithmic and Geometric batch size distributions, the last row – the distance between Zipf and Uniform distributions. Statistics show that the distances are dependent from each other. So, for the next step of our investigation we can use any appropriate norm.

Let find out how to change the values N and \(\tau \) in formulas (3)–(4), if probability variation of f(k) is low. Let a new distribution can be expressed as \(\tilde{f}(k)=f(k)+\varepsilon (k)f(k)\), moreover, under the same norming the equality \(\sum \limits _{k}\varepsilon (k)f(k) =0\) is fulfilled. Let introduce the variable \( E=\mathop {\sup }\limits _{k} \left| \varepsilon (k)\right| \). Then we get the following estimation of distance between distributions in L1 norm:

$$\begin{aligned} \varepsilon =\left\| f-\tilde{f}\right\| _{L1} =\sum \limits _{k}\left| f(k)-\tilde{f}(k)\right| =\sum \limits _{k}\left| \varepsilon (k)\right| f(k) \le E. \end{aligned}$$
(5)

Let use (5) to get estimation of some differentiable function variation depending on average batch size in case \(E<<1\):

$$\begin{aligned} \begin{array}{l} \displaystyle {\left| \delta l^{(1)} \right| =\left| \sum _{k}k\left( f(k)-\tilde{f}(k)\right) \right| <\sum _{k}k\left| f(k)-\tilde{f}(k)\right| =\sum _{k}k\left| \varepsilon (k)\right| f(k) \le El^{(1)} ;} \\ {} \\ \displaystyle \, \, \, \,\, \, \, \,\, \, \, \,\, \, \, \, \, \, \,\, \, \, \,\, \, \, \,\, \, \, \, {\left| \delta u\left( l^{(1)} \right) \right| =\left| \frac{\partial u\left( l^{(1)} \right) }{\partial \left( l^{(1)} \right) } \right| \cdot \left| \delta l^{(1)} \right| \le Eu\left| \frac{\partial \ln u}{\partial \ln l} \right| \left| _{l=l^{(1)} } \right. +o\left( E\right) .} \end{array} \end{aligned}$$
(6)

Logarithmic derivative of function with respect to parameter’s logarithm is called function sensitivity to parameter variation. Then, from (6) comes that variation of some function from the mean value, obtained due to distribution variation, at linear approximation on E does not exceed this function multiplied by the supremum of distribution density variation and by modulus of specified sensitivity. In our case estimations of average queue length (3) and average waiting time (4), that are linear for E, are expressed as follows:

$$\begin{aligned} \begin{array}{l} \displaystyle {\left| \delta N\right| \le \frac{E\rho }{2} \cdot \left| \frac{v_{2} }{v_{1} b_{1} } +\frac{l^{(2)} -l^{(1)} }{l^{(1)} } \frac{b_{1} }{\left( 1-\rho \right) ^{2} } +\frac{b_{2} }{b_{1}^{2} } \left( 2-\rho \right) \frac{\rho }{\left( 1-\rho \right) ^{2} } \right| ;} \\ {} \\ \displaystyle \, \, \,\, \, \, \,\, \, \, \,\, \, \, \, \, \, \,\, \, \, \,\, \, {\left| \delta \tau \right| \le \frac{E\rho }{2\left( 1-\rho \right) ^{2} } \cdot \left| \frac{l^{(2)} -l^{(1)} }{l^{(1)} } b_{1} +\frac{b_{2} }{b_{1} } \right| .} \end{array} \end{aligned}$$
(7)

However, theoretical estimations (7) do not possess adequate accuracy as they appear to be too excessive. Despite this fact they cannot be improved within of functions to be chosen for empirical distribution functions. Unimprovability comes out of existence of a variation when \(\varepsilon (k)=\left\{ 0;\pm E\right\} \). Inadequacy of accuracy comes out of condition (5): as far as \(\varepsilon \le E\), then for heavily nonuniform distributions the variation norm in the form of is too crude estimate, since for such kind of distributions the distance between distributions can be significantly less than E. That is why in [4] an analysis of sensitivity of these parameters based on the numerical results for various functions f(k) was carried out. It was found out that four types of norms – L1 and C for F(k), L1 for f(k) and similar to them the forth norm that is a supplement for total area S to the unity of two densities – determine rather exactly the variation of values N and \(\tau \) under variation of densities.

Let us denote variation of f(k) by \(\delta f\), which is denominated in norm C for distribution function. We denote by \(\delta N(\rho )\) variation of average queue length and by \(\delta \tau (\rho )\) variation of average waiting time for a given value of load \(\rho \). Data analysis showed that under variation of uniform distribution, which determined on the interval from 1 to the maximum batch size (in our case maximum is equal to 8), there is a relationship between \(\delta N(\rho )\) and \(\delta f\), also \(\delta \tau (\rho )\) and \(\delta f\) with determination 0.99:

$$\begin{aligned} \begin{array}{l} \displaystyle {\, \, \, \left| \frac{\delta N(\rho )}{N(\rho )} \right| =0,2\left( 1-\ln \rho \right) \left( \delta f\right) ^{0,27} ;} \\ {} \\ \displaystyle \, \, \,\, {\left| \frac{\delta \tau (\rho )}{\tau (\rho )} \right| =\frac{0,106+0,041\ln \rho }{\rho } \left( \delta f\right) ^{0,27} ;} \\ {} \\ \displaystyle {\, \, \, \, \, \, \, \, \, \, \, \, \rho \in [0,1;\; 0,9].} \end{array} \end{aligned}$$
(8)

4 Algorithm for Average Queue Length Calculation

Practical application of the described method is the algorithm for average queue length calculation.

Step 1. Choose the basic predicted batch size distribution of f(k) on the interval \(1\le k\le M\), for example, uniform distribution: \(f(k)=1/8\).

Step 2. Calculate the average queue length \(N_{0} \; \) for the basic distribution:

$$\begin{aligned} N_{0} =\frac{v_{2} }{2v_{1} b_{1} } \rho +\frac{M-1}{3} \frac{\rho }{1-\rho } +\frac{b_{2} }{2b_{1}^{2} } \frac{\rho ^{2} }{1-\rho } , \end{aligned}$$
(9)

For basic distribution function Eq. (3) is considered as null approximation.

Step 3. Get the empirical batch size distribution function F(k) from measurements. Let consider that empirical distribution, being investigated, is stationary, F(k) is its distribution function.

Step 4. Calculate the distance between empirical and uniform distributions:

$$\begin{aligned} \delta f=\mathop {\sup }\limits _{k} \left| F(k)-k/M\right| . \end{aligned}$$
(10)

Step 5. Substituting the result of (10) in (8) we get estimation of average queue length that corresponds to the following empirical distribution:

$$\begin{aligned} \begin{array}{l} {N/N_{0} \approx 1+0,2\left( 1-\ln \rho \right) \left( \delta f\right) ^{0,27} ,\, \, \rho \in [0,1;\; 0,9]} \\ {\, \, \, \, \, \, \, \, \quad } \end{array} \end{aligned}$$
(11)

Estimation for average waiting time variation is expressed in the same way.

Equation (11) is computationally much simpler than calculation of the generating function in accordance with (2), where L(z) is calculated through empirical distribution of F(k). That is, firstly, rather difficult and, secondly, leads to calculation errors that may exceed approximation inaccuracy for (11).

5 Average Queue Length for Geometric Batch Size Distribution

For example, let consider that an empirical distribution of \(f_{n} (k)\) is taken from a general population f(k) that has geometric distribution with a parameter q on the interval \(1\le k\le M\). That means \(f(k)=\frac{1-q}{1-q^{M} } q^{k-1} \).

We show you algorithm for average queue length calculation with geometric distribution function.

Step 1. Basic batch size distribution:

\(f(k)=1/8\), \(1\le k\le M\) - uniform distribution.

Step 2. Average queue length \(N_{0} \; \) for the uniform distribution:

$$\begin{aligned} N_{0} \left( \rho \right) ,\; \; \rho \in [0,1;\; 0,9].\end{aligned}$$

Step 3. Empirical batch size distribution is geometric distribution with following parameters: \(q=0,67\), \(M=8\) [8].

$$\begin{aligned} F(k)=\frac{1-q}{1-q^{M} } q^{k-1} ,\mathrm{\; \; }1\le k\le M.\end{aligned}$$

Step 4. Distance between empirical and basic distributions:

$$\begin{aligned}\delta f=0,35.\end{aligned}$$

Step 5. Estimation of average queue length:

$$\begin{aligned}N\approx 0,14\left( 1-\ln \rho \right) N_{0} (\rho ),\; \; \rho \in [0,1;\; 0,9].\end{aligned}$$

6 Conclusion

This paper presents the approach to estimation of the performance measures for SIP server model with batch arrivals and vacations depending on the batch size distribution. Investigation of this particular dependence was motivated by the fact that the batch size distribution is not known as a general population and, moreover, cannot be recognized as far as empirical evaluations of this population are non-stationary. That is why approximate evaluation methods, that are not associated with a specified functional class of mentioned distributions, are of great significance and actuality. Therefore, the method that considers coefficients of the model parameters sensitivity to adjustment of the distance between distribution functions seems to be efficient among nonparametric techniques. This method may be used for non-stationery distributions when non-stationary behavior is interpreted as definite variation of some basic distribution (for example, uniform). This approach enables to circumvent technical difficulty coming from absence of convergence theorem both for probability and the norm for random variables being investigated.

Proposed approach to evaluation of performance measures of a Session Initiation Protocol server model and given analysis of parameters sensitivity leads to recommendations for engineers to use simple formulas for preliminary evaluation of presence signaling messages service.