Variance-GGC Asset Price Models and Their Sensitivity Analysis

Abstract

This paper reviews the variance-gamma asset price model as well as its symmetric and non-symmetric extensions based on generalized gamma convolutions (GGC). In particular we compute the basic characteristics and decomposition of the variance-GGC model, and we consider its sensitivity analysis based on the approach of Kawai and Kohatsu-Higa in Appl Math Finance 17(4):301–321, 2010 [8].

1 Introduction

Lévy processes play an important role in the modeling of risky asset prices with jumps. In addition to the Black-Scholes model based on geometric Brownian motion, pure jump and jump-diffusion processes have been used by Cox and Ross [5] and Merton [13] for the modeling of asset prices. More recently, Brownian motions time-changed by non-decreasing Lévy processes (i.e. subordinators) have become popular, in particular the Normal Inverse Gaussian (NIG) model [1], the variance-gamma (VG) model [11, 12], and the CGMY/KoBol models [3, 4].

The normal inverse Gaussian (NIG) process [1] can constructed as a Brownian motion time-changed by a Lévy process with the inverse Gaussian distribution, whose marginal at time t is identical in law to the first hitting time of the positive level t by a drifted Brownian motion.

The variance-gamma process [11, 12] is built on the time change of a Brownian motion by a gamma process, and has been successful in modeling asset prices with jumps and in addressing the issue of slowly decreasing probability tails found in real market data.

The CGMY/KoBol models [3, 4] are extensions of the variance-gamma model by a more flexible choice of Lévy measures. However, this extension loses some nice properties of variance-gamma model, for example variance-gamma processes can be decomposed into the difference of two gamma processes, whereas this property does not hold in general in the CGMY/KoBol models.

In [6] the variance-gamma model has been extended into a symmetric variance-GGC model, based on generalized gamma convolutions (GGCs), see [2] for details and a driftless Brownian motion. In this paper we review this model and propose an extension to non-symmetric case using a drifted Brownian motion.

GGC random variables can be constructed by limits in distribution of sums of independent gamma random variables with varying shape parameters. As a result, the variance-GGC model allows for more flexibility than standard variance-gamma models, while retaining some of their properties. The skewness and kurtosis of variance-GGC processes can be computed in closed form, including the relations between skewness and kurtosis of the GGC process and of the corresponding variance-GGC process. In addition, variance-GGC processes can be represented as the difference of two GGC processes.

On the other hand, the sensitivity analysis of stochastic models is an important topic in financial engineering applications. The sensitivity analysis of time-changed Brownian motion processes has been developed and the Greek formulas have been obtained by following the approach in [8]. In addition, the sentivity analysis of the variance-gamma, stable and tempered stable processes has been performed in [9] and [10] respectively. As an extension of the variance-gamma process, we study the corresponding sensitivity analysis of the variance-GGC model along the lines of [9].

In the remaining of this section we review some facts on generalized gamma convolutions, (GGCs) including their variance, skewness and kurtosis. We also discuss an asset price model based on GGCs and its sensitivity analysis.

Wiener-gamma integrals

Consider a gamma process $(\gamma _t )_{t\in {\mathord {\mathbb R}}_+}$, i.e. $(\gamma _t )_{t\in {\mathord {\mathbb R}}_+}$ is a process with independent and stationary increments such that $\gamma _t$ at time $t>0$ has a gamma distribution with shape parameter t and probability density function $e^{-x} x^{t-1} / \varGamma (t)$, $x>0$. We denote by

$$\begin{aligned} \int _0^\infty g(t) d\gamma _t, \end{aligned}$$

(1)

the Wiener-gamma stochastic integral of a deterministic function

$$ g:\mathbb R_+ \longrightarrow \mathbb R_+ $$

with respect to the standard gamma process $(\gamma _t)_{t\in {\mathord {\mathbb R}}_+}$, provided g satisfies the condition

$$\begin{aligned} \int _0^\infty \log (1+g(t))dt<\infty , \end{aligned}$$

(2)

which ensures the finiteness of Eq. (1), cf. Sect. 1.2, page 350 of [7] for details. In particular, there is a one-to-one correspondence between GGC random variables and Wiener-gamma integrals, Proposition 1.1, page 352 of [7].

Generalized gamma convolutions

A random variable Z is a generalized gamma convolution if its Laplace transform admits the representation

$$ {\mathord {\mathbb E}}[e^{-uZ}]=\exp \left( -t\int _0^\infty \log \left( 1+\frac{u}{s} \right) \mu (ds) \right) ,\qquad u\ge 0 $$

where $\mu (ds)$ is called the Thorin measure and should satisfy the conditions

$$ \int _{(0,1]}|\log s|\mu (ds)<\infty \quad \text{ and } \quad \int _{(1,\infty )}s^{-1}\mu (ds)<\infty . $$

Generalized gamma convolutions (GGC) can be defined as the limits of independent sums of gamma random variables with various shape parameters, cf. [2] for details.

In particular, the density of the Lévy measure of a GGC random variable is a completely monotone function. From the Laplace transform of Z we find

$$ {\mathord {\mathbb E}}[Z]=\int _0^\infty t^{-1} \mu (dt) , $$

and the first central moments of Z can be computed as

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle {\mathord {\mathbb E}}[(Z-{\mathord {\mathbb E}}[Z])^2] = \int _0^\infty t^{-2}\mu (dt), \\ \\ \displaystyle {\mathord {\mathbb E}}[(Z-{\mathord {\mathbb E}}[Z])^3]=2\int _0^\infty t^{-3}\mu (dt), \\ \\ \displaystyle {\mathord {\mathbb E}}[(Z-{\mathord {\mathbb E}}[Z])^4]= 3\left( {\mathrm {\mathrm{Var}}}[ Z] \right) ^2 + 6\int _0^\infty t^{-4}\mu (dt) . \end{array} \right. \end{aligned}$$

(3)

As a consequence we can compute the

$$ \text{ Skewness } [Z] =\frac{{\mathord {\mathbb E}}[(Z-{\mathord {\mathbb E}}[Z])^3]}{({\mathrm {\mathrm{Var}}}[Z])^{3/2}}=\frac{2\int _0^\infty t^{-3}\mu (dt)}{( {\mathrm {\mathrm{Var}}}[Z] )^{3/2}}, $$

and

$$ \text{ Kurtosis } [Z] =\frac{{\mathord {\mathbb E}}[(Z-{\mathord {\mathbb E}}[Z])^4]}{({\mathrm {\mathrm{Var}}}[Z])^2}=3 +6\frac{\int _0^\infty t^{-4}\mu (dt)}{({\mathrm {\mathrm{Var}}}[ Z] )^2} $$

of Z. We refer the reader to Proposition 1.1 of [7] for the relation between the integrand in a Wiener-gamma representation and the cumulative distribution function of the associated generalized gamma convolution.

Market model and sensitivity analysis

As an extension of the model of [9] to GGC random variables we consider an asset price process $S_T$ defined by the exponent

$$ S_T=S_0\exp \left( \theta \int _0^\infty g(s) d\gamma _s +\tau \sqrt{T}\varTheta +Z_T+c(\theta ,\tau )T \right) , $$

of a variance-GGC process, i.e. $\int _0^\infty g(s) d\gamma _s$ is a GGC random variable represented as a Wiener-gamma integral, $\varTheta$ is an independent Gaussian random variable, $(Z_t)_{t\in {\mathord {\mathbb R}}_+}$ is another GGC-Lévy process, and $\theta \in \mathbb R$, $\tau \ge 0$, $T>0$.

In Sect. 3 the sensitivity $\displaystyle \frac{\partial }{\partial S_0}{\mathord {\mathbb E}}[\varPhi (S_T)]$ of an option with payoff $\varPhi$ with respect to the initial value $S_0$ in a variance-GGC model is shown to satisfy

$$ \frac{\partial }{\partial S_0}{\mathord {\mathbb E}}[\varPhi (S_T)] = \frac{1}{S_0}{\mathord {\mathbb E}}[\varPhi (S_T)L_T], $$

where

$$ L_T :=\frac{2 \theta \int _0^\infty g(s)f^2(s) d\gamma _s}{(\theta \int _0^\infty g(s)f(s)d\gamma _s+\tau \sqrt{T}\eta )^2}+\frac{\int _0^\infty f(s) d\gamma _s-T\int _0^\infty f(s)ds+ \eta \varTheta }{\theta \int _0^\infty g(s)f(s)d\gamma _s+\tau \sqrt{T}\eta } $$

for any positive function $f:\mathbb R_+\rightarrow (0,a)$ and $\eta >0$. In Theorem 1 we will compute this sensitivity as well as orther Greeks based on the model parameters $\theta$ and $\tau$.

The remaining of this paper is organized as follows. In Sect. 2 we introduce a model for Brownian motion time-changed by a GGC subordinator. The variance, skewness and kurtosis of variance-GGC processes are calculated in relation with the corresponding parameters of GGC processes, and several example of variance-GGC models are considered. A Girsanov transform of GGC processes is also stated. The sensitivity analysis with respect to $S_0$, $\theta$ and $\tau$ is conducted in Sect. 3.

2 Variance-GGC Processes

Given $(W_t)_{t\in {\mathord {\mathbb R}}_+}$ a standard Brownian motion and $\theta \in {\mathord {\mathbb R}}$, $\sigma >0$, consider the drifted Brownian motion

$$ B_{t}^{\theta ,\sigma } : =\theta t+\sigma W_t, \qquad t\in {\mathord {\mathbb R}}_+. $$

Next, consider a generalized gamma convolution (GGC) Lévy process $(G_t)_{t\in {\mathord {\mathbb R}}_+}$ such that $G_1$ is a GGC random variable with Thorin measure $\mu (ds)$ on ${\mathord {\mathbb R}}_+$. We define the variance-GGC process $(Y_t^{\sigma ,\theta })_{t\in {\mathord {\mathbb R}}_+}$ as the time-changed Brownian motion

$$ Y_t^{\sigma ,\theta } : = B_{G_t}^{\theta ,\sigma }, \qquad t\in {\mathord {\mathbb R}}_+. $$

The probability density function of $Y_t^{\sigma ,\theta }$ is given by

$$ f_{Y_t^{\sigma ,\theta }}(x) = \frac{1}{\sigma \sqrt{2\pi }} \int _0^\infty \exp \left( -\frac{| x-\theta y |^2}{2\sigma ^2 y} \right) h_t (y) \frac{dy }{\sqrt{y}} , \qquad x \in {\mathord {\mathbb R}}, $$

where $h_t (y)$ is the probability density function of $G_t$, cf. Relation (6) in [11].

The Laplace transform of $Y_t^{\sigma ,\theta }$ is

$$\begin{aligned} {\mathord {\mathbb E}}\left[ \exp \left( -uY_t^{\sigma ,\theta } \right) \right]= & {} \int _0^\infty e^{-uy} f_{Y_t}(y)dy \nonumber \\= & {} \varPsi _{G_t} \left( \theta u-\frac{\sigma ^2}{2} u^2 \right) \nonumber \\= & {} \exp \left( -t \int _0^\infty \log \left( 1+\frac{\theta u-\sigma ^2 u^2/2}{s} \right) \mu (ds) \right) , \end{aligned}$$

(4)

where $\varPsi _{G_t}$ is the Laplace transform of $G_t$.

This construction extends the symmetric variance-GGC model constructed in Sect. 4.4, pages 124–126 of [6]. In particular, the next proposition extends to variance-GGC processes Relation (8) in [11, 12], which decomposes the variance-gamma process into the difference of two gamma processes. Here, we are writing $Y_t$ as the difference of two independent GGC processes, i.e. $Y_t$ becomes an Extended Generalized Gamma Convolution (EGGC) in the sense of Chap. 7 of [2], cf. also Sect. 3 of [14].

Proposition 1

The time-changed process $Y_t$ can be decomposed as

$$ Y_t = U_t - W_t, $$

where $U_t$ and $W_t$ are two independent GGC processes with Thorin measures $\mu _A$ and $\mu _B$ which are the image measures of $\mu (dt)$ on ${\mathord {\mathbb R}}_+$ respectively, by the mappings

$$ s\longmapsto B(s):=\frac{\theta }{\sigma ^2} +\frac{1}{\sigma }\sqrt{\frac{\theta ^2}{\sigma ^2}+2s}, \qquad s\in {\mathord {\mathbb R}}_+, $$

and

$$ s \longmapsto A(s)= - \frac{\theta }{\sigma ^2} + \frac{1}{\sigma }\sqrt{ \frac{\theta ^2}{\sigma ^2} +2s}, \qquad s\in {\mathord {\mathbb R}}_+. $$

Proof

From (4), the Laplace tranform of $Y_t$ can be decomposed as

$\square$

The Laplace tranform of $Y_t$ can also be decomposed as

(5)

where $\mu _{-B}$ is the image measure of $\mu _B$ by $s\mapsto -s$, and in particular, $Y_t$ is an extended GGC (EGGC) with Thorin measure $\mu _A+\mu _{-B}$ in the sense of Chap. 7 of [2].

In the next proposition we compute the variance, skewness and kurtosis of variance-GGC processes.

Proposition 2

We have

• (i) $\displaystyle {\mathrm {\mathrm{Var}}}[Y_1] = \theta ^2 {\mathrm {\mathrm{Var}}}[G_1]+\sigma ^2 {\mathord {\mathbb E}}[G_1]$.

• (ii) $\displaystyle \mathrm{Skewness}[Y_1] = - \frac{{\mathord {\mathbb E}}[(G_1-{\mathord {\mathbb E}}[G_1])^3] + 2 ( \sigma / \theta )^2 {\mathrm {\mathrm{Var}}}[G_1 ]}{ 2 ({\mathrm {\mathrm{Var}}}[G_1]+ ( \sigma / \theta )^2 {\mathord {\mathbb E}}[G_1] )^{3/2}}$

  $$\begin{aligned}&\quad \,\,&= -\frac{\theta ^3}{2}\mathrm{Skewness}[G_1] \frac{({\mathrm {\mathrm{Var}}}[G_1])^{3/2}}{({\mathrm {\mathrm{Var}}}[Y_1])^{3/2}} -\frac{\theta \sigma ^2{\mathrm {\mathrm{Var}}}[G_1]}{({\mathrm {\mathrm{Var}}}[Y_1])^{3/2}}. \end{aligned}$$

  (6)

• (iii) $\displaystyle \mathrm{Kurtosis} [Y_1] = 3+ 3 \theta ^4 \frac{ {\mathord {\mathbb E}}[(G_1-{\mathord {\mathbb E}}[G_1])^4]-3({\mathrm {\mathrm{Var}}}[G_1])^2}{8 (\theta ^2 {\mathrm {\mathrm{Var}}}[G_1]+\sigma ^2 {\mathord {\mathbb E}}[G_1])^2}$

  $$\begin{aligned}&\,\,\qquad +\,\,3 \frac{3\theta ^2\sigma ^2{\mathord {\mathbb E}}[(G_1-{\mathord {\mathbb E}}[G_1])^3]/4+\sigma ^4{\mathrm {\mathrm{Var}}}[G_1]}{(\theta ^2 {\mathrm {\mathrm{Var}}}[G_1]+\sigma ^2 {\mathord {\mathbb E}}[G_1])^2} \nonumber \\&\quad \,\, = 3 + \theta ^4 \frac{(\mathrm{Kurtosis} [G_1] -3)({\mathrm {\mathrm{Var}}}[G_1])^2}{16({\mathrm {\mathrm{Var}}}[Y_1])^2} \nonumber \\&\,\, \qquad +\,\,9\sigma ^2\theta ^2 \frac{\mathrm{Skewness}[G_1] ({\mathrm {\mathrm{Var}}}[G_1])^{3/2}}{4({\mathrm {\mathrm{Var}}}[Y_1])^2} + 3 \frac{\sigma ^4 {\mathrm {\mathrm{Var}}}[G_1]}{({\mathrm {\mathrm{Var}}}[Y_1])^2}. \end{aligned}$$

  (7)

Proof

Using the Thorin measure $\mu _A+\mu _{-B}$ of $Y_t$ and (3) we have

$$\begin{aligned} {\mathrm {\mathrm{Var}}}[Y_1]= & {} \int _0^\infty t^{-2}\mu _A(dt)+\int _{-\infty }^0 t^{-2}\mu _{-B}(dt) \\= & {} \int _0^\infty \frac{1}{A^2 (t)} \mu (dt)+\int _0^\infty \frac{1}{B^2(t)} \mu (dt) \\= & {} \int _0^\infty \frac{\theta ^2+t\sigma ^2}{t^2}\mu (dt) \\= & {} \theta ^2 {\mathrm {\mathrm{Var}}}[G_1]+\sigma ^2 {\mathord {\mathbb E}}[G_1] , \end{aligned}$$

and

$$\begin{aligned} {\mathord {\mathbb E}}[(Y_1-{\mathord {\mathbb E}}[Y_1])^3]= & {} 2 \int _0^\infty t^{-3}\mu _A(dt) + 2 \int _{-\infty }^0 t^{-3}\mu _{-B}(dt) \\= & {} \frac{1}{2} \int _0^\infty \frac{{\theta }^3+\theta \sigma ^2 \left( \theta ^2 / \sigma ^2 +2t\right) }{t^3}\mu (dt) \\= & {} \frac{\theta ^3}{2}{\mathord {\mathbb E}}[(G_1-{\mathord {\mathbb E}}[G_1])^3]+\theta \sigma ^2{\mathrm {\mathrm{Var}}}[G_1], \end{aligned}$$

and

and this yields (6) and (7). $\square$

Girsanov theorem

Consider the probability measure $Q_\lambda$ defined by the Radon-Nikodym density

$$\begin{aligned} \frac{dQ_\lambda }{dP}: =\frac{e^{\lambda Y_T}}{{\mathord {\mathbb E}}[e^{ \lambda Y_T}]} = ( 1-\lambda )^{a T} e^{ \lambda Y_T } = e^{ \lambda Y_T + a T \log ( 1-\lambda ) }, \qquad \lambda <1, \end{aligned}$$

(8)

cf. e.g. Lemma 2.1 of [9], where $Y_T$ is a gamma random variable with shape and scale parameters (aT, 1) under P. Then, under $Q_\lambda$, the random variable $Y_t$ has a gamma distribution with parameter $(aT,1/(1-\lambda )$, i.e. the distribution of $Y_t/(1-\lambda )$ under P.

In the next proposition we extend this Girsanov transformation to GGC random variables.

Proposition 3

Consider the probability measure $P_{f}$ defined by its Radon-Nikodym derivative

$$ \frac{dP_{f} }{dP} =\frac{e^{ \int _0^\infty f(s) d\gamma _s}}{{\mathord {\mathbb E}}[e^{\int _0^\infty f(s) d\gamma _s}]} = e^{ \int _0^\infty f(s) d\gamma _s+ \int _0^\infty \log \left( 1-f(s) \right) ds }, $$

where $f:\mathbb R_+\rightarrow (0,1)$ satisfies

$$\begin{aligned} \int _0^\infty \log \left( \frac{1+f(t)}{1- f(t)}\right) dt<\infty . \end{aligned}$$

(9)

Assume that $g:\mathbb R_+\rightarrow \mathbb R_+$ satisfies (2), and

$$ \int _0^\infty \log \left( 1+ug(s)- f(s) \right) ds>-\infty ,\qquad u>0. $$

Then, under $P_{f}$, the law of $\int _0^\infty g(s)d\gamma _s$ is the GGC distribution of the Wiener-gamma integral

$$ \int _0^\infty \frac{g(s)}{1-f(s)}d\gamma _s $$

under P.

Proof

For all $u>0$, we have

$\square$

Note that (8) is recovered by taking $g(s)=\mathbf{1}_{[0,aT]}(s)$ and $f(s) =\lambda \mathbf{1}_{[0,aT]}(s)$ for $\lambda \in (0,1)$, i.e. $G_T=\int _0^\infty g(s) d\gamma _s$ is a gamma random variable with shape parameter aT and we have

$$ {\mathord {\mathbb E}}_{P_{f}} [e^{-u G_T}]= \left( 1+\frac{u}{1- \lambda } \right) ^{-aT} ={\mathord {\mathbb E}}\left[ \exp \left( - \frac{u}{1-\lambda } G_T \right) \right] , $$

$u>0$, $\lambda <1$. Next we consider several examples and particular cases.

Gamma case

In case the Thorin measure $\mu$ is given by

$$ \mu (dt) = \gamma \delta _c(dt), $$

where $\delta _c$ is the Dirac measure at $c>0$ we find the variance-gamma model of [12]. Here, $G_t$, $t>0$, has the gamma probability density

$$ \phi _t (x) = c^{\gamma t} \frac{x^{\gamma t -1} e^{-c x }}{\varGamma (\gamma t )}, \qquad x \in {\mathord {\mathbb R}}_+ , $$

with mean and variance $\gamma t /c$ and $\gamma t /c^2$, and $G_t$ becomes a gamma random variable with parameters $(\gamma t, c)$. In this case, the decomposition in Proposition 1 reads

$$ \varPsi _{Y_t} (u) = \left( 1-\frac{\sigma ^2 u^2}{2c} \right) ^{- t \gamma } = \left( 1-\frac{\sigma u}{\sqrt{2c}} \right) ^{-t \gamma } \left( 1+\frac{\sigma u}{\sqrt{2c}} \right) ^{-t \gamma } , $$

and we have

$$ \mu _A (dt) =\mu _B (dt) = \gamma \delta _{\sqrt{2c}/\sigma } (dt), $$

thus $(U_t)_{t\in {\mathord {\mathbb R}}_+}$, $(W_t)_{t\in {\mathord {\mathbb R}}_+}$ become independent gamma processes with parameter $(\gamma t, \sqrt{2c}/\sigma )$. The mean and variance of $U_1$ are

$$ {\mathord {\mathbb E}}[U_1]=\int _0^\infty t^{-1} \mu _A(dt) = \frac{\sigma \gamma }{\sqrt{2c}} $$

and

$$ {\mathrm {\mathrm{Var}}}[U_1] = {\mathord {\mathbb E}}[(U_1-{\mathord {\mathbb E}}[U_1])^2] = \int _0^\infty t^{-2} \mu _A(dt) =\frac{\gamma \sigma ^2}{2c} . $$

Symmetric case

When $\theta =0$ we recover the symmetric variance-GGC process

$$ Y_t: = B^\sigma (G_t), \qquad t\in {\mathord {\mathbb R}}_+, $$

defined in Sect. 4.4, page 124–126 of [6], i.e. the time-changed Brownian motion is a symmetric variance-GGC process. Here, $Y_t$ is a centered Gaussian random variable with variance $\sigma ^2 G_t$ given $G_t$, where $B^\sigma _t$ is a standard Brownian motion with variance $\sigma ^2$.

The Laplace transform of $Y_t$ in Proposition 1 shows that $Y_t$ decomposes into two independent processes with same GGC increments since $\mu _A$ and $\mu _B$ are the same image measures of $\mu (dt)$ on ${\mathord {\mathbb R}}_+$, by $s\mapsto \sqrt{2s}/\sigma$.

Variance-stable processes

Let $(G_t)_{t\in {\mathord {\mathbb R}}_+}$ be a Lévy stable process with index parameter $\alpha \in (0,1)$ and moment generating function $h(s)=e^{-s^\alpha }$. In this section we consider a non-symmetric extension of the symmetric variance stable process considered in Sect. 4.5, pages 126–127 of [6]. The Thorin measure of the stable distribution is given by

$$ \mu (dt) = \varphi (t) dt = \frac{\alpha }{\pi } \sin (\alpha \pi ) t^{\alpha -1} dt, $$

cf. page 35 of [2]. By Proposition 1, $Y_t$ can be decomposed as

$$ Y_t=U_t-W_t , $$

where $U_t$ and $W_t$ are processes with independent stable increments and Thorin measures

$$\begin{aligned} \mu _A (dt) = \varphi _A (t) dt =\frac{\alpha }{\pi }\sin (\alpha \pi ) (\sigma ^2 t+\theta ) \left( \frac{1}{2} ( \sigma t- \theta / \sigma )^2-\frac{\theta ^2}{2\sigma ^2}\right) ^{\alpha -1}dt, \end{aligned}$$

and

$$\begin{aligned} \mu _B (dt) = \varphi _B (t) dt = \frac{\alpha }{\pi }\sin (\alpha \pi ) (\sigma ^2 t-\theta ) \left( \frac{1}{2} ( \sigma t- \theta / \sigma )^2-\frac{\theta ^2}{2\sigma ^2} \right) ^{\alpha -1}dt. \end{aligned}$$

In the symmetric case $\theta =0$ we find

$$ \mu _A (dt) = \varphi _A (t) dt=\mu _B (dt) = \varphi _B (t) dt = \sigma ^2 t \varphi \left( \frac{\sigma ^2 t^2}{2} \right) dt = \frac{\alpha \sin (\alpha \pi )}{2^{\alpha -1}\pi }\sigma ^{2\alpha } t^{2\alpha -1} dt , $$

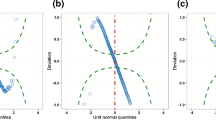
i.e. $\sqrt{2} U_t / \sigma$ and $\sqrt{2} W_t / \sigma$ are stable processes of index $2\alpha$. Note that the skewness and kurtosis of $G_t$ and $Y_t$ are undefined. Figure 1 presents a simulation of the variance-stable process.

Fig. 1

Sample paths of variance-stable process with $\alpha =0.99$

Variance product of stable processes

Here we take $G_1 = Z^{1/\alpha }X_\alpha$ where Z is a $\varGamma (\gamma ,1)$ random variable and $X_\alpha$ is a stable random variable with index $\alpha <1$. The MGF of $G_1$ is $h(s)=(1+s^\alpha )^\gamma$, cf. page 38 of [2], i.e. $G_1$ is a GGC with Thorin measure

$$ \mu (dt) = \varphi (t) dt = \frac{1}{\pi }\frac{\gamma \alpha t^{\alpha -1}\sin (\alpha \pi )}{1+t^{2\alpha }+2t^\alpha \cos (\alpha \pi )} dt, $$

and $Y_t$ decomposes as

$$ Y_t=U_t-W_t , $$

where $U_t$ and $W_t$ are processes of independent product of stable increment and Thorin measures

and

In the symmetric case

$$\begin{aligned} \mu _A(dt)= & {} \varphi _A (t) dt=\mu _B(dt) =\varphi _B (t) dt\\= & {} \sigma ^2 t \varphi \left( \frac{\sigma ^2 t^2}{2} \right) dt = \frac{\gamma \alpha \sigma ^{2\alpha }t^{2\alpha -1}\sin (\alpha \pi )}{\pi (2^{\alpha -1}+2^{-\alpha -1}\sigma ^{4\alpha }t^{4\alpha }+\sigma ^{2\alpha }t^{2\alpha }\cos (\alpha \pi ))}dt. \end{aligned}$$

The skewness and kurtosis of $G_t$ and $Y_t$ are undefined. Figure 2 presents the corresponding simulation.

Fig. 2

Sample paths of variance-product of stable process with $\alpha =0.99$ and $\gamma =0.2$

3 Sensitivity Analysis

In this section we extend approach of [8] to the sensitivity analysis of variance-GGC models. Consider $(B_t)_{t\in {\mathord {\mathbb R}}_+}$ a standard one-dimensional standard Brownian motion independent of the Lévy process $(Y_t)_{t\in [0,T]}$ generated by

$$ Y_T : =\int _0^\infty g(s) d\gamma _s. $$

Let $\varTheta$ be a standard Gaussian random variable independent of $(Y_t)_{t\in [0,T]}$. For each $t \in [0,T]$, we denote by ${\mathscr {F}}_t$ the filtration generated by $\varTheta$ and $\sigma ( Y_s \ : \ s\in [0,t])$.

Let $(Z_t)_{t\in {\mathord {\mathbb R}}_+}$ be a real-valued stochastic process in $\mathbb R$ independent of $(Y_t)_{t\in {\mathord {\mathbb R}}_+}$ and $(B_t)_{t\in {\mathord {\mathbb R}}_+}$. Finally we denote by and let $C^n_b(\mathbb R_+;\mathbb R)$ denote the class of n-time continuously differentiable functions with bounded derivatives, whereas ${\mathscr {C}}_c (\mathbb R_+;\mathbb R)$ denotes the space of continuous functions with compact support.

Given $\theta \in \mathbb R$ and $\tau \in \mathbb R_+$ we consider the asset price $S_T$ written as

$$ S_T=S_0\exp \left( \theta Y_T +\tau \sqrt{T}\varTheta +Z_T + T c(\theta ,\tau ) \right) , $$

where the function $g(s): \mathbb R_+\rightarrow \mathbb R_+$ verifies (2).

Remark 1

When $\theta =0$ the above model reduces to the standard Black-Scholes model, and in case $\theta \ne 0$ we find the variance-GGC model by taking $(Z_t)_{t\in [0,T]}$ to be a GGC process.

For example, we can take the Wiener-gamma integral $\int _0^\infty g(s) d\gamma _s$ to be a stable random variable and set $Z_T$ to be another stable random variable, then the exponent of $S_t$ is a variance-stable process. This example will be developed in the next section.

The next theorem deals with the sensitivity analysis of the variance-GGC model with respect to $S_0$, $\theta$ and $\tau$, and is the main result in this section. Define the classes of functions

$$ {\mathscr {C}}_L(\mathbb R_+;\mathbb R):=\{f\in C(\mathbb R_+;\mathbb R) \ : \ |f(x)|\le C(1+|x|) \text{ for } \text{ some } C>0\}, $$

and

Theorem 1

Let $\varPhi \in D(\mathbb R_+;\mathbb R)$. Assume that the law of $Z_T$ is absolutely continuous with respect to the Lebesgue measure, with

$$\begin{aligned} \int _0^\infty \log \left( 1+\frac{g(s)f^k (s)}{(1-\lambda f(s))^{k+1}}\right) ds<\infty , \qquad k = 1,2,3. \end{aligned}$$

(10)

Then

• (i) (Delta—sensitivity with respect to $S_0$). We have

  $$ \frac{\partial }{\partial S_0}{\mathord {\mathbb E}}[\varPhi (S_T)]=\frac{1}{S_0}{\mathord {\mathbb E}}[\varPhi (S_T)L_T], $$

  where

  $$ L_T=\frac{2 \theta \int _0^\infty g(s)f^2(s) d\gamma _s}{(\theta \int _0^\infty g(s)f(s)d\gamma _s+\tau \sqrt{T}\eta )^2}+\frac{\int _0^\infty f(s) d\gamma _s-T\int _0^\infty f(s)ds+ \eta \varTheta }{\theta \int _0^\infty g(s)f(s)d\gamma _s+\tau \sqrt{T}\eta }. $$

• (ii) (Sensitivity with respect to $\theta$). We have

  $$\begin{aligned} \frac{\partial }{\partial \theta }{\mathord {\mathbb E}}[\varPhi (S_T)]= & {} {\mathord {\mathbb E}}\left[ \varPhi (S_T)\left( L_T\int _0^\infty g(s)d\gamma _s-\frac{1}{H_T}\int _0^\infty g(s)f(s)d\gamma _s\right) \right] \\&+\,\,TS_0 \frac{\partial c}{\partial \theta }(\theta ,\tau )\frac{\partial }{\partial S_0}{\mathord {\mathbb E}}[\varPhi (S_T)], \end{aligned}$$

  where $\displaystyle H_T = \theta \int _0^\infty g(s)f(s)d\gamma _s+\tau \sqrt{T}\eta$.

• (iii) (Theta—sensitivity with respect to $\tau$). We have

  $$ \frac{\partial }{\partial \tau }{\mathord {\mathbb E}}[\varPhi (S_T)] ={\mathord {\mathbb E}}\left[ \varPhi (S_T)L_T\sqrt{T}\left( \varTheta -\frac{\eta }{H_T}\right) \right] + TS_0 \frac{\partial c }{\partial \tau } (\theta ,\tau ) \frac{\partial }{\partial S_0}{\mathord {\mathbb E}}[\varPhi (S_T)]. $$

• (iv) (Gamma—second derivative with respect to $S_0$). We have

  

  where

  $$ K_T=2\theta \int _0^\infty g(s)f^2(s) d\gamma _s, \quad M_T= \int _0^\infty f(s) d\gamma _s-T\int _0^\infty f(s)ds+ \eta \varTheta , $$

  and

  $$ I_T=6\theta \int _0^\infty g(s)f(s)^3d\gamma _s, \quad N_T= \left( \int _0^\infty f(s) d\gamma _s-T\int _0^\infty f(s)ds+ \eta \varTheta \right) ^2. $$

Next we state two lemmas which are needed for the proof of Theorem 1.

Lemma 1

Assume that ${\mathord {\mathbb E}}[e^{2\gamma Z_T}]<\infty$ for some $\gamma >1$. Let $f: \mathbb R\rightarrow (0,a)$ be a positive function and $\lambda \in (0,\varepsilon )$ for $\varepsilon <1/a$ such that (10) holds. Fix $\eta > 0$ and suppose that one of the following conditions holds:

• (i) The density function of $Y_T = \int _0^\infty g(s)d\gamma _s$ decays exponentially, or

• (ii) ${\mathord {\mathbb E}}\left[ e^{2\gamma (1+\theta \delta )Y_T}\right] <\infty$ for all $\delta >0$.

Let also

$$\begin{aligned} S_T^{(\lambda f)}= & {} S_0\exp \left( \theta \int _0^\infty \frac{g(s)}{1-\lambda f(s)}d\gamma _s \right. + \left. \tau \sqrt{T}(\varTheta +\eta \lambda )+Z_T+c(\theta ,\tau )T\right) , \end{aligned}$$

and

$$\begin{aligned} H_T^{\left( \lambda f\right) }= & {} \frac{\partial }{\partial \lambda } \log S_T^{(\lambda f)} =\theta \int _0^\infty \frac{g(s)f(s)}{(1-\lambda f(s))^2}d\gamma _s+\tau \sqrt{T}\eta , \quad H_T=H_T^{(0)}, \end{aligned}$$

and

$$\begin{aligned} K_T^{(\lambda f)}= & {} \frac{\partial }{\partial \lambda }H_T^{(\lambda f)}=2\theta \int _0^\infty \frac{g(s)f^2(s)}{(1-\lambda f(s))^3}d\gamma _s,\quad K_T=K_T^{(0)}. \end{aligned}$$

Then we have the $L^2(\varOmega )$-limits

$$ \lim _{\lambda \rightarrow 0} S_T^{(\lambda f)}H_T^{(\lambda f)} = S_TH_T \quad \text{ and } \quad \lim _{\lambda \rightarrow 0} \frac{K_T^{(\lambda f)}}{(H_T^{(\lambda f)})^2} = \frac{K_T}{(H_T)^2}. $$

Proof

For any $\lambda \in (0,\varepsilon )$, we have

where $C_1$ is a positive constant. Under condition (i) or (ii) above we have

$$\begin{aligned} {\mathord {\mathbb E}}\left[ Y_T^{2\gamma } \exp \left( \frac{ 2\gamma \theta }{1-\varepsilon a}Y_T \right) \right]\le & {} {\mathord {\mathbb E}}\left[ \exp \left( 2\gamma \left( 1+\frac{\theta }{1-\varepsilon a} \right) Y_T \right) \right] <\infty , \end{aligned}$$

and similarly we have $\displaystyle {\mathord {\mathbb E}}\left[ e^{\frac{2\gamma \theta }{1-\varepsilon a}Y_T}\right] <\infty$. Finally, we have ${\mathord {\mathbb E}}[e^{2\gamma Z_T}]<\infty$ by assumption, and it is clear that ${\mathord {\mathbb E}}[e^{2\gamma \tau \sqrt{T}\varTheta }]<\infty$. Then $|S_T^{(\lambda f)}H_T^{(\lambda f)}|$ is $L^{2\gamma }(\varOmega )$-integrable, hence $(S_T^{(\lambda f)}H_T^{(\lambda f)})^2$ is uniformly-integrable since $\gamma >1$. Therefore, we have proved that $S_T^{(\lambda f)}H_T^{(\lambda f)}$ converges to $S_TH_T$ in $L^{2}(\varOmega )$ as $\lambda \rightarrow 0$.

Next, for any $\lambda \in (0,\varepsilon )$ we have

since ${\mathord {\mathbb E}}\left[ \left( \int _0^\infty g(s)d\gamma _s\right) ^{2\gamma }\right]$ is finite under Condition (i) or (ii) above. Therefore $(K_T^{(\lambda f)}/(H_T^{(\lambda f)})^2)^2$ is uniformly-integrable since $\gamma >1$, and this shows that $K_T^{(\lambda f)}/(H_T^{(\lambda f)})^2$ converges to $K_T/(H_T)^2$ as $\lambda \rightarrow 0$ in $L^{2}(\varOmega )$. $\square$

Lemma 2

Assume that ${\mathord {\mathbb E}}[e^{2\gamma Z_T}]<\infty$ for some $\gamma >1$ and that (10) holds. Suppose in addition that one of the following conditions holds:

• 1. The density function of $\int _0^\infty g(s)d\gamma _s$ decays exponentially.

• 2. ${\mathord {\mathbb E}}\left[ \left| e^{2\gamma (1+\theta \delta )Y_T}\right| \right] <\infty$ for all $\delta >0$, where $Y_T=\int _0^\infty g(s)d\gamma _s$.

Then for $\varPhi \in {\mathscr {C}}_b^1(\mathbb R_+,\mathbb R)$ it holds that

• (i) $\displaystyle {\mathord {\mathbb E}}\left[ \varPhi '(S_T)S_TH_T\right] ={\mathord {\mathbb E}}\left[ \left( \int _0^\infty f(s)d\gamma _s-T\int _0^\infty f(s)ds+ \eta \varTheta \right) \varPhi (S_T)\right] .$

• (ii) $\displaystyle {\mathord {\mathbb E}}[\varPhi '(S_T)S_T]={\mathord {\mathbb E}}[\varPhi (S_T)L_T].$

• (iii) $\displaystyle {\mathord {\mathbb E}}\left[ \varPhi '(S_T)S_T\int _0^\infty g(s)d\gamma _s\right] =\nonumber {\mathord {\mathbb E}}\left[ \varPhi (S_T)\left( L_T\int _0^\infty g(s)d\gamma _s-\frac{1}{H_T}\int _0^\infty g(s)f(s)d\gamma _s\right) \right] .$

• (iv) $\displaystyle {\mathord {\mathbb E}}[\varPhi '(S_T)S_TB_T] = \sqrt{T} {\mathord {\mathbb E}}\left[ \varPhi (S_T)L_T \left( \varTheta -\frac{\eta }{H_T} \right) \right] .$

• (v) If in addition $\varPhi \in {\mathscr {C}}_b^2(\mathbb R_+,\mathbb R)$ and (10) is satisfied then we have

  

Proof

We have

$$\begin{aligned} {\mathord {\mathbb E}}[(\varPhi (S_T))^2]\le & {} 2{\mathord {\mathbb E}}[(\varPhi (S_T)-\varPhi (S_0))^2]+2{\mathord {\mathbb E}}[(\varPhi (S_0))^2]\\\le & {} 2{\mathord {\mathbb E}}[(\varPhi (S_0))^2] + 2\int _0^1{\mathord {\mathbb E}}[(\varPhi '( r S_T+(1- r )S_0))^2(S_T-S_0)^2]dr \\< & {} \nonumber \infty , \end{aligned}$$

since $\varPhi \in C^1_b(\mathbb R_+;\mathbb R)$. As for (i) we have

$$\begin{aligned} {\mathord {\mathbb E}}\left[ \varPhi (S_T^{(\lambda f)})\right]= & {} {\mathord {\mathbb E}}\left[ \frac{dP_{\lambda f}}{dP}_{\big | {{\mathscr {F}}_T}}\varPhi (S_T)\right] , \end{aligned}$$

(11)

where we define the probability measure $P_{\lambda f}$ via its Radon-Nikodym derivative

$$ \frac{dP_{\lambda f} }{dP}_{\big | {{\mathscr {F}}_T}} =\frac{e^{\lambda \int _0^\infty f(s) d\gamma _s}}{{\mathord {\mathbb E}}[e^{ \lambda \int _0^\infty f(s) d\gamma _s}]}\frac{e^{\lambda \eta \varTheta }}{{\mathord {\mathbb E}}[e^{\lambda \eta \varTheta }]}= e^{ \lambda \int _0^\infty f(s) d\gamma _s+T\int _0^\infty \log \left( 1- \lambda f(s) \right) ds +\lambda \eta \varTheta - \lambda ^2 \eta ^2 / 2 } , $$

where $f:\mathbb R\rightarrow (0,a)$ and $\lambda \in (0,\varepsilon )$. In this way the GGC random variable $\int _0^\infty g(s)d\gamma _s$ and the Gaussian random variable $\varTheta$ under $P_{\lambda f}$ are transformed to $\int _0^\infty \frac{g(s)}{1-\lambda f(s)}d\gamma _s$ and $\varTheta +\eta \lambda$ under P.

First we prove that $\displaystyle \frac{\partial }{\partial \lambda }{\mathord {\mathbb E}}\left[ \varPhi (S_T^{(\lambda f)})\right]$ exists and equals the left hand side of (i). For every $\varepsilon \in (-\lambda , \lambda )$ we have

$$ \frac{\varPhi (S_T^{(\varepsilon f)})-\varPhi (S_T)}{\varepsilon }=\int _0^1 \varPhi '(S_T^{( r \varepsilon f)})S_T^{( r \varepsilon f)}H_T^{( r \varepsilon f)}d r, $$

and by the Cauchy-Schwarz inequality we get

(12)

From the boundedness and continuity of $\varPhi '(S_T^{(\varepsilon f)})$ with respect to $\varepsilon$ in $L^{2}(\varOmega )$, we have

$$ {\mathord {\mathbb E}}[(\varPhi '(S_T^{(\varepsilon f)}))^2]<\infty \quad \text{ and } \quad \lim _{\varepsilon \rightarrow 0 } {\mathord {\mathbb E}}[(\varPhi '(S_T^{(\varepsilon f)})-\varPhi '(S_T))^2] = 0. $$

By Lemma 1 we get that $S_T^{(\lambda f)}H_T^{(\lambda f)}$ converges in $L^{2}(\varOmega )$. Finally, we take the limit on both sides of (12) as $\varepsilon \rightarrow 0$. Next we prove that $\displaystyle \frac{\partial }{\partial \lambda }{\mathord {\mathbb E}}\left[ \frac{dP_{\lambda f}}{dP}_{\big | {{\mathscr {F}}_T}}\varPhi (S_T)\right]$ exists and equals the right hand side of (i).

For every $\varepsilon \in ( -\lambda , \lambda )$ the Cauchy-Schwarz inequality yields

It is then straightforward to check that ${\mathord {\mathbb E}}[|\varPhi (S_T)|^2]<\infty$ and

$$ \frac{1}{\lambda } \left( \exp \left( \lambda \int _0^\infty f(s) d\gamma _s+T\int _0^\infty \log \left( 1- \lambda f(s) \right) ds +\lambda \eta \varTheta - \lambda ^2 \eta ^2 / 2 \right) -1 \right) $$

converges to

$$ \int _0^\infty f(s)d\gamma _s-T\int _0^\infty f(s)ds+ \eta \varTheta $$

in $L^2(\varOmega )$ as $\lambda$ tends to 0 since $\lambda ^{-1}(e^{\lambda \int _0^\infty f(s) d\gamma _s}-1)$ converges to $\int _0^\infty f(s)d\gamma _s$ in $L^2(\varOmega )$ as $\lambda \rightarrow 0$. We conclude by taking the limit on both sides as $\lambda \rightarrow 0$.

For (ii) we start with the identity

$$\begin{aligned} {\mathord {\mathbb E}}\left[ \frac{\varPhi (S_T^{(\lambda f)})}{H_T^{(\lambda f)}}\right]= & {} {\mathord {\mathbb E}}\left[ \frac{dP_{\lambda f} }{dP}_{\big | {{\mathscr {F}}_T}} \frac{\varPhi (S_T)}{H_T}\right] . \end{aligned}$$

First we prove that $\displaystyle \frac{\partial }{\partial \lambda }{\mathord {\mathbb E}}\left[ \frac{\varPhi (S_T^{(\lambda f)})}{H_T^{(\lambda f)}}\right]$ exists and equals the left hand side of (ii). For every $\varepsilon \in [-\lambda , \lambda ]$ we have

$$ \frac{1}{\varepsilon }\left( \frac{\varPhi (S_T^{(\varepsilon f)})}{H_T^{(\varepsilon f)}}-\frac{\varPhi (S_T^{(0)})}{H_T}\right) =\int _0^1 \frac{\varPhi '(S_T^{( r \varepsilon f)})S_T^{(r \varepsilon f)}(H_T^{(r \varepsilon f)})^2-\varPhi (S_T^{(r \varepsilon f)})K_T^{(r \varepsilon f)}}{(H_T^{(r \varepsilon f)})^2}dr, $$

and by the Cauchy-Schwarz inequality we get

(13)

We have shown ${\mathord {\mathbb E}}[(\varPhi (S_T))^2]<\infty$ in the proof of (i). Then

where the Cauchy-Schwarz inequality and the Fubini theorem have been used for the second inequality. The convergence of $S_T^{(\varepsilon f)}H_T^{(\varepsilon f)}$ as $\varepsilon \rightarrow 0$ in $L^2(\varOmega )$ has been proved in Lemma 1. Note that ${\mathord {\mathbb E}}[(\varPhi (S_T^{(\varepsilon f)}))^2]<\infty$ also implies

$$ {\mathord {\mathbb E}}[(\varPhi (S_T^{(\varepsilon f)})-\varPhi (S_T))^2]\rightarrow 0\qquad as\qquad \varepsilon \rightarrow 0. $$

By Lemma 1, we get $K_T^{(\varepsilon f)}/(H_T^{(\varepsilon f)})^2$ converges to $K_T/(H_T)^2$ as $\varepsilon \rightarrow 0$ in $L^{2}(\varOmega )$. Taking the limit on both sides of (13) as $\varepsilon \rightarrow 0$.

Next, we prove that $\displaystyle \frac{\partial }{\partial \lambda }{\mathord {\mathbb E}}\left[ \frac{dP_{\lambda f} }{dP}_{\big | {{\mathscr {F}}_T}}\frac{\varPhi (S_T)}{H_T}\right]$ exists and is equal to the right hand side of (ii). For all $p>0$ we have

$$ {\mathord {\mathbb E}}[(H_T^{(\lambda f)})^{-2p}]=\int _0^\infty \left( \theta \int _0^\infty \frac{g(s)f(s)}{(1-\lambda f(s))^2}d\gamma _s+\tau \sqrt{T}\eta \right) ^{-2p}f_1(y) dy< ( \tau \sqrt{T}\eta )^{-2p}, $$

where $f_1$ is the density function of $\int _0^\infty \frac{g(s)f(s)}{(1-\lambda f(s))^2}d\gamma _s$. Therefore, the moment is uniformly bounded.

We conclude as in the second part of proof of (i). The proof of $(iii)-( {iv})$ is similar to that of (ii). As for (iii) we have

$$ {\mathord {\mathbb E}}\left[ \frac{\varPhi (S_T^{(\lambda f)})}{H_T^{(\lambda f)}}\int _0^\infty \frac{g(s)}{1-\lambda f(s)}d\gamma _s\right] ={\mathord {\mathbb E}}\left[ \frac{dP_{\lambda f} }{dP}_{\big | {{\mathscr {F}}_T}}\frac{\varPhi (S_T)}{H_T}\int _0^\infty g(s)d\gamma _s\right] . $$

For the first part, the existence of the derivative can be obtained as

Similarly, $\displaystyle \int _0^\infty \frac{g(s)f(s)}{(1-\lambda f(s))^2} d\gamma _s$ converges to $\int _0^\infty g(s)f(s) d\gamma _s$ in $L^2{(\varOmega )}$ as $\lambda \rightarrow 0$. The second part is almost the same as (i) by uniform boundedness of $H_T^{(\lambda f)}$.

For $( {iv})$ we have

$$ (\varTheta +\eta \lambda ) {\mathord {\mathbb E}}\left[ \frac{\varPhi (S_T^{(\lambda f)})}{H_T^{(\lambda f)}} \right] = \varTheta {\mathord {\mathbb E}}\left[ \frac{dP_ {\lambda f} }{dP}_{\big | {{\mathscr {F}}_T}}\frac{\varPhi (S_T)}{H_T} \right] . $$

For the first part, the existence of the derivative follows from the fact that $\varTheta$ has a Gaussian distribution. The second part is proved similarly.

Finally, for (v), define $\varPsi (x)=\varPhi '(x)x$, and by the result of (ii) we have

$$ {\mathord {\mathbb E}}[\varPhi ''(S_T) ( S_T )^2]={\mathord {\mathbb E}}[(\varPsi '(S_T)-\varPhi '(S_T))S_T]= {\mathord {\mathbb E}}[\varPsi (S_T)L_T]-{\mathord {\mathbb E}}[\varPhi '(S_T)S_T]. $$

Hence, we obtain the desired equation by differentiating

$$ {\mathord {\mathbb E}}\left[ \varPhi (S_T^{(\lambda f)}) \frac{L_T^{(\lambda f)}}{H_T^{(\lambda f)}} \right] ={\mathord {\mathbb E}}\left[ \frac{dP_{\lambda f} }{dP}_{\big | {{\mathscr {F}}_T}}\varPhi (S_T)\frac{L_T}{H_T} \right] $$

at $\lambda =0$. $\square$

Now we can prove Theorem 1.

Proof

The proof of Theorem 1 uses the same argument as in the proof of Corollary 3.6 of [9]. The only difference is that $S_T$ is a variance-gamma process in the proof of Corollary 3.6 of [9], while $S_T$ is a variance-GGC process in this proof.

When $\varPhi \in {\mathscr {C}}_b^2(\mathbb R_+,\mathbb R)$, all four formulas in Theorem 1 are direct consequences of $(ii)-( {v})$ in Lemma 2, and we now extend this result to the class $D(\mathbb R_+;\mathbb R)$. In general, in order to obtain an extension to $\varPhi$ in a class $\mathfrak {R}_1$ of functions based on an approximating sequence $( \varPhi _n )_{n\in \mathbb N}$ in a class $\mathfrak {R}_2 \subset \mathfrak {R}_1$, it suffices to show that for each compact set $K \subset \mathbb R$ we have

$$\begin{aligned} \sup _{S_0\in K}|{\mathord {\mathbb E}}[\varPhi _n(S_T)]-{\mathord {\mathbb E}}[\varPhi (S_T)]|\rightarrow 0 \qquad as\qquad n\rightarrow \infty , \end{aligned}$$

(14)

and

$$\begin{aligned} \lim _{n\rightarrow \infty } \sup _{S_0\in K}\left| \frac{\partial }{\partial S_0}{\mathord {\mathbb E}}[\varPhi _n(S_T)]-\frac{1}{S_0}{\mathord {\mathbb E}}[\varPhi (S_T)L_T]\right| = 0. \end{aligned}$$

(15)

The extension is then based on the above steps, first from ${\mathscr {C}}_b^2(\mathbb R_+,\mathbb R)$ to ${\mathscr {C}}_c (\mathbb R_+,\mathbb R)$, then to ${\mathscr {C}}_b(\mathbb R_+,\mathbb R)$ and to the class of finite linear combinations of indicator functions on an interval of $\mathbb R$. Finally the result is extended to the class of functions $\varPhi$ of the form $\varPhi =\varPsi \times \mathbf{1}_A$ where $\varPsi \in {\mathscr {C}}_L(\mathbb R_+,\mathbb R)$ and A is an interval of $\mathbb R_+$. This shows that (14) and (15) are satisfied, and the details of each step are the same as in the proof of Corollary 3.6 of [9]. $\square$