Sensitivity Analysis for Time-Inhomogeneous Lévy Process: A Malliavin Calculus Approach and Numerics

Abstract

The main goal of this paper is to study sensitivity analysis, with respect to the parameters of the model, in the framework of time-inhomogeneous Lévy process. This is a slight generalization of recent results of Fournié et al. (Finance Stochast 3(4):391–412, 1999 [9]), El-Khatib and Privault (Finance Stochast 8(2):161–179, 2004 [7]), Bally et al. (Ann Appl Probab 17(1):33–66, 2007 [1]), Davis and Johansson (Stochast Process Appl 116(1):101–129, 2006 [5]), Petrou (Electron J Probab 13(27):852–879, 2008 [12]), Benth et al. (Commun Stochast Anal 5(2):285–307, 2011 [2]) and El-Khatib and Hatemi (J Statist Appl Probab 3(1):171–182, 2012 [8]), using Malliavin calculus developed by Yablonski (Rocky Mountain J Math 38:669–701, 2008 [16]). This relatively recent result will help us to provide tools that are necessary for the calculation of the sensitivities. We provide some simple examples to illustrate the results achieved. In particular, we discussed the time-inhomogeneous versions of the Merton model and the Bates model.

1 Introduction

A trader selling a financial product to a customer usually tends to avoid any risk involved in that product and therefore wants to get rid of these risks by hedging. In some cases we can make use of a static hedge and we can hedge—and—forget it, additionally we can calculate the price from the products used for hedging. But for most options this is not possible and we have to use a dynamic hedging strategy. The price sensitivities with respect to the model parameters—the Greeks—are vital inputs in this context.

The Greeks are calculated as differentials of the derivative price, which can be expressed as an expectation (in risk—neutral measure) of the discounted payoff. The Greeks are traditionally estimated by means of a finite difference approximation. This approximation contains two errors: one on the approximation of the derivative function by means of its finite difference and another one on the numerical computation of the expectation. In addition the theoretical convergence rates for finite difference approximations are not met for discontinuous payoff functions.

Fournié et al. [9] propose a method with faster convergence which consists in shifting the differential operator from the payoff functional to the diffusion kernel, introducing a weighting function. The main idea is the use of the Malliavin integration by parts formula to transform the problem of calculating derivatives by finite difference approximations to calculating expectations of the form

$$\begin{aligned} \mathrm {E}[H(S_{T}) \pi |S_{0}=x] \end{aligned}$$

where the weight $\pi$ is a random variable and the underling price process is a Markov diffusion given by:

$$\begin{aligned} dS_{t} =b(S_{t}) dt+\sigma (S_{t}) dW_{t},\;\; S_{0} =x. \end{aligned}$$

There have been several studies that attempt to produce similar results for markets governed by processes with jumps. We mention León et al. [10], have approximated a jump—diffusion model for a simple Lévy process, and hedged an european call option using a Malliavin Calculus approach. El-Khatib and Privault [7] where a market generated by Poisson processes is considered. Their setup allows for random jump sizes, and by imposing a regularity condition on the payoff they use Malliavin calculus on Poisson space to derive weights for Asian options. Bally et al. [1] reduce the problem to a setting in which only ‘finite—dimensional’ Malliavin calculus is required in the case where stochastic differential equations are driven by Brownian motion and compound Poisson components. Davis and Johansson [5] have developed the Malliavin calculus for simple Lévy process which allows them to calculate the Greeks in a jump diffusion setting which satisfy a separability condition. Petrou [12] has calculated the sensitivities using Malliavin Calculus for markets generated by square integrable Lévy processes which is a extension of the paper [9]. Benth et al. [2] studied the computation of the deltas in model variation within a jump—diffusion framework with two approaches, the Malliavin calculs technics and the Fourier method. El-Khatib and Hatemi [8] estimated the price sensitivities of a trading position with regard to underlying factors in jump—diffusion models using jump times Poisson noise.

While Lévy processes offer nice features in terms of analytical tractability, the constraints of independence and stationarity of their increments prove to be rather restrictive. On one hand, the stationarity of increments of Lévy processes leads to rigid scaling properties for marginal distributions of returns, which are not observed in empirical time series of returns. On the other hand, from the point of view of risk neutral modeling, the Lévy models allow to reproduce the phenomenon of volatility smile for a given maturity, but it becomes more complicated when one tries to stick to several maturities. The inhomogeneity in time increments can improve it, hence the importance of introducing the additive processes in financial modeling. Each of the previous papers has its advantages in specific cases. However, they can only treat subclasses of Lévy processes except that of [12] but in time-homogeneous case setting.

The objective of this work is to derive stochastic weights in order to compute the Greeks in market models with jump when the discontinuity is described by a Poisson random measure with time-inhomogeneous intensity and then to use different numerical methods to compare the results for simpler time dependent models. The main tool uses Malliavin calculus, developed by Yablonski [16] for additive processes, that will be presented shortly at the appendix of the present document for the sake of completeness. Essentially, we introduce the time-inhomogeneity in the jump component of the risky asset price. In particular, we focus on a class of models in which the price of the underlying asset is governed by the following stochastic differential equation:

$$\begin{aligned} \left\{ \begin{array}{l} dS_{t}=b(t,S_{t-}) dt+\sigma (t,S_{t-}) dW_{t} \\ \quad \qquad \, +\int _{\mathbb {R}^{d}_{0}}\varphi (t,S_{t-},z) \widetilde{N}(dt,dz), \\ S_{0}=x \end{array} \right. \end{aligned}$$

(1)

where $\mathbb {R}^{d}_{0}:=\mathbb {R}^{d}\setminus \{0_{\mathbb {R}^{d}}\}$, $x=(x_{i}) _{1\le i\le d}\in \mathbb {R}^{d}$. The functions $b: \mathbb {R}^{+}\times \mathbb {R}^{d}\longrightarrow \mathbb {R}^{d}$, $\sigma : \mathbb {R}^{+}\times \mathbb {R}^{d}\longrightarrow \mathbb {R}^{d\times d}$ and $\varphi : \mathbb {R}^{+}\times \mathbb {R}^{d}\times \mathbb {R}^{d}\longrightarrow \mathbb {R}^{d\times d}$, are continuously differentiable with bounded derivatives. Here

$$W_{t}=(W_{1}(t),\ldots , W_{d}(t) ) $$

is a d-dimensional standard Brownian motion and

$$\widetilde{N}(dt,dz) ^{\top }=(N_{1}(dt,dz_{1}) -\nu ^{1}_{t}(z_{1}),\ldots , N_{d}(dt,dz_{d}) -\nu ^{d}_{t}(z_{d}) ) $$

where $N_{k}, k=1,\dots , d$ are independent Poisson random measures on $[0,T]\times \mathbb {R}_{0}$, $\mathbb {R}_{0}:=\mathbb {R}_{0}^1$, with time-inhomogeneous Lévy measures $\nu _{t}^{k}, k=1,\ldots , d$ coming from d independent one-dimensional time-inhomogeneous Lévy processes. The family of positive measures $(\nu _{t}^k) _{1\le k\le d}$ satisfies

$$\sum _{k=1}^{d}\int _{0}^{T}\int _{\mathbb {R}_{0}}(|z_k|^{2}\wedge 1) \nu ^k_{t}(dz_k) dt<\infty $$

and $\nu ^k_{t}(\{0\}) =0, k=1,\ldots , d$. Let $b(t,x) =b_{i}(t,x) ) _{1\le i\le d}$, $\sigma (t,x) =\sigma _{ij}(t,x) _{1\le i\le d, 1\le j\le d}$ and $\varphi (t,x,z) =\varphi _{ik}(t,x,z) _{1\le i\le d, 1\le k\le d}$ be the coefficients of (1) in the component form. Then $S_t=(S_i(t) ) _{1\le i\le d}$ in (1) can be equivalently written as

$$\begin{aligned} \left\{ \begin{array}{l} dS^{i}_{t}=b_i(t,S_{t-}) dt+\sum _{j=1}^{d}\sigma _{ij}(t,S_{t-}) dW_{j}(t) \\ \quad \qquad \, +\sum _{k=1}^{d}\int _{\mathbb {R}_{0}}\varphi _{ik}(t,S_{t-},z_{k}) \widetilde{N}_{k}(dt,dz_{k}), \\ S^{i}_{0}=x_i. \end{array} \right. \end{aligned}$$

(2)

To guarantee a unique strong solution to (1), we assume that the coefficients of (1) satisfy linear growth and Lipschitz continuity, i.e.,

$$\begin{aligned} \Vert b(t,x) \Vert ^{2}+\Vert \sigma (t,x) \Vert ^{2}+\sum _{k=1}^{d}\sum _{i=1}^{d}\int _{\mathbb {R}_{0}}|\varphi _{ik}(t,x,z_{k}) |^{2}\nu _{t}^{k}(dz_{k}) \le C(1+\Vert x\Vert ^{2})\nonumber \\ \end{aligned}$$

(3)

and

$$\begin{aligned} \Vert b(t,x) -b(t,y) \Vert ^{2}+\Vert \sigma (t,x) -\sigma (t,y) \Vert ^{2}\le K_1\Vert x-y\Vert ^{2} \end{aligned}$$

(4)

for all $x, y \in \mathbb {R}^{d}$ and ${t\in [0,T]}$, with C and $K_1$ are positive constants.

We suppose that there exists a family of functions $\rho _{k} :\mathbb {R} \longrightarrow \mathbb {R}$, $k=1,\dots , d$ such that

$$\begin{aligned} \sup _{0\le t\le T}\int _{\mathbb {R}_{0}}\sum _{k=1}^{d}|\rho _k(z_k) | ^{2}\nu ^k_{t}(dz_k) <\infty , \end{aligned}$$

(5)

and a positive constant $K_2$ such that

$$\begin{aligned} \sum _{i=1}^{d}|\varphi _{ik}(t,x,z_{k}) -\varphi _{ik}(t,y,z_{k}) |^{2}\le K_2|\rho (z_k) |^2\Vert x-y\Vert ^2, \end{aligned}$$

(6)

for all $x,y\in \mathbb {R}^{d}$, ${t\in [0,T]}$ and $z_k\in \mathbb {R}$, $k=1,\dots , d$. Similarly to the homogeneous case, we have the following lemma:

Lemma 1.1

Under the above conditions there exists a unique solution $(S_{t}) _{t\in [0,T]}$ for (1). Moreover, there exists a positive constant $C_{0}$ such that

$$\begin{aligned} \mathrm {E}\left[ \underset{0\le t\le T}{\sup }\Vert S_{t}\Vert ^{2}\right] <C_{0}. \end{aligned}$$

2 Regularity of Solutions of SDEs Driven by Time-Inhomogeneous Lévy Processes

The aim of this section is to prove that under specific conditions the solution of a stochastic differential equation belongs to the domains $\mathbb {D}^{1,2}$ (see Sects. 4.14 and 4.16). Having in mind the applications in finance, we will also provide a specific expression for the Wiener directional derivative of the solution.

Remark 2.1

The theory developed in the Appendix also holds in the case that our space is generated by an d-dimensional Wiener process and d-dimensional random Poisson measures. However, we will have to introduce new notation for the directional derivatives in order to simplify things. For the multidimensional case,

$$D_{t,0}=(D^{(1) }_{t,0},\ldots , D^{(d) }_{t,0}) $$

will denote a row vector, where the element $D^{(j) }_{t,0}$ of the jth row is the directional derivative for the Wiener process $W_{j}$, for all $j=1,\ldots , d$. Similarly, for all $z=(z_k) _{1\le k\le d}\in \mathbb {R}_{0}^d$ we define the row vector

$$D_{t,z}=(D^{(1) }_{t,z_1},\ldots , D^{(d) }_{t,z_d}) $$

where the element $D^{(k) }_{t,z_k}$ of the kth row is the directional derivative for the random Poisson measure $\widetilde{N}_{k}$, for all $k=1,\ldots , d$. For what follows we denote with $\sigma _{j}$ the jth column vector of $\sigma$ and $\varphi _{k}$ the kth column vector of $\varphi$.

Theorem 2.2

Let $(S_{t}) _{t\in [0,T]}$ be the solution of (1). Then $S_{t}\in \mathbb {D}^{1,2}$ for all $t\in [0,T]$, and we have

• 1. The Malliavin derivative $D^{(j) }_{r,0}S_{t}$ with respect to $W_j$ satisfies the following linear equation:

  $$\begin{aligned} D^{(j) }_{r,0}S_{t}= & {} \sum _{i=1}^{d}\int _{r}^{t}\frac{\partial b}{\partial x_i} (u,S_{u-}) D^{(j) }_{r,0}S^{i}_{u-}du+\sigma _{j}(r,S_{r-}) \\&+\sum _{i=1}^{d}\sum _{\alpha =1}^{d}\int _{r}^{t}\frac{\partial \sigma _{\alpha } }{\partial x_i} (u,S_{u-}) D^{(j) }_{r,0}S^{i}_{u-}dW_{\alpha }(u) \\&+\sum _{i=1}^{d}\int _{r}^{t}\int _{\mathbb {R}^{d}_{0}}\frac{\partial \varphi }{\partial x_i} (u,S_{u-},y) D^{(j) }_{r,0}S^{i}_{u-}\widetilde{N}(du,dy), \end{aligned}$$

  for $0\le r\le t$ a.e. and $D^{(j) }_{r,0}S_{t}=0$ a.e. otherwise.

• 2. For all $z\in \mathbb {R}^{d}_{0}$, The Malliavin derivative $D_{r,z}S_{t}$ with respect to $\widetilde{N}$ satisfies the following linear equation:

  $$\begin{aligned} D_{r,z}S_{t}= & {} \int _{r}^{t}D_{r,z}b(u,S_{u-}) du+\int _{r}^{t}D_{r,z}\sigma (u,S_{u-}) dW_{u} \\&+\,\varphi (r,S_{r-},z) +\int _{r}^{t}\int _{\mathbb {R}^{d}_{0}}D_{r,z}\varphi (u,S_{u-},y) \widetilde{N}(du,dy), \end{aligned}$$

  for $0\le r\le t$ a.e. and $D_{r,z}S_{t}=0$ a.e. otherwise.

Proof

• 1. We consider the Picard approximations $S_{t}^{n},\;n\ge 0$, given by

  $$\begin{aligned} \left\{ \begin{array}{l} S_{t}^{0}=x \\ S_{t}^{n+1}=\displaystyle x+\int _{0}^{t}b(u,S_{u-}^{n}) du+\int _{0}^{t}\sigma (u,S_{u-}^{n}) dW_{u} \\ \ \ \ \ \ \ \ \ \ \ \displaystyle +\int _{0}^{t}\int _{\mathbb {R}^{d}_{0}}\varphi (u,S_{u-}^{n},z) \widetilde{N}(du,dz) . \end{array} \right. \end{aligned}$$

  (7)

  From Lemma 1.1 we know that

  $$\begin{aligned} \mathrm {E}\left[ \underset{0\le t\le T}{\sup }|S_{t}^{n}-S_{t}|^{2}\right] \underset{n\rightarrow \infty }{\longrightarrow }0. \end{aligned}$$

  By induction, we prove that the following statements hold true for all $n\ge 0$.

  Hypothesis (H)

  • (a) $S_{t}^{n}\in \mathbb {D}^{1,2}$ for all ${t\in [0,T]}$.

  • (b) $\xi _{n}(t) =\underset{0\le r\le t}{\sup }\mathrm {E}\left[ \underset{ r\le u\le t}{\sup }\left| D_{r,0}S_{u}^{n}\right| ^{2}\right] <\infty$.

  • (c) $\xi _{n+1}(t) \le \alpha +\beta \int _{0}^{t}\xi _{n}(u) du$ for some constants $\alpha$, $\beta$.

  For $n=0$, it is straightforward that (H) is satisfied. Assume that (H) holds for a certain n. We would prove it for $n + 1$. By Proposition 4.12 $b(u,S_{u-}^{n})$, $\sigma (u,S_{u-}^{n})$ and $\varphi (u,S_{u-}^{n},z)$ are in $\mathbb {D}^{1,2}$. Furthermore,

  $$\begin{aligned} D_{r,0}b_{i}(u,S_{u-}^{n})= & {} \sum _{\alpha =1}^{d}\dfrac{\partial b_{i}}{\partial x_{\alpha }} (u,S_{u-}^{n}) D_{r,0}S_{u-}^{n,\alpha }\mathbf{1 }_{\{r\le u\}}, \\ D_{r,0}\sigma _{ij} (u,S_{u-}^{n})= & {} \sum _{\alpha =1}^{d}\dfrac{\partial \sigma _{ij}}{\partial x_{\alpha }} (u,S_{u-}^{n}) D_{r,0}S_{u-}^{n,\alpha }\mathbf{1 }_{\{r\le u\}}, \\ D_{r,0}\varphi _{ik}(u,S_{u-}^{n},z_k)= & {} \sum _{\alpha =1}^{d}\dfrac{\partial \varphi _{ik} }{\partial x_{\alpha }} (u,S_{u-}^{n},z_k) D_{r,0}S_{u-}^{n,\alpha }\mathbf{1 }_{\{r\le u\}}. \end{aligned}$$

  Since the functions b, $\sigma$ and $\varphi$ are continuously differentiable with bounded first derivatives in the second direction and taking into account the conditions (4) and (6) we have

  $$\begin{aligned} \left\| D_{r,0}b_{i}(u,S_{u-}^{n}) \right\| ^{2}\le & {} K_{1}\left\| D_{r,0}S_{u-}^{n}\right\| ^{2}, \nonumber \\ \left\| D_{r,0}\sigma _{ij} (u,S_{u-}^{n}) \right\| ^{2}\le & {} K_{1}\left\| D_{r,0}S_{u-}^{n}\right\| ^{2}, \\ \left\| D_{r,0}\varphi _{ik} (u,S_{u-}^{n},z_{k}) \right\| ^{2}\le & {} K_{2}|\rho (z_{k}) |^{2}\left\| D_{r,0}S_{u-}^{n}\right\| ^{2}. \nonumber \end{aligned}$$

  (8)

  However, $\int _{0}^{t}b(u,S_{u-}^{n}) du$, $\int _{0}^{t}\sigma (u,S_{u-}^{n}) dW_{u}$ and $\int _{0}^{t}\int _{\mathbb {R}_{0}^{d}}\varphi (u,S_{u-}^{n},z) \widetilde{N}(dt,dz)$ are in $\mathbb {D}^{1,2}$. Which implies that $S_{t}^{n+1}$ to $\mathbb {D}^{1,2}$ and we have

  $$\begin{aligned}&D^{(j) }_{r,0}\int _{0}^{t}b_{i}(u,S_{u-}^{n}) du \ =\ \int _{r}^{t}D^{(j) }_{r,0}b_{i}(u,S_{u-}^{n}) du, \\&D^{(j) }_{r,0}\sum _{\alpha =1}^{d}\int _{0}^{t}\sigma _{i\alpha } (u,S_{u-}^{n}) dW^{\alpha }_{u} \ =\ \sigma _{ij} (r,S_{r-}^{n}) +\sum _{\alpha =1}^{d}\int _{r}^{t}D^{(j) }_{r,0}\sigma _{i\alpha } (u,S_{u-}^{n}) dW_{\alpha }(u), \\&D^{(j) }_{r,0}\sum _{k=1}^{d}\int _{0}^{t}\int _{\mathbb {R}_{0}}\varphi _{ik}(u,S_{u-}^{n},z_{k}) \widetilde{N}_{k} (dt,dz_{k}) \ =\ \sum _{k=1}^{d}\int _{r}^{t}\int _{\mathbb {R}_{0}}D^{(j) }_{r,0}\varphi _{ik}(u,S_{u-}^{n},z_k) \widetilde{N}_{k}(dt,dz_k). \end{aligned}$$

  Thus

  $$\begin{aligned} D^{(j) }_{r,0}S_{t}^{n+1}= & {} \int _{r}^{t}D^{(j) }_{r,0}b(u,S_{u-}^{n}) du+\sigma _{j} (r,S_{r-}^{n}) +\sum _{\alpha =1}^{d}\int _{r}^{t}D^{(j) }_{r,0}\sigma _{\alpha }(u,S_{u-}^{n}) dW_{\alpha }(u) \\&+\sum _{k=1}^{d}\int _{r}^{t}\int _{\mathbb {R}_{0}}D^{(j) }_{r,0}\varphi _{k}(u,S_{u-}^{n},z_{k}) \widetilde{N}_{k} (dt,dz_{k}). \end{aligned}$$

  We conclude that

  $$\begin{aligned}&\mathrm {E}\left[ \underset{r\le v\le t}{\sup }|D^{(j) }_{r,0}S_{v}^{n+1}|^{2} \right] \le 4\left\{ \mathrm {E}\left[ \underset{r\le v\le t}{\sup } \left| \int _{r}^{v}D^{(j) }_{r,0}b(u,S_{u-}^{n}) du\right| ^{2}\right] \right. \\&+\,\mathrm {E}\left[ \underset{0\le t\le T}{\sup }|\sigma _{j} (t,S_{t}^{n}) |^{2}\right] +\mathrm {E}\left[ \underset{r\le v\le t}{\sup }\left| \sum _{\alpha =1}^{d}\int _{r}^{v}D^{(j) }_{r,0}\sigma _{\alpha }(u,S_{u-}^{n}) dW_{\alpha }(u) \right| ^{2}\right] \\&+\left. \mathrm {E}\left[ \underset{r\le v\le t}{\sup }\left| \sum _{k=1}^{d}\int _{r}^{v}\int _{\mathbb {R}_{0}}D^{(j) }_{r,0}\varphi _{k}(u,S_{u-}^{n},z_{k}) \widetilde{N}_{k} (dt,dz_{k}) \right| ^{2}\right] \right\} . \end{aligned}$$

  Using Cauchy–Schwarz inequality and Burkholder–Davis–Gundy inequality (see [14], Theorem 48 p. 193), there exists a constant $K>0$ such that

  $$\begin{aligned}&\mathrm {E}\left[ \underset{r\le v\le t}{\sup }|D^{(j) }_{r,0}S_{v}^{n+1}|^{2} \right] \le K\left\{ (t-r) \mathrm {E}\left[ \int _{r}^{t}|D^{(j) }_{r,0}b(u,S_{u-}^{n}) |^{2}du\right] \right. \\&+\,\mathrm {E}\left[ \underset{0\le t\le T}{\sup }|\sigma _{j} (t,S_{t}^{n}) |^{2}\right] +\mathrm {E}\left[ \sum _{\alpha =1}^{d}\int _{r}^{t}|D^{(j) }_{r,0}\sigma _{\alpha }(u,S_{u-}^{n}) |^{2}du\right] \\&+\left. \mathrm {E}\left[ \sum _{k=1}^{d}\int _{r}^{v}\int _{\mathbb {R}_{0}}|D^{(j) }_{r,0}\varphi _{k}(u,S_{u-}^{n},z_{k}) |^{2}\nu ^{k} _{u}(dz_k) du\right] \right\} . \end{aligned}$$

  From (6) and (8) we reach

  $$\begin{aligned}&\mathrm {E}\left[ \underset{r\le u\le t}{\sup }|D^{(j) }_{r,0}S_{u}^{n+1}|^{2} \right] \le K\mathrm {E}\left[ \underset{0\le t\le T}{\sup }|\sigma _{j} (t,S_{t}^{n}) |^{2}\right] \\&\quad +K\left( K_{1}(T+1) +K_{2}\underset{0\le t\le T}{\sup }\int _{\mathbb {R} _{0}}\sum _{k=1}^{d}|\rho _k(z_k) | ^{2}\nu ^k_{t}(dz_k) \right) \int _{r}^{t}\mathrm {E}\left[ |D^{(j) }_{r,0}S_{u-}^{n}|^{2}\right] du. \end{aligned}$$

  Then, from (3)

  $$\begin{aligned}&\mathrm {E}\left[ \underset{r\le u\le t}{\sup }|D^{(j) }_{r,0}S_{u}^{n+1}|^{2} \right] \le KC\left( 1+\mathrm {E}\left[ \underset{0\le t\le T}{\sup }|S_{t}^{n}|^{2}\right] \right) \\&\quad +K\left( K_{1}(T+1) +K_{2}\underset{0\le t\le T}{\sup }\int _{\mathbb {R} _{0}}\sum _{k=1}^{d}|\rho _k(z_k) | ^{2}\nu ^k_{t}(dz_k) \right) \int _{r}^{t}\mathrm {E}\left[ \underset{r\le v\le u}{\sup }|D^{(j) }_{r,0}S_{v-}^{n}|^{2}\right] du. \end{aligned}$$

  Consequently

  $$\begin{aligned} \xi _{n+1}(t) \le \alpha +\beta \int _{0}^{t}\xi _{n}(u) du, \end{aligned}$$

  where

  $$\begin{aligned} \alpha :=KC\left( 1+\underset{n\in \mathbb {N}}{\sup }\mathrm {E}\left[ \underset{0\le t\le T}{\sup }|S_{t}^{n}|^{2}\right] \right) <\infty \end{aligned}$$

  and, using (5), we have

  $$\begin{aligned} \beta :=K\left( K_{1}(T+1) +K_{2}+\underset{0\le t\le T}{\sup }\int _{\mathbb { R}_{0}}\sum _{k=1}^{d}|\rho _k(z_k) | ^{2}\nu ^k_{t}(dz_k) \right) <\infty . \end{aligned}$$

  By induction, we can easily prove that, for all $n\in \mathbb {N}$ and $t\in [0,T]$

  $$\begin{aligned} \xi _{n}(t) \le \alpha \sum _{i=0}^{n}\frac{(\beta t) ^{i}}{i!}. \end{aligned}$$

  Hence, for all $n\in \mathbb {N}$ and $t\in [0,T]$

  $$\begin{aligned} \xi _{n}(t) \le \alpha e^{\beta t}<\infty , \end{aligned}$$

  which implies that the derivatives of $S_{t}^{n}$ are bounded in $\mathrm {L} ^{2}(\varOmega \times [0,T])$ uniformly in n. Hence, we deduce that the random variable $S_{t}$ belongs to $\mathbb {D}^{1,2}$ and by applying the chain rule to (1) we achieve our proof.

• 2. Following the same steps we can prove the second claim of the theorem.

As in the classical Malliavin calculus we are able to associate the solution of (1) with the first variation process $Y_{t}:=\nabla _{x}S_{t}$. We reach the following proposition which provides us with a simpler expression for $D_{r,0}S_{t}$.

Proposition 2.3

Let $(S_{t}) _{t\in [0,T]}$ be the solution of (1). Then the derivative satisfies the following equation:

$$\begin{aligned} D_{r,0}S_{t}=Y_{t}Y_{r-}^{-1}\sigma (r,S_{r-}) \mathbf{1 }_{\{r\le t\}}\;\;a.e. \end{aligned}$$

(9)

where $(Y_{t}) _{t}$ is the first variation process of $(S_{t}) _{t}$.

Proof

Let $(S_{t}) _{t\in [0,T]}$ be the solution of (1). Then

$$\begin{aligned} D^{(j) }_{r,0}S^{i}_{t}= & {} \sum _{\beta =1 }^{d}\int _{r}^{t}\frac{\partial b_{i}}{\partial x_\beta } (u,S_{u-}) D^{(j) }_{r,0}S^{\beta }_{u-}du+\sigma _{ij}(r,S_{r-}) \\&+\sum _{\beta =1}^{d}\sum _{\alpha =1}^{d}\int _{r}^{t}\frac{\partial \sigma _{i\alpha } }{\partial x_\beta } (u,S_{u-}) D^{(j) }_{r,0}S^{\beta }_{u-}dW_{\alpha }(u) \\&+\sum _{\beta =1}^{d}\sum _{k=1}^{d}\int _{r}^{t}\int _{\mathbb {R}_{0}}\frac{\partial \varphi _{ik}}{\partial x_\beta } (u,S_{u-},z_{k}) D^{(j) }_{r,0}S^{\beta }_{u-}\widetilde{N}_{k}(du,dz_{k}). \end{aligned}$$

The $d\times d$ matrix–valued process $Y_t$ is given by

$$\begin{aligned} Y^{ij}_{t}:= & {} \frac{\partial S^{i}_{t}}{\partial x_j}\\= & {} \delta _{ij}+\sum _{k=1 }^{d}\int _{0}^{t}\frac{\partial b_{i}}{\partial x_k} (u,S_{u-}) Y^{k j}_{u-}du \\&+\sum _{k=1}^{d}\sum _{\alpha =1}^{d}\int _{0}^{t}\frac{\partial \sigma _{i\alpha } }{\partial x_k} (u,S_{u-}) Y^{k j}_{u-}dW_{\alpha }(u) \\&+\sum _{k=1}^{d}\sum _{\beta =1}^{d}\int _{0}^{t}\int _{\mathbb {R}_{0}}\frac{\partial \varphi _{i\beta }}{\partial x_k} (u,S_{u-},z_{\beta }) Y^{kj}_{u-}\widetilde{N}_{\beta }(du,dz_{\beta }) \end{aligned}$$

with $\delta _{ii}=1$ and $\delta _{ij}=0$ if $i\ne j$. Let $(Z_{t}) _{0\le t\le T}$ be a $d\times d$ matrix–valued process that satisfies the following equation

$$\begin{aligned} Z^{ij}_{t}= & {} \delta _{ij}+\sum _{k=1}^{d}\int _{0}^{t}\left( -\frac{\partial b_{k}}{\partial x_j} (u,S_{u-}) +\sum _{n=1}^{d}\sum _{\alpha =1}^{d}\frac{\partial \sigma _{k\alpha }}{\partial x_n} (u,S_{u-}) \frac{\partial \sigma _{n\alpha }}{\partial x_j} (u,S_{u-}) \right) Z^{ik}_{u-}du \\&+\sum _{k=1}^{d}\sum _{\beta =1}^{d}\int _{0}^{t}\int _{\mathbb {R}_{0}}\frac{\sum _{n=1}^{d}\frac{\partial \varphi _{k\beta }}{\partial x_n} (u,S_{u-},z_{\beta }) \frac{\partial \varphi _{n\beta }}{\partial x_j} (u,S_{u-},z_{\beta }) }{1+\frac{\partial \varphi _{k\beta }}{\partial x_j} (u,S_{u-},z_{\beta }) }Z^{ik}_{u-}\nu ^{\beta }_{u}(dz_{\beta }) du\\&-\sum _{k=1}^{d}\sum _{\alpha =1}^{d}\int _{0}^{t}\frac{\partial \sigma _{k\alpha }}{\partial x_j} (u,S_{u-}) Z^{ik}_{u-}dW_{\alpha }(u) \\&-\sum _{k=1}^{d}\sum _{\beta =1}^{d}\int _{0}^{t}\int _{\mathbb {R}_{0}}\frac{\frac{\partial \varphi _{k\beta }}{\partial x_j} (u,S_{u-},z_{\beta }) }{1+\frac{\partial \varphi _{k\beta }}{\partial x_j} (u,S_{u-},z_{\beta }) }Z^{ik}_{u-}\widetilde{N}_{\beta }(du,dz_{\beta }). \end{aligned}$$

By means of Itô’s formula, one can check that

$$\sum _{j=1}^{d}Z^{ij}_{t}Y^{jk}_{t}=\delta _{ik}.$$

Hence $Z_{t}Y_{t}=Z_{t}Y_{t}=I_{d}$ where $I_{d}$ is the unit matrix of size d. As a consequence, for any $t\ge 0$ the matrix $Y_{t}$ is invertible and $Y_{t}^{-1}=Z_{t}$. Applying again Itô’s formula, it holds that

$$D^{(j) }_{r,0}S^{i}_{t}=\sum _{n=1}^{d}\sum _{k=1}^{d}Y^{ik}_{t}Z^{kn}_{r}\sigma _{nj}(r,S_{r-}) \quad \text {for all}\quad r\le t.$$

Then the result follows.

2.1 Greeks

For $n\in \mathbb {N}^{*}$ we define the payoff $H:=H(S_{t_{1}},S_{t_{2}},\ldots , S_{t_{n}})$ to be a square integrable function discounted from maturity T and evaluated at the times $t_{1},t_{2},\ldots , t_{n}$ with the convention that $t_{0}=0$ and $t_{n}=T$. Under a chosen, since we do not have uniqueness, risk neutral measure, denoted by $\mathbb {Q}$, the price $\mathscr {C}(x)$ of the contingent claim given an initial value is then expressed as:

$$\begin{aligned} \mathscr {C}(x) =\mathrm {E}_{\mathbb {Q}}\left[ H(S_{t_{1}},S_{t_{2}},\ldots ,S_{t_{n}}) \right] . \end{aligned}$$

In what follows, we assume the next ellipticity¹ condition for the diffusion matrix $\sigma$.

Assumption 2.4

The diffusion matrix $\sigma$ satisfies the uniform ellipticity condition:

$$\exists \; \eta>0 \;\;\xi ^{*}\sigma ^{*}(t,x) \sigma (t,x) \xi >\eta \Vert \xi \Vert ^{2}, \;\; \forall \; \xi , x \in \mathbb {R}^{d}.$$

Using the Malliavin calculus developed in the Sect. 2.1 we are able to calculate the Greeks for the one–dimensional process $(S_{t}) _{t\in [0,T]}$ that satisfies equation (1).

2.2 Variation in the Initial Condition

In this section, we provide an expression for the derivatives of the expectation $\mathscr {C}(x)$ with respect to the initial condition x in the form of a weighted expectation of the same functional.

Let us define the set:

$$\begin{aligned} T_{n}=\left\{ a\in L^{2}([0,T]) :\int _{0}^{t_{i}}a(u) du=1\;\;\forall \ i=1,2,\dots , n\right\} \end{aligned}$$

where $t_{i}$, $i=1,2,\ldots , n$ are as defined in the Sect. 2.1.

Proposition 2.5

Assume that the diffusion matrix $\sigma$ is uniformly elliptic. Then for all $a\in T_{n}$,

$$\begin{aligned} \nabla _{x}\mathscr {C}(x) =\mathrm {E}_{\mathbb {Q}}\left[ H(S_{t_{1}},S_{t_{2}},\ldots , S_{t_{n}}) \int _{0}^{T}a(u) \sigma ^{-1}(u,S_{u-}) Y_{u-}dW_{u}\right] . \end{aligned}$$

Proof

Let H be a continuously differentiable function with bounded gradient. Then we can differentiate inside the expectation (see Fournié et al. [9] for details) and we have

$$\begin{aligned} \nabla _{x}\mathscr {C}(x)= & {} \mathrm {E}_{\mathbb {Q}}\left[ \sum _{i=1}^{n}\nabla _{i}H(S_{t_{1}},S_{t_{2}},\ldots , S_{t_{n}}) \nabla _{x}S_{t_{i}}\right] \\= & {} \mathrm {E}_{\mathbb {Q}}\left[ \sum _{i=1}^{n}\nabla _{i}H(S_{t_{1}},S_{t_{2}},\ldots , S_{t_{n}}) Y_{t_{i}}\right] \end{aligned}$$

where $\nabla _{i}H(S_{t_{1}},S_{t_{2}},\ldots , S_{t_{n}})$ is the gradient of H with respect to $S_{t_{i}}$ for $i=1,\ldots , n$. For any $a\in T_{n}$ and $i=1,\ldots , n$ and using (9) we find

$$\begin{aligned} Y_{t_{i}}=\int _{0}^{T}a(u) D_{u,0}S_{t_{i}}\sigma ^{-1}(u,S_{u-}) Y_{u-}du. \end{aligned}$$

From Proposition 4.12 we reach

$$\begin{aligned} \nabla _{x}\mathscr {C}(x)= & {} \mathrm {E}_{\mathbb {Q}}\left[ \int _{0}^{T}\sum _{i=1}^{n}\nabla _{i}H(S_{t_{1}},S_{t_{2}},\ldots ,S_{t_{n}}) a(u) D_{u,0}S_{t_{i}}\sigma ^{-1}(u,S_{u-}) Y_{u-}du\right] \\= & {} \mathrm {E}_{\mathbb {Q}}\left[ \int _{0}^{T}D_{u,0}H(S_{t_{1}},S_{t_{2}}, \ldots , S_{t_{n}}) a(u) \sigma ^{-1}(u,S_{u-}) Y_{u-}du\right] \\= & {} \mathrm {E}_{\mathbb {Q}}\left[ \int _{0}^{T}\int _{\mathbb {R} }D_{u,z}H(S_{t_{1}},S_{t_{2}},\ldots , S_{t_{n}}) a(u) \sigma ^{-1}(u,S_{u-}) Y_{u-}du\delta _{0}(dz) \right] . \\ \end{aligned}$$

Into measure $\pi (dudz)$ defined in Sect. 4.12 we replace $\varDelta$ by 0 and $\mu (du)$ by a Lebesgue measure du. Then

$$\begin{aligned} \nabla _{x}\mathscr {C}(x)= & {} \mathrm {E}_{\mathbb {Q}}\left[ \int _{0}^{T}\int _{\mathbb {R} }D_{u,z}H(S_{t_{1}},S_{t_{2}},\ldots , S_{t_{n}}) a(u) \sigma ^{-1}(u,S_{u-}) Y_{u-}\mathbf{1 }_{\{0\}}(z) \pi (dudz) \right] . \end{aligned}$$

Using the integration by parts formula (see Sect. 4.14), we have

$$\begin{aligned} \nabla _{x}\mathscr {C}(x) =\mathrm {E}_{\mathbb {Q}}\left[ H(S_{t_{1}},S_{t_{2}},\ldots , S_{t_{n}}) \delta \left( a(\cdot ) \sigma ^{-1}(\cdot ,S_{\cdot }) Y_{\cdot }\mathbf {1}_{\{z=0\}}(\cdot ) \right) \right] . \end{aligned}$$

However, $\left( a(u) \sigma ^{-1}(t,S_{t-}) Y_{t-}\right) _{0\le t\le T}$ is a predictable process, thus the Skorohod integral coincides with the Itô stochastic integral.

$$\begin{aligned} \nabla _{x}\mathscr {C}(x) =\mathrm {E}_{\mathbb {Q}}\left[ H(S_{t_{1}},S_{t_{2}},\ldots , S_{t_{n}}) \int _{0}^{T}a(u) \sigma ^{-1}(u,S_{u-}) Y_{u-}dW_{u}\right] . \end{aligned}$$

Since the family of continuously differentiable functions is dense in $L^2$, the result hold for any $H\in L^2$ (see Fournié et al. [9] for details).

2.3 Variation in the Drift Coefficient

Let $\widetilde{b}:\mathbb {R}^{+}\times \mathbb {R}^{d}\longrightarrow \mathbb {R}^{d}$ be a function such that for every $\varepsilon \in [-1,1]$, $\widetilde{b}$ and $b+\varepsilon \widetilde{b}$ are continuously differentiable with bounded first derivatives in the space directions.

We then define the drift–perturbed process $(S_{t}^{\varepsilon }) _{t}$ as a solution of the following perturbed stochastic differential equation:

$$\begin{aligned} \left\{ \begin{array}{c} dS_{t}^{\varepsilon }=(b(t,S_{t-}^{\varepsilon }) +\varepsilon \widetilde{b} (t,S_{t-}^{\varepsilon }) ) dt+\sigma (t,S_{t-}^{\varepsilon }) dW_{t} \\ \ \ \ \ \ \ \ \ \ \ +\int _{\mathbb {R}_{0}^{d}}\varphi (t,S_{t-}^{\varepsilon },z) \widetilde{N}(dt,dz),\; \text {with}\; S_{0}^{\varepsilon }=x. \end{array} \right. \end{aligned}$$

(10)

We can relate to this perturbed process the perturbed price $\mathscr {C} ^{\varepsilon }(x)$ defined by

$$\begin{aligned} \mathscr {C}^{\varepsilon }(x) =\mathrm {E}_{\mathbb {Q}}\left[ H(S_{t_{1}}^{\varepsilon },S_{t_{1}}^{\varepsilon },\ldots ,S_{t_{n}}^{\varepsilon }) \right] . \end{aligned}$$

Proposition 2.6

Assume that the diffusion matrix $\sigma$ is uniformly elliptic. Then we have

$$\begin{aligned} Rho=\frac{\partial \mathscr {C}^{\varepsilon }}{\partial \varepsilon }(x) \biggm |_{\varepsilon =0}=\mathrm {E}_{\mathbb {Q}}\left[ H(S_{t_{1}},S_{t_{2}},\ldots , S_{t_{n}}) \int _{0}^{T}(\sigma ^{-1}\widetilde{b} ) (t,S_{t-}) dW_{t}\right] . \end{aligned}$$

Proof

We introduce the random variable

$$\begin{aligned} \widetilde{D}_{T}^{\varepsilon }=\exp \left( \varepsilon \int _{0}^{T}(\sigma ^{-1}\widetilde{b}) (t,S_{t-}^{\varepsilon }) dW_{t}-\frac{\varepsilon ^{2}}{2}\int _{0}^{T}\Vert (\sigma ^{-1}\widetilde{b}) (t,S_{t-}^{\varepsilon }) \Vert ^{2}dt\right) . \end{aligned}$$

The Novikov condition is satisfied since

$$\begin{aligned} \mathrm {E}_{\mathbb {Q}}\left[ \exp \left( \frac{\varepsilon ^{2}}{2} \int _{0}^{T}\Vert (\sigma ^{-1}\widetilde{b}) (t,S_{t-}^{\varepsilon }) \Vert ^{2}dt\right) \right] <+\infty . \end{aligned}$$

As well as $\mathrm {E}_{\mathbb {Q}}[\widetilde{D}_{T}^{\varepsilon }]=1$, then we can define new probability measure $\mathbb {Q}^{\varepsilon }$ by its Radon–Nikodym derivative with respect to the risk–neutral probability measure $\mathbb {Q}$:

By changing of measure, we can write

$$\begin{aligned} \mathrm {E}_{\mathbb {Q}}\left[ H(S_{t_{1}}^{\varepsilon },S_{t_{1}}^{\varepsilon },\ldots , S_{t_{n}}^{\varepsilon }) \right]= & {} \mathrm {E}_{\mathbb {Q}^{\varepsilon }}\left[ H(S_{t_{1}}^{\varepsilon },S_{t_{1}}^{\varepsilon },\ldots , S_{t_{n}}^{\varepsilon }) \frac{d\mathbb {Q} }{d\mathbb {Q}^{\varepsilon }}\right] \\= & {} \mathrm {E}_{\mathbb {Q}}\left[ H(S_{t_{1}},S_{t_{2}},\ldots ,S_{t_{n}}) D_{T}^{\varepsilon }\right] \end{aligned}$$

where

$$\begin{aligned} D_{T}^{\varepsilon }= & {} \exp \left( -\varepsilon \int _{0}^{T}\left( (\sigma ^{-1}\widetilde{b}) (t,S_{t-}) \right) dW_{t}-\frac{\varepsilon ^{2}}{2} \int _{0}^{T}\Vert (\sigma ^{-1}\widetilde{b}) (t,S_{t-}) \Vert ^{2}dt\right) \\= & {} 1-\varepsilon \int _{0}^{T}\left( (\sigma ^{-1}\widetilde{b}) (t,S_{t-}) \right) D_{t}^{\varepsilon }dW_{t} \end{aligned}$$

which implies that

$$\begin{aligned}&\left| \frac{\mathrm {E}_{\mathbb {Q}}\left[ H(S_{t_{1}}^{\varepsilon },S_{t_{1}}^{\varepsilon },\ldots , S_{t_{n}}^{\varepsilon }) \right] -\mathrm { E}_{\mathbb {Q}}\left[ H(S_{t_{1}},S_{t_{2}},\ldots , S_{t_{n}}) \right] }{ \varepsilon }\right. \\&\left. - \,\mathrm {E}_{\mathbb {Q}}\left[ H(S_{t_{1}},S_{t_{2}},\ldots ,S_{t_{n}}) \int _{0}^{T}(\sigma ^{-1}\widetilde{b}) (t,S_{t-}) dW_{t}\right] \right| ^{2} \\= & {} \left| \mathrm {E}_{\mathbb {Q}}\left[ H(S_{t_{1}},S_{t_{2}},\ldots ,S_{t_{n}}) \left( \frac{D_{T}^{\varepsilon }-1}{\varepsilon }-\left( \int _{0}^{T}(\sigma ^{-1}\widetilde{b}) (t,S_{t-}) dW_{t}\right) \right) \right] \right| ^{2} \\\le & {} \mathrm {E}_{\mathbb {Q}}\left[ |H(S_{t_{1}},S_{t_{2}},\ldots ,S_{t_{n}}) |^{2}\right] \mathrm {E}_{\mathbb {Q}}\left[ \left| \frac{ D_{T}^{\varepsilon }-1}{\varepsilon }-\int _{0}^{T}\left( (\sigma ^{-1}\widetilde{b}) (t,S_{t-}) dW_{t}\right) \right| ^{2}\right] . \end{aligned}$$

2.4 Variation in the Diffusion Coefficient

In this section, we provide an expression for the derivatives of the price $\mathscr {C}(x)$ with respect to the diffusion coefficient $\sigma$. We introduce the set of deterministic functions

$$\begin{aligned} \widetilde{T}_{n}=\left\{ a\in L^{2}([0,T]) :\int _{t_{i-1}}^{t_{i}}a(u) du=1\;\;\forall \ i=1,2,\dots ,n\right\} \end{aligned}$$

where $t_{i}$, $i\,{=}\,1,\ 2,\ldots , n$ are as defined in the Sect. 2.1. Let $\widetilde{\sigma }:\mathbb {R}^{+}\,{\times }\,\mathbb {R}^{d}\,{\longrightarrow }\,\mathbb {R}^{d}\,{\times }~\mathbb {R}^{d}$ a direction function for the diffusion such that for every $\varepsilon \in [-1,1]$, $\widetilde{\sigma }$ and $\sigma +\varepsilon \widetilde{\sigma }$ are continuously differentiable with bounded first derivatives in the second direction and verify Lipschitz conditions such that the following assumption is satisfied:

Assumption 2.7

The diffusion matrix $\sigma +\varepsilon \widetilde{\sigma }$ satisfies the uniform ellipticity condition for every $\varepsilon \in [-1,1]$:

$$\exists \; \eta>0 \;\;\xi ^{*}\left( \sigma +\varepsilon \widetilde{\sigma }\right) ^{*}(t,x) \left( \sigma +\varepsilon \widetilde{\sigma }\right) (t,x) \xi >\eta \Vert \xi \Vert ^{2}, \quad \forall \; \xi , x \in \mathbb {R}^{d}.$$

We then define the diffusion–perturbed process $(S_{t}^{\varepsilon ,\widetilde{\sigma }}) _{0\le t\le T}$ as a solution of the following perturbed stochastic differential equation:

$$\begin{aligned} \left\{ \begin{array}{c} dS_{t}^{\varepsilon ,\widetilde{\sigma } }=b(t,S_{t-}^{\varepsilon ,\widetilde{\sigma } }) dt+\left( \sigma (t,S_{t-}^{\varepsilon ,\widetilde{\sigma } }) +\varepsilon \widetilde{\sigma }(t,S_{t-}^{\varepsilon ,\widetilde{\sigma } }) \right) dW_{t} \\ \ \ \ \ \ \ \ \ \ \ \ \ +\int _{\mathbb {R}_{0}^{d}}\varphi (t,S_{t-}^{\varepsilon ,\widetilde{\sigma } },z) \widetilde{N}(dt,dz),\text { with }S_{0}^{\varepsilon ,\widetilde{\sigma } }=x. \end{array} \right. \end{aligned}$$

We can also relate to this perturbed process the perturbed price $\mathscr {C} ^{\varepsilon ,\widetilde{\sigma } }(x)$ defined by

$$\begin{aligned} \mathscr {C}^{\varepsilon ,\widetilde{\sigma } }(x) :=\mathrm {E}_{\mathbb {Q}}\left[ H(S_{t_{1}}^{\varepsilon ,\widetilde{\sigma } },S_{t_{1}}^{\varepsilon ,\widetilde{\sigma } },\ldots ,S_{t_{n}}^{\varepsilon ,\widetilde{\sigma } }) \right] . \end{aligned}$$

We will need to introduce the variation process with respect to the parameter $\varepsilon$

$$\begin{aligned} dZ_{t}^{\varepsilon ,\widetilde{\sigma } }= & {} b^{\prime }(t,S_{t-}^{\varepsilon ,\widetilde{\sigma } }) Z_{t-}^{\varepsilon ,\widetilde{\sigma } }dt+\left( \sigma ^{\prime }(t,S_{t-}^{\varepsilon ,\widetilde{\sigma } }) +\varepsilon \widetilde{\sigma }^{\prime }(t,S_{t-}^{\varepsilon ,\widetilde{\sigma } }) \right) Z_{t-}^{\varepsilon ,\widetilde{\sigma } }dW_{t} \\&+\,\widetilde{\sigma }(t,S_{t-}^{\varepsilon ,\widetilde{\sigma } }) dW_{t}+\int _{\mathbb {R}^d _{0}}\varphi ^{\prime }(t,S_{t-}^{\varepsilon ,\widetilde{\sigma } },z) Z_{t-}^{\varepsilon ,\widetilde{\sigma } } \widetilde{N}(dt,dz) \;\text {and}\;Z_{0}^{\varepsilon ,\widetilde{\sigma } }=0, \end{aligned}$$

so that $\frac{\partial S_{t}^{\varepsilon ,\widetilde{\sigma } }}{\partial \varepsilon } =Z_{t}^{\varepsilon ,\widetilde{\sigma } }$. We simply use the notation $S_{t}$, $Y_{t}$ and $Z^{\widetilde{\sigma }}_{t}$ for $S_{t}^{0,\widetilde{\sigma }}$, $Y_{t}^{0,\widetilde{\sigma }}$ and $Z_{t}^{0,\widetilde{\sigma }}$ where the first variation process is given by $Y_{t}^{0,\widetilde{\sigma }}:=\nabla _{x}S_{t}^{0,\widetilde{\sigma }}$. Next, consider the process $(\beta ^{\widetilde{\sigma }}_{t})_{t\in [0,T]}$ defined by

$$\begin{aligned} \beta ^{\widetilde{\sigma }} _{t}:=Y_{t}^{-1}Z^{\widetilde{\sigma }}_{t},\;\;0\le t\le T\;\;a.e. \end{aligned}$$

Proposition 2.8

Assume that Hypothesis 2.7 holds. Set

$$\begin{aligned} \widetilde{\beta }_{t}^{a,\widetilde{\sigma }}=\sum _{i=1}^{n}a(t) \left( \beta ^{\widetilde{\sigma }} _{t_{i}}-\beta ^{\widetilde{\sigma }} _{t_{i-1}}\right) \mathbf {1}_{[t_{i-1},t_{i}[}(t). \end{aligned}$$

Suppose further that the process $(\sigma ^{-1}(t,S_{t}) Y_{t}\widetilde{\beta }_{t}^{a,\widetilde{\sigma }}\delta _{0}(z) ) _{(t,z) }$ belongs to $Dom(\delta )$, then we have for any $a\in \widetilde{T}_{n}$:

$$\begin{aligned} Vega=\frac{\partial \mathscr {C}^{\varepsilon ,\widetilde{\sigma } }}{\partial \varepsilon }(x) \biggm |_{\varepsilon =0}=\mathrm {E}_{\mathbb {Q}}\left[ H(S_{t_{1}},S_{t_{2}},\ldots , S_{t_{n}}) \delta \left( \sigma ^{-1}(\cdot ,S_{\cdot }) Y_{\cdot }\widetilde{\beta }_{\cdot }^{a,\widetilde{\sigma }}\delta _{0}(\cdot ) \right) \right] . \end{aligned}$$

Moreover, if the process $\left( \beta ^{\widetilde{\sigma }}_{t}\delta _{0}(z) \right) _{t\in [0,T]}$ belongs to $\mathbb {D}^{1,2}$, then

$$\begin{aligned} \delta \left( \sigma ^{-1}(\cdot ,S_{\cdot }) Y_{\cdot }\widetilde{\beta }_{\cdot }^{a,\widetilde{\sigma }}\delta _{0}(\cdot ) \right)= & {} \sum _{i=1}^{n}\left\{ \beta ^{\widetilde{\sigma }} _{t_{i}}\delta _{0}(z) \int _{t_{i-1}}^{t_{i}}a(t) (\sigma ^{-1}(t,S_{t-}) Y_{t-}) dW_{t}\right. \\&-\int _{t_{i-1}}^{t_{i}}a(t) \left( (D_{t,0}\beta ^{\widetilde{\sigma }}_{t_{i}}) \sigma ^{-1}(t,S_{t-}) Y_{t-}\right) dt \\&-\left. \int _{t_{i-1}}^{t_{i}}a(t) (\sigma ^{-1}(t,S_{t-}) Y_{t-}\beta ^{\widetilde{\sigma }} _{t_{i-1}}\delta _{0}(z) dW_{t}\right\} . \end{aligned}$$

Proof

Let H be a continuously differentiable function with bounded gradient. Then we can differentiate inside the expectation

$$\begin{aligned} \frac{\partial \mathscr {C}^{\varepsilon ,\widetilde{\sigma } }}{\partial \varepsilon }(x)= & {} \mathrm {E}_{\mathbb {Q}}\left[ \sum _{i=1}^{n}\nabla _{i}H(S_{t_{1}}^{\varepsilon ,\widetilde{\sigma } },S_{t_{2}}^{\varepsilon ,\widetilde{\sigma } },\ldots ,S_{t_{n}}^{\varepsilon ,\widetilde{\sigma } }) \frac{\partial S_{t_{i}}^{\varepsilon ,\widetilde{\sigma } }}{\partial \varepsilon }\right] \\= & {} \mathrm {E}_{\mathbb {Q}}\left[ \sum _{i=1}^{n}\nabla _{i}H(S_{t_{1}}^{\varepsilon ,\widetilde{\sigma } },S_{t_{2}}^{\varepsilon ,\widetilde{\sigma } },\ldots ,S_{t_{n}}^{\varepsilon ,\widetilde{\sigma } }) Z_{t_{i}}^{\varepsilon ,\widetilde{\sigma } }\right] . \end{aligned}$$

Hence

$$\begin{aligned} \frac{\partial \mathscr {C}^{\varepsilon ,\widetilde{\sigma }}}{\partial \varepsilon }(x) \biggm | _{\varepsilon =0}=\mathrm {E}_{\mathbb {Q}}\left[ \sum _{i=1}^{n}\nabla _{i}H(S_{t_{1}},S_{t_{2}},\ldots , S_{t_{n}}) Z_{t_{i}}^{\widetilde{\sigma }}\right] . \end{aligned}$$

On the other hand we have

$$\begin{aligned} Z_{t_{i}}^{\widetilde{\sigma }}= & {} Y_{t_{i}}\beta ^{\widetilde{\sigma }} _{t_{i}} \\= & {} Y_{t_{i}}\sum _{j=1}^{i}(\beta ^{\widetilde{\sigma }} _{t_{j}}-\beta ^{\widetilde{\sigma }} _{t_{j-1}}) \\= & {} Y_{t_{i}}\sum _{j=1}^{i}\int _{t_{j-1}}^{t_{j}}a(t) (\beta ^{\widetilde{\sigma }} _{t_{j}}-\beta ^{\widetilde{\sigma }} _{t_{j-1}}) dt \\= & {} \int _{t_{0}}^{t_{i}}Y_{t_{i}}\widetilde{\beta }_{t}^{a,\widetilde{\sigma }}dt. \end{aligned}$$

From Proposition 2.3, we conclude that

$$\begin{aligned} Z_{t_{i}}^{\widetilde{\sigma }}=\int _{0}^{T}D_{u,0}S_{t_{i}}\sigma ^{-1}(u,S_{u-}) Y_{u-}\widetilde{\beta }_{u}^{a,\widetilde{\sigma }}du. \end{aligned}$$

Which implies that

$$\begin{aligned} \frac{\partial \mathscr {C}^{\varepsilon ,\widetilde{\sigma } }}{\partial \varepsilon }(x) \biggm | _{\varepsilon =0}= & {} \mathrm {E}_{\mathbb {Q}}\left[ \int _{0}^{T} \sum _{i=1}^{n}\nabla _{i}H(S_{t_{1}},S_{t_{2}},\ldots ,S_{t_{n}}) D_{u,0}S_{t_{i}}\sigma ^{-1}(u,S_{u-}) Y_{u-}\widetilde{\beta }_{u}^{a,\widetilde{\sigma }}du\right] \\= & {} \mathrm {E}_{\mathbb {Q}}\left[ \int _{0}^{T}D_{u,0}H(S_{t_{1}},S_{t_{2}}, \ldots , S_{t_{n}}) \sigma ^{-1}(u,S_{u-}) Y_{u-}\widetilde{\beta }_{u}^{a,\widetilde{\sigma }}du\right] \!. \end{aligned}$$

Using the duality formula in Sect. 4.14 and taking into account the fact that $(\sigma ^{-1}(t,S_{t}) Y_{t}\widetilde{\beta }_{t}^{a,\widetilde{\sigma }}\delta _{0}(z) ) _{(t,z) }$ belongs to $Dom(\delta )$, we reach

$$\begin{aligned} \frac{\partial \mathscr {C}^{\varepsilon ,\widetilde{\sigma } }}{\partial \varepsilon }(x) \biggm | _{\varepsilon =0}=\mathrm {E}_{\mathbb {Q}}\left[ H(S_{t_{1}},S_{t_{2}},\ldots ,S_{t_{n}}) \delta \left( \sigma ^{-1}(\cdot ,S_{\cdot }) Y_{\cdot }\widetilde{\beta }_{\cdot }^{a,\widetilde{\sigma }}\delta _{0}(\cdot ) \right) \right] . \end{aligned}$$

2.5 Variation in the Jump Amplitude

To derive a stochastic weight for the sensitivity with respect to the amplitude parameter $\varphi$ we use the same technique as in the Proposition 2.6. To do this, we consider the perturbed process

$$\begin{aligned} \left\{ \begin{array}{l} dS_{t}^{\varepsilon ,\widetilde{\varphi } }=b(t,S_{t-}^{\varepsilon ,\widetilde{\varphi } }) dt+\sigma (t,S_{t-}^{\varepsilon ,\widetilde{\varphi } }) dW_{t} \\ \qquad \qquad \,+\int _{\mathbb {R}_{0}^{d}}(\varphi (t,S_{t-}^{\varepsilon ,\widetilde{\varphi } },z) +\varepsilon \widetilde{\varphi }(t,S_{t-}^{\varepsilon ,\widetilde{\varphi }},z) ) \widetilde{N}(dt,dz), \\ S_{0}^{\varepsilon ,\widetilde{\varphi } }=x \end{array} \right. \end{aligned}$$

where $\varepsilon \in [-1,1]$ and $\widetilde{\varphi }:\mathbb {R}^{+}\times \mathbb {R}^{d}\times \mathbb {R}^{d}\longrightarrow \mathbb {R}^{d\times d}$ is continuously differentiable function with bounded first derivative in the second direction. The variation process with respect to the parameter $\varepsilon$ becomes

$$\begin{aligned} \left\{ \begin{array}{lll} dZ_{t}^{\varepsilon ,\widetilde{\varphi } }&{}=&{}b^{\prime }(t,S_{t-}^{\varepsilon ,\widetilde{\varphi } }) Z_{t-}^{\varepsilon ,\widetilde{\varphi } }dt+\sum _{k=1}^{d}\sigma _{k}^{\prime }(t,S_{t-}^{\varepsilon ,\widetilde{\varphi } }) Z_{t-}^{\varepsilon ,\widetilde{\varphi } }dW_{t}^{(k) } \\ &{}&{} +\int _{\mathbb {R}_{0}^{d}}\left( \varphi ^{\prime }(t,S_{t-}^{\varepsilon ,\widetilde{\varphi } },z) +\varepsilon \widetilde{\varphi }^{\prime }(t,S_{t-}^{\varepsilon ,\widetilde{\varphi } },z) \right) Z_{t-}^{\varepsilon ,\widetilde{\varphi } }\widetilde{N}(dt,dz) \\ &{}&{} +\int _{\mathbb {R}_{0}^{d}}\widetilde{\varphi }(t,S_{t-}^{\varepsilon ,\widetilde{\varphi }},z) \widetilde{N}(dt,dz), \\ Z_{0}^{\varepsilon ,\widetilde{\varphi } }&{}=&{}0. \end{array} \right. \end{aligned}$$

We can also relate to this perturbed process the perturbed price $\mathscr {C} ^{\varepsilon ,\widetilde{\varphi } }(x)$ defined by

$$\begin{aligned} \mathscr {C}^{\varepsilon ,\widetilde{\varphi } }(x) :=\mathrm {E}_{\mathbb {Q}}\left[ H(S_{t_{1}}^{\varepsilon ,\widetilde{\varphi } },S_{t_{1}}^{\varepsilon ,\widetilde{\varphi } },\ldots ,S_{t_{n}}^{\varepsilon ,\widetilde{\varphi } }) \right] . \end{aligned}$$

Hence, the statement of the following proposition is practically identical to Proposition 2.8:

Proposition 2.9

Assume that the diffusion matrix $\sigma$ is uniformly elliptic and the process $(\sigma ^{-1}(t,S_{t}) Y_{t}\widetilde{\beta }_{t}^{a,\widetilde{\varphi }}\delta _{0}(z) ) _{(t,z) }\in Dom(\delta )$, then we have for any $a\in \widetilde{T}_{n}$:

$$\begin{aligned} Kappa=\frac{\partial \mathscr {C}^{\varepsilon ,\widetilde{\varphi } }}{\partial \varepsilon }(x) \biggm |_{\varepsilon =0}=\mathrm {E}_{\mathbb {Q}}\left[ H(S_{t_{1}},S_{t_{2}},\ldots , S_{t_{n}}) \delta \left( \sigma ^{-1}(\cdot ,S_{\cdot }) Y_{\cdot }\widetilde{\beta }_{\cdot }^{a,\widetilde{\varphi }}\delta _{0}(\cdot ) \right) \right] . \end{aligned}$$

Moreover, if the process $(\beta ^{\widetilde{\varphi }}_{t}\delta _{0}(z) ) _{t\in [0,T]}$ belongs to $\mathbb {D}^{1,2}$, then

$$\begin{aligned} \delta \left( \sigma ^{-1}(\cdot ,S_{\cdot }) Y_{\cdot }\widetilde{\beta } _{\cdot }^{a,\widetilde{\varphi }}\delta _{0}(\cdot ) \right)= & {} \sum _{i=1}^{n}\left\{ \beta ^{\widetilde{\varphi }}_{t_{i}}\delta _{0}(z) \int _{t_{i-1}}^{t_{i}}a(t) (\sigma ^{-1}(t,S_{t-}) Y_{t-}) dW_{t}\right. \\&-\int _{t_{i-1}}^{t_{i}}a(t) \left( (D_{t,0}\beta ^{\widetilde{\varphi }}_{t_{i}}) \sigma ^{-1}(t,S_{t-}) Y_{t-}\right) dt \\&-\left. \int _{t_{i-1}}^{t_{i}}a(t) (\sigma ^{-1}(t,S_{t-}) Y_{t-}\beta ^{\widetilde{\varphi }}_{t_{i-1}}\delta _{0}(z) ) dW_{t}\right\} . \end{aligned}$$

3 Numerical Experiments

In this section, we provide some simple examples to illustrate the results achieved in the previous section. In particular, we will look at time-inhomogeneous versions of the Merton model and the Bates model.

3.1 Examples

3.1.1 Time-Inhomogeneous Merton Model

We consider time-inhomogeneous versions of the Merton model when the riskless asset is governed by the equation:

$$\begin{aligned} dS_{t}^{0}=S_{t}^{0}r(t) dt,\;\ S_{0}^{0}=1, \end{aligned}$$

and the evolution of the risky asset is described by:

$$\begin{aligned} dS_{t}=S_{t-}dL_{t},\;\ S_{0}=x, \end{aligned}$$

where

$$\begin{aligned} L_{t}=\int _{0}^{t}b(u) du+\int _{0}^{t}\sigma (u) dW_{u}+\int _{0}^{t}\varphi (u) dX_{u},\quad t\ge 0. \end{aligned}$$

• $\{W_{t},0\le t \le T\}$ is a standard Brownian motion.

• The process $\{X_{t},0\le t\le T\}$ is defined by $X_{t}:=\sum _{j=1}^{N_{t}}Z_{j}$ for all $t\in [0,T]$, such that $\{N_{t},t\ge 0\}$ is a inhomogeneous Poisson process with intensity function $\lambda (t)$ and $(Z_{n}) _{n\ge 1}$ is a sequence of square integrable random variables which are i.i.d. (we set $\kappa :=\mathrm {E}_{ \mathbb {Q}}[Z_{1}]$).

• $\{W_{t},t\ge 0\}$, $\{N_{t},t\ge 0\}$ and $\{Z_{n},n\ge 1\}$ are independent.

• r, b, $\sigma$ and $\varphi$ are deterministic functions.

We can write

$$\begin{aligned} L_{t}= & {} \int _{0}^{t}b(u) du+\int _{0}^{t}\sigma (u) dW_{u}+\int _{0}^{t}\int _{ \mathbb {R}_{0}}\varphi (u) zJ_{X}(du,dz) \\= & {} \int _{0}^{t}\left( b(u) +\kappa \varphi (u) \lambda (u) \right) du+\int _{0}^{t}\sigma (u) dW_{u}+\int _{0}^{t}\int _{\mathbb {R}_{0}}\varphi (u) z \widetilde{J}_{X}(du,dz), \end{aligned}$$

where $J_{X}(du,dz)$ and $\widetilde{J}_{X}(du,dz)$ are, respectively, the jump measure and the compensated jump measure of the process X. By Itô’s formula, we have for all $t\in [0,T]$:

$$\begin{aligned} \ln (S_{t})= & {} \ln (x) +\int _{0}^{t}\left( b(u) -\frac{1}{2}\sigma ^{2}(u) \right) du \\&+\int _{0}^{t}\sigma (u) dW_{u}+\int _{0}^{t}\int _{\mathbb {R}_{0}}\ln (1+\varphi (u) z) J_{X}(du,dz). \end{aligned}$$

Set $A_{t}=\exp (-\int _{0}^{t}r(u) du)$, we conclude that the process $(A_{t}S_{t}) _{t\in [0,T]}$ is a martingale if and only if the following condition is satisfied:

$$\begin{aligned} b(t) -r(t) +\kappa \varphi (t) \lambda (t) =0\;\;\forall \ t\in [0,T]. \end{aligned}$$

Hence, for all $t\in [0,T]$:

$$\begin{aligned} \ln (S_{t})= & {} \ln (x) +\int _{0}^{t}\left( r(u) -\frac{1}{2}\sigma ^{2}(u) -\kappa \varphi (u) \lambda (u) \right) du \\&+\int _{0}^{t}\sigma (u) dW_{u}+\int _{0}^{t}\int _{\mathbb {R}_{0}}\ln (1+\varphi (u) z) J_{X}(du,dz). \end{aligned}$$

The price of a contingent claim $H(S_{T})$ is then expressed as

$$\begin{aligned} \mathscr {C}(x) =\mathrm {E}_{\mathbb {Q}}\left[ A_{T}H(S_{T}) \right] , \end{aligned}$$

and for all $t\in [0,T]$, the processes $Y_{t}$, $Z_{t}^{\widetilde{\sigma }}$, $\beta _{t}^{\widetilde{\sigma }}$, $Z_{t}^{\widetilde{\varphi }}$ and $\beta _{t}^{ \widetilde{\varphi }}$ are, respectively, given by

$$\begin{aligned} Y_{t}= & {} \frac{S_{t}}{x} \\ Z_{t}^{\widetilde{\sigma }}= & {} \left( \int _{0}^{t}\widetilde{\sigma } (u) dW_{u}-\int _{0}^{t}\widetilde{\sigma }(u) \sigma (u) du\right) S_{t} \\ \beta _{t}^{\widetilde{\sigma }}= & {} x\left( \int _{0}^{t}\widetilde{\sigma } (u) dW_{u}-\int _{0}^{t}\widetilde{\sigma }(u) \sigma (u) du\right) \\ Z_{t}^{\widetilde{\varphi }}= & {} \left( \int _{0}^{t}\int _{\mathbb {R}_{0}}\frac{ \widetilde{\varphi }(u) z}{1+\varphi (u) z}J_{X}(du,dz) -\int _{0}^{t}\kappa \widetilde{ \varphi }(u) \lambda (u) du\right) S_{t} \\ \beta _{t}^{\widetilde{\varphi }}= & {} x\left( \int _{0}^{t}\int _{\mathbb {R}_{0}} \frac{\widetilde{\varphi }(u) z}{1+\varphi (u) z}J_{X}(du,dz) -\int _{0}^{t}\kappa \widetilde{\varphi }(u) \lambda (u) du\right) . \end{aligned}$$

By using the general formulae developed in the previous section, we are able to compute analytically the values of the different Greeks $(a(u) =\frac{1}{T} )$:

$$\begin{aligned} \nabla _{x}\mathscr {C}(x)= & {} \mathrm {E}_{\mathbb {Q}}\left[ A_{T}H(S_{T}) \int _{0}^{T}a(u) \left( \sigma ^{-1}(u,S_{u-}) Y_{u-}\right) dW_{u}\right] \\= & {} \mathrm {E}_{\mathbb {Q}}\left[ A_{T}H(S_{T}) \int _{0}^{T}\frac{1}{xT\sigma (u) }dW_{u}\right] \end{aligned}$$

$$\begin{aligned} Rho_{\widetilde{r}}= & {} \mathrm {E}_{\mathbb {Q}}\left[ A_{T}H(S_{T}) \int _{0}^{T} \left( \sigma ^{-1}(t,S_{t-}) \widetilde{r}(t,S_{t-}) \right) dW_{t}\right] \\&-\,\mathrm {E}_{\mathbb {Q}}\left[ \int _{0}^{T}\widetilde{r}(u) duA_{T}H(S_{T}) \right] \\= & {} \mathrm {E}_{\mathbb {Q}}\left[ A_{T}H(S_{T}) \left( \int _{0}^{T}\frac{ \widetilde{r}(u) }{\sigma (u) }dW_{u}-\int _{0}^{T}\widetilde{r}(u) du\right) \right] \end{aligned}$$

$$\begin{aligned} Vega_{\widetilde{\sigma }}= & {} \mathrm {E}_{\mathbb {Q}}\left[ A_{T}H(S_{T}) \int _{0}^{T}\sigma ^{-1}(t,S_{t-}) Y_{t-}\widetilde{\beta }_{t-}^{a}dW_{t}\right] \\= & {} \mathrm {E}_{\mathbb {Q}}\left[ A_{T}H(S_{T}) \left( \int _{0}^{T}a(t) \beta _{T}(\sigma ^{-1}(t,S_{t-}) Y_{t-}) dW_{t}\right) \right] \\= & {} \mathrm {E}_{\mathbb {Q}}\left[ A_{T}H(S_{T}) \left( \int _{0}^{T}\frac{a(t) }{ \sigma (t) }\left( \int _{0}^{T}\widetilde{\sigma }(u) (dW_{u}-\sigma (u) du) \right) dW_{t}\right) \right] \end{aligned}$$

$$\begin{aligned} Kappa_{\widetilde{\varphi }}= & {} \mathrm {E}_{\mathbb {Q}}\left[ A_{T}H(S_{T}) \int _{0}^{T}\sigma ^{-1}(t,S_{t-}) Y_{t-}\widetilde{\beta }_{t-}^{a}dW_{t}\right] \\= & {} \mathrm {E}_{\mathbb {Q}}\left[ A_{T}H(S_{T}) \left( \int _{0}^{T}a(t) \beta _{T}(\sigma ^{-1}(t,S_{t-}) Y_{t-}) dW_{t}\right) \right] \\= & {} \mathrm {E}_{\mathbb {Q}}\left[ A_{T}H(S_{T}) \left( \int _{0}^{T}\frac{a(t) }{ \sigma (t) }dW_{t}\right) \right. \\&\left. \qquad \times \left( \int _{0}^{T}\int _{\mathbb {R}_{0}}\frac{\widetilde{ \varphi }(u) z}{1+\varphi (u) z}J_{X}(du,dz) -\int _{0}^{T}\kappa \widetilde{\varphi } (u) \lambda (u) du\right) \right] \end{aligned}$$

For numerical simplicity we suppose that the coefficients $r>0$, $\sigma >0$ are real constants and $\varphi =1$ such that $\ln (1+Z_{1}) \sim \mathscr {N}(\mu , \delta ^{2})$ where $\mu \in \mathbb {R}$ and $\delta >0$. The intensity function $\lambda (t)$ is exponentially decreasing given by $\lambda (t) =a e^{-b t}$ for all $t\in [0,T]$, where $a >0$ and $b >0$.

In this case we have $\kappa =\mathrm {E}[Z_{1}]=e^{\mu +\frac{\delta ^{2}}{2}}-1$ and the mean–value function of the Poisson process $\{N_{t},t\ge 0\}$ is $m(t) =\int _{0}^{t}\lambda (s) ds=\frac{a }{b } \left( 1-e^{-b t}\right) ,\;\;\forall \ t\in [0,T]$.

3.1.2 Binary Call Option

We consider the payoff of a digital call option of strike $K>0$ and maturity T i.e. $H(S_{T}) =\mathbf {1}_{\left\{ S_{T}\ge K\right\} }$, such that:

$$\begin{aligned} S_{T}=x\exp \left\{ \left( r-\frac{1}{2}\sigma ^{2}\right) T-\frac{a \kappa }{b }(1-e^{-b T}) +\sigma W_{T}+\sum _{j=1}^{N_{T}}\ln (1+Z_{j}) \right\} . \end{aligned}$$

The price of a digital option is given by:

Delta: variation in the initial condition

• Delta computed from a derivation under expectation: By conditioning on the number of jumps, we can express the price as a weighted sum of Black–Scholes prices:

  $$\begin{aligned} \mathscr {C}_{bin}^{M}=\sum _{n\ge 0}\frac{e^{-m(T) }(m(T) ) ^{n}}{n!}\mathscr {C} _{bin}^{BS}(0,T,S_{n},K,r,\sigma _{n}) \end{aligned}$$

  where $m(T) =\frac{a }{b }(1-e^{-b T})$, $S_{n}=x\exp (n(\mu +\frac{\delta ^{2}}{2}) -m(T) \kappa )$, $\sigma _{n}^{2}=\sigma ^{2}+n\frac{\delta ^{2}}{2}$ and $\mathscr {C} _{bin}^{BS}(0,T,S_{n},K,r,\sigma _{n})$ stands for the Black–Scholes price of a digital option.

  $$\begin{aligned} \varDelta _{bin}^{M}:=\frac{\partial \mathscr {C}_{bin}^{M}}{\partial x} =\sum _{n\ge 0}\frac{e^{-m(T) }(m(T) ) ^{n}}{n!}\frac{S_{n}}{x}\frac{\partial \mathscr {C}_{bin}^{BS}(0,T,S_{n},K,r,\sigma _{n}) }{\partial S_{n}}. \end{aligned}$$

  Recall that

  $$\begin{aligned} \mathscr {C}_{bin}^{BS}(0,T,S_{n},K,r,\sigma _{n}) =e^{-rT}\mathscr {N}(d_{2,n}) \end{aligned}$$

  and

  $$\begin{aligned} \frac{\partial \mathscr {C}_{bin}^{BS}(0,T,S_{n},K,r,\sigma _{n}) }{\partial S_{n}}=\frac{e^{-rT}}{S_{n}\sigma _{n}\sqrt{T}}\Phi (d_{2,n}) \end{aligned}$$

  where $d_{1,n}=\frac{\ln (\frac{S_{n}}{K}) +(r+\frac{\sigma _{n}^{2}}{2}) T}{ \sigma _{n}\sqrt{T}}$, $d_{2,n}=d_{1,n}-\sigma _{n}\sqrt{T}$ and $\Phi (z) = \frac{1}{\sqrt{2\pi }}e^{\frac{-z^{2}}{2}}$. Consequently

  $$\begin{aligned} \varDelta _{bin}^{M}=\frac{e^{-(rT+m(T) ) }}{x\sqrt{T}}\sum _{n\ge 0}\frac{ (m(T) ) ^{n}}{n!}\frac{\Phi (d_{2,n}) }{\sigma _{n}}. \end{aligned}$$

• Finite difference approximation scheme of Delta:

  $$\begin{aligned} \varDelta _{bin}^{M,DF}=\frac{\partial }{\partial x}\mathrm {E}_{\mathbb {Q} }[e^{-rT}H(S_{T}^{x}) ]\simeq \frac{\mathrm {E}_{\mathbb {Q} }[e^{-rT}H(S_{T}^{x+\varepsilon }) ]-\mathrm {E}_{\mathbb {Q} }[e^{-rT}H(S_{T}^{x-\varepsilon }) ]}{2\varepsilon }. \end{aligned}$$

• Global Malliavin formula for Delta:

  The stochastic Malliavin weight for the delta is written:

  $$\begin{aligned} \delta (\omega ) =\int _{0}^{T}\frac{1}{T}\frac{S_{t}}{x\sigma S_{t}}dW_{t}= \frac{W_{T}}{x\sigma T} \end{aligned}$$

  where $\omega (t) =a(t) \frac{Y_{t}}{\sigma S_{t}}$ and $Y_{t}=\frac{S_{t}}{x}$ and $a(t) =\frac{1}{T}$

  

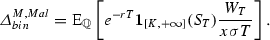
• Localized Malliavin formula for Delta:

  Empirical studies have shown that the theoretical estimators produced by the techniques of Malliavin are unbiased. We will adopt the localization technique introduced by Fournié et al. [9], which aims is to reduce the variance of the Monte–Carlo estimator for the sensitivities by localizing the integration by part formula around the singularity at K.

  Consider the decomposition:

  $$\begin{aligned} H(S_{T}) =H_{\varepsilon , loc}(S_{T}) +H_{\varepsilon , reg}(S_{T}). \end{aligned}$$

  The regular component is defined by:

  $$\begin{aligned} H_{\varepsilon , reg}(S_{T}) :=G_{\varepsilon }(S_{T}-K). \end{aligned}$$

  where $\varepsilon$ is a localization parameter and the localization function $G_{\varepsilon }$, that we propose, is given by:

  $$\begin{aligned} G_{\varepsilon }(z) =\left\{ \begin{array}{ll} 0; &{} z\le -\varepsilon \\ \frac{1}{2}\left( 1-\frac{z}{\varepsilon }\right) \left( 1+\frac{z}{ \varepsilon }\right) ^{3}; &{} -\varepsilon<z<0 \\ 1-\frac{1}{2}\left( 1+\frac{z}{\varepsilon }\right) \left( 1-\frac{z}{ \varepsilon }\right) ^{3}; &{} 0\le z<\varepsilon \\ 1; &{} z\ge \varepsilon . \end{array} \right. \end{aligned}$$

  Then

  $$\begin{aligned} H_{\varepsilon , reg}(S_{T})= & {} \frac{1}{2}\left( 1-\frac{S_{T}-K}{ \varepsilon }\right) \left( 1+\frac{S_{T}-K}{\varepsilon }\right) ^{3} \mathbf {1}_{\left\{ K-\varepsilon<S_{T}<K\right\} } \\&+\left( 1-\frac{1}{2}\left( 1+\frac{S_{T}-K}{\varepsilon }\right) \left( 1- \frac{S_{T}-K}{\varepsilon }\right) ^{3}\right) \mathbf {1}_{\left\{ K\le S_{T}<K+\varepsilon \right\} } \\&+\,\mathbf {1}_{\left\{ S_{T}\ge K+\varepsilon \right\} }. \end{aligned}$$

  The localized component is given by:

  $$\begin{aligned} H_{\varepsilon , loc}(S_{T}) =H(S_{T}) -H_{\varepsilon , reg}(S_{T}). \end{aligned}$$

  We find that the Delta computed by localized Malliavin formula:

  $$\begin{aligned} \varDelta _{LocMall}=e^{-rT}\mathrm {E}_{\mathbb {Q}}\left[ H_{\varepsilon ,loc}(S_{T}) \frac{W_{T}}{x\sigma T}\right] +e^{-rT}\mathrm {E}_{\mathbb {Q}} \left[ H_{\varepsilon , reg}^{\prime }(S_{T}) \frac{S_{T}}{x}\right] . \end{aligned}$$

In Fig. 1 we plot the delta for a digital option for a simplest time-inhomogeneous Merton model.

Fig. 1

Delta of a digital option computed by global, localized Malliavin like formula and finite difference. The parameters are $S_0=100$, $K=100$, $\sigma =0.10$, $T=1$, $r=0.02$, $\mu =-0.05$, $\delta =0.01$, $\varphi =1$, the intensity function $\lambda$ is exponentially decreasing given by $\lambda (t) =a e^{-b t}$ for all $t \in [0,T]$, where $a=1$ and $b=1$

Furthermore, we have

$$\begin{aligned} Rho= & {} e^{-rT}\mathrm {E}_{\mathbb {Q}}\left[ \left( \frac{W_{T}}{\sigma } -T\right) \mathbf {1}_{\left\{ S_{T}\ge K\right\} }\right] \\ Vega= & {} e^{-rT}\mathrm {E}_{\mathbb {Q}}\left[ \left( \frac{W_{T}^{2}-\sigma TW_{T}-T}{\sigma T}\right) \mathbf {1}_{\left\{ S_{T}\ge K\right\} }\right] \\ Kappa= & {} e^{-rT}\mathrm {E}_{\mathbb {Q}}\left[ \left( \sum _{j=1}^{N_{T}}\frac{ Z_{j}}{1+\varphi Z_{j}}-\kappa \frac{a }{b }(-e^{-b T}+1) \right) \frac{W_{T}}{\sigma T}\mathbf {1}_{\left\{ S_{T}\ge K\right\} }\right] . \end{aligned}$$

Rho: variation in the drift coefficient

• Rho computed from a derivation under expectation: Recall that

  $$\begin{aligned} \mathscr {C}_{bin}^{BS}(0,T,S_{n},K,r,\sigma _{n}) =e^{-rT}\mathscr {N}(d_{2,n}) \end{aligned}$$

  and

  $$\begin{aligned} \frac{\partial \mathscr {C}_{bin}^{BS}(0,T,S_{n},K,r,\sigma _{n}) }{\partial r} =-Te^{-rT}\mathscr {N}(d_{2,n}) +\frac{\sqrt{T}e^{-rT}}{\sigma _{n}}\Phi (d_{2,n}) \end{aligned}$$
  $$\begin{aligned} Rho_{bin}^{M}:= & {} \frac{\partial \mathscr {C}_{bin}^{M}}{\partial r} \\= & {} \sum _{n\ge 0}\frac{e^{-m(T) }(m(T) ) ^{n}}{n!}\frac{\partial \mathscr {C} _{bin}^{BS}(0,T,S_{n},K,r,\sigma _{n}) }{\partial r} \\= & {} \sum _{n\ge 0}\frac{e^{-m(T) }(m(T) ) ^{n}}{n!}(-Te^{-rT}\mathscr {N} (d_{2,n}) +\frac{\sqrt{T}e^{-rT}}{\sigma _{n}}\Phi (d_{2,n}) ) \\= & {} Te^{-(rT+m(T) ) }\sum _{n\ge 0}\frac{(m(T) ) ^{n}}{n!}\left( -\mathscr {N} (d_{2,n}) +\frac{\Phi (d_{2,n}) }{\sqrt{T}\sigma _{n}}\right) . \end{aligned}$$

• Finite Difference Approximation scheme of Rho:

  $$\begin{aligned} Rho_{FD}:=\frac{\partial }{\partial r}\mathrm {E}_{\mathbb {Q} }[e^{-rT}H(S_{T}) ]\simeq \frac{\mathrm {E}_{\mathbb {Q}}[e^{-(r+\varepsilon ) T}H(S_{T}^{r+\varepsilon }) ]- \mathrm {E}_{\mathbb {Q}}[e^{-(r-\varepsilon ) T}H(S_{T}^{r-\varepsilon }) ]}{2\varepsilon }. \end{aligned}$$

• Global Malliavin formula for Rho:

  $$\begin{aligned} Rho_{GMall}=e^{-rT}\mathrm {E}_{\mathbb {Q}}\left[ \left( \frac{W_{T}}{\sigma } -T\right) \mathbf {1}_{\left\{ S_{T}\ge K\right\} }\right] . \end{aligned}$$

• Localized Malliavin formula for Rho:

  $$\begin{aligned} Rho_{LocMall}= & {} e^{-rT}\mathrm {E}_{\mathbb {Q}}\left[ H_{ \varepsilon ,loc}(S_T) \left( \frac{W_{T}}{\sigma }-T\right) \right] \\&+e^{-rT}\mathrm {E}_{\mathbb {Q}}\left[ H^{\prime }_{\varepsilon ,reg}(S_T) TS_T\right] -Te^{-rT}\mathrm {E}_{\mathbb {Q}}\left[ H'_{\varepsilon ,reg}(S_T) \right] . \end{aligned}$$

In Fig. 2 we plot the Rho for a digital option for a simplest time-inhomogeneous Merton model.

Fig. 2

Rho of a digital option computed by global, localized Malliavin like formula and finite difference. The parameters are $S_0=100$, $K=100$, $\sigma =0.1$, $T=1$, $r=0.03$, $\mu =-0.05$, $\delta =0.01$, $\varphi =1$, the intensity function $\lambda$ is exponentially decreasing given by $\lambda (t) =a e^{-b t}$ for all $t \in [0,T]$, where $a=1$ and $b=1$

Vega: variation in the diffusion coefficient

• Vega computed from a derivation under expectation:

  $$\begin{aligned} Vega_{bin}^{M}: & {} =\frac{\partial \mathscr {C}_{bin}^{M}}{\partial \sigma } \\= & {} \sum _{n\ge 0}\frac{e^{-m(T) }(m(T) ) ^{n}}{n!}\frac{\partial \sigma _{n}}{ \partial \sigma }\frac{\partial \mathscr {C}_{bin}^{BS}(0,T,S_{n},K,r,\sigma _{n}) }{\partial \sigma _{n}} \\= & {} \sum _{n\ge 0}\frac{e^{-m(T) }(m(T) ) ^{n}}{n!}\frac{\sigma }{\sigma _{n}} (-e^{-rT}) (\sqrt{T}+\frac{d_{2,n}}{\sigma _{n}}) \Phi (d_{2,n}) \\= & {} -\sigma e^{-(rT+m(T) ) }\sum _{n\ge 0}\frac{(m(T) ) ^{n}}{n!}\left( \frac{ \sigma _{n}\sqrt{T}+d_{2,n}}{\sigma _{n}^{2}}\right) \Phi (d_{2,n}). \end{aligned}$$

• Finite Difference Approximation scheme of Vega:

  $$\begin{aligned} Vega_{FD}:=\frac{\partial }{\partial \sigma }\mathrm {E}_{\mathbb {Q} }[e^{-rT}H(S_{T}^{\sigma }) ]\simeq e^{-rT}\frac{\mathrm {E}_{\mathbb {Q} }[H(S_{T}^{\sigma +\varepsilon }) ]-\mathrm {E}_{\mathbb {Q}}[H(S_{T}^{\sigma -\varepsilon }) ]}{2\varepsilon }. \end{aligned}$$

• Global Malliavin formula for Vega:

  $$\begin{aligned} {Vega_{GMall}=e^{-rT}\mathrm {E}_{\mathbb {Q}}\left[ \left( \frac{ W_{T}^{2}-\sigma TW_{T}-T}{\sigma T}\right) \mathbf {1}_{\left\{ S_{T}\ge K\right\} }\right] .} \end{aligned}$$

• Localized Malliavin formula for Vega:

  $$\begin{aligned} Vega_{LocMall} =&e^{-rT}\mathrm {E}_{\mathbb {Q}}\left[ H_{\varepsilon ,loc}(S_{T}) \left( \frac{W_{T}^{2}-\sigma TW_{T}-T}{\sigma T}\right) \right] \\&+e^{-rT}\mathrm {E}_{\mathbb {Q}}\left[ H_{\varepsilon , reg}^{\prime }(S_{T}) \left( W_{T}-\sigma T\right) S_{T}\right] . \end{aligned}$$

In Fig. 3 we plot the Vega for a digital option for a simplest time-inhomogeneous Merton model.

Fig. 3

Vega of a digital option computed by global, localized Malliavin like formula and finite difference. The parameters are $S_0=100$, $K=100$, $r=0.02$, $\sigma =0.20$, $T=1$, $r=0.05$, $\mu =-0.05$, $\delta =0.01$, $\varphi =1$, the intensity function $\lambda$ is exponentially decreasing given by $\lambda (t) =a e^{-b t}$ for all $t \in [0,T]$, where $a=1$ and $b=1$

Alpha: variation in the jump amplitude

• Alpha computed from a derivation under expectation:

  $$\begin{aligned} Alpha_{bin}^{M}:= & {} \frac{\partial \mathscr {C}_{bin}^{M}}{\partial \varphi } \\= & {} \sum _{n\ge 0}\frac{e^{-m(T) }(m(T) ) ^{n}}{n!}\frac{\partial S_{n}}{ \partial \varphi }\frac{\partial \mathscr {C}_{bin}^{BS}(0,T,S_{n},K,r,\sigma _{n}) }{\partial S_{n}} \\= & {} \sum _{n\ge 0}\frac{e^{-m(T) }(m(T) ) ^{n}}{n!}\frac{m(T) \kappa S_{n}}{\varphi }\frac{ \partial \mathscr {C}_{bin}^{BS}(0,T,S_{n},K,r,\sigma _{n}) }{\partial S_{n}} \\= & {} \frac{\kappa e^{-(rT+m(T) ) }}{\varphi \sqrt{T}}\sum _{n\ge 0}\frac{(m(T) ) ^{n+1}}{ n!}\frac{\Phi (d_{2,n}) }{\sigma _{n}}. \end{aligned}$$

• Finite Difference Approximation scheme of Alpha:

  $$\begin{aligned} Alpha_{FD}:=\frac{\partial }{\partial \varphi }\mathrm {E}_{\mathbb {Q} }[e^{-rT}H(S_{T}^{\varphi }) ]\simeq e^{-rT}\frac{\mathrm {E}_{\mathbb {Q} }[H(S_{T}^{\varphi +\varepsilon }) ]-\mathrm {E}_{\mathbb {Q}}[H(S_{T}^{\varphi -\varepsilon }) ]}{2\varepsilon }. \end{aligned}$$

• Global Malliavin formula for Alpha:

  $$\begin{aligned} Alpha_{GMall}=e^{-rT}\mathrm {E}_{\mathbb {Q}}\left[ \left( \sum _{j=1}^{N_{T}} \frac{Z_{j}}{1+\varphi Z_{j}}-\kappa \frac{a }{b }(-e^{-b T}+1) \right) \frac{W_{T}}{\sigma T}\mathbf {1}_{\left\{ S_{T}\ge K\right\} } \right] . \end{aligned}$$

• Localized Malliavin formula for Alpha:

  $$\begin{aligned} Alpha_{LocMall}= & {} e^{-rT}\mathrm {E}_{\mathbb {Q}}\left[ H_{\varepsilon ,loc}(S_{T}) \left( \sum _{j=1}^{N_{T}}\frac{Z_{j}}{1+\varphi Z_{j}}-\kappa \frac{a }{b }(-e^{-b T}+1) \right) \frac{W_{T}}{\sigma T}\right] \\&+\,e^{-rT}\mathrm {E}_{\mathbb {Q}}\left[ H_{\varepsilon , reg}^{\prime }(S_{T}) \left( \sum _{j=1}^{N_{T}}\frac{Z_{j}}{1+\varphi Z_{j}}-\kappa \frac{ a }{b }(-e^{-b T}+1) \right) S_{T}\right] . \end{aligned}$$

In Fig. 4 we plot the sensitivity with respect to the jump size parameter $\varphi$ for a digital option for a simplest time-inhomogeneous Merton model.

Fig. 4

Alpha of a digital option computed by global, localized Malliavin like formula and finite difference. The parameters are $S_0=100$, $K=100$, $\sigma =0.20$, $T=1$, $r=0.02$, $\mu =-0.05$, $\delta =0.01$, $\varphi =1$, the intensity function $\lambda$ is exponentially decreasing given by $\lambda (t) =a e^{-b t}$ for all $t \in [0,T]$, where $a=1$ and $b=1$

3.1.3 Time-Inhomogeneous Bates Model:

We consider the solution of the stochastic differential equation:

$$\begin{aligned} \left\{ \begin{array}{l} dS^{1}_{t}=rS^{1}_{t-}dt+\sqrt{V_{t}}S^{1}_{t-}dW_{t}^{1}+S^{1}_{t-}\int _{ \mathbb {R}_{0}}(e^{z}-1) \widetilde{N}(dt,dz),\;\;S_{0}^{1}=x_{0}, \\ dV_{t}=\kappa (\theta -V_{t}) dt+\sigma \sqrt{V_{t}}dB_{t},\;\;V_{0}=v_{0}, \\ \left\langle W^{1},B\right\rangle _{t}=\rho t, \end{array} \right. \end{aligned}$$

where $(W_{t}^{1},B_{t}) _{t\in [0,T]}$ is a two–dimensional correlated Brownian motion with correlation parameter $\rho \in ]-1,1[$. The stochastic process $(S^{1}_{t})$ is the underling price process and $(V_{t})$ is the square of the volatility process which follows a CIR² process with an initial value $v_{0}>0$, with long–run mean $\theta$, and rate of reversion $\kappa$, $\sigma$ is referred to as the volatility of volatility.

For all ${t\in [0,T]}$, we define

$$\begin{aligned} W_{t}^{2}:=\frac{1}{\sqrt{1-\rho ^{2}}}\left( B_{t}-\rho W_{t}^{1}\right) . \end{aligned}$$

The process $(W_{t}^{2}) _{t\in [0,T]}$ is a Brownian motion which is independent of $(W_{t}^{1}) _{t\in [0,T]}$. Then, the system of stochastic differential equations can be rewritten in a matrix form

$$\begin{aligned} dS_{t}=b(t,S_{t-}) dt+\sigma (t,S_{t-}) dW_{t}+\int _{\mathbb {R}_{0}}\varphi (t,S_{t-},z) \widetilde{N}(dt,dz),\ S_{0}=(x_0,v_0) \end{aligned}$$

where $S_{t}=(S^{1}_{t},V_{t})$, $W_{t}^{*}=(W_{t}^{1},W_{t}^{2}) ^{*}$, $b^{*}(t,S_{t-}) =(rS^{1}_{t-},\kappa (\theta -V_{t}) ) ^{*}$, $\varphi ^{*} (t,S_{t-},z) =((e^{z}-1) S^{1}_{t-},0) ^{*}$ and

$$\begin{aligned} \sigma (t,S_{t-}) =\left( \begin{array}{cc} \sqrt{V_{t}}S^{1}_{t-} &{} 0 \\ &{} \\ \rho \sigma \sqrt{V_{t}} &{} \sigma \sqrt{1-{\rho ^{2}}}\sqrt{V_{t}} \end{array} \right) . \end{aligned}$$

The inverse of $\sigma$ is

$$\begin{aligned} {\sigma ^{-1}}(t,S_{t-}) =\frac{1}{\sigma \sqrt{1-\rho ^{2}}S^{1}_{t-}V_{t}} \left( \begin{array}{cc} \sigma \sqrt{1-\rho ^{2}}\sqrt{V_{t}} &{} 0 \\ &{} \\ -\rho \sigma \sqrt{V_{t}} &{} \sqrt{V_{t}}S^{1}_{t-} \end{array} \right) . \end{aligned}$$

The price of the contingent claim in this setting is expressed as:

$$\begin{aligned} \mathscr {C}=\mathrm {E}_{\mathbb {Q}}\left[ e^{-rT}H(S_{t}) \right] . \end{aligned}$$

Note that by Itô’s formula we have for all $t\in [0,T]$

$$\begin{aligned} \ln (S^{1}_{t})= & {} \int _{0}^{t}\left( r-\frac{1}{2}V_{u}\right) du+\int _{0}^{t}\int _{\mathbb {R}_{0}}\left[ z-(e^{z}-1) \right] \nu _{u}(dz) du \\&+\int _{0}^{t}\sqrt{V_{u}}dW_{u}^{1}+\int _{0}^{t}\int _{\mathbb {R}_{0}}z \widetilde{N}(du,dz). \end{aligned}$$

The Rho

In the drift—perturbed process $(S_{t}^{\varepsilon }) _{t}$ which is a solution of the stochastic differential equation (10), we take $\widetilde{b}^{*}(t,x) =(x_{1},0) ^{*}$ and we get

$$\begin{aligned} (\sigma ^{-1}(t,S_{t-}) \widetilde{b}(t,S_{t-}) ) ^{*}=\left( \frac{1}{\sqrt{ V_{t}}},\frac{-\rho }{\sqrt{1-\rho ^{2}}\sqrt{V_{t}}}\right) . \end{aligned}$$

From Proposition 2.6, we have

$$\begin{aligned} Rho=e^{-rT}\mathrm {E}_{\mathbb {Q}}\left[ H(S_{t}) \left( \int _{0}^{T} \frac{dW_{t}^{1}}{\sqrt{V_{t}}}-\frac{\rho }{\sqrt{1-\rho ^{2}}}\int _{0}^{T} \frac{dW_{t}^{2}}{\sqrt{V_{t}}}\right) \right] -Te^{-rT}\mathrm {E}_{\mathbb {Q }}\left[ H(S_{t}) \right] . \end{aligned}$$

The Delta

The first variation process is given by

$$\begin{aligned} \left\{ \begin{array}{l} dY_{t}=b'(t,S_{t-}) Y_{t-}dt+ \sigma '_{1}(t,S_{t-}) Y_{t-}dW_{t}^{1} \\ \qquad \qquad +\,\sigma '_{2} (t,S_{t-}) Y_{t-}dW_{t}^{2}+\int _{\mathbb {R}_{0}}\varphi '(t,S_{t-},z) Y_{t-}\widetilde{N}(dt,dz), \\ Y_{0}=I_{2} \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} b'(t,S_{t-}) =\left( \begin{array}{cc} r &{} 0 \\ 0 &{} -\kappa \end{array} \right) , \quad \varphi '(t,S_{t-},z) =\left( \begin{array}{cc} (e^{z}-1) &{} 0 \\ 0 &{} 0 \end{array} \right) , \end{aligned}$$

$$\begin{aligned} \sigma '_{1}(t,S_{t-}) =\left( \begin{array}{cc} \sqrt{V_{t}} &{} \frac{S^{1}_{t-}}{2\sqrt{V_{t}}} \\ 0 &{} \frac{\sigma \rho }{2\sqrt{V_{t}}} \end{array} \right) \; \text {and} \quad \sigma '_{2}(t,S_{t-}) =\left( \begin{array}{cc} 0 &{} 0 \\ 0 &{} \frac{\sigma \sqrt{1-\rho ^{2}}}{2\sqrt{V_{t}}} \end{array} \right) , \end{aligned}$$

$$\begin{aligned} \left( \sigma ^{-1}(t,S_{t-}) Y_{t-}\right) ^{*}=\left( \begin{array}{cc} \frac{Y_{t-}^{1,1}}{S^{1}_{t-}\sqrt{V_{t}}} &{} \frac{-\rho }{\sqrt{1-\rho ^{2} }}\frac{Y_{t-}^{1,1}}{S^{1}_{t-}\sqrt{V_{t}}} \\ \frac{Y_{t-}^{2,1}}{S^{1}_{t-}\sqrt{V_{t}}} &{} \frac{1}{\sqrt{1-\rho ^{2}} \sqrt{V_{t}}}\left( \frac{-\rho Y_{t-}^{1,2}}{S^{1}_{t-}}+\frac{Y_{t-}^{2,2} }{\sigma }\right) \end{array} \right) . \end{aligned}$$

By Proposition 2.5 we conclude that

$$\begin{aligned} Delta:= & {} \frac{\partial \mathscr {C}}{\partial x_{0}}\\= & {} e^{-rT} \mathrm {E}_{\mathbb {Q}}\left[ H(S_{t}) \left( \int _{0}^{T}a(t) \frac{Y_{t-}^{1,1}}{S^{1}_{t-}\sqrt{V_{t}}}dW_{t}^{1}-\int _{0}^{T}a(t) \frac{-\rho }{\sqrt{1-\rho ^{2} }}\frac{Y_{t-}^{1,1}}{S^{1}_{t-}\sqrt{V_{t}}}dW_{t}^{2}\right) \right] .\\ \end{aligned}$$

Since $Y_{t-}^{1,1}=\frac{S^{1}_{t-}}{x_{0}}$ and if we take $a(t) = \frac{1}{T}$, we get

$$\begin{aligned} Delta= & {} \frac{e^{-rT}}{x_{0}T} \mathrm {E}_{\mathbb {Q}}\left[ H(S_{t}) \left( \int _{0}^{T}\frac{dW_{t}^{1} }{\sqrt{V_{t}}}-\frac{\rho }{\sqrt{1-\rho ^{2}}}\int _{0}^{T}\frac{dW_{t}^{2} }{\sqrt{V_{t}}}\right) \right] . \end{aligned}$$

The Vega

We perturb the original diffusion matrix with $\widetilde{\sigma }$ to get the perturbed process given by (11) such that

$$\begin{aligned} \widetilde{\sigma }(t,x) =\left( \begin{array}{cc} x_{1} &{} 0 \\ 0 &{} 0 \end{array} \right) . \end{aligned}$$

For all $t\in [0,T]$, the processes $Z_{t}^{\widetilde{\sigma }}$ and $\beta _{t}^{\widetilde{\sigma }}$ are, respectively, given by

$$\begin{aligned} Z_{t}^{1,\widetilde{\sigma }}= & {} \left( W_{t}^{1}-\int _{0}^{t}\sqrt{V_{u}} du\right) S_{t},\;Z_{t}^{2,\widetilde{\sigma }}=0 \\ \beta _{t}^{1,\widetilde{\sigma }}= & {} x_{0}\left( W_{t}^{1}-\int _{0}^{t}\sqrt{ V_{u}}du\right) ,\;\beta _{t}^{2,\widetilde{\sigma }}=0. \end{aligned}$$

Using the chain rule (Proposition 4.12) on a sequence of continuously differentiable functions with bounded derivatives approximating $\sqrt{V_{u}}$, together with Proposition 2.3 we obtain

$$\begin{aligned} D_{t,0}\beta _{T}^{1,\widetilde{\sigma }}= & {} x_{0}\left( (1,0) ^{*}-\int _{0}^{T}\frac{1}{2\sqrt{V_{u}}}D_{t,0}\sqrt{V_{u}}du\right) \\= & {} x_{0}\left( (1,0) -\frac{\sigma }{2}\int _{t}^{T}\frac{\sqrt{V_{t}}}{\sqrt{ V_{u}}}\frac{Y_{u}^{2,2}}{Y_{t}^{2,2}}\left( \rho , \sqrt{1-\rho ^{2}}\right) du\right) . \end{aligned}$$

Thus

$$\begin{aligned} Tr\left( (D_{t,0}\beta _{T}) \sigma ^{-1}(t,S_{t-}) Y_{t-}\right) =\frac{1}{ \sqrt{V_{t}}}. \end{aligned}$$

Then

$$\begin{aligned} \delta \left( \sigma ^{-1}(\cdot ,S_{\cdot }) Y_{\cdot }\widetilde{\beta } _{\cdot }^{a}\delta _{0}(\cdot ) \right)= & {} \beta _{T}^{\widetilde{\sigma }*}\int _{0}^{T}a(t) (\sigma ^{-1}(t,S_{t-}) Y_{t-}) ^{*}dW_{t} \\&-\int _{0}^{T}a(t) Tr\left( (D_{t,0}\beta _{T}) \sigma ^{-1}(t,S_{t-}) Y_{t-}\right) dt \\= & {} \left( W_{T}^{1}-\int _{0}^{T}\sqrt{V_{u}}du\right) \\&\quad \times \left( \int _{0}^{T}\frac{a(t) }{\sqrt{V_{t}}}dW_{t}^{1}-\frac{ \rho }{\sqrt{1-\rho ^{2}}}\int _{0}^{T}\frac{a(t) }{\sqrt{V_{t}}} dW_{t}^{2}\right) \\&-\int _{0}^{T}\frac{a(t) }{\sqrt{V_{t}}}dt. \end{aligned}$$

Consequently,

$$\begin{aligned} Vega_{\widetilde{\sigma }}= & {} \frac{e^{-rT}}{T}\mathrm {E}_{\mathbb {Q}}\left[ H(S_{T}) \left( \left( W_{T}^{1}-\int _{0}^{T}\sqrt{V_{u}}du\right) \right. \right. \\&\left. \left. \quad \times \left( \int _{0}^{T}\frac{dW_{t}^{1}}{\sqrt{ V_{t}}}-\frac{\rho }{\sqrt{1-\rho ^{2}}}\int _{0}^{T}\frac{dW_{t}^{2}}{\sqrt{ V_{t}}}\right) -\int _{0}^{T}\frac{dt}{\sqrt{V_{t}}}\right) \right] . \end{aligned}$$

The alpha

We consider the perturbed process

$$\begin{aligned} \left\{ \begin{array}{l} dS_{t}^{\varepsilon }=b(t,S_{t-}^{\varepsilon }) dt+\sigma (t,S_{t-}^{\varepsilon }) dW_{t} \\ \qquad \qquad +\int _{\mathbb {R}_{0}}(\varphi (t,S_{t-}^{\varepsilon },z) +\varepsilon \widetilde{\varphi }(t,S_{t-}^{\varepsilon },z) ) \widetilde{N}(dt,dz), \\ S_{0}^{\varepsilon }=x, \end{array} \right. \end{aligned}$$

with

$$\begin{aligned} \widetilde{\varphi }(t,x,z) =\left( \begin{array}{c} x_{1} \\ 0 \end{array} \right) . \end{aligned}$$

For all $t\in [0,T]$, the processes $Z_{t}^{\widetilde{\varphi }}$ and $\beta _{t}^{\widetilde{\varphi }}$ defined above are, respectively, given by

$$\begin{aligned} Z_{t}^{1,\widetilde{\varphi }}= & {} \left( \int _{0}^{t}\int _{\mathbb {R}_{0}}e^{-z} \widetilde{N}(du,dz) -\int _{0}^{t}\int _{\mathbb {R}_{0}}(1-e^{-z}) \nu _{u}(dz) du\right) S_{t},\;\;Z_{t}^{2,\widetilde{\varphi }}=0 \\ \beta _{t}^{1,\widetilde{\varphi }}= & {} x_{0}\left( \int _{0}^{t}\int _{\mathbb {R} _{0}}e^{-z}\widetilde{N}(du,dz) -\int _{0}^{t}\int _{\mathbb {R}_{0}}(1-e^{-z}) \nu _{u}(dz) du\right) ,\;\;\beta _{t}^{2,\widetilde{\varphi }}=0. \end{aligned}$$

Then

$$\begin{aligned}&\delta \left( \sigma ^{-1}(\cdot , S_{\cdot }) Y_{\cdot }\widetilde{\beta } _{\cdot }^{a}\delta _{0}(\cdot ) \right) =\beta _{T}^{\widetilde{\varphi }*}\int _{0}^{T}a(t) (\sigma ^{-1}(t,S_{t-}) Y_{t-}) ^{*}dW_{t} \\&-\int _{0}^{T}a(t) Tr\left( (D_{t,0}\beta _{T}) \sigma ^{-1}(t,S_{t-}) Y_{t-}\right) dt \\= & {} \left( \int _{0}^{T}\int _{\mathbb {R}_{0}}e^{-z}\widetilde{N} (du,dz) -\int _{0}^{T}\int _{\mathbb {R}_{0}}(1-e^{-z}) \nu _{u}(dz) du\right) \\&\times \left( \int _{0}^{T}\frac{a(t) }{\sqrt{V_{t}}}dW_{t}^{1}-\frac{\rho }{ \sqrt{1-\rho ^{2}}}\int _{0}^{T}\frac{a(t) }{\sqrt{V_{t}}}dW_{t}^{2}\right) . \end{aligned}$$

Consequently

$$\begin{aligned} Alpha_{\widetilde{\varphi }}= & {} \frac{e^{-rT}}{T}\mathrm {E}_{\mathbb {Q}}\left[ H(S_{T}) {\left( \int _{0}^{T}\int _{\mathbb {R}_{0}}e^{-z}\widetilde{N} (du,dz) -\int _{0}^{T}\int _{\mathbb {R}_{0}}(1-e^{-z}) \nu _{u}(dz) du\right) } \right. \\&\left. {\times \left( \int _{0}^{T}\frac{dW_{t}^{1}}{\sqrt{V_{t}}}-\frac{ \rho }{\sqrt{1-\rho ^{2}}}\int _{0}^{T}\frac{dW_{t}^{2}}{\sqrt{V_{t}}}\right) }\right] . \end{aligned}$$

4 Malliavin Calculus for Square Integrable Additive Processes

4.1 Additive Processes

Definition 4.1

( see Cont [3], Definition 14.1 ) A stochastic process $(S_{t}) _{t\ge 0}$ on $\mathbb {R}^{d}$ is called an additive process if it is càdlàg, satisfies $S_{0}=0$ and has the following properties:

• 1. Independent increments: for every increasing sequence of times $t_{0},\ldots , t_{n}$, the random variables $S_{t_{0}},S_{t_{1}}-S_{t_{0}}, \ldots , S_{t_{n}}-S_{t_{n-1}}$ are independent.

• 2. Stochastic continuity: $\forall \ \varepsilon >0\ \text {and}\ \forall \ t\ge 0,\ \lim _{h\rightarrow 0}\mathbb {P} [|S_{t+h}-S_{t}|\ge \varepsilon ]=0.$

Theorem 4.2

(see Sato [15], Theorems 9.1–9.8) Let $(S_{t}) _{t\ge 0}$ be an additive process on $\mathbb {R}^{d}$. Then $S_{t}$ has an infinitely divisible distribution for all t. The law of $(S_{t}) _{t\ge 0}$ is uniquely determined by its spot characteristics $(A_{t},\mu _{t},\varGamma _{t}) _{t\ge 0}$:

$$\begin{aligned} \mathrm {E}[\exp (iuS_{t}) ]=\exp (\psi _{t}(u) ) \end{aligned}$$

where

$$\begin{aligned} \psi _{t}(u) =-\frac{1}{2}u\cdot A_{t}u+iu\cdot \varGamma _{t}+\int _{\mathbb {R} ^{d}}(e^{iu\cdot z}-1-iu\cdot z\mathbf {1}_{\{|z|\le 1\}}) \mu _{t}(dz). \end{aligned}$$

The spot characteristics $(A_{t},\mu _{t},\varGamma _{t}) _{t\ge 0}$ satisfy the following conditions

• 1. For all t, $A_{t}$ is a positive definite $d\times d$ matrix and $\mu _{t}$ is a positive measure on $\mathbb {R}^{d}$ satisfying $\mu _{t}({0} ) =0$ and $\int _{\mathbb {R}^{d}_0}(|z|^{2}\wedge 1) \mu _{t}(dz) <\infty$.

• 2. Positiveness: $A_{0}=0$, $\mu _{0}=0$, $\varGamma _{0}=0$ and for all s, t such that $s\le t$, $A_{t}-A_{s}$ is a positive definite $d\times d$ matrix and $\mu _{t}(B) \ge \mu _{s}(B)$ for all measurable sets $B\in \mathscr {B}( \mathbb {R}^{d})$.

• 3. Continuity: if $s\longrightarrow t$ then $A_{s}\longrightarrow A_{t}$, $\varGamma _{s}\longrightarrow \varGamma _{t}$ and $\mu _{s}(B) \longrightarrow \mu _{t}(B)$ for all $B\in \mathscr {B}(\mathbb {R}^{d})$ such that $B\subset \{z:|z|\ge \varepsilon \}$ for some $\varepsilon >0$.

Conversely, for a family of $(A_{t},\mu _{t},\varGamma _{t}) _{t\ge 0}$ satisfying the conditions (1) , (2) and (3) above there exists an additive process $(S_{t}) _{t\ge 0}$ with $(A_{t},\mu _{t},\varGamma _{t}) _{t\ge 0}$ as spot characteristics.

Example 1

We consider a class of spot characteristics $(A_{t},\mu _{t},\varGamma _{t}) _{t \ge 0}$ constructed in the following way:

• A continuous matrix valued function $\sigma : [0,T]\longrightarrow M_{d\times d}(\mathbb {R})$ such that $\sigma _t$ is symmetric for all $t\in [0,T]$ and verifies $\int _{0}^{T}\sigma ^{2}_tdt<\infty$.

• A family $(\nu _{t}) _{t\in [0,T]}$ of Lévy measures verifying $\int _{0}^{T}\left( \int _{\mathbb {R}^{d}_0}(|z|^{2}\wedge 1) \nu _{t}(dz) \right) dt< \infty$.

• A deterministic function with finite variation $\gamma : [0,T]\longrightarrow \mathbb {R}^d$ (e.g., a piecewise continuous function).

Then the spot characteristics $(A_{t},\mu _{t},\varGamma _{t}) _{t\ge 0}$ defined by

$$\begin{aligned} A_{t}= & {} \int _{0}^{t}\sigma ^{2}_sds \\ \mu _{t}= & {} \int _{0}^{t}\nu _{s}ds \\ \varGamma _{t}= & {} \int _{0}^{t}\gamma _sds \end{aligned}$$

satisfy the conditions 1, 2, 3 and therefore define a unique additive process $(S_{t}) _{t\ge 0}$ with spot characteristics $(A_{t},\mu _{t},\varGamma _{t}) _{t\in [0,T]}$. The triplet $(\sigma _{t}^{2},\nu _{t},\gamma _{t}) _{t\in [0,T]}$ are called local characteristics of the additive process.

Remark 4.3

Not all additive processes can be parameterized in this way, but we will assume this parametrization in terms of local characteristics in the rest of this paper. In particular, the assumptions above on the local characteristics implies that the process $(S_{t}) _{t\ge 0}$ is a semimartingale which will allow us to apply the Itô formula.

The local characteristics of an additive process enable us to describe the structure of its sample paths: the positions and sizes of jumps of $(S_{t}) _{t\ge 0}$ are described by a Poisson random measure on $[0,T]\times \mathbb {R}^{d}$

$$\begin{aligned} J_{S}(\omega , \cdot ) =\sum _{0\le t\le T;\varDelta S_{t}\ne 0}\delta _{(t,\varDelta S_{t}) } \end{aligned}$$

with (time-inhomogeneous) intensity given by $\nu _{t}(dz) dt$:

$$\begin{aligned} \mathrm {E}[J_{S}([t_{1},t_{2}]\times B) ]=\mu _{T}([t_{1},t_{2}]\times B) =\int _{t_{1}}^{t_{2}}\nu _{s}(B) ds. \end{aligned}$$

The compensated Poisson random measure can therefore be defined by:

$$\begin{aligned} \widetilde{J}_{S}(\omega , dt,dz) =J_{S}(\omega , dt,dz) -\nu _{t}(dz) dt. \end{aligned}$$

4.2 Isonormal Lévy Process (ILP)

Let $\mu$ and $\nu$ are $\sigma$–finite measures without atoms on the measurable spaces $(\mathrm {T},\mathscr {A})$ and $(\mathrm {T\times X_{0}}, \mathscr {B})$ respectively.

Define a new measure

$$\begin{aligned} \pi (dt,dz) :=\mu (dt) \delta _{\varDelta }(dz) +\nu (dt,dz) \end{aligned}$$

(11)

on a measurable space $(\mathrm {T\times X},\mathscr {G})$, where $\mathrm {X}= \mathrm {X_0}\cup {\varDelta }$, $\mathscr {G}=\sigma (\mathscr {A}\times {\varDelta }, \mathscr {B})$ and $\delta _{\varDelta }(dz)$ is the measure which gives mass one to the point $\varDelta$.

We assume that the Hilbert space $\mathscr {H}=\mathrm {L}^{2}(\mathrm {T\times X },\mathscr {G},\pi )$ is separable.

Definition 4.4

We say that a stochastic process $\mathrm {L}=\{\mathrm {L}(h), h\in \mathscr {H} \}$ defined in a complete probability space $(\varOmega ,\mathscr {F},P)$ is an isonormal Lévy process (or Lévy process on $\mathscr {H}$) if the following conditions are satisfied:

• 1. The mapping $h\longrightarrow L(h)$ is linear.

• 2. $\mathrm {E}[e^{ixL(h) }]=\exp (\Psi (x,h) )$, where

  $$\begin{aligned} \Psi (x,h) =\int _{\mathrm {T\times X}}\left( (e^{ixh(t,z) }-1-ixh(t,z) ) {\mathbf {1}}_{\mathrm {X}_{0}}(z) -\frac{1}{2}x^{2}h^{2}(t,z) \mathbf {1}_{\varDelta }(z) \right) \pi (dt,dz). \end{aligned}$$

4.3 Generalized Orthogonal Polynomials (GOP)

Denote by $\overline{x}=(x_{1},x_{2},\ldots , x_{n},\ldots )$ a sequence of real numbers. Define a function $F(z,\overline{x})$ by

$$\begin{aligned} F(z,\overline{x}) =\exp \left( \sum _{k=1}^{\infty }\frac{(-1) ^{k+1}}{k} x_{k}\, z^{k}\right) . \end{aligned}$$

(12)

If

$$\begin{aligned} R(\overline{x}) =\left( \limsup |x_{k}|^{\frac{1}{k}}\right) ^{-1}>0 \end{aligned}$$

then the series in (12) converge for all $|z|<R(\overline{x})$. So the function $F(z,\overline{x})$ is analytic for $|z|<R(\overline{x})$.

Consider an expansion in powers of z of the function $F(z,\overline{x})$:

$$\begin{aligned} F(z,\overline{x}) =\sum _{n=0}^{\infty }z^{n}P_{n}(\overline{x}). \end{aligned}$$

One can easily show the following equalities:

$$\begin{aligned} (n+1) P_{n+1}(\overline{x})= & {} \sum _{k=0}^{n}(-1) ^{k}x_{k+1}P_{n-k}(\overline{ x}),\;\;n\ge 0, \\ \frac{\partial P_{n}}{\partial x_{l}}(\overline{x})= & {} \left\{ \begin{array}{llc} 0 &{} \text {if} &{} l>n, \\ \frac{(-1) ^{l+1}}{l}P_{n-l}(\overline{x}) &{} \text {if} &{} l\le n. \end{array} \right. \end{aligned}$$

4.4 Examples

• 1. If $\overline{x}(h) =(x,\lambda , 0,\ldots , 0,\ldots )$, then

  $$\begin{aligned} F(z,\overline{x}) =\exp \left( zx-\frac{z^{2}}{2}\lambda \right) =\sum _{n=0}^{\infty }H_{n}(x,\lambda ) z^{n}, \end{aligned}$$

  where $H_{n}(x,\lambda )$ are the Hermite polynomials (Brownian case). So

  $$\begin{aligned} P_{n}(x,\lambda , 0,\ldots , 0) =H_{n}(x,\lambda ). \end{aligned}$$

• 2. If $\overline{x}(h) =(x-t,x,\ldots , x,\ldots )$, then

  $$\begin{aligned} F(z,\overline{x}) =(1+z) ^{x}e^{-tz}=\sum _{n=0}^{\infty }C_{n}(x,\lambda ) \frac{z^{n}}{n!}, \end{aligned}$$

  where $C_{n}(x,\lambda )$ are the Charlier polynomials (Poissonian case). So

  $$\begin{aligned} n!P_{n}(x-t,x,\ldots , x) =C_{n}(x,\lambda ). \end{aligned}$$

4.5 Relationship Between Generalized Orthogonal Polynomials and Isonormal Lévy Process

For $h\in \mathscr {H}\cap L^{\infty }(T\times X_{0},\mathscr {B},\nu )$, let $\overline{x}(h) =(x_{k}(h) ) _{k=1}^{\infty }$ denote the sequence of the random variables such that

$$\begin{aligned} x_{1}(h)= & {} L(h) ; \\ x_{2}(h)= & {} L(h^{2}\mathbf {1}_{X_{0}}) +\Vert h\Vert _{\mathscr {H}}^{2}; \\ x_{k}(h)= & {} L(h^{k}\mathbf {1}_{X_{0}}) +\int _{T\times X_{0}}h^{k}(t,x) \nu (dt,dx),\;\;k\ge 3. \end{aligned}$$

Lemma 4.5

Let h and $g\in \mathscr {H}\cap L^{\infty }(T\times X_{0},\mathscr {B},\nu )$. Then for all $n,m\ge 0$ we have $P_{n}(\overline{x}(h) )$ and $P_{m}(\overline{x} (g) ) \in L^{2}(\varOmega )$, and

$$\begin{aligned} \mathrm {E}\left[ P_{n}(\overline{x}(h) ) P_{m}(\overline{x}(g) ) \right] =\left\{ \begin{array}{llc} 0 &{} \text {if} &{} n\ne m, \\ \dfrac{1}{n!}\left( \mathrm {E}\left[ L(h) L(g) \right] \right) ^{n} &{} \text {if} &{} n=m. \end{array} \right. \end{aligned}$$

4.6 The Chaos Decomposition

Lemma 4.6

The random variables $\{e^{L(h) }, h\in \mathscr {H}\cap L^{\infty }(T\times X_0, \mathscr {B},\nu ) \}$ form a total subset of $L^{2}(\varOmega ,\mathscr {F} ,P)$.

For each $n\ge 1$ we will denote by $\mathscr {P}_n$ the closed linear subspace of $L^{2}(\varOmega ,\mathscr {F},P)$ generated by the random variables $\{P_{n}(\overline{x}(h) ), h\in \mathscr {H}\cap L^{\infty }(T\times X_0,\mathscr {B} ,\nu ) \}$. $\mathscr {P}_0$ will be the set of constants. For $n=1$, $\mathscr { P}_1$ coincides with the set of random variables $\{L(h),h\in \mathscr {H}\}$. We will call the space $\mathscr {P}_n$ chaos of order n.

Theorem 4.7

The space $L^{2}(\varOmega ,\mathscr {F},P)$ can be decomposed into the infinite orthogonal sum of the subspace $\mathscr {P}_n$:

$$\begin{aligned} L^{2}(\varOmega ,\mathscr {F},P) =\bigoplus _{n=0}^{\infty }\mathscr {P}_n. \end{aligned}$$

4.7 The Multiple Integral

Set $\mathscr {G}_{0}=\left\{ A\in \mathscr {G}|\pi (A) <\infty \right\}$. For any $m\ge 1$ we denote by $\mathscr {E}_{m}$ the set of all linear combinations of the following functions $f\in \mathrm {L}^{2}((T\times X) ^{m}, \mathscr {G}^{m},\pi ^{m})$

$$\begin{aligned} f(t_{1},x_{1},\ldots , t_{m},x_{m}) =\mathbf {1}_{A_{1}\times A_{2}\times \ldots A_{m}}(t_{1},x_{1},\ldots , t_{m},x_{m}), \end{aligned}$$

(13)

where $A_{1},\ldots , A_{m}$ are pairwise–disjoint sets in $\mathscr {G}_{0}$.

The fact that $\pi$ is a measure without atoms implies that $\mathscr {E} _{m}$ is dense in $\mathrm {L}^{2}((T\times X) ^{m})$. (See, e.g. Nualart [11] pp. 8–9).

For the function of the form (13) we define the multiple integral of order m

$$\begin{aligned} I_{m}(f) =L(A_{1}) \ldots L(A_{m}). \end{aligned}$$

Then, by linearity we conclude $I_{m}(f)$ for all functions $f\in \mathscr {E} _{m}$ and by continuity $I_{m}(f)$ for all functions $f\in \mathrm {L} ^{2}((T\times X) ^{m})$.

The following properties hold:

• 1. $I_m$ is linear.

• 2. $I_{m}(f) =I_{m}(\widetilde{f})$, where $\widetilde{f}$ denotes the symmetrization of f, which is defined by

  $$\begin{aligned} \widetilde{f}(t_{1},x_{1},\ldots , t_{m},x_{m}) =\frac{1}{m!}\sum _{\sigma \in \mathscr {S}_{m}}f(t_{\sigma (1) },x_{\sigma (1) },\ldots , t_{\sigma (m) },x_{\sigma (m) }). \end{aligned}$$
• 3.
  $$\begin{aligned} \mathrm {E}\left[ I_{n}(f) I_{m}(g) \right] =\left\{ \begin{array}{llc} 0 &{} if &{} n\ne m, \\ m!<\widetilde{f},\widetilde{g}>_{\mathrm {L}^{2}((T\times X) ^{m}) } &{} if &{} n=m. \end{array} \right. \end{aligned}$$

4.8 Relationship Between Generalized Orthogonal Polynomials And multiple Stochastic Integrals

Proposition 4.8

Let $P_{n}$ be the nth generalized orthogonal polynomial and $\overline{x} (h) =(x_{k}(h) ) _{k=1}^{\infty }$, where $h\in \cap _{p\ge 2}L^{p}(T\times X_{0},\mathscr {B},\nu ) \cap \mathscr {H}$ and

$$\begin{aligned} x_{1}(h)= & {} L(h) ; \\ x_{2}(h)= & {} L(h^{2}\mathbf {1}_{X_{0}}) +\Vert h\Vert _{\mathscr {H}}^{2}; \\ x_{k}(h)= & {} L(h^{k}\mathbf {1}_{X_{0}}) +\int _{T\times X_{0}}h^{k}(t,x) \nu (dt,dx),\;\;k\ge 3. \end{aligned}$$

Then it holds that

$$\begin{aligned} n!P_{n}(\overline{x}(h) ) =I_{n}(h^{\otimes n}), \end{aligned}$$

where

$$\begin{aligned} h^{\otimes n}(t_{1},x_{1},\ldots , t_{m},x_{m}) =h(t_{1},x_{1}) \times \cdots \times h(t_{m},x_{m}). \end{aligned}$$

4.9 Expansion into a Series of Multiple Stochastic Integrals

Corollary 4.9

Any square integrable random variable $\xi \in L^{2}(\varOmega , \mathscr {F},P)$ can be expanded into a series of multiple stochastic integrals:

$$\begin{aligned} \xi =\sum _{k=0}^{\infty }I_{k}(f_{k}). \end{aligned}$$

(14)

Here $f_{0}=\,$E$[\xi ]$, and $I_{0}$ is the identity mapping on the constant. Furthermore, this representation is unique provided the functions $f_{k}\in L^{2}((T\times X) ^{k})$ are symmetric.

4.10 The Derivative Operator

Let $\mathscr {S}$ denote the class of smooth random variables such that a random variable $\xi \in \mathscr {S}$ has the form

$$\begin{aligned} \xi =f(L(h_{1}),\ldots , L(h_{n}) ), \end{aligned}$$

(15)

where f belongs to $\mathrm {C}_{b}^{\infty }(\mathbb {R}^{n}),h_{1},\ldots ,h_{n}$ are in $\mathscr {H}$, and $n\ge 1$. The set $\mathscr {S}$ is dense in $L^{p}(\varOmega )$, for any $p\ge 1$.

Definition 4.10

The stochastic derivative of a smooth functional of the form (15) is the $\mathscr {H}$–valued random variable $D\xi =\{D_{t,x}\xi , (t,x) \in T\times X\}$ given by

$$\begin{aligned} D_{t,x}\xi= & {} \sum _{k=1}^{n}\frac{\partial f}{\partial y_{k}} (L(h_{1}),\ldots , L(h_{n}) ) h_{k}(t,x) \mathbf {1}_{\varDelta }(x) \\&+\left( f(L(h_{1}) +h_{1}(t,x),\ldots , L(h_{n}) +h_{n}(t,x) ) \right. \nonumber \\&\left. -f(L(h_{1}),\ldots , L(h_{n}) ) \right) \mathbf {1}_{X_{0}}(x). \nonumber \end{aligned}$$

(16)

We will consider $D\xi$ as an element of $\xi \in L^{2}(T\times X \times \varOmega ) \cong L^{2}(\varOmega ;\mathscr {H})$, namely, $D\xi$ is a random process indexed by the parameter space $T\times X$.

• 1. If the measure $\nu$ is zero or $h_{k}(t,x) =0$, $k=1,\ldots , n$ when $x\ne \varDelta$ then $D\xi$ coincides with the Malliavin derivative (see, e.g. Nualart [11] Def. 1.2.1 p. 38).

• 2. If the measure $\mu$ is zero or $h_{k}(t,x) =0$, $k=1,\ldots , n$ when $x=\varDelta$ then $D\xi$ coincides with the difference operator (see, e.g. Picard [13]).

4.11 Integration by Parts Formula

Theorem 4.11

Suppose that $\xi$ and $\eta$ are smooth functionals and $h\in \mathscr {H}$. Then

• 1.
  $$\begin{aligned} \mathrm {E}[\xi L(h) ]=\mathrm {E}[\left\langle D\xi ;h\right\rangle _{\mathscr {H}}]. \end{aligned}$$
• 2.
  $$\begin{aligned} \mathrm {E}[\xi \eta L(h) ]=\mathrm {E}[\eta \left\langle D\xi ;h\right\rangle _{\mathscr {H}}]+\mathrm {E}[\xi \left\langle D\eta ;h\right\rangle >_{\mathscr {H}}]+\mathrm {E} [\left\langle D\eta ;h\mathbf {1}_{X_{0}}D\xi \right\rangle _{\mathscr {H}}]. \end{aligned}$$

As a consequence of the above theorem we obtain the following result:

• The expression of the derivative $D\xi$ given in (16) does not depend on the particular representation of $\xi$ in (15).

• The operator D is closable as an operator from $L^2(\varOmega )$ to $L^2(\varOmega ;\mathscr {H})$.

We will denote the closure of D again by D and its domain in $L^2(\varOmega )$ by $\mathbb {D}^{1,2}$.

4.12 The Chain Rule

Proposition 4.12

(See Yablonski [16], Proposition 4.8) Suppose $F=(F_{1},F_{2},\ldots , F_{n})$ is a random vector whose components belong to the space $\mathbb {D}^{1,2}$. Let $\phi \in \mathscr {C}^{1}(\mathbb {R}^{n})$ be a function with bounded partial derivatives such that $\phi (F) \in \mathrm {L}^{2}(\varOmega )$. Then $\phi (F) \in \mathbb {D}^{1,2}$ and

$$\begin{aligned} D_{t,x}\phi (F) =\left\{ \begin{array}{llc} \displaystyle \sum _{i=1}^{n}\frac{\partial \phi }{\partial x_{i}}(F) D_{t,\varDelta }F_{i}; &{} x=\varDelta \\ &{}&{}\\ \phi (F_{1}+D_{t,x}F_{1},\ldots , F_{n}+D_{t,x}F_{n}) -\phi (F_{1},\ldots ,F_{n}) ; &{} x\ne \varDelta \end{array} \right. \end{aligned}$$

4.13 The Action of the Operator D via the Chaos Decomposition

Lemma 4.13

It holds that $P_{n}(\overline{x}(h) ) \in \mathbb {D}^{1,2}$ for all $h\in \mathscr {H}\cap L^{\infty }(T\times X_{0},\mathscr {B},\nu )$, $n=1,2,\ldots$ and

$$\begin{aligned} D_{t,x}P_{n}(\overline{x}(h) ) =P_{n-1}(\overline{x}(h) ) h(t,x). \end{aligned}$$

Proposition 4.14

Let $\xi \in L^{2}(\varOmega , \mathscr {F},P)$ with an expansion $\xi =\sum _{k=0}^{\infty }I_{k}(f_{k})$ where $f_{k}\in L^{2}((T\times X) ^{k})$ are symmetric for all k. Then $\xi \in \mathbb {D}^{1,2}$ if and only if

$$\begin{aligned} \sum _{k=0}^{\infty }kk!\Vert f_{k}\Vert _{L^{2}((T\times X) ^{k}) }^{2}<\infty , \end{aligned}$$

and in this case we have

$$\begin{aligned} {D_{t,x}\xi =\sum _{k=0}^{\infty }kI_{k-1}(f_k(\cdot ,t,x) ) } \end{aligned}$$

and

$$\begin{aligned} \mathrm {E}\left[ \int _{T\times X}(D_{t,x}\xi ) ^{2}\pi (dt,dx) \right] \end{aligned}$$

coincides with the sum of the series (14).

4.14 The Skorohod Integral

We recall that the derivative operator D is a closed and unbounded operator defined on the dense subset $\mathbb {D}^{1,2}$ of $\mathrm {L} ^{2}(\varOmega )$ with values in $\mathrm {L}^{2}(\varOmega ;\mathscr {H})$.

Definition 4.15

We denote by $\delta$ the adjoint of the operator D and we call it the Skorohod integral.

The operator $\delta$ is a closed and unbounded operator on $\mathrm {L} ^{2}(\varOmega ;\mathscr {H})$ with values in $\mathrm {L}^{2}(\varOmega )$ defined on $Dom(\delta )$, where $Dom(\delta )$ is the set of processes $u\in \mathrm {L} ^{2}(\varOmega ;\mathscr {H})$ such that

$$\begin{aligned} \left| \mathrm {E}\left[ \int _{T\times X}D_{t,z}Fu(t,z) \pi (dt,dz) \right] \right| \le c\left\| F\right\| _{\mathrm {L}^{2}(\varOmega ) } \end{aligned}$$

for all $F\in \mathbb {D}^{1,2}$, where c is some constant depending on u.

If $u\in Dom(\delta )$, then $\delta (u)$ is the element of $\mathrm {L} ^{2}(\varOmega )$ such that

$$\begin{aligned} \mathrm {E}\left[ F\delta (u) \right] =\mathrm {E}\left[ \int _{T\times X}D_{t,z}Fu(t,z) \pi (dt,dz) \right] \end{aligned}$$

(17)

for any $F\in \mathbb {D}^{1,2}$.

4.15 The Behavior of $\delta$ in Terms of the Chaos Expansion

Proposition 4.16

Let $u\in \mathrm {L}^{2}(\varOmega ;\mathscr {H})$ with the expansion

$$\begin{aligned} u(t,z) =\sum _{k=0}^{\infty } I_k(f_k(\cdot ,t,z) ). \end{aligned}$$

(18)

Then $u\in Dom(\delta )$ if and only if the series

$$\begin{aligned} \delta (u) =\sum _{k=0}^{\infty } I_{k+1}(\widetilde{f}_k) \end{aligned}$$

(19)

converges in $\mathrm {L}^{2}(\varOmega )$.

It follows that $Dom(\delta )$ is the subspace of $\mathrm {L}^{2}(\varOmega )$ formed by the processes that satisfy the following condition:

$$\begin{aligned} \sum _{k=1}^{\infty }(k+1) ! \Vert \widetilde{f}_k\Vert ^2_{\mathrm {L}^{2}(T\times X) ^{k+1}}<\infty . \end{aligned}$$

(20)

Note that the Skorohod integral is a linear operator and has a zero mean, e.g. $\mathbb {E}\left[ \delta (u) \right] =0$ if $u\in Dom(\delta )$. The following statements prove some properties of $\delta$.

Proposition 4.17

Suppose that u is a Skorohod integrable process. Let $F\in \mathbb {D}^{1,2}$ be such that $\mathrm {E}\left[ \int _{T\times X}\left( F^{2}+(D_{t,z}F) ^{2}\mathrm {1}_{X_0}\right) u(t,z) ^{2}\pi (dt,dz) \right] <\infty$. Then it holds that

$$\begin{aligned} \delta \left( \left( F+(D_{t,z}F) \mathrm {1}_{X_0}\right) u\right) =F\delta (u) -\int _{T\times X}(D_{t,z}F) u(t,z) \pi (dt,dz), \end{aligned}$$

(21)

provided that one of the two sides of the equality (21) exists.

4.16 Commutativity Relationship Between the Derivative and Divergence Operators

Let $\mathbb {L}^{1,2}$ denote the class of processes $u\in \mathrm {L} ^{2}(T\times X\times \varOmega )$ such that $u(t,x) \in \mathbb {D}^{1,2}$ for almost all (t, x) , and there exists a measurable version of the multi–process $D_{t,x}u(s,y)$ satisfying

$$\begin{aligned} \mathrm {E}\left[ \int _{T\times X}\int _{T\times X}(D_{t,x}u(s,y) ) ^{2}\pi (dt,dx) \pi (dsdy) \right] <\infty . \end{aligned}$$

Proposition 4.18

Suppose that $u\in \mathbb {L}^{1,2}$ and for almost all $(t,z) \in T\times X$ , the two–parameter process $\left( D_{t,z}u(s,y) \right) _{(s,y) \in T\times X}$ is Skorohod integrable, and there exists a version of the process $\left( \delta (D_{t,z}u(\cdot ,\cdot ) ) \right) _{(t,z) \in T\times X}$ which belongs to $\mathrm {L}^{2}(T\times X\times \varOmega )$. Then $\delta (u) \in \mathbb {D}^{1,2}$, and we have

$$\begin{aligned} D_{t,z}\delta (u) =u(t,z) +\delta (D_{t,z}u(\cdot ,\cdot ) ). \end{aligned}$$

(22)

4.17 The Itô Stochastic Integral as a Particular Case of the Skorohod Integral

Let $W=\{W_{t},0\le t\le T\}$ is a be an d-dimensional standard Brownian motion, $\widetilde{N}$ a compensated Poisson random measure on $[0,T]\times \mathbb {R}_{0}^d$ with (time-inhomogeneous) intensity measure $\nu (dt,dx) =\beta _{t}(dx) dt$, where $(\beta _{t}) _{t\in [0,T]}$ is a family of Lévy measures verifying $\int _{0}^{T}\left( \int _{ \mathbb {R}^{d}}(\Vert z\Vert ^{2}\wedge 1) \beta _{t}(dz) \right) dt<\infty$. Here $\mathbb {R}_{0}:=\mathbb {R}\setminus \{0\}$ and for each $t\in [0,T]$, $\mathscr {F}_{t}$ is the $\sigma$–algebra generated by the random variables

$$\begin{aligned} \{W_{s}^{j},\widetilde{N}((0,s]\times A) ;0\le s\le t,j=1,\dots , d,\, A\in \mathscr {B}(\mathbb {R}_{0}^d),\underset{0\le s\le t}{\sup } \beta _{s}(A) <\infty \} \end{aligned}$$

and the null sets of $\mathscr {F}$.

We denote by $L_{p}^{2}$ the subset of $L^{2}(\varOmega ;\mathscr {H})$ formed by $( \mathscr {F}_{t})$–predictable processes.

Proposition 4.19

$L_{p}^{2}\subset Dom(\delta )$, and the restriction of the operator $\delta$ to the space coincides with the usual stochastic integral, that is

$$\begin{aligned} \delta (u) =\sum _{j=1}^{d}\int _{0}^{T}u^j(t,0) dW^{j}_t+\int _{0}^{T}\int _{ \mathbb {R}_{0}^d}u(t,z) \widetilde{N}(dt,dz). \end{aligned}$$

(23)