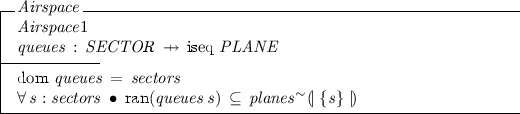The Z Notation: Whence the Cause and Whither the Course?

Abstract

The Z notation for the formal specification of computer-based systems has been in existence since the early 1980s. Since then, an international Z community has emerged, academic and industrial courses have been developed, an ISO standard has been adopted, and Z has been used on a number of significant software development projects, especially where safety and security have been important. This chapter traces the history of the Z notation and presents issues in teaching Z, with examples. A specific example of an industrial course is presented. Although subsequent notations have been developed, with better tool support, Z is still an excellent choice for general purpose specification and is especially useful in directing software testing to ensure good coverage.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Whence the Cause?

“Mathematical reasoning may be regarded rather schematically as the exercise of a combination of two facilities, which we may call intuition and ingenuity.”

– Alan M. Turing

The Purpose of Ordinal Logics (1938)

1.1 History

The computing pioneer Alan Turing (1912–1954) [13, 22] and the physicist Albert Einstein (1879–1955), who died only a year after Turing although after a considerably longer lifespan, are two of the western scientists who are celebrated with busts on the campus of Southwestern University in Chongqing, China (see Fig. 1). Einstein is of course extremely well-known internationally, but Turing has been less well-known until more recently when his achievements have become increasingly visible to the public. He is considered by many to be the founding father of modern computer science with his 1936/7 paper on the Entscheidungsproblem (“decision problem” in German), establishing what is computable through the theoretical computing device that has become known as a Turing Machine [42]. This is an abstract model of a computing machine that is useful for demonstrating what is and what is not computable. This astoundingly novel approach has had a profound effect on the theory of computation subsequently, effectively founding the field of theoretical computer science.

Fig. 1.

Busts of Alan Turing and Albert Einstein on the campus of Southwest University, Chongqing, China. (Photographs by Jonathan Bowen.)

Turing produced what is considered by many as the first paper on proving a program correct [43]. However, sadly this short paper had little impact on the development of formality in computing until it was rediscovered and evaluated in its historical context much later [34]. Instead, Tony Hoare’s much later 1969 paper on an axiomatic basis for computer programming, introducing Hoare logic and assertions, was a turning point in providing a formal approach to program proving [29].

Formal methods [18] emerged during the 1970s as a mathematically-based approach to software development. Jean-Raymond Abrial’s 1974 paper on data semantics [1] was in hindsight a seminar paper leading to the development of the Z notation for the formal specification of computer-based systems. In the early 1980s, Abrial visited the Programming Research Group (PRG) in the Oxford University Computing Laboratory (OUCL) and sowed the seeds for thedevelopment of the Z notation there. A Z course was established for bothacademics and industry. Projects such as the Distributed Computing Software Project used Z to specify network services at OUCL [15, 24]. A series of Z User Meetings was established, first in Oxford from 1986, with written proceedings from 1987 [5], then around the UK from 1992 [36], and finally internationally from 1998 [14].

A “Z Reference Manual” (ZRM) was published as a book originally in 1989, with a second edition in 1992, and further revisions online in 2001 [39]. This was and even remains a de facto standard, with an associated type-checker, [40]. However, an ISO/IEC standard with a formal semantics written in the Z notation itself was issued in 2002 [32]. The development of a formal semantics revealed some issues in Z that were clarified in the final semantics in the ISO/IEC standard [27].

Turing is associated with Cambridge University and later Manchester University. There is no known record of him ever having even visited Oxford University. However, Turing did liaise with Christopher Strachey (1916–1975), at one time a teacher at Harrow School, but also an expert early programmer. His program for the game of draughts impressed Turing. Strachey went on to found the Programming Research Group at Oxford in the 1960s, where he developed denotational semantics with colleagues there. Strachey’s untimely death in 1975 led to the appointment of Tony Hoare as the next head of the PRG. It was Hoare who fostered a suitable environment at Oxford for the Z notation to emerge and flourish in the 1980s and 1990s.

1.2 Background

The Z notation is an industrial-strength formal specification notation based on typed set theory and first order predicate logic, used in the specification of discrete computer-based systems [10, 39]. As well as standard mathematical operators, Z also includes a number of additional operators that have proved to be useful for specifications in practice, using more specialised sets such as relations, functions, and sequences. In addition to the mathematical notation, Z also includes a schema notation that collects the mathematical description into schema boxes containing declarations and predicates. These schemas may be combined to form larger specifications using schema operators that largely match logical operators, aiding the structuring of large specifications at an industrial scale.

This chapter includes a description of an industrially used course that covers the mathematical and schema notation of Z. Delivery of the course is in the form of lectures interspersed with paper-and-pencil exercises. The course is based around an ongoing case study example and finished with a further example for study. Previous experience of standard mathematical set theory and predicate logic is helpful although not essential.

1.3 Brief Survey

Formal methods are useful for improving software engineering where high integrity is desirable or required [18, 19, 28]. Examples of real industrial use are available [2, 3, 25]. There are a number of formal methods available with various strengths – and weaknesses – depending on the situation in which they are applied. See http://formalmethods.wikia.com for a wiki with information on formal methods in general and the Z notation in particular. Z’s strength is its use as a general purpose specification language in a human-readable form, interspersed with informal text, that can be scaled up to an industrial level. A weakness is its lack of good tools.

Z can be used for formal specification with the aim of designing and documenting mainly software but also hardware systems [6]. For example, Z has been used to specify microprocessor instruction sets [4]. It can also be used to specify software tools [7] and even window-based user interfaces [8].

Z is not executable in the general case, although an executable semantics for Z has been explored [20]. It is possible to embed Z within other formal systems. For example, see a shallow embedding of Z in HOL (Higher Order Logic) [16].

Z has good type-checking support, notably the type-checker [40] based on the Z Reference Manual [39]. This is based around the document preparation system, widely used in academia. There are a number of style files available to allow formatting of the Z symbols and schema structures. These include zed.sty (the original style file), fuzz.sty (designed for use with ), zed-csp.sty (also including support for CSP [30]), and oz.sty (supporting the object-oriented extension of Z, Object-Z [38]). All these styles are essentially compatible with the core parts of the Z notation. This chapter has been formatted using zed-csp.sty, mainly because it is very comprehensive for the Z glossary in Appendix A.

is not widely used in industrial, where Word is much more common. There is a Z Word Tools plug-in for Word that allows Z symbols and schemas to be written in Word using an additional menu entry [26]. It also integrates the type-check to allow convenient type-checking of Z from within Word. Z has the potential to allow proofs, either at an informal level, or with tool support. Leading Z proof tools include Z/EVES [37] and ProofPower [33]. However, learning to use such a tool effectively requires a significant amount of time and effort, longer than is normally available on an industrial project,

Despite the issues of proof support for Z, a Z specification is still extremely useful for another important part of the development process in industrial-scale projects. It can be used to aid much more effective and comprehensive testing of a software artefact [21, 23, 31, 41], helping to ensure more complete coverage of branches in a program for example. It can even be used to specify testing criteria, which are often defined in a rather loose way, in a more precise manner [44, 45].

1.4 Overview of Z Structuring

The Z notation includes mathematics based on logic and set theory (see a glossary in Appendix A) together with the schema box structuring notation. It is the latter than makes Z powerful and useful for very large specifications (potentially consisting of thousands of pages) as well as small specifications, as typically presented by academics for didactic purposes. In this section we present some of the important basic aspects of a Z specification, especially with respect to structuring using schemas.

All Z specifications have the set of integers ($\mathbb {Z}$) included by default as a given set, with the standard arithmetic operators available. Additional given sets (or basic types) may be specified as needed, providing distinct types of sets from which more complex abstract data structures can be constructed. For example, to declare given sets X and Y, the following could be included at the start of a Z specification:

A Z schema has the form of a name (used to reference it later in the specification), a declaration part, and a predicate part that optionally relates components that have been declared in the schema (defaulting to true if omitted). For example, the following simple schema T declares an integer n with no constraints on its value:

It is possible to include a schema within another schema. For example, the following schema S includes the declarations and predicates of T. It also declares an additional set x and constrains the value of n to be the size of the set (an “invariant” predicate for the state schema S):

Note that $\mathbb {P}$ indicates a power set (the set of all subsets of X in this case). x is drawn from this set (i.e., it is some subset of X, possibly the empty set $\emptyset$, possible the full set X, or somewhere in between). The complete version of S if the included schema T is expanded is as follows:

Schemas may be “decorated” with appended subscripts and superscripts. The most normal decoration is the prime (or “dash”, $'$), used by convention to indicate the “after state” of an operation schema (with a matching unprimed “before state”). All the components of the schema $S'$ are also renamed with an appended prime (i.e., $n'$ and $x'$ in this simple example). Thus $S'$ expands to:

In a state-based Z specification, the system is modelled as a series of operations (with related before and after states) that change the state of the system. For the system to start in the first place, there needs to be an initial state that is the system state, but normally together with some initial constraints (specified as predicates). Since this is the state after initialisation, it is normally specified in terms of an after state, namely $S'$ in this example:

The constraint that $n'$ is zero means that the size of $x'$ is also zero and thus $x'$ is empty. The predicate $x' = \emptyset$ could equally well have been used.

For an operation schema in Z, a before state (undecorated) and an after state (decorated with primes) are related together. The most general operation, where the after state may take on any arbitrary value with respect to the before state, can be specified using schema inclusion as follows with the example S state schema:

This expands to:

Note that predicates on separate lines in a schema are joined with logical conjunction by default.

Most operation schemas in Z will include this general change of state together with further constraining predicates relating the after-state components (here $n'$ and $x'$) with the before-state components (here n and x). Since the ChangeofState schema above is likely to be useful in a number of operation schemas in practice and since a real Z specification may specify operations on a number of sub-states that can later be combined into a complete system, there is a convention that a schema named $\varDelta S$ (in the case of the S schema for example) is automatically available for the specification, with the same meaning as ChangeOfState above.

For the specification of operations, typically these may have inputs and outputs as well as the change of state. Inputs and outputs are conventionally indicated with an appended “?” and “!” respectively. So, as an example, consider an operation to add an input element e? to the set x:

Here there is a “precondition” predicate that e? is not already a member of the set x, There is also a “postcondition” predicate meaning that the set $x'$ is the original set x with the element e? added to it. Note that the value of $n'$ has not been specified explicitly, but implicitly it has a value of the size of the set $x'$ due to the invariant predicate in $S'$. The full expanded version of AddOp is as follows:

Sometimes operation schemas do not actually change the state of the system, for example in status operations where part of the state is returned as an output. Z includes a convention similar to the $\varDelta$ convention, with matching before and after states where the values of the matching before and after components maintain their value. For example in this case:

Similarly to the $\varDelta$ convention described earlier, there is a convention that a schema named $\varXi S$ (again for example) is automatically available within the specification, having the same meaning as NoChangeOfState above. So in the running example, for a status operation that returns, using the output n!, the size of the set x (which is always constrained to be the same is n), the following status operation scheme could be specified:

This could be expanded as:

As can be seen, there is much clutter in the expanded version of the schema that obscures its actual purpose. Thus the use of schema inclusion is a very important part of the structuring techniques used by Z in practice, making the specification much shorter, less repetitive, and more readable.

There are further features for combining schemas, using operators that match the logical operators, but the introduction above should be sufficient for non-experts in Z to follow the example questions and answers in the next section.

2 Whither the Course?

“Teaching to unsuspecting youngsters the effective use of formal methods is one of the joys of life because it is so extremely rewarding.”

– Edsger W. Dijkstra (1930–2002)

A. M. Turing Award winner in 1972

There have been many Z courses over the years, since the original one at Oxford University started in the 1980s, initially inspired by Jean-Raymond Abrial (see Fig. 2) and later developed as a course for academic and industry, as well as being presented on the Masters degree course on Computation at the Programming Research Group there. Subsequently many universities incorporated Z into their undergraduate Computer Science degree programmes [35]. and it continues to be used for teaching, especially in software engineering courses, to this day.

Fig. 2.

The front page of the hand-written notes on the Z course during the 1980s at the Programming Research Group, Oxford University. (Drawing by Ib Sørensen, from an idea by Bernard Sufrin.)

In addition to academic courses on Z, industrial courses have also developed for training practitioners in software engineering. On of these was at Praxis (later Altran Praxis and now Altran UK). The course, written in the troff document markup language of UNIX, is in use to this day. It has been presented by the author at Altran Praxis in Bath, UK, and more recently in abbreviated form, with some additional material, at the Summer School on Engineering Trustworthy Software Systems (SETSS) held at Southwest University, Chongqing, China, in September 2014. The course is proprietary and copyright by Altran so cannot be published publicly in full. However extracts are including in Appendix B to give a flavour of the material. The course is normally presented intensively over a period of around four days, with lectures together with paper-and-pencil exercises intermingled.

An interesting feature is that the course is actually really two courses, one for “readers” of Z and one for “writers” of Z. In practice, many more engineers must learn to read Z on a particular project and far fewer are needed to write Z. This is because Z is typically used by both programmers, implementing the software product, and by software testers, who can use the Z specification to direct the tests that are needed in a very systematic way [23]. Neither implementers nor testers need to be able to write Z, but both must read and understand Z effectively in a project where the specification is written in Z. These tend to be major teams on a typical software project, the testing team often outnumbering even the implementation team. Most professional and experienced software engineers are able to assimilate the ability to read Z relatively easily, in a similar way to the fact that reading a book such as a novel is much easier than writing one. After a few day’s on a Z course, followed by a week or two of using Z documents, a good software engineer can read and understand Z effectively.

In contrast, writing a Z specification is a much more difficult skill to acquire. Thus the course by Altran has additional material on this aspect. Writing an effective Z specification that is amendable to both implementation and testing in a cost effective manner is something that only comes with experience, typically over months, arguably for greatest effectiveness over years. Fortunately the number of people needed to specify a software product on a large software project is much smaller the the numbers needed for implementation and testing, perhaps even by an order of magnitude. A wise decision is only to include the most experienced software engineers on the specification team, ideally with several years of at least reading Z.

2.1 Exercise

Since the Z course produced by Altran/Praxis cannot be reproduced in full here, we include an example exercise and solutions for part of a Z course that has been delivered as a component of the final year of an undergraduate degree programme in Computer Science at Birmingham City University.

We use, as an example, a simplified air traffic control system. The questions are informal in nature and the task is to write Z that formally specifies the informal description in the questions. This emulates the task of a software specifier on a real project, where some informal requirements written in a natural language such as English, perhaps augmented with some diagrams, need to be formalised in a more rigorous and mathematically-based notation such as Z.

One issue of learning a notation like Z is that there are often examples of a completed specification available, but there is very little indication of how to reach that specification [11]. An example has previously been given of a simple invoicing system specified using a number of different notations, including Z [12], where the questions that should be answered as the specification is developed are explicitly stated. Here we first present the questions and then example solutions with an indication of how these can be derived mentally.

2.2 Questions

The following are questions on a simple air traffic control system that need to be answered using Z notation. A comprehensive glossary of the Z notation is available in Appendix A for reference.

• Question 1: An air traffic control system involves a number of airspace sectors and a number of planes. Define two given sets to model these.

• Question 2: The airspace consists of a number of sectors. Each sector may have a number of adjacent sectors, which are then related to each other. Note that the adjacency relation is symmetric; i.e., if a sector is adjacent to another sector, then the reverse is also true. Sectors cannot be adjacent to themselves (i.e., sectors cannot map to themselves in the adjacency relation). In addition, all sectors in the airspace have adjacent sectors. Define a state schema that models sectors and a relation indicating which sectors are adjacent, with appropriate constraining predicates. Note that $\mathop {\mathrm {id}}X$ in Z is a one-to-one function that maps all elements in X to themselves.

• Question 3: Each sector may contain a number of planes at any given time. Extend the previous state schema with a function that models planes in sectors. Planes can only be in valid sectors within the airspace.

• Question 4: In each sector, some of the planes may be queued to leave the sector, in a sequence of planes. Extend the state schema in Question 3 to include a function that models the queued planes in each sector. Such queues can only be in valid sectors in the airspace. In addition these queues can only include a subset of the planes that are in each sector.

• Question 5: There is more than one sector in the airspace. Initially there are no planes in the airspace. Define an initialisation schema that ensures these conditions.

• Question 6: Define operations for the following, assuming success in each case, but including preconditions as needed:

  • 1. Have a new plane added to one of the sectors (both specified as inputs), but not in the queue for the sector (e.g., after taking off from an airport or arriving from another airspace).

  • 2. Queue an existing plane (specified as an input) that is not yet in a queue. The plane should be added to the last position of the queue in its sector.

  • 3. Remove the plane at the head of a queue in a specified sector from the airspace (e.g., land at an airport or be transferred to another airspace). Output the plane involved.

  • 4. Have the plane at the head of a queue in a sector move to an adjacent sector. Both sectors should be specified as inputs and the plane should not be included in the queue of the new sector.

• Question 7: (optional)

  • 1. Extend your answers in Question 6 to handle errors and provide total operations, with appropriate error messages.

  • 2. Informally describe and formally specify further operations (e.g., changing airspace sectors).

2.3 Answers

Here for each question in the previous subsection we present the thought processes that lead to a solution, together with an example model answer in Z.

• Answer 1: In Z, “given sets” (or “basic types”) are potentially infinite sets with no implicit structure on which the specification is going to operate. Z is typed so these sets are non-overlapping and are not compatible with standard set operations (e.g., union $\cup$ or intersection $\cap$). The question suggests two such sets, which we could name SECTOR to model all the possible airspace sectors in the system and PLANE for all the possible airplanes in the system. Obviously these are two different types of entity, so comparing them, subsets of them, or elements of them in any way (e.g., with equality $=$) is not correct and in Z would produce a type error if the specification is mechanically type-checked.

  In our simple example, we can define these two given sets in Z at the beginning of a specification as follows:

  

  Note that a convention (but not a requirement) in Z is to use all upper case name for given sets. This is not required, but it does make identifying them easier in a specification and is widely used in practice.

• Answer 2: Once we have some given sets in Z, we can start to use these to build up more complex structures. Typically we do this with “schema” boxes, that collect together mathematical objects such as sets, relations, functions, sequences, etc. A feature of Z is that all these are modelled as various types of set, so many Z operators can be reused on more specific structures. For example, standard set operators like union and intersection can be used on all these more refined set-based structures if desired. In addition, further more specific operators are available in Z that can be applied only to restricted forms of sets (e.g., relations). Schemas in Z are often used to specify abstract state structures on which operations can perform changes to those structures.

  In thisquestion, we require a number of sectors. We can do this by defining a set sectors (for example) to be drawn from a set of subsets of SECTOR (a “power set” $\mathbb {P}\ SECTOR$). In the declarations below, “:” is much like that used in many programming languages to declare variables. In Z, it can be considered as meaning “is a member of” a set (written as $\in$ when used in predicates (in the lower half of a schema box) rather than the declaration part (the upper half of the schema box). So x : X can be thought of as $x\in X$. Further, a declaration of the form $x_1\in \mathbb {P}x_2$ can be considered as meaning $x_1\subseteq x_2$ (i.e., $x_1$ is a subset of $x_2$). So below, $sectors\subseteq SECTOR$ holds. This is because we wish to model the airspace is a number of sectors, which are a subset of all the possible sectors (the set SECTOR).

  Another property of airspace is that some sectors are adjacent to each other. I.e., it is possible for airplanes to fly directly between them. We model this as pairs of sectors that are considered to be next to each other. Adjacent sectors have a number of properties that always hold for all configurations of sectors in the airspace. For example, if a sector is adjacent to another sector, then the second sector is also adjacent to the first sector (i.e., it is symmetric, $adjacent^\sim = adjacent$). Sectors cannot be adjacent to themselves, so the intersection of adjacent sectors and sectors mapped to themselves is empty ($adjacent \cap \mathop {\mathrm {id}}sectors = \emptyset$). All sectors in the airspace have at least one adjacent sector (i.e., the domain of the adjacent sectors is the same as the set of sectors in the airspace, $sectors = \mathop {\mathrm {dom}}adjacent$). This means that the range of the adjacency relation is also the same as all the sectors in the airspace ($sectors = \mathop {\mathrm {ran}}adjacent$) since this relation is symmetric. So in all, the following holds:

  

• Answer 3: All planes in the airspace are in one of the sectors. We can model this as a partial function from airplanes to sectors. (). The sector for each plane must be one of those that is in the airspace ($\mathop {\mathrm {ran}}planes \subseteq sectors$). We can augment the state space by adding this information to the existing airspace Airspace0 (an “included” schema with all the information in that schema too) as follows:

  

• Answer 4: Within each sector there is a queue of planes (possibly empty) waiting to leave the sector, again modelled as a partial function, this time from sectors to an injective sequence of airplanes (). Being injective meane that the planes in the sequence are all different. Queues of planes waiting to leave each sector. Each sector in the airspace has a (possibly empty) queue associated with it ($\mathop {\mathrm {dom}}queues = sectors$). What is more, the planes in the queues within each sector are a subset of the planes in that sector ($\forall s:sectors \bullet \mathop {\mathrm {ran}}(queues~s) \subseteq planes^\sim$ ). Some planes in the sector may not (yet) be waiting in the queue for that sector. Again we can augment the state space to create our complete abstract state scheme Airspace: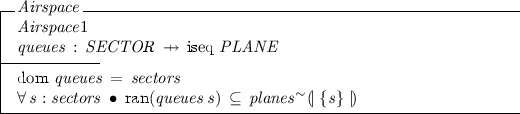

  

• Answer 5: The airspace at initialisation has more than one sector in it ($\#sectors' > 1$) and no planes ($planes' = \emptyset$). Thus the state after initialisation, indicated with a postpended prime ($'$) by convention in Z, is as follows:

  

  Note that the prime appended with the Airspace schema means that all its components (in this case sectors, adjacent, planes, and queues) all have primes appended to them as well (i.e., $sectors'$, $planes'$, etc.). In formulating the state at initialisation, we should consider all the state components. However it is normal for there to be invariant predicates relating some of these components. It is often the case that specifying one state component to be empty implies that one or more other related state components are restricted in some appropriate way, typically to be empty too. For example in this case, because there are no planes in the airspace initially, the queues in each sector (modelled by the queues state component) are restricted by the universally quantified predicate in Airspace to be empty too since a subset of an empty set can only be the empty set too. Note that nothing specific has been said about the adjacent state component apart from the constraints that are already in the predicate part of the Airspace0 schema since there is no additional predicate involving $adjacent'$.

• Answer 6: Below are various operations on the airspace, specified as schemas with a “before state” (with “unprimed” state components) and a matching “after state” (with “primed” state components, postfixed with the prime symbol $'$). $\varDelta Airspace$ indicates both a before state Airspace and an after state $Airspace'$ where the prime $'$ filters through to the names of all the components parts of the state in the schema too.

  • 1. A plane entering the airspace can be specified as follows:

    

    The $\varXi Airspace0$ is similar to $\varDelta Airspace0$ but with all the primed state components in $Airspace0'$ constrained to be the same as the unprimed equivalents in Airspace0. In this case, the state components in Airspace0 are sectors and adjacent. Inputs to operation schemas (with before and after states) are appended with a question mark (?) by convention to differentiate them from state components. Here there are two inputs, p? for the plane that is entering the airspace and s? for the sector that it enters.

    Next the predicates for the schema need to be formulated. First consider the precondition for the operation to be valid, only dealing with the before (unprimed) state and inputs. The plane p? must not be one of the planes already in the airspace. It is worth considering especially if there are any limitations on inputs for the operation to be successful. This is very often the case and it is helpful to specify this explicitly even if it is implied indirectly by other predicates. The implementer will find it useful and it will help in testing the implementation later too if the specification is used to direct the tests.

    Now consider the postcondition for the operation. I.e., how are the after state and outputs related to the before state and inputs? The plane p? is added to the sector s? that it enters. It is not in the queue to leave the sector initially so the queues are unchanged. The rest of the airspace state is also unchanged. It is important to explicitly specify when the after state is the same as the before state in a specification of an operation if this is what is required. Otherwise the after state may take on any value. It is important to go through all the after-state components and outputs in an operation and ensure that they are specified in some way. It is unusual to allow an after state or output to take on any value. This is easy for the implementer, but normally not very useful or desirable for the customer. Similarly, it is normally for all the inputs to be used in some way in the predicate part of the schema and all the outputs to be set in some useful way,

    Here $\varXi Airspace0$ ensures that the rest of the otherwise unmentioned state components remain the same after the operation. This is a technique often used in Z to “frame” operations on selected parts of the state of interest in a particular set of operations. It helps in structuring the specification when there are several similar operations where much of the state is unchanged but a particular part is changed in a different way for individual operations. In this case, $\varXi Airspace0$ in the declaration part of the schema acts as a short form for the predicate $sectors'=sectors \wedge adjacent'=adjacent$, which would become repetitive if needed in multiple operations and would also obscure the important predicates in the operations.

  • 2. Queueing a plane to leave a sector can be specified as follows. The plane starts at the back of the queue.

    

    In this case, $\varXi Airspace1$ is used to specify the fact that all the state components sectors, adjacent, and planes, remain the same. It is only queues that changes, in fact only one queue in one particular sector. p? is the input plane that is to be queued.

    Again, for the predicate part, we consider the precondition first. The plane p? is in the airspace but it is not in any of the queues in all of the sectors in the airspace. In considering the postcondition, only one individual queue is changed. All of the rest of the state remains the same since the sector where the plane is located does not change. The plane p? is added to the end of the queue for the sector in which it is located. The overriding operator ($\oplus$) is one that is commonly used in Z when a small part of a relation, often a function, is to be change to have a different value in the range associated with a particular element in the domain.

    The use of $\varXi Airspace1$ in the declaration part of the schema above ensures that other state components apart from queues remain the same, so only queues needs to be considered explicitly for the postcondition.

  • 3. The plane at the head of the waiting queue in a given sector leaves the airspace (e.g., comes in for landing or passes to another airspace).

    

    Here there is an input s? to specify the sector to which the operation applies and an output p! giving the plane at the head of the queue that is leaving the sector. An appended exclamation mark (!) is used to indicate an output by convention in Z.

    As a precondition, the queue for the sector s? must be non-empty. This is an important precondition since at least one plane is needed in the queue to allow one to be removed. The plane p! is the one at the head of the queue. It is removed from the overall airspace. It must also be removed from the queue for the specified sector s?.

  • 4. The plane at the head of the waiting queue in a given sector moves from that sector to an adjacent sector.

    

    Two sectors are declared as inputs, s1? for the sector where the plane at the head of the queue is to be moved and s2? for an adjacent sector where it is to be moved.

    Again, a precondition is that the queue for the sector s1? must be non-empty. Another precondition is that the sector s2? must be immediately adjacent to the sector s1?. A postcondition is that the plane is moved from sector s1? to sector s2?. It is also removed from the queue in sector s1?. Note that it is not added to the queue in sector s2?.

• Answer 7: (optional) There are a variety of answers possible for this part. It is designed to be more open-ended for the better students to tackle. Only those aiming for top marks are likely to attempt this question.

2.4 Z Course

The Z course produced by Altran is a commercial course and as such the copyright is owned by the company. Thus some extracts are included as Appendix B of this chapter to give a sample of the style of the course. Full model answers are also available, but these are not reproduced here for obvious reasons.

The following is a timetable for a typical four-day Z Readers Course. There are normally four sessions each day, two in the morning and two in the afternoon, with breaks between the sessions. These sessions are typically of 90 min duration. Lectures are interspersed with exercises, normally at the end of sessions.

• Day 1

  • Session 1: General Introduction

  • Session 2: Case Study Introduction

  • Session 3: Underlying Mathematics: Sets

  • Session 4: Case Study (continued) and Relations

• Day 2

  • Session 1: Relations (continued)

  • Session 2: Functions

  • Session 3: Case Study (continued)

  • Session 4: Underlying Mathematics: Logic

• Day 3

  • Session 1: Introduction to Schemas

  • Session 2: Case Study Operations

  • Session 3: Schema Calculus

  • Session 4: Analysing Specifications

• Day 4

  • Session 1: Schemas as Types

  • Session 2: Alternative Case Study

  • Session 3: Syndicate Exercise

  • Session 4: Syndicate Exercise (continued)

The Z Writers Course is longer than the Z Readers Course. In particular, more time is allocated to actually writing a Z specification, e.g., as a mini-project in small groups.

3 Conclusion

This chapter has presented the formal specification language Z, including information on an industrial Z course and some example Z questions and answers, with commentary on how to approach developing a formal Z specification from an informal description. A glossary of Z is included in Appendix A and parts of an industrial Z course are included in Appendix B, with some commentary,

Z is now a mature formal specification language with an ISO standard. It is still lacking in good industrial-strength tools but despite this deficiency it has been used in significant industrial projects involving teams of more than a hundred engineers and associated personnel. Research in Z has now slowed but that is an indication of its maturity. It is likely to continue to play an important part of safety and security-related projects when high integrity is essential. It can play an important part in a safety case, especially with respect to its use in improving the efficacy of testing. To paraphrase a well-known quotation by Winston Churchill, reports of Z’s death are greatly exaggerated!

Appendices

APPENDICES

A   Glossary of Z Notation

A comprehensive glossary of the Z mathematical and schema notation as used in this chapter is included here for easy reference. Earlier versions of this Z glossary have been distributed to students on Z courses delivered by the author and others. These have also been made available online and in published form [9]. The notation is only explained in summary form. For more detailed information on the formal meaning of Z constructs, see [32, 39].

Z Glossary

1.1 Names

1.2 Definitions

1.3 Logic

1.4 Sets and expressions

1.5 Relations

1.6 Functions

1.7 Numbers

1.8 Sequences

1.9 Bags

1.10 Schema notation

1.11 Conventions

B   Altran Z Course Description and Extracts

Here an overview of the material is given, together with sample pages from the Altran Z Course, which are reproduced with permission as examples of the style of the course material. The examples are intersperse with some commentary on the various parts of the course. Note that all the material reproduced from the Z course itself in this Appendix is Copyright $\copyright$ Altran. The sample pages are designed to give a feel for the style of the course. For the full Z course and its delivery, contact Altran UK.

Altran has two overlapping Z courses for Z “readers” and a longer course for Z “writers”. The extracts included here are from the more widely delivered Z Readers Course. Introductory slides on questions such as what is a specification, what is a formal specification, what is a Z specification, and what is taught during the main part of the material are presented at the start of the course.

The course starts with a gentle introduction to specifications in general, followed by formal and Z specifications in particular. In summary, a specification covers what a system does as opposed to how it does it. The specification documentation provides an interface between the specification team and the implementation team. A “black-box” specification concentrates on the external behaviour, as visible from outside the system. A specification must cover how the system affects its environment. Of course, the specification can only cover the immediate environment relevant to and controlled by the system.

The system being specified needs a model of the environment. This system can use information within the model and also change the model’s state. This model is an abstract view of the actual world environment. It is an engineering judgement to decide what model is reasonable and appropriate for a given system. It should include all the relevant features of the real world in a simplified manner, but not so simple that pertinent information is not included in the model.

A formal specification is based on mathematics. This is useful because of various properties of mathematics, such as the ability to abstract, its power to specify in a simple and universal way with the soundness that mathematics can provide, enabling formal reasoning for example. One widely used approach is “model-based” specification. Formal notations and methods appropriate for a model-based approach include ASM, B, VDM, Z, etc. [17]. This type of approach includes a mathematical model of the state associated with the system and operations that change the state of that system. This in operation, there is an initial state, followed by the first operation, a modified state after that operation, another possibly different operation, yet another modified state, and so on.

Such a specification covers functional attributes of the systems behaviour. Non-functional aspects such as availability of the system, performance, reliability, usability, size aspects, etc., are normally covered in alternative ways. More implementation-oriented aspects such as features like concurrency and real-time issues, may not be covered by all formal notations in a convenient manner. This is certainly true of the Z notation, which is a general purpose specification language. A formal specification does not normally cover design aspects of the system. In fact, it is quite possible to produce a specification that cannot be implemented in practice (by introducing false into the specification, typically through some incompatible logic, e.g., $P\wedge \lnot P$), obviously something to avoid in a real engineering situation.

The Z notation is normally used in a model-based style, although this is by convention and for convenience rather than being a built-in aspect of the notation. A Z specification includes mathematics (logic and set theory), a structuring approach (using the schema box notation), some conventions for the model-based aspects, and accompanying interleaved natural language text (typically English). Typically the informal description is of a similar length to the formal specification, providing an aid to the understanding of the mathematics and emphasising the connection with the real world.

The mathematics employed by Z is relatively simple, being based on first-order predicate logic and set theory. The sets in Z are strongly typed with basic sets (also known as given types) and simple constructors. More complex sets can be created, such as relations (normally sets of pairs), functions (relations where at most one element in the range is associated with each element in the domain) and sequences (modelled as finite functions mapping a contiguous set of natural numbers from one upwards to the elements in the sequence). All of these are thus modelled as sets in Z. Many Z operators can be applied across these different set structures.

Both infinite and finite sets may be specified in Z, although practical implementations of the specification will be finite of course. The Z notation has a relatively few number of constructs that are fundamental to the language. There is a library (a “toolkit” [39]) of generally useful notation that is formally defined in Z. Additional constructs can be formally defined for a particular specification in a similar way if desired.

The mathematical notation of Z alone would be adequate for a very small specification but a structuring technique is needed for a specification of any size. Z has such a mechanism in the form of schemas, which use a box-like visual notation to encapsulate the mathematical description. Schema boxes have names and can thus be referenced later in the specification. Common fragments of specification can be formulated and explained once, then used through reference to their schema name subsequently. This allows partial specifications to be formulated and then combined by including schemas within other schemas and also using a calculus of schema operators that match the logical operators in Z. Conjunction for building up specifications and disjunction for dealing with error cases are the most useful operators in practice.

There are a number of conventions in Z that make both writing and reading Z easier once they are understood. These conventions are used in the naming of both variable components and schemas. They aid in the concise specification of operations with state changes and also the identification of inputs and outputs for such operations.

1.1 B.1   Approach Sequencing Case Study

The Altran Z course includes an extended case study for approach sequencing of aircraft for an airport. This is gradually developed with features to introduce aspects of the Z notation in a measured manner. Initially sets and their associated operators are introduced.

First the informal requirements are presented, using an English description covering messages that can be sent and simple diagrams, such as a system context diagram to aid in analysing the requirements and an entity-relationship diagram to help in modelling the world under consideration. Next the operations that the system must perform are considered. Once a list of operations has been formulated, it is possible consider a formal specification of the system in terms of an abstract state and operations on that state. Each operation has inputs, a starting state, a finishing state, and outputs.

To formulate any specification in Z, sets are needed, so the course first introduces the simplest form of sets available, with no internal structure. Venn diagrams are used to introduce the standard set operators of union ($\cup$), intersection ($\cap$), set difference ($\setminus$). The concept of the size of a set using the “$\#$” operator is also introduced. In Z, the set of integers ($\mathbb {Z}$) is assumed to exist for all specifications. Additional basic sets can also be introduced (e.g., [X] to introduce a set called X). More complex sets can be constructed using sets of sets ($\mathbb {P}$ for infinite sets, $\mathbb {F}$ for finite sets, and $\mathbb {F}_1$ for finite sets with the empty set excluded), sets of pairs (using $\times$), and also schemas for more complex internal structure where needed. Sets can contain sets themselves, and so on in a nested manner if desired.

Using simple sets, a system state is specified, with a specific initial state for the system when it starts. Operations with before and after states, as well as inputs, are also defined. The conventions for schema operations are introduced informally (e.g., $\varDelta$ for change of state schemas, $'$ appended for after-state components, and ? appended for inputs).

1.2 B.2   Relations and Functions

Sets are the most basic form of structuring abstract data in Z. For more structure where pairs of elements are associated with each other, relations are available, with further specific operators available for handling them. Elements in the domain and range of a relation may be related in arbitrary ways (i.e., a many-to-many mapping). Functions are a special sort of relation in Z where elements in the domain map to at most one element in the range (i.e., a many-to-one mapping). This allows standard function application for example in the form f(x) (or even just $f\,x$ in Z), where f is a function and x is an element in the function’s domain. Care must be take if f is a partial function (i.e., the entire domain is not necessarily mapped) to ensure that x is in the domain of f (formally, $x \in \mathop {\mathrm {dom}}f$). Otherwise f(x) will be undefined, resulting in an arbitrary value in the two-state (true/false) logic of Z.

Pairs of elements using the Cartesian product operator ($\times$), together with the “maplet” notation ($\mapsto$) are introduced. Relations ($\leftrightarrow$) are explained using simple diagrams with a domain($``\mathop {\mathrm {dom}}$”), range (“$\mathop {\mathrm {ran}}$”), and mappings between elements in the domain and range. Additional operators that only apply to relations are introduced, such as domain restriction, ), domain subtraction (or anti-restriction (), range restriction (), and range subtraction (or anti-restriction, ), are covered. These operators are not so common in standard set theory, but have been found to be useful for manipulating relations in practical Z specifications so are included as part of the standard language. The use of infix relational operators (such as $\in$ and $\subset$) in Z is explained.

Next functions, a special sort of relation in Z, are covered, including function application (e.g., f(x)). Relational overriding ($\oplus$), often used with functions, is also explained. This operator is another more unusual feature of Z, but is very useful in cases where a function needs a part of it modifying in some way.

With some basic aspects of relations and functions covered, the course material continues with the case study, adding a state component that uses a partial function (), using schema inclusion, which is also explained. The concept of a state invariant (a predicate in a state schema that applies to all possible states in the system), is introduced. The initial state and operations schemas previously defined using sets are augmented with the newly defined partial state schema using schema inclusion, together with additional inputs and predicates as needed.

1.3 B.3   Sequences

Sequences in Z are modelled as a special sort of function where the domain consists of natural numbers from one up to the size (length) of the sequence. Further operators are available specifically for sequences, notably concatenation of two sequences to form a new sequence.

The sequence notation of Z (“$\mathop {\mathrm {seq}}$” and “$\langle \ldots \rangle$”) is introduced and an example is presented. Injective sequences (“$\mathop {\mathrm {iseq}}$”), in which all the elements of the sequence are different, are also covered. Sequences can be concatenated (). It is also possible to select from (or filter) a sequence using a set of elements that may be in the sequence (), resulting in a new sequence with potentially fewer elements in it.

The state for the case study example is augmented with an injective sequence, related to an existing state component with an invariant predicate.

There are a significant number of further operators for use with sequences in Z, as listed in Appendix A. Perhaps the most useful are the functions head for returning the first element in a non-empty sequence, tail for returning all except the head of a sequence as a new sequence, last for returning the last element in a non-empty sequence, and front for returning all but the last element of a sequence as a new sequence. In addition, rev can be used to reverse any sequence, even the empty sequence.

A further but less-used feature of Z is a “bag” (also known as a multiset), which is like a set but used where multiple copies of the same element are needed. This is modelled in Z as a partial function from the type of the elements in the bag (e.g., X), to strictly positive natural numbers ($\mathbb {N}_1$, i.e., all natural numbers except zero), indicating the number of elements in the bag. If this number as always one, the bag would act like a normal set. There are various built-in operators in Z for handling bags, as listed in Appendix A. Some of these have counterparts with operators on standard sets, such as bag membership, the sub-bag relation, bag union, and bag difference, but need different definitions to handle the multiplicity of elements appropriately.

Most of the operators used in Z are defined formally within Z using generic definitions, as part of a mathematical “toolkit” [39]. It is often the case for large specifications that some additional operators will also be specified in this way, to enable a shorter and more understandable specification overall. Some could be deemed generally useful and form the basis for an augmented toolkit at an organisation that produces many Z specifications.

1.4 B.4   Logic

As well as sets in Z, first order predicate logic is also used as the main form of detailed specification, with standard logical operators on predicates. Note that the logic of Z is two-valued, with only true or false possible. There is no “undefined” logical value, unlike some other logics. If any expressions are undefined in a predicate, Z handles this by allowing the predicate to take either a true or false value. This is normally something that is not desirable in real specifications, so it is avoided in practice through careful formulation of the specification, with appropriate error handling where needed.

The course initially introduces propositional logic in which statements are true or false. The standard logical connectives of negation (“not”, $\lnot$), conjunction (“and”, $\wedge$), disjunction (inclusive “or”, $\vee$), implication (“implies”, $\Rightarrow$), and equivalence (“equivalent”, $\Leftrightarrow$) are introduced using truth tables. The binding powers (strongest binding first in the list above) and use of brackets to override this if needed are explained. An example of a truth table for a more complex expression is also presented.

Next predicate logic is covered, in which variables are also included. In Z, variable components are typed, so predicates and expressions in them must respect this typing. Existential quantification ($\exists$), universal quantification ($\forall$), and the nesting of quantifications are introduced. All quantified variables in Z must be declared with a type when introduced since Z is a typed language. Selective quantification is explained, in which a predicate is included after the declaration part (separated by “$\mid$”) to restrict the quantified variables further before the main predicate of the quantification (separated by “”) is stated.

Next, set comprehension (of the form ) is explained, with a number of examples. This has a similar form to quantification in Z. Set comprehension can always be used to define a set in Z if there is no other more convenient way to do it.

The case study is then used to demonstrate an axiomatic description that introduces a global constant to the specification, a typical use of this construct. Then a concept of time is introduced to the state, using a natural number that increases as time progresses. Next an illustration of how a quantified predicate may be determined and added as an invariant for the state is explained, as several possible candidate invariants. An operation to model time passing is presented, including a change of state to the system that may occur as time passes. This is an operation that the user cannot directly control, but will be interleaved with other user operations.

The schema operations are augmented to handle the additional state now being modelled in the system. The complete state, and initial state, and final versions of the operations are presented.

1.5 B.5   Analysing the Specification

Once a specification has been formulated, it is possible to reason about it. This may be informally in the head of the engineer or more formally. The former if most typical in industrial use of Z. The Altran Z course illustrates some of the thought processes and the techniques that are helpful in such reasoning.

Proofs associated with a specification can check a number of properties. Firstly an initial state must exist for the system to be able to start at all. Then preconditions of operations can be checked. If they are not true, it is normal to add schemas to cover the error conditions (the negation of the precondition for the successful operation) so a complete “total” operation can be produced that has an overall precondition of true and typically an output that indicates if an error occurred. Any invariant predicates are consistently applied to the state are all times. If these or other predicates reduce to false, operations may not be implementable.

Finally, challenge theorems demonstrating desirable properties are beneficial when checking a specification. If true, they increase confidence in the specification since our understanding is compatible with the mathematical description. If false, it indicates a possible misunderstanding and may necessitate a change in the specification. Even with all these checks, the specification may still not be “correct” with respect to informal notions of what the system should do. For that, engineering judgement, expertise, and experience is needed.

The course material provides examples of checking these issues using the case study specification. It also includes its own summary of the Z notation.

1.6 B.6   Exercises

On the following page is part of a sample exercise from the Altran Z course. Matching model answers are also available for both presentation by the course teacher once the exercises have been attempted by students and also distribution to the students after that have tackled the questions.

Exercises cover sets, relations, functions, propositional logic, and predicate logic. The exercise on sets includes questions on the understanding of enumerated sets, the use of set operators in expressions, predicates involving sets, and the selection of given sets for a specification. The exercise on relations covers the understanding of notation relevant to relations, expressions using relations, and the understanding of a small specification involving a relation. The exercise on functions includes questions on the difference between a relation and a function, followed by the understanding of a small specification involving a number of functions.

The exercise on logic has questions on propositional logic and predicate logic. Propositional logic questions include determining the truth value of propositions, choosing a value to make propositions true, explicitly adding brackets to complex logical statements, and producing truth tables for logical statements. Questions on predicate logic cover rewriting logical statements using quantifiers, determining if quantified predicates are true or false, and expressing informal sentences as formal quantified predicates.

1.7 B.7   Introduction to Schemas

This part of the Z course covers the schema as a structuring concept, schemas in use as abstract state, schema inclusion enabling the building up of a specification, and schemas as operations involving relating a before state with an after state.

First the idea of schemas is introduced informally. A schema box has a name, a declaration part, and a predicate part (which may be omitted if the predicate is true):

Some examples of schemas are explained, based around the well-known “Birthday Book” example in Z [39]. A schema can specify the abstract state of a system and this is explained in terms of the state components and invariant predicates that can constrain those components, normally by relating them together in some way.

Generic schemas are also introduced briefly, although these are less used within Z in practice. Next the important concept of schema inclusion is covered, explaining how declarations are merged (especially if component names match) and how predicates are conjoined.

As well as being used for specifying state, schemas can also be used to specify operations, with both a before state and a matching after state (in which the components are decorated with primes, $'$). In fact schemas can be decorated with arbitrary subscripts and superscripts if desired, but the use of primes for decoration is but far the most common style of decoration with Z schemas in typical specifications.

An example of schema inclusion is given, including the expansion of the overall schema to include all the constituent state components. It is important to be able to do this mentally when using Z, so an understanding of schema inclusion is critical when reading most Z specifications. The technique is a key part of Z and may be used to specialise an existing partial specification for a particular specification, potentially multiple times even in a single overall specification.

As well as specifying abstract state, an important use of Z schemas in practice is to specify a change of state (with before and after states), in which typically some state components change their values and others remain the same. The standard naming convention for state components in an operation schema is that undecorated state components are in the before state, matching primed (or “dashed”) components ($'$) are in the after state, inputs have a “?” appended, and outputs have a “!” appended to their names. These conventions are extremely common in Z specifications in the standard model-based style. Subscripts and superscripts can also be used for decoration if desired for a special purpose, although this is less common in practice.

An operation schema will typically have a number of predicates conjoined together (often implicitly on separate lines). Normally preconditions are included first and postconditions afterwards, but the order is logically immaterial since logical conjunction ($\wedge$) is commutative and conjunction is assumed between lines of predicates by default if no other logical operator is included since it is the most common connective for predicates in Z specification in practice.

Preconditions are constraining predicates that only involve before-state unprimed components and inputs. Postconditions also include after-state primed components and outputs. It is normally very important to check that all after-state components and outputs are constrained in some way since it is unusual for these to be allowed to take on any value after an operation has been performed.

Often an after-state component is constrained deterministically in terms of a function involving the matching before-state component (e.g., $x'=\ldots x\ldots$). If no change of state is required, this must be explicitly specified (e.g., $x'=x$), although often it is possible to do this conveniently using the $\varXi$ convention with included schemas that adds this constraint for all the components in the relevant schema.

It should be noted that it is possible to include hidden preconditions in what appear to be postconditions. For example, $x'\in xs$ implicitly assumes that $xs\ne \emptyset$ (i.e., xs is not an empty set), which is thus a precondition if this is included in an operation. Thus, formally the precondition in a schema should be calculated (by existentially quantifying all the after-state components and outputs), although in practice this can often just be done mentally.

The important $\varDelta$ and $\varXi$ conventions for state schemas are covered. $\varDelta$ may be prefixed to a state schema name to produce a schema with a before state and matching primed after state. $\varXi$ is similar, but adds the constraint that all the after-state components have the same value as the matching before-state components (e.g., $x'=x$, etc.).

There are associated exercises with questions on schemas, together with model answers. Aspects of schemas covered include understanding of the purpose of schemas, their constituent parts, and conventions associated with schemas. Example state and operations schemas are provided and questions explore their meaning and use. Finally, a more advanced question covers the use of a generic schema. These are less used in simple Z specifications, but can be more useful in larger specifications, as found in industrial-scale examples.

1.8 B.8   Schema Calculus

There are matching logical operators on schemas such as conjunction ($\wedge$) and disjunction ($\vee$) that allow larger specifications to be constructed from earlier schemas. This is a very important aspect of Z that allows large specifications, potentially thousands of pages long, to be created and used effectively. If only the mathematical aspects of Z were available, it would not be possible to use it on an industrial scale.

First the most used schema operator, namely schema conjunction ($\wedge$), is introduced and explained. This is used for building up specifications from constituent schemas that have specified part of the overall system. Declarations are merged and predicates are logically conjoined, in a similar way to schema inclusion.

If schema components have the same name and are type-compatible, they map on top of each other. This is a useful feature but some care is needed because Z declarations can and often do include additional constraints as well as type information. If the component is declared in exactly the same way, the issue is easy. However, say there is a declaration of $x:\mathbb {N}$ (a natural number of zero or more) in one schema and $x:\mathbb {Z}$ (an integer of arbitrary value) in another. These are type-compatible since $\mathbb {N}$ is a subset of $\mathbb {Z}$ but when logically conjoined, the value of x must be a natural number, not an arbitrary integer.

Thus an important aspect of combining schemas using schema operators (or schema inclusion) is the normalisation of the types of components. In the example above, $x:\mathbb {N}$ is normalised to $x:\mathbb {Z}$ with the constraining predicate that $x\in \mathbb {N}$. The same issue applies to functions, which are a constrained form of relation. Thus 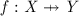normalises to $f:\mathbb {P}(X \times Y)$, for example, with the constraint that 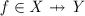, assuming that X and Y are given sets and thus already normalised. Remembering that $X\leftrightarrow Y$ is the same as $\mathbb {P}(X\times Y)$ is a useful fact to memorise to understand typing in Z.

Components with the same name must be type-compatible (i.e., have the same normalised types) for the specification to be meaningful. Components with different names are just merged in the declaration part of the new schema. Note that component declaration order is immaterial in a schema. A common mistake is to try to relate two schema components in the declaration part, but this is invalid since the declarations are only meaningful in the predicate part of the schema, which is where such relationships should be specified.

Schema disjunction ($\vee$) is covered next since this is also an important way that schemas can be combined, especially when dealing with error cases. The declarations are combined in exactly the same way as for schema conjunction, with the same normalisation of types needed when combining components with the same name. However in this case the predicates of the two schemas are combined using logical disjunction.

Robust (or “total”) operations can be produced using disjunction to give an overall precondition of true. Typically if there is a precondition P in a successful operation schema (e.g., Op), an error schema (e.g., Err) with a precondition $\lnot P$ can handle the error case, and $Op\vee Err$ gives a total operation schema with a precondition of true. If an operation schema has two preconditions $P\wedge Q$, there can be two error schemas with preconditions $\lnot P$ and $\lnot Q$, and so on.

Typically error schemas output an error result of some sort (e.g., report!). For example, the successful operation schema could output $report! = ok$ (perhaps specified once is a single schema, e.g., Success, for reuse later) and the error schema could output $report! = error$. Further error reports can be introduced as needed. A robust total operation (TotalOp in this case) could be specified in the form of combined schemas as follows:

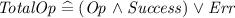
In a typical Z specification with total operations, there would be a number of such total operations specified in this form.

There is also a schema negation operator ($\lnot$), although this is less used in practice. However it is included for completeness and is covered by the Z course. Again, the schema is first normalised with respect to all the declarations and then the entire predicate part is logically negated, including any predicates introduced through normalisation. For example, if the declarations in a schemas S included $x:\mathbb {N}$, the negated schema $\lnot S$ would include a declaration of $x:\mathbb {Z}$ and a predicate of $\lnot x\in \mathbb {N}$ (or $x\notin \mathbb {N}$). Thus the x component in $\lnot S$ would be constrained to be a negative integer ($x<0$). An example of schema negation is included in the course. A schema normalisation example where a similarly named component has different but compatible declarations in the two schemas that are to be combined (using disjunction) is also included.

Z includes a facility to rename individual schema components if needed. If a schema S includes a component variable old, it is possible to create a new schema T with that component renamed to new as follows:

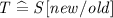
This is not used much in small specifications, but can be useful in industrial-scale specifications, allowing reuse of a schema in a different context. Several component variables can be renamed simultaneously and renaming can also be combined with a generically defined schema for even more possibilities of reuse. An example is given in the course material.

Again, there are associated questions on schema calculus with model answers. These include a general question on schema operators and their use. An example of schema disjunction is given for explanation. A more complex example with schema conjunction and disjunction must also be understood and explained informally.

1.9 B.9   Schemas as Types

Z is a typed language and standard types are built up from basic types (or given sets) that are unstructured. Of course, relations, functions, sequences, etc., can be specified as well. For more complex structuring, the use of schemas as types is helpful. Schemas can be used somewhat like records in many programming languages, with the named state components in the schema identifying different parts of the structure.

An example of a simple schema being used in a type declaration is explained. It should be noted that the ordering of declarations in schemas is unimportant, unlike a Cartesian product where the ordering is meaningful. Even if two schemas have different predicates, they can still be type-compatible since it is the normalisation of the schema components that matters.

If a component variable has a schema type, components in that schema can be selected. For example, with a declaration of s : S where S is a schema with components x and y in its declaration, s.x and s.y can be used to refer to those components. With two variables declared using type-compatible (or identical) schema types, they can be made equal in a predicate. E.g., with declarations s, t : S using a schema S, the predicate $s=t$ is valid.

If the variables of S are in scope within a schema (e.g., it has been included in another schema), then $\theta S$ is an instance of the schema type S with all the components have the values in the current context. The schema may be decorated, so $\theta S'$ is also meaningful. This is especially useful in specifying the meaning of $\varXi S$ (for example) formally:

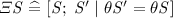
The technique of schema promotion is also covered. This is very important in larger specifications since it allows a smaller specification to be embedded in a larger specification in a convenient manner, especially if the rest of the larger system is to remain unchanged while the smaller subsystem is updated in some way. An example of this approach is provided by the course. The approach is particularly useful in industrial-scale Z specifications. First the course material explains a specific example and then this is generalised. The template can be used in many real examples of the specification of large systems and solves the framing problem of dealing with a small update of a large system in a convenient manner in the context of Z.

Associated questions and model answers are available. Firstly a schema is provided and the compatibility of this with other schemas when used as a schema type must be determined. This especially checks schema normalisation skills. Then a more complex example is presented including two schema component variables declared using schema types with a complex predicate relating the two. The relationship that this conveys must be explained in English.

1.10 B.10   Syndicate Exercise

An extended Z specification is available for students to learn how to discuss and use a more realistic formal specification. This is an optional but useful part of the course, taking around half a day. Example questions are provided, but this part of the course is more open-ended and the course teacher can lead a discussion with students on the course once they have studied the case study material.

The specification is provided with Z and associated English explanation in a way that is typical for a Z specification. A number of operations are covered. The example questions start with detailed technical issues, why certain features have been selected in the Z specification, and what effect these have in practice. The questions become more general as they proceed, allowing more discussion. Further questions could easily be formulated and discussed either by the course leader or by more able participates on the course.

Those participants who are able to provide sensible input to the discussions on this specifications are the ones that are likely to be more productive in reading Z specification on a real project. This could be helpful in deciding the roles of participants subsequently on a subsequent project involving Z specification.

1.11 B.11   Summary

As well as material for distribution to students on the Altran Z course, there are also matching teaching notes with an expanded form of the material. Slides are available with reduced material for presentation by the course teacher on a screen during lectures. The exercises have full associated model answers in general.

An expanded version of the Z Readers Course is available, the Z Writers Course, designed for people who are going to need to write specifications. On a typical industrial project using Z, the number of people who need to be able to read Z vastly outnumbers the team needed to write Z. Typically the Z specification may be used to guide the software tests that are undertaken, by partitioning the specification for the various tests that are required. It will always be used to guide the implementation by programmers. Both these large teams only require engineers that are able to read Z, a much easier task than writing good Z specifications.

For more information on Altran, see http://www.altran.com. For specific information on “Formal Computing” from Altran, see:

http://intelligent-systems.altran.com/technologies/software-engineering/formal-computing.html