Temperature Effects in Hot-Wire Measurements on Higher-Order Moments in Wall Turbulence

Abstract

The effect of temperature fluctuations—as they are e.g. encountered in non-isothermal flows—on the mean, variance and spectra in wall-bounded turbulent flows when utilising hot-wire anemometry has recently been documented. The present work extends these efforts on the effect of temperature fluctuations on the skewness and flatness factors as well as assesses the performance of commonly employed temperature compensations.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction and Approach

Measuring turbulent fluctuations using hot-wire anemometry is still the method that provides the highest degree of accuracy, in particular when it comes to temporal and spatial resolution. The question of spatial resolution of hot-wires has been treated in the past in a number of publications [1], and corresponding correction schemes, both heuristic [2] and data-driven [3], have been suggested. Nonetheless, there are still unresolved open questions in wall turbulence, such as the proper scaling of the near-wall and secondary peak (or even its existence) in the variance profile of the streamwise velocity component or the scaling behaviour of its higher-order moments [4]. While the effect of temporal and spatial resolution on these quantities has been investigated in a number of studies it was only very recently that the effect of temperature fluctuations—as they are e.g. encountered in non-isothermal flows—on the mean, variance and spectra in wall-bounded turbulent flows when utilising hot-wire anemometry has been documented and corrections were proposed [5].

The aim of the present investigation is to extend the aforementioned efforts on the effect of temperature fluctuations on the skewness and flatness factors as well as to assess the performance of commonly employed temperature compensations. For this purpose, the response of a hot-wire is simulated through the use of velocity and temperature (i.e. passive scalar) data from a turbulent channel flow generated by means of direct numerical simulations (DNS) at a friction Reynolds number of $Re_\tau =590$ as done in Örlü et al. [5] to which the reader is referred for details. In particular, the effect of a 2, 4, and 6 K temperature gradient across the channel height will be simulated and the performance of temperature compensations of the instantaneous velocity signals will be demonstrated utilising common techniques, i.e. the mean centreline (or external) temperature $\left\langle T_{CL}\right\rangle$, the mean local temperature $\left\langle T(y^+)\right\rangle$, and the newly proposed synthetic instantaneous temperature by Örlü et al. [5], henceforth denoted $T_\text {synt}(t;y^+)$ given through

$$\begin{aligned} T_\text {synt}(t;y^+) = \langle T \rangle (y^+) + \frac{u(t) T_\tau }{u_\tau } \left( \frac{\langle uu \rangle }{\langle uu \rangle _{max}} \right) , \end{aligned}$$

(1)

where $u_\tau$ and $T_\tau$ is the friction velocity and temperature, while $\langle \cdot \rangle$ and $^+$ denote the time-average operator and wall units, respectively. In all these exercises $u_\tau$ is taken from the simulation and is therefore unaffected by the temperature gradient. This procedure is comparable to an experimental where $u_\tau$ is obtained independently from velocity measurements, as e.g. from the pressure drop in internal flows.

Fig. 1

Inner-scaled mean streamwise velocity $U^+$ profile from DNS (

) and sensed by virtual hot-wire probe for $\varDelta T = 2$ (—), 4 (– –), and 6 K (– $\cdot$ –), which is temperature-compensated by means of $\left\langle T_{CL}\right\rangle$, as well as the relative errors when utilising $\left\langle T_{CL}\right\rangle$ and $\left\langle T(y^+)\right\rangle$

2 Results and Discussions

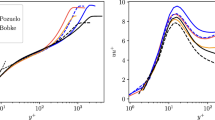
In situations where $\left\langle T_{CL}\right\rangle$ is monitored throughout an experiment, it is common to employ this temperature for the compensation of the instantaneous hot-wire (voltage) readings. The effect on the mean velocity profile for temperature gradients of 2, 4, and 6 K is depicted in Fig. 1 together with their relative errors. Although not directly apparent from the mean velocity profile, the relative errors are considerable. Utilising instead $\left\langle T(y^+)\right\rangle$, as is common practise (if one is aware of possible temperature gradients), one is able to recover the correct mean velocity profile.

Based on this result, one would assume that $\left\langle T(y^+)\right\rangle$ is superior to $\left\langle T_{CL}\right\rangle$ when it comes to the variance profile. Although this is the case as shown in Fig. 2, the obtained variance profile is significantly attenuated around the near-wall peak when utilising $\left\langle T(y^+)\right\rangle$, while it is nearly fully recovered when $\left\langle T_{CL}\right\rangle$ is used, which makes it interesting for practical purposes, since it is the near-wall peak that is effected the most in absolute terms. Consequently, there is no clear favourite between the two temperatures when it comes to corrections beyond the mean velocity and hence the correction scheme suggested in Ref. [5], i.e. Eq. (1), is compared to the previous ones in the following for the higher-order moments.

Fig. 2

Inner-scaled variance profile of the streamwise velocity component $\left\langle uu \right\rangle ^+$ obtained when utilising $\left\langle T(y^+)\right\rangle$ for the compensation as well as the relative errors when using $\left\langle T(y^+)\right\rangle$ and $\left\langle T_{CL}\right\rangle$

Contrary to the previous figures, where relative errors were presented, Fig. 3 documents the absolute errors for higher-order moments, since relative errors become problematic for odd moments due to zero-crossings and values close to zero. As apparent, the utilisation of $\left\langle T_{CL}\right\rangle$ is not recommended although it might yield (only) the correct amplitude of the variance near-wall peak; errors (obviously) amplify in the limit of $y^+\rightarrow 0$. This becomes in particular important when assessing the limiting behaviour of the variance, i.e. amplitude of the wall shear stress fluctuations, and skewness or flatness factors. While both $\left\langle T(y^+)\right\rangle$ and $T_\text {synt}(t;y^+)$ yield the correct mean velocity profile, the advantage of utilising $T_\text {synt}(t;y^+)$ becomes apparent when inspecting the absolute errors for the higher-order moments. Consequently, in the absence of simultaneous, spatially and temporally resolved, temperature and (hot-wire) velocity measurements, the correction scheme proposed in Örlü et al. [5] is recommended whenever temperature gradients are unavoidable, be it for the purpose of correcting or assessing errors due to temperature fluctuations.

Fig. 3

Absolute errors for the variance, skewness factor, third-order moment, flatness factor and fourth-order moment of the streamwise velocity fluctuations, temperature compensated with $\left\langle T_{CL}\right\rangle$, $\left\langle T(y^+)\right\rangle$, as well as the method proposed in Örlü et al. [5], i.e. $T_\text {synt}(t;y^+)$. To appreciate the relative importance of the absolute errors compared to the actual amplitudes see e.g. Ref. [4]