Keywords

1 Introduction

Induction machines, a type of AC drives, are used widely in practice for variable speed applications in wide power ranges. These machines are very economical, rugged and reliable [8]. However, the control and estimation of important quantities of AC drives with induction motors is difficult because of variable frequency of a supply stator phase voltages realized by frequency converters, complex dynamics of AC machines, machine parameters variations, and signal processing of feedback signals [6]. In many decades, induction motor control methods are developed. The control methods of induction machines can be listed as scalar controlling, field oriented control (FOC) and direct torque and flux control (DTC) [4, 6]. Scalar control is simple, easy to implement in practice but it disregards the coupling effect. So it has inferior performance, especially in low speed applications and now scalar control diminished in real world. The DTC, an advanced scalar control method, is introduced in the mid-1980s. The torque and stator flux are controlled by inverter voltage space vector through look-up table [4]. The disadvantage of DTC is that DTC is not stable at low speed. The field-oriented control or vector control was introduced firstly in 1970s. The vector control has been used in industry for high performance, especially in low speed [7]. This method is complicated. However, with developing of semiconductor technology, powerful microcontroller or DSP are used so that FOC overcome its disadvantages and become an industry standard control for AC drives.

In FOC, a flux control loop has been added for precision control of flux. The torque component is generated from the speed control loop. So induction motor control requires accurate flux and motor rotor speed. The flux and rotor speed can be achieved by using Hall sensor and encoder. However, in recent researches, sensors are eliminated because of complexity, higher cost and lower reliability [3, 8, 9, 13]. The observers are used instead. Many kinds of observers are proposed, such as Extended Kalmanm Filter (EKF), Luenberger Observer (LO) and Sliding Mode Observer (SMO) [3–6, 8–10, 12, 13]. Among the observers, the EKF observers get high accuracy at medium and high speed range [9, 13]. They can operate well at the rotor speed above 60 rpm while the SMO and LO observers can work well at very low speed, about 15 rpm [8, 9, 13]. In case of parameters of induction motor not known exactly and noise, the SMOs and LOs have superior performance over to the EKF observers [9, 13]. Among these observers, sliding mode observers have strong robustness to parameter variations such as stator resistance, mutual inductance, etc. [13]. They also have superior performance when the noise increases and they can handle nonlinear systems like IM very well [4, 13]. Moreover, LO and SMO are more applicable in practical than EKF [13].

Because of their outstanding characteristics in nonlinear systems and parameter variations, sliding mode observers are focused in this paper. The mathematical model of induction machines is introduced in Sect. 2. Sliding mode observer and the current model are used to estimate the rotor flux and speed are presented in Sect. 3. In this section, the stability of the method based on Lyapunov’s theory is also analyzed. Next, Sect. 4 introduces vector control of induction motor. Some simulation results are presented in Sect. 4. At last, the conclusions are in Sect. 5.

2 Mathematical Model of Induction Machines

Dynamic model of an induction motor in two-phase stationary frame are described as follows [5, 6, 14]:

$$ \begin{aligned} \frac{{di_{S\alpha } }}{dt} = & - \frac{{\left( {L_{h}^{2} R_{R} + L_{R}^{2} R_{S} } \right)}}{{\sigma L_{S} L_{R}^{2} }}i_{S\alpha } + \frac{{L_{h} R_{R} }}{{\sigma L_{S} L_{R}^{2} }}\psi_{R\alpha } + \frac{{L_{h} \omega_{r} }}{{\sigma L_{S} L_{R} }}\psi_{R\beta } + \frac{1}{{\sigma L_{S} }}v_{S\alpha } \\ \frac{{di_{S\beta } }}{dt} = & - \frac{{\left( {L_{h}^{2} R_{R} + L_{R}^{2} R_{S} } \right)}}{{\sigma L_{S} L_{R}^{2} }}i_{S\beta } - \frac{{L_{h} \omega_{r} }}{{\sigma L_{S} L_{R} }}\psi_{R\alpha } + \frac{{L_{h} R_{R} }}{{\sigma L_{S} L_{R}^{2} }}\psi_{R\beta } + \frac{1}{{\sigma L_{S} }}v_{S\beta } \\ \frac{{d\psi_{R\alpha } }}{dt} = &\frac{{L_{h} R_{R} }}{{L_{R} }}i_{S\alpha } - \frac{{R_{R} }}{{L_{R} }}\psi_{R\alpha } - \omega_{r} \psi_{R\beta } \\ \frac{{d\psi_{R\beta } }}{dt} = &\frac{{L_{h} R_{R} }}{{L_{R} }}i_{S\beta } + \omega_{r} \psi_{R\alpha } - \frac{{R_{R} }}{{L_{R} }}\psi_{R\beta } \\ \end{aligned} $$
(1)

where \( i_{S\alpha } \), \( i_{S\beta } \)—stator current vector components in \( \left[ {\alpha ,\beta } \right] \) stator coordinate system; \( v_{S\alpha } ,\,v_{S\beta } \)—stator voltage vector components in \( \left[ {\alpha ,\beta } \right] \) stator coordinate system; \( \psi_{R\alpha } ,\,\psi_{R\beta } \)—rotor magnetic flux in \( \left[ {\alpha ,\beta } \right] \) stator coordinate system; \( L_{h} \)—magnetizing inductance; \( L_{R} \)—rotor inductance; \( L_{S} \)—stator inductance; \( R_{R} \)—rotor phase resistance; \( R_{S} \)—stator phase resistance; \( \omega_{r} \)—rotor angular speed; \( \sigma \)—total leakage factor \( \left( {\sigma = 1 - \frac{{L_{m}^{2} }}{{L_{R} L_{S} }}} \right) \); \( p \)—the number of poles.

The electrical torque produced by induction motor is:

$$ T_{e} = \frac{3}{2}\frac{p}{2}\frac{{L_{h} }}{{L_{R} }}\left( {\psi_{R\alpha } i_{S\beta } - \psi_{R\beta } i_{S\alpha } } \right) $$
(2)

3 Sliding Mode Observer

3.1 Sliding Mode Observer for Speed Estimation

Depending on field oriented control of induction motor, the stator currents, rotor fluxes and rotor speed need to be estimated. The stator currents \( i_{S\alpha } ,\,i_{S\beta } \), rotor speed \( \omega_{r} \) are estimated by using sliding mode observer.

According to Eq. (1), the dynamic model of induction motor is rewritten under state space as follows:

$$ \begin{aligned} & \dot{x} = A \cdot x + B \cdot v \\ & y = C \cdot x \\ \end{aligned} $$
(3)
$$ x = \left[ {i_{S\alpha } \,\,\,i_{S\beta } \,\,\,\psi_{R\alpha } \,\,\,\psi_{R\beta } } \right]^{T} ;\quad v = \left[ {v_{S\alpha } \,\,v_{S\beta } } \right]^{T} $$
(4)
$$ A = \left[ {\begin{array}{*{20}l} {a_{11} } \hfill & {a_{12} } \hfill & {a_{13} } \hfill & {a_{14} } \hfill \\ {a_{21} } \hfill & {a_{22} } \hfill & {a_{23} } \hfill & {a_{24} } \hfill \\ {a_{31} } \hfill & {a_{32} } \hfill & {a_{33} } \hfill & {a_{34} } \hfill \\ {a_{41} } \hfill & {a_{42} } \hfill & {a_{43} } \hfill & {a_{44} } \hfill \\ \end{array} } \right], \quad B = \frac{1}{{\sigma L_{S} }}\left[ {\begin{array}{*{20}l} 1 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill \\ \end{array} } \right], \quad C = \left[ {\begin{array}{*{20}l} 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right] $$
(5)
$$ \begin{aligned} & a_{11} = a_{22} = - \frac{{\left( {L_{h}^{2} R_{R} + L_{R}^{2} R_{S} } \right)}}{{\sigma L_{S} L_{R}^{2} }}, \quad a_{12} = a_{21} = 0, \quad a_{13} = a_{24} = \frac{{L_{h} R_{R} }}{{\sigma L_{S} L_{R}^{2} }}, \quad a_{14} = - a_{23} = \frac{{L_{h} \omega_{r} }}{{\sigma L_{S} L_{R} }} \\ & a_{31} = a_{42} = \frac{{L_{h} R_{R} }}{{L_{R} }}, \quad a_{32} = a_{41} = 0, \quad a_{33} = a_{44} = - \frac{{R_{R} }}{{L{}_{R}}}, \quad a_{34} = - a_{43} = - \omega_{r} \\ \end{aligned} $$
(6)

The sliding mode observer can be given as:

$$ \begin{aligned} & \frac{d}{dt}\hat{x} = \hat{A} \cdot \hat{x} + B \cdot v + G \cdot sign\left[ {y - \hat{y}} \right] \\ & y = C \cdot \hat{x} \\ \end{aligned} $$
(7)
$$ \hat{A} = A_{{\left( {\omega_{r} = \hat{\omega }_{r} } \right)}} ;\quad G = \left[ {\begin{array}{*{20}l} {g_{1} } \hfill & { - g_{2} } \hfill \\ {g_{2} } \hfill & {g_{1} } \hfill \\ {g_{3} } \hfill & { - g_{4} } \hfill \\ {g_{4} } \hfill & {g_{3} } \hfill \\ \end{array} } \right] $$
(8)

Sliding surface is chosen:

$$ S = y - \hat{y} $$
(9)

The time derivation of sliding mode observer is:

$$ \dot{S} = \dot{y} - \dot{\hat{y}} = C\dot{x} - C\dot{\hat{x}} $$
(10)
$$ \begin{aligned} \dot{S} =\,& C \cdot \left( {A \cdot x + B \cdot v - \hat{A} \cdot \hat{x} - B \cdot v - G \cdot sign\left[ {y - \hat{y}} \right]} \right) \\ =\,& C \cdot \left( {\left( {A - \hat{A}} \right) \cdot x + \hat{A} \cdot \tilde{x} - G \cdot sign\left[ {y - \hat{y}} \right]} \right) \\ \end{aligned} $$
(11)

where \( \tilde{x} = x - \hat{x} \)—the error between the real value and estimated value.

$$ A - \hat{A} = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 0 \hfill & {\frac{{L_{h} }}{{\sigma L_{S} L_{R} }}} \hfill \\ 0 \hfill & 0 \hfill & { - \frac{{L_{h} }}{{\sigma L_{S} L_{R} }}} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & { - 1} \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ \end{array} } \right]\tilde{\omega }_{r} = W\tilde{\omega }_{r} $$
(12)

where \( \tilde{\omega }_{r} = \omega_{r} - \hat{\omega }_{r} \)—speed difference between actual rotor speed and estimated rotor speed.

Choosing the positive definite Lyapunov function as follows [7]:

$$ V = \frac{1}{2}\left( {S^{2} + \frac{{\tilde{\omega }_{r}^{2} }}{a}} \right) $$
(13)

The time derivation of Lyapunov function is derived:

$$ \begin{aligned} \dot{V} =\,& S^{T} \cdot \dot{S} - \frac{1}{\alpha }\dot{\hat{\omega }}_{r} \tilde{\omega }_{r} =\, S^{T} \cdot C \cdot \left( {\hat{A} \cdot \tilde{x} + W \cdot \tilde{\omega }_{r} \cdot x - G \cdot sign\left[ {y - \hat{y}} \right]} \right) - \frac{1}{a}\dot{\hat{\omega }}_{r} \tilde{\omega }_{r} \\ =\,& S^{T} \cdot C \cdot \hat{A} \cdot \tilde{x} - S^{T} \cdot C \cdot G \cdot sign\left[ {y - \hat{y}} \right] \\ & + \tilde{\omega }_{r} \left( { - \frac{{\dot{\hat{\omega }}_{r} }}{a} + \frac{{L_{h} }}{{\sigma L_{R} L_{S} }}\left( {i_{S\alpha } - \hat{i}_{S\alpha } } \right)\psi_{R\beta } - \frac{{L_{h} }}{{\sigma L_{R} L_{S} }}\left( {i_{S\beta } - \hat{i}_{S\beta } } \right)\psi_{R\alpha } } \right) \\ \end{aligned} $$
(14)

For global asymptotic stability, the time derivation of Lyapunov function \( \dot{V} \) must be negative definite function. We obtain:

$$ \left\{ {\begin{array}{*{20}l} {S^{T} \cdot C \cdot \hat{A} \cdot \tilde{x} - S^{T} \cdot C \cdot G \cdot sign\left[ {y - \hat{y}} \right] < 0} \hfill \\ {\tilde{\omega }_{r} \left( { - \frac{{\dot{\hat{\omega }}_{r} }}{a} + \frac{{L_{h} }}{{\sigma L_{R} L_{S} }}\left( {i_{S\alpha } - \hat{i}_{S\alpha } } \right)\psi_{R\beta } - \frac{{L_{h} }}{{\sigma L_{R} L_{S} }}\left( {i_{S\beta } - \hat{i}_{S\beta } } \right)\psi_{R\alpha } } \right) = 0} \hfill \\ \end{array} } \right. $$
(15)

We can derive the following equations for the calculation of G matrix elements [17]:

$$ \begin{aligned} & g_{1} = \lambda \left( {k - 1} \right)\left( {R_{S} L_{R} + R_{R} L_{S} } \right); \quad g_{2} = - \left( {k - 1} \right)\hat{\omega }_{r} \\ & g_{3} = - \frac{{\left( {k - 1} \right)\left( {R_{R} L_{S} - kR_{S} L_{R} } \right)}}{{L_{h} }}; \quad g_{4} = \frac{{\left( {k - 1} \right)}}{{\lambda L_{h} }}\hat{\omega }_{r} \\ & \lambda = \frac{1}{{L_{R} L_{S} - L_{h}^{2} }} \\ \end{aligned} $$
(16)

Moreover, the rotor speed of induction motor satisfies:

$$ - \frac{{\dot{\hat{\omega }}_{r} }}{a} + \frac{{L_{h} }}{{\sigma L_{R} L_{S} }}\left( {i_{S\alpha } - \hat{i}_{S\alpha } } \right)\psi_{R\beta } - \frac{{L_{h} }}{{\sigma L_{R} L_{S} }}\left( {i_{S\beta } - \hat{i}_{S\beta } } \right)\psi_{R\alpha } = 0 $$
(17)
$$ \hat{\omega }_{r} = K_{R} \int {zdt} $$
(18)

where \( z = \left( {i_{S\alpha } - \hat{i}_{S\alpha } } \right) \cdot \psi_{R\beta } - \left( {i_{S\beta } - \hat{i}_{S\beta } } \right) \cdot \psi_{R\alpha } \)

According to the (18), the rotor speed of induction motor can be estimated depending on the following update law:

$$ \hat{\omega }_{r} = K_{P} \cdot z + K_{I} \int {z \cdot dt} $$
(19)

3.2 Flux Estimator

After estimating the stator currents \( i_{S\alpha } \), \( i_{S\beta } \), the rotor fluxes \( \psi_{R\alpha } \), \( \psi_{R\beta } \) are observed by using current model.

The current model is as follows:

$$ \begin{aligned} \frac{{d\psi_{R\alpha } }}{dt} & = \frac{{L_{h} }}{{T_{R} }}i_{S\alpha } - \frac{1}{{T_{R} }}\psi_{R\alpha } - \omega_{r} \psi_{R\beta } \\ \frac{{d\psi_{R\beta } }}{dt} & = \frac{{L_{h} }}{{T_{R} }}i_{S\beta } + \omega_{r} \psi_{R\alpha } - \frac{1}{{T_{R} }}\psi_{R\beta } \\ \end{aligned} $$
(20)

where \( T_{R} = \frac{{L_{R} }}{{R_{R} }} \) is the rotor circuit time constant. The stator currents \( i_{S\alpha } \), \( i_{S\beta } \), and rotor speed \( \omega_{r} \) are the output of sliding mode observer mentioned above.

4 Simulations

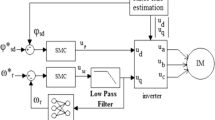
The vector control with sliding mode observer diagram is shown in Fig. 1.

Fig. 1
figure 1

Schematic of induction motor control

Full size image

All simulations were carried out in MATLAB—SIMULINK, on the three phase two pole machine. The motor parameters used are listed as follows.

  • \( P_{n} = { 2}. 7 {\text{ kW}},\,T_{n} = {\text{ 19 Nm}},\,\omega_{mn} = { 136}0{\text{ rpm}},\,p = 2 \)

  • \(I_{Sn} = { 7}. 5 1 {\text{ A}},\,I_{Rn} = {\text{ 17 A}},\, I_{Sxn} = 6. 8 {\text{ A}},\,I_{Syn} = 8.16 \)

  • \(U_{Sn} = { 4}00/ 2 30{\text{ V}},\,\psi_{Sn} = 0.877\,\text{Wb} \)

  • \(R_{S} = { 1}. 8 3 \,\Omega , \,R_{R} = { 2}. 1 9 \,\Omega ,\,L_{S} = \, 0. 1 3 7 {\text{ H}}, \,L_{R} = \, 0. 1 3 7 {\text{ H}},\,L_{m} = \, 0. 1 2 9 {\text{H}}, T_{R} = \, 0.0 5 4 6 {\text{ s}} \)

In controlling induction machine, the flux is needed to get the reference flux as fast as possible. In this application, the time response of flux is chosen 10 ms so in flux loop control, PI parameters are chosen \( T\_R\_Im = 10\,{\text{ms}},\,K\_Rm = 10. \) In torque loop control, the time respone is chosen about 50 ms, so PI parameters of this loop are \( T\_R\_omega = 50\,\text{ms,}\,K\_Romega = 2 \) The simulation results are shown in following figures.

The estimated stator current vector components \( i_{S\alpha \_est} ,\,i_{S\beta \_est} \) are shown in Fig. 2. Figure 3 shows the error between the real and the estimated of stator current vector \( i_{S\alpha \_est} ,\,i_{S\beta \_est} \). The error between the real stator current vector components and the estimated stator current vector components is small, the maximum is just only 0.04 and oscilations are around −0.02 and 0.02 in average.

Fig. 2
figure 2

Estimated stator current vector components \( i_{S\alpha \_est} \), \( i_{S\beta \_est} \)

Full size image
Fig. 3
figure 3

Current differences \( e_{S\alpha } \), \( e_{S\beta } \)

Full size image

In Fig. 4, firstly, the reference speed is zero, the magnetizing current component \( i_{Sx} \) is maximum (8A) so that the flux goes to the reference flux. The rising time of magnetizing current component is about 10 ms. After that, the flux reach to reference flux so the magnetizing current component \( i_{Sx} \) is unchanged, the torque current component changes depending on the reference torque. The time response of torque current component is about 50 ms. Figure 5 is the estimated rotor flux vector components \( \psi_{R\alpha \_est} ,\,\psi_{R\beta \_est} \).

Fig. 4
figure 4

Magnetizing current component \( i_{Sx} \) and torque current component \( i_{Sy} \)

Full size image
Fig. 5
figure 5

Estimated rotor flux vector components \( \psi_{R\alpha \_est} \), \( \psi_{R\beta \_est} \)

Full size image

Figures 6 and 7 show estimated speed compared to reference speed and the speed difference between the actual speed and the estimated speed. The characteristics of speed are very good. The time response is about 0.1 s, the overshoot is about 10 %, the static error between the actual speed and reference speed is zero. The maximum speed difference between the actual speed and the estimated speed is 1 rpm (1 %) in Fig. 7.

Fig. 6
figure 6

Reference rotor speed \( \omega_{m\_ref} \) and estimated rotor speed \( \omega_{m\_est} \)

Full size image
Fig. 7
figure 7

Speed difference between actual rotor speed \( \omega_{m} \) and estimated rotor speed \( \omega_{m\_est} \)

Full size image

5 Conclusions

The estimation technique for sensorless induction motor drive with vector control was presented in the paper. The sliding mode observer was used to estimate the speed of induction motor. The induction motor drive with the presented speed estimator gives good dynamic responses and the estimation of the mechanical speed is good in steady state and also in transient state, even with the presence of torque load. The disadvantage of this paper is that the speed estimator does not work well when the errors between the real parameters of the induction motor and the nominal parameters occur. In the next research, a sliding mode controller will be proposed together with the sliding mode observer to improve the control characteristics, even with the noise and parameter variations.