Applications of Coherent Potential Approximation to HEAs

Abstract

This chapter details the coherent potential approximation (CPA) to describe the chemically and magnetically disordered phases for systems of arbitrary number of components. Two widely used CPA implementations, namely, the exact muffin-tin orbitals (EMTO) and the Korringa–Kohn–Rostoker (KKR) methods, are briefly reviewed. Applications to predict lattice stability, electronic and magnetic structure, elasticity properties, and stacking fault energies of single-phase HEAs are presented.

9.1 The Coherent Potential Approximation

Ab initio density functional theory (DFT) [1, 2], as a powerful ground state theory, has been widely applied to investigate the structural and electronic properties of solids. In the case of the random solid solutions modeling, the coherent potential approximation (CPA) represents the most efficient alloy theory for the electronic structure calculations in multicomponent random solid solutions. The CPA was introduced by Soven [3] for the electronic structure problem and by Taylor [4] for phonons in random alloys. Later, Győrffy [5] formulated the CPA in the framework of the multiple scattering theory using the Green function technique.

The CPA is based on the assumption that the alloy may be replaced by an ordered effective medium, the parameters of which are determined self-consistently. The impurity problem is treated within the single-site approximation. This means that one single impurity is placed in an effective medium and no information is provided about the individual potential and charge density beyond the sphere or polyhedral around this impurity. Below, we illustrate the principal idea of the CPA within the conventional muffin-tin formalism.

We consider a substitutional alloy A _a B _b C _c …, where A, B, C, … are the randomly distributed atoms on an underlying crystal lattice and a, b, c, … stand for the corresponding atomic fractions. The system is characterized by the Green function g _alloy and the alloy potential P _alloy. In a real alloy, for a selected type of atom, P _alloy shows small variations due to the different local chemical environments. There are two main approximations within the CPA. First, it is assumed that the local potentials around a certain type of atom from the alloy are the same, i.e., the effect of local environments is neglected. These local potentials are described by the functions P _A, P _B, P _C, .... Second, the system is replaced by a monoatomic setup described by the site-independent coherent potential $\tilde{P}$. In terms of Green functions, one approximates the real Green function g _alloy by a coherent Green function $\tilde{g}$. For each alloy component i = A, B, C, …, a single-site Green function g _i is introduced.

The main steps to construct the CPA effective medium are as follows. First, the coherent Green function is calculated from the coherent potential using an electronic structure method. Within a multiple scattering method, we have

$$ \tilde{g}={[ S-\tilde{P} ]}^{-1}, $$

(9.1)

where S denotes the structure constant matrix describing the underlying lattice [6– 9]. Next, the Green functions of the alloy components, g _i, are determined by substituting the coherent potential of the CPA medium by the real atomic potentials P _i . Mathematically, this condition is expressed via the real-space Dyson equation

$$ {g}_i = \tilde{g}+\tilde{g}\left({P}_i-\tilde{P} \right){g}_i $$

(9.2)

for each i = A, B, C, … Finally, the average of the individual Green functions should reproduce the single-site part of the coherent Green function, i.e.,

$$ \tilde{g}=a{g}_{\mathrm{A}}+a{g}_{\mathrm{B}}+c{g}_{\mathrm{C}}+\dots . $$

(9.3)

Equations (9.1, 9.2, and 9.3) are solved iteratively, and the output $\tilde{g}$ and g _is are used to determine the electronic structure, charge density, and total energy of the random alloy. According to the single-site impurity equation (9.2), the impurity Green function g _i describes the single impurity (one single atom) with potential P _i as embedded in the effective medium specified by the coherent potential $\tilde{P}$.

Nowadays, the CPA has become a state-of-the-art technique for electronic structure calculations in random alloys. Numerous applications have shown that within this approximation, one can calculate lattice parameter, bulk modulus, mixing enthalpy, etc., with an accuracy similar to that obtained for ordered solids. At the same time, the CPA, being a single-site approximation to the impurity problem, has intrinsic limitations. For instance, within the CPA, one cannot take into account the short-range order effects. Moreover, systems with large-size mismatch between the alloy components are difficult to describe because of the sizable local lattice relaxations. More specifically, the average lattice dilation is well captured by CPA but not the element-specific local displacements of the lattice sites.

Probably, the most important failure of the existing CPA methods happens in the case of anisotropic lattice distortions in random alloys. This problem has erroneously been attributed to the inherent single-site approximation. However, one should bear in mind that certain limitations of the CPA are not directly related to the approximation itself. Rather, they originate from additional approximations introduced by particular DFT implementations. The most common electronic structure calculation methods used in combination with the CPA are based on the Atomic Sphere Approximation (ASA). The associated shape approximation turned out to be insufficient for the accurate description of the behavior of the total energy upon anisotropic lattice distortions. Thus, one cannot calculate, for example, elastic constants in random alloys or relax the axial ratio in alloys with a tetragonal, hexagonal, or lower symmetry. In addition, such DFT methods do not give a proper description of the open structures or structural energy differences between structures with different packing fractions, to the extent that even the energy difference between the bcc and fcc structures of the late transition metals is often incorrectly described. However, a recent reformulation of the CPA [10–12] demonstrates that this approximation implemented within the framework of the exact muffin-tin orbitals (EMTO) method, in contrast to several previous implementations, is suitable to reproduce the structural energy differences and energy changes related to small lattice distortions in random alloys with high accuracy.

In addition to the CPA, the virtual crystal approximation (VCA), the cluster expansion method, and the supercell approach [13], in particular, the so-called special quasi-random structure (SQS) [14], are often used to study random alloys. Recently, the SQS was employed in describing the CoCrFeMnNi high-entropy alloys [15]. However, today, the SQS calculations for the paramagnetic state are still very cumbersome. The reader is referred to Chap. 10 for more details about SQS. Another important method to describe atomic structure of HEAs is through hybrid Monte Carlo/Molecular Dynamic (MCMD) simulations as detailed in Chap. 8. The advantages of SQS and MCMD are that they allow atomic relaxation and render reliable prediction of temperature-dependent thermodynamic properties. On the other hand, due to the constraint associated with the supercell, they cannot account for small compositional changes as discussed, for example, in Ref. [15]. A brief comparison among the above methods in treating HEAs is presented in Chap. 10 in this book.

In the present chapter, we describe two widely used CPA implementations, namely, the EMTO-CPA and the Korringa–Kohn–Rostoker (KKR)-CPA methods, and demonstrate them through several recent applications. The structure of the chapter is as follows: in Sect. 9.2, we review the main features of the EMTO-CPA method relevant for the HEAs and in Sect. 9.3, we assess it using supercell calculations. In Sects. 9.4 and 9.5, we present results obtained for 3d and refractory HEAs, respectively. Section 9.6 puts forward a first attempt to determine the stacking fault energies of HEAs using a combined experimental–theoretical effort. Finally, the KKR-CPA method is introduced and demonstrated in Sects. 9.7 and 9.8. The chapter ends with brief conclusions.

9.2 The EMTO-CPA Method

The EMTO theory belongs to the third-generation muffin-tin approximation family. This theory is an improved KKR method, which uses large overlapping muffin-tin potential spheres which can describe the exact one-electron potential rather accurately. In the calculation of the total energy, the EMTO method employs the Full Charge Density (FCD) technique, which not only improves the calculation efficiency but also ensures total energies with accuracy similar to that of the full-potential methods [12]. For numerical details of the present EMTO-CPA calculations, see Refs. [16–18].

It should be mentioned that most of the present EMTO-CPA calculations of the 3d HEAs are based on the paramagnetic state. We employed the disordered local magnetic moment (DLM) [19] picture to describe the paramagnetic state of these HEAs. According to that model, an alloy component M of concentration m is presented by its spin-up (↑) and spin-down (↓) counterparts assumed to be distributed randomly on the underlying sublattice, i.e., each magnetic alloy component is treated as M _m → ${\mathrm{M}}_{m/2}^{\uparrow }{\mathrm{M}}_{m/2}^{\downarrow }$. For example, CoCrFeNi is described as a quasi-eight-component random solid solution, viz., ${\mathrm{Co}}_{0.125}^{\uparrow }{\mathrm{Co}}_{0.125}^{\downarrow }{\mathrm{Cr}}_{0.125}^{\uparrow }{\mathrm{Cr}}_{0.125}^{\downarrow }{\mathrm{Fe}}_{0.125}^{\uparrow }{\mathrm{Fe}}_{0.125}^{\downarrow }{\mathrm{Ni}}_{0.125}^{\uparrow }{\mathrm{Ni}}_{0.125}^{\downarrow }.$

9.3 Assessing the EMTO-CPA Method for HEAs

In order to assess the performance of EMTO-CPA in the case of HEAs, we select CoCrFeNi and set up a simple supercell (SC) with fcc underlying lattice. To mimic a homogeneous solid solution, we distribute the four alloying elements so that they are neighbors to each other within a conventional fcc unit cell, as shown in Fig. 9.1. We notice that CoCrFeNi is found to show no tendency for long-range chemical ordering [20]. Taking into account that the long-range order has a rather small effect on the elastic properties of alloys [21], it seems to be reasonable to assume that one may directly compare the result from CPA with the SC results calculated for the present ordered structure. In this test, ferromagnetic order was assumed in both CPA and SC calculations. Table 9.1 lists the results obtained from the above SC method and those calculated for the corresponding Co_0.25Cr_0.25Fe_0.25Ni_0.25 (equivalent to CoCrFeNi) random solid solution using the single-site CPA as implemented in EMTO. More DFT calculations on the effect of the SC size to the energy and elastic properties of HEAs are presented in Chap. 10.

Fig. 9.1

The simple supercell (SC) used to model the CoCrFeNi high-entropy alloy

Table 9.1 Theoretical bulk parameters for fcc CoCrFeNi HEA calculated using the CPA and SC (see text) methods

The average SC equilibrium Wigner–Seitz (WS) radius is 2.601 Bohr, which is rather close to 2.607 Bohr obtained for solid solution via CPA. The agreement between the SC (207 GPa) and CPA (208 GPa) bulk moduli is also excellent. For all theoretical parameters, we find a good consistency between the CPA and SC results. In particular, the three cubic elastic constants, c ₁₁, c ₁₂ and c ₄₄, obtained with the two methods differ on the average by ~4 %. The larger relative differences in the Zener anisotropy (c ₄₄/c′) and the Cauchy pressure (c ₁₂–c ₄₄) are still acceptable, especially if we consider that the present SC is the simplest periodic approximant of the four-component random alloy considered in the CPA calculations. The good agreement seen for the shear and Young’s modulus (G and E), Poisson ratio (v), and polycrystalline anisotropy ratio A _VR indicates that the CPA is an efficient and accurate method to investigate the bulk properties of these multicomponent alloys.

In order to further assess the performance of the calculations derived from the mean-field CPA, we construct two 2 × 2 × 2 cubic supercells shown in Fig. 9.2. The supercell formed by the bcc (fcc) unit cells is treated as simple cubic (body-centered cubic), where we introduce one (two) Al atom per 16 (32) atomic sites. All other sites are occupied by an equimolar four-component CoCrFeNi alloy. We note that similar partially ordered solid solution has been reported in Al_0.3CoCrFeNi HEA [23]. The present supercells have the molar radio Al₁Co_15/4Cr_15/4Fe_15/4Ni_15/4, corresponding to Al_0.2667CoCrFeNi HEA. The Wigner–Seitz radii obtained for these supercells are 2.620 Bohr for fcc and 2.634 Bohr for bcc, which are practically the same as those obtained in the corresponding CPA calculations (2.620 Bohr for fcc and 2.635 for bcc). The corresponding bulk moduli are 197 and 193 GPa for the fcc and bcc supercells, respectively, which are also close to the CPA results (198 GPa for fcc and 193 GPa for bcc).

Fig. 9.2

Schematic plot of the 2 × 2 × 2 bcc supercell (a) and the 2 × 2 × 2 fcc supercell (b) for Al_0.2667CoCrFeNi HEA. Label M represents an equimolar four-component CoCrFeNi alloy, and label Al is aluminum at the center or vertex sites

9.4 EMTO-CPA Applications to 3d HEAs

9.4.1 Equilibrium Volumes

In Table 9.2, we compare the EMTO-CPA Wigner–Seitz (WS) radii calculated for CoCrFeNi, CoCrCuFeNi, CoCrFeMnNi, and CoCrFeNiTi with available experimental values measured by x-ray diffraction. Using the Wigner–Seitz radii for the alloy constituents, we may estimate the equilibrium volume of the HEAs via Vegard’s rule. In Table 9.2, ${\overline{w}}_{\mathrm{t}}$ stands for the estimated volume based on the previous PBE-level theoretical data, and ${\overline{w}}_{\mathrm{e}}$ the one obtained from the experimental data. It is found that the calculated average WS radii are smaller than the averaged experimental data. The calculated WS radii are also slightly smaller than the experimental values except for CoCrFeNiTi (we notice that the as-cast CoCrFeNiTi is not a single fcc structure, but the main fcc matrix with two minor phases [27]). The connection between the WS radius and the lattice parameter a is ${a}^3=2*\frac{4}{3}\pi {w}^3$ (${a}^3=4*\frac{4}{3}\pi {w}^3$) for bcc (fcc) structure.

Table 9.2 Theoretical and experimental Wigner–Seitz radii (Bohr) for CoCrFeNi, CoCrFeMnNi, CoCrCuFeNi, and CoCrFeNiTi _x [22, 24–26]

9.4.2 Magnetic Properties

Figure 9.3 shows the local magnetic moments (↑or↓) versus the Wigner–Seitz radius for the magnetic sublattices in paramagnetic CoCrCuFeNi, CoCrFeNi, and CoCrFeNiTi high-entropy alloys. According to the calculations, the local magnetic moments vanish on the Cu, Ni, and Ti sites for all volumes and thus, they are not shown in Fig. 9.3. We should note that thermal effects would eventually induce local magnetic moments on the Ni sites as well at finite temperature. Such longitudinal spin fluctuations have been neglected in the present study. For all alloys, Fe possesses a significant (~1.8–2.0 μ _B) local magnetic moment around the equilibrium volume. Cobalt remains nonmagnetic in CoCrFeNi and CoCrFeNiTi but shows a small (~0.6 μ _B) magnetic moment for CoCrCuFeNi.

Fig. 9.3

Local magnetic moments of Co, Cr, and Fe in paramagnetic fcc CoCrFeNi, CoCrCuFeNi, and CoCrFeNiTi alloys as a function of the WS radius. For each HEA, the vertical (green) line stands for the calculated equilibrium SW radius (Data taken from Ref. [16])

We plot the paramagnetic total density of state (DOS) and partial density of state (pDOS) for CoCrCuFeNi, CoCrFeNi, and CoCrFeNiTi in Fig. 9.4. For all alloys, Fe has a moderate pDOS peak located very close to the Fermi level (E _F). It is found that the size of the DOS at E _F (D _Fe(E _F)) is the largest among all pDOS at E _F, followed by D _Co(E _F) and D _Cr(E _F). This distinct Fe peak at E _F leads to magnetic instability in Fe sublattice. Indeed, as shown in Fig. 9.4, the spin-polarized pDOS of Fe has two separate peaks: one above the Fermi level and one below the Fermi level. These two Fe peaks hybridize with the Cr and Co peaks, respectively. As a result of the magnetic splitting, the total D(E _F) drops significantly in all three alloys.

Fig. 9.4

Total (upper panels) and Co, Cr, and Fe partial (lower panels) density of states (pDOS) for the paramagnetic fcc CoCrCuFeNi, CoCrFeNi, and CoCrFeNiTi HEAs. In the lower panels, only the Co, Cr, and Fe partial densities of state are shown (Ni, Cu, and Ti are no local magnetic moments). Apart from the sign (spin up versus spin down) difference, the partial densities of states for Co, Cr, and Fe are identical to those shown in the figure (Data taken from Ref. [16])

9.4.3 Elastic Properties of 3d HEAs

The three cubic elastic constants c ₁₁, c ₁₂, c ₄₄ and c′ of CoCrFeNi, CoCrFeMnNi, CoCrCuFeNiTi _x , and CoCrFeNiTi are listed in Table 9.2. The elastic constants and elastic moduli for CoCrCuFeNiTi _x are also plotted in Fig. 9.5 as a function of Ti content. As seen from Table 9.2, all 3d HEAs considered here are mechanically stable. Titanium decreases the tetragonal elastic constant c′ both in CoCrFeNiTi and CoCrCuFeNiTi _x , as compared to that of CoCrFeNi. This indicates that Ti decreases the mechanical stability of the fcc phase, which is in line with the expectation based on the effective number of d electrons.

Fig. 9.5

Panel (a): Three independent elastic constants c ₁₁, c ₁₂, and c ₄₄ as well as c′ ((c ₁₁–c ₁₂)/2), c ₄₄/c′, and (c ₁₂–c ₄₄) for CoCrCuFeNiTi _x (x = 0–0.5,1.0) HEAs. Panel (b): Polycrystalline elastic moduli B, G, and E as well as B/G, v, and A _VR for CoCrCuFeNiTi _x (x = 0–0.5,1.0) HEAs (All data are from Ref. [16])

Theory predicts a moderate elastic anisotropy and small negative Cauchy pressure for CoCrFeNi. We recall that negative (c ₁₂–c ₄₄) has been associated with the covalent nature of the metallic bond and is characteristic to brittle alloys. In the absence of any experimental data, we compare the present results calculated for paramagnetic CoCrFeNi with those obtained for paramagnetic austenitic stainless steel alloys composed of ~18 % Cr, ~8 % Ni, and balance Fe [28]. The three cubic elastic constants reported for this stainless steel are c ₁₁ = 208.6 GPa, c ₁₂ = 143.5 GPa, and c ₄₄ = 132.8 GPa, which yield 4.07 for the Zener anisotropy ratio and 10.7 GPa for the Cauchy pressure. Therefore, compared to the austenitic stainless steels, the paramagnetic CoCrFeNi is predicted to be more brittle. Equimolar Cu addition to CoCrFeNi is found to increase slightly the Cauchy pressure from −14.3 GPa obtained for CoCrFeNi to −10.7 GPa calculated for CoCrCuFeNi. For reference, fcc Ir has Cauchy pressure of −13 GPa and undergoes both transgranular and intergranular fracture.

Before continuing our discussion, we mention that the validity of the correlation between brittle–ductile behavior and the Cauchy pressure has not yet been confirmed in the case of HEAs, so the above theoretical prediction regarding the brittleness of CoCrFeNi should be treated with precautions. On the other hand, we should recall that the present calculations correspond to static conditions (0 K), which substantially underestimates the equilibrium volume of the alloy. Computing the elastic parameters close to the experimental volume (i.e., accounting for the lattice expansion) leads to positive Cauchy pressures for both CoCrFeNi and CoCrFeMnNi [15]. Employing the Vienna ab initio simulation packages (VASP) in combination with special quasi-random structure (SQS) yields somewhat different elastic parameters as compared to EMTO-CPA and positive (negative) Cauchy pressure for CoCrFeNi (CoCrFeMnNi) [15]. Research focusing on the above trends and differences is in progress. In the rest of this chapter, the discussions related to the brittle–ductile behavior of HEAs should be considered in the mirror of the above results.

Titanium is found to change the CoCrFeNi host into a more ductile but strongly anisotropic material. Equimolar fcc CoCrFeNiTi has c ₄₄/c′ = 18.7 and (c ₁₂–c ₄₄) =43.9 GPa. Such high anisotropy ratio is rather unusual. For comparison, the Zener anisotropy of paramagnetic bcc and fcc Fe was found to be around 8.6 and 3.6, respectively. Considering the change of the Cauchy pressure upon equimolar doping, we may conclude that although Cu also improves the ductility of the 3d HEAs, Ti makes it especially ductile. Indeed, as seen in the case of CoCrCuFeNiTi _x , Ti can substantially increase the Cauchy pressure of the host alloy. It gradually increases the metallic character of the bonds turning the static (0 K) Cauchy pressure positive somewhere between x = 0.3 and x = 0.4. We find that all elastic parameters of CoCrCuFeNiTi _x change monotonously with the amount of Ti in Fig. 9.5b. According to the present theoretical calculations, the bulk parameters of single-crystal CoCrCuFeNiTi_0.5 HEAs, which are still believed to be single-phase alloys, are surprisingly close to those reported for the Cr_0.18 Fe_0.74Ni_0.08 austenitic stainless steel alloy [28].

Next, we compare the theoretical results with the available experimental data. It is particularly surprising that for CoCrCuFeNi, our Young’s modulus of 234 GPa is about four times larger than 55.6 GPa found in experiment [24]. This alloy shows relatively low anisotropy and thus, the uncertainty associated with the Voigt–Reuss–Hill averaging is expected to be small. Furthermore, as shown in Fig. 9.6, the Young’s modulus of a single-crystal CoCrCuFeNi changes between 102.79 GPa obtained for the <001> direction and 379.18 GPa calculated for the <111> direction. Therefore, even for a highly textured material, theory would predict the lowest E to be around 100 GPa, which is still almost double of the experimental value. For the two Ti-containing CoCrCuFeNiTi_0.5 and CoCrCuFeNiTi alloys, the calculated Young’s moduli differ from the reported experimental values by ~ 90 %. On the other hand, the agreement between theory and experiment is almost perfect for CoCrFeNiTi. Such good agreement is rather unexpected since for this alloy, we obtained very large anisotropy ratio. The single-crystal Young’s modulus of CoCrFeNiTi changes significantly with direction (Fig. 9.6), the lowest value being close to 20 GPa (for <001> direction) and the largest around 307 GPa (for <111 >direction). One should also point out that the recent experiments show that CoCrFeNiTi is not a single fcc phase alloy [27]. Finally, we note that the paramagnetic CoCrFeNi and CoCrFeMnNi HEAs have very close Young’s moduli E as a function of direction.

Fig. 9.6

Theoretical Young’s modulus for five HEAs (CoCrFeNi, CoCrCuFeNi, CoCrCuFeNiTi, CoFeCrFeNiTi, and CoCrFeMnNi) as a function of direction including the three main cubic directions

Regarding the difference between the theoretical and experimental Young’s moduli for CoCrCuFeNi, one possible reason is that all present calculations were carried out at static conditions (0 K) while the experimental measurements were performed at room temperature. In addition, our calculations assumed an ideal solid solution phase with fcc underlying lattice in contrast to the real alloys having complex microstructure. For instance, in CoCrCuFeNi, Cu segregation to the interdendrite region was observed. More extensive experimental as well as theoretical studies are necessary to understand the large deviation between the theoretical and experimental Young’s modulus for these important category of engineering materials.

9.4.4 The fcc–bcc Phase Transformation in Al-Doped 3d HEAs

In Fig. 9.7, we show the theoretical equilibrium volume (V) and structural energy difference ΔE = E _t(bcc)-E _t(fcc) for the Al _x CoCrFeNi alloys as a function of Al content. Experimental volumes are available for the single fcc phase for x ≤ 0.5 and for single bcc phase for x ≥ 0.9 [29–31]. Aluminum addition is found to increase the equilibrium volume of the solid solution, which is consistent with the fact that w of Al is larger than those of the other alloy components. Using a cubic spline fit for the calculated energy points, we find that the structural energy difference between ideal bcc and fcc lattices vanishes at x = 1.11 Al fraction.

Fig. 9.7

Theoretical fcc and bcc equilibrium volumes and structural energy difference for Al _x CoCrFeNi (x = 0–2.5) HEAs

Because of the large atomic volume of Al, the interatomic distance between Al and the other elements is larger than the average bulk value. We estimated the size of the local lattice relaxation (LLR) around the Al atoms in Al _x CoCrFeNi alloys by making use of the above 2 × 2 × 2 supercells, each of them containing one single Al atom. We relaxed the first 12 nearest neighbor CoCrFeNi sites in the fcc supercell and the first eight nearest neighbor CoCrFeNi sites in the bcc supercell. For the energy gain upon the LLR, we obtained δE _bcc = 0.17 mRy and δE _fcc = 0.32 mRy. The larger relaxation effect in the fcc lattice is in line with our previous observation that the bcc lattice can accommodate the large substitutional Al more easily than the fcc lattice. Then, we consider ΔE′ ≡ x(δE _bcc − δE _fcc) as the measure of the LLR effect on the structural energy difference per Al fraction. Adding ΔE′ to ΔE, we obtain that the total structural energy difference vanishes around x = 1.2, i.e., at only slightly larger Al content than the one predicted from the total energies obtained for rigid underlying lattices.

Two phases arrive at equilibrium when their Gibbs free energies become equal. Here, we consider the Al _x CoCrFeNi system as a pseudo-binary Al _y (CoCrFeNi)_1-y alloy (with y = x/(4 + x)) and compute the relative formation energy according to Δ G ^α(y) = G ^α(y)-(1-2y)G ^fcc(0)-2yG ^fcc(0.5), where α stands for fcc or bcc and G ^α(y) is the Gibbs free energy per atom for Al _y (CoCrFeNi)_1-y in the α phase. This is approximated as G ^α(y) ~ E ^α(y)-TS _mix(y)-TS ^α _mag (y), where E ^α(y) is the total energy per atom for Al _y (CoCrFeNi)_1-y in the α phase and T is the temperature. The two entropy terms are estimated within the mean-field approximation. Namely, the mixture entropy of ideal solutions is S _mix = −k _B ${\displaystyle \sum_{i=1}^5}{c}_i \ln\ {c}_i$, and the magnetic entropy S _mag = k _B ${\displaystyle \sum_{i=1}^5}{c}_i\ \ln \left(1+{\mu}_i\right)$, where c _i is the concentration and μ _i the magnetic moment of the ith alloying element. Accordingly, all chemical and magnetic short-range order effects and the longitudinal spin fluctuations are neglected (i.e., for each alloy composition, we assume constant local magnetic moments with temperature). The above phenomenological approximation for the magnetic entropy was previously used to estimate the free energy of paramagnetic Fe and Fe-based alloys having non-integer magnetic moments.

The present Gibbs free energies at different temperature are plotted in Fig. 9.8. According to the rule of common tangent line, we find that at room temperature, Al _x CoCrFeNi has single fcc phase for x ≤ 0.597 (y ≤ 0.130), single bcc phase for x ≥ 1.229 (y ≥ 0.235), and two phases (duplex) between the above limits. In terms of valence electron concentration, the present theory predicts that at 300 K, the fcc phase is stable for valence electronic concentration (VEC) ≥7.57 and the bcc one for VEC ≤ 7.04. These theoretical solubility limits should be compared to 8.0 and 6.87 estimated by Guo et al. and 7.67–7.88 and 7.06–7.29 observed in experiments [32].

Fig. 9.8

The Gibbs free energies as a function of the content of Al for bcc and fcc Al _y (CoCrFeNi)_1-y (y = 0–0.5) at T = 0, 300, and 600 K. Note that y = x/(4 + x), where x is the atomic fraction of Al in Al _x CoCrFeNi HEAs (All data are from Ref. [17])

9.4.5 Elastic Properties of Al-Doped 3d HEAs

The calculated elastic parameters of Al _x CoCrFeNi HEAs are listed in Table 9.3. We notice that the elastic parameters obtained for the fcc and bcc phases around x = 1 are surprisingly close to each other. When considering the fcc or bcc structure separately, it is found that the three cubic elastic constants (c _ij) and the polycrystal elastic moduli (B, G, and E) decrease with increasing Al content. However, the Cauchy pressure (c ₁₂–c ₄₄), the two anisotropy ratios (A _Z and A _VR), the Poisson’s ratio (v), and the B/G ratio increase with x in the fcc phase.

Table 9.3 Wigner–Seitz radius w (Bohr), three cubic elastic constants (c _ij, c′ = (c _11– c ₁₂)/2, A _Z = c ₄₄/c′), Cauchy pressure (c ₁₂–c ₄₄), and polycrystalline elastic moduli (B, G, E, A _VR, v, and B/G) for fcc and bcc Al _x CoCrFeNi HEAs as a function of the content of Al

From Table 9.3, we find that the somewhat different impact of Al on the elastic parameters of fcc and bcc AlCoCrFeNi leads to local maxima in (c ₁₂–c ₄₄), v, and B/G with increase of Al content. According to the calculated trend of c′(x), Al strongly reduces the dynamical stability of the fcc lattice and slightly increases that of the bcc lattice. At the same time, Al stabilizes thermodynamically the bcc structure relative to the fcc one (Fig. 9.8). Combining these two effects, we obtain that around the duplex region (x = 0.597–1.229), the Al _x CoCrFeNi system has two very similar distinct local minima within the Bain configurational space (described by c/a and volume) with a clear barrier between them (Fig. 9.9). One local minimum corresponds to the bcc phase (c/a = 1) and another to the fcc phase (c/a = $\sqrt{2}$). This situation is rather unusual for elemental cubic transition metals and their alloys, for which the thermodynamically unstable cubic structure is usually also dynamically unstable.

Fig. 9.9

Energy contour (mRy) for paramagnetic AlCoCrFeNi as a function of the tetragonal ratio (c/a) and the Wigner–Seitz radius (Bohr) (Data taken from Ref. [17])

According to Pugh, materials with B/G ratio above 1.75 are ductile. For isotropic materials, the Pugh criteria for ductility imply μ > 0.26, which has been confirmed for bulk metallic glasses [33]. In the case of Al _x CoCrFeNi, alloys close to x = 1 in both phases have large positive Cauchy pressure, and large B/G and μ, indicating strong metallic character and enhanced ductility for these systems. Our calculated Young’s moduli are very close for the fcc (201 GPa) and bcc (204 GPa) AlCoCrFeNi. The single-crystal Young’s modulus changes from 70 to 370 GPa (77–355 GPa) for the fcc (bcc) AlCoCrFeNi along the different crystallographic directions. We note that the reported experimental value of 127 GPa [34] is within the range of our calculations.

9.5 Refractory HEAs

9.5.1 Structural Properties

For NbTiVZr and MoNbTiV _x Zr (x = 0–1.5), the EMTO-CPA theory predicts the bcc structure to be the most stable one among the three close-packed lattices, namely, fcc, bcc, and hcp. The corresponding equilibrium Wigner–Seitz radii and total energy difference compared to bcc structure are listed in Table 9.4. The theoretical predictions are fully supported by experiments. At this point, we should note that local lattice relaxation (neglected in the present study) could slightly alter the structural energy difference. According to our previous estimation of the influence of the lattice relaxation on the bcc–fcc energy difference [17], the effect of relaxation is well below the energy differences from Table 9.4.

Table 9.4 Theoretical Wigner–Seitz radius w (Bohr) for HEAs with bcc, fcc, and hcp structures, respectively

Experimentally, the HEAs composed of refractory elements were found to have a single bcc structure. It should be noted that the present refractory elements Ti, Zr, V, Nb, and Mo all adopt a bcc crystal structure below their melting temperature, but Ti and Zr are stable in the hcp phase at ambient conditions (the allotropic transition from hcp to bcc happens at temperatures of 1155 K and 1136 K for Ti and Zr, respectively).

We show the calculated equilibrium WS radii for bcc NbTiVZr and MoNbTiV _x Zr (x = 0–1.50) HEAs in Table 9.5. The only experimental equilibrium radius we could find in the literature is 3.094 Bohr [35] reported for NbTiVZr. To further assess the theoretical volumes predicted for the present HEAs, we make use of Vegard’s rule and estimate the mean equilibrium WS radii for alloys using those of the alloy components. First, we study the atomic radius of the refractory elements. For the Wigner–Seitz radius of bcc Ti and Zr at 0 K, we extrapolate the high-temperature data assuming a linear thermal expansion, i.e., w(T) = w(0 K)(1 + αT), where w(0 K) is the WS radius at 0 K and w(T) at temperature T and α is the linear thermal expansion coefficient. Using the experimental values w _Ti(1155 K) = 3.077 Bohr and w _Zr (1140 K) = 3.358 Bohr together with the reported thermal expansion coefficients for bcc Ti (10.9 × 10⁻⁶ K⁻¹) and Zr (9 × 10⁻⁶ K⁻¹) [36], we get 3.039 Bohr and 3.324 Bohr for w(0 K) of the hypothetical bcc Ti and Zr, respectively. For bcc V, Nb, and Mo, the Wigner–Seitz radii at 0 K were extrapolated by fitting the selected lattice parameters in Ref.[37]. Considering the quoted estimated values in Table 9.5, we conclude that the present theory correctly describes the equilibrium properties of all five refractory elements.

Table 9.5 Wigner–Seitz radius w (Bohr), bulk modulus B (GPa), and elastic constants c ₁₁, c ₁₂, c ₄₄, and c′ (GPa) for NbTiVZr and MoNbTiV _x Zr (x = 0–1.5) HEAs

It is interesting to note that for all HEAs considered here, the calculated equilibrium WS radius w _t is slightly smaller than w̅ _t. Hence, all alloys show a small but systematic negative deviation relative to Vegard’s rule. Similar to CoCrCuFeNiTi _x , the WS radius of MoNbTiV _x Zr has a linear change as a function of the content of Vanadium x (x = 0–1.50).

9.5.2 Electronic Structure

In the following, we discuss the electronic structure of the refractory HEAs. The total and partial DOSs for the NbTiVZr, MoNbTiZr, and MoNbTiVZr HEAs are shown in the middle and lower panels of Fig. 9.10, respectively. Although the chemical disorder smears out most of the structure characteristic to the elemental DOSs (upper panels), a weak peak survives in the vicinity of the Fermi level for all three alloys (middle panels). This peak is located at the Fermi level for NbTiVZr and shifted toward the descending zone when equimolar Mo replaces V or is added to the alloy. This feature may explain why NbTiVZr has smaller dynamical stability against tetragonal deformation (smaller c′) as compared to the other alloys (Table 9.5). We should notice that the aforementioned lattice distortion mechanism is expected to be less effective in HEAs due to the disorder-driven smearing of the DOS. Monitoring the total DOS curves (Fig. 9.10), one may conclude that the two Mo-containing HEAs should exhibit similar anomalous temperature dependence as found in V and Nb metals [38]. These theoretical predictions need to be verified by future theoretical and experimental analysis.

Fig. 9.10

Density of state (DOS) of bcc Ti, Zr, V, Nb, and Mo refractory metals (upper panels); total (middle panels) and partial (lower panels) DOS for bcc NbTiVZr, MoNbTiZr, and MoNbTiVZr high-entropy alloys. The vertical dashed lines stand for the positions of the Fermi level (All data are from Ref. [18])

The partial DOSs (Fig. 9.10, lower panels) are somewhat different from the DOSs of the elemental metals (upper panels). In all three cases, Ti and Zr contribute with a peak to the DOS at the Fermi level. The partial DOSs resemble the pure metal DOSs the most in NbTiVZr. Here, the small charge redistribution between the alloy components shifts slightly the peaks in V and Nb partial DOSs close to E _F, resulting in the global peak seen in the total DOS (left middle panel). The partial DOS of Mo is strongly altered compared to that of pure Mo. However, the presence of Mo makes the V and Nb partial DOSs more V- and Nb-like, respectively (having E _F in the descending zone). That is the reason why the Mo-containing alloys are mechanically more stable than the Mo-free NbTiVZr alloy.

9.5.3 Elastic Properties

The three cubic elastic constants c ₁₁, c ₁₂, and c ₄₄ and the tetragonal shear modulus c′ are listed in Table 9.6. All HEAs considered here are predicted to be mechanically stable. Adding equimolar V to MoNbTiZr-based alloy produces small changes in the elastic parameters. The weak increase of the tetragonal elastic constant c′ with V content in MoNbTiV _x Zr alloys indicates that V slightly enhances the elastic stability of the bcc phase against tetragonal deformation. At the same time, V addition decreases c ₄₄, resulting in a small increases of the elastic anisotropy. In Table 9.6, we also list the theoretical elastic constants, the Zener anisotropy A _Z, and Cauchy pressure (c₁₂–c₄₄) (GPa), as well as polycrystalline elastic moduli (B, G, E, v, B/G, A _VR) and VEC of the present refractory HEAs. One can see that the ductility is slightly enhanced with increasing V content. However, these changes are too small and the quoted correlation between the elastic parameters and ductility too vague to be able to draw more solid conclusions here.

Table 9.6 The Cauchy pressure (c ₁₂–c ₄₄) (GPa) and Zener anisotropy A _Z (c ₄₄ /c′); polycrystalline elastic moduli G and E (GPa) and Poisson’s ratio v; the B/G ratio, elastic anisotropy ratio A _VR, and VEC for selected refractory HEAs

The VEC has often been used to classify the single solid solution phases (bcc, fcc, or mixture of bcc and fcc). According to the experimental findings, HEAs prefer to form bcc solid solution when VEC < 7.55. This correlation is fully supported by the present theory and former experiments. In addition to the phase stability, the VEC should also reflect the changes of the metallic bonds and thus the changes of the polycrystalline elastic moduli. Indeed, as shown in Fig. 9.11, we find a correlation between the bulk and shear moduli of MoNbTiV _x Zr and the VEC. The increase in the VEC with V content (we should remember that HEAs are equimolar systems) is followed by an increase (slightly decrease) of the bulk (shear) modulus. The opposite trends in B and G explain the enhanced ductility of MoNbTiV _x Zr for large x values.

Fig. 9.11

Correlation between the bulk moduli B and shear moduli G and Pugh ratio B/G of MoNbTiV _x Zr (x = 0–1.5) and VEC (All data are from Ref. [18])

In order to illustrate the effect of alloying on the elastic anisotropy of refractory HEAs, in Fig. 9.12, we plot the three-dimensional E for NbTiVZr, MoNbTiZr, and MoNbTiVZr. Here, E is the Young’s modulus along [hlk] crystallographic direction. For NbTiVZr alloy, the E exhibits rather strong orientation dependence, so this system may be regarded as being anisotropic. The largest value of E is 140.2 GPa realized along the [111] direction, whereas the smallest value of 97.7 GPa belongs to the [100] direction.

Fig. 9.12

Characteristic surfaces of the Young’s modulus E for NbTiVZr, MoNbTiZr, MoNbTiVZr, and Mo_0.8NbTi V_0.5Zr. The values on the color scale and on the axes are in GPa. Note that the same color bar applies to NbTiVZr and Mo_0.8NbTiV_0.5Zr and another to MoNbTiZr and MoNbTiVZr

In contrast to the Mo-free alloy, the Mo-containing alloys seem to be almost isotropic. Namely, their three-dimensional E shown in Fig. 9.12 have almost spherical shapes. The Young’s modulus changes between 136.0 and 149.2 GPa for MoNbTiVZr and between 139.9 and 144.3 GPa for MoNbTiZr. Previous theoretical calculations predicted nearly isotropic surface energies for bcc Mo and, as a consequence, spherically shaped nanoparticles for this metal.

For a fully isotropic material, the tetragonal shear modulus c′ = (c ₁₁–c ₁₂) equals the cubic shear modulus c ₄₄, so we have A _Z = 1 and A _VR = 0. The latter condition reflects the fact that all statistical averaging methods (in the present case, the Voigt and Reuss methods) lead to the same polycrystalline shear modulus. According to our calculations, V slightly enhances the anisotropy of MoNbTiV _x Zr, whereas equimolar Mo addition to NbTiVZr turns the alloy almost isotropic. Based on this information, we propose that one can optimize the content of Mo and V in Mo _y NbTiV _x Zr so that the resulting alloy is fully isotropic. We demonstrate this by performing calculations for Mo _y NbTiV _x Zr as a function of x and y (keeping the Ti, Zr, and Nb atomic fractions to 1). Some of the results of this additional study are shown in the lower part of Table 9.6. We find that Mo _y NbTiV _x Zr becomes almost perfectly isotropic for (x, y) = (0, 0.9) or (x, y) = (0.5, 0.8). The Young’s modulus for Mo_0.8NbTiV_0.5Zr is shown in Fig. 9.12.

Very interestingly, for both isotropic Mo_0.9NbTiZr and Mo_0.8NbTiV_0.5Zr HEAs, the VEC is about 4.72. On this ground, we suggest that VEC ~ 4.72 (valid within the present approximations) is an important criterion for the isotropic HEAs. For comparison, Li et al. predicted that the Ti–V alloys (Gum Metals) become elastically isotropic for VEC ~ 4.7 [39].

In addition to the above cases, we used the EMTO-CPA method to calculate some other equimolar refractory HEAs reported in experiments. Table 9.7 lists the Wigner–Seitz radii, elastic constants, and polycrystalline elastic moduli as well as VEC of the HfNbTiXZr (X = V, Cr, Ta), MoNbTaW, MoNbTaVW, as well as HfNbTiZr and HfNbZr refractory HEAs. Like before, we used Vegard’s law to estimate the WS radius of the solid solution, i.e., w _mix. Our ab initio predications are slightly smaller than w _mix for these seven refractory HEAs. Hence, all alloys show a small but systematic positive deviation relative to Vegard’s rule. We note that for all HEAs considered here, the calculated lattice parameter w _t is slightly larger than the experiments w _e, except for HfNbTiZr and CrHfNbTiZr. It is very likely that this deviation is due to the employed frozen-core approximation, which is known to yield somewhat larger lattice parameters as compared to all-electron calculations.

Table 9.7 Wigner–Seitz radius w (Bohr) and elastic properties of refractory HEAs

The seven refractory HEAs listed in Table 9.7 are predicted to be mechanically stable according to the dynamical stability conditions c ₄₄ > 0, c ₁₁ > |c ₁₂|, and c ₁₁ + 2c ₁₂ > 0. For the HfNbTiXZr (X = V, Cr, Ta) refractory HEAs, the polycrystalline elastic moduli are very similar. It is found that V has a small effect on B, G, and E of MoNbTaW alloys.

The experimental Young’s modulus is 128 (112) GPa for HfNbTiVZr (CrHfNbTiZr), whereas the ab initio E is 95 (104.4) GPa. We should note that Hf₂₀Nb₂₀Ti₂₀V₂₀Zr₂₀ is almost a single bcc phase, whereas CrHfNbTiZr consists of a mixture of bcc and Laves phases. The theoretical results are expected to be valid for the completely random and homogeneous bcc solid solutions.

The calculated large positive Cauchy pressure (c ₁₂−c ₁₄) suggests that these refractory HEAs have strong metallic character and enhanced ductility. Keeping in mind our previous discussion from Sect. 9.4.3, we find that all values in Table 9.7 would indicate enhanced ductility for these refractory alloys. Good ductility has indeed been reported for the single-phase HfNbTaTiZr alloy, while limited ductility at room temperature and extensive compressive plasticity above 873 K has been found for the single-phase MoNbTaW and MoNbTaVW alloys. The reduced ductility of CrHfNbTiZr alloy may result from the precipitation of Laves phase.

9.6 Stacking Fault Energy of HEAs

It has been established in this chapter that EMTO-CPA is a valuable tool to make independent predictions on the structure and properties of HEAs. Beyond independent calculation of properties of HEAs, this method can also be coupled to available experimental measurements to aid in the extraction of physical properties. Here, we review a recent example of the extraction of the stacking fault energy (SFE) from multicomponent alloys, including HEAs, using this combined approach.

Determination of SFEs is important in alloy design because it indicates the predominant plastic deformation mechanism to be expected in the alloys. High SFE materials tend to deform via a dislocation glide mechanism with little splitting into partial dislocations, while lower SFEs more readily split into partial dislocation pairs and the stacking fault widths tend to increase as the SFE is reduced. Solid solution alloying has been one route to engineer lower SFE alloys experimentally, typically successful in Cu- or Mg- based where a wide range of solid solubility is achievable. Although successful, these materials have not retained sufficient strength to suit all potential applications. HEAs, however, provide a unique opportunity to tune the SFE as they form as solid solutions on fcc lattices in materials typically known for having higher strength and over a wider compositional range. The ability to extract trends in SFE from new alloys is essential as these provide a means of evaluating success of experiment and also provide for comparison with independent predictive simulation.

One route to assess the SFE experimentally is accomplished through x-ray diffraction (XRD) measurements. However, this approach is only possible if elastic properties of the alloy are known ahead of the measurement. If this is not the case, first principles methods, such as EMTO + CPA, can play a valuable role of assessing the elastic constants of alloy as a function of their components and concentrations and make the extraction of SFEs possible. From XRD (and EMTO + CPA), the SFE is calculated by use of Eq. 9.4 for fcc materials

$$ \gamma =\frac{6.6}{\pi \sqrt{3}}\kern0.5em \cdot \underset{\mathrm{Theory}}{\underbrace{G_{(111)}{\left(\frac{2{c}_{44}}{c_{11}-{c}_{12}}\right)}^{-0.37}}}\ \dot{c}\ \underset{\mathrm{Experiment}}{\underbrace{\frac{a_o{\varepsilon}^2}{\alpha }}} $$

(9.4)

In this expression, theoretical calculations provide values for the shear modulus in (111) determined from the elastic constants, G ₍₁₁₁₎, and the Zener elastic anisotropy determined from the independent elastic constants for fcc (i.e., c ₁₁, c ₁₂, and c ₄₄), and experiment provides information on the lattice parameter (a _o ), mean square microstrain (ε ²), and the stacking fault probability (α). The microstrain can be extracted by fitting XRD peaks with a Lorentzian function. The width of these fitted peaks yields the microstrain through the procedure of Williamson and Hall [41] and can be converted to the mean square microstrain through the procedure of Klug and Alexander [42]. The stacking fault probability can be extracted by use of the PM2K software package [43]. The elastic constants can be extracted through fits to both equations of state as well as quadratic fits to volume conserving orthorhombic strains to the unit cell [12].

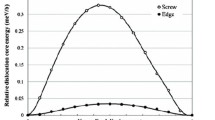
Using the XRD together with EMTO-CPA approach, Zaddach et al. recently explored the SFE in equiatomic alloys as a function of the number of components up to five-component HEAs [15]. The SFEs presented in this work are plotted in Fig. 9.13. Each equiatomic alloy was found to be a single-phase random solid solution on the fcc lattice. The data in Fig. 9.13 shows a clear trend of a reduction in the SFE with the number of components.

Fig. 9.13

Stacking fault energy for elements and alloys. Alloys without subscripts are equiatomic, while alloys with subscripts are given in atomic percent. The all gray values are from the literature, while the bar graphs with the patterned fill came from Ref. [15] using the combined XRD + EMTO approach discussed in this section (All data are taken from Ref. [15])

Although the SFEs were able to be reduced as a function of the number of components, the lowest achievable value still exceeds those of conventional low SFE Cu alloys, which have been shown to exhibit an SFE in the range of 7–14 mJ/m² depending on composition [44–46]. To further explore the ability to tune the SFE, Zaddach et al. relaxed the equiatomic constraint and explored non-equiatomic compositions for the five-component HEA. The authors added and removed Cr at the expense of Ni, a typical high SFE material, and found that higher Cr content alloys further reduced the SFE while retaining the single-phase solid solution fcc structure. Ultimately, the authors found the Cr₂₆Co₂₀Fe₂₀Mn₂₀Ni₁₄ non-equiatomic HEA, with the subscripts representing atomic percent with unlabeled values fixed at 20 at. %, to have an SFE slightly less than 4 mJ/m², which is below current reported values of Cu-based alloys.

9.7 The KKR-CPA Method

In the previous sections, we have discussed theoretical studies of HEAs of four and five elements using EMTO-CPA. In this section, we present a KKR-CPA approach to the ab initio electronic structure calculation for Al _x CrCoCuFeNi. In its conventional implementation, the KKR-CPA takes muffin-tin approximation, in which the one-electron potential in DFT is assumed to be spherically symmetric within a nonoverlapping “muffin-tin” sphere centered at each atom and constant in the interstitial region. In contrast, the EMTO-CPA method uses the optimized overlapping muffin-tin potential, in order to employ the “best possible” spherical representation of the one-electron potential. The KKR-CPA method is based on the multiple scattering theory, where the single-site scattering and the scattering path matrices are of fundamental interest. On the other hand, the EMTO-CPA method is based on muffin-tin orbitals theory. Because of these differences, the CPA mediums in these two methods are somewhat different. For the completeness of this chapter, we present here the basic theoretical features of the KKR-CPA method adopting the usual multiple scattering terminology.

The KKR-CPA method uses Green’s function technique within the framework of multiple scattering theory and is uniquely designed for the theoretical investigation of random alloys from the first principles. In multiple scattering theory, the Green function in the vicinity of an impurity “i” at site 1, embedded in the host with atoms “C”, is given by [47, 48]

$$ {g}_i\left(\overrightarrow{r},{\overrightarrow{r}}^{\prime };\varepsilon \right)={\displaystyle \sum_{L,{L}^{\prime }}{Z}_L^i\left({\overrightarrow{r}}_{<};\varepsilon \right){\left[{\underline{\tau}}_i^{11}\left(\varepsilon \right)\right]}_{L{L}^{\prime }}{Z}_L^{i\bullet}\left({\overrightarrow{r}}_{<};\varepsilon \right)}-{\displaystyle \sum_L{Z}_L^i\left({\overrightarrow{r}}_{<};\varepsilon \right){J}_L^{i\bullet}\left({\overrightarrow{r}}_{>};\varepsilon \right)}, $$

(9.5)

where ${r}_{<}= \min \left(r,{r}^{\prime}\right)\ \mathrm{and}\ {r}_{>}= \max \left(r,{r}^{\prime}\right),$ L and L′ are the index of the combination of angular momentum and magnetic quantum numbers l and m, and ${Z}_L^i\left(\overrightarrow{r};\varepsilon \right)\ \mathrm{and}\ {J}_L^i\left(\overrightarrow{r};\varepsilon \right)$ are regular and irregular solutions, respectively, of single atom “i” with appropriate boundary condition at the origin and at the bounding sphere of the atomic cell. The symbol “•” in the superscript of the single-site solutions implies that complex conjugate is applied to the complex spherical harmonic function in the boundary condition. The scattering path matrix [49], ${\underline{\tau}}_i^{11}\left(\varepsilon \right),$ describes multiple scattering processes, starting from and ending at site 1 and is given by [5]

$$ {\underline{\tau}}_i^{11}\left(\varepsilon \right)={\left[{\underline{\tau}}_C^{11}\left(\varepsilon \right)\left({\underline{t}}_i^{-1}\left(\varepsilon \right)-{\underline{t}}_C^{-1}\left(\varepsilon \right)\right)+1\right]}^{-1}{\underline{\tau}}_C^{11}\left(\varepsilon \right), $$

(9.6)

where ${\underline{t}}_i\left(\varepsilon \right)\ \mathrm{and}\ {\underline{t}}_C\left(\varepsilon \right)$ are the t-matrix of atoms i and C, respectively. If the host atoms are on a periodic lattice, the scattering path matrix can be calculated using Brillouin zone (BZ) integration technique as follows:

$$ {\underline{\tau}}_C^{11}\left(\varepsilon \right)=\frac{1}{\varOmega_{BZ}}{\displaystyle {\int}_{\varOmega_{BZ}}\left[{\underline{t}}_C^{-1}\left(\varepsilon \right)-\underline{S}\left(\overrightarrow{k};\varepsilon \right)\right]{d}^3\overrightarrow{k}}, $$

(9.7)

where Ω _BZ is the BZ volume and $\underline{S}\left(\overrightarrow{k};\varepsilon \right)$ is the KKR structure constant matrix.

For a random alloy made of N atomic species with contents c _i , i = 1, 2, …, N, the CPA condition is such that the average of τ ¹¹ _i (ε) is the scattering path matrix ${\underline{\tau}}_C^{11}\left(\varepsilon \right)$ of the CPA medium, in which the “host” atom is described by ${\underline{t}}_C\left(\varepsilon \right)$. In practice, it is useful to define following matrices [50]

$$ {\underline{X}}_i\left(\varepsilon \right)=-{\left[{\underline{\tau}}_C^{11}\left(\varepsilon \right)+{\left({\underline{t}}_i^{-1}\left(\varepsilon \right)-{\underline{t}}_C^{-1}\left(\varepsilon \right)\right)}^{-1}\right]}^{-1},\ \mathrm{and}\kern0.5em {\underline{X}}_C\left(\varepsilon \right)={\displaystyle \sum_{i=1}^N{c}_i{\underline{X}}_i\left(\varepsilon \right)}, $$

(9.8)

and it is easy to verify that the CPA condition gives rise to ${\underline{X}}_C\left(\varepsilon \right)=0.$ To solve for ${\underline{t}}_C\left(\varepsilon \right)$, one may start with an initial guess of ${\underline{t}}_C\left(\varepsilon \right)$, ${\underline{t}}_C^{(1)}\left(\varepsilon \right)={\displaystyle \sum_{i=1}^N{c}_i{\underline{t}}_i\left(\varepsilon \right)},$ and obtain ${\underline{\tau}}_C^{11,(1)}\left(\varepsilon \right)$ and ${\underline{X}}_C^{(1)}\left(\varepsilon \right)$ using (9.7) and (9.8), respectively. A better guess of ${\underline{t}}_C\left(\varepsilon \right)$ can be obtained from the previous one by using

$$ {\underline{t}}_C^{\left(n+1\right),-1}\left(\varepsilon \right)={\underline{t}}_C^{(n),-1}\left(\varepsilon \right)-{\underline{X}}_C^{(n)}\left(\varepsilon \right){\left[1+{\underline{\tau}}_C^{11,(n)}\left(\varepsilon \right){\underline{X}}_C^{(n)}\left(\varepsilon \right)\right]}^{-1}. $$

(9.9)

This recursive procedure is iterated until the convergence is obtained. Once the CPA medium ${\underline{t}}_C\left(\varepsilon \right)$ is determined, one is able to calculate τ ¹¹ _i (ε) and then the Green function. If the system is in ferromagnetic state, the calculations described above are carried out for each spin channel, which means there are CPA mediums for spin up and spin down, respectively. The configurationally averaged electron density $\rho \left(\overrightarrow{r}\right)$ and density of state n(ε) associated with each spin channel are given by the imaginary part of the averaged Green function as follows:

$$ \rho \left(\overrightarrow{r}\right)= - \frac{1}{\pi}\mathrm{I}\mathrm{m}{\displaystyle \sum_{i=1}^N{c}_i{\displaystyle {\int}_{\varepsilon_B}^{\varepsilon_F}{g}_i\left(\overrightarrow{r},\overrightarrow{r};\varepsilon \right)d\varepsilon }},\ \mathrm{and}\kern0.5em n\left(\varepsilon \right)=-\frac{1}{\pi}\mathrm{I}\mathrm{m}{\displaystyle \sum_{i=1}^N{\displaystyle {\int}_{\varOmega }{g}_i\left(\overrightarrow{r},\overrightarrow{r};\varepsilon \right){d}^3\overrightarrow{r}}}, $$

(9.10)

where Ω is atomic cell volume, and the energy integration is usually carried out along a contour, in the upper half of complex energy plane, from the bottom of the valence bands ε _B to the Fermi energy ε _F .

Despite the fact that all of KKR-CPA calculations carried out so far have been using the muffin-tin approximation, which is a reasonable approximation for most metallic alloys, the formalism of the KKR-CPA method shown above is valid in general. A full-potential KKR-CPA method is currently under development by one of the authors.

9.8 Application of the KKR-CPA Approach

To investigate the phase stability and the mechanical and magnetic properties of Al _x CoCrCuFeNi high-entropy alloys, we performed ab initio, spin-polarized, electronic structure calculation using KKR-CPA method described above. Like many other HEAs, this category of six-element alloys exhibits a combination of good material properties, including high hardness, high compressive strength, and excellent resistance to softening, corrosion, oxidation, and wearing, especially at elevated temperatures [51]. It has also been reported that this category of alloys shows ferromagnetic behavior [52]. In the KKR-CPA calculation, we chose von Barth-Hedin LSDA potential [53] and applied the muffin-tin approximation to the potential. The angular momentum quantum number cutoff was chosen to be l _max = 3, for which the size of the scattering matrices is 16 × 16. We used an adaptive method for the Brillouin zone integration and used 30 Gaussian points for the integration of the Green function along the energy contour. To determine the equilibrium state, we ran the calculation for both fcc and bcc structures for x up to 0.3.

The computational results are summarized in Table 9.8 in which the bulk modulus and the lattice constant are obtained by fitting the calculated average total energy versus the atomic volume to the Murnaghan equation of state. The sizable average magnetic moment shows that the alloys are ferromagnetic for $x\le 0.3.$ The average magnetic moment in the bcc structure is found to be higher than that in fcc. While Cu and Al appear to be nonmagnetic in both fcc and bcc structures, Cr exhibits antiferromagnetism, but its moment in bcc is few times smaller than in fcc. For the fcc phase (x < 2.5), Al _x CoCrCuFeNi shows significant positive enthalpy of mixing as shown in Fig. 9.14.

Table 9.8 The calculated energetic, mechanical, and magnetic properties of Al _x CoCrCuFeNi high-entropy alloys

Fig. 9.14

The calculated enthalpy of mixing of Al _x CoCrCuFeNi high-entropy alloys in fcc (solid circle) and bcc (solid square) structures. The data are obtained using KKR-CPA method

9.9 Conclusions

In this chapter, we have introduced two CPA-based ab initio approaches, EMTO-CPA and KKR-CPA, to the theoretical study of HEAs. We have investigated 3d HEAs with magnetic elements both in paramagnetic and in ferromagnetic states. For paramagnetic alloys, Fe remains magnetic due to its local moment nature, while most of the other alloy components are essentially in the nonmagnetic state. For ferromagnetic alloys, Cr moment appears to be antiferromagnetic or suppressed at small Wigner–Seitz radius, which may be related to the fact that we are only considering the collinear magnetic states in the spin-polarized calculations.

It is found that all the 3d HEAs under investigation are mechanically stable. As a base alloy, CoCrFeNi is found to be brittle at static conditions (0 K). However, when the calculations are performed at room temperature volume, CoCrFeNi is predicted to be ductile, in line with the observations. This finding highlights the importance of thermal effect in the case of HEAs. By adding Cu or Ti to CoCrFeNi, the material becomes more ductile. On the other hand, addition of Al to CoCrFeNi or CoCrCuFeNi is found to increase the equilibrium volume of the solid solution and reduce the dynamical stability of the fcc lattice, and as the Al content increases, the alloy undergoes phase changes from single fcc phase to fcc–bcc duplex phase and to single bcc phase.

We have investigated HEAs with refractory elements. These HEAs show large positive Cauchy pressure which suggests strong metallic character and enhanced ductility. We also found that Mo tends to enhance the isotropic elasticity while V tends to enhance the anisotropy. It is therefore possible to optimize the content of Mo and V in MoNbTiVZr so that the resulting alloy is fully isotropic.

The stacking fault energy of CoCrFeNi-based alloys has been studied using a combined theoretical–experimental approach. We have demonstrated that non-equiatomic HEAs offer additional degrees of freedom for a precise optimization of the deformation mechanism controlling the plasticity of this promising class of engineering alloys.