Physical Metallurgy

Abstract

Physical metallurgy is a branch of materials science, especially focusing on the relationship between composition, processing, crystal structure and microstructure, and physical and mechanical properties. Because all properties are the manifestation of compositions, structure and microstructure, thermodynamics, kinetics, and plastic deformation, factors as encountered in processing control become very important to control phase transformation and microstructure and thus properties of alloys. All the underlying principles have been well built and physical metallurgy approaches mature. However, traditional physical metallurgy is based on the observations on conventional alloys. As composition is the most basic and original factor to determine the bonding, structure, microstructure, and thus properties to a certain extent, physical metallurgy principles might be different and need to be modified for HEAs which have entirely different compositions from conventional alloys. The most distinguished effects in HEAs are high-entropy, severe lattice distortion, sluggish diffusion, and cocktail effects. This chapter will present and discuss the corresponding subjects of physical metallurgy based on these effects.

3.1 Introduction

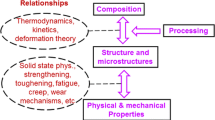
Physical metallurgy is a science focusing on the relationships between composition, processing, crystal structure and microstructure, and physical and mechanical properties [1, 2]. Figure 3.1 shows the scheme of physical metallurgy, in which straightforward correlations can be seen. Composition and processing determine structure and microstructure, which in turn determine properties. The relationships between composition, processing, and crystal structure and microstructure are thermodynamics, kinetics, and deformation theory. Those between crystal structure, microstructure, and physical and mechanical properties are solid-state physics and theories for strengthening, toughening, fatigue, creep, wear, etc. Therefore, the understanding of physical metallurgy is very helpful to manipulate, develop, and utilize materials. Physical metallurgy has been gradually built over 100 year since using optical microscope to observe the microstructure of materials. The underlying principles were thought to become mature [2]. However, traditional physical metallurgy is based on the observations on conventional alloys. As compositions of high-entropy alloys (HEAs) are entirely different from those of conventional alloys, physical metallurgy principles might need to be modified for HEAs and thus require more future research.

Fig. 3.1

The scheme of physical metallurgy in which those areas influenced by four core effects of HEAs are indicated

Because of their uniqueness, four core effects of HEAs were proposed in 2006 [3]. They are high-entropy effect for thermodynamics, sluggish diffusion effect for kinetics, severe lattice distortion effect for structure, and cocktail effect for properties, respectively. Figure 3.1 also shows the influence positions of these four core effects in the scheme of physical metallurgy. High-entropy effect should be involved in thermodynamics to determine the equilibrium structure and microstructure. Sluggish diffusion effect affects kinetics in phase transformation. Severe lattice distortion effect not only affects deformation theory and all the relationships between each property, structure, and microstructure but also affects thermodynamics and kinetics. As for the cocktail effect, it is the overall effect from composition, structure, and microstructure. Properties of HEAs are not as simple as those predicted from the rule of mixture, but mutual interactions between unlike atoms and the feature of phases and microstructure would give excess quantity to each property. Therefore, physical metallurgy principles of HEAs might be different from those of current physical metallurgy because of these influences. We need to review every aspect of physical metallurgy through the four core effects of HEAs. It can be expected that when physical metallurgy encompasses all alloys including tradition alloys and HEAs, the whole understanding of the alloy world becomes realized.

3.2 Four Core Effects of HEAs

3.2.1 High-Entropy Effect

As the name of HEAs implies, high entropy is the first important core effects [4]. This effect could enhance the formation of solution phases and render the microstructure much simpler than expected before. This effect thus has the potential to increase the strength and ductility of solution phases due to solution hardening. Why high entropy could enhance the formation of solution phases? Before answering this, it is necessary to know that there are three possible categories of competing states in the solid state of an alloy: elemental phases, intermetallic compounds (ICs), and solid solution phases [4]. Elemental phase means the terminal solid solution based on one metal element as seen in the pure component side of a phase diagram. Intermetallic compound means stoichiometric compounds having specific superlattices, such as NiAl having B2 structure and Ni₃Ti having D0₂₄ structure, as seen at certain concentration ratios in phase diagrams. Solid solution phase could be further divided into random solid solution and ordered solid solution. Random solid solutions are those with crystal structure in which different components occupy lattice sites by probability although short-range ordering might exist. They could be the phases with the structures of BCC, FCC, or HCP. Ordered solid solutions are intermetallic phases (IPs) or intermediate phase. They are solid solutions with the crystal structure based on intermetallic compounds, as seen in the broader composition ranges around different stoichiometric compounds in phase diagrams [5, 6]. In such phases, different constituent elements tend to occupy different sets of lattice sites. Their degree of ordering is smaller than that of completely ordered structure and thus they can be called partially ordered solid solutions. Although they have the structure of intermetallic compounds and might be classified to intermetallic compounds, they are classified as solid solution phases here with the emphasis on their significant solubility between constituent elements. This is the same thing to separate random solid solutions from terminal phases.

• 1. General trend in phase competition

According to the second law of thermodynamics, a system reaches its thermodynamic equilibrium when its Gibbs free energy is the lowest at given temperature and pressure. In order to elucidate high-entropy effect in enhancing the formation of solid solution phases and inhibiting the formation of IMs, HEAs composed of constituent elements with stronger bonding energies between each other are considered first. If strain energy contribution to mixing enthalpy due to atomic size difference is not considered for simplicity, as shown in Table 3.1, elemental phases based on one major element would have small-negative ΔH _mix and small ΔS _mix, compound phases would have large-negative ΔH _mix but small ΔS _mix, and solid solution phases containing multi-elements would have medium-negative ΔH _mix and high ΔS _mix. As a result, solid solution phases become highly competitive with compound phases for attaining the equilibrium state especially at high temperatures.

Table 3.1 Comparisons of ΔH _mix, ΔS _mix, and ΔG _mix between elemental phases, compounds, and solid solutions. Strain energy from atomic size difference is not included in ΔH _mix

Why multi-principal-element solid solutions have medium ΔH _mix? This is because there has a proportion of unlike atomic pairs in solution phases [4]. For example, by taking a mole of atoms, N ₀, a binary intermetallic compound (B2) NiAl in complete ordering would have (1/2) × 8 N ₀ Ni-Al bonds as the coordination number is 8, whereas a mole of NiAl random solid solution would have (1/2) × (1/2) × 8 N ₀ Ni-Al bonds. Thus, the mixing enthalpy in the random state is one-half of that of the completely ordered state. Similarly, for a five-element equimolar alloy, that in the random solid solution state is 4/5 of that in binary compounds assuming each compound of the ten possible binary compounds has the same mixing enthalpy, i.e., all heats of mixing for unlike atom pairs are the same. Similarly, for an eight-element equimolar alloy, the ratio becomes 7/8. Therefore, higher number of element would allow the random state to have the mixing enthalpy closer to that of the completely ordered state and to become even more competitive with the ordered state under the aid of its high mixing entropy.

If the average of the mixing enthalpy of unlike pairs (28 unlike pairs in total) in an equiatomic eight-element alloy ABCDEFGH is assumed to be −23 kJ/mol, ΔH _mix of completely ordered structure, i.e., forming 28 intermetallic compounds (each has N ₀/8 atoms), is −46 kJ/mol, and that of complete disordered structure, i.e., random solid solution, is −46 × 7/8 = −40.25 kJ/mol. On the other hand, the configurational entropy (ΔS _conf) of completely ordered structure is 0 and that of complete disordered structure is 17.29 J/Kmol. At 1473 K, which is often lower than the melting points of most HEAs, ΔG _mix of completely ordered structure is thus equal to −46 kJ/mol and that of completely disordered structure is equal to −65.72 kJ/mole. Therefore, completely disordered structure is the stable phase at 1473 K. Furthermore, completely disordered structure is also stable at temperature down to 333 K since the temperature of free energy equivalence between these two states can be calculated to be 333 K. However, it should be mentioned that due to the difference of mixing enthalpy between different unlike pairs and the effect of strain energy, partially ordered state might have lower mixing free energy than the random state and form at 1473 K or become the stable state by phase separation. Obviously, the assumption of the 10 or 28 binary compounds having the same or similar mixing enthalpies is almost impossible from the elements in the periodical table. They are hypothetical alloy systems which are used to emphasize the fact that there are lots of unlike pairs with strong bonding and have medium-negative mixing enthalpy in the random solutions or partially ordered solid solutions. They still have low free energy of mixing because some loss of mixing enthalpy could be compensated by higher mixing entropy.

• 2. The effect of the diversity of mixing enthalpy between unlike atom pair

In general, if mixing enthalpies for unlike atomic pairs do not have large difference, solid solution phases would be dominant in the equilibrium state [4]. For example, CoCrFeMnNi alloy can form a single FCC solution even after full-annealing treatments [7, 8]. Ductile refractory HfNbTaTiZr alloy has single BCC phase in the as-cast state [9] and in the as-homogenized state. Conversely, large difference might generate more than two phases. For example, Al has stronger bonding with transition metals but Cu has no attractive bond with most transition metals. As a result, AlCoCrCuFeNi alloy forms Cu-rich FCC + multi-principal-element FCC + multi-principal-element BCC (A2) at high temperatures above 600 °C and have B2 precipitates in the Cu-rich FCC and spinodally decomposed structure of A2 + B2 phases from A2 phase during cooling. B2 solid solution containing multi-principal-elements is in fact derived from the NiAl-type compound [10]. Even larger difference in mixing enthalpies for unlike atomic pairs in those alloys containing O, C, B, or N would generate oxides, carbides, borides, or nitrides in the microstructure. However, it can be found that these strong phases often have certain solubilities of other elements with similar strong bonding due to mixing entropy effect, for example, in Al_0.5B _x CoCrCuFeNi (x = 0–1) alloys, strong boride phase rich in Cr, Fe, and Co forms [11].

• 3. The effect of atomic size difference

To include the effect of atomic size difference on the phase formation, Zhang et al. [12] first proposed the forming trend of disordered solid solutions, ordered solid solution, intermediate phases, and bulk metallic glass (BMG) by comparing ΔS _mix, ΔH _mix, and atomic size difference (δ). The former three are commonly found in HEAs, in which disordered solid solutions and ordered (or partially ordered) ones are those with BCC, FCC, or HCP structures, and intermediate phases are those with more complex compound structures. Guo et al. [13] also used these factors to lay out the phase selection rule for such kinds of phase. Moreover, Yeh [14], Chen et al. [15], and Yang et al. [16] used δ and the ratio of TΔS _mix to ΔH _mix to describe the order-disorder competition in HEAs and also the existing range of intermetallics and BMG. All these have been discussed in Chap. 2. The main point is that solution-type phases tend to form in highly alloyed multicomponent alloys. Disordered solutions preferentially form under smaller δ, smaller |ΔH _mix|, and higher ΔS _mix.

In summary, high-entropy effect is the first important effect for HEAs because it can inhibit the formation of many different kinds of stoichiometric compounds which have strong ordered structures and are usually brittle. Conversely, it enhances the formation of solution-type phases and thus reduces the number of phases much lower than the maximum number (i.e., n + 1, n is the number of components) of phases predicted by Gibbs’ phase rule. This renders the microstructure simpler than expected before, with the positive expectation in displaying better properties.

3.2.2 Severe Lattice Distortion Effect

Because of high-entropy effect, a solid solution phase in HEAs is often a whole-solute matrix no matter its structure is BCC, FCC, HCP, or other more complex compound structures [17]. Thus, every atom in the multi-principal-element matrix is surrounded by different kinds of atom and suffers lattice strain and stress as shown in the right side of Fig. 3.2. In addition to the atomic size difference, different bonding energies and crystal structure tendencies among constituent elements are expected to cause even higher lattice distortion since the nonsymmetrical neighboring atoms, i.e., nonsymmetrical bindings and electronic structure, around an atom, and the variation of such non-symmetry from site to site would affect the atomic position [8, 18]. In conventional alloys, most matrix atoms (or solvent atoms) have the same kind of atoms as their neighbors. The overall lattice distortion is much smaller than that in HEAs.

Fig. 3.2

Schematic diagram showing the severely distorted lattice and the various interactions with dislocations, electrons, phonons, and x-ray beam

• 1. Crystal structure effect on lattice distortion

Wang has used Monte Carlo method in combination with MaxEnt (the principles of maximum entropy) to demonstrate the entropy force to maximize mixing entropy for single-phase solid solution [19]. He built atomic structure models of bulk equiatomic alloys with BCC and FCC lattices from four to eight principal elements. Based on the built models, the atomic structure features are analyzed. Table 3.2 shows the information on the structure analyses of these models. The shortest distance of an atom is the distance of the atom to its nearest-same-element atom. It is surprising to note that an atom to have another atom of same element (like-pair) in the first nearest neighbor can all be avoided for those BCC alloys with five or more elements, and most of the same elements in quaternary and quinary BCC are found in the second nearest-neighbor shell. This peak region providing highest number of like-pairs moves to the third nearest-neighbor shell as the element number increases. On the other hand, there are still a larger proportion of same elements in the first shell in quaternary (74.3 %) and quinary FCC alloys (47.3 %). Because larger proportion of unlike pairs between the center atom and dissimilar atoms in the first shell would give larger distortion (contributions from second and higher shell are diminishingly minor), it can be expected from Table 3.2 that larger number of elements would tend to give larger distortion, and BCC structure has larger distortion than FCC if constructed by the same set of elements with same proportion. This might suggest that BCC solid solution could have larger solution hardening effect than FCC solid solution by the same set of elements with same proportion. This will be discussed in Sect. 3.6.4.

Table 3.2 Distribution of the shortest distances between the same-element atoms on the nearest-neighbor lattice sites in the created BCC and FCC MaxEnt models

• 2. Factors on lattice distortion and relaxation

Lattice distortion might be described by different ways but the most common way only considers atomic size factor [16, 20, 21]. That is, lattice distortion could be directly related to differences in atomic size (δ) by the following equation for a multiple-element matrix:

$$ \delta =100\sqrt{{\displaystyle \sum_{i=1}^n{c}_i{\left(1-{r}_i/\overline{r}\right)}^2}} $$

(3.1)

where $\overline{r}={\displaystyle \sum_{i=1}^n{c}_i{r}_i}$ and c _i and r _i are the atomic percentage and atomic radius of the ith element, respectively. This equation is based on the assumption similar to conventional assumption for the misfit strain of a solute in a matrix, in which the solute atom occupies the exact lattice site. In the multiple-element matrix, pseudo-unary matrix with solvent atoms with an average radius $\overline{r}$ is used. Therefore, this equation gives the average misfit strain in the pseudo-unary matrix. Apparently, this equation is still not accurate since positions of solute atoms in the multiple-element matrix would have some deviations from the exact site of the average lattice. Therefore, better descriptions of lattice distortion are still the issue in the future. Furthermore, it should be mentioned that the lattice distortion is not only from atomic size difference but also from bonding difference and crystal structure difference among components. Assuming a case that distortion strain is only 1 %, the local atomic stress could be estimated to be around 0.01E (or ~0.01 × 8G/3 = 0.027 G) in tension and 0.0135G in shear for isotropic solid at every lattice site where E and G are Young’s modulus and shear modulus, respectively. As the theoretical shear strength is about 0.039–0.11G and actual (or observed) shear strength is orders of magnitude below that [22], in general lower than 0.001G [22], it can be realized that such a small distortion strain is still not negligible. Furthermore, it is easy to find that the critical lattice distortion above which local atomic stress exceeds theoretical shear strength (∼G/15) is ∼5 %, supposing that Hooke’s law is still valid. This suggests that higher distortion would cause instability in forming random or disordered solid solution. But this is underestimated since the lattice distortion of 6.6 % is empirically found to be the borderline between disordered solid solution and other complex crystal structures, as discussed in Chap. 2. This indicates that the final lattice distortion would be resulted from some relaxation by adjusting relative atom positions in the lattice sites for the sake of reducing the distortion energy and maintaining the local atomic stress balance. By this, the critical lattice distortion just for maintaining disordered solid solution, calculated by misfit strain concept, is relaxed to 6.6 %.

• 3. Evidences of lattice distortion effect

Severe lattice distortion not only affects properties but also reduces the thermal effect on properties. Figure 3.2 also shows that interactions will occur when dislocations, electrons, phonons, and x-ray beams passing through the distorted lattice. In general, it can effectively increase hardness and strength by large solution hardening. For example, refractory MoNbTaW alloy and MoNbTaVW alloy have Hv 4455 MPa and 5250 MPa, respectively. Their hardness values are three times that obtained by the mixture rule [23]. In addition, severe lattice distortion significantly decreases electrical and thermal conductivity since it can markedly scatter free electrons and phonons [24]. For example, Lu et al. studied the thermal diffusivity as a function temperature for four HEAs and pure Al as shown in Fig. 3.3. It was found that the slopes of thermal diffusivities of HEAs with respect to temperature are positively small and thus insensitive to temperature whereas those of conventional metal Al are negatively large and sensitive to temperature [25]. In x-ray diffraction, peak intensity largely decreases due to diffuse scattering on the distorted atomic planes [18]. Lots of x-ray cannot fulfill Bragg’s law during diffraction and are scattered to the background. It is also noted that all these properties in HEAs become quite insensitive to temperature. This is explainable since the lattice distortion caused by thermal vibration of atoms is relatively small as compared with the severe lattice distortion [4, 18].

Fig. 3.3

Thermal diffusivities as a function of temperature for pure aluminum and HEA-a(Al_0.3CrFe_1.5MnNi_0.5), HEA-b(Al_0.5CrFe_1.5MnNi_0.5), HEA-c(Al_0.3CrFe_1.5MnNi_0.5Mo_0.1), and HEA-d(Al_0.5CrFe_1.5MnNi_0.5Mo_0.1) [25]

3.2.3 Sluggish Diffusion Effect

Phase transformations in HEAs would require cooperative diffusion of many different kinds of atoms to accomplish the partitioning of composition between phases. However, the vacancy concentration for substitutional diffusion is still limited in HEAs as found in traditional alloys since each vacancy in crystalline HEAs is also associated with a positive enthalpy of formation and an excess mixing entropy. The competition between these two factors yields a certain equilibrium vacancy concentration with minimum free energy of mixing at a given temperature [26]. A vacancy in the whole-solute matrix is in fact surrounded and competed by different element atoms during diffusion. Either a vacancy or an atom would have a fluctuated diffusion path to migrate and have slower diffusion and higher activation energy. As a result, diffusional phase transformation would be slower in HEAs. In brief, the sluggish diffusion effect implies slower diffusion and phase transformation.

• 1. Diffusion couple experiment on HEAs

Although there are many indirect evidences of sluggish diffusion effect, direct diffusion measurement is more persuasive. In order to verify this effect, a near-ideal solution system of Co-Cr-Fe-Mn-Ni with stable single FCC solid solution was selected by Tsai et al. to do diffusion experiment [8]. Four quasi-binary diffusion couples were made as listed in Table 3.3. In the two end members of each couple, only two elements differed in concentration. The diffusion couple was tightly fixed in a molybdenum tube which was then sealed in a vacuum quartz tube. From the concentration profiles obtained after diffusion at 1173, 1223, 1273, and 1323 K, diffusion coefficients and activation energy were calculated. Figure 3.4 shows the temperature dependence of the diffusion coefficient of a different element, revealing that the sequence of elements in the order of decreasing diffusion rate was Mn, Cr, Fe, Co, and Ni. It was also found that diffusion coefficients of each elements at T/T _m in the Co-Cr-Fe-Mn-Ni alloy system were the smallest in similar FCC matrices including Fe-Cr-Ni(-Si) alloys and pure Fe, Co, and Ni metals (see Fig. 3.5). In addition, the melting-point-normalized activation energies, Q/T _m, in the HEA were the largest as shown in Fig. 3.6. It was also noted that for the same element, the degree of sluggish diffusion is related to the number of principal elements in the matrix. For example, the Q/T _m values in the present HEAs are the highest; those in Fe-Cr-Ni(-Si) alloys are the second; and those in pure metals are the lowest. In brief, all these are direct evidences for the sluggish diffusion effect in HEAs.

Table 3.3 The concentrations of end members of three diffusion couples [8]

Fig. 3.4

Temperature dependence of the diffusion coefficients for Co, Cr, Fe, Mn, and Ni obtained from Co-Cr-Fe-Mn-Ni diffusion couple experiments [8]

Fig. 3.5

Temperature dependence of the diffusion coefficients for Cr, Mn, Fe, Co, and Ni in different matrices

Fig. 3.6

Melting-point-normalized activation energy of diffusion for Cr, Mn, Fe, Co, and Ni in different matrices [8]

• 2. Positive benefits from sluggish diffusion effect

Sluggish diffusion effect might provide several important advantages as found in many related researches [10, 27–34]. They include easiness to get supersaturated state and fine precipitates, increased recrystallization temperature, slower grain growth, reduced particle coarsening rate, and increased creep resistance. These advantages might benefit microstructure and property control for better performance. For example, Liu et al. studied the grain growth of cold-rolled and annealed sheet of CoCrFeMnNi HEA and found that activation energy is much higher than AISI 304LN stainless steels, which is consistent with the sluggish diffusion effect [33].

3.2.4 Cocktail Effect

The term “multimetallic cocktails” was first proposed by Ranganathan to emphasize alloy pleasures in alloy design and development [35]. Although this effect is also possessed by conventional alloys, cocktail effect is emphasized in HEAs because at least five major elements are used to enhance the properties of materials. As stated above, HEAs might have simple phase, two phases, three phases, or more depending on the composition and processing. As a result, the whole properties are from the overall contribution of the constituent phases by the effect of grain morphology, grain-size distribution, grain and phase boundaries, and properties of each phase. However, each phase is a multi-principal-element solid solution and can be regarded as atomic-scale composites. Its composite properties not only come from the basic properties of elements by the mixture rule but also from the mutual interactions among all the elements and from the severe lattice distortion. Interaction and lattice distortion would bring excess quantities to the quantities predicted by the mixture rule. As a whole, “cocktail effect” ranges from atomic-scale multi-principal-element composite effect to microscale multi-phase composite effect. Therefore, it is important for an alloy designer to understand related factors involved before selecting suitable composition and processes based on the cocktail effect [4]. For example, refractory HEAs developed by Air Force Research Laboratory have melting points very much higher than those of Ni-base and Co-base superalloys [23, 29]. This is simply because refractory elements were selected as constituent elements. By the mixture rule, quaternary alloy MoNbTaW and quinary alloy MoNbTaVW have melting point above 2600 °C. As a result, both alloys display much higher softening resistance than superalloys and have yield strength above 400 MPa at 1600 °C as shown in Fig. 3.7 [29]. Such refractory HEAs are thus also expected to have potential applications at very high temperatures. In another example, Zhang et al. studied FeCoNi(AlSi)_0–0.8 alloys for finding the composition with the optimum combination of magnetic, electrical, and mechanical properties. The best was achieved in alloy FeCoNi(AlSi)_0.2 with saturation magnetization (1.15 T), coercivity (1400 A/m), electrical resistivity (69.5 μΩcm), yield strength (342 MPa), and strain without fracture (50 %), which makes the alloy an excellent soft magnetic materials for many potential applications [36]. Obviously, this alloy design relied on the selection of equimolar ferromagnetic elements (Fe, Co, and Ni) for forming ductile FCC phase with higher atomic packing density than BCC and suitable addition of nonmagnetic elements (Al and Si having slightly antiparallel magnetic coupling with Fe, Co, and Ni) to increase lattice distortion. It led to a positive cocktail effect in achieving high magnetization, low coercivity, good plasticity, high strength, and high electrical resistance.

Fig. 3.7

Temperature dependence of the yield stress of Nb₂₅Mo₂₅Ta₂₅W₂₅ and V₂₀Nb₂₀Mo₂₀Ta₂₀W₂₀ HEAs and two superalloys, Inconel 718 and Haynes 230 [29]

3.3 Crystal Structures and Phase Transformation in HEAs

3.3.1 The Number of Crystal Structures in Alloy World

• 1. Mackey’s statistical analysis on crystal number

In the periodic table, there are 80 metal elements and most of them are of three simple structures: FCC, HCP, and BCC. However, there exist different kinds of ICs and IPs in binary alloys, as seen in binary phase diagrams. Moreover, more ternary ICs or IPs exist in lots of ternary alloy systems. Thus, it is easy to have the concept that higher-order alloy systems would generate more ICs or IPs and an alloy with a large number of elements would have many different kinds of ICs and IPs in equilibrium although Gibbs’ phase rule places the limitation for the maximum number of phases. Is this right? Mackay has reported the statistics of inorganic crystal structures in his paper entitled “On Complexity” [37]. He wrote “The Inorganic Crystal Structure Database contains some 50,000 structures (many of which are duplicated), which can be searched according to various parameters. Figure 3.1 (i.e., Fig. 3.8 in this chapter) shows a plot of the numbers of structures containing 1, 2, 3, …, N different elements. A cursory examination shows that many of the structures with large values of N contain solid solutions, different elements occupying the same sites, but the result is nevertheless clear. There is a sharp limit to complexity.” He tried to explain this phenomenon by two approaches. One is “The problem could be considered thermodynamically. For example, a soup of many elements does not produce very complex crystals but minimizes the configurational entropy by forming ordered crystal of several simpler compositions.” The other is based on the similarity between Planck distribution of energy in an absolutely black body and the distribution of numbers of crystal structure: “In fact, in a one-dimensional crystal, the number of atoms in a repeat must be an integer and similar effects are to be expected in three-dimensions. Space is “quantized” by atomicity, and not all dimensions of unit cells are possible.” As a result, the explanations for the distribution are still not clear and require further confirmation. On the other hand, if we select 2 elements from 80 metal elements in the periodic table, there are 3160 combinations. Furthermore, the selection of 40 elements from 80 metal elements give possible combinations with a number 1.075 × 10²³, which is about one-sixth of an Avogadro’s number. As there are around 6500 inorganic crystal structures found from binary systems and 19,000 structures from ternary systems (see Fig. 3.8), it could be expected that the number of crystal structure would be huge by extrapolation. It has been estimated that the number of compounds for metal systems could be up to 10⁹⁰, which exceed the number of atoms, around 10⁸⁰, in the universe. Thus, the number of compounds is inconceivable except some factors interfere with this extrapolation.

Fig. 3.8

Points denote the numbers of inorganic crystal structures with 1, 2, 3, … . N different elements. N = 3 has a maximum of 19,000. The line follows the Planck distribution of energy in an absolutely black body [34]. Three alloy regions, LEAs, MEAs, and HEAs, are indicated

• 2. Entropy and dilution effects on the statistical distribution of crystal number

What are the interfering factors? Considering the high-entropy effect in HEAs, high entropy is thought to be one important factor to interfere those factors which cause the formation of compounds such as larger atomic size difference which promotes size-factor compounds with highest-neighboring atoms to maximize bond number and also lower the strain energy, valence bonding which promotes valence compounds to maximize the ionic and/or covalent bond strength and satisfy the valence balance, and certain valence electron concentration (e/a) ranges which stabilize electron phases [38, 39]. Entropy effect can be seen in binary and ternary systems. It can enhance the substitution in compounds between different elements with similar chemical features. As the electronegativity and valence of elements in the same group or close groups of the periodic table generally have close chemical feature, the substitution is common. It is apparent that this partial substitution is favored by increasing mixing entropy with some gain or loss in mixing enthalpy depending on the substituting element. For example, NiAl compound (with B2 crystal structure) has a range of composition (also called as NiAl intermediate phase) in Ni-Al phase diagram. By alloying, Co and Pt can substitute a portion of Ni, and Ti and Ta can substitute a portion of Al in the compounds. By the same reason, even high mixing entropy in high-order compositions could enhance the substitution and the mixing in the compounds. This means the ability to accommodate more elements in compounds to form IPs could consume a portion of components. Besides compounds, similar substitution and consumption also occur in the terminal phases based on the component’s structures. Furthermore, there is a dilution effect in high-order alloy such as HEAs. For equiatomic quinary alloys in which each component possesses 20 % in atomic concentration, its tendency to form compounds is lower since the ratio in A _x B _y -type compounds is often 2:5, 3:4, 1:1, 4:3, or 2:5. Only the ratios, 2:5 and 5:2, are possible except the cases in which the components could be grouped into two and form pseudo-binary alloys. Even for this, solution-type compounds (or IPs) are formed due to high-entropy effect. Therefore, in high-order alloys such as HEAs, high-entropy and dilution effect could enhance the formation of solution-type phase including terminal solid solutions or IPs. This is the main reason, as referred to Fig. 3.8, why there are a sharp decrease in the number of crystal structures with four elements and a further decrease with elements more than four. It is noted that the number of crystal structure with more than eight elements is nearly at the same level of that with one element. As observed by Mackay, many of the structures with large values of N contain solid solutions, different elements occupying the same sites. This is clearly the evidence to support the above explanation based on high-entropy and dilution effects.

What is the entropy effect on the shape of crystal number distribution? The large decrease in the number of crystal structures in fact echoes the definition of HEAs emphasizing the number of major elements being at least five. Two lines are set in the plot of Fig. 3.8 to mark the degree of entropy effect. Mixing entropy is pronounced for crystal structures with at least five elements, moderately pronounced for those with three to five elements and less pronounced for those with one or two elements. As a result, the fast increase of crystal structure number from one element to three elements is due to weaker entropy effect, the slowdown and concave-down are due to increased entropy effect from three to five elements, and further decrease to small number after five elements is related to strong entropy effect. In brief, the distribution curve can be related to entropy effect. This correlation explains the classification of alloy world into HEAs, MEAs, and LEAs based on the number of major elements [3]. Based on the above reasons, it can be expected that most crystal structures in HEAs are also found in LEAs or MEAs. Furthermore, a lot of crystals are of BCC, FCC, and HCP solid solutions since terminal phases of 80 elements almost belong to three kinds of structures: FCC, HCP, and BCC.

3.3.2 Factors Affecting Solubility Between Metal Elements

According to crystallography [40], a lattice is a regular periodic array of points in space. The crystal structure is formed when a basis of atoms (atom or a group of atoms or ions) is attached identically to every lattice point. This can be expressed as

$$ \mathrm{Lattice} + \mathrm{basis} = \mathrm{crystal}\ \mathrm{structure} $$

(3.2)

where every basis is identical in composition, arrangement, and orientation.

Hume-Rothery (H-R) rules are rules in judging the mutual solubility of the two elements at high temperatures in substitutional solid solution of a binary alloy. For example, the solubilities of Ni, Co, Cr, Mo, and Si in Fe are regarded as larger than 15 at.% although their solubility is much lower than 15 at.% at room temperature [41]. He is the first to propose three empirical rules to explain the formation of solid solutions in 1920s. [42, 43]: (1) the atomic sizes of the solvent and solute must not differ by more than 15 %, (2) the electrochemical nature of the two elements must be similar, and (3) a higher-valent metal is more soluble in a lower-valent metal than vice versa. Through a number of latter research, H-R rule are generally stated as [44]:

• 1. The radii of the solute and solvent atoms must not differ by more than about 15 %: For complete solubility, the atomic size difference should be less than 8 %.

• 2. The crystal structures of the two elements must be the same for extended solid solubility.

• 3. Extended solubility occurs when the solvent and solute have the same valency.

• 4. The two elements should have similar electronegativity so that intermetallic compounds will not form.

Therefore, the similarity and difference of crystal structure, valence, electronegativity, and atomic size are considered to affect the maximum solubility which occurs in the high temperature range below solidus line as seen in phase diagrams. For example, Cu-Ag system has an atomic size difference of 12.5 % (r _Cu = 0.128 nm, r _Ag = 0.145 nm [40]), same electronegativity (Cu and Ag are both 1.9), same crystal structure (both are FCC), and small difference in valences (+1 for Ag and +1 and +2 for Cu). Thus, due to its atomic size difference larger than 8 %, the maximum solubility of Ag in Cu at 779 °C is 8 wt.% (~5 at.%) and that of Cu in Ag is 8.8 wt.% (~14.3 at.%).

Alonso and Simozar [41] have correlated the mixing enthalpy, atomic size difference, and maximum solubility quite well. In fact, mixing enthalpy can be regarded as the result of interaction between two elements, which have been more precisely treated by Miedema model using work function, the electron density of the Wigner-Seitz cell, and molar volume of the two elements. This parameter is obviously better than crystal structure, electronegativity, and valence between two elements in the solubility prediction [41, 45]. However, mixing entropy hasn’t been considered as a factor in the solubility prediction although it is known to have a contribution of − TΔS to the mixing free energy. This neglect might be due to the thinking that binary alloys have low mixing entropy as compared with mixing enthalpy. In fact, mixing entropy is still important at high temperatures. Co-Cr binary system is an example. Although Co is FCC at above 810 °C and Cr is BCC, the mutual solubility is very high (37 wt.%Cr in Co side and 56.1 wt.%Co in Cr side at 1395 °C). This could not be explained adequately with H-R rules since they are different in crystal structure, atomic size (Co, 0.125 nm, and Cr, 0.128 nm), and electronegativity (Co, 1.7, and Cr, 1.6) and quite different in valence (Co, +2 and +3; Cr, +3, +4, and +6). Obviously, mixing entropy could relax the strictness of H-R rules. In HEAs, there are many examples which reveal the relaxation of H-R rules. That means large mutual solubilities in BCC and FCC solid solutions and partially ordered solid solutions with compound structures at high temperatures are often found in those alloys not fulfilling the rules, such as in AlCoCrCuFeNi [10], AlCrCuFeMnNi [46], CoCrFeMnNi [7, 8], and HfNbTaTiZr [9]. This is also why most of the phase formation criteria for HEAs discussed in Chap. 2 already consider high-entropy effect for the extended solubility.

3.3.3 Phase Transformation in Different Processing for HEAs

• 1. High-entropy effect on phase evolution from liquid state

High-entropy effect plays an important role on the phase transformation of HEAs. It should be reminded that mixing entropy is compared at the liquid solution or random solid-solution state in the definition of HEAs. That means HEAs have high mixing entropy at such states as compared with those of conventional alloys. Why high mixing entropy at such states is emphasized? Figure 3.9 shows the typical phase evolution during solidification and cooling [4]. If an alloy has high mixing entropy, simple solid-solution phases will form at high temperatures due to the large TΔS _mix. During subsequent cooling, mixing entropy become less important and short-range ordering, long-range ordering, or even precipitation of second phases might occur. But sluggish diffusion effect may either yield fine precipitates or inhibit precipitation depending on alloys and processing, which is important for improving mechanical properties. Santodonato et al. studied the evolution of structure, microstructure, phase composition, long-range ordering, short-range ordering, and configurational entropy of Al_1.3CoCrCuFeNi HEA from room temperature to above 1315 °C by using atom probe tomography, SEM, TEM, EDS, EBSD, neutron diffraction, synchrotron x-ray powder diffraction, and ab initio molecular dynamics simulation [10, 47]. At above 1315 °C, the alloy becomes 100 % liquid, with some preferred nearest-neighbor pair correlations: Al-Ni, Cr-Fe, and Cu-Cu. At 1230–1315 °C, Cu-rich liquid plus BCC crystals (Al_1.3CoCrCu_1-zFeNi) with chemical short-range order are obtained. Total configurational entropy of BCC phase is 1.73R ≤ ΔS _conf ≤ 1.79R calculated by the phase composition and degree of ordering. At 1080–1230 °C, 95 % B2 phase (Al_1.3CoCrCu_0.7FeNi) and 5 % Cu-rich liquid are obtained. The total configurational entropy of B2 phase is 1.63R ≤ ΔS _conf ≤ 1.73R. At 600–1080 °C, 85 % B2 phase (Al_1.3CoCrCu_0.1FeNi) plus 10 % Cu-rich rod FCC phase and 5 % Cu-rich interdendrite are obtained. The total configurational entropy of B2 phase is ΔS _conf = 1.50R. At room temperature to 600 °C, 84 % spinodal BCC/B2 (Co_0.2CrFe_0.5/Al_1.3Co_0.8Fe_0.5Ni) plus 16 % various Cu-rich FCC phases are obtained. The total configurational entropy is 0.89R. They concluded that when the alloy undergoes elemental segregation, precipitation, chemical ordering, and spinodal decomposition with decreased temperature, a significant amount of disorder remains due to the distributions of multiple elements in the major phases. That means an enhancement of the overall disorder due to the entropy effect still exists at room temperature as reflected by the multi-principal-element composition in most phases.

Fig. 3.9

Phase evolution during solidification and cooling of HEAs [4]

Conversely, if multi-principal-element alloys do not have high mixing entropy at high temperatures, intermetallic phases would form at high temperatures. And in subsequent cooling, the microstructure would become even more complex. Such complex microstructures obviously become very difficult to understand and manipulate and very brittle to be utilized. Therefore, the fortune to avoid the complexity at low temperatures essentially comes from the high-entropy effect which is amplified by high temperature and becomes stronger in competing with mixing enthalpies of intermetallic compounds.

How about the phase diagrams of HEAs? Due to high-entropy effect involved, phase diagram of a HEA system in the composition hyperspace may not be too complicated. Single-phase region, two-phase region, and three-phase region might exist. Each region has their composition and temperature range. Thus, if the phase diagram of a HEA system is known, the equilibrium phases of a composition in the system can be predicted. Figure 3.10 shows the approximate phase diagrams of different alloy series of Al-Co-Cr-Fe-Mo-Ni system [48]. Each diagram was obtained by investigating an alloy series varied with the content of one element with SEM, TEM, room-temperature and high-temperature x-ray diffractometer, and differential thermal analyzer (DTA). Taking the AlCoCrFeMo_0.5Ni as an example, three phases, FCC + B2 + σ, coexist at 1000 °C and two phases, B2 + σ, coexist at 400 °C. From the viewpoint of thermodynamics, the two and three solid solutions would have lower free energies than that of the single random solid-solution phase. Figure 3.11 shows the schematic curves of mixing Gibbs’ free energy at 400 and 1000 °C, respectively, for such a comparison. Although the mixing free energy for each solid solution and thus the overall mixing free energy were not calculated due to their complexity and almost impossible to take a common tangent plane for the equilibrium compositions in the hyperspace, the role of high mixing entropy in further lowering free energy of solution-type phase from pure elements or compounds is obvious in the figure. That is to say that an existence of a mixture of several multi-principal-element solution phases in equilibrium is still a result of high-entropy effect.

Fig. 3.10

Schematic phase diagrams of different alloy systems: (a) Al_uCoCrFeMo_0.5Ni, (b) AlCo_vCrFeMo_0.5Ni, (c) AlCoCr_wFeMo_0.5Ni, (d) AlCoCrFe_xMo_0.5Ni, (e) AlCoCrFeMo_yNi, and (f) AlCoCrFeMo_0.5Ni_z alloys [48]

Fig. 3.11

Schematic curves of mixing Gibbs’ free energy for the AlCoCrFeMo_0.5Ni alloy at (a) 673 K and (b) 1273 K [49]

• 2. Lattice distortion and sluggish diffusion effects on solid-state transformation

What factors affect phase transformation? Phase transformation has two categories: diffusional type and diffusionless type. Diffusion type one includes solidification, eutectic reaction, eutectoid reaction, precipitation, spinodal decomposition, ordering transformation, and dissolution as found in phase diagram when cooling or heating is exerted. In addition, long holding time at high temperatures will cause grain coarsening and Oswald ripening of second phase particles. One example of diffusionless type one is martensitic transformation. Up to 2015, HEAs have provided many examples for different diffusional phase transformations in the literature. However, examples for martensitic transformation are still rare. Nucleation and growth are commonly seen in addition to spinodal transformation. In nucleation-and-growth transformation process, surface energy required to form a nucleus results in the nucleation energy barrier for an embryo to become a stable nucleus. In addition, free energy difference between new and old phases (or new state and old state) provides driving force for the transformation. Because lattice distortion affects interfacial energy and driving force, and sluggish diffusion affects nucleation rate and growth rate, their detailed effects need to be considered for each HEA. But, the general trend of these effects will be considered and explained in Sects. 3.4, 3.5, 3.6 and 3.7.

• 3. Lattice distortion and sluggish diffusion effects under severe deformation or extremely high cooling rate

What is the lattice distortion and sluggish diffusion effects under severe deformation and extremely high cooling rate? Mechanical alloying and sputtering deposition are easy ways to obtain non-equilibrium simple solid solutions due to the kinetic reason by which sufficient long-range diffusion is inhibited. In addition to crystalline structures, amorphous structure is especially easy to form either by mechanical alloying [49–52] and by sputtering deposition from HEA targets [31, 53] since atomic size difference required to form amorphous structure is smaller than that required for solidification route. Egami’s criterion based on topological instability is suitable to explain which compositions tend to form amorphous solid because the alloy synthesized by mechanical alloying or sputtering deposition is directly formed from elemental state [51]. His criterion is that topological instability would happen when the critical volume expansion, 6.3 %, by atoms of different sizes is exceeded [51, 54, 55]. It has been found that diverse atomic size in HEAs enhances the topological stability and sluggish diffusion of HEAs is helpful in freezing the atom configuration and avoiding crystallization. The combination of a deposition temperature at 400–500 °C and a deposition time 1 h is still easy to obtain the HEA amorphous films with lesser atomic size difference. On the other hand, by solidification route, stricter alloy design is required for obtaining amorphous structure by rapid solidification with at least one dimension very small in thickness or by moderate cooling with bulk forms. Because nucleation and growth of solid phases should be involved during the cooling through freezing range, compositions near deep eutectic composition and fulfilling Inoue’s rules tend to have high glass formability [56]. Another viewpoint to increase the glass formability relates with confusion principle which says more components will have a lower chance to select viable crystal structures and thus have greater glass formability [57–60]. To summarize the general factors for forming amorphous structure, increased atomic size difference, negative mixing enthalpy, number of components, and deviation in crystal structures could increase the glass formability of a solid solution [54–60].

3.4 Defects and Defect Energies in HEAs

3.4.1 Defects in Distorted Lattice and Origin of Defect Energy

It is well known that even in very pure crystals, it is inevitable to have a certain amount of crystal defects such as vacancies and impurity atoms, which exist at least because of their contribution in mixing entropy. In addition, during preparation of materials, dislocations and grain boundaries and even voids are easily to be introduced into the materials. In HEAs, their structure could be either amorphous structure or crystal structure which depends on the composition and process used. In amorphous structure with multiple elements, residual strain energy might exist since atoms in the structure could suffer from atomic-scale compressive or tensile stress although there is no net stress to cause plastic flow. This stress is different from the external applied stress or residual stress balanced in a long-range scale. Residual distortion energy in amorphous structure could be relaxed to a lower level if suitable thermal energy is provided, such as annealing at below glass transition temperature. In crystal structure with multiple elements, the crystal lattice is distorted due to the difference in atomic size, crystal structure tendency, and chemical bonding as discussed in Sect. 3.2.2. Any atom at a lattice site might have position deviation from exact lattice site. In addition, the electron configuration around the atom has no symmetry as compared with that of crystal structure of pure component. All the deviation and non-symmetry depends on its neighboring atoms. Apparently, such a severe lattice distortion, i.e., distortion exists everywhere, affects phase stability, microstructure, and properties.

Topologically, strain and strain energy might be used to describe the degree of lattice distortion in the whole-solute lattice. Because vacancies, dislocations, stacking faults, twins, and grain boundaries are all formed from the lattice, the atomic configuration of these defects would be different between pure lattice and whole-solute lattice with distortion. In addition, the energy level of distorted lattice would be higher than pure lattice without distortion if average chemical bonding is the same. In other words, the deviation of energy level of a kind of defect from the energy level of distorted lattice would be smaller than its deviation from that of pure lattice. This concept could be realized from the typical textbook on phase transformation [61]. The origin of interface energy is discussed in the book. It says, as shown in Fig. 3.12, “The free energy of a system containing an interface of area A and free energy γ per unit area is given by $G = {G}_0 + A\gamma$ where G ₀ is the free energy of the system assuming that all material in the system has the properties of the bulk—γ is therefore the excess free energy arising from the fact that some material lies in or close to the interface. It is also the work that must be done at constant T and P to create unit area of interface.” Another textbook on thermodynamics of solids [62] also says, “The interface is a site of disturbance on an atomic scale, since the environment of atoms at the interface is not regular as it is in the interior of the phase. As a result, to increase the area of an interface, work must be expended by the system.” Although this concept is for interfacial energy, it is similarly applied to the energy of other defects since all these other defects are generated by doing work from the distorted lattice.

Fig. 3.12

A portion of material is shown, which contains an interface with interface area A. Total free energy G is equal to G ₀ + γA, where γ is the excess free energy per unit interface area arising from the generation of the interface

The energies of vacancies, dislocations, stacking faults, twin boundaries, and high-angle grain boundaries in most pure metals have been well established in the literature. Table 3.4 selects typical examples of FCC metals, Al, Cu, Ag, Au, and Ni and lists their values for comparison. In the multiple-principal-element matrix, the lattice distortion energy would increase the energy level of the distorted lattice and thus reduce the defect energy from the undistorted lattice to a lower level. Therefore, it is important to estimate the distortion energy so that the importance of distortion energy in affecting defect energy could be determined. The estimation will be presented in the next section.

Table 3.4 The energies of vacancies, dislocations, stacking faults, twin boundaries, and high-angle grain boundaries in FCC metals: Al, Cu, Ag, Au, and Ni

3.4.2 Lattice Distortion and Distortion Energy

In Sect. 3.2.2, it was discussed that besides atom size difference, different bonding energies and crystal structure tendencies among constituent elements also increase lattice distortion. The lattice distortion energy due to atomic size difference has been formulated in the literature. However, the effects of crystal structure difference, bonding difference, and the extent of lattice relaxation on distortion energy are still difficult to estimate in a quantitative way. Nevertheless, the lattice distortion energy could increase the lattice energy level due to chemical bonding energy. In other words, lattice energy level per mole is equal to the sum of that contributed by chemical bonding and lattice strain per mole:

$$ {U}_{\mathrm{lattice},\ \mathrm{per}\ \mathrm{mole}} = {U}_{\mathrm{bonding},\ \mathrm{per}\ \mathrm{mole}} + {U}_{\mathrm{strain},\ \mathrm{per}\ \mathrm{mole}} $$

(3.3)

The common calculation of distortion strain is the average misfit strain by using Eq. 3.1. It was also mentioned that actual lattice distortion is not as large as predicted by misfit strain. There would have relaxation process to adjust the atomic configuration in the lattice so that local stress balance and overall minimum free energy could be reached at the equilibrium state. The lattice for such an atomic configuration is just the average lattice as measured by XRD method. Therefore, the lattice strain of this atomic configuration should be based on the average lattice. The calculation of lattice distortion strain and strain energy was proposed by Huang et al. who investigated inhibition mechanism why original grain-size strengthening of high-entropy AlCrNbSiTiV nitride film with NaCl-type structure in the as-deposited state changes little, even after annealing at 1000 °C for 5 h [20]. They calculated the strain and strain energy based on the average lattice constant of average lattice measured by XRD. The strain caused by a component is the deviation between its lattice constant at the pure component state and the experimental average lattice constant. This calculation is based on the tendency that each component would take their original lattice if no constraint for local atomic stress balance and minimum free energy is exerted. The fitting of their original lattices to average lattice brings about the strain energy. Thus, by assuming average strain energy per unit volume is U ₀, and per atom, U _{0, per atom}, the following equations could be obtained under the hypothesis of isotropic elastic solids:

$$ {U}_0=\frac{1}{2}{\varepsilon}_x^2E+\frac{1}{2}{\varepsilon}_y^2E+\frac{1}{2}{\varepsilon}_z^2E, $$

(3.4)

$$ {\varepsilon}_x^2={\varepsilon}_y^2={\varepsilon}_z^2={\displaystyle \sum_i{x}_i}{\varepsilon}_i^2, $$

(3.5)

$$ {\varepsilon}_i=\frac{a_i-{a}_{\exp }}{a_{\exp }}, $$

(3.6)

and

$$ {U}_{0,\ \mathrm{per}\;\mathrm{atom}}=\frac{U_0}{\rho_v}, $$

(3.7)

where E is Young’s modulus; ε _x , ε _y , and ε _z are strains in the [100], [010], and [001] directions, respectively; ε _i is the lattice strain from component i; x _i is the molar fraction of component i; a _i is the lattice constant of component i; a _exp is average lattice constant of the whole-solute lattice obtained by XRD method; and ρ _v is the mole number density.

By using the above equation to calculate the distortion energy of AlCrNbSiTiV nitride film with NaCl-type structure, it is successful to explain low driving force for subgrain growth and grain growth and also the actual subgrain size and grain size observed with TEM. The agreement suggests the distortion energy calculation is persuasive.

As an example for the calculation, an equimolar alloy series from Ni, NiCo, NiCoFe, NiCoFeCr, and CoNiFeCrMn alloy with single FCC structure is used. The basic features of the elements used in this alloy series are listed as Table 3.5 [67]. In the table, the atomic radius and lattice constants are of FCC structure, in which those of non-FCC Cr and Mn, although not found directly in the literature, have been calculated using the equation: ${a}_{\mathrm{FCC}}=4{r}_i/\sqrt{2}$, where r _i is the atomic radius of element i in 12-coordinated metals as listed in the table. Average lattice constants measured by XRD and Burgers’ vector, Young’s modulus measured by tensile test, and density measured by Archimedes’ method for the alloy series are listed in Table 3.6 [68]. Based on this and Eqs. 3.4 and 3.7, we can calculate the distortion energies also listed in Table 3.6. It can be seen that the distortion energy increases with increased addition of element. Although Mn does not have the largest lattice constant, distortion energy still increases after its addition.

Table 3.5 Properties of constituent elements in Ni-Co-Fe-Cr-Mn alloy series [67]

Table 3.6 Related data of Ni-Co-Fe-Cr-Mn alloy series

3.4.3 Vacancies

In HEAs, what is the formation enthalpy of vacancy? Is the vacancy concentration influenced by high mixing entropy? How about the diffusivity of vacancy? All these answers are important for understanding the kinetics of phase transformation and creep behaviors.

It is well known that vacancies are inevitable in materials because of entropy reason. The formation of a vacancy by removing an atom would destroy the bonds with its neighboring atoms and thus raise the energy state with an increase, ΔH _v, in enthalpy although some relaxation would occur. Besides, the formation would also be associated with an excess entropy ΔS _v mainly by vibrational randomness around vacancy. However, an amount of vacancy would increase the configuration entropy by configurational randomness. For a pure metal, it can be derived that there exists a critical concentration at which the total free energy of mixing is minimum [26]. Consider a crystal containing N ₀ atoms and N _v vacancies, the free energy change from perfect crystal without vacancies could be written as

$$ G\ - \ {G}_0 = {N}_{\mathrm{v}}\Delta {H}_{\mathrm{v}} - \ kT\ \ln \left[\left({N}_0+{N}_{\mathrm{v}}\right)!/{N}_0!{N}_{\mathrm{v}}!\right]\ - \ {N}_{\mathrm{v}}T\Delta {S}_{\mathrm{v}} $$

(3.8)

where k is Boltzmann’s constant. Using Stirling’s approximation and rearrangement,

$$ G-{G}_0 = {N}_{\mathrm{v}}\Delta {H}_{\mathrm{v}}-kT\left[\left({N}_0+{N}_{\mathrm{v}}\right)\ \ln \left({N}_0+{N}_{\mathrm{v}}\right)-{N}_0\kern0.2em \ln \kern0.2em {N}_0-{N}_{\mathrm{v}}\kern0.2em \ln \kern0.2em {N}_{\mathrm{v}}\right]-{N}_{\mathrm{v}}T\Delta {S}_{\mathrm{v}} $$

(3.9)

Since $d\left(G-{G}_0\right)/d{N}_{\mathrm{v}} = 0$ at equilibrium and N ₀ is very small, it leads to the equilibrium vacancy concentration

$$ {X}_{\mathrm{v}}={N}_{\mathrm{v}}/\left({N}_0+{N}_{\mathrm{v}}\right)={e^{\Delta {S}_{\mathrm{v}}}}^{/ kT}{e^{-\Delta {H}_{\mathrm{v}}}}^{/ kT}={e^{-\Delta G}}^{{}_{\mathrm{v}}/ kT} $$

(3.10)

How about the vacancy concentration in HEAs? Consider the simplest case, an equimolar random ideal solid solution with n metal elements which have the same atomic size, then the above equation becomes

$$ {G}_{\mathrm{h}}-{G}_{0\mathrm{h}}={N}_{\mathrm{vh}}\Delta {H}_{\mathrm{vh}}-kT\left[\left({N}_0+{N}_{\mathrm{vh}}\right)\ \ln \left({N}_0+{N}_{\mathrm{vh}}\right)-{N}_0\kern0.5em \ln \left({N}_0/n\right)-{N}_{\mathrm{vh}}\kern0.5em \ln {N}_{\mathrm{vh}}\right]-{N}_{\mathrm{vh}}T\Delta {S}_{\mathrm{vh}} $$

(3.11)

Since $d\left({G}_{\mathrm{h}} - \ {G}_{0\mathrm{h}}\right)/d{N}_{\mathrm{v}} = 0$ at equilibrium and N ₀ is very small, it leads to the equilibrium vacancy concentration

$$ {X}_{\mathrm{vh}}={N}_{\mathrm{vh}}/\left({N}_0+{N}_{\mathrm{vh}}\right)={e^{\Delta {S}_{\mathrm{vh}}}}^{/ kT}{e^{-\Delta {H}_{\mathrm{vh}}}}^{/ kT} = {e^{-\Delta {G}_{\mathrm{vh}}}}^{/ kT} $$

(3.12)

Therefore, the number of elements does not alter the equation form of vacancy concentration for pure metal. For a non-equimolar and non-ideal solid solution in which atomic size and bonding are different between elements, the equation form is still the same except using its own excess enthalpy, excess entropy, and excess free energy. This demonstrates that the equation of vacancy concentration for each solid-solution phase of HEAs is essentially the same as that for pure metals. Does lattice distortion of multiple-element matrix affect the excess enthalpy? The answer is that lattice distortion would be very small and negligible since lattice distortion energy per mole of atoms as shown in Table 3.6 is far below the heat of formation of vacancy per mole. The largest distortion energy, 500 J/mole, of quinary alloy is about five thousandth of the formation enthalpy of vacancy as seen in Table 3.4. This is reasonable because the formation of a vacancy needs to break chemical bonds with its neighboring atoms whereas lattice distortion only changes bond length or angle. In brief, the concept of vacancy concentration for conventional alloys still holds for HEAs.

3.4.4 Solutes

Solute atoms come from the impurity inherent from the extraction and fabrication processes or intended alloying from initial alloy design for improving properties. In HEAs, most phases are of solid solutions (disordered or partially ordered). In each solid solution, a variety of elements are mixed in the matrix which can be regarded as a whole-solute matrix. Larger atoms are mostly in compressive strain or stress whereas smaller atoms mostly are in tensile strain or stress. Thus, each lattice point of the whole-solute matrix has atomic-scale lattice strain and the whole lattice suffers severe lattice distortion as compared with conventional lattice with a major element. As mentioned previously, besides atomic size effect, different crystal structure tendencies and different bondings among unlike neighboring atoms would influence atomic position and cause further distortion. However, due to the tendency to lower the total free energy, lattice strain at each site would be relaxed by adjusting the relative positions of neighboring atoms.

• 1. Stress field around an atom

Despite the relaxation, the atomic-scale stresses exist in the whole-solute matrix. Egami has pointed out the existence [54, 55]. Even in amorphous structure, such atomic-scale stresses still exist. Although such atomic-scale stress varies from site to site in the lattice, some in compression and some in tension, local balance between their stresses should be attained in the steady state. That is, their overall contribution to microscale or macroscale stress is zero on average basis. Because the stress field around a solute atom would be shielded or eliminated by the stress field of surrounding atoms, the long-range atomic stress of any atom would be small. That is, the stress around an atom is atomic scale or short range.

• 2. Distortion effect on lattice constant

As the whole-solute matrix of HEA solid solution is a mixture of various elements, the lattice constant of the real crystal structure would have some relation with the lattice constant of pure element. For the simplest case of random solid solution, is Vegard’s law valid? Vegard’s law in a binary A-B solid solution can be expressed as

$$ {a}_{\mathrm{A}\mathrm{B}} = \left(1-x\right){a}_{\mathrm{A}} + x{a}_{\mathrm{B}} $$

(3.13)

where x is the fraction of component B. Vegard’s law can be regarded as the rule of mixtures, which was proposed based on his observation on continuous solid solution of ionic salts, such as KCl-KBr. However, this law is not strictly obeyed by metallic solid solutions [6]. But the reason for the deviation is still unclear. For this, we need to consider the effects of lattice distortion and excess chemical bonding. It is proposed that lattice distortion could expand the average lattice predicted by Vegard’s law and stronger excess chemical bonding would give shorter bond length and thus smaller lattice constant. The superposition of these two main effects determines the real lattice constant. For the first effect, let’s consider the equilibrium structure without lattice distortion and used pure Ni as example. Figure 3.13a shows the equilibrium case in which atoms in pure Ni are in their equilibrium positions at the minimum of potential well, bond strengths are maximized, and its lattice constant attains the minimum. Figure 3.13b shows the perturbation case. In this structure, any offset of an atom from the minimum of potential well would decrease local bond strength and increase overall bond length or lattice constant. In other words, a distorted lattice with zigzag atomic directions and planes would disturb the original equilibrium lattice to have a certain expansion of volume. In the extreme case, amorphous solid could have a lower density than crystalline solid by 0.3–0.5 %.

Fig. 3.13

(a) Equilibrium structure of pure Ni without lattice distortion and (b) expanded structure of pure Ni with lattice distortion

This thinking could be applied to binary solid solution. Because the average lattice predicted by Vegard’s law is a linear combination of two component lattices and total free energy would be raised by atomic size difference or other differences in electrochemical properties, a certain offset from the composite minimum position of potential well is needed in order to relax total free energy. Under such a lattice distortion, the effective bond strength is reduced and lattice constant is increased. Similarly, for Ni-Co-Fe-Cr-Mn alloy series which is near-ideal FCC solid solution, the lattice distortion ${\varepsilon}_x^2={\varepsilon}_y^2={\varepsilon}_z^2={\displaystyle \sum_i{x}_i}{\varepsilon}_i^2$ increases with increased number of elements explaining why the lattice constant of real crystal structure generally has more deviation from that predicted by Vegard’s law. The deviations from binary to quinary alloys are −5.66 × 10⁻⁴, 7.91 × 10⁻³, 7.86 × 10⁻³, and 1.43 × 10⁻², respectively (see Table 3.6). It should be mentioned that the quinary alloy has a negative mixing enthalpy −4.16 kJmol⁻¹ which would reduce bond length and thus lattice constant. Hence, the increased lattice constants as compared with ideal average lattice constant indeed give a strong suggestion that lattice distortion has the effect to expand the lattice (see the quinary alloy in Fig. 3.14).

Fig. 3.14

(a) Equilibrium structure of CoCrFeMnNi without lattice distortion and (b) expanded structure of CoCrFeMnNi with lattice distortion

3.4.5 Dislocations

• 1. Lattice distortion and pinning effect on dislocation energy

Dislocations exist in metals by various sources including nucleation and growth of solid during solidification and cooling, collapse of quenched vacancies, stress concentration, and multiplication of dislocation sources [69]. However, due to severe lattice distortion in the whole-solute matrix, dislocation energy, typically written as Gb ² for conventional alloys (G, shear modulus; b, Burgers’ vector), needs to be modified by considering two factors: the interaction between dislocations and surrounding atoms and lattice distortion energy level. If no interaction occurs between dislocations and nearby atoms, the stress field equations are the same as that in a perfect lattice in the literature [69]. However, interaction would occur for the sake of reducing total energy if thermal activation and time are sufficient to let flexible dislocation and nearby atoms to adjust their relative position to lower total energy and form dislocation atmosphere. Since this adjustment does not require long-range diffusion and could be achieved by pipe diffusion in the core with the abundant solutes everywhere, such an adjustment within several atomic distances is possible at relatively lower temperature than that for conventional alloys. This is unique for HEAs since conventional matrix with one major element would require long-range diffusion to attract solutes from faraway regions toward dislocation cores and thus higher temperature to enhance the diffusion to form atmospheres.

The core radius of a dislocation, in which stress and strain do not follow linear elastic mechanics, is usually thought to be 5b (i.e., 5 atoms in the radius), and the stress built up in the core is theoretical stress which is around Gb/30 [70]. This core energy could account for one-tenth of dislocation energy [69, 70]. In the core, large atoms such as Cr and Fe could migrate into tensile region beneath the edge dislocation whereas smaller atoms could diffuse into compressive region just above dislocation line through fast dislocation-pipe diffusion, as shown in Fig. 3.15. Although such a rearrangement could release the overall energy, the stress field around a dislocation is essentially unchanged because it is a long-range field formed initially with dislocation and not affected by the short-range interaction in the core.

Fig. 3.15

Atomic configurations around a dislocation: (a) before relaxation and (b) after relaxation. Relaxation means that overall strain energy is lowered by rearrangement of different atoms. Dashed circle presents the range of dislocation core

On the other hand, lattice distortion could reduce the effective energy of dislocations since the defect energy is a relative difference of the energy level between defects (vacancy, dislocation, grain boundary, and surface) and lattice. This means when we create the defect by doing work, the work would be smaller in distorted lattice than in perfect lattice without distortion energy. Alternately, when two opposite dislocations cancel with each other and return to distorted lattice, the energy release would be lower. Therefore, the dislocation energy is reduced and becomes smaller than the expected Gb ². Here, quinary alloy CoCrFeMnNi is chosen for the estimation. As seen in Table 3.6, the core volume per unit length (m) of a dislocation in this alloy is

$$ \mathrm{Core}\ \mathrm{volume}\ \mathrm{per}\ \mathrm{unit}\ \mathrm{length}={(5b)}^2\pi \times 1\kern0.5em \mathrm{m} = 5.12\times {10}^{-18}\;{\mathrm{m}}^3 $$

(3.14)

The distortion energy of the same volume in the distorted lattice without dislocations is

$$ \mathrm{Equivalent}\ \mathrm{distortion}\ \mathrm{energy}/\mathrm{m}=5.12\times {10}^{-18}\;{\mathrm{m}}^3\times {\rho}_v\times {U}_{0\mathrm{per}\ \mathrm{mole}}=3.58\times {10}^{-10}\;\mathrm{J}/\mathrm{m} $$

(3.15)

$$ \mathrm{Dislocation}\ \mathrm{energy}/\mathrm{m}=G{b}^2-3.58\times {10}^{-10}\;\mathrm{J}/\mathrm{m}=4.3\times {10}^{-9}\;\mathrm{J}/\mathrm{m}-3.58\times {10}^{-10}\;\mathrm{J}/\mathrm{m}=3.94\times {10}^{-9}\;\mathrm{J}/\mathrm{m} $$

(3.16)

Thus, lattice distortion in the quinary alloy CoCrFeMnNi reduces about one-tenth of the dislocation energy. In brief, the two factors could lower dislocation energy to a certain extent: easy relaxation effect to lower the overall strain energy (but un-estimated) by forming atmosphere and distorted lattice effect to lower the dislocation energy by increasing the energy level of lattice. For other systems with larger atomic size difference and thus U _{0 per mole}, the dislocation energy would be significantly lower. It should be mentioned that the stress required to form a dislocation is similar to the theoretical shear stress to shear a crystal along slip plane. The theoretical stress is about G/15. In real crystals having dislocations to aid the slip deformation, the actual stress required to shear only ranges from 1/100 to 1/10,000 of theoretical shear stress. This means, even if the above two factors result small energy reduction of dislocation energy, their effects on real strength can be significant. Therefore, compared to the undistorted lattice, dislocations in the whole-solute matrix have a relatively lower energy state which are more difficult to move in the slip plane, not only to overcome strong atmospheres but also to overcome the abundant solute obstacles even after releasing from atmospheres. This will be further discussed in the later section of solution hardening. However, it should be pointed out that more fundamental research to derive exact dislocation energy by simulation or theoretical calculation is required in the future. Direct observations or indirect evidences are also required to check the existence of strain aging (solute pinning on dislocations).

• 2. Vitual force on dislocations under applied stress

The virtual force that results from a shear stress applied to a conventional crystal needs to be checked for HEA crystal. Since the virtual force is derived by equating the external work done by applied stress with the internal work done by the virtual force, which does not concern with lattice distortion, the virtual force equation for dislocations in HEAs is the same as that in conventional alloys. That is, all the virtual force per unit length on screw, edge, or mixed dislocations in the slip plane is

$$ F={\tau}_{\mathrm{o}}b $$

(3.17)

where τ _o is the applied shear stress in parallel with Burgers’ vector. If the stress is not parallel with Burgers’ vector, the virtual force could be calculated by a general equation called Peach-Koehler equation: the cross product of stress tensor and Burgers’ vector [69, 70].

3.4.6 Stacking Faults

• 1. Lattice distortion and Suzuki effect on stacking fault energy

Stacking faults relate with dislocations. Discontinuities in the stacking order of atomic planes are called stacking faults. If a stacking fault terminates in the crystal, its boundary is a partial dislocation. In FCC, it could be Shockley partial dislocations or Frank partial dislocations [69]. Stacking fault can be regarded as a planar defect and have a surface energy because the atoms on either side of a stacking fault are not in normal positions and lose some bonding energy. The stacking fault is in fact a HCP layer with four atomic layers. However, strain fields and chemical tendency in FCC or HCP structure of those atoms near or along stacking fault could be used to lower the stacking fault energy (SFE) by segregation and adjusting their positions if suitable thermal energy is provided. This is the so-called Suzuki interaction. Conventionally Suzuki interaction is used for explaining the reduction of SFE due to alloying effect. For HEAs, this interaction also holds true and can be considered as one factor in lowering SFE. In the whole-solute matrix, this local adjustments or rearrangements of atoms will change the composition in atomic-scale range (without long-range diffusion as in the conventional matrix) but might not change it when measured in nanoscale or larger range. Therefore, the proof on such an interaction requires very careful analysis on identifying the segregation.

Besides Suzuki interaction, there is in fact another factor, lattice distortion energy, in reducing SFE for HEAs. Figure 3.16 shows the schematic diagram for the effect of Suzuki interaction and lattice distortion, in which different free energy levels of stacking fault, perfect lattice without distortion, and distorted lattice are shown. The hypothetical lattice without distortion means solute atoms simply occupy lattice sites and do not cause the lattice distortion. The energy level of stacking fault is assumed to be constant although it could be somewhat lower by relaxation in distorted lattice. The stacking fault energy in such a lattice is γ _perfect. After Suzuki interaction which releases some energy, U _suzuki, of stacking fault, the stacking fault energy is reduced. In reality, lattice is distorted by solute atoms and has a higher energy level due to distortion energy. As a result, real SFE, γ _real, is even lower than γ _perfect − U _suzuki. Therefore, as all atoms in the HEA matrix are solutes, the SFE in HEA matrix is inherently low because of Suzuki interaction and lattice distortion energy. However, Suzuki interaction occurs when thermal energy is suitably provided to cause the diffusion for segregation. Thus, suitable temperature is required. Low temperature could not afford the diffusion for segregation whereas high temperature would destroy the interaction or segregation toward randomness. If a specimen is processed to avoid the suitable temperature range for Suzuki interaction, SFE becomes γ′_real which is larger than γ _real by U _suzuki.

Fig. 3.16

Diagram shows the effect of Suzuki interaction and lattice distortion on stacking fault energy. Different free energy levels of stacking fault, perfect lattice without distortion, and distorted lattice are compared

As Suzuki interaction and lattice distortion energy depend on the constituent elements in the matrix, the relative positions of energy levels and thus real SFE also depend on compositions.

It should be pointed out that lattice distortion energy effect should be also considered as the second factor in reducing SFE of conventional alloys such as FCC Cu-Al bronze and FCC Cu-Zn brass in considering the origin of interface energy mentioned above. The additions of Al and Zn into the copper matrix have been found to effectively lower SFE. In view of the second factor, the significant atomic size difference between Al (1.43 Å) and Cu (1.28 Å) and between Zn (1.39 Å) and Cu and other differences in crystal structure tendency and chemical bonding can cause lattice distortion and decrease SFE.

• 2. Stacking fault energies measured for HEAs

By using XRD patterns taken from powder samples, stacking fault energy of the equiatomic alloy series with single FCC structure, Ni, NiCo, NiCoFe, NiCoFeCr, and NiCoFeCrMn has been measured [68]. The powders were obtained from two bulk samples by using a high-speed steel rasp. One is cold-rolled sample obtained by cold-rolling the sheet homogenized at 1100 °C for 6 h and quenched. The cold reduction is 70 % so that fully work hardening is ensured. The other is full-annealed sample which is obtained by heat-treating the cold-rolled sample at 1100 °C for 10 min. Table 3.7 shows the related data for deriving stacking fault energy by using related equations as reported in the literature [71]. The SFE, 108 mJ/m², of pure Ni obtained by this XRD method agrees well with that, 128 mJ/m², obtained by TEM node method in the literature [72, 73]. Figure 3.17 shows the variation of SFE with the number of composing elements. Stacking fault energy decreases with increasing number of elements. It is noted that there is a large reduction of SFE from Ni to NiCo and NiCoFeCrMn has the lowest SFE, 6.2 mJ/m². As SFE of FCC Co is 15 mJ/m² [73], the SFE value, 40.8 mJ/m², of NiCo in Table 3.7 is reasonable since the SFE predicted by the rule of mixture is 71.5 mJ/m². Suzuki interaction and lattice distortion energy in NiCo alloy would cause a further reduction of SFE. In fact, the value is similar to that found for NiCo in the literature [72].

Table 3.7 Related data and related equations for deriving stacking fault energy by XRD method [61]

Fig. 3.17

SFE as a function of the number of composing elements from Ni to NiCoFeCrMn alloy [68]

Koch’s group used mechanical alloying method to prepare another equiatomic alloy series and derived stacking fault energy by using XRD method and different simulations [74]. They found that SFE decreases with increased number of elements, and five-element alloy has the lowest SFE (see Fig. 3.18). However, there exists a larger difference between the SFEs of equiatomic CoCrFeMnNi in Figs. 3.17 and 3.18. Hence, further research is required for clarification. In addition, by varying Ni content and Cr content, Kock’s group found that Ni₁₄Fe₂₀Cr₂₆Co₂₀Mn₂₀ alloy has an extremely low SFE 3.5 mJ/m² [74]. If one plots SFEs as a function of atomic size difference (see Eq. 3.1) for these Co-Cr-Fe-Mn-Ni alloys, Fig. 3.19 is obtained revealing the trend which rationalizes the combined effect of increased energy level of the distorted matrix and the increased strain energy relief of stacking fault by in situ atom position adjustment since larger atomic size difference could enhance these two factors. However, all these phenomena require new model and theory to explain the mechanisms.

Fig. 3.18

Stacking fault energies of equiatomic FCC metals from pure Ni to NiFeCrCoMn measured by XRD methods combined with different simulations [74]

Fig. 3.19

Stacking fault energies [74] and atomic size differences of non-equiatomic and equiatomic Co-Cr-Fe-Mn-Ni alloys

• 3. Effect of stacking fault energy on slip bands

Stacking fault energy is very important in affecting dislocation movement, dislocation substructure, twinning, strength, strain hardening, ductility, climb, creep, stress corrosion, and hydrogen embrittlement. For example, low SFE will give larger separation between partial dislocations. For the stacking fault bounded by Shockley partial dislocations in FCC structure, the cross-slip or double cross-slip process becomes more difficult since far-spaced partial dislocations need to combine into complete screw dislocations for finishing such processes. The resulting dislocation structure will be more uniform in planar array and slip bands are finer and more uniform. In addition, both the stress and energy required to form twins is lower because a coherent twin boundary is basically half-thickness of a stacking fault. Figure 3.20 shows the optical micrographs of the slip bands in grains after cold-rolling with a reduction of 50 % from Ni to NiCoFeCrMn alloy [68]. It can be seen under such a reduction that there is essentially one slip system operated. However, the average spacing between slip bands first decreases and then increases with increasing number of elements. Their spacings are 15.8, 9.0, 3.3, 5.4, and 6.0 μm. As dislocation etching pits represent dislocation, dark slip bands in Ni, NiCo, and NiCoFe suggest that dislocation density in slip bands is high enough to let pits seen under optical microscope. This means the plastic strain in their slip bands is also large. However, NiCoFe has the densest slip bands, which is helpful to release the strain concentration in each slip band and helpful to enhance ductility. It is noted that NiCoFeCr and NiCoFeCrMn alloys have discrete etching pits in slip bands and between slip bands. The spreading of etching pits is obviously large in NiCoFeCr as compared with NiCoFeCrMn alloy. However, because NiCoFeCrMn alloy has much smaller SFE than that of NiCoCrFe, nanotwinning deformation is much easier to operate especially between slip bands. To sum up, decreased SFE from Ni to NiCoFeCr could increasingly inhibit cross-slip and double cross-slip and thus enhance strain hardening and the activation for other slip bands. Higher strain hardening and lesser strain concentration in turn delay the fracture and improve the ductility. On the other hand, low SFE of NiCoFeCr and NiCoFeCrMn is expected to induce nanotwinning deformation, in which NiCoFeCrMn would be much easier than NiCoFeCr. So, a portion of strain is expended in nanotwinning which is expected to form between slip bands. Similar phenomena could be observed in low SFE stainless steel such as 310S (Fe-25Cr-19Ni) having a SFE of 14/m² [71, 75]. This is why etching pits of NiCoFeCrMn are not so dense in between slip band. The large formation of nanotwinning (during rolling or tensile deformation at low temperatures) is especially beneficial for ductility due to large strain hardening and induced plasticity.

Fig. 3.20

Slip bands observed in the grains after cold-rolling with a reduction of 50 %: (a) Ni, (b) NiCo, (c) NiCoFe, (d) NiCoFeCr, and (e) NiCoFeCrMn [68]

As the cold-rolling reduction is increased up to 90 %, second slip systems are induced in deformed grains [68]. Coarse slip bands in Ni and NiCo become intersected and wavy. Fine slip bands in NiCoFe are also found to be interwoven. NiCoFeCr alloy has even fine and dense interwoven structure of slip lines. NiCoFeCrMn alloy has very fine network structure in which substructures with deformed subgrains and nanograins exist.

• 4. Texture of FCC NiCoFeCrMn alloy

Figure 3.21 shows the cross-sectional microstructure and texture of the NiCoFeCrMn after 90 % cold-rolling [76]. Figure 3.21a, b shows the EBSD (electron backscatter diffraction) image quality (IQ) maps overlaid with the typical FCC rolling texture components while Fig. 3.21c, d shows the (111) pole figures for two different regions, respectively. The IQ maps show submicron-cell structure. Thin shear band (marked by the arrow) inclined to the rolling direction (RD) about ~25° could be observed in region I. The HAGB (high-angle grain boundary) fractions in the two regions are similar. The orientation maps show strong presence of the brass ({110} < 112>; designated as B _S and highlighted in green), S ({123}< 634>; highlighted in yellow), and Goss ({110} < 001>; designated as G and highlighted in orange) components but very little presence of the copper orientation ({112} < 111>; designated as Cu and highlighted in red). The appearance of the (111) pole figures (Fig. 3.21c, d) clearly reveals the development of a predominantly B _S texture after 90 % cold-rolling. The volume fractions of the different texture components obtained from the two regions are very similar, which indicate that the microtexture in the HEA following heavy deformation is reasonably homogeneous brass texture. Besides the volume fraction of random components is 42 %, and that of brass component is the largest, around 22 %, among the rest components.

Fig. 3.21

(a) and (b) are IQ maps with overlaid orientations obtained from two different regions of 90 % cold-rolled NiCoFeCrMn; (c) and (d) are the corresponding (111) pole figures [76]

3.4.7 Grain Boundaries

• 1. Lattice distortion and local rearrangement effect on grain boundary energy

Grain boundaries are the interface between adjacent grains with different orientations. There are low-angle boundaries constructed with dislocation arrays, high-angle boundaries with disordered structure along with it, and coincident boundaries at specific misorientation angles. They all have interface energy because the energy level is higher than that of the matrix. Similar to stacking fault discussed in Sect. 3.4.6, the effective boundary energy of all kinds of grain boundary could be lowered by the segregation layer of solute atoms along boundaries and by the higher energy level of the distorted matrix as compared with the pure matrix. This means grain boundaries in HEAs are smaller in boundary energy and thus become more stable and difficult to migrate than that in conventional alloys during annealing. Furthermore, the driving force for grain coarsening is also lower in HEAs. All these are beneficial to have more stable grain structure at high temperatures. To understand the distortion energy effect on grain boundary energy, an extreme case of distorted matrix, that is, amorphous structure, could be used as an example. As high-angle boundaries except those specific orientations could be regarded as disordered interface layer in the matrix, any boundary line in amorphous structure would be completely disordered in atomic configuration and equivalent to other disordered structure besides boundary line. Thus, no boundary energy of the boundary line could exist. This is why amorphous structure has no grain boundaries.

• 2. Factors affecting grain and particle coarsening in HEAs

Consider a metal with an average grain size D and assume the polyhedral grains to be spherical for simplifying the calculation. Then for one unit volume, the total grain boundary area is

$$ {A}_{\mathrm{g}} = \left(1/2\right){D}^2\pi \left(1/\left({D}^3\pi /6\ \right)\right) = 3/D. $$

(3.18)

Thus, the total grain boundary energy per unit volume is

$$ {U}_{\mathrm{g}}=3\gamma /D. $$

(3.19)

Assume grains grow with an incremental size dD, the loss of U _g will be

$$ d{U}_{\mathrm{g}}=\left(3\gamma /{D}^2\right)dD. $$

(3.20)

Assume the virtual driving force on unit grain boundary area is F _g, then the work done by driving force is equal to the loss of U _g:

$$ \left(3/D\right)\ {F}_{\mathrm{g}}\kern0.2em dD/2=\left(3\gamma /{D}^2\right)dD. $$

(3.21)

This gives

$$ {F}_{\mathrm{g}}=2\gamma /D. $$

(3.22)

Since this derivation is only based on grain size and boundary energy, the result is equally applied to single-phase HEAs. It implies that driving force of grain growth is proportional to grain boundary energy and inversely proportional to grain size.

In reality, grain growth concerns with boundary migration. Assuming the mobility is M _g and grain growth rate is ν _g, the phenomenological equation becomes

$$ {\nu}_{\mathrm{g}}={M}_{\mathrm{g}}\kern0.2em {F}_{\mathrm{g}}. $$

(3.23)

The mobility of boundary is determined by the successful jumping rate of atoms across the boundary which has an energy barrier to overcome and thus lower energy barrier and higher temperature would result in higher mobility [61]. Besides these two factors in affecting mobility and growth rate, other structural factors solute segregation and precipitates along grain boundary also drag the boundary directly. The drag force F _d will cancel a portion of driving force and the above equation becomes

$$ {\nu}_{\mathrm{g}}={M}_{\mathrm{g}}\left({F}_{\mathrm{g}}-{F}_{\mathrm{d}}\right). $$

(3.24)

Because driving force is inversely proportional to grain size, it is apparent that a stable grain size is attained at the treating temperature when driving force is equal to drag force. This also implies smaller grain boundary energy and larger drag force would get a smaller grain size. It is well known that higher temperature could eliminate the segregation and second phase along boundaries (except oxides or similar stable phases) and might lead to abnormal grain growth. All these phenomena and phenomenological relations also hold true for single-phase HEAs.

However, there is something different between conventional matrix and the whole-solute matrix in HEAs. First, the grain boundary energy is inherently low in HEAs as discussed above. This would reduce the driving force and thus lower the growth rate. Second, the successful jumps across grain boundary would be more difficult in HEAs since many kinds of component are involved and need to cooperate to make the same composition of adjacent grains. This in turn lowers the mobility of boundary. Third, segregation along grain boundary is easy in HEAs since grain boundary has relatively higher diffusion rate than grain interiors and segregation to lower grain boundary energy could be obtained by atomic-scale rearrangement of solutes along grain boundaries, which might be accomplished even at room temperature within a suitable aging time. As a result, drag force is easy to be attained during grain growth and retard grain growth. In brief, the grain growth is effectively slower than conventional alloys with similar melting points. Several researches also reported such an observation on a typical FCC CoCrFeMnNi HEA [33, 76]. Liu et al. found the growth kinetics could be described by a power law of 3 (see Fig. 3.22), suggesting that grain boundary motion is controlled by a solute-drag mechanism. The activation energy for growth was about 321.7 kJ mol⁻¹ which is close to the highest activation energy, 317.5 kJ mol⁻¹ of Ni among the five elements as described in Sect. 3.2.3 [8]. This demonstrates that the grain boundary migration during grain growth is rate-controlled by the diffusion of slowest Ni atoms through lattice diffusion, instead of grain boundary diffusion as seen for conventional alloys. This is very particular in consideration of the smaller activation energy of AISI 304LN stainless steels, which is only about 150 kJ mol⁻¹ [33].

Fig. 3.22

(a) Grain size as a function of the annealing time for the CoCrFeMnNi alloy specimens at different temperatures; a linear relation between the cube of the grain size and time is observed. (b) Grain-growth constant, C, as a function of the reciprocal of absolute temperature. Activation energy is calculated [33]

In binary alloys, if an impurity has small solubility in the matrix, the relative segregation (or enrichment ratio) to grain boundary is large and causes slow grain growth rate. If an impurity has large solubility, the inhibiting effect on grain growth becomes small at the same content due to lesser segregation [61]. However, this phenomenon is not applied to HEAs with the whole-solute matrix, since grain boundaries in HEAs already have many different components to rearrange the best segregation to lower overall free energy. The rearrangement is mainly confined in the grain boundary layer with a typical width about 0.5 nm. That means the average composition in this layer would be similar to that in the grain interiors. For the case with minor impurity and alloying elements, the observation in binary alloy mentioned above could be applied if the whole-solute matrix is regarded as a pseudo-unary matrix. The minor elements having low solubility in the pseudo-unary matrix would segregate a large portion to enrich grain boundaries. But, they might bring brittleness to HEAs and need our precaution.

Phase boundary is the interface between two phases. In equilibrium, chemical potential of each component in both phases and their phase boundary are equal. But, the free energy level of both phases could be different with each other. Thus, the phase boundary energy could be regarded as the energy difference between the energy level of phase boundary and the arithmetic average of the energy levels of both phases. Similarly, lattice distortion in both phases raises their energy level and also might lower the phase boundary energy under no distortion effect. This would also affect the particle coarsening or phase coarsening in two-phase alloys.

3.5 Basic Mechanism of Sluggish Diffusion

For a multi-principal-element solid solution, the mechanism of substitutional diffusion is still vacancy mechanism except that the diffusion is sluggish and the kinetic process is lower due to larger activation energy of diffusion. This sluggish diffusion effect has been confirmed with the diffusion couple experiment on Co-Cr-Fe-Mn-Ni HEA system as discussed in Sect. 3.2.3 [8]. In this section, the sluggish diffusion was explained based on the distorted lattice. The distorted multi-principal-element lattice would have fluctuated lattice potential energy (LPE) for the migration of an atom from one site to site because each site is surrounded by different kinds of atoms and has different types of bonds. Consider an atom-vacancy pair (A-V) and their nearest-neighboring atoms in an FCC lattice, as shown in Fig. 3.23. The nearest-neighboring atoms of the A-V pair can be divided into three types. Type-1 (T1) atoms are adjacent to A (A ₁–A ₇), type-2 (T2) atoms are adjacent to V (V ₁–V ₇), and type-3 (T3) atoms are adjacent to both A and V (S ₁–S ₄). When atom A exchanges with vacancy V, four T3 atoms remain to be the neighbors of A, but the seven A − T1 bonds are broken and seven new A − T2 bonds are established instead. Therefore, when an atom migrates, the change in LPE comes from the interaction energy difference between A − T1 bonds and A − T2 bonds. As a result, this fluctuated LPE would let the diffusion of atoms be more difficult than that in the lattice with uniform LPE, as shown in Fig. 3.24. This is analogue to the driving of a car along a rugged road. The barrier is higher and the speed is lower than those along a smooth road. As for the self-diffusion of vacancies, the activation energy required is also lower than that in undistorted lattice with uniform lattice potential energy. By the same thinking, the interstitial diffusion of small atoms would be slowed down and its activation energy is higher in the distorted lattice although vacancy aid is not required.

Fig. 3.23

Illustration of an atom-vacancy pair (A−V) and their neighboring atoms in an FCC lattice: A _1–7, atoms adjacent to A only, type 1; V _1–7, atoms adjacent to V only, type 2; and S _1–4, atoms adjacent to both A and V, type 3 [8]

Fig. 3.24

Schematic diagram showing the fluctuation of lattice potential energy along the diffusion path for an atom in the lattice. Deep traps are indicated

High diffusion paths along dislocations and grain boundaries also exist in the whole-solute matrix in HEAs. In conventional alloy matrix, the diffusivity along dislocation, D _p, and that along high-angle grain boundaries, D _g, have similar order in magnitude because high-angle grain boundaries could be regarded as an array of dislocations with very small spacing between two neighboring dislocations. But both diffusivities are larger than those through defect-free lattice, D _l, at any temperature. For example, at 500 °C, D _p/D _l and D _g/D _l in silver are 2 × 10⁶ and at 1 × 10⁶, respectively [77, 78]. Moreover, its activation energy of diffusion in grain boundary is about 0.45 of that in the lattice. The increased diffusivity could be explained with the increased degree of opening in the defect structure. That means the jumping frequency of an atom in these defect structures is much higher than that of an atom in the lattice. Similar trend of diffusivity for lattice, dislocation, and grain boundary holds for the whole-solute matrix in HEAs although atom diffusion in such a distorted lattice is more difficult than that in undistorted lattice.

However, all the above discussions still need to be justified by more researches on different-structured HEAs, such as BCC and HCP. More rigorous mechanisms are also required. In addition, isotopic elements should be also incorporated in the diffusion couples for non-ideal solutions in order to get diffusion coefficients of each component and assist the understanding of mechanisms.

3.6 Plastic Deformation in HEAs

All basic processes for plastic deformation such as dislocation slip, twinning, and grain boundary sliding in conventional alloys are also seen in HEAs but their detailed mechanisms might be significantly different between conventional alloys and HEAs. This is at least because the whole-solute matrices in HEAs are distorted at all lattice points which directly affect the behaviors of plastic deformation.

3.6.1 Yielding and Serration Phenomenon

As discussed in Sect. 3.4.5, there are two factors in lowering dislocation energy: easy relaxation effect to lower the overall strain energy by forming atmosphere and distorted lattice effect to lower the dislocation energy by increasing the energy level of lattice. Compared with the undistorted lattice, dislocations require extra stress to overcome atmospheres and to overcome the whole-solute obstacles even after releasing from atmospheres. This lattice distortion effect is the structural factor contributing to solution hardening, in addition to other factors relating to excess chemical bonding, shear modulus difference, short-range order, and dipole interaction. If temperature is sufficiently low in inhibiting pipe diffusion, atmosphere could not automatically form around dislocations through aging. The extra stress to overcome atmosphere is absent. As diffusion increases with increasing temperature, the relaxation effect to form atmosphere becomes easier because of abundant solutes everywhere. This aging might increase the yield strength by an extra stress for dislocations releasing from atmospheres at room temperature. This might be used to explain the small load drops after yielding observed at 77 K, 293 K, and 473 K (not at higher temperatures) for fine-grained FCC CoCrFeMnNi alloy which received a recrystallization treatment at 1073 K for 1 h for obtaining a grain size of 4.4 μm [79]. In addition, the relaxation effect at higher temperatures could result in serration phenomena (dynamic strain aging) during deformation. However, at much higher temperatures, thermal vibration becomes too large to make successful structural relaxation, and serration behavior would disappear. This also explains why CoCrFeMnNi alloy displayed serration behavior on stress-strain curves at 673 K for three grain sizes: 4.4, 50, and 155 μm [79]. So, the relaxation behavior of HEAs is different from that in conventional alloys in which solutes are limited in concentration and require long-distance diffusion to release the strain energy and pin the dislocations.

3.6.2 Effect of Low Stacking Fault Energy on Ductility and Toughness

In fact, a perfect dislocation would tend to decompose itself into two Shockley partial dislocations with wide stacking fault in FCC HEA solid solution which generally has low stacking fault energy. As discussed in Sect. 3.4.6, this feature causes the cross-slip and double cross-slip of screw dislocations to be more difficult and tend to form a substructure characterized by banded, linear arrays of dislocations. This is because each double cross-lip could form a Frank-Reed source which in turn generates new dislocation loops in the slip plane. In contrast, high stacking fault metals tend to exhibit tangled dislocations and dislocation cell structure after deformation. Thus, deformation in HEA solid solution tends to be more uniform with more planar slips. This tendency gives an advantage in enhancing ductility because stress concentration on interface between the matrix and inclusions or on grain boundaries becomes smaller without coarse slip band impingement. In addition, less cross-slip gives smaller dynamic recovery and strain hardening. Both effects could be beneficial for the good ductility of FCC HEAs.

The inherent low stacking fault energy of FCC HEAs also enhances the nanotwinning deformation mechanism which benefits strain hardening rate and overall ductility. Basically, low SFE in FCC means that coherent twin boundary energy (one-half of SFE because a coherent twin boundary, e.g., C in ABCABCBACBA… stacking sequence, is similar to one-half of an intrinsic stacking fault, ABCABCBCABC… bounded by Shockley partial dislocations) and thus the critical stress for nucleation and growth are also low. On the other hand, the yield stress of FCC HEAs is increased by solution hardening and other strengthening mechanism, which make the movement of dislocation more difficult. As a result, the formation of deformation twinning becomes easier in FCC HEA solid solution under the competition between the two critical stresses required for twinning and slip deformations, respectively. By this competition, both low temperatures and high strain rates will enhance the nanotwinning deformation since the yield strength increases faster than critical stress for twinning. Twinning during deformation is very important to induce higher plasticity. Twin-induced plasticity steels (TWIP steels) are a famous example in which twinning causes high strain hardening rate and lets the onset of necking delayed to occur at higher strain according to Considere’s criterion. Therefore, FCC HEA solid solution generally has an excellent combination of strength and toughness. Otto et al. [79] observed the temperature effect on the mechanical properties of FCC CoCrFeMnNi HEA and found that yield strength, strain hardening, and ductility are increased as temperature decreases from 293 to 77 K. Moreover, Gludovatz et al. reported similar results as shown in Fig. 3.25 [80]. They also showed that CoCrFeMnNi HEA displays remarkable fracture toughness properties at tensile strengths of 730–1280 GPa, which exceed 200 MPa · m^1/2 at crack initiation and rise to >300 MPa · m^1/2 for stable crack growth at cryogenic temperatures down to 77 K. The alloy has toughness levels that are comparable to the very best cryogenic steels, specifically certain austenitic stainless steels and high-Ni steels. Wu et al. reported the temperature dependence of the mechanical properties of various equiatomic alloys which are subsets of the CoCrFeMnNi HEA [81]. The UTS and uniform elongation to fracture of all the equiatomic alloys such as CoCrNi, CoCrMnNi, and CoCrFeNi also increase with decreasing temperature, with the largest increase occurring between 77 and 293 K. To sum up, this phenomenon was attributed to a transition from planar-slip dislocation activity at room temperature to deformation by mechanical nanotwinning with decreasing temperature, which results in continuous steady strain hardening at cryogenic temperatures.

Fig. 3.25

Typical stress-strain curves obtained by tensile testing at 77, 200, and 293 K. Yield strength, ultimate tensile strength, and ductility (strain to failure) all increase with decreasing temperature [80]

Easy twinning has another advantage in producing abundant twins which will effectively reduce the grain size and increase the grain-size strengthening approximately at below recrystallization temperatures. Also, fine grain size could enhance superplasticity at above recrystallization temperatures by grain boundary sliding. Thus, low stacking fault energy of FCC HEAs is very beneficial for microstructure refining and property enhancement.

3.6.3 Deformation Mechanisms in BCC or HCP HEAs

The last two sections concern with the deformation behaviors in FCC HEAs. As for the dislocation behavior in BCC HEAs, the study is quite lack. This is because most BCC HEAs have high strength but brittle. The dislocation structure has been found in refractory BCC HEA HfNbTaTiZr in the as-cast state, as shown in Fig. 3.26 [82]. There is the presence of numerous dislocations, the majority of which are arranged in subgrain boundaries. In addition, pileups are observed and some dislocation reactions have led to the formation of hexagonal networks. This indicates that dislocations exist in the as-cast alloys, which suggests that plastic deformation could assist by dislocation movement. Senkov et al. reported that refractory BCC HEA HfNbTaTiZr has compressive fracture strain higher than 50 %. The microstructure observation on the cross section of compression-tested specimen revealed deformation twins and cracking along some grain boundaries as shown in Fig. 3.27 [9]. This further demonstrates that twinning is also a possible deformation mechanism. Although lesser investigations could be found for HCP HEAs, it is believed that basic deformation mechanisms are similar to conventional HCP alloys except suitable modifications mentioned above.

Fig. 3.26

TEM observations on refractory BCC HfNbTaTiZr HEA: (a) selected area diffraction (inset) indicating the [001] zone-axis pattern; (b) bright-field micrograph of the as-cast microstructure. Symbols highlight the presence of subgrain boundaries and hexagonal dislocation network [82]

Fig. 3.27

SEM backscatter electron image of a longitudinal cross section of the HIP’d Ta₂₀Nb₂₀Hf₂₀Zr₂₀Ti₂₀ alloy after compression deformation at room temperature [9]

3.6.4 Strengthening Mechanisms in HEAs

Strengthening mechanisms in physical metallurgy include solution hardening, strain hardening, grain-size strengthening, precipitation hardening, dispersion hardening, martensitic strengthening, and composite strengthening. Except martensitic strengthening, they have been also found in the literature on HEAs and HEA-related composites.

• 1. Solution hardening

For solution hardening, the whole-solute matrix inherently has a very large solution hardening effect when real strength (or hardness) and rule-of-mixture strength (or hardness) are compared. The ratio could be as high as 3–4 for HfNbTaTiZr [9] and NbMoTaW and VNbMoTaW [23]. This is surprising because such high strength could be attained only by solution hardening. However, the ratio is about 1–2 for FCC HEAs. This might be related to the fact that the distortion in FCC HEA is smaller than that in BCC HEA as discussed in Sect. 3.2.2. In the strengthening through the addition of one component to the whole-solute matrix, Lin et al. studied a series of refractory Al_0–1HfNbTaTiZr HEA and found the linear relation, $\sigma = 1031\kern0.5em + 26.1\ c\left(\mathrm{M}\mathrm{P}\mathrm{a}\right)$, between yield strength and atomic percentage, c, of Al, as shown in Fig. 3.28 [83]. They proposed that the strengthening effect of a certain element in a single-phase HEA alloy can be explained based on quasi-binary alloy concept. The fact of linearity is thus originated from the strengthening contribution per Al atom. Strong bonding factor in combination with atomic-size-difference factor (or lattice distortion) is the main contributor of Al addition to strengthening. However, a number of metals follow the less-effective c ^1/2 dependence of solution hardening with substitutional solutes and interstitial ones [84]. Although exponent from 1/3 to 1 was also observed in conventional metals, theoretical models for HEAs are required to be established.

Fig. 3.28

Effects of solute concentration of Al on the yield strength of the Al_xHfNbTaTiZr HEAs [83]

• 2. Grain-size strengthening

In grain-size strengthening, Liu et al. systematically investigated the grain growth behavior of FCC CoCrFeMnNi equiatomic HEA by cold-rolling and subsequently annealing at different temperatures [33]. One can see from Fig. 3.29 [33] that Hall-Petch relation also holds for this alloy. But it is noted that the hardening coefficient, 677 MPa μm^−0.5, is quite large since the upper bound of hardening coefficient in BCC, FCC, and HCP metals is about 600 MPa μm^−0.5. This suggests that grain boundary hardening efficiency in the current CoCrFeMnNi alloy is much higher. The reason might relate to the large strain hardening of this alloy [80]. Furthermore, Al_0.2CoCrFeMnNi alloy has even larger hardening coefficient, 2199 MPa μm^−0.5, because addition of Al provides larger lattice distortion and stronger bonding and thus larger work hardening [85]. This might be explained with Li’s theory. He explained that grain-size strengthening in fact arises from the strain hardening of the near-grain boundary regions due to the dislocation pumping from grain boundary ledges under the elastic incompatibility stresses between adjacent grains before macroyielding [86]. Therefore, larger strain hardening such as FCC HEAs would imply larger hardening coefficient.

Fig. 3.29

Hardness as a function of grain size in the CoCrFeMnNi alloy [33]

• 3. Strain hardening

Strain hardening is commonly observed in the deformation of HEAs. In FCC HEAs, slip and nanotwinning could be the main mechanisms because their stacking fault energies are effectively lower. Higher temperature and lower strain rate enhance the deformation by dislocation motion whereas lower temperature such as at subzero and higher strain rate such as forging and rolling, nanotwins are more pronounced in the deformed structure. It can be observed that both mechanisms can give high strain hardening. In the slip mechanism, low stacking fault energy makes dislocation cross-slip more difficult and thus delay dynamic recovery to cause softening. In the nanotwinning mechanism, grain-size strengthening due to the formation of nanotwins is involved during deformation. Both factors increase large strain hardening and thus result in enhanced ductility based on Considere’s criterion [79–81]. In BCC HEAs, twinning is less found during deformation suggesting its formation is difficult as compared with slip. Strain hardening is generally smaller than that of FCC HEAs [9]. This could be attributable to three factors: (1) high strength due to large solution hardening, (2) easy cross-slip to cause dynamic recovery, and (3) difficult twinning. The first factor relates to large lattice distortion which is similar to severe cold-work structure. The second and third factors relate to the lack of partial dislocations and many slip systems for cross-slip. Cryo-rolling might enhance twinning because the stress for dislocation glide is significantly increased. However, more researches for taking more data (including HCP HEAs and other structures) and building rigorous theories are required.

• 4. Precipitation, dispersion, and composite hardenings

Precipitation hardening is often observed in HEAs. To the first approximation, conventional theories on these are also applicable to HEAs. Precipitate shape, size, coherency, degree of ordering, shear modulus, and volume fraction are factors affecting the strengthening [86]. But, in HEAs, multi-principal-element matrix and multi-principal-element precipitates might be stronger than conventional ones and have higher strength level. Interface energy and strain field between precipitates and the matrix should be further considered. Dispersion hardening is obtained by adding hard particles to the alloy in the molten liquid, to the alloy by powder metallurgy, or to the alloy by internal oxidation [86]. Their strengthening mechanism is essentially similar to precipitation hardening for HEAs. Composite strengthening is obtained by in situ phase formation such as eutectic and eutectoid structure or by extrinsically adding large amount of second phases or reinforcements. Finer lamellae, fine particles, and fine fibers would provide higher strength. HEA-related hard metals such as sintered carbides and cermets with HEA binders have been reported [87, 88]. Wettability, interface bonding, morphology, grain size, distribution, volume fraction, and binder strength are needed to be considered. It is noted that HEA binders might change all these factors and thus properties. Understanding of the mechanisms is very important for improving properties.

3.7 Creep and Creep Mechanisms in HEAs

3.7.1 Creep Behavior and Extrapolation Method to Predict Creep

Creep deformation is a very important aspect for the materials used at high temperatures [84, 89–91]. A number of high-temperature failures are due to creep or creep plus fatigue since failures and insufficient yield strength and tensile strength could be observed instantly or in the early stage failure. A material creep at high temperatures means its dimension changes with time under a load. Creep test at constant load could give a creep curve, i.e., strain (ε) as a function of time (t). It typical displays three distinct stages after the initial rapid elongation: I (primary), II (secondary), and III (tertiary). The slope, dε/dt, of the curve is creep rate. In primary stage, the creep rate decreases with time; in secondary stage, the creep rate changes little and remains constant; and in tertiary stage, the creep rate increases rapidly with time until fracture occurs. In general, higher load will result in higher creep rate and shorten the time to rupture. In the intermediate stress range (10⁻⁴ < σ/G < 10⁻²; σ is applied stress and G is shear modulus), constant creep rate in stage II could be described by power law:

$$ d\varepsilon /dt=A\ {\sigma}^n{e}^{-Qc/RT} $$

(3.25)

where A and n are constants depending on creep mechanism and Qc the activation energy for creep. It should be noted that Qc is approximately equal to the activation energy for self-diffusion for pure metals and solid-solution alloys if T > 0.5 T _m.

Usually, an industrial equipment is designed to have a reasonable life for customers. For jet turbine, power plant turbine, and nuclear reactors, the reasonable lives are 10,000 h (~1 year), 100,000 h (~10 years), and 350,000 h (~40 years), respectively. To avoid the lengthy tests, the extrapolation methods have been developed. The Larson-Miller equation with the following form has been commonly accepted and used for the extrapolation:

$$ T\left( \log\ {t}_{\mathrm{r}}+C\right)=m, $$

(3.26)

where C is the Larson-Miller constant depending on the alloy, t _r is the time to failure, and m is the Larson-Miller parameter depending on stress. Thus, one can use the shorter rupture time obtained by creep testing at higher temperature to predict rupture time at lower temperatures under the same stress. It is note that higher m would be better by giving longer rupture time under the same stress.

3.7.2 Creep Mechanisms

The creep deformation mechanisms have been well-established and can be approximately grouped into four kinds [84, 89–91]:

• 1. Diffusion creep: σ/G < 10⁻⁴

This involves a flow of vacancies and atoms through the material. Two mechanisms are possible. Nabarro and Herring mechanism states that the vacancies move in such a way to produce an increase in length under the direction of applied stress. The grain boundaries could act as sources or sinks. Coble proposed another mechanism which is based on the diffusion along grain boundaries. The activation energies of both creep mechanisms are the self-diffusion activation energy in lattice and grain boundary, respectively. Coble mechanism is predominant for lower temperatures and small grain size where grain boundary is more important than bulk diffusion. Both mechanisms could be operated in parallel and creep rate is the summation of both creeps. The summation equation is [84]

$$ d\varepsilon /dt={A}_{\mathrm{NH}}\left({D}_{\mathrm{L}}/{d}^2\right)\left(\sigma \Omega /kT\right)+{A}_{\mathrm{C}}\left({D}_{\mathrm{GB}}\kern0.5em \delta /{d}^3\right)\left(\sigma \Omega /kT\right) $$

(3.27)

where D _L and D _GB are diffusion coefficients of lattice and grain boundary, respectively. Ω is the atomic volume, d is grain size, and δ is grain boundary thickness. Thus, Coble creep is more sensitive to grain size.

• 2. Dislocation creep: 10⁻⁴ < σ/G < 10⁻²

This also involves vacancy diffusion which assists dislocations to overcome obstacles by climb during their glide, called climb-plus-glide mechanism. Since the rate of climb is determined by the rate at which the vacancies arrive at (as vacancy sinks) or leave (as vacancy sources) the dislocation, higher rate of climb process enhanced by larger stress and higher temperature would enhance dislocation climb and glide and cause higher creep rate. The creep rate in this stage is described by power law as mentioned above. For pure metals in which dislocation climb is easier, glide contributes most of creep strain and becomes the rate-controlling process; n is commonly about 5 and can be derived as in the following formula based on the balance between softening mode and hardening mode [91]:

$$ d\varepsilon /dt={A}^{\prime }{\left({\gamma}_{\mathrm{SF}}/Gb\right)}^3{\left(\sigma /G\right)}^5{e}^{-Qc/\mathrm{R}\mathrm{T}} $$

(3.28)

where A′ is a constant and γ _SF is the stacking fault energy (SFE). This mechanism is also evidenced by the formation of dislocation cell substructure observed by TEM and same cell size remains during stage II creep but inversely proportional to applied stress.

Sherby and Burke further divided solid-solution alloys into two classes with different mechanisms [89, 91]. In class I alloys, dislocation glide is controlled by the drag of solutes and n is about 3, such as in Ni-Au binary system with larger atomic size difference. In class II alloys with small atomic size difference such as Ni-Fe, Ni-Co, and Ni-Cr, the creep is controlled by dislocation climb as in pure metals; thus n is also about 5.

• 3. Dislocation glide: σ/G > 10⁻²

At high stress, power law breaks down and dislocation climb is replaced by dislocation glide which does not involve diffusion. Thermally activated dislocation glide is the rate-controlling step. When a dislocation encounters the obstacles, thermal energy is required to overcome the obstacles with energy barrier U ₀. Applied stress could provide a work to reduce the thermal energy required to overcome the barriers. Thus larger stress and higher temperature could increase such “dislocation glide” creep. This process occurs from low temperature to high temperature [84, 89, 90].

• 4. Grain boundary sliding

Grain boundary sliding occurs during the stage II to accommodate the grain shape change under creep strain. Smaller steady-state creep rate in stage II also has smaller grain boundary sliding. But, it becomes important in stage III with higher creep rate because it causes intergranular crack initiation and propagation. As grain boundary slides, diffusional mass flow is required to accommodate the incompatibility between grains. When this is not sufficient, voids at grain boundaries will form. However, single-crystal components do not have grain boundary sliding and have improved creep resistance [84, 89, 90].

3.7.3 Potential of HEAs to Have Improved Creep Resistance

Based on the above creep mechanisms, different factors could be considered to increase creep resistance and rupture life. Combining the positive factors would have superposition effect on creep resistance. Following factors are thus discussed to find the potential of HEAs to get improved creep resistance.

• 1. Sluggish diffusion factor

As mentioned above, for both diffusion and dislocation creeps, steady-state creep rate is directly related to the diffusion rate in the alloy. Activation energy for creep is essentially equal to that for diffusion. In this regard, sluggish diffusion in HEAs has the benefit to have a better resistance to creep. Similarly, grain boundary sliding is also inhibited because diffusion in the vicinity of grain boundaries to support the diffusion and dislocation creeps is sluggish. This leads to enhanced resistance to creep. In addition, the component having the slowest diffusion rate could become the rate-determining component in creep. This demonstrates the benefit from HEA composition which contains appreciable amounts of major elements. If the slowest component is added, its power to determine the creep rate would be significant. In refractory BCC-type HEAs which have a common melting point over 2000 °C, all these sluggish diffusion effects might compensate the higher diffusion rate in the open-packed structure of BCC matrix.

• 2. Low stacking fault energy factor

Solute addition has been found to lower the SFE such as Cu-Al bronze and Cu-Zn brass due to interactions between solutes and stacking fault. It is well known that low stacking fault energy of pure metals and solid-solution-strengthened alloys have low creep rate [91, 92]. This trend can be explained because low SFE causes the dislocation difficult to overcome obstacles by cross-slip. This makes the dislocation mainly use climb process to overcome the obstacles. Although the actual model/mechanism is still not clear, this trend suggests that low stacking fault energy has the advantage in reducing creep rate. As FCC-HEAs have quite low stacking fault energy, they have the potential to have a better creep resistance.

• 3. Atomic size difference factor

In polycrystalline nickel, solid-solution strengthening has been found to increase the time to fracture under the same stress. In addition, larger atomic size difference gives larger creep resistance (higher stress at the same stage-II strain rate). Even larger atomic size difference could reduce stress component from five to three as mentioned above. Furthermore, higher content of solutes gives smaller creep rate [91]. Based on the same trend, it appears that multi-principal-element solid-solution phases in HEAs would be beneficial to the creep resistance because they essentially possess the whole-solute matrix and have solute-dislocation interaction everywhere.

• 4. Precipitate factor

In nickel alloys, γ′ phase not only enhances high-temperature strength but also increases creep resistance [91]. Higher volume fraction of γ′ phase could increase creep resistance. For example, the Nimonic 80A, 90, 105, and 115 alloys having γ′ fractions of 0.17, 0.18, 0.32, and 0.62, respectively, also have improved creep resistance. The temperature of the last alloy for 1000 h creep life at 137 MPa is higher than the first by about 120 °C. In addition, lattice misfit between γ′ phase and γ matrix and solvus temperature of γ′ phase are important factors for creep resistance [91]. Small lattice misfit means less coarsening rate of γ′ precipitates and higher solvus temperature means higher thermal stability of γ′ phase at higher working temperature. As different solute elements have different partitions between γ′ phase and γ matrix affecting lattice misfit, shear modulus, coherency, and stability, how to design high-entropy superalloys based on conventional superalloys is a good research topic to obtain improved properties.

• 5. Carbide and boride factors

Small addition of boron and carbon for forming boride and carbide particles could increase the resistance of grain boundary sliding and thus improve creep resistance. For example, Che and Knowles [91] tested an experimental second-generation superalloy in creep at 950 °C and 290 MPa; addition of 0.09 wt.%C and 0.01 wt.%B could improve the rupture life from 10 h to 100 h. This is due to small carbide M₂₃C₆ formed along grain boundaries. This method is also required for improving creep resistance of polycrystalline HEAs.

Up to 2015, direct data on creep properties of HEAs are lack in the literature. He et al. reported the steady-state flow behavior of CoCrFeMnNi HEA in strain-rate jump tension tests at temperatures ranging from 1023 to 1123 K (~0.65–0.7 T _m) [93]. They used the power law Eq. 3.24 to fit flow behavior with stress and temperature shown in Fig. 3.30. Two regions, region I with a low stress exponent at the low strain rates (or stresses) and region II with a high stress exponent at the high strain rates (or stresses), are observed. The activation energies are 284 kJ/mol in region I and 333 kJ/mol in region II. They emphasized that these values are comparable to the activation energies for lattice diffusion in the FeCoNiCrMn alloy [8], for example, Ni (317.5 kJ/mol), Cr (292.9 kJ/mol), and Mn (288.4 kJ/mol). The stress exponent about 5 in region II suggests that the dominant deformation process is dislocation climb. The activation energy around 330 kJ/mol can be rationalized by that (317.5 kJ/mol) of the slowest-diffusing species Ni which controls the rate process. On the other hand, the stress exponent about three in region I suggests that the mechanism is the drag of gliding dislocations. However, the lower activation energy, 284 kJ/mol, is difficult to rationalize by the slowest Ni. But when region I in Fig. 3.30 is rechecked, an activation energy same as region I might be expected. This again confirms that rate controlling is still the slowest Ni.

Fig. 3.30

(a) Steady-state strain rate as a function of the true stress on a double logarithmic plot shows apparently two deformation regions (marked as region I and region II) and (b) the steady-state strain rate vs. the inverse of temperature on an Arrhenius plot showing the apparent activation energy of ~280 kJ/mol for region I and ~330 kJ/mol for region II, respectively

Besides, the measurement of hot hardness to see the softening resistance at high temperatures could provide an indicator to compare creep resistance between materials [94]. In addition, indentation creep test is also a way to compare the creep resistance [94–96]. Figure 3.31 shows the plots of hot hardness vs. temperature for Al _x CoCrFeNi cast alloys (x = 0–1.8) from room temperature to 1273 K [94]. In this alloy series, Al_0–0.3 alloys form single FCC structure. Al_0.5–0.9 alloys form FCC plus BCC mixture in which BCC phase further decomposes into modulated spinodal structure. Al_0.9–1.8 alloys form complete spinodal structure [94, 97].

Fig. 3.31

Hot hardness vs. temperature plots for Al_xCoCrFeNi alloys (x = 0−1.8) from room temperature to 1273 K [94]

Although hot hardness represents the strength at high temperatures, their variation could provide information about deformation mechanism. The hot hardness as a function of temperature can be represented by the following equation suggested by Westbrook [94, 95, 98–100]:

$$ H=A \exp \left(-BT\right) $$

(3.29)

where A is the intrinsic hardness or the value of hardness at 0 K and B is called softening coefficient. There are two set of constants A and B in low-temperature and high-temperature regions, respectively, suggesting a change in the deformation mechanism. In most metals and alloys, the transition temperature T _T is known to occur at about 0.5 T _m, where T _m is the melting point. It has been suggested that the deformation mechanism for low temperatures is slip and that for high temperatures (>0.5 T _m) is dislocation climb and glide [95, 99, 100]. The activation energy is also same as that of lattice diffusion. This is reasonable since at temperatures above T _T the indentation size does not attain a constant value after a certain time but continues to increase with time [99]. Because the plastic zone gradually built beneath the indenter, dislocations are generated in the interface and multiplied in the zone. As the diffusion is high, dynamic recovery occurs during indenter descending. This is mainly due to the climb of edge dislocations to overcome obstacles and the movement of jogged screw dislocations to facilitate cross-slip. If dwell time increases, creep deformation continues and hardness decreases.

Table 3.8 lists and compares hot-hardness transition temperature (T _T), homologous temperature (T _T/T _m), and two sets of intrinsic hardness (A) and softening coefficient (B): A _I and B _I for low temperatures and A _II and B _II for high temperatures, for Al _x CoCrFeNi cast alloys and three commercial alloys, T-800, In718, and In718H [94]. One can see that all the homologous temperatures are about 0.5 except that 0.66 of In718. Furthermore, the softening coefficients, B _I, are similar to those of the comparing alloys, whereas the softening coefficients, B _II, are in general smaller than those of the compared commercial alloys. This suggests that the present alloy system has a higher softening resistance than compared alloys at above T _T. The explanation is related to sluggish diffusion effect in the multi-principal-element solid-solution phases such as ordered BCC, disordered BCC, FCC, and sigma phases in the alloy series. It is noted that Al₀ and Al_0.3 alloys with single FCC phase have the lowest B _II values. This demonstrates the combined effects of the lower diffusion rate of FCC structure than other structures and the sluggish diffusion in the multi-principal-element matrix.

Table 3.8 Transition temperature (T _T), intrinsic hardness (A), softening coefficient (B), melting point, and homologous temperature of the Al _x CoCrFeNi alloys and commercial alloys T-800, In718, and In718H [94]

Indentation creep test was also used for measuring the hot hardness as a function of dwell time (5, 10, and 30 s) on Al_0.3, Al_0.5, Al_0.7, Al_0.9, and Al_1.5 alloys at 773, 873, 973, 1073, and 1173 K [94]. The results also confirm that the FCC Al_0.3 alloy has negligible creep and the Al _x alloys with x ≥ 0.5 display some creep at above T _T. This is consistent with the variation of the B _II values with aluminum content.

3.8 Conclusions and Perspective

This chapter emphasizes the four core effects of HEAs, which influence many aspects of physical metallurgy. By these core effects, many aspects have been discussed as detailed as possible with the author’s knowledge. One can see that their effects on microstructure and properties are mostly positive and encouraging. Alloy design utilizing these positive effects becomes very promising to develop application-oriented HEAs. Nevertheless, the discussion and explanation are still far from completeness. More experimental data and evidences and clear mechanisms and theories are required for HEAs in the future. When physical metallurgy from conventional alloys to HEAs is built, the whole understanding of the alloy world becomes realized.