Keywords

1 Introduction

During the past several decades, robust tracking control of nonlinear systems has attracted considerate attention [1–3]. Many significant approaches have been proposed. Among these methods, the feedback linearization approach is often employed. However, to use the feedback linearization method, the control matrix needs to be invertible. This requirement is usually hard to satisfy in applications.

Recently, adaptive dynamic programming (ADP) [4] is applied to give the optimal tracking control of nonlinear systems. In [5], Heydari and Balakrishnan proposed a single network adaptive critic architecture to obtain the optimal tracking control for continuous-time (CT) nonlinear systems. By employing the architecture, the control matrix was no longer required to be invertible. After that, Modares and Lewis [6] introduced a discounted value function for the CT constrained-input optimal tracking control problem. By proposing an ADP algorithm, the optimal tracking control was obtained without requiring the control matrix to be invertible either. Though the aforementioned literature provides important insights into deriving optimal tracking control for CT nonlinear systems, the ADP-based robust tracking control for CT uncertain nonlinear systems is not considered.

In this paper, an ADP-based robust tracking control is developed for CT matched uncertain nonlinear systems. By choosing a discounted value function for the nominal augmented error dynamical system, the robust tracking control problem is transformed into an optimal control problem. The control matrix is not required to be invertible in the present method. Meanwhile, a single critic neural network (NN) is used to approximate the solution of the Hamilton-Jacobi-Bellman (HJB) equation. Based on the developed critic NN, the optimal tracking control is obtained without using policy iteration. In addition, all signals in the closed-loop system are proved to be uniformly ultimately bounded (UUB) via Lyapunov’s direct method.

The rest of the paper is organized as follows. Preliminaries are presented in Sect. 2. The problem transformation is given in Sect. 3. Approximating the HJB solution via ADP is shown in Sect. 4. Simulation results are provided in Sect. 5. Finally, several conclusions are given in Sect. 6.

2 Preliminaries

Consider the CT uncertain nonlinear system given by

$$\begin{aligned} \dot{x}(t)=f(x(t))+g(x(t))u(t)+\varDelta f(x(t)) \end{aligned}$$
(1)

where \(x(t)\in \mathbb {R}^n\) is the state vector available for measurement, \(u(t)\in \mathbb {R}^m\) is the control vector, \(f(x(t))\in \mathbb {R}^n\) and \(g(x(t))\in \mathbb {R}^{n\times m}\) are known functions with \(f(0)=0\), and \(\varDelta f(x(t))\in \mathbb {R}^n\) is an unknown perturbation. \(f(x)+g(x)u\) is Lipschitz continuous on a compact set \(\varOmega \subset \mathbb {R}^n\) containing the origin, and system (1) is assumed to be controllable.

Assumption 1

There exists a constant \(g_M>0\) such that \(0<\Vert g(x)\Vert \le g_M\) \(\forall x\in \mathbb {R}^n\). \(\varDelta f(x)=g(x)d(x)\), where \(d(x)\in \mathbb {R}^{m}\) is unknown function bounded by a known function \(d_{M}(x)>0\). Moreover, \(d(0)=0\) and \(d_M(0)=0\).

Assumption 2

\(x_d(t)\) is the desired trajectory of system (1). Meanwhile, \(x_d(t)\) is bounded and produced by the command generator model \(\dot{x}_d(t)=\eta (x_d(t))\), where \(\eta :\mathbb {R}^n\rightarrow \mathbb {R}^n\) is a Lipschitz continuous function with \(\eta (0)=0\).

Objective of Control: Without the requirement of the control matrix g(x) to be invertible, a robust control scheme based on ADP is developed to keep the state of system (1) following the desired trajectory \(x_d(t)\) to a small neighborhood of the origin in the presence of the unknown term d(x).

3 Problem Transformation

Define the tracking error as \(e_\mathrm{err}(t)=x(t)-x_d(t)\). Then, the tracking error dynamics system is derived as

$$\begin{aligned} \dot{e}_\mathrm{err}(t)=&\ f(x_d(t)+e_\mathrm{err}(t))+g(x_d(t)+e_\mathrm{err}(t))u(t)\nonumber \\&-\eta (x_d(t))+\varDelta f(x_d(t)+e_\mathrm{err}(t)). \end{aligned}$$
(2)

In this sense, the robust tracking control can be obtained by giving a control such that, without the requirement of \(g(\cdot )\) to be invertible, system (2) is stable in the sense of uniform ultimate boundedness and the ultimate bound is small.

Denote \(z(t)=[e^{\mathsf {T}}_\mathrm{err}(t), x^{\mathsf {T}}_d(t)]^{\mathsf {T}}\in \mathbb {R}^{2n}\). By Assumption 2 and using (2), we derive an augmented system for the error dynamics as

$$\begin{aligned} \dot{z}(t)=F(z(t))+G(z(t))u(t)+\varDelta F(z(t)) \end{aligned}$$
(3)

where \(F:\mathbb {R}^{2n}\rightarrow \mathbb {R}^{2n}\) and \(G:\mathbb {R}^{2n}\rightarrow \mathbb {R}^{2n\times m}\) are, respectively, defined as

$$\begin{aligned} F(z(t))= \begin{bmatrix}f(x_d(t)+e_\mathrm{err}(t))-\eta (x_d(t))\\ \eta (x_d(t)) \end{bmatrix}, \ \ G(z(t))= \begin{bmatrix}g(x_d(t)+e_\mathrm{err}(t))\\ 0\end{bmatrix} \end{aligned}$$

and \(\varDelta F(z(t))=G(z(t))d(z(t))\) with \(d(z(t))\in \mathbb {R}^m\) and \(\Vert d(z(t))\Vert \le d_M(z(t))\).

In what follows we show that the robust tracking control problem can be transformed into the optimal control problem with a discounted value function for the nominal augmented error system (i.e., system (3) without uncertainty).

The nominal augmented system is given as

$$\begin{aligned} \dot{z}(t)=F(z(t))+G(z(t))u(t). \end{aligned}$$
(4)

The value function for system (4) is described by

$$\begin{aligned} V(z(t))=\int _{t}^{\infty }e^{-\alpha (\tau -t)} \big [\rho d_{M}^2(z(\tau ))+\bar{U}\big (z(\tau ),u(\tau )\big )\big ]\mathrm {d}\tau \end{aligned}$$
(5)

where \(\alpha >0\) is a discount factor, \(\rho =\lambda _{\max }(R)\), and \(\lambda _{\max }(R)\) denotes the maximum eigenvalue of R, \(\bar{U}(z,u)=z^{\mathsf {T}}\bar{Q}z+u^{\mathsf {T}}Ru\) with \(\bar{Q}=\mathrm{diag}\{Q,0_{n\times n}\}\), and \(Q\in \mathbb {R}^{n\times n}\) and \(R\in \mathbb {R}^{m\times m}\) are symmetric positive definite matrices.

According to [7], the optimal control for system (4) with the value function (5) is

$$\begin{aligned} u^{*}(z)=-(1/2)R^{-1}G^{\mathsf {T}}(z)V_{z}^{*} \end{aligned}$$
(6)

where \(V^{*}_{z}=\partial V^{*}(z)/\partial z\) and \(V^{*}(z)\) denotes the optimal value of V(z) given in (5). Meanwhile, the corresponding HJB equation is derived as

$$\begin{aligned} \rho d_{M}^2(z)+V_z^{\mathsf {*T}}\left( F(z)+G(z)u^{*}\right) -\alpha V^{*}(z)+z^{\mathsf {T}}\bar{Q}z+u^{\mathsf {*T}}Ru^{*}=0. \end{aligned}$$
(7)

Theorem 1

Consider the CT nominal system described by (4) with the value function (5). Let Assumptions 1 and 2 hold. Then, the optimal control \(u^{*}(x)\) given in (6) ensures system (2) to be stable in the sense of uniform ultimate boundedness and the ultimate bound can be kept small.

Proof

Taking the derivative of \(V^{*}(z)\) along the system trajectory \(\dot{z}=F(z)+G(z)u^{*}+\varDelta F(z)\), we have \(\dot{V}^{*}(z)=V_{z}^{*\mathsf {T}}\big (F(z)+G(z)u^{*}\big ) +V_{z}^{*\mathsf {T}}\varDelta F(z)\). Noticing that \(V_{z}^{*\mathsf {T}}\varDelta F(z)=-2u^{*\mathsf {T}}Rd(z)\) and by (7), we obtain \(\dot{V}^{*}(z)=-\rho d_{M}^2(z)-z^{\mathsf {T}}\bar{Q}z-u^{\mathsf {*T}}Ru^{*}-2u^{*\mathsf {T}}Rd(z) +\alpha V^{*}(z)\). Then it can be rewritten as \(\dot{V}^{*}(z)=-\rho d_{M}^2(z)-e_\mathrm{err}^{\mathsf {T}}Qe_\mathrm{err}-\big (u^{*}+d(z)\big )^{\mathsf {T}}R\big (u^{*}+d(z)\big ) +d^{\mathsf {T}}(z)Rd(z)+\alpha V^{*}(z)\). Observing that \(\rho =\lambda _{\max }(R)\) and \(\Vert d(z)\Vert \le d_M\), we derive \(\dot{V}^*(z)\le -\lambda _{\min }(Q)\Vert e_\mathrm{err}\Vert ^2+\alpha V^{*}(z)\). Because \(u^*\) is actually an admissible control, there exists a constant \(b_{v^*}>0\) such that \(\Vert V^*(z)\Vert \le b_{v^*}\). Thus, \(\dot{V}^*(z)\le -\lambda _{\min }(Q)\Vert e_\mathrm{err}\Vert ^2+\alpha b_{v^*}\). So, \(\dot{V}(z)<0\) as long as \(e_\mathrm{err}\) is out of the set \(\tilde{\varOmega }_{e_\mathrm{err}}=\{e_\mathrm{err}:\Vert e_\mathrm{err}\Vert \le \sqrt{\alpha b_{v^*}/\lambda _{\min }(Q)}\}\). By Lyapunov Extension Theorem [8], we obtain that the optimal control \(u^*\) guarantees \(e_\mathrm{err}(t)\) to be UUB with ultimate bound \(\sqrt{\alpha b_{v^*}/\lambda _{\min }(Q)}\). Moreover, if \(\alpha \) is selected to be very small, then \(\sqrt{\alpha b_{v^*}/\lambda _{\min }(Q)}\) can be kept small enough.

From Theorem 1, we can find that the robust tracking control can be obtained by solving the optimal control problem (4) and (5). In other words, we need get the solution of (7). In what follows, a novel ADP-based control scheme is developed to obtain the approximate solution of (7). Before proceeding further, we present an assumption used in [9, 10].

Assumption 3

Let \(L_1(z)\in C^1\) be a Lyapunov function candidate for system (4) and satisfied \(\dot{L}_1(z)=L^\mathsf {T}_{1z}\big (F(z)+G(z)u^*\big )<0\) with \(L_{1z}\) the partial derivative of \(L_1(z)\) with respect to z. In addition, there exists a symmetric positive definite matrix \(\varLambda (z)\in \mathbb {R}^{2n\times 2n}\) such that \(L^\mathsf {T}_{1z}\big (F(z)+G(z)u^{*}\big ) =-L_{1z}^\mathsf {T}\varLambda (z)L_{1z}\).

4 Approximate the HJB Solution via ADP

By using the universal approximation property of NNs, \(V^{*}(z)\) given in (7) can be represented by a single-layer NN on a compact set \(\tilde{\varOmega }\) as

$$\begin{aligned} V^{*}(z)=W_c^{\mathsf {T}}\sigma (z)+\varepsilon (z) \end{aligned}$$
(8)

where \(W_c\in \mathbb {R}^{N_0}\) is the ideal NN weight, \(\sigma (z)=[\sigma _1(z), \sigma _2(z),\ldots ,\sigma _{N_0}(z)]^{\mathsf {T}}\in \mathbb {R}^{N_0}\) is the activation function with \(\sigma _{j}(z)\in C^{1}(\tilde{\varOmega })\) and \(\sigma _j(0)=0\), the set \(\{\sigma _{j}(z)\}_{1}^{N_0}\) is often selected to be linearly independent, \({N_0}\) is the number of neurons, and \(\varepsilon (z)\) is the NN function reconstruction error.

Substituting (8) into (6), we have

$$\begin{aligned} u^{*}(z)=-(1/2)R^{-1}G^{\mathsf {T}}(z) \nabla \sigma ^{\mathsf {T}}W_c+\varepsilon _{u^{*}} \end{aligned}$$
(9)

where \(\nabla \sigma =\partial \sigma (z)/\partial z\) and \(\varepsilon _{u^{*}}=-(1/2)R^{-1}G^{\mathsf {T}} (z)\nabla \varepsilon \). Meanwhile, by using (8), (7) becomes

$$\begin{aligned} W_c^{\mathsf {T}}\nabla \sigma F-\alpha W_c^{\mathsf {T}}\sigma +z^{\mathsf {T}}\bar{Q}z+\rho d_{M}^2(z)-(1/4)W_c^{\mathsf {T}}\nabla \sigma \mathcal {A}\nabla \sigma ^{\mathsf {T}}W_c=\varepsilon _\mathrm{HJB} \end{aligned}$$
(10)

where \(\mathcal {A}=G(z)R^{-1}G^{\mathsf {T}}(z)\) and \(\varepsilon _\mathrm{HJB}=-\nabla \varepsilon ^{\mathsf {T}}F +\alpha \varepsilon +(1/2)W_c^{\mathsf {T}}\nabla \sigma \mathcal {A}\nabla \varepsilon +(1/4)\nabla \varepsilon ^{\mathsf {T}}\mathcal {A}\nabla \varepsilon \) is the HJB approximation error [11].

Due to the unavailability of \(W_c\), \(u^{*}(z)\) given in (9) cannot be implemented in real control process. Therefore, we use a critic NN to approximate \(V^{*}(z)\) as

$$\begin{aligned} \hat{V}(z)=\hat{W}_c^{\mathsf {T}}\sigma (z) \end{aligned}$$
(11)

where \(\hat{W}_c\) is the estimated weight of the ideal weight \(W_c\). The weight estimation error for the critic NN is defined as \(\tilde{W}_c=W_c-\hat{W}_c\).

Using (11), the estimated value of optimal control \(u^{*}(z)\) is

$$\begin{aligned} \hat{u}(z)=-(1/2)R^{-1}G^{\mathsf {T}} (z)\nabla \sigma ^{\mathsf {T}}\hat{W}_c. \end{aligned}$$
(12)

Combining (7), (11) and (12), we obtain the residual error as \(\delta =\hat{W}_c^{\mathsf {T}}\nabla \sigma F -\alpha \hat{W}_c^{\mathsf {T}}\sigma +z^{\mathsf {T}}\bar{Q}z+\rho d_{M}^2(z)-(1/4)\hat{W}_c^{\mathsf {T}}\nabla \sigma \mathcal {A}\nabla \sigma ^{\mathsf {T}}\hat{W}_c\). By utilizing (10), we have \(\delta =-\tilde{W}_c^{\mathsf {T}}\phi +(1/4)\tilde{W}_c^{\mathsf {T}} \nabla \sigma \mathcal {A} \nabla \sigma ^{\mathsf {T}}\tilde{W}_c+\varepsilon _\mathrm{HJB}\) with \(\phi =\nabla \sigma \big (F(z)+G(z)\hat{u}\big )-\alpha \sigma (z)\).

To get the minimum value of \(\delta \), we develop a novel critic NN tuning law as

$$\begin{aligned} \dot{\hat{W}}_c=&-\gamma \bar{\phi }\Big (Y(z)+\rho d_{M}^2(z) -(1/4)\hat{W}_c^{\mathsf {T}} \nabla \sigma \mathcal {A}\nabla \sigma ^{\mathsf {T}}\hat{W}_c\Big ) +\frac{\gamma }{2}\varSigma (z,\hat{u})\nabla \sigma \mathcal {A}L_{1z}\nonumber \\&+\gamma \Big (\big (K_1\varphi ^{\mathsf {T}}-K_2\big )\hat{W}_c +(1/4)\nabla \sigma \mathcal {A}\nabla \sigma ^{\mathsf {T}} \hat{W}_c\frac{\varphi ^{\mathsf {T}}}{m_s}\hat{W}_c\Big ) \end{aligned}$$
(13)

where \(\bar{\phi }=\phi /m_s^2\), \(\varphi =\phi /{m_s}\), \(m_s=1+\phi ^{\mathsf {T}}\phi \), \(Y(z)=\hat{W}_c^{\mathsf {T}}\nabla \sigma F -\alpha \hat{W}_c^{\mathsf {T}}\sigma +z^{\mathsf {T}}\bar{Q}z\), \(L_{1z}\) is given as in Assumption 3, \(K_1\) and \(K_2\) are tuning parameter matrices with suitable dimensions, and \(\varSigma (z,\hat{u})\) is an indicator function defined as

$$\begin{aligned} \varSigma (z,\hat{u})=\left\{ \begin{aligned}&0,\ \ \ \mathrm{if}\ L_{1z}^{\mathsf {T}}\big (F(z)+G(z)\hat{u}\big )<0,\\&1,\ \ \ \mathrm{otherwise}. \end{aligned} \right. \end{aligned}$$
(14)

Then, we obtain the weight estimation error dynamics of the critic NN as

$$\begin{aligned} \dot{\tilde{W}}_c =&\ \gamma \bar{\phi }\left( -\tilde{W}_c^{\mathsf {T}}\phi +(1/4)\tilde{W}_c^{\mathsf {T}} \nabla \sigma \mathcal {A} \nabla \sigma ^{\mathsf {T}}\tilde{W}_c+\varepsilon _\mathrm{HJB}\right) -\frac{\gamma }{2}\varSigma (z,\hat{u})\nabla \sigma \mathcal {A}L_{1z}\nonumber \\&-\gamma \left( \big (K_1\varphi ^{\mathsf {T}}-K_2\big ) -(1/4)\nabla \sigma \mathcal {A}\nabla \sigma ^{\mathsf {T}} \big (W_c-\tilde{W}_c\big )\frac{\varphi ^{\mathsf {T}}}{m_s}\right) \big (W_c-\tilde{W}_c\big ). \end{aligned}$$
(15)

In what follows we develop a theorem to show the stability of all signals in the closed-loop system. Before proceeding further, an assumption is provided as follows.

Assumption 4

\(W_c\) is bounded by a known constant \(W_{M}>0\). There exist constants \(b_\varepsilon >0\) and \(b_{\varepsilon z}>0\) such that \(\Vert \varepsilon (z)\Vert <b_\varepsilon \) and \(\Vert \nabla \varepsilon (z)\Vert <b_{\varepsilon z}\) \(\forall z\in \tilde{\varOmega }\). There exists a constant \(b_{\varepsilon _{u^*}}>0\) such that \(\Vert \varepsilon _{u^{*}}\Vert \le b_{\varepsilon _{u^*}}\). In addition, there exist constants \(b_{\sigma }>0\) and \(b_{\sigma z}>0\) such that \(\Vert \sigma (z)\Vert \le b_{\sigma }\) and \(\Vert \nabla \sigma (z)\Vert \le b_{\sigma z}\) \(\forall z\in \tilde{\varOmega }\).

Theorem 2

Consider the CT nominal system given by (4) with associated HJB equation (7). Let Assumptions 1–4 hold and take the control input for system (4) as given in (12). Meanwhile, let the critic NN weight tuning law be (13). Then, the function \(L_{1z}\) and the weight estimation error \(\tilde{W}_c\) are guaranteed to be UUB.

Proof

We provide an outline of the proof due to the space limit. Consider the Lyapunov function candidate \(L(t)=L_1(z)+(1/2)\tilde{W}_c^\mathsf {T}\gamma ^{-1}\tilde{W}_c\). Taking the time derivative of L(t), we have \(\dot{L}(t)= L_{1z}^\mathsf {T}\big (F(z)+G(z)\hat{u}\big ) +\dot{\tilde{W}}_c^\mathsf {T}\gamma ^{-1}\tilde{W}_c\). By using (15) and simplification, and noticing that \(\dot{z}=F(z)+G(z)\hat{u}\), we obtain

$$\begin{aligned} \dot{L}(t)\le&\ L_{1z}^\mathsf {T}\dot{z} -\lambda _{\min }(M)\Vert \mathcal {Z}\Vert ^2+b_N\Vert \mathcal {Z}\Vert -(1/2)\varSigma (z,\hat{u})L^{\mathsf {T}}_{1z}\mathcal {A} \nabla \sigma ^{\mathsf {T}}\tilde{W}_c \end{aligned}$$
(16)

where \(\mathcal {Z}=\big [\tilde{W}_c^{\mathsf {T}}\varphi , \tilde{W}^{\mathsf {T}}_c\big ]^{\mathsf {T}}\), \(b_N\) is the upper bound of \(\Vert N\Vert \), M and N are, respectively, given as

$$\begin{aligned} M=\begin{bmatrix}I&-\frac{W^\mathsf {T}_c\mathcal {B}}{8m_s}-\frac{K^\mathsf {T}_1}{2}\\ -\frac{\mathcal {B}W_c}{8m_s}-\frac{K_1}{2}&K_2-\frac{\varphi ^\mathsf {T}W_c\mathcal {B}}{4m_s} \end{bmatrix},\ \ N=\begin{bmatrix} \frac{\varepsilon _\mathrm{HJB}}{m_s} \\ \frac{\mathcal {B}W_c\varphi ^{\mathsf {T}}W_c}{4m_s} +K_2W_c-K_1\varphi ^{\mathsf {T}}W_c \end{bmatrix} \end{aligned}$$

with \(\mathcal {B}=\nabla \sigma \mathcal {A}\nabla \sigma ^{\mathsf {T}}\). Due to the definition of \(\varSigma (z,\hat{u})\) given in (14), we divide (16) into the following two cases for discussion:

  • (i) \(\varSigma (z,\hat{u})=0\). In this circumstance, we have \(L_{1z}^\mathsf {T}\dot{z}<0\). By employing dense property of \(\mathbb {R}\) [12], we can obtain a positive constant \(\beta \) such that \(0<\beta \le \Vert \dot{z}\Vert \) implies \(L_{1z}^\mathsf {T}\dot{z}\le -\Vert L_{1z}\Vert \beta <0\). Then (16) can be developed as \(\dot{L}(t)\le -\Vert L_{1z}\Vert \beta +(1/4)b_N^2/\lambda _{\min }(M) -\lambda _{\min }(M)\big (\Vert \mathcal {Z}\Vert -(1/2)b_N/\lambda _{\min }(M)\big )^2\). Notice that \(\Vert \mathcal {Z}\Vert \le \sqrt{1+\Vert \varphi \Vert ^2}\Vert \tilde{W}_c\Vert \le (\sqrt{5}/2)\Vert \tilde{W}_c\Vert \). Therefore, \(\dot{L}(t)<0\) is valid only if \( \Vert L_{1z}\Vert >b_N^2/(4\beta \lambda _{\min }(M))\) or \(\Vert \tilde{W}_c\Vert >2b_N/(\sqrt{5}\lambda _{\min }(M))\).

  • (ii) \(\varSigma (z,\hat{u})=1\). In this case, (16) can be developed as \(\dot{L}(t)\le L_{1z}^\mathsf {T}\big (F(z)+G(z)u^{*}\big ) +L_{1z}^\mathsf {T}G(z)(\hat{u}-u^{*})-\lambda _{\min }(M)\Vert \mathcal {Z}\Vert ^2 +b_N\Vert \mathcal {Z}\Vert -\frac{1}{2}L^{\mathsf {T}}_{1z}\mathcal {A}\nabla \sigma ^{\mathsf {T}}\tilde{W}_c\). By using Assumption 3 and similar with (i), we can obtain that \(\dot{L}(t)<0\) is valid only if \( \Vert L_{1z}\Vert >g_{M}b_{\varepsilon _{u^*}}/(2\lambda _{\min }(\varLambda (z))) +\sqrt{\ell /\lambda _{\min }(\varLambda (z))}\) or \(\Vert \tilde{W}_c\Vert >b_N/(\sqrt{5}\lambda _{\min }(M)) +\sqrt{4\ell /(5\lambda _{\min }(M))}\), where \(\ell =g^2_{M}b^2_{\varepsilon _{u^*}} /(4\lambda _{\min }(\varLambda (z)))+b^2_N/(4\lambda _{\min }(M))\).

Combining (i) and (ii) and using the standard Lyapunov Extension Theorem [8], we derive that the function \(L_{1z}\) and the weight estimation error \(\tilde{W}_c\) are UUB.

5 Simulation Results

Consider the CT uncertain nonlinear system given by

$$\begin{aligned} \dot{x}_1&=-x_1+x_2 \nonumber \\ \dot{x}_2&=-(x_1+1)x_2-49x_1+u+q\cos ^{3}(x_1)\sin (x_2) \end{aligned}$$
(17)

where \(x=[x_1,x_2]^\mathsf {T}\in \mathbb {R}^2\), and the uncertain term \(d(x)=q\cos ^{3}(x_1)\sin (x_2)\) with unknown parameter \(q\in [-1,1]\). We choose \(d_M(x)=\Vert x\Vert \). The reference trajectory \(x_d\) is generated by \(\dot{x}_{1d}=x_{2d}\) and \(\dot{x}_{2d}=-49x_{1d}\) with the initial condition \(x_d(0)=[0.2,0.4]^\mathsf {T}\). Then the augmented tracking error system is derived as

$$\begin{aligned} \dot{z}=C(z)+D(z)(u+d(z)) \end{aligned}$$
(18)

where \(z=[z_1,z_2,z_3,z_4]^\mathsf {T}=[e_{err_1},e_{err_2},x_{1d},x_{2d}]^\mathsf {T}\) with \(e_{err_i}=x_i-x_{id}\), and \(D(z)=[0,1,0,0]^\mathsf {T}\), and \( C(z)=[-z_1+z_2-z_3;-(z_1+z_3)(z_2+z_4)-49z_1-z_2-z_4;z_4;-49z_3]\). The nominal augmented system is \(\dot{z}=C(z)+D(z)u\) with C(z) and D(z) is given in (18). The cost function V(z) for nominal augmented error system is given as (5), where \(R=1\) and \(Q=2I_2\). The activation function of the critic NN is chosen with \(N_0=10\) as \(\sigma (x)= \big [z_1^2,z_2^2,z_3^2,z_4^2,z_1z_2,z_1z_3, z_1z_4,z_2z_3,z_2z_4,z_3z_4\big ]^{\mathsf {T}}\), and the weight of the critic NN is written as \(\hat{W}_c=[W_{c1},W_{c2},\ldots ,W_{c10}]^{\mathsf {T}}\).

Fig. 1.
figure 1

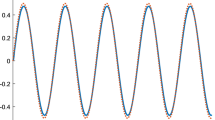
(a) Convergence of critic NN weights (b) Control input u (c) Evolution of tracking errors \(e_{err_i}(t)\) (\(i=1,2\)) during NN learning process (d) Tracking errors \(e_{err_i}\) (\(i=1,2\)) between the state of system (17) and the desired trajectory \(x_d\) under the approximate optimal control

Full size image

The initial system state is \(x(0)=[0.5,-0.5]^{\mathsf {T}}\), and the initial weight for the critic NN is selected randomly within an interval of [0, 1], which implies that no initial stabilizing control is required. In addition, \(\alpha =0.15\) and \(\gamma =0.5\). The developed control algorithm is implemented via (12) and (13). The computer simulation results are shown by Fig. 1(a)–(d). Figure 1(a) and (b) indicate convergence of critic NN weights and control input u, respectively. Figure 1(c) shows the evolution of tracking errors \(e_{err_i}\) (\(i=1,2\)) during NN learning process. Figure 1(d) illustrates tracking errors \(e_{err_i}\) (\(i=1,2\)) between the state of system (17) and the desired trajectory \(x_d\) under the approximate optimal control. From simulation results, it is observed that the state x(k) tracks the desired trajectory \(x_d(k)\) very well, and all signals in the closed-loop system are bounded.

6 Conclusions

We have developed an ADP-based robust tracking control for CT matched uncertain nonlinear systems. The robust tracking control is obtained without the requirement of the control matrix to be invertible. By using Lyapunov’s method, the stability of the closed-loop system is proved, and all signals involved are UUB. The computer simulation results show that the developed control scheme can perform successfully control and attain the desired performance. In our future work, we focus on studying robust control for CT nonaffine nonlinear systems.