1 Introduction

Optimization of the structures is one of the main research areas in civil and structural engineering. As a branch of applied and computational mathematics, optimization usually tries to find the best-fitted solution of the problem within a domain that contains acceptable values of design variables subject to some design restrictions or constraints. The optimum solution of the problem may be achieved by minimizing or maximizing a real objective function satisfying predefined restrictions at the same time. Such a solution is supposed to be the best one among a large feasible solution space that can satisfy all the constraints of the optimization problem. The function to be minimized or maximized is referred to as objective function, while the functions to represent restrictions are called as constraints. The design parameters of an optimization problem are called design variables. While the geometric properties of members can be considered as design variables in structural weight optimization, coordinates of nodal points can be treated as design variables for shape or topology design of structures. So the objective function, constraints, and variables can vary widely according to the type of the problem. For the minimum weight design of 3D truss structures, the objective function represents the weight of the truss, variables can be the areas of cross sections of the structural members, and the constraints may be the maximum allowable stresses and displacements of nodal joints.

2 Mathematical Formulations of Optimization Problems

An optimization problem subject to some constraints can be formulated as the following mathematical form:

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{{{\mathbf{x}} \in \,S}} \,f({\mathbf{x}}) \\ & S = \left\{ {\,{\mathbf{x}}|h_{j} ({\mathbf{x}}) = 0,\,j = 1, \ldots ,p;\,\,\,g_{k} ({\mathbf{x}}) \le 0,\,k = 1, \ldots ,m\,} \right\} \\ \end{aligned} $$
(1)

where f(x), h j (x), and g k (x) are a C 1 function of x ∈ IR n. In addition, p and m are the total numbers of h j (x) and g k (x), respectively. S represents the feasible set for the optimization problem, S \( \subset \) IR n.

However, in the engineering field, an optimization problem can also be generally defined as follows:

$$ \begin{aligned} & {\text{find}}\,\,\,\,\,{\mathbf{x}} = \left\{ {\,x_{1} ,\,x_{2} , \ldots ,\,x_{n} \,} \right\} \\ & \hbox{min} .\,\,\,\,W({\mathbf{x}}) \\ & {\text{s}} . {\text{t}} .\,\,\,\,\,\,\,g_{k} ({\mathbf{x}}) \le 0,\,\,\,k = 1\,{\text{to}}\,m \\ & \,\,\,\,\,\,\,\,\,\,\,x_{il} \le \,\,x_{i} \le x_{iu} ,\,\,i = 1\,{\text{to}}\,n \\ \end{aligned} $$
(2)

In Eqs. (1) and (2), x is an n-dimensional vector representing the design variables of the optimization problem. Depending on the optimization type, the cross-sectional areas of the members, the nodal coordinates of the member connections, and the members itself are treated as the design variables. f(x) and W(x) are called objective functions or cost functions, which usually correspond to a real number to be used to evaluate how good a solution is. Since weight is usually adopted as the objective function of the optimization problem in structural engineering, W(x) corresponds to the weight of the related structure. h j (x) and g k (x) are the equality and inequality constraints functions, respectively. In contrast, h j (x) in the engineering fields, the type of inequality constraint functions, g k(x), are often encountered. And it generally requires a structural analysis to obtain the structural response such as displacements, forces, etc. Here, x il and x iu show the lower and upper boundaries of x i . Strictly speaking, x i might be continuous, discrete, and real but since it is preferred in practice to select the cross-sectional areas of members from the predefined list, x i is taken as the discrete in structural engineering applications.

3 Genetic Algorithms

To find the value of x obeying the h j (x) and g k (x) and minimizing W(x) requires an optimization method to be employed. Optimization methods, generally speaking, are classified as the gradient-based and gradient-free techniques. Of course, various categorizations can be encountered for the optimization methods available in the literature [1–3]. In fact, although they are referred with various classifications and names, there is not much difference in the main properties of the methods. For example, one of the most commonly used classifications is deterministic and stochastic. While the former uses derivatives of the objective function and constraints in the search of the optimum solution, the latter works with probabilistic transition rules instead of the gradient information of the objective function and constraints [4–12]. As seen from the example, deterministic and stochastic techniques are easily put into the classification of the gradient-based and the gradient-free optimization methods, respectively.

Genetic algorithm (GA) is probably one of the first optimization methods, which simulates the natural phenomena into a numerical algorithm. It mimics the procedure known as survival of the fittest. GA was firstly proposed by Holland [13]. Since new some valuable improvements in the GA such as adaptive operators, distinct coding schemes for the design variables, immigration, elitism, breeding, hybridization, etc., have been presented by the researcher [19–30].

After the study of Rajeev and Krishnamoorthy [14] which was a well-documented study for the application of the GA in the structural optimization problems, GA has gained more popularity in this area than that proposed for the first time. By studying Rajeev and Krishnamoorthy [14], it is realized at first glance that GA is very primitive compared with the level recently reached. For instance, the design variables were coded with binary scheme in the GA process proposed by Rajeev and Krishnamoorthy [14], while at the moment the design variables are treated as discrete and even that mixed [15–18]. Figure 1 demonstrates the binary scheme for the design variables of the structural optimization problems. Herein, it is assumed that the corresponding optimization problem has three design variables which are the cross-section areas of the grouped members. And they are selected from 16 different sections available in practice.

Fig. 1
figure 1

Coding in binary system for design variables

Full size image

When this scheme is chosen to find the value of the design variables in decimal system, a transformation is needed. Through this transformation, the sequence numbers of the sections related to the design variables are determined from a predefined list sections. The steps of the transformation and mapping can be summarized as the main steps shown in Fig. 2. After mapping with the predefined list, the cross-section area for the related design variable is directly used in the corresponding process, i.e., in calculating the structural responses via a structural analyzer.

Fig. 2
figure 2

Decoding and mapping steps for the design variables represented in the binary system

Full size image

Then the structure should be analyzed to determine its responses and then the requirements of the optimization problems defined by the constraints functions are evaluated. The next step is to calculate the value of W(x). As mentioned before, it shows the goodness of the solution that consists of coupling the design variables (see Fig. 1)—the string is called as a solution. However, since the GA is an unconstrained optimization method like other gradient-free optimization techniques, W(x) also includes the value of a function known as the penalty function which reflects the violation level of the constraints in normalized form for the solution. Equation (3) shows the objective function, incorporating the constraints violation as expressed in Rajeev and Krishnamoorthy [14].

$$ \begin{aligned} & W({\mathbf{x}}) = W^{\prime}({\mathbf{x}})\,\left( {1 + KC} \right) \\ & {\text{where }}C = \sum\limits_{k = 1}^{m} {c_{k} } \\ \end{aligned} $$
(3)

where K is a parameter that is taken as 10, C is the violation coefficient computed in the following manner: if g k (x > 0, then c k  = g k (x); or if g k (x ≤ 0), then c k  = 0. Finally, W′(x) represents the weight of the structure. Note that g k (.) is in the normalized form expressed as σ/σ a −1 ≤ 0 for stress and d/d a −1 ≤ 0 for displacement. σ a and d a in these expressions show the allowable values for stress and displacement for the problem considered.

3.1 Genetic Operators

The search procedures of GA were based on the mechanics of natural genetics and natural selection. With the help of the genetic operators adapted from nature, the concept of the survival of the fittest is simulated to form a robust search mechanism. Following the steps summarized above, the GA search procedure proposed by Rajeev and Krishnamoorthy [14] applies two genetic operators successively.

The first one is the reproduction operator which reflects the concept of the survival of the fittest in nature. It proceeds according to the individual fitness calculated as follows:

$$ F_{i} = \left( {W_{\hbox{max} } + W_{\hbox{min} } } \right) - W_{i} (x) $$
(4)

where F i is the fitness of the ith individual in the population, W max and W min are the maximum and minimum values of W(x) computed using Eq. (3). Thus, the individuals with higher fitness values have a higher probability to survive, whereas the less fit ones get fewer chances of survival. And the worst fit individuals will be removed from the population.

Then, to exchange the solution segments between the individuals in the population, crossover operator is implemented. Double point crossover is applied to the pairs selected randomly as an example. Figure 3 demonstrates the application of the two genetic operators explained in Rajeev and Krishnamoorthy [14].

Fig. 3
figure 3

Two genetic operators given in Rajeev and Krishnamoorthy [14]. a Reproduction operator. b Crossover operator

Full size image

The genetic algorithm continues the process by following the above steps outlined in detail so as to modify the new population. To terminate the GA process, a criterion based on the similarity of the individuals in the population was imposed by Rajeev and Krishnamoorthy [14]. In addition, although mutation operator was not implemented in [14], the GA search process employed it to preserve the diversity among the population. Figure 4 illustrates the basic concept behind the mutation operator. It proceeds in three steps. First, an individual within the population is randomly selected. Then, a binary position to be changed is determined randomly. After that, the corresponding position value is switched to 1 if it is equal to 0 or to 0 if it is equal to 1.

Fig. 4
figure 4

Mutation operator

Full size image

All search procedures based on GA were called simple genetic algorithms in Rajeev and Krishnamoorthy [14] and since then, numerous modifications have been proposed by researchers in order to improve the search and/or computational performances of the GA in this area. For example, the coding scheme [19–21], the penalization [22–27], and new operators [28–30] are some of them. Other improvements based on adaptive concept have attracted more attention. The following section will review this concept.

4 Strategies Based on the Adaptive Concept

Some improvement or renewal in the GA operators or the GA algorithms have been made by researchers to increase the probability of finding the global solution and to enhance the performance of GA. Other improvements of GA are to relieve the user from the burden of determining sensitive parameter(s) existed in GA. The vast majorities of these efforts have been focused on the adaptive approaches in GA for both the penalty function, and the mutation and crossover. The key idea behind the adaptive approaches is to adjust itself automatically during the optimization procedure using genetic algorithms.

4.1 Adaptive Penalty Scheme

Although it is not a genetic operation, the penalty function is important in GA to demonstrate the extent of the violation of the constraints quantitatively. Penalty techniques can be classified as multiplicative or additive. A positive penalty factor is introduced in the multiplicative case to amplify the value of the fitness function of an infeasible individual in a minimization problem. This type of penalty has received less attention in the evolutionary computation community, compared with the additive type. A penalty functional is added to the objective function in the additive case to define the fitness value of an infeasible element [24].

An adaptive penalty scheme to be able to adjust itself automatically during the GA process is proposed by Toğan and Daloğlu [31] as follows:

$$ \begin{aligned} & f_{\text{penalty}} = \left( {C_{ \hbox{max} } + C(r)} \right)/\left( {C_{\hbox{max} } + C_{\text{ave}} } \right)\quad \quad C(r) \ge C_{\text{ave}} \\ & f_{\text{penalty}} = \left( {C_{\text{ave}} + C(r)} \right)/\left( {C_{\text{ave}} - C_{\hbox{min} } } \right)\quad \quad \quad C(r) < C_{\text{ave}} \\ & f_{\text{penalty}} = 0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;C(r) = 0\,\,\,\,\,\,\,\,\,\,\,r = 1, \ldots ,{\text{nps}} \\ \end{aligned} $$
(5)

where f penalty is the penalty function, C(r) is the violation value of normalized constraints of the rth individual in the generation, and nps represents the population size. In addition, C max , C min, and C ave are, respectively, the maximum, minimum and average violation values of generation. According to this formulation, Eq. (3) becomes

$$ W({\mathbf{x}}) = W^{\prime}({\mathbf{x}})\,\left( {1 + f_{\text{penalty}} } \right) . $$
(6)

The penalty function is, therefore, kept free from any predefined or user-defined constants. Also the magnitudes of the violations are not characterized by a static rate for both near feasible and infeasible solutions during the design process. With the expressions in Eq. (5), the infeasible solutions will not be penalized with the same rate of penalty. The magnitude of the penalty tends to get heavier instead, as the level of the violation of the infeasible solution tends to get bigger. Moreover, the magnitude of penalty increases as the violation value gets closer to C max. On the other hand, it decreases as the violation value gets closer to C min. Thus, some infeasible individuals that are close to the feasible region in the search space will not disappear through the penalty scheme and they will find a chance to survive. This may sustain the capacity of finding the global solution for design problem using GA.

4.2 Adaptive Crossover and Mutation Schemes

Genetic operators are applied to mimic the natural evolution. Among these operators, crossover provides the genetic information exchange between the couples randomly, and mutation enables the development of new genetic material, and both play an effective role to reach the optimum or to get close to the optimum solution. It is arbitrary and up to the user to incorporate the rates of these operators in optimization process. The choices of mutation, p m , and crossover, p c , rates as well as generating positions to be shifted by mutation and mapping the individuals for crossover are also arbitrary.

Many refinements using adaptive controls provide significant improvements in performance for some situations [32]. Keeping all of these in mind, it can be concluded that the randomness on mapping for crossover, and specifying the gene position(s) for mutation may be removed. Mutation and crossover should be adapted for both the individual and the generation because it is possible to lose the best-fitted individual with this random process in mutation. Therefore, in contrast to traditional crossover and mutation operator based on randomization mechanisms, i.e., generating the pairs, and determining position of bit shifted by mutation of the solution, the mutation and the crossover operators can be adaptive and adjust themselves from generation to generation since the population is renewed from iteration to iteration. Adaptive means adjusting itself automatically depending on the fitness value of the individual and the other individuals in the generation.

The adaptive mutation and crossover operators suggested by Srivinas and Patnaik [33] are modified as follows and applied by Toğan and Daloğlu [31, 34–36], for the optimization of 2d and 3d truss structures:

$$ p_{m} = \left\langle {\begin{array}{*{20}l} {0.5\left( {W_{\hbox{max} } - W(r)} \right)/\left( {W_{\hbox{max} } - W_{\text{ave}} } \right)} & {W(r) \ge W_{\text{ave}} } \\ {\left( {W_{\text{ave}} - W(r)} \right)/\left( {W_{\text{ave}} - W_{\hbox{min} } } \right)} & {W(r) < W_{\text{ave}} } \\ \end{array} } \right. $$
(7a)
$$ p_{c} = \left\langle {\begin{array}{*{20}l} {\left( {W_{\hbox{max} } - W^{*} \,} \right)/\left( {W_{\hbox{max} } - W_{\text{ave}} } \right)} & {W^{*} \ge W_{\text{ave}} } \\ 1 & {W^{*} < W_{\text{ave}} } \\ \end{array} } \right. $$
(7b)

Here, W(r) is the fitness of the rth individual, W ave is the average fitness value of the population, W max and W min are the maximum and minimum fitness values of an individual in the population, respectively, and W * is the larger of the fitness values of the solutions to be crossed. p m and p c are mutation and crossover rates, respectively.

After the mutation rate, p m , is determined using Eq. (7a), the numbers of design variables, m des, disrupted by mutation are calculated by multiplying p m with the string length of the solution. Then design variables in the individual are arranged according to the level of violation of normalized constraints, and they are renewed with m des starting with the most violated one. Thus design variables in the individuals are classified and the good individuals are kept unchanged. Also the diversity of population is maintained since the design variables that violate the constraints are renewed.

Unlike Srivinas and Patnaik [33], and Bekiroğlu [37], W * represents the lower value of the two fitness values of the solutions for crossover. The reason for that is because if the lower value of fitness is bigger than W ave, the crossover will take place between the pairs having good fitness value, whereas when W * represents the higher of the fitness values, there is a possibility for crossover to take place between the pairs having bad fitness values. Since the adaptive crossover is incorporated, information exchange between pairs can be done with various crossover points changing from 1 to string length of the individual (flexible point crossover). The numbers of design variables, c des, exchanged by crossover between pairs are specified by multiplying p c with string length for the solution. So if p c is equal to 1, the individual of pairs will not be subjected to crossover operator.

5 Innovative Approaches in Genetic Algorithms

The enhancements developed by the researchers to increase the performance of GA are not limited to adaptive schemes. Besides, some refinements are proposed for making the search procedures of GA computationally effective. Member grouping and initial population strategies are some of them as described in the next subsections in detail.

5.1 Initial Population Strategy

To start the evolution process in GA, the initial population within the solution space is generated. All individuals constituting the initial population are selected from the solution space of the problem notwithstanding any condition. In other words, this step is random. However, even though the process of creating initial population seems ordinary, it critically affects the convergence, the performance and the ability of the GA. This case becomes more crucial for very complicated and large solution space which is mostly encountered in the practical application of GA in the area of structural engineering.

The idea starting the search of the solution space without a randomly generated set is the key rationale of creating the initial population automatically. So, adopting the list number of the maximum area of cross sections as the starting point for the design variables leads to more efficiency than randomly generated. And it is stored as the initial point for each group of tension members to create the initial population. For the groups of the compression members, two or three surplus of the list number of the member that has he maximum area of cross section in the group is taken from the list of sections. The value of cross-sectional area and radius of gyration of that section must be bigger than the values found previously. And the corresponding section list number gives the initial points for each group of compression members and is stored to create the initial population (see Toğan and Daloğlu [31, 34] for more details).

5.2 Member Grouping Strategies

In the structural optimization terminologies, the design variables refer to the variables affecting the value of the objective function, and they generally represent the areas of the cross section of the structural members. Since the GA completely independent from the characteristic of the problem, the design variables of the optimization problems should be coded in some encoding schemes such as binary, decimal, real, and so on. GA evolves those solutions by creating in terms of design variables and randomly selecting into the potential solutions space of the problem. A set of possible feasible or unfeasible solutions construct the population or generation. Each solution in the populations is known as the individual.

For a given problem, all of the cross-sectional areas of the structural members can be taken as design variables. In this case, however, the computation time gets very high and the results obtained from optimization process will probably be the local optima due to the expanded design space. Therefore in the GA applications, member grouping is generally applied for the members of the structural system in order to reduce the size of the problem. On the other hand, the member grouping adopted a priori might not lead to an accurate grouping and if the number of members of the structural systems becomes very large; i.e., for 3D roof trusses, transmission towers, this leads to very large string lengths, which delays convergence and precludes useful exchange of information [38].

Two new member grouping strategies are proposed by Toğan and Daloğlu [31, 34] to reduce the size of the search space of the design problem as much as possible, to increase the probability of catching the global optimum solution and enhance the performance of the GA. The key idea behind the member grouping strategies is to make a convenient member grouping that will end up with as few numbers of cross sections as possible in the final set, and reduce the size of the design space of the problem as much as possible. The efforts are also made to relieve the user from the burden of determining the member groups.

5.2.1 First Member Grouping Strategy

The first strategy (strategy 1) is based on the one proposed by previous researchers [31, 38, 39]. To implement this strategy, the same cross-section areas are assigned for all the structural members first as stated in [31, 38, 39]. Then the analysis of the structure is performed using these initial areas for each load cases. Following the static analysis, the entire range of internal forces is divided into several ranges both for tension and compression members. And members are grouped according to the internal forces in the members.

An additional group is added in Toğan and Daloğlu [34] to the system for zero force members or members with very low internal forces. Hence, all the members of the truss structure are grouped conveniently and accurately. Moreover, a complex solution space may be avoided under some conditions.

5.2.2 Second Member Grouping Strategy

For strategy 2, while the magnitude of the axial force is considered as the factor for grouping the tension members [31, 38, 39], slenderness ratio is considered as the main factor for the compression members to set the groups. Therefore, due to the importance of slenderness ratio, it may be more convenient to group the compression members according to their slenderness ratio in terms of radius of gyration of the cross section and the effective length of the member instead of grouping them depending on the magnitude of the axial force. This is the key idea behind strategy 2. Hence, as the tension members of the truss structure are grouped depending on the axial forces, the compression members are grouped according to their slenderness ratio. An extra member group for the zero force members or members with very low internal forces is also arranged (Toğan and Daloğlu [31, 34]).

6 Examples

In this section, in the light of the information given in the previous sections, two types of design examples are presented. In the first one, a 160-bar space truss is considered as an example to demonstrate the effectiveness and robustness of proposed adaptive approaches for GA and member grouping strategy over simple GA. Later, an investigation is performed to demonstrate the efficiency, accuracy, and reliability of the proposed initial population strategies by solving numerical examples taken from previous studies in the literature for comparison.

The population size is taken as 40 for all the examples and real-value coding is employed in the genetic algorithm.

At the beginning of the genetic process 40 % of the initial population is created by using the proposed initial population strategy automatically. Therefore the diversity of the population is preserved and the algorithm may be less likely to get stuck at local minima and may also avoid some early convergence. It is possible to create all the individuals of the initial population automatically. However, in this case, the initial population consists of the same individual only and the search performed in the solution space start in a certain region. On the other hand, as the adaptive schemes applied for both penalty functions and mutation and crossover operators are able to adjust itself automatically during the genetic process [31], they completely disrupt the initial population. So, creating all the individuals in the initial population automatically is not meaningful.

6.1 Example 1: 160-Bar Truss Tower

The 160-bar truss tower shown in Fig. 5 was optimized by Rajaev and Krishnamoorthy [14] and Galante [40] in advance. 32 cross-section types were used to optimize the tower and taken from the AISC Manual [41]. The members are classified into 16 groups. Details of the member groups were presented in Galante [40]. Rajaev and Krishnamoorthy [14] used in GA with one criterion (minimum weight) and without taking the buckling effect into account. As Galante [40] stated, it can be observed that the buckling effect plays an important role in truss optimization. So if it is not taken into account the truss obtained will not be suitable as load carrying structural system. Galante [40] optimized the transmission tower with the aim of the minimum weight and minimum number of cross-section types of bars taken from the market and also taking buckling and the slenderness limits recommended by AISC [41] into account.

Fig. 5
figure 5

160-bar trussed steel transmission tower

Full size image

The tower is optimized for the objective indicated by Galante [40] with the proposed algorithm. All parameters needed to start the optimization process are taken from the reference studies. The structure is optimized with the implemented improvements in GA and two member grouping strategies for the aim of that the final design forms three groups at one for tension and two for compression members. An extra member group for zero force members is not formed. This is because of the fact that Galante [40] reported that 51 bars have a higher compression stress than the limit recommended by AISC [41] to prevent buckling and 68 have higher slenderness ratio than the AISC advice. It is also observed from the optimization process of the tower that the arrangement of an extra member group for zero force members does not make any difference in the weight of the tower drastically and the two member grouping strategies give the same result. Therefore, the tower is optimized with three, four, and five member groups.

The final design obtained by the proposed strategies and the ones reported by Galante [40] are presented in Table 1. Galante [40] used both GA and the simple rebirth process in GA for the optimization of this example and mentioned that the GA with the rebirth process achieves a better truss. However, the optimum designs obtained with the proposed improvements in the algorithm ended up with a lighter truss than the design by Galante [40]. A question may arise: as the values of design variables presented in Table 1 for the three groups are the same, why are the optimum weight of truss different? The answer is hidden in Fig. 6a. It is shown in Fig. 6a that some members that belong to the first group skipped to the second group and a better solution from the previous one is reached. However, the most interesting result is obtained when the four member groups are adopted at two for tension and two for compression member for this example. Although this optimum design has more groups than the result obtained by Galante [40] and previously performed optimization cases, in this study, it seems still reasonable to achieve that the number of sections in the final set must be as few as possible to make fabrication and workmanship easier [31, 39, 40]. The reduction in the total weight of the tower is about 28 % compared to the designs summarized in Table 1. As mentioned above, when the number of groups is taken as five, the optimized weight is slightly changed. In other words, arranging an extra group for the zero force members did not affect the weight of the tower drastically. Hence, the design at four groups is more meaningful than the design at five groups for the design objective. Figure 6b shows the genetic histories of the value of the objective function taken as the weight of tower for three optimization cases.

Table 1 Comparison of results for 160-bar transmission tower
Full size table
Fig. 6
figure 6

a Member groups for 160-bar tower, b Variation of weight for the three cases with number of generations

Full size image

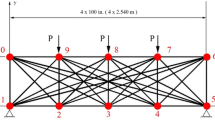
6.2 Example 2: 640-Bar Space Deck Truss

A trussed space deck shown in Fig. 7 has 179 joints and 640 members. The truss was first studied by Jenkins [32] in order to assess the decimal GA on a more substantial structural problem. Jenkins [32] found the optimum height of truss in addition to optimum volume. The truss members were subjected to compressive stress limitation given in BS 5950 and tensile stress limitation, 275 N/mm2. This trussed space deck was subjected to the one loading condition, which a single load of 300 kN was applied at the center of the upper plane (joint 90). A maximum displacement limitation of ±40 mm was imposed on every node in vertical direction. 21 discrete values of data for each design variable were taken from rectangular hollow steel sections with cross-sectional areas varying from 142 mm2 in intervals to 4350 mm2. Jenkins [32] collected the members of the structure in five distinct groups as follows: (1) upper deck longitudinal members, (2) upper deck transverse members, (3) lower deck longitudinal members, (4) lower deck transverse members, and (5) diagonal members connecting the upper and lower planes.

Fig. 7
figure 7

640 trussed space deck truss

Full size image

For this example, 23 pipe sections given in AISC [41] are adopted for each design variables. The allowable tensile stress is taken as 275 N/mm2 and the modulus of elasticity is 210 kN/mm2. The allowable compressive stress is calculated according to AISC [41] for the compression members and the maximum deflection imposed is 40 mm. The truss is subjected to one loading condition as specified in [32]. The optimization of the space truss is first carried out by using five groups imposed by Jenkins [32]. Then the optimal volume of the truss is obtained with four groups of members that were assumed as one for tension, two for compression members, and one for zero force members after preliminary analysis. Table 2 shows the optimum volume for each trial and the maximum deflection of the truss. The algorithm proposed in this study achieved a design with the best solution vector after approximately 29,000 searches for each trial. When four groups for the members are adopted after the preliminary analysis, the volume of the truss gets smaller than the result obtained by using five groups imposed by Jenkins [32]. Moreover, nearly 50 % reduction is obtained with both the member grouping and the new initial population strategies adopted in this study. This design obtained with the proposed algorithm confirms the intension of “both the weight of the structure and the number of cross section should be minimized to obtain an economical structure” as indicated in [31, 33–36, 38–40].

Table 2 Results for the 640-bar space deck truss
Full size table

6.3 Example 3: 1512-Bar Shed Truss

In order to demonstrate the performance, efficiency, and practical capability of the algorithm with the proposed strategies, the design of 1512-bar shed truss is studied as a final design problem. A shed structure illustrated in Fig. 8 covers a square field with size of 40,000 × 40,000 mm2 and has a height of 5359 mm. The structure is designed in a way that its sub-parts are reproduced along direction Z per 5000 mm and are connected by lateral elements on the lower arch level in that direction. In a sub-part each node on lower arch connects to four nodes on upper arches with diagonals. So, it consists of 409 nodes and 1512 truss elements. The structure is supported at two edges in the Z direction. The material density and modulus of elasticity are 7.85 × 10–8 kN/mm3 and 210 kN/mm2, respectively. It is subjected to a load scheme that is applied to all nodes of upper arches. 35,000 N is applied the nodes along Z direction and it increases 10,000 N per each node level in Y direction so that at the two nodes near symmetry axis the value is 55000 N (see Fig. 8). The allowable value of 250 N/mm2 is employed for tensile stresses and the formulation of buckling obeying AISC [41] considered for compressive stresses. The algorithm is provided with 26 discrete values of data for each design variable. The structural properties are taken from the pipe sections as given in [41]. The maximum displacement limitation imposed is 50 mm.

Fig. 8
figure 8

1512-bar shed truss

Full size image

As seen in Fig. 8, since the shed truss is a large structural system with more than 1000 members, it might be very difficult to optimize the area of individual members if the member groups become very large. Besides, very large string length causes the solution space of the problem to increase and becomes very complicated. Therefore, member grouping adopted to reduce the size of the problem and initial points to search the solution space are crucial to get an optimum design which is closer the global optimum.

The truss is designed by adopting the four groups at one for tension, two for compression, and one for zero members after the preliminary analysis. Table 3 gives the best solution vectors and the corresponding weight. An optimal structural weight of 692.43 kN was obtained considering the constraints, which gives a feasibility to construct it in practice. The algorithm obtained the optimum solution after approximately 43,600 searches.

Table 3 Result for the 1512-bar shed truss
Full size table

7 Conclusion

An optimum design approach is proposed based on the GA for truss structures with the help of self-adaptive strategies for member grouping, penalty function, mutation and crossover operators, and the initial population, which is then employed for the optimization of large 3D truss structures. An investigation has been performed to demonstrate the performance and workability of the enhanced GA (eGA). It is shown from the design examples that the eGA works well for the large structural systems. It is also worth pointing out that self-adaptive strategies in eGA help user to start the GA process automatically. It can be expected that proposed eGA may also be a useful search technique and a tool for solving discrete sizing variables of the large 3D truss structures.