Numerical Experiments with a Linear Convection–Diffusion Problem Containing a Time-Varying Interior Layer

Abstract

We examine a time dependent singularly perturbed convection-diffusion problem, where the convective coefficient contains an interior layer. A smooth transformation is introduced to align the grid to the location of the interior layer. A numerical method consisting of an upwinded finite difference operator and a piecewise-uniform Shishkin mesh is constructed in this transformed domain. Numerical results are presented which indicate that the numerical approximations converge at a rate of first order (up to logarithmic factors) uniformly in the pointwise maximum norm.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In addition to boundary layers, interior layers can appear in the solutions of singularly perturbed problems. In the context of time dependent problems, an additional issue with interior layers is that the location of the layer can move with time. Here we focus on parabolic problems with moving interior layers.

Consider singularly perturbed convection-diffusion parabolic problems of the general form: Find u such that

$$\displaystyle{ -\varepsilon u_{ss} + au_{s} + bu + cu_{t} = f,\quad (s,t) \in (0,1) \times (0,T],\quad b,c > 0; }$$

(1a)

$$\displaystyle{ 0 <\varepsilon \ll 1,\qquad u(0,t),u(1,t),u(s,0)\quad \mbox{ specified}. }$$

(1b)

Interior layers can appear in the solutions of problem (1), if the coefficients a, b, c or the inhomogenous term f are discontinuous [1]. Strong interior layers [1, 7] are generated, when the convective coefficient a is discontinuous and assumed to have the particular sign pattern a(s, t) > 0, s < d(t); a(s, t) < 0, s > d(t). In [7] a piecewise-linear map $X: (s,t) \rightarrow (x,t)$ was introduced, which transforms the curve Γ ₁: = { (d(t), t) | t ∈ [0, T], 0 < d(t) < 1} into a vertical line x = d(0). Using this transformed domain as the computational domain, a piecewise-uniform Shishkin mesh [3] was constructed and centered around the point x = d(0). Under the assumption that the convective coefficient a(s) is discontinuous and independent of time, the resulting numerical method was shown to be (essentially) first order $\varepsilon$-uniformly convergent to the solution of (1). In [4], interior layers appeared in the solution of (1), in the case where the initial condition u(s, 0), contained it’s own interior layer. In the case of [4], the convective coefficient a(t) was assumed to be smooth, space independent and of one sign. The reduced initial condition (set $\varepsilon = 0$) was discontinuous at some point x = d and this discontinuity was transported along the characteristic curve $\varGamma _{2}:=\{ (d(t),t)\vert t \in [0,T],d^{{\prime}}(t) = a(t),d(0) = d.\}$, associated with the reduced hyperbolic problem av _s + bv + cv _t  = f. Again, a parameter-uniform numerical method (akin to the method analysed in [1]) was shown [4] to be (essentially) first order uniformly convergent.

In the current paper, an interior layer appears in the solution of (1) due to the fact that the convective coefficient $a_{\varepsilon }(s,t)$ is assumed to be smooth, but to contain a layer and to smoothly, but rapidly, switch from positive to negative values along some given curve Γ ₁ within the domain. In Sect. 2, the space derivative of the convective coefficient $a_{\varepsilon }$ will be of order $O(\varepsilon ^{-1})$ in a neighbourhood of Γ ₁. With this scaling, the problem may be viewed as a linearization of the quasilinear problem $-\varepsilon y_{xx} + yy_{x} + by + y_{t} = f$, with a moving interior layer present in the solution y(x, t). If the space derivative of the convective coefficient a was uniformly bounded at the turning point, then the width of the layer would not be $O(\varepsilon )$ and an alternative numerical method (to what is examined in this paper) would be required (see, e.g., [2]). For the current paper, in the limiting case of $\varepsilon = 0$, the convective coefficient will be discontinuous. Unlike [4, 7], a smooth transformation of the discontinuity curve Γ ₁ is utilized here, so that the data for the transformed problem is as smooth as the data of the original problem. Based on the theoretical results established in [6] for a related convection-diffusion problem, restrictions are placed on the possible admissible transformations, in order that the central assumptions on the convective coefficient, required for the numerical analysis in [6] to apply, are satisfied. In turn, this motivates a particular choice for the transition parameter in the layer-adapted Shishkin mesh. Numerical results are presented for the resulting numerical method, which suggest that the constructed numerical method is also a first order (ignoring logarithmic effects) uniformly convergent numerical method. In previous related papers examining interior layers [1, 4, 7], the location of the interior layer was tracked exactly. In this paper, the fine mesh is centered at an approximate location of the interior layer.

Notation

Throughout this paper C denotes a generic constant which is independent of $\varepsilon$ and all mesh parameters.

2 Continuous Problem

Consider singularly perturbed linear parabolic problems, posed on the domain Ω: = (0, 1) × (0, T], of the form

$$\displaystyle{ -\varepsilon \tilde{u}_{ss} +\tilde{ k}(s,t)\tilde{\kappa }_{\varepsilon }(s,t)\tilde{u}_{s} +\tilde{ b}(s,t)\tilde{u} +\tilde{ c}(s,t)\tilde{u}_{t} =\tilde{ f}(s,t),\ (s,t) \in \ \varOmega; }$$

(2a)

$$\displaystyle{ \tilde{k}(s,t) \geq \alpha _{1} > 0,\ \tilde{b}(s,t) \geq \alpha _{2} > 0,\quad \tilde{c}(s,t) \geq \alpha _{3} > 0,\quad (s,t) \in \overline{\varOmega }; }$$

(2b)

$$\displaystyle{ \tilde{u}(0,t) =\phi _{L}(t),\ \tilde{u}(1,t) =\phi _{R}(t),\ \tilde{u}(s,0) =\tilde{\phi } _{0}(s); }$$

(2c)

$$\displaystyle{ \tilde{\kappa }_{\varepsilon }(s,t):=\tanh (\frac{q(t) - s} {\varepsilon } ),\quad 0 < q(t) < 1,\ \forall t; }$$

(2d)

where for each value of t, the convection coefficient $(\tilde{k}\tilde{\kappa }_{\varepsilon })(s,t)$ has a single zero at s = q(t) and this point may vary with time. The data is assumed to be sufficiently regular so that the solution $u \in \mathcal{C}^{4+\gamma }(\overline{\varOmega })$. In this problem, the convective coefficient is positive to the left of the curve Γ: = { (q(t), t), t ≥ 0} and it is negative to the right. This results in an interior layer forming in the vicinity of the curve Γ. Below we deploy a coordinate transformation so that in the transformed domain the location of the interior layer lies within $O(\varepsilon )$ of a fixed point in time.

Consider maps X: (s, t) ↦ (x, t) of the form $X(s,t) = (\varXi (s,t),t)$. Below we will design invertible maps $\varXi: \overline{\varOmega }\mapsto [0,1]$ so that

$$\displaystyle\begin{array}{rcl} & \varXi (0,t) = 0,\quad \varXi (q(t),t) = q(0),\quad \varXi (1,t) = 1, & {}\\ & \varXi: [0,q(t)] \times [0,T]\mapsto [0,q(0)]\qquad \mbox{ and}\qquad \varXi: [q(t),1] \times [0,T]\mapsto [q(0),1].& {}\\ \end{array}$$

Moreover, we assume that the inverse map $\varXi ^{-1}$ is a polynomial in x. Hence, if $u(x,t):=\bar{ u}(s,t)$ and since $\varXi (s,t) = x$, we have that

$$\displaystyle{\frac{\partial \tilde{u}} {\partial t} = -\frac{s_{t}} {s_{x}} \frac{\partial u} {\partial x} + \frac{\partial u} {\partial t},\quad \frac{\partial \tilde{u}} {\partial s} = \frac{1} {s_{x}} \frac{\partial u} {\partial x};\quad \frac{\partial ^{2}\tilde{u}} {\partial s^{2}} = -\frac{s_{xx}} {s_{x}^{3}} \frac{\partial u} {\partial x} + \frac{1} {s_{x}^{2}} \frac{\partial ^{2}u} {\partial x^{2}}.}$$

Using a map of this form, the differential equation (2a) will transform into

$$\displaystyle{ L_{\varepsilon }u:= -\varepsilon u_{xx} + (a_{\varepsilon } +\varepsilon g)u_{x} + s_{x}^{2}(bu + cu_{ t}) = (s_{x}^{2}f)(x,t),\quad (x,t) \in \varOmega, }$$

(3a)

$$\displaystyle{ \mbox{ where}\quad a_{\varepsilon }:= (ks_{x})(\kappa _{\varepsilon } - s_{t} \frac{c} {k})\quad \mbox{ and}\quad g:= \frac{s_{xx}} {s_{x}}. }$$

(3b)

To ensure the map is invertible and that s(0, t) = 0, s(1, t) = 1, we require that s _x (x, t) > 0 for all (x, t) ∈ Ω. Since s(x, t) is assumed to be a polynomial in x, and given that s(q(0), t) = q(t) with 0 < q(t) < 1, it follows that there exists a smooth positive function r(x, t) such that

$$\displaystyle{q(t) - s(x,t) = (q(0) - x)r(x,t),\quad r(x,t) \geq \beta > 0,(x,t) \in \bar{\varOmega }.}$$

Using this fact and ze ^−z ≤ 2e ^−z∕2, z ≥ 0, one can deduce that

$$\displaystyle{{\bigl \Vert\frac{\partial ^{m}a_{\varepsilon }} {\partial t^{m}} \bigr \Vert}_{\varOmega } \leq C,\quad m = 1,2,3.}$$

Thus by aligning the coordinate system along the direction of the layer movement (along the curve Γ), the time derivatives of the convective coefficient $a_{\varepsilon }(x,t)$ are $\varepsilon$-uniformly bounded. Observe that the time derivatives of the convective coefficient $\tilde{\kappa }_{\varepsilon }(s,t)$ are not, in general, $\varepsilon$-uniformly bounded in the original (s, t) coordinate system. However, the space derivatives in the transformed variables do depend adversely on the singular perturbation parameter as

$$\displaystyle{{\bigl \Vert\frac{\partial ^{i}a_{\varepsilon }} {\partial x^{i}}\bigr \Vert}_{\varOmega } \leq C\varepsilon ^{-i},\quad i = 1,2,3,4.}$$

In general, the point at which the convective coefficient $a_{\varepsilon }(x,t)$ is zero, is not always located at x = q(0). However, if $\vert cs_{t}k^{-1}\vert < 1,\ t \leq T,0 \leq x \leq 1$ then for $\varepsilon$ sufficiently small the coefficient $a_{\varepsilon }(x,t)$ will be zero within an $O(\varepsilon )-$ neighbourhood of x = q(0). Hence, we restrict the problem class being examined by imposing the following two constraints on the data. The q(t), T are restricted so that there exists a smooth inverse mapping $s: [0,1] \times [0,T] \rightarrow [0,1]$ such that

$$\displaystyle{ s_{x}(x,t)\geqslant \beta _{0} > 0,\quad \vert \frac{cs_{t}} {k} (x,t)\vert \leqslant \beta _{1} < 1,\quad \forall \quad (x,t) \in [0,1] \times [0,T], }$$

(3c)

$$\displaystyle{ s(0,t) = 0,\quad s(1,t) = 1,\quad s(q(0),t) = q(t). }$$

(3d)

Under these constraints and for sufficiently small $\varepsilon$, there exists a unique d(t) ∈ (0, 1) such that

$$\displaystyle{ a_{\varepsilon }(d(t),t) = 0\quad \text{and}\quad \vert d(t) - q(0)\vert \leq C\varepsilon,\qquad \mbox{ for all}\ t \in [0,T]. }$$

Moreover, the sign pattern of the convective coefficient $a_{\varepsilon }$ is essentially preserved as

$$\displaystyle{(d(t) - x)a_{\varepsilon }(x,t) > 0,\qquad x\not\in (d(t) - C\varepsilon,d(t) + C\varepsilon ).}$$

Using the equality

$$\displaystyle{\frac{\partial a_{\varepsilon }} {\partial d} \frac{\partial d} {\partial t} + \frac{\partial a_{\varepsilon }} {\partial t} = 0}$$

we deduce that $\vert d^{{\prime}}(t)\vert \leq C\varepsilon$ and by repeating the differentiation we conclude that

$$\displaystyle{\vert d^{(m)}(t)\vert \leq C\varepsilon,m = 1,2,3.}$$

Hence, in the transformed domain, the location of the interior layer lies within an $O(\varepsilon )$-neighbourhood of the initial point x = q(0) at all values of time. In the original domain, the position of the turning point of the convective coefficient is explicitly know (as s = q(t)), but in the computational domain the position of the turning point is only approximately known as $x = d(t),\ d(t) \in (q(0) - C\varepsilon,q(0) + C\varepsilon )$. Note further, that due to the nature of the convective coefficient, although $a_{\varepsilon }(d(t),t) = 0$, we have that $a_{\varepsilon }(d(t) \pm C\varepsilon,t) = O(1)$.

3 Bounds on the Continuous Solution

In this section, the solution is decomposed into the sum of a discontinuous regular component and a discontinuous layer component. We obtain a pointwise bound on the singular component, which identifies the rate of exponential decay of the singular component within the interior layer. This rate depends both on the location of the curve Γ and the particular choice of transformation s, introduced in the previous section.

Lemma 1

For the solution u of (3) we have the following bounds

$$\displaystyle{{\Bigl \Vert \frac{\partial ^{j+m}u} {\partial x^{j}\partial t^{m}}\Bigr \Vert}\leqslant C\varepsilon ^{-(j+m)},\quad 0 \leq j + 2m \leq 4.}$$

Proof

The bound on ∥ u ∥ is established using a maximum principle. Use the stretched variables $\zeta:= (x - q(0))/\varepsilon,\eta:= t/\varepsilon$ and the a priori bounds [5, pg. 320, Theorem 5.2] to deduce the bounds on the partial derivatives of the solution. □ 

For all points in $\varOmega \setminus \varGamma$, define the differential operator

$$\displaystyle{\mathcal{L}_{\varepsilon }u:= -\varepsilon u_{xx}+(a_{0}+\varepsilon g)u_{x}+s_{x}^{2}(bu+cu_{ t}),\ a_{0}(x,t):= ks_{x}\left \{\begin{array}{lll} + (1 - s_{t} \frac{c} {k}),&x < q(0), \\ - (1 + s_{t} \frac{c} {k}),&x > q(0) \end{array} \right.}$$

Observe that the convective coefficient in the operator $\mathcal{L}_{\varepsilon }$ is discontinuous across the curve Γ.

Lemma 2

For sufficiently small $\varepsilon$ , there exists functions r ^± (t) such that the solutions v ^± of the problems

$$\displaystyle\begin{array}{rcl} & \mathcal{L}_{\varepsilon }v^{-} = f(x,t),\quad (x,t) \in \varOmega ^{-}:= (0,d(t)) \times (0,T], & {}\\ & v^{-}(x,0) =\phi (x),\ 0 \leq x \leq d(t),\ v^{-}(0,t) =\phi _{L}(t),\ v^{-}(d(t),t) = r^{-}(t),\ 0 < t \leq T,& {}\\ & \mathcal{L}_{\varepsilon }v^{+} = f(x,t),\quad (x,t) \in \varOmega ^{+}:= (d(t),1) \times (0,T], & {}\\ & v^{+}(x,0) =\phi (x),\ d(t)\leqslant x\leqslant 1,\ v^{+}(1,t) =\phi _{R}(t),\ v^{+}(d(t),t) = r^{+}(t),\ 0 < t \leq T, & {}\\ \end{array}$$

are, respectively, in $\mathcal{C}^{4+\gamma }(\overline{\varOmega }^{\pm })$ and satisfy the bounds

$$\displaystyle{{\Bigl \Vert\frac{\partial ^{j+m}v^{\pm }} {\partial x^{j}\partial t^{m}} \Bigr \Vert}_{\overline{\varOmega }^{\pm }} \leq C(1 +\varepsilon ^{2-(j+m)}),\quad 0 \leq j + 2m \leq 4.}$$

Proof

As in [6]. □ 

We now define the interior layer components $w^{\pm }\in \mathcal{C}^{4+\gamma }(\overline{\varOmega }^{\pm })$ as

$$\displaystyle{w^{\pm }(x,t):= u(x,t) - v^{\pm }(x,t),\quad (x,t) \in \overline{\varOmega }^{\pm },}$$

which satisfy the problems

$$\displaystyle{ L_{\varepsilon }w^{\pm }(x,t) = (a_{ 0}(x,t) - a_{\varepsilon }(x,t))v_{x}^{\pm }(x,t),\quad (x,t) \in \varOmega ^{\pm }; }$$

(4a)

$$\displaystyle{ w^{-}(0,t) = 0,\quad w^{-}(d(t),t) = (u - v^{-})(d(t),t),\quad t \geq 0; }$$

(4b)

$$\displaystyle\begin{array}{rcl} & w^{-}(x,0) = 0,\quad 0 < x < d(t),\qquad w^{+}(x,0) = 0,\quad d(t) < x < 1;& \\ & w^{+}(1,t) = 0,\quad w^{+}(d(t),t) = (u - v^{+})(d(t),t),\quad t \geq 0. &{}\end{array}$$

(4c)

Observe that

$$\displaystyle{\vert L_{\varepsilon }w^{\pm }(x,t)\vert \leq Ce^{-\frac{2\beta \vert x-q(0)\vert } {\varepsilon } }.}$$

Lemma 3

Assume that α ₁ β ₀ ≤ 2β. The solutions w ^± of the problems specified in (4) satisfy the following pointwise bounds

$$\displaystyle{{\Bigl \vert w^{\pm }(x,t)\Bigr \vert}_{\overline{\varOmega }^{ \pm }} \leq Ce^{-\frac{\theta }{2\varepsilon } \vert q(0)-x\vert },\quad \mbox{ where}\quad \theta:=\alpha _{ 1}\beta _{0}(1 -\beta _{1}).}$$

Proof

We outline how to establish the bound in the region Ω ⁻. For $\varepsilon$ sufficiently small, there exists a C ₁ such that for all t ≥ 0, and $x \in (0,d(t) - C_{1}\varepsilon )$

$$\displaystyle\begin{array}{rcl} a_{\varepsilon }(x,t)& =& s_{x}k(\tanh \frac{r(q(0) - x)} {\varepsilon } -\frac{s_{t}c} {k} )\ \geq \alpha _{\varepsilon }(x,t) > 0,\ {}\\ \mbox{ where}\quad \alpha _{\varepsilon }(x,t)&:=& \alpha _{1}\beta _{0}(\tanh \frac{\beta (q(0) - x)} {\varepsilon } -\beta _{1}),\quad x \leq d(t) {}\\ \end{array}$$

Since $\vert z\vert \mbox{ sech}^{2}z \leq C,\forall z$, we have that

$$\displaystyle\begin{array}{rcl} -2\varepsilon \frac{\partial \alpha _{\varepsilon }} {\partial x} +\alpha _{ \varepsilon }^{2}& =& A^{2}\tanh ^{2}\frac{\beta (q(0) - x)} {\varepsilon } + (A\beta _{1})^{2} {}\\ & +& A(2\beta \mbox{ sech}^{2}\frac{\beta (q(0) - x)} {\varepsilon } - 2A\beta _{1}\tanh \frac{\beta (q(0) - x)} {\varepsilon } ),\quad A:=\alpha _{1}\beta _{0}\ {}\\ & =& A^{2}(\tanh ^{2}z +\beta _{ 1}^{2}) + A(2\beta \mbox{ sech}^{2}z - 2A\beta _{ 1}\tanh z), {}\\ & & \qquad \quad \mbox{ where}\ z:= \frac{\beta (q(0) - x)} {\varepsilon } {}\\ & =& A^{2}\beta _{ 1}^{2} + 2A\beta + A(A - 2\beta )\tanh ^{2}z - 2A^{2}\beta _{ 1}\tanh z {}\\ & \geq & A^{2}(1 -\beta _{ 1})^{2},\quad \mbox{ if}\quad A \leq 2\beta. {}\\ \end{array}$$

Consider the following layer function

$$\displaystyle{B(x,t):=\varepsilon ^{-1}e^{-\int _{s=x}^{d(t)} \frac{\alpha _{\varepsilon }(s,t)} {2\varepsilon } ds}\ dp,\qquad x \leq d(t);}$$

and noting that $\int _{0}^{t}\tanh x\ dx = t +\log ((1 + e^{-2t})/2) \geq t -\log 2$, we have that

$$\displaystyle\begin{array}{rcl} \int _{s=x}^{d(t)}\alpha _{ \varepsilon }(s,t)ds& \geq & A{\bigl (\int _{s=x}^{q(0)}\tanh (\frac{\beta (q(0) - x)} {\varepsilon } ) -\beta _{1}\ dx\bigr )} + O(\varepsilon ) {}\\ & \geq & A(1 -\beta _{1})(d(t) - x) + O(\varepsilon ). {}\\ \end{array}$$

Using the above lower bound, we have that

$$\displaystyle\begin{array}{rcl} C_{1}e^{-\frac{A(1-\beta _{1})} {\varepsilon } (d(t)-x)}& \leqslant & e^{-\frac{1} {\varepsilon } \int _{s=x}^{d(t)}\alpha _{ \varepsilon }(s,t)\ ds}\leqslant C_{2}e^{-\frac{A(1-\beta _{1})} {\varepsilon } (d(t)-x)} {}\\ {\Bigl \vert\frac{\partial B} {\partial t} (x,t)\Bigr \vert}& \leq & CB(x,t),\quad \mbox{ as}\quad \vert d^{{\prime}}(t)\vert \leq C\varepsilon. {}\\ \end{array}$$

Using these bounds, for $\varepsilon$ sufficiently small, one can deduce that

$$\displaystyle{L_{\varepsilon }B \geq (\frac{A^{2}(1 -\beta _{1})^{2}} {4\varepsilon } - C)B \geq \frac{A^{2}(1 -\beta _{1})^{2}} {8\varepsilon } B}$$

where we have also used the fact that $a_{\varepsilon } -\alpha _{\varepsilon }\geq -C\varepsilon,\ x \in (d(t) - C_{1}\varepsilon,d(t))$. Hence we can choose C so that CB(x, t) − w ⁻(x, t) ≥ 0, (x, t) ∈ Ω ⁻. □ 

In [6] a similar class of problems to the problem class (3) was studied. A numerical method was constructed and shown to be (essentially) first order $\varepsilon$-uniformly convergent on a suitably constructed Shishkin mesh. This motivates the choice of numerical method in this paper. The choice of the transition parameter in the mesh is dictated by the bounds established in this section. A proof of an associated error bound for the numerical method presented in Sect. 4, as applied to problems of the form (2), would require some modifications in the analysis in [6]. Due to space restrictions, we do not discuss these modifications here.

4 Numerical Method

A numerical approximation $\tilde{U } _{I}(s,t)$ to the solution of (2) is generated by discretizing the transformed problem (3) (with an upwind finite difference method) to generate a discrete nodal solution U(x _i , t _j ). which is interpolated (using bilinear interpolation) to produce a global approximation U _I (x, t) and then this is subsequently transformed back to the original domain to produce $\tilde{U }_{I}(s,t)$. To capture the interior layer we will design a layer-adapted piecewise uniform mesh.

The discrete problem is: Find a mesh function U such that:

$$\displaystyle{ L_{\varepsilon }^{N,M}U(x_{ i},t_{j}) = s_{x}f(x_{i},t_{j}),\quad (x_{i},t_{j}) \in \varOmega _{\varepsilon }^{N,M}, }$$

(5a)

$$\displaystyle{ U(0,t_{j}) = u(0,t_{j}),\quad U(1,t_{j}) = u(1,t_{j}),\quad U(x_{i},0) = u(x_{i},0), }$$

(5b)

$$\displaystyle{ L_{\varepsilon }^{N,M}:= -\varepsilon \delta _{ x}^{2} + (a_{\varepsilon } +\varepsilon g)D_{ x} + s_{x}bI + s_{x}cD_{t} }$$

(5c)

$$\displaystyle{ \delta _{x}^{2}Z(x_{ i},t_{j}):= \frac{D_{x}^{+}Z(x_{i},t_{j}) - D_{x}^{-}Z(x_{i},t_{j})} {(h_{i+1} + h_{i})/2},\quad h_{i}:= x_{i} - x_{i-1} }$$

(5d)

$$\displaystyle{ (AD_{x}Z)(x_{i},t_{j}):= \tfrac{1} {2}\left ((A + \vert A\vert )D_{x}^{-} + (A -\vert A\vert )D_{ x}^{+}\right )Z(x_{ i},t_{j}), }$$

(5e)

where $D_{x}^{+}$ and $D_{x}^{-}$ are the standard forward and backward finite difference operators in space, respectively. We define the piecewise-uniform Shishkin mesh $\overline{\varOmega }_{\varepsilon }^{N,M}$ by

$$\displaystyle{ \sigma _{1}:=\min \{\frac{q(0)} {2}, \tfrac{2\varepsilon } {\theta } \ln N\},\ \sigma _{2}:=\min \{\frac{1 - q(0)} {2}, \tfrac{2\varepsilon } {\theta } \ln N\}, }$$

(6a)

$$\displaystyle{ H_{0}:= \tfrac{4} {N}(q(0) -\sigma _{1}),\ h:= \tfrac{2} {N}(\sigma _{1} +\sigma _{2}),\ H_{1}:= \tfrac{4} {N}(1 - q(0) -\sigma _{2}),\ k = \tfrac{T} {M}, }$$

(6b)

$$\displaystyle{ \overline{\varOmega }_{\varepsilon }^{N,M}:= \left \{(x_{ i},t_{j})\left \vert \begin{array}{cc} x_{i} = H_{0}i, & 0\leqslant i\leqslant \tfrac{N} {4}, \\ x_{i} = x_{\frac{N} {4} } + h(i -\tfrac{N} {4} ), & \tfrac{N} {4} < i\leqslant \tfrac{3N} {4}, \\ x_{i} = x_{\frac{3N} {4} } + H_{1}(i -\tfrac{3N} {4} ),& \tfrac{3N} {4} < i\leqslant N, \\ t_{j} = jk, &0\leqslant j\leqslant M = N, \end{array} \right.\right \} }$$

(6c)

where the parameter $\theta$ in (6b) is defined in the statement of Lemma 3.

5 Numerical Experiments

Let us consider the following particular map, whose inverse is of the form

$$\displaystyle{ s(x,t) = x - A(t)(x(1 - x)),\quad A(t):= \frac{q(0) - q(t)} {q(0)(1 - q(0))}. }$$

(7)

The transformed differential equation (3a) can be written in the form

$$\displaystyle\begin{array}{rcl} a_{\varepsilon }(x,t):=\tanh \left (\tfrac{r(x,t)} {\varepsilon } (q(0) - x)\right ) - s_{t},\quad g(x,t) = \tfrac{2A(t)} {s_{x}},& &{}\end{array}$$

(8a)

$$\displaystyle\begin{array}{rcl} s_{x} = 1 + A(t)(2x - 1),\ \ s_{t} = A^{{\prime}}(t)x(x - 1),\ \ r(x,t):= \tfrac{q(t)} {q(0)} + A(t)x.& &{}\end{array}$$

(8b)

Imposing the constraints from the previous sections on the particular map (7) yield

$$\displaystyle\begin{array}{rcl} \vert q(t) - q(0)\vert & \leqslant & (1 -\beta _{0})q(0)(1 - q(0)),\quad \beta _{0} > 0\;{}\end{array}$$

(9a)

$$\displaystyle\begin{array}{rcl} \Vert ck^{-1}\Vert \vert q^{{\prime}}(t)\vert & <& 4\beta _{ 1}q(0)(1 - q(0)),\quad \beta _{1} < 1\;{}\end{array}$$

(9b)

$$\displaystyle\begin{array}{rcl} r(x,t) \geq \min _{0\leq t\leq T}\{ \frac{q(t)} {q(0)}, \frac{1 - q(t)} {1 - q(0)}\}& =& \beta \geq 0.5\beta _{0};{}\end{array}$$

(9c)

which are more stringent than the natural constraint of $0 < q(t) < 1,\ 0 \leq t\leqslant T$.

As an example from the problem class (3), let us examine

$$\displaystyle{ q(t) = \tfrac{1} {2} + mt(1 - t),\quad f(x,t) = t(2 + t)\cos (\pi x), }$$

(10a)

$$\displaystyle{ c = b \equiv 1,\quad u(x,0) \equiv 0, }$$

(10b)

$$\displaystyle{ u(0,t) = t^{2},\quad u(1,t) = -t^{2},\quad t\leqslant T = 1. }$$

(10c)

This example has been designed so that the level one compatibility conditions (i.e. $u \in C^{0}(\bar{\varOmega })$ and $(Lu_{\varepsilon })(0,0) = f(0,0),\quad (Lu_{\varepsilon })(1,0) = f(1,0)$) at the points (0, 0), (1, 0) are satisfied. Then all the constraints (9), on the allowed time variation on the interior layer location, are met if

$$\displaystyle{\vert m\vert < 1,\qquad \beta _{0}:= 1 -\vert m\vert,\ \beta _{1}:=\vert m\vert,\quad \beta = 1 - 0.5\vert m\vert \geq 0.5\beta _{0}.}$$

Hence we take $\theta:= (1 -\vert m\vert )^{2}.$

We estimate the order of convergence using the double mesh principle [3]. The linear interpolants of the numerical solutions on the coarse and fine mesh will be denoted by $U_{I}^{N,M}$ and $U_{I}^{2N,2M}$ respectively. We compute the maximum global two-mesh differences $d_{\varepsilon }^{N,M}$ and the uniform global differences d ^N, M from

$$\displaystyle{ d_{\varepsilon }^{N,M}:=\max _{\varOmega ^{ N,M}\cup \varOmega ^{2N,2M}}\left \vert (U_{I}^{N,M} - U_{ I}^{2N,2M})(x_{ i},t_{j})\right \vert,\quad d^{N,M}:=\max _{ S_{\varepsilon }}d_{\varepsilon }^{N,M}, }$$

where $S_{\varepsilon }:=\{ 2^{0},2^{-1},\ldots,2^{-20}\}.$ From these values we calculate the corresponding computed orders of global convergence $q_{\varepsilon }^{N,M}$ and the computed orders of uniform global convergence q ^N, M using

$$\displaystyle{ q_{\varepsilon }^{N,M}:=\log _{ 2}\left (d_{\varepsilon }^{N,M}/d_{\varepsilon }^{2N,2M}\right ),\quad q^{N,M}:=\log _{ 2}\left (d^{N,M}/d^{2N,2M}\right ). }$$

(11)

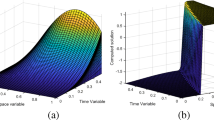
For all $\varepsilon \in S_{\varepsilon }$ the computed orders of uniform convergence q ^N, M for test problem (8), (9) and (10) for sample values of m, N are given in Table 1. A selection of particular values of global convergence $q_{\varepsilon }^{N,M},\varepsilon = 2^{-10},2^{-15},2^{-20}$ are also presented. Observe that as the parameter m approaches the limiting value of 1, the number of mesh points (N) must be sufficiently large before the asymptotic rate of convergence is established. Nevertheless, for the sample values of m examined, one observes rates of global convergence tending to rates corresponding to an error bound of the form $N^{-1}\ln N$. A sample computed solution is displayed in Fig. 1, where the interior layer is visible.

Fig. 1

Numerical approximation to solution of (8), (9) and (10); with m = 0. 5 using the numerical method (5), (6) for $\varepsilon = 2^{-12}$ and N = 128 transformed to the s and t variables using the map (7)

Table 1 Computed rates of convergence, (11), generated from applying the numerical scheme (5), (6) to test problem (8), (9) and (10) for sample values of m, N and $\varepsilon$