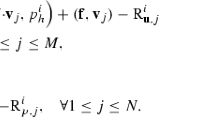A Note on the Stabilised Q₁ − P₀ Method on Quadrilaterals with High Aspect Ratios

Abstract

This work deals with the stabilisation of mixed methods for the Stokes problem on anisotropic meshes. For this, we extend a method proposed previously in Liao and Silvester (IMA J Numer Anal 33(2):413–431, 2013), to cover the case in which the mesh contains anisotropically refined corners. This modification consists of adding extra jump terms in selected edges connecting small shape regular with large anisotropic elements. We prove stability and convergence of the proposed method, and provide numerical evidence for the fact that our approach successfully removes the dependence on the anisotropy.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

This work deals with a stabilised discretisation of the Stokes problem. In a bounded, connected, polygonal domain $\varOmega \subset \mathbb{R}^{2}$, this problem reads as follows: Find a velocity $\mathbf{u}$ and a pressure p such that

$$\displaystyle{ -\varDelta \mathbf{u} + \nabla p =\mathbf{ f}\,,\quad \mathrm{div}\,\mathbf{u} = 0\quad \mbox{ in}\quad \varOmega }$$

(1)

subject to $\mathbf{u} = {\boldsymbol 0}$ on ∂ Ω and $\left < \,p\right >_{\varOmega } = 0$, where $\left < \,p\right >_{\omega }$ denotes the mean value of p over $\omega \subset \varOmega$, and $\mathbf{f} \in L^{2}(\varOmega )^{2}$ is a given source term.

For the discrete space we choose the $\mathbf{Q}_{1}\times \mathbf{P}_{0}$ pair and allow the mesh to be anisotropic. It is well known that the $\mathbf{Q}_{1}\times \mathbf{P}_{0}$ pair is not inf-sup stable (cf. [5]). Over the years several stabilised finite element methods have been proposed (see the introduction in [7] and the references therein).

In this work, we focus on the case in which the mesh used contains anisotropic elements. This possibility is considered in [7], but the method needs to be extended to accommodate the anisotropies we consider in this paper. More precisely, the method considered in [7] is an extension of the locally stabilised FEM [6]. To build the method, the mesh $\mathcal{P}$ used in the discretisation has to be a uniform refinement of an initial partition $\mathcal{P}_{0}$ (see Fig. 1). In this initial partition, each macro element M is divided into four quadrangles by connecting the mid-points of opposite edges (see Fig. 1, right). The stability of the locally stabilised method is a consequence of the stability of the $\mathbf{Q}_{2}\times \mathbf{P}_{0}$ space over the initial partition $\mathcal{P}_{0}$. Now, it is well-known (see [2]) that the following fact holds

$$\displaystyle{ \inf _{q\in \mathbf{P}_{0}}\sup _{\mathbf{v}\in \mathbf{Q}_{2}} \frac{\left (q,\mathrm{div}\,\mathbf{v}\right )_{\varOmega }} {\left \vert \mathbf{v}\right \vert _{1,\varOmega }\left \Vert q\right \Vert _{0,\varOmega }} \geq C\sqrt{\kappa }\, }$$

(2)

where $\kappa = h/H$ is the grading factor.¹ This leads to a deterioration of the stability constant when the grading factor κ tends to zero, as in Fig. 1. This dependence is still present in [7], since that method only considers jumps inside the macro-elements $M \in \mathcal{P}_{0}$, and then, in such a case, a deterioration of stability of the type (2) will not be corrected.

Fig. 1

Partition $\mathcal{P}_{0}$ (left) and $\mathcal{P}$ (right). We call this $\mathcal{P}_{0}$ corner patch

The objective of this work is to propose an extension of the method from [7] which remains uniformly stable as the grading factor goes to zero. For this, we apply the techniques recently developed in [3] and augment the method by adding jumps in selected edges of the partition $\mathcal{P}$ (not present in the original method). More precisely, we add jumps to the formulation that allow to “connect” the small (shaded) corner macro-element in $\mathcal{P}_{0}$ to the rest of the corner patch from Fig. 1.

Throughout, we use standard notation for Sobolev spaces [1]. The variational form of (1) consists of seeking $\mathbf{u} \in \mathbf{V }:=\mathbf{ H}_{0}^{1}(\varOmega )$ and $p \in M:= L_{0}^{2}(\varOmega )$ such that

$$\displaystyle{ \mathfrak{B}\left (\mathbf{u},p;\mathbf{v},q\right ) = \left (\mathbf{f},\mathbf{v}\right )_{\varOmega }\quad \mbox{ for all}\quad (\mathbf{v},q) \in \mathbf{V } \times M }$$

(3)

where

$$\displaystyle{ \mathfrak{B}\left (\mathbf{u},p;\mathbf{v},q\right ) = \left (\nabla \mathbf{u},\nabla \mathbf{v}\right )_{\varOmega } -\left (\mathrm{div}\,\mathbf{v},p\right )_{\varOmega } -\left (\mathrm{div}\,\mathbf{u},q\right )_{\varOmega }\,. }$$

(4)

Problem (3) is well-posed as consequence of inf-sup condition [5, pp. 58–61]:

$$\displaystyle{ \inf _{q\in M}\sup _{\mathbf{v}\in \mathbf{V }}\frac{\left (\mathrm{div}\,\mathbf{v},q\right )_{\varOmega }} {\left \vert \mathbf{v}\right \vert _{1,\varOmega }\left \Vert q\right \Vert _{0,\varOmega }} =\beta _{\varOmega } > 0. }$$

(5)

The rest of this paper is organised as follows. We define required notation and extend the stabilisation terms of the method in [7] by a few jumps. Then, the stability, a-priori estimates and numerical experiments are stated. These experiments confirm the dependency on the grading factor κ and that the additional jumps remove it. The proof of the main results is given after the concluding remarks. An appendix justifies the numerical experiments made.

1.1 The Finite Element Approximation

Let $\mathcal{P}$ be a given conforming partition of Ω into the union of closed parallelograms for which the non-empty intersection of distinct elements K and K′ is either a single common point or an edge of both elements. We define the spaces

$$\displaystyle{ \mathbf{Q}_{\ell,\mathcal{P}}:= \left \{\mathbf{v} \in \mathbf{V }: \mathbf{v}\vert _{K} \in \mathbb{Q}_{\ell}(K)^{2}\quad \forall K \in \mathcal{P}\right \}\,,\quad \ell = 1,2 }$$

(6)

and

$$\displaystyle{ M_{\mathcal{P}}:= \left \{q \in M: q\vert _{K} \in \mathbb{P}_{0}(K)\quad \forall K \in \mathcal{P}\right \}\,. }$$

(7)

Then, the approximation of the solution of Problem (3) is sought within $\mathbf{Q}_{1,\mathcal{P}}\times M_{\mathcal{P}}$.

It is well known that the pair $\mathbf{Q}_{1,\mathcal{P}}\times M_{\mathcal{P}}$ does not satisfy a discrete version of (5) (cf. [7] and the references therein). Adding stabilisation terms can circumvent this disadvantage. We now introduce notation and requirements on the partition $\mathcal{P}$:

• The partition $\mathcal{P}$ is a uniform refinement of a macro element partition $\mathcal{P}_{0}$. That is, each $M \in \mathcal{P}_{0}$ is split into $K_{1},K_{2},K_{3},K_{4} \in \mathcal{P}$ such that $\left \vert K_{i}\right \vert = \left \vert M\right \vert /4\,(i = 1,\ldots,4)$ by connecting the midpoints of opposite edges of $\mathcal{P}_{0}$. Here and throughout $\left \vert \omega \right \vert$ denotes the area of $\omega \subset \mathbb{R}^{2}$ and length of $\omega \subset \mathbb{R}$.

• Let $\mathcal{E}_{\mathcal{P}}$ denote the interior edges of partition $\mathcal{P}$. For each $M \in \mathcal{P}_{0}$, let $\mathcal{E}_{M}$ be the collection of its interior edges (dashed in Fig. 1, right). Every $e \in \mathcal{E}_{\mathcal{P}}$ satisfies $e = K \cap K'$, for two $K,K' \in \mathcal{P}$.

• For each corner in the initial partition $\mathcal{P}_{0}$ (shaded in Fig. 3) we select a single edge $\gamma _{\mathbf{c}} \in \mathcal{E}_{\mathcal{P}_{0}}$ that separates a (possibly) extremely small corner macro element (shaded) from a highly stretched neighbouring macro element, e.g. the embraced edges in Fig. 1 or Fig. 3. We collect all the edges $\gamma _{\mathbf{c}}$ in the set $\mathcal{E}_{c}$.

Now, we present the stabilised method: Find $(\mathbf{u}_{\mathcal{P}}^{s},p_{\mathcal{P}}^{s}) \in \mathbf{ Q}_{1,\mathcal{P}}\times M_{\mathcal{P}}$ such that

$$\displaystyle{ \mathfrak{B}_{s}\left (\mathbf{u}_{\mathcal{P}}^{s},p_{ \mathcal{P}}^{s};\mathbf{v},q\right ) = \left (\mathbf{f},\mathbf{v}\right )_{\varOmega }\quad \mbox{ for all}\quad (\mathbf{v},q) \in \mathbf{ Q}_{ 1,\mathcal{P}}\times M_{\mathcal{P}}\,. }$$

(8)

Here,

$$\displaystyle{ \mathfrak{B}_{s}\left (\mathbf{u},p;\mathbf{v},q\right ) = \mathfrak{B}\left (\mathbf{u},p;\mathbf{v},q\right ) -\frac{1} {4}\widetilde{S}(\,p;q)\,, }$$

(9)

the stabilisation terms are

$$\displaystyle{ \widetilde{S}(\,p;q):=\sum _{M\in \mathcal{P}_{0}}S_{M}(\,p;q) +\sum _{\gamma _{\mathbf{c}}\in \mathcal{E}_{c}}S_{\gamma _{\mathbf{c}}}(\,p;q) }$$

(10)

where, if $\left [\![\cdot \right ]\!]$ stands for the jump of a function across edge $e = K \cap K'$, then

$$\displaystyle{\begin{array}{lll} S_{M}(\,p;q)&:=&\sum _{e\in \mathcal{E}_{M}}\frac{\left \vert M\right \vert } {4\left \vert e\right \vert }\int _{e}\left [\![\,p\right ]\!]\left [\![q\right ]\!]\,\mathrm{d}s\,, \\ S_{\gamma _{\mathbf{c}}}(\,p;q) &:=&\sum _{e\subset \gamma _{\mathbf{c}}}\frac{\min \left \{\left \vert K\right \vert,\left \vert K'\right \vert \right \}} {\left \vert e\right \vert } \int _{e}\left [\![\,p\right ]\!]\left [\![q\right ]\!]\,\mathrm{d}s\,.\end{array} }$$

Remark

The method proposed in [7] seeks $(\mathbf{u},p) \in \mathbf{ Q}_{1,\mathcal{P}}\times M_{\mathcal{P}}$, such that

$$\displaystyle{ \mathfrak{B}\left (\mathbf{u},p;\mathbf{v},q\right ) -\frac{1} {4}\sum _{M\in \mathcal{P}_{0}}S_{M}(\,p;q) = \left (\mathbf{f},\mathbf{v}\right )_{\varOmega }\quad \mbox{ for all}\quad (\mathbf{v},q) \in \mathbf{ Q}_{1,\mathcal{P}}\times M_{\mathcal{P}}\,. }$$

(11)

Then, the difference is given by additional jumps across a few selected edges.

For simplicity, we restrict ourselves to axis-parallel meshes (although the results can be easily extended to meshes consisting of parallelograms). We summarise the existence and a-priori results here, the proofs are postponed until after the numerical experiments.

Theorem 1

Let $\left \vert \!\left \vert \!\left \vert (\mathbf{v},q)\right \vert \!\right \vert \!\right \vert ^{2}:= \left \vert \mathbf{v}\right \vert _{1,\varOmega }^{2} + \left \Vert q\right \Vert _{0,\varOmega }^{2}$ . Then, there exists a constant μ _s > 0 independent of grading factors κ and aspect ratios $\varrho$ , such that

$$\displaystyle{ \sup _{(\mathbf{v},q)\in \mathbf{Q}_{1,\mathcal{P}}\times M_{\mathcal{P}}}\frac{\mathfrak{B}_{s}\left (\mathbf{w},r;\mathbf{v},q\right )} {\left \vert \!\left \vert \!\left \vert (\mathbf{v},q)\right \vert \!\right \vert \!\right \vert } \geq \mu _{s}\,\left \vert \!\left \vert \!\left \vert (\mathbf{w},r)\right \vert \!\right \vert \!\right \vert \quad \mbox{ for all}\quad (\mathbf{w},r) \in \mathbf{ Q}_{1,\mathcal{P}}\times M_{\mathcal{P}}\,. }$$

(12)

Consequently, Problem (8) has a unique solution $(\mathbf{u}_{\mathcal{P}}^{s},p_{\mathcal{P}}^{s}) \in \mathbf{ Q}_{1,\mathcal{P}}\times M_{\mathcal{P}}$ . Moreover, if $p \in H^{1}(\varOmega )$ , then there exists a positive constant C such that

$$\displaystyle\begin{array}{rcl} & & \left \vert \!\left \vert \!\left \vert (\mathbf{u} -\mathbf{ u}_{\mathcal{P}}^{s},p - p_{ \mathcal{P}}^{s})\right \vert \!\right \vert \!\right \vert \leq (1 + C\mu _{ s}^{-1})\bigg\{\sum _{ K\in \mathcal{P}}\Big(h_{K,x}\left \Vert \partial _{x}p\right \Vert _{0,K} + h_{K,y}\left \Vert \partial _{y}p\right \Vert _{0,K}\Big) \\ & & \qquad \qquad \qquad \qquad \qquad \qquad +\inf _{(\mathbf{v}_{\mathcal{P}},q_{\mathcal{P}})\in \mathbf{Q}_{1,\mathcal{P}}\times M_{\mathcal{P}}}\left \vert \!\left \vert \!\left \vert (\mathbf{u} -\mathbf{ v}_{\mathcal{P}},p - q_{\mathcal{P}})\right \vert \!\right \vert \!\right \vert \bigg\} {}\end{array}$$

(13)

where h _K,x and h _K,y is the length of cell $K \in \mathcal{P}$ in x- and y-direction, respectively.

Fig. 2

Stability constants μ _s in (12) and $\xi$ in [7, (3.12)] for various grading factors κ. Left: on the mesh of Fig. 1, right: on mesh in Fig. 3

Fig. 3

An anisotropic mesh on a T-shaped domain

1.2 Numerical Results

We compare μ _s from (12) and the stability constant $\xi$ from [7] given by

$$\displaystyle{\xi =\inf _{(\mathbf{w},r)\in \mathbf{Q}_{1,\mathcal{P}}\times M_{\mathcal{P}}}\sup _{(\mathbf{v},q)\in \mathbf{Q}_{1,\mathcal{P}}\times M_{\mathcal{P}}}\frac{\mathfrak{B}\left (\mathbf{w},r;\mathbf{v},q\right ) - 4^{-1}\sum _{M\in \mathcal{P}_{0}}S_{M}(r;q)} {\left \vert \!\left \vert \!\left \vert (\mathbf{v},q)\right \vert \!\right \vert \!\right \vert \left \vert \!\left \vert \!\left \vert (\mathbf{w},r)\right \vert \!\right \vert \!\right \vert } \,.}$$

The experiments in Fig. 2 were performed on partitions $\mathcal{P}$ shown in Fig. 1 (right) and Fig. 3 on the domains $\varOmega = (-3,3)\times (0,2) \cup (-1,1)\times (-2,0]$ and Ω = (0, 1)×(0, 1), respectively. The set of additional edges $\mathcal{E}_{c}$ was set to contain all edges enclosed by a jump symbol $\left [\![\cdot \right ]\!]$. We observe for κ → 0, that while μ _s remains uniformly bounded away from zero, $\xi$ degrades and tends to zero. Hence, the additional jumps correct the dependency of $\xi$ on κ. We used Corollary 1 (cf. Appendix) to calculate the values of $\xi$ and μ _s .

1.3 Conclusions

In this work we have extended the method from [7] to cover the case in which the meshes contain anisotropically refined corners. We have enhanced the aforementioned method with selected, appropriately weighted jumps that improve the stability constant by curing its dependency on the grading factor. Finally, it is worth mentioning that the refinement strategy proposed in [7] leads to meshes for which the method is as stable as it was on the initial mesh. This explains some numerical results in that reference, since the original mesh used was shape-regular.

2 Proof of Stability

In this section we prove the stability estimate (12). We start by deriving a uniformly inf-sup-stable subspace $G \subset M_{\mathcal{P}}$ and an inf-sup deficiency. To this end, we recall the definition of $\mathcal{E}_{c}$.

Lemma 1

For the subspace $G \subset M_{\mathcal{P}_{0}} \subset M_{\mathcal{P}}$ , defined by

$$\displaystyle{ G:= \left \{q \in M_{\mathcal{P}_{0}}: \left [\![q\right ]\!]_{\gamma _{\mathbf{c}}} = 0\quad \mbox{ for}\quad \gamma _{\mathbf{c}} \in \mathcal{E}_{c}\right \}, }$$

(14)

there exists a constant β _G independent of aspect ratios and grading factors such that

$$\displaystyle{ \sup _{\mathbf{v}_{\mathcal{P}}\in \mathbf{Q}_{1,\mathcal{P}}}\frac{\left (\mathrm{div}\,\mathbf{v}_{\mathcal{P}},q_{\mathcal{P}}\right )_{\varOmega }} {\left \vert \mathbf{v}_{\mathcal{P}}\right \vert _{1,\varOmega }} \geq \beta _{G}\left \Vert q_{\mathcal{P}}\right \Vert _{0,\varOmega }\quad \mbox{ for all}\quad q \in G\,. }$$

(15)

Proof

We reason by similarity of the velocity spaces $\mathbf{Q}_{1,\mathcal{P}}$ and $\mathbf{Q}_{2,\mathcal{P}_{0}}$. For the pair $\mathbf{Q}_{2,\mathcal{P}_{0}} \times G$ the result is a consequence of [3, Theorem 1]. □

The result above induces the following inf-sup deficiency of $\mathbf{Q}_{1,\mathcal{P}}\times M_{\mathcal{P}}$.

Lemma 2

Let $G$ be defined by (14) and let $\varPi _{G}: M_{\mathcal{P}}\rightarrow G$ be an operator. Then

$$\displaystyle{ \sup _{\mathbf{v}\in \mathbf{Q}_{1,\mathcal{P}}}\frac{\left (\mathrm{div}\,\mathbf{v},q\right )_{\varOmega }} {\left \vert \mathbf{v}\right \vert _{1,\varOmega }} \geq \beta _{G}\left \Vert \varPi _{G}q\right \Vert _{0,\varOmega } -\left \Vert q -\varPi _{G}q\right \Vert _{0,\varOmega }\quad \mbox{ for all}\quad q \in M_{\mathcal{P}}\,. }$$

(16)

Furthermore, if $\varPi _{G}q = q$ for all $q \in G$ , then (16) implies (15).

Proof

Let $q \in M_{\mathcal{P}}$, then $\varPi _{G}q \in G$ and by (15) there exists a non-zero $\mathbf{v} \in \mathbf{ Q}_{1,\mathcal{P}}$ such that

$$\displaystyle{\beta _{G}\left \vert \mathbf{v}\right \vert _{1,\varOmega }\left \Vert \varPi _{G}q\right \Vert _{0,\varOmega } \leq \left (\mathrm{div}\,\mathbf{v},\varPi _{G}q\right )_{\varOmega } \leq \left \vert \mathbf{v}\right \vert _{1,\varOmega }\left \Vert q -\varPi _{G}q\right \Vert _{0,\varOmega } + \left (\mathrm{div}\,\mathbf{v},q\right )_{\varOmega }\,.}$$

Dividing by $\left \vert \mathbf{v}\right \vert _{1,\varOmega }$ gives (16) for one $\mathbf{v} \in \mathbf{ Q}_{1,\mathcal{P}}$. The rest follows easily. □

The last results can be read as follows: The inf-sup deficiency (2) is caused by functions whose jumps do not vanish across edges in $\mathcal{E}_{c}$. Then, in the rest of this section, we show that it is enough to control such jumps to obtain uniform stability.

We recall that each selected edge $\gamma _{\mathbf{c}} \in \mathcal{E}_{c}$ can be written as $\gamma _{\mathbf{c}} = M \cap M'$ where $M,M' \in \mathcal{P}_{0}$ and M is the small and M′ is the large one. In order to simplify the proof we define $\omega _{\gamma _{\mathbf{ c}}}:= M \cup M'$. Now, let $G$ be defined by (14) and let $\varPi _{G}: M_{\mathcal{P}}\rightarrow G$ be the L ²-projection given by the rule

$$\displaystyle{ \varPi _{G}q\big\vert _{M} = \left \{\begin{array}{@{}l@{\quad }l@{}} \left < q\right >_{\omega _{\gamma _{\mathbf{c}}}} \quad &\text{if }M \subset \omega _{\gamma _{\mathbf{c}}}\,, \\ \left < q\right >_{M}\quad &\text{otherwise.} \end{array} \right. }$$

(17)

Now, Lemma 3 proves properties of the stabilisation terms (10). The proof uses the characteristic function on subdomains $\omega \subset \overline{\varOmega }$ given by

$$\displaystyle{\chi _{\omega }(\mathbf{x}):= \left \{\begin{array}{@{}l@{\quad }l@{}} 1\quad &\text{if }\mathbf{x} \in \omega \,,\\ 0\quad &\text{otherwise.} \end{array} \right.}$$

Lemma 3

Let $q_{\mathcal{P}}\in M_{\mathcal{P}}$ . On $M \in \mathcal{P}_{0}$ with $M\not\subset \omega _{\gamma _{\mathbf{c}}}$ we have the equivalence

$$\displaystyle{ 2\left \|q_{\mathcal{P}}-\varPi _{G}q_{\mathcal{P}}\right \|_{0,M}^{2} \leq S_{ M}(q_{\mathcal{P}};q_{\mathcal{P}}) \leq 4\left \|q_{\mathcal{P}}-\varPi _{G}q_{\mathcal{P}}\right \|_{0,M}^{2}\,, }$$

(18a)

on $\omega _{\gamma _{\mathbf{c}}} = M \cup M'$ we have

$$\displaystyle{ \frac{1} {4}\left \|q_{\mathcal{P}}-\varPi _{G}q_{\mathcal{P}}\right \|_{0,\omega _{\gamma _{\mathbf{c}}}}^{2} \leq \big (S_{ M} + S_{M'} + S_{\gamma _{\mathbf{c}}}\big)(q_{\mathcal{P}};q_{\mathcal{P}}) \leq 6\left \|q_{\mathcal{P}}-\varPi _{G}q_{\mathcal{P}}\right \|_{0,\omega _{\gamma _{\mathbf{c}}}}^{2}\,. }$$

(18b)

Furthermore, let $\widetilde{S}\vert _{M}:= S_{M}$ and $\widetilde{S}\vert _{\omega _{\gamma _{\mathbf{c}}}}:= S_{M} + S_{M'} + S_{\gamma _{\mathbf{c}}}$ , then

$$\displaystyle{ \left.\widetilde{S}(q_{\mathcal{P}};q_{\mathcal{P}})\right \vert _{\omega }\leq C\left \{\begin{array}{@{}l@{\quad }l@{}} \left \Vert q_{\mathcal{P}}\right \Vert _{0,\omega }^{2} \quad \\ \sum _{K\subset \omega }\left (\left \Vert p - q_{\mathcal{P}}\right \Vert _{0,K}^{2} + h_{K,x}^{2}\left \Vert \partial _{x}p\right \Vert _{0,K}^{2} + h_{k,y}^{2}\left \Vert \partial _{y}p\right \Vert _{0,K}^{2}\right )\quad \end{array} \right. }$$

(19)

for all $p \in H^{1}(\varOmega )$ , where $\omega = M \in \mathcal{P}_{0}$ or $\omega =\omega _{\gamma _{\mathbf{c}}}$ .

Proof

Equivalence (18a) has been proved in [7], however, we include an alternative proof because it supplies us with notation and arguments for (18b). To this end, let $M \in \mathcal{P}_{0}$ be a 2-by-2 macro element such that $M\not\subset \omega _{\gamma _{\mathbf{c}}}$, $\gamma _{\mathbf{c}} \in \mathcal{E}_{c}$. We define $r_{a}:= \left.(q_{\mathcal{P}}-\varPi _{G}q_{\mathcal{P}})\right \vert _{M}$ and realise $r_{a} \in M_{\mathcal{P}}\cap L_{0}^{2}(M)$. Since, all cells $K \subset M$ have the same area, an orthogonal (w.r.t. the inner product in L ²) basis of $M_{\mathcal{P}}\cap L_{0}^{2}(M)$ is given by (cf. Fig. 4, left)

$$\displaystyle{ \begin{array}{lll} \phi _{1,M}&:=&\chi _{K_{1}} -\chi _{K_{2}}\,, \\ \phi _{2,M}&:=&\chi _{K_{1}\cup K_{2}} -\chi _{K_{3}\cup K_{4}}\,, \\ \phi _{3,M}&:=&\chi _{K_{3}} -\chi _{K_{4}}\,. \end{array} }$$

(20)

Fig. 4

A macro element $M \in \mathcal{P}_{0}$ (left) and set $\omega _{\gamma _{\mathbf{ c}}}$ (right) with cells $K_{i,M} \in \mathcal{P}$

Below, we omit the subscript M when it is clear from the context. Therefore, by definition (20) we get $r_{a} =\sum _{ i=1}^{3}\alpha _{i}\phi _{i,M}$. Then, using $\left \vert K_{i}\right \vert = \left \vert M\right \vert /4,\,(i = 1,\ldots,4)$ and adding the jumps counter-clockwise we get

$$\displaystyle\begin{array}{rcl} S_{M}(q_{\mathcal{P}};q_{\mathcal{P}})& =& \frac{\left \vert M\right \vert } {4} \sum _{e\in \mathcal{E}_{M}}\frac{1} {\left \vert e\right \vert }\int _{e}\left [\![q_{\mathcal{P}}\right ]\!]^{2} = \frac{\left \vert M\right \vert } {4} \sum _{e\in \mathcal{E}_{M}}\frac{1} {\left \vert e\right \vert }\int _{e}\left [\![r_{a}\right ]\!]^{2} = \frac{\left \vert M\right \vert } {4} \sum _{e\in \mathcal{E}_{M}}\left [\![r_{a}\right ]\!]_{e}^{2} \\ & =& \frac{\left \vert M\right \vert } {4} \left [(2\alpha _{1})^{2} + (2\alpha _{ 2} -\alpha _{1} -\alpha _{3})^{2} + (2\alpha _{ 3})^{2} + (-2\alpha _{ 2} -\alpha _{3} -\alpha _{1})^{2}\right ] \\ & =& \frac{\left \vert M\right \vert } {4} \left [4\alpha _{1}^{2} + 4\alpha _{ 3}^{2} + 8\alpha _{ 2}^{2} + 2(\alpha _{ 1} +\alpha _{3})^{2}\right ] \\ & =& 2\left \Vert \alpha _{1}\phi _{1}\right \Vert _{0,M}^{2} + 2\left \Vert \alpha _{ 3}\phi _{3}\right \Vert _{0,M}^{2} + 2\left \Vert \alpha _{ 2}\phi _{2}\right \Vert _{0,M}^{2} + \frac{\left \vert M\right \vert } {2} (\alpha _{1} +\alpha _{3})^{2} \\ & =& 2\left \Vert r_{a}\right \Vert _{0,M}^{2} + \frac{\left \vert M\right \vert } {2} (\alpha _{1} +\alpha _{3})^{2}\,, {}\end{array}$$

(21)

which proves the lower bound of (18a). Applying $(\alpha _{1} +\alpha _{3})^{2}\left \vert M\right \vert /2 \leq 2\left \Vert r_{a}\right \Vert _{0,M}^{2}$ proves the upper bound. Now, we fix an edge $\gamma _{\mathbf{c}} \in \mathcal{E}_{c}$ and let $r_{b}:= \left.(q_{\mathcal{P}}-\varPi _{G}q_{\mathcal{P}})\right \vert _{\omega _{\gamma _{\mathbf{c}}}}$. Then $r_{b} =\alpha _{0}\phi _{0} + r_{a} + r_{a}'$, where $\phi _{0} = \left \vert M\right \vert ^{-1}\chi _{M} -\left \vert M'\right \vert ^{-1}\chi _{M'}$ and $r_{a} =\sum _{ i=1}^{3}\alpha _{i}\phi _{i,M}$ and $r_{a}' =\sum _{ i=1}^{3}\alpha _{i}'\phi _{i,M'}$. Using (21), the definition of ϕ ₀ and $\left \vert K\right \vert \leq \left \vert K'\right \vert$ (since $\left \vert M\right \vert \leq \left \vert M'\right \vert$), the stabilisation terms (10) inside $\omega _{\gamma _{\mathbf{c}}}$ satisfy

$$\displaystyle{ \big(S_{M} + S_{M'} + S_{\gamma _{\mathbf{c}}}\big)(q_{\mathcal{P}};q_{\mathcal{P}}) \geq 2\left \Vert r_{a}\right \Vert _{0,M}^{2} + 2\left \Vert r_{ a}'\right \Vert _{0,M'}^{2} +\sum _{ e\subset \gamma _{\mathbf{c}}}\frac{\left \vert K\right \vert } {\left \vert e\right \vert } \int _{e}\left [\![r_{b}\right ]\!]^{2} }$$

(22)

where the two additional edges $e \subset \gamma _{\mathbf{c}}$ satisfy $e \subset M \cap M'$.

We only need a lower bound for the last term. In fact

$$\displaystyle{\begin{array}{ll} &\sum _{e\subset \gamma _{\mathbf{c}}}\int _{e}\frac{\left [\![r_{b}\right ]\!]^{2}} {\left \vert e\right \vert } \\ &\qquad = \left (\left [\![\alpha _{0}\phi _{0}\right ]\!]_{\gamma _{\mathbf{c}}} -\alpha _{2} +\alpha _{2}' -\alpha _{3} -\alpha _{3}'\right )^{2} + \left (\left [\![\alpha _{0}\phi _{0}\right ]\!]_{\gamma _{\mathbf{c}}} +\alpha _{2} -\alpha _{2}' -\alpha _{1} -\alpha _{1}'\right )^{2} \\ & \qquad = 2\left [\![\alpha _{0}\phi _{0}\right ]\!]_{\gamma _{\mathbf{c}}}^{2} + 2(\alpha _{2} -\alpha _{2}')^{2} + (\alpha _{1} +\alpha _{1}')^{2} + (\alpha _{3} +\alpha _{3}')^{2} \\ & \qquad \quad - 2(\left [\![\alpha _{0}\phi _{0}\right ]\!]_{\gamma _{\mathbf{c}}} +\alpha _{2} -\alpha _{2}')(\alpha _{1} +\alpha _{1}') - 2(\left [\![\alpha _{0}\phi _{0}\right ]\!]_{\gamma _{\mathbf{c}}} -\alpha _{2} +\alpha _{2}')(\alpha _{3} +\alpha _{3}') \\ &\qquad \geq \left [\![\alpha _{0}\phi _{0}\right ]\!]_{\gamma _{\mathbf{c}}}^{2} + (\alpha _{2} -\alpha _{2}')^{2} - (\alpha _{1} +\alpha _{1}')^{2} - (\alpha _{3} +\alpha _{3}')^{2} \\ & \qquad \geq \left [\![\alpha _{0}\phi _{0}\right ]\!]_{\gamma _{\mathbf{c}}}^{2} + (\alpha _{2} -\alpha _{2}')^{2} - 2(\alpha _{1}^{2} +\alpha _{1}'^{2} +\alpha _{ 3}^{2} +\alpha _{3}'^{2})\,.\end{array} }$$

By multiplying with $\left \vert K\right \vert = \left \vert M\right \vert /4 \leq \left \vert M'\right \vert /4$ we get

$$\displaystyle{\left \vert K\right \vert \left [\![\alpha _{0}\phi _{0}\right ]\!]_{\gamma _{\mathbf{c}}}^{2} =\alpha _{ 0}^{2}\frac{\left \vert M\right \vert } {4} \left ( \frac{1} {\left \vert M\right \vert } + \frac{1} {\left \vert M'\right \vert }\right )^{2} \geq \frac{1} {4}\alpha _{0}^{2}\left ( \frac{1} {\left \vert M\right \vert } + \frac{1} {\left \vert M'\right \vert }\right ) = \frac{1} {4}\left \|\alpha _{0}\phi _{0}\right \|_{0,\omega _{\gamma _{\mathbf{c}}}}^{2}}$$

and

$$\displaystyle{\begin{array}{lll} 2\left \vert K\right \vert \left (\alpha _{1}^{2} +\alpha _{1}'^{2} +\alpha _{ 3}^{2} +\alpha _{3}'^{2}\right )& \leq &\frac{\left \vert M\right \vert } {2} (\alpha _{1}^{2} +\alpha _{ 3}^{2}) + \frac{\left \vert M'\right \vert } {2} (\alpha _{1}'^{2} +\alpha _{ 3}'^{2}) \\ & \leq &\left \Vert r_{a}\right \Vert _{0,M}^{2} + \left \Vert r_{a}'\right \Vert _{0,M}^{2}\,. \end{array} }$$

Gathering (22), these estimates and using the fact that ϕ ₀ is orthogonal to ϕ _i, M and ϕ _i, M′ yields the lower bound

$$\displaystyle{ \big(S_{M} + S_{M'} + S_{\gamma _{\mathbf{c}}}\big)(q_{\mathcal{P}};q_{\mathcal{P}}) \geq \left \Vert r_{a}\right \Vert _{0,M}^{2} + \left \Vert r_{ a}'\right \Vert _{0,M}^{2} + \frac{1} {4}\left \|\alpha _{0}\phi _{0}\right \|_{0,\omega _{\gamma _{\mathbf{c}}}}^{2} \geq \frac{1} {4}\left \Vert r_{b}\right \Vert _{0,\omega _{\gamma _{\mathbf{c}}}}^{2}\,. }$$

(23)

The upper bound follows using that r _b is constant on each $K \subset \omega _{\gamma _{\mathbf{c}}}$ with value r _K and that jumps across at most three edges $e \subset \partial K$ are penalised, i.e.

$$\displaystyle\begin{array}{rcl} & & \qquad \quad \big(S_{M} + S_{M'} + S_{\gamma _{\mathbf{c}}}\big)(q_{\mathcal{P}};q_{\mathcal{P}}) =\big (S_{M} + S_{M'} + S_{\gamma _{\mathbf{c}}}\big)(r_{b};r_{b}) {}\\ & & \leq \sum _{e\in \mathcal{E}_{M}\cup \mathcal{E}_{M'}\cup \left \{e: e\subset \gamma _{\mathbf{c}}\right \}}2\frac{\left \vert K\right \vert } {\left \vert e\right \vert } \int _{e}(r_{K}^{2} + r_{ K'}^{2}) \leq 6\sum _{ K\subset \omega _{\gamma _{\mathbf{c}}}}\left \vert K\right \vert r_{K}^{2} = 6\left \Vert r_{ b}\right \Vert _{0,\omega _{\gamma _{\mathbf{c}}}}^{2}\,. {}\\ \end{array}$$

Now, equivalence (18b) follows from estimate (23) and this upper bound.

The first estimate in (19) is a consequence of (18) and $\left \|q_{\mathcal{P}}-\varPi _{G}q_{\mathcal{P}}\right \|_{0,\omega }^{2} + \left \|\varPi _{G}q_{\mathcal{P}}\right \|_{0,\omega }^{2} = \left \|q_{\mathcal{P}}\right \|_{0,\omega }^{2}$ for $\omega = M \in \mathcal{P}_{0}$ or $\omega =\omega _{\gamma _{\mathbf{c}}}$. Finally, the second estimate in (19) follows using $p \in H^{1}(M)$ and the arguments used to prove [7, Estimate (3.24)]. □

Proof (of Theorem 1)

First, by Lemma 1 we notice that the pressure space $M_{\mathcal{P}}$ contains a uniformly inf-sup stable subspace $G$. Then, thanks to (18), the stabilisation terms control the non-stable part of $M_{\mathcal{P}}$. Then, (12) follows by standard arguments, as in [3, 4, 7]. Using (19) the a-priori estimate also follows known arguments, see for instance [3]. □

Appendix

For completeness we include a standard result Lemma 4. Corollary 1 is a direct consequence of Lemma 4 and justifies our numerical experiments.

Lemma 4

Let $\mathcal{A},\mathcal{B}\in \mathbb{R}^{n\times n}$ be symmetric matrices and let $\mathcal{B}$ be positive definite.Then, the generalised eigenvalue problem

$$\displaystyle{ \mathcal{A}\mathbf{v} =\xi \, \mathcal{B}\mathbf{v}\,, }$$

(24)

has n real eigenvalues $\left \{\xi _{i}\right \}_{i}$ , and an $\mathcal{A},\mathcal{B}$ -orthogonal basis of eigenvectors of $\mathbb{R}^{n}$ , $\left \{\mathbf{v}_{i}\right \}_{i}$ , such that

$$\displaystyle{ \left < \mathbf{v}_{j},\mathcal{A}\mathbf{v}_{i}\right > =\xi _{i}\,\delta _{ij}\quad \mbox{ and}\quad \left < \mathbf{v}_{j},\mathcal{B}\mathbf{v}_{i}\right > =\delta _{ij}\,. }$$

(25)

Moreover, we have the (sharp) discrete inf-sup condition:

$$\displaystyle{ \sup _{\mathbf{v}\in \mathbb{R}^{n}} \frac{\mathbf{v}^{\top }\mathcal{A}\mathbf{u}} {\sqrt{\mathbf{v}^{\top } \mathcal{B}\mathbf{v}}} \geq \left \vert \xi _{1}\right \vert \sqrt{\mathbf{u}^{\top } \mathcal{B}\mathbf{u}}\quad \mbox{ for all}\quad \mathbf{u} \in \mathbb{R}^{n} }$$

(26)

where $\xi _{1}$ is an eigenvalue of problem (24) of smallest magnitude.

Proof

A proof for a special case is given in [8, Section 3.B]. The extension to the general case presented here is straightforward. □

Corollary 1

Let $\mathfrak{B}$ be as in (4) and let $s: M_{\mathcal{P}}\times M_{\mathcal{P}}\rightarrow \mathbb{R}$ be an arbitrary symmetric non-negative bilinear form. Then

$$\displaystyle{\inf _{(\mathbf{u},p)\in \mathbf{Q}_{1,\mathcal{P}}\times M_{\mathcal{P}}}\sup _{(\mathbf{v},q)\in \mathbf{Q}_{1,\mathcal{P}}\times M_{\mathcal{P}}}\frac{\mathfrak{B}\left (\mathbf{u},p;\mathbf{v},q\right ) - s(\,p;q)} {\left \vert \!\left \vert \!\left \vert (\mathbf{v},q)\right \vert \!\right \vert \!\right \vert \left \vert \!\left \vert \!\left \vert (\mathbf{u},p)\right \vert \!\right \vert \!\right \vert } = \left \vert \xi _{1}\right \vert }$$

where $\xi _{1}$ is an eigenvalue of smallest magnitude of the problem

$$\displaystyle{ \left (\begin{array}{*{10}c} A & B\\ B^{\top } &-S \end{array} \right )\mathcal{U} =\xi \left (\begin{array}{*{10}c} A& 0\\ 0 &M \end{array} \right )\mathcal{U} }$$

(27)

with matrices A,B and S defined as usual from $\mathfrak{B}$ and s, the mass-matrix M on the pressure space $M_{\mathcal{P}}$ and $\mathcal{U}\in \mathbb{R}^{n},\,n =\dim (\mathbf{Q}_{1,\mathcal{P}}\times M_{\mathcal{P}})$ .