Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
5.1 Introduction
As discussed in Chaps. 2 and 3, a wide variety of experimental techniques have allowed to obtain a wealth of information of upd systems. This information concerns:
-
Structure of the adsorbed monolayer, as determined by GIXS, surface EXAFS , X-ray standing waves , SHG, and SPM (AFM, STM) techniques.
-
Coverage degree of the different adsorbed species as a function of the applied potential, as determined from cyclic or linear sweep voltammograms under quasi-equilibrium conditions (at slow sweep rates), from the integral analysis of potentiostatic and galvanostatic transients, or from radiometric measurements.
-
Kinetic information, via transient electrochemical techniques, eventually coupled to some of the other in situ techniques, as long as the time scale of the evens allows it.
-
Chemical information, as the oxidation state of the adsorbate, as obtained from XANES.
-
Ex situ information on structure using LEED, RHEED and chemical composition (using AES).
It will come out below that depending on the type of property to be analyzed, there are different theoretical approaches that may be used with interpretative or predictive purposes.
The first attempt to understand a given problem within upd starts with a model, that is, a description of the upd problem using mathematical concepts and language.
According to quantum mechanics, the most precise description that we can get for a system, stems from its wave function Ψ(r, R, t), which can be obtained from the solution of Schrödinger equation :
where we have emphasized that the wave function is a function of the coordinates of the light (electrons) the heavy (nuclei) particles, and the time, which were denoted with r, R and t respectively. Ĥ is the Hamiltonian of the system, which contains the kinetic energy of all the particles and the potential energy describing the interaction between them, say U(r, R, t). To the best of our knowledge, the dynamic Eq. (5.1) has never been solved for an upd system. The closest that has been done to the problem stated in Eq. (5.1) in the upd field was the resolution of the dynamic behavior of a system of electrons, with the purpose of calculating the plasmon spectrum of Au nanoparticles decorated with upd Ag atoms [1]. In the case that Ĥ is time independent, the previous problem reduces to the resolution of the eigenvalue equation:
where E corresponds to the energy eigenvalues. In order to make the latter equation solvable, a further simplification is required: the Born-Oppenheimer approximation , where the wave function is splitted as:
where ψelec and ψnuc correspond to wave function of the electrons and nucleus, respectively. The latter approximation leads to two further equations:
where Ĥel is an operator that contains the kinetic energy of electrons and the electron–electron and electron-nuclei potential energy interactions. Thus, Ĥel and the eigenvalues E el(R) in Eq. (5.4) contain the nuclear coordinates as parameters. Making some further approximations, many of the computer codes based on Density Functional Theory (DFT) (see Sect. 5.2 below) are able to solve Eq. (5.4) quite accurately for a few tens of atoms. Eq. (5.5) is the wave equation for the nuclei of the system, moving in a potential energy provided by the nuclei-nuclei interaction energy and the potential energy delivered by the eigenvalues E nuc. In most cases, the inner electrons (core electrons) are frozen to solve Eq. (5.4), so Eq. (5.5) actually represents the motion of ion cores. For elements heavier than hydrogen and relatively high temperatures, Eq. (5.5) is usually replaced by its classical version:
where m i is the mass, the index i runs over the N heavy particles of the system 5 and f i is the force exerted on particle i. The f i can be calculated from the potential energy of the system U({R i }) according to:
where (x i , y i , x i ) are the cartesian coordinates of particle i. As stated above, the potential energy for an arbitrary atomic configuration can be obtained from the eigenvalues E nuc and the repulsive interaction between the heavy particles. Thus, the resolution of equations of motion (5.6) using the eigenvalues (5.4) along with Eqs. (5.7) and (5.4) would allow to describe the time evolution of the system. Unfortunately, such a resolution can be made, with the most powerful computers nowadays available, for times of the order of picoseconds for a reduced number of atoms. Thus, what can quantum mechanics be of aid to the upd problem? As stated above, Eq. (5.4) can be solved very efficiently with modern computer codes for a given configuration. The eigenvalues E el(R), together with the repulsive interaction between heavy particles yields the potential energy U({R}). Thus, theoreticians can obtain efficiently equilibrium configurations by solving the problem:
With the information resulting from these calculations, relevant (static) physical quantities can be obtained, like lattice contants, bulk modulus and surface energies, which can be compared with experiment to check the accuracy of the obtained results. Some first-principles results are compared with experimental values in Table 5.1, showing a reasonably good overall agreement. Similarly, the binding energy of an adatom on a foreign substrate can be obtained with a good accuracy, and underpotential shifts, as were discussed in Chap. 3, can be calculated quite accurately. A detailed discussion on the application of first-principles calculations to upd is given in the following Sect. 5.2.
To summarize this introductory discussion on the application of first-principles calculations to upd, we can state that these methods may deliver essentially information on static equilibrium properties, like lattice constants and binding energies. Other electronic properties like densities of states, partial charges of adsorbates and some basic vibrational properties, in the harmonic approximation, can also be obtained. Thus, all the analysis is usually restricted to ground-state properties (0 K) or same elementary vibrational properties.
To move forward to the prediction of other properties of upd system, like those involving a finite temperature, we get into the realm of statistical mechanics. Using the two postulates of statistical mechanics [3], it can be shown that the eigenvalues of Eq. (5.2) may be used to predict any equilibrium property of the system. For example, considering a system of N particles enclosed in a volume V at temperature T it can be shown that the average value of a mechanical property A may be calculated through:
where the brackets denotes statistical average, the sum runs over all the i energy states of the system, say E i ; A i is the value of A at the state i and the probability of observing it is given by:
The denominator of this equation is the so-called canonical partition function, usually denoted with Q. The classical versions of Eqs. (5.9) and (5.10) look very similar, but replacing the state sums by the integrals over momenta (p) and configurational space (r). In the case of the partition sum, we have:
where Ĥ(r, p) is the classical Hamiltonian of the system, h is the Planck constant. Thus, the probability density becomes:
Since the Hamiltonian can be usually separated into space and momentum components, \( \widehat{\mathrm{H}}\left(\mathbf{r},\mathbf{p}\right)=K\left(\mathbf{p}\right)+V\left(\mathbf{r}\right) \), Eq. (5.12) can be splitted as:
The previous equation may be integrated over the momenta to give:
Which yields the probability density of finding a given configuration independently from the momentum of the particles. The denominator of this equation is termed configuration integral, since the integral runs over all possible configurations of the system.
In the case where the number of particles in a system fluctuates in a constant volume V, in contact with a reservoir at the chemical potential , μ , the equations for the partition function (5.11) and probability density (5.14) must be replaced by:
where we note the occurrence of a new sum over the number of particles. The present statistical mechanical description is often used to describe the electrochemical interphase, since the latter may be envisaged as an open system with respect to the particles being absorbed, while the volume under study considered encloses the immediate neighborhood of the substrate/adsorbate system.
The generalization of Eqs. (5.15) and (5.16) to multicomponents systems is relatively straightforward, involving sums over the different species involved.Footnote 1 This is the basis of the theories developed in Sect. 5.4. A word of caution is necessary here. While, as we say, the generalization of the mathematical form of the partition function and the probability density is simple, their calculation may be quite involved, if not impossible in general. There are two ways out of this problem. One of them is to introduce an extremely simplified mathematical form for the potential energy function V(r), and thus the integral in Eq. (5.15) can be evaluated, after some simplifying assumptions. The other way out is to calculate the averages in Eq. (5.9) without going through the partition functions. Although this may sound some sort of magic, this can be done by means of the Monte Carlo methods, as explained in Sect. 5.4. For the reader who is eager to know how this incredibly useful method works, we can advance that the trick consists in making moves (create or destroy particles, displace them, etc.) on the configuration of the system, such that the probability of accepting these moves depends on a ratio of probability densities given in Eq. (5.14) or Eq. (5.16), (i.e. \( P\left({\mathbf{r}}_i\right)/P\left({\mathbf{r}}_j\right)= \exp \left[-\left(V\left({\mathbf{r}}_i\right)-V({\mathbf{r}}_j)\right)/{k}_{\mathrm{B}}T\right] \)) so that the denominators become simplified.
The structure of the present chapter is as follows: we start with the first-principles approaches to the study of upd. We then describe the applications of statistical mechanics and follow with Monte Carlo applications. We end describing miscellaneous theoretical approaches, not included in the previous items.
5.2 Application of Quantum Mechanical Methods to Underpotential Deposition
5.2.1 Quantum Mechanical Modeling of Underpotential Deposition Previous to the Application of Density Functional Theory
Pioneering modeling on metal adatom formation in electrochemistry using quantum mechanical tools is due to Schmickler [4] and Kornyshev and Schmickler [5]. These authors used a model for electrosorption based on the Anderson-Newns model for adsorption from the gas phase. The later topic has been reviewed by Muscat and Newns [6], and Gadzuk [7], and the application of this model to electrochemistry has been reviewed by Schmickler and Henderson [8]. Figure 5.1 depicts the main ideas involved in the Anderson-Newns model applied to describe an adsorbate in contact with a metal at the metal/gas interphase.
Scheme of the Anderson-Newns used model to describe the interaction of an adatom with a metal substrate. The electronic states |k〉 of the metal interact with the electronic state of the adsorbate |a〉. The interaction between them is represented by a hopping matrix V ka . ε F denotes the Fermi level of the metal
In the electrochemical approach [4, 5], the total Hamiltonian of the interface contains the contributions of the valence electrons of the adatoms, the metal electrons and the solvent molecules. To give a flavor of this model, we briefly state its components and the interactions between them, as it was discussed in detail in Ref. [9], where Schmickler considered the occurrence of charge transitions in metal adsorbates on foreing metal substrates. Assuming that only one adatom orbital is interacting with the metal, the Hamiltonian of the system was:
where ε denotes energy, n are number operators, \( {c}^{+} \) and c are creation and anhilation operators, the index a denotes adsorbate, σ is the spin, k labels the electronic states in the metal, and v labels the solvent modes (vibrational, librational). According to this notation, ε a is the energy level of the adsorbate, U is the repulsive interaction between two electrons in the same orbital, V ka represent the off-diagonal elements for electron exchange between metal and adsorbate. The first line in Eq. (5.17) is that present in the Anderson model mentioned above. The second line contains slow solvent modes, which are represented as a set of harmonic oscillators of frequencies ω v , momentum p ν, and coordinates q v . The model considers, via the third line of Eq. (5.17), the coupling of the adsorbate with the slow (vibrational, librational) modes of the solvent molecules, whose interaction with the adatom is proportional to the adsorbate charge. The term g v represents the corresponding coupling constants. The allowance of electron exchange between the substrate and the adsorbate results in a broadening of the energy levels of the latter and produces a shift of their values with respect to the bulk value. Thus, a partial charge arises naturally as a consequence of adsorption. Kornyshev and Schmickler [5] evaluated partial charge transfer coefficients for several systems, considering different broadenings of the adsorbate level and different degrees of adatom solvation. The upd couples showed an intermediate behaviour between the extreme cases of adsorption of alkali and halide ions on mercury. In the case of upd, multiple solutions were found to exist for the occupation probability <n> of the adsorbate orbital as a function of the energies of the adsorbate relative to the Fermi level of the metal (see Fig. 5.2). According to the theoretical analysis, the existence of these multiple solutions would be associated with a weak interaction of the adsorbate with the metal and a strong interaction with the solvent, behavior that would be expected in the case of adsorption on flat terraces. As discussed by Schmickler in his work, the occurrence of multiple solutions could lead to current spikes in cyclic voltammograms.
Total occupancy of the adatom orbital as a function of the adsorbate energy ε a (Reprinted with permission from Ref. [9])
Extensions of the present model were the inclusion of the dependence of the partial charge transfer coefficient on the coverage degree [10], the consideration of two kinds of ions with opposite charge [11], the treatment of a random adsorbate layer with arbitrary coverage [Mishra AK, (1999) J Phys Chem B 103:1484] and the formulation by Schmickler of a unified approach to electrochemical electron and ion transfer reactions [12], with the subsequent inclusion of spin effects [13]. Recent work by Santos et al. [14] showed that the combination of the previous type of electron transfer theory with density functional theory calculations (see below) gives results that agree very well with experimental data for complex reaction like hydrogen evolution. In the future, this kind of modeling may provide further insight into the problem of charge transfer in upd systems.
5.2.2 Early Applications of Density Functional Theory to Underpotential Deposition
As stated in the Sect. 5.1, the most accurate, but computationally demanding approach to the study of upd systems is the quantum mechanical one. The early articles that applied quantum mechanics to understand the upd phenomenon based on Density Functional Theory (DFT) were those of Leiva and Schmickler [15], Schmickler [16] and Lehnert and Schmickler [17], within the so-called jellium model for a metal. In the first of these articles, the substrate was modeled as a semi-infinite positive charge background with a given charge density, and the adsorbate was represented as a slab of a different, positive charge density, see Fig. 5.3. This work showed that two different mechanisms are operative in upd systems. One is the fact, already known, that the electrons flow from the adsorbate, usually having a lower work function , to the substrate, usually having a larger one. The other mechanism is related to the surface energy. Metals with a high work function usually tend to have a high surface energy, a behavior which is also supported by predictions of the jellium model for high electronic densities [18]. In this way, energy is gained when a substrate is covered with an adsorbate having a surface energy lower than its own. This fact explained why most substrates employed in upd have particularly high surface energies.
Positive background charge and electronic density profile of the jellium model used to analyze monolayer adsorption on a foreign substrate. The susbstrate extends over the region \( x<0 \), while the adsorbate layer is confined to the region \( 0\le x\le \mathrm{d} \) (Reprinted with permission from Ref. [15])
In the subsequent improvements of the model, the substrate was represented through a lattice of local pseudopotentials [19] appropriate to the single crystal plane, while the adsorbate layer was represented as a thin layer of jellium with a two-dimensional lattice of pseudopotentials commensurate with the substrate [16, 17]. Lehnert and Schmickler used local pseudopotentials to describe the metal ion cores, with the aim of calculating the surface dipole induced by the adsorbate, the work function of the substrate and the substrate/adsorbate system, and the relationship between the latter and the upd shift for a number of sp metals.
Subsequent DFT calculations within the jellium model used more sophisticated self-consistent calculations of the electronic density to draw general trends concerning underpotential deposition on single crystal surfaces. For example, Leiva and Schmickler [20] analyzed the average electronic density profile for Pb on Ag (111) , as shown in Fig. 5.4. In the bulk of the metal (near to zero) it oscillates about its average value. There is a maximum at the positions near to the ions and there is a minimum at the interphase between the Pb overlayer and the Ag(111) surface. Since the electronic density of Pb is higher than that of Ag there is an accumulation of electronic charge in the top layer, which rapidly decays to zero outside of the metal surface. Towards the bulk of the metal the electronic density becomes identical to that for bulk Ag after a few lattice spacing.
(a) Electronic density profile and (b) position of the effective image charge as a function of the surface charge density, for a monolayer of lead on Ag(111) according to Jellium model (Reprinted with permission of Ref. [20])
Figure 5.4b shows the position of the image plane, measured with respect to the metal surface, as a function of the surface charge on the metal for Ag (111) , Ag(111)/Pb , and for a surface of Pb(111). The curve for Ag(111)/Pb is close to that of Pb(111) indicating that a monolayer of Pb on Ag(111) should have almost the same interfacial capacity as a surface of Pb(111). When the electrode is negatively charged the excess electrons accumulate mainly in front of the metal surface, and the image charge is pushed further away from the surface. In contrast, when the electrode is positively charged the surface electrons withdraw towards the bulk, and the image plane moves towards the surface.
The same model was used to analyze the electronic surface properties of the upd system Ag (111)/Tl [21]. Figure 5.5a shows the electronic density before and after the deposition of a Tl monolayer on Ag(111) . The response of the surface electrons to an external electrostatic field is shown in Fig. 5.5b.
(a) Electronic density profile and (b) position of the effective image charge as a function of the surface charge density, for a monolayer of Tl on Ag(111) according to Jellium model (Reprinted with permission of Ref. [21])
The jellium model was also used to analyze the lattice constants of adsorbed metallic incommensurate layers [22], corresponding to upd systems. For surfaces, the attractive interaction with the neighboring ions is missing, so the lateral pressure on the electron gas is smaller than in the bulk. Consequently the electronic density expands in the direction perpendicular to the lattice plane and contracts within the plane. This results in a shortening of the interplanar distance. When an adsorbate layer is added to the surface, the interplanar distance increases again.
5.2.3 Density Functional Theory Calculations for Underpotential Deposition Systems
While local pseudopotentials have been found to deliver reasonably good results for sp metals, they are not adequate for d metals, which are the most widely used as substrates in upd. A pioneering step to improve this situation in the field of DFT calculations applied to upd was given by Kramar et al. [23]. These authors analyzed the Pt (001)/Cu (2 × 2) system using the self-consistent, semirelativistic, all electron full-potential-linearized plane wave method. In the analysis they considered lattice parameter relaxation, band structure, partial density of states, electronic density and work function . This article was pioneering in determining the magnitude of the Cu-Pt bond, but the Cu cohesive energy was not considered, so that the underpotential shift was not evaluated. A next step forward was undertaken by Sánchez and Leiva [24], who analyzed both the binding energy of the adsorbate to the substrate \( {U}_{{\mathrm{S}\hbox{-} \mathrm{M}}_{\theta}}^{\mathrm{bind}} \) Footnote 2 and the cohesive energy of the adsorbate U cohS for a number of systems, thus obtaining the underpotential shift according to:
It is important to note that this equation is approximate and only contains energetic contributions, so that it is rigorously valid at 0 K. Figure 5.6 shows schematically the supercell used by these authors to represent the substrate/adsorbate system. The structure of the substrate was represented by a 5 (111)-planes wide atomic slab, on which an adsorbate plane was located at each side with (1 × 1) adsorption geometry on the threefold fcc adsorption sites. The supercell is periodically repeated in the three directions. Two surfaces (top and bottom) were separated by a vacuum region considered as six times the distance between (111) lattice planes.
Schematic illustration of the supercell geometry employed by Sánchez and Leiva, in order to represent the substrate/adsorbate system. d 111 denotes the distance between (111) lattice planes. The metal slabs representing the system extend over planes perpendicular to the plane of the page (Reprinted with permission from Ref. [24])
Within DFT, the energy of the electronic system illustrated in Fig. 5.6 is given by:
where T s[n] is the functional describing the kinetic energy of a system of non interacting electrons with density n(r), U H[n] is the Hartree energy, calculated from the corresponding potential v H(r) and U xc[n] is the exchange and correlation energy. The remaining terms correspond to the electron–nuclei (U e ‐ nuc[n]) and nuclei–nuclei (U nuc ‐ nuc) electrostatic interactions. The electronic density n(r) is obtained through the self-consistent solution of the corresponding Kohn-Sham equation s:
where V ext, V H and V xc are the external potential, the Hartree and the exchange-correlation potentials, respectively, which are given by:
and
Thus, n(r) is given by:
where f(i) is the occupation number of state i. The effects of the core electrons and the nuclei on the valence electrons were replaced by suitable non local, relativistic pseudopotentials [24]. Table 5.1 shows the work functions for the substrate and substrate/adsorbate systems obtained by Sánchez and Leiva . Ag (111) /Cu (1 × 1) yields a work function which is lower than that of both bulk metals. This is reasonable, since the atomic density of Ag(111)/Cu (1 × 1) is considerably lower than that of a Cu(111) surface.
The underpotential shift, calculated according to Eq. (5.18), is also shown in the fourth column of Table 5.1. A small ΔU updS‐M (theoretical) /eV was obtained for the Au (111)/Ag (1 × 1) system, in agreement with experimental results, and overpotential deposition (opd) is predicted for Ag(111) /Cu , as found in experiment [26]. However, for the Au(111)/Cu (1 × 1) and Ag(111)/Au(1 × 1) systems the theoretical predictions are at odds with the experimental results. No upd is predicted for Au(111)/Cu(1 × 1), while an underpotential shift of 0.12 V results for Ag(111)/Au(1 × 1) . For the later system no upd has been reported in the literature so far. The case of Au(111)/Cu(1 × 1) has been the subject of a long controversy between experiment and theoretical predictions. Sánchez and Leiva [25] analyzed the application of different DFT functionals (Local Density Approximation –LDA- and Gradient Generalized Approximation – GGA) in calculations for different single crystal surfaces of the system Au(hkl)/Cu. In all cases opd was predicted. However, a strong change in the work function of the Au(hkl)/Cu(1 × 1) system, of the order of 1 eV, was obtained upon metal upd monolayer formation. These authors noted the possibility that anion coadsorption, due to the concomitant shift of the potential of zero charge of the system, may be providing the extra free energy required for upd (Table 5.2).
Another important information that can be obtained from the DFT calculations are the (pseudo)electronic density profiles, and the differential electronic density plots. The latter may allow to visualize the increase or reduction of electronic density, as a consequence of bond formation. Accumulation and depletion regions should lead to an apparent increase of the corrugation of the surface when it is observed by scanning tunnel microscopy in the constant height mode, if a pure M surface is taken as a reference. The differential electronic density, δρ(r), is calculated from:
where ρ S/M, ρ S and ρ M correspond to the electronic densities of the substrate/adsorbate system and the separated substrate and adsorbate, respectively. Figure 5.7 presents images of the differential electronic densities, showing the charge rearrangement that takes places upon bond formation in the system. Figure 5.7a shows accumulation plots, while Fig. 5.7b shows depletion plots. It is found that charge accumulates more strongly at the plane between substrate and adsorbate, and is slightly depleted at the sites corresponding to the first substrate layer.
Electronic accumulation (a) and depletion (b) plots for the Ag (111) /Cu (1 × 1) systems. In (a) the darker regions indicate the highest accumulation of the electronic density. In (b) the darker regions indicate the highest depletion of the electronic density (Reprinted with permission from Ref. [24])
A further systematic calculation of upd shifts using DFT and first-principles pseudopotentials was undertaken in 2001 by Sánchez et al. [2]. The excess binding energies, corresponding to the term in brackets of Eq. (5.18), are given in Table 5.3 for different adsorbates on the fcc (111) face of single crystals of several substrates.
From Table 5.3 it can be observed that for a given substrate, with some notable exceptions, the excess binding energy tends to decrease for increasing surface energy of the adsorbate. Conversely, a given adsorbate usually exhibits larger excess binding energies on high surface energy substrates. These results support the same general trend already found within the framework of the jellium model , shown in the first part of this section, that represents the simplest approach to bulk metals and metal surfaces that takes into account explicitly the electronic component.
5.2.4 Relationship Between Excess Binding Energy and Surface Energy
Based on the hypothesis that the upd shift is related to the surface energy difference between substrate and adsorbate, Sánchez et al. [2] considered the thermodynamic cycle shown in Fig. 5.8. The left part of the figure shows two alternative ways to generate a free substrate surface and bulk adsorbate material from the substrate/adsorbate system. On one side, going through the unprimed way (I, II, III), the process involves: (I) detachment of the M adsorbate monolayer from the substrate S, (II) dissasemblement of the monolayer into its constituting atoms and (III) reassemblement of the isolated M atoms to yield the bulk M material. The energy change calculated along this cycle corresponds to the quantity in the bracket of Eq. (5.18). The primed path (I′, II′, III′) has the same initial and final states as the unprimed one, but involves: (I′) compression (expansion) of the adsorbed M monolayer to fit the lattice parameter of the bulk M material; (II′) setting the compressed (expanded) monolayer in contact with its bulk material (III′) detachment of the bulk piece of M from the substrate. The excess of binding energy, as calculated from the primed cycle, results in:
(a) Two alternative pathways to calculate the excess of binding energy of a metal M adsorbed on a substrate S. For more details see the text. (b) Excess of binding energy vs difference of surface energies between substrate and adsorbate (Reprinted with permission from Ref. [2])
Neglecting the compression (expansion term), that is, setting \( \Delta {U}_{\mathrm{I}\prime}\approx 0 \), leads to the following relationship between the binding energy excess and the difference of surface energies:
where a S y a M denote the lattice parameters and A S and A M are the atomic areas of substrate and adsorbate, respectively. Figure 5.8b shows the excess of binding energy as a function of the difference of surface energies between substrate and adsorbate, f(γ M, γ S), as plotted according to Eq. (5.26). It is evident that the points scatter around a straight line with slope one, although the systems Cu (111)/Ag (1 × 1) and Cu(111)/Au (1 × 1) deviate strongly from this general trend. This indicates that the approximation \( {\Delta \mathrm{U}}_{\mathrm{I}\prime}\approx 0 \) is not good for these systems. Less meaningful deviations are observed for the Ag(111) /Cu(1 × 1) and Au(111)/Cu(1 × 1) systems.
Recently, Greeley [29] has extended the previous work, using DFT calculations to determine periodic trends in the reversible deposition/dissolution potentials of admetals on a variety of transition metal substrates. A total of 81 systems were analyzed using the DACAPO code [30]. Greeley performed calculations involving adsorbed monomer, dimer and kink adatoms. Calculated underpotential shift results of that work are given in Table 5.4. For the sake of the analysis we perform below, we have ordered the metals in the table by increasing cohesive energy.
Since the diagonal terms correspond to metal adsorption on the same material and should be zero, they can be taken as a measure for the precision of the calculation method. On the average, we find that the error is of the order of 0.02 eV. From this table, it can be easily visualized that many of the systems over the main diagonal exhibit positive underpotential shifts. On the contrary, many systems below the main diagonal exhibit negative values, predicting overpotential deposition. Remarkable exceptions to this rule are Rh, Ni and Co adsorbates on Pt , Pt and Co adsorbates on Rh, Cu adsorbate on Au and Pt and Au adsorbates on Cu. Of all these systems, the most striking result is that of Cu on Au, where upd is not predicted, at odds with the occurrence of one of the most popular upd systems, as already discussed in the previous paragraphs.
5.2.5 Density Function Theory Calculations for Expanded Monolayers
As discussed in Sect. 3.1, and illustrated in Table 3.1, Ag upd on Au (111) yields a number of expanded structures, as determined by LEED [32]. This work motivated the study of expanded Ag adlayers adsorbed on Au(111) performed by Sánchez et al. [33]. These first-principles calculations on the stability of expanded Ag adlayers adsorbed on Au(111) were performed using the SIESTA program [34]. Different structures were considered for the adlayer : p(1 × 1), (3 × 3), p(\( \sqrt{3}\times \sqrt{3} \))R30°, p(2 × 2), p(3 × 3), and p(4 × 4), all adsorbed on Au(111). The corresponding coverage degrees were \( \uptheta =1 \), 0.44, 0.33, 0.25, 0.11 and 0.07, respectively. Table 5.5 reports the upd shift and changes in work function values for these systems, according to Sánchez et al. [33]. These calculations showed that in a vacuum environment, all Ag expanded monolayers are less stable than the bulk Ag phase and hence should not present upd. This is a striking discrepancy between experimental results and theoretical calculations. To rationalize this, it must be taken into account that DFT calculations consider a vacuum phase environment. The previous authors mentioned that at least three different effects, related to changes in the double layer, may contribute to stabilize these expanded structures: adsorption of anions, negative shift of the potential of zero charge [32, 35] and the influence of the electric field on the binding energy [33, 36].
Adsorption of various d-metals (Pd , Pt , Cu , Au ) and p-metals (Sn , Pb , Bi ) at different coverages on the Pt(111) surface was studied by means of DFT calculations by Pasti and Mentus [37] using the PWscf code of the Quantum ESPRESSO distribution [38]. The Perdew–Burke–Ernzerhof (PBE) [39] functional for the general gradient approximation (GGA) was employed. Upd shifts were determined at different coverages between 0.25 and 1, using (2 × 2) and \( \left(\sqrt{3}\times \sqrt{3}\right)\mathrm{R}30{}^{\circ} \) surface structures. A (2 × 2) cell was used to model coverages of 1/4 and 1/2 of a monolayer, while a \( \left(\sqrt{3}\times \sqrt{3}\right)\mathrm{R}30{}^{\circ} \) cell was used to model a clean Pt(111) surface and coverages of 1/3 and 2/3 of a monolayer.
Table 5.6 shows that the fcc-hollow adsorption site is generally the most stable one. For the d- and p-metals, the adsorption energy increases in the order fcc ≈ hcp > bridge > atop.
5.2.6 Analysis of Substrate and Adsorbate Interaction Energy
The adsorption energy of adatoms may be formally decomposed as [37]:
where \( {U}_{\mathrm{S}-{\mathrm{M}}_{\uptheta}} \) is the binding of a free standing adlayer to the substrate,Footnote 3 and \( {U}_{\mathrm{M}-\mathrm{M}} \) is the binding energy of M atoms in a free standing adlayer, referred to isolated atoms in vacuum. Due to the nature of metallic bond, both quantities are a function of coverage degree. Figure 5.9 shows \( {U}_{\mathrm{S}-{\mathrm{M}}_{\uptheta}} \) and \( {U}_{\mathrm{M}-\mathrm{M}} \) as a function of θ as obtained from the DFT-GGA calculations of Pasti and Mentus [37]. The magnitude of \( {U}_{\mathrm{S}-{\mathrm{M}}_{\theta }} \) decreases (the deposit becomes more unstable) with increasing coverages for all systems, concomitantly with the negative shift of the Pt d-band center in the formation process of the adsorbed monolayer. On the other hand, the magnitude of \( {\mathrm{U}}_{\mathrm{M}-\mathrm{M}} \) increases with increasing coverage degrees. In the case of Pd, Pt, Cu and Au the magnitude of \( {U}_{\mathrm{M}-\mathrm{M}} \) increases with increasing coverage in the entire coverage range. In the cases of Sn , Pb and Bi , the magnitude of \( {U}_{\mathrm{M}-\mathrm{M}} \) passes through a maximum at an intermediate coverage degree. This can be understood taking into account the appearance of pronounced repulsive forces due to the adatom sizes at high coverages.
5.2.7 Growth of Deposits Underpotentially formed on Stepped Surfaces
Theoretical studies of upd growth on stepped surfaces were undertaken by Danilov et al. in Ref. [40], performing DFT calculations with the Gaussian 03 program. These authors employed a scheme to construct additive pair potentials from DFT calculations. These potentials were then used to simulate the growth of Cu overlayers on different Pt stepped surfaces. The surfaces analyzed comprised (111) terraces, with (100) and (110) monoatomic steps, including some kink sites at these steps, see Fig. 5.10a. Figure 5.11 shows the evolution of the system energy as a function of the number of Cu atoms deposited onto the stepped Pt(111) surface. First, the Cu atoms are deposited onto the most active sites, that is, on the kink-positions, see Fig. 5.10a (black spheres) and step 1 in Fig. 5.11. Then, Cu atoms are deposited at the (110) and (100) steps sparsely (Fig. 5.10b). This process corresponds to step 2 in Fig. 5.11. A new plateau in the U vs. N curve (step 3 in Fig. 5.11) appears, corresponding to the formation of a continuous row of Cu atoms at the step, see Fig. 5.10c, d. Then, Cu atoms are deposited preferentially on the wide terraces as shown in Fig. 5.10e. Figure 5.10f, g displays a Cu \( \left(\sqrt{3}\times \sqrt{3}\right)\mathrm{R}30{}^{\circ} \) motif on the Pt terraces. The authors pointed out that the open structures shown in Fig. 5.10f, g were formed as a result of the mutual repulsion between Cu atoms, carrying a partial positive charge. It must be emphasized that the present model leads to open adlayers, without the need of assuming the presence of anions on the surface. Finally, Cu deposition at terraces builds a Cu(1 × 1) epitaxial monolayer , as show in Fig. 5.10h.
Snapshots of the different surface structures resulting from the quantum-chemical modeling of Cu deposition onto a stepped Pt(111) single crystal surface. From (a) to (d) Cu atoms are represented as black spheres, while Pt atoms are represented with gray and white spheres. From (e) to (h) the Cu atoms at steps are represent with black spheres, while Cu atoms on terraces are represented with gray, and Pt atoms are represented as white spheres (Reprinted with permission from Ref. [40])
Change in the energy of the system as copper atoms are deposited on a stepped Pt(111) surface (Reprinted with permission from Ref. [40])
5.3 A Statistical-Mechanical Approach to Underpotential Deposition
Blum and Huckaby developed pioneering work in the field of statistical mechanics devoted to describe chemisorption of a single type of species at the liquid/solid interface [41, 42] that was latter extended to the study of complex systems, as we analyze below.
We will not address the technical details of the models, since they are extensively explained in the corresponding papers, and a complete review on phase transitions at electrode interfaces has been given by Blum et al. in Ref. [43]. We just point out here their most relevant features, which are illustrative of the methodology employed. In this approach, a fluid of N molecules with a spherical hard core σ C was considered interacting with a smooth, hard wall with sticky sites, each of them having q nearest neighbours. This was called sticky sites model (SSM). The sticky interaction with the wall U s(r) at the point \( \mathbf{r}=\left(x,y,z\right) \) was defined as:
where z denotes the distance to the contact plane, located at a distance σC/2 from the electrode surface. \( \mathbf{R}=\left(x,y,0\right) \) is the position of the surface plane, δ represents the Dirac delta function, λ is a parameter that represents the likelihood of adsorption of an individual atom or molecule onto the sticky site. n 1 and n 2 are integer numbers, a 1 and a 2 are lattice vectors spanning a two-dimensional lattice L. The Hamiltonian describing the fluid was:
where Ĥ0 is the Hamiltonian of the system in the absence of the sticky sites on the hard wall, and ĤS represents the interaction with the sticky sites:
The analysis of the partition function of this model showed that the SSM maps for the adsorption on a flat surface onto a two-dimensional lattice problem with an arbitrary number of interactions. A further approximation was writing the n-body correlation g 0 n (R 1 … R n ) for the smooth wall problem as a product of pair correlation functions \( {g}_2^0\left({\mathbf{R}}_i,{\mathbf{R}}_j\right)={g}_2^0\left(\left|{\mathbf{R}}_i-{\mathbf{R}}_j\right|\right) \) according to:
The atoms in the 2-d lattice were assumed to have a nearest-neighbor interaction w(r), which corresponded to the pair potential of mean force of the adsorbed species interacting at the distance r:
For a constant distance between lattice sites, g 2 can be visualized as an interaction parameter, which can be used to fit experimental results. If the lateral interactions between the adsorbates are attractive and \( {g}_2>{g}_2\left(\mathrm{critical}\right) \) then a first-order phase transition occurs, which is seen as a sharp spike in the voltammogram. If the interactions are repulsive then only second order (order-disorder) phase transitions can occur. Since second-order phase transitions are discontinuous in the first derivative of coverage, they should be seen as small cusps in the voltammogram.
The relationship between the contact density and the potential bias, referred to the PZC , was assumed to be given by:
The coverage degree θ was written in terms of Padé approximants for low and high fugacities f. The latter was given by:
Once the coverage is obtained as a function of the electrode potential, cyclic voltammograms may be constructed calculating the current from:
Adsorption isotherm s and cyclic voltammograms for different interaction parameters are shown in Fig. 5.12. A sharp peak results for the case \( {g}_2=3.1 \) which has a transition, whereas a rather broad peak occurs for the case \( {g}_2=2.3 \), for which there is no transition.
Adsorption isotherms (left) and voltammograms (right) for two different interaction parameters as given in the figure. Ψ is a reduced potential referred to the pzc, \( \varPsi =\left(E-{E}_{\mathrm{pzc}}\right)/{k}_{\mathrm{B}}T \) (Reprinted with permission from Ref.[43])
The previous modeling was extended to a two-adsorbate system, in order to investigate the upd of Cu on the Au (l11) surface in the presence of sulfate ions [44]. According to this formulation, the following sequence of events occurs in the case of a cathodic potential sweep:
-
I- Formation of a \( \sqrt{3}\times \sqrt{3} \) sulfate phase on the gold substrate. See Fig. 5.13.
Fig. 5.13 Scheme of the geometrical model used by Huckaby and Blum for the theoretical study of upd of Cu on Au(111) in the presence of sulfate ions. Gold atoms are represented by large white disks, the adsorption sites for sulfate and copper are depicted as small black disks, and the adsorbed sulfate groups are depicted as sets of three lines emerging from the adsorption sites to the neighboring gold atoms (Reprinted with permission from Ref. [44])
-
II- Adsorption of Cu ions on the free adsorption sites, yielding a honeycomb lattice.
-
III- Replacement of adsorbed sulfate ions by Cu ions.
The mathematical model was similar to that described above, but the interaction of the copper ions with the Au (111) surface containing the \( \sqrt{3}\times \sqrt{3} \) sulfate film was introduced. Denoting with λ T, the stickiness parameter for the sites on the triangular sublattice LT, associated with the sulfate groups, and with λ H, the stickiness parameter for sites on the vacant honeycomb lattice LH, the fugacities of the copper atoms on the different sites were:
And
and the equivalent of equation (5.32) becomes:
for two copper atoms on neighbouring sites of LH, and
for two copper atoms on neighbouring sites of LT. In this first approach, the coupling between the two lattices was ignored to make the calculations straightforward. The theoretical voltammograms, shown in Fig. 5.14, exhibited features similar to those of the experimental ones.
Theoretical voltammogram from Huckaby and Blum [44] corresponding to two first-order phase transitions (Reprinted with permission from Ref. [44]). The peak couple on the right corresponds to adsorption/desorption of Cu atoms on/from the adsorption sites left free by a \( \sqrt{3}\times \sqrt{3} \) sulfate phase on the gold substrate. The peak couple on the left corresponds to replacement of adsorbed sulfate ions by Cu atoms, leaving a full adsorbed Cu monolayer (or to the reverse reaction)
The previous model was then extended by Huckaby and Blum to include the dynamics of the sulfate adsorption-desorption process, assuming a strong coadsorption of copper with bisulfate [45, 46]. In these articles second nearest neighbour configurations were also included, and the foot of the voltammetric spike for Cu upd on Au (111) located at more positive potentials was explained by a second-order order-disorder hard hexagon surface phase transition. The better agreement with the experiment introduced by this improved formulation can be seen in Fig. 5.15.
A further improvement of the model was achieved when kinetic features were introduced [47], including diffusion reaction kinetics. This extension of the model to the dynamic regime delivered phenomenological rate constants by fitting the theory to the experiment and produced a theoretical cyclic voltammogram that was in fairly good agreement with the experiment, in both the anodic and cathodic sweeps, as can be seen in Fig. 5.16
The subsequent approaches to upd using statistical mechanics were devoted to understand the shapes of the voltammogram spikes [48–50] since the simulated voltammetric profiles obtained from microscopic theory or computational modeling did not agree straightforwardly with the shapes of the experimental spikes. It must be reminded here that the width of the peaks in Figs. 5.14, 5.15, 5.16 and 5.17 were tuned by fitting a free parameter, introduced in an error function [44], or in a power functional form [46, 47]. Also the voltammogram simulated by lattice gas models exhibits peaks which are considerably sharper than the experimental results, see for example Fig. 5.35 of Sect. 5.4.3.2.
Comparison between experimental results for underpotential deposition of Cu on Pt (111) from 1 mM Cu2+ and 0.1 M H2SO4 at a scan rate of 1 mV/s [53] (broken line) and the theoretical modeling of Huckaby and Medvev [48]. The parameters fitted in the theoretical model were the effective electrovalence of the adsorbed ion \( {\gamma}_{\mathrm{v}}=1.981 \), the reference potential for the voltammogram \( {E}_{\mathrm{ref}}=-0.31\ \mathrm{V} \), the interaction parameter between adsorbed species \( \varsigma =-0.4334\ \mathrm{eV} \) and the probability of occurrence of line defects \( P=0.1 \). The latter quantity determines the distribution of lattice domains sizes on the surface (Reprinted with permission from Ref. [48])
It was shown by Huckaby and Medved [48] that the rigorous Borgs–Kotecky theory [51, 52] of finite-size effects near first-order transitions implies that a current spike from a lattice of a “reasonable” size is about 100 times taller and sharper than experimental spikes. Although kinetic effects could be invoked to understand this discrepancy, many experiments involve very low sweep rates and there is no indication for kinetic limitations, in the sense that the current profiles obtained in the anodic and cathodic sweeps are practically the mirror image of each other. The hypothesis put forward by Huckaby and Medved is that an electrode surface is made of a huge number of domains (regular arrays of adsorption sites) separated by small areas of defects (irregular arrays of sites), so that the emerging current spike from an electrode is the addition of the current spikes from each domain. In Ref. [48] Huckaby and Medved showed that the lone use of periodic boundary conditions to simulate voltammograms fail to agree with experiment, so that boundary effects on the electrode crystals must be of real importance, and therefore, they derived expressions to obtain the total electrode current density as an average of the current densities of single crystals having a distribution of sizes and boundary interaction strengths.
Figure 5.17 shows the agreement between experimental results and the model prediction for Cu upd on Pt (111) . The fitting parameters are the effective electrovalence of the adsorbed ion, the reference potential for the voltammogram, the interaction parameter between adsorbed species (see discussion on the lattice gas model in Chap. 3, Sect. 3.6), and the probability of occurrence of line defects. The latter quantity determines the distribution of lattice domains sizes on the surface.
The previous studies were extended by the authors to consider Cu upd on Pt (100) and to the more complex system Cu upd on Au (111) [49, 50], allowing an evaluation of interaction parameters between deposited ions.
5.4 Monte Carlo Methods
5.4.1 Introduction and Generalities
The term Monte Carlo (MC) is often used to describe a wide variety of numerical techniques that are applied to solve mathematical problems by means of the simulation of random variables (the name MC itself makes a reference to the random nature of the gambling at MC, Monaco). These methods first emerged in the late 1940s and 1950s as electronic computers came into use.
Computer simulations generate information at a microscopic level (atomic positions and momenta, etc.) that has to be converted into macroscopic information (pressure, internal energy, etc.). As mentioned in Sect. 5.1, a thermodynamic property A may be calculated through a weighted average in which the weighting factors are the Boltzmann probabilities of each microscopic state and in which the sum runs over all of the states of the system (Eq. 5.9).
In practice, it is impossible to calculate a sum over all of the microscopic states of a system and, hence, we must propose a way to circumvent this problem.
In a first stage, we might be tempted to approximate the calculation of this average just by randomly generating a sufficiently large number of configurations and calculating the weighted average of the instantaneous value of the property A for each one of the generated states.
Two practical problems arise when we consider the calculation of the property A through this methodology:
-
1.
Most randomly generated configurations will have a very low probability and, hence, a very small contribution to the average (which makes this a very inefficient approach).
-
2.
As mentioned before in Sect. 5.1, the evaluation of these probabilities involves the calculation of the partition function which, for most systems of practical interest, is very difficult (if not downright impossible).
An elegant solution to these problems was provided by Metropolis and co-workers of the Los Alamos team [54]. In the Metropolis approach, instead of randomly accumulating configurations and then evaluating their probability-weighed contribution to the desired average, configurations according to their Boltzmann probability can be accumulated and then a simple arithmetic average can be taken.
Thereby the problem is not solved, but merely reformulated. Now we need a way to generate a set of states in which each state appears a number of times that is proportional to its Boltzmann probability.
The way this is accomplished in the Metropolis approach can be summarized as follows:
Given a starting configuration i, a new configuration j is generated by means of a random change (which can be the simple movement, addition or removal of a particle). This new state j is accepted with a transition probability \( {P}_{i\to j} \), which is calculated as follows:
-
If the probability of state j is greater than the probability of state i, then the transition probability is equal to 1 (i.e. the new configuration is automatically accepted).
-
If the probability of state j is smaller than the probability of state i, then the transition probability is equal to the ratio between the probabilities of states j and i (\( {P}_{i\to j}={P}_j/{P}_i \)).
Or, in a compact form:
where min(a,b) denotes the minimum value between a and b. This way of defining the transition probabilities allows us to skip the calculation of the partition function because, when evaluating the ratio between the probabilities (as defined in Eqs. (5.12) or (5.13)), the partition functions (which are in the denominators of the r.h.s. of such equations) become simplified.
Taking this into account, the transition probability becomes:
The chain of states constructed by this way has a limiting distribution equal to the probability distribution of the corresponding thermodynamic ensemble. This means that, at the end, a set of configurations is obtained according to Boltzmann statistics and the expectation value of the property of interest is obtained simply as the arithmetic average of values from individual accepted configurations.
So far we have said nothing about the way of generating these new configurations in order to construct the required chain of states. The different ways of doing so will be addressed in the following sections.
5.4.2 Off-Lattice Monte Carlo
In the Off-Lattice approach to the MC method, when attempting a move, the new random configurations are chosen from a continuous set, i.e., the atoms are allowed to move continuously.
Several ways of accomplishing this condition have been proposed. One of the simplest (and the most used one) is the following one: At the beginning of a MC move, an atom is randomly selected and given a uniform random displacement along each one of the coordinate directions, as shown in Fig. 5.18. The maximum displacement, δr max, is an adjustable parameter that governs the size of the region.
After the new configuration j is generated, the transition is accepted with a probability \( {P}_{i\to j} \) as defined in Eq. (5.41). The whole process is then repeated.
The efficiency of the exploration of the configuration space depends on the value of δr max in the following way: if it is too small, the energy changes associated with the transition will be small and a large fraction of moves will be accepted, but the configuration space will be explored slowly (i.e., consecutive moves will be highly correlated). If δr max is too large, then nearly all the trial moves will be rejected (due to the high probability of overlapping with other atoms) and, again, there is little movement through the configuration space. To maximize the efficiency of the exploration, the value of the parameter δr max is adjusted during the simulation so as to keep the acceptance ratio close to 50 %.
In the case of a simulation in the Grand Canonical Ensemble , the chemical potential is fixed while the number of molecules fluctuates. In order to construct the chain of states, the most used method is the one proposed by Norman and Filinov [55]. In this technique there are three different types of move:
-
(a)
a particle is displaced.
-
(b)
a particle is destroyed (no record of its position is kept).
-
(c)
a particle is created at a random position.
The displacement of a particle is handled using the normal Metropolis method described above. If a particle is destroyed, the ratio of the probabilities of the two states is given by:
where N is the number of molecules initially in state i, V is the volume of the system, and Λ is the thermal de Broglie wavelength , defined as \( \varLambda ={\left({h}^2/2\pi m{k}_{\mathrm{B}}T\right)}^{1/2} \). Similarly, for the creation of a particle, the ratio of probabilities is given by:
In both cases of destruction and creation, the final transition probability is calculated (like in the case of displacement), as min(1, P j /P i ).
5.4.2.1 Off-Lattice Monte Carlo: Applications to Underpotential Deposition
Off-Lattice Monte Carlo methods were early applied not to upd but to an overpotential deposition system: Cu on Ag (111) [56]. We explain now shortly the motivation for such work. As pointed very often in the literature [57], important phenomenological criteria exist to determine if the type of deposit to be formed by metal on metal deposition is a two dimensional or a three-dimensional one. These criteria are based on the interaction energy of the adsorbate with the substrate, \( {U}_{\mathrm{S}-\mathrm{M}} \), the interaction energy of M atoms with a substrate of the same type, \( {U}_{\mathrm{M}-\mathrm{M}} \), and the crystallographic misfit M-S. According to this analysis, three types of growth modes of a deposit on a foreign surface can be established. In the case where \( {U}_{\mathrm{S}-\mathrm{M}}\gg {U}_{\mathrm{M}-\mathrm{M}} \), crystal growth is expected to proceed via a 3D island growth or a Volmer-Weber mechanism . In the case where \( {U}_{\mathrm{S}-\mathrm{M}}\ll {U}_{\mathrm{M}-\mathrm{M}} \) two possibilities may in turn be distinguished, depending on the misfit with the substrate. If the misfit is small, a layer by layer growth (Frank-van der Merwe ) mode should be expected. On the other hand, if the misfit is large, a 3D growth on top of predeposited monolayers (Stranski-Krastanov ) should occur. Even when a wide variety of systems appear to fit adequately into the previous scheme, the measurements made by Dietterle et al. [58] on Cu deposition on Ag(111) showed that in this system a particular situation occurs, where the classical view seems to be challenged. While Cu deposition on Ag(111) presents no upd, a fact that would indicate that \( {U}_{\mathrm{S}-\mathrm{M}}<{U}_{\mathrm{M}-\mathrm{M}} \) ,the formation of a pseudomorphic monolayer can be observed at low deposition overpotentials. On the other hand, three dimensional clusters are formed only at higher overpotentials, a situation where the deposition reaction is considerably accelerated. This fact lead Dietterle et al to suggest that a “delicate balance of adatom -adatom and adatom-substrate interactions” should take place, to explain this anomalous behavior.
Going back to the theoretical work of Cu deposition on Ag (111) , it involved MC simulations where, like in most of the work discussed in this section, the interatomic potentials where those of the embedded atom method, which is discussed in more detail in Sect. 5.4.4.2. Figure 5.19 shows results from these simulations, for trajectories corresponding to the motion of a single atom (left) and of a full monolayer (right).
MC simulation results for Cu deposited on Ag(111). Left: trajectory of a single Cu adatom indicated as a thin line; spots show the position of the first layer of Ag atoms. Right: Atomic positions for a monolayer of Cu adatoms (grey clouds) on a Ag( 111) surface (Ag atoms in the first layer are shown as black clouds). Dashed lines show arbitrary unit cells (Reprinted with permission from Ref. [56])
The binding energy of the Cu atoms was evaluated as a function of the coverage degree, as shown in Table 5.7. It is found that in all cases the binding energies of Cu are below the cohesive energy of Cu (3.54 eV), so that overpotential deposition is predicted.
Off-Lattice MC simulations using EAM potentials have been also found useful to calculate surface stress changes Δσ s upon island and monolayer formation of metal on foreign substrates. Based on a previous work devoted to study the properties of metallic islands [59], Rojas et al. [60] have developed a model to calculate Δσ s using a statistical mechanical argument.
Using the relationship between the Helmholz free energy and the canonical partition function:
and the fact that when the stress tensor is diagonal, we can obtain the surface stress from the derivative:
Rojas et al. [60] arrived to the following equation to calculate the surface stress change of the system:
where N M is the number of adatoms, S is the surface, \( {U}_{\mathrm{S}-\mathrm{M}} \) and U M are the interaction potential energies of the substrate-adsorbate and the substrate system respectively, and the quantities in brackets are evaluated from an isotropic stretching and compression of the simulation box in the direction parallel to the surface for each configuration of the production run.
The relaxation of islands on different substrate/adsorbate systems is illustrated in Fig. 5.20, together with a scheme of the simulation box. The arrows in the figure denote the displacement of the atoms in the island with respect to their pseudomorphic adsorption sites, and the colors indicate the magnitude of the displacement.
Top: scheme of the simulation cell used to study the relaxation of an island of adatoms on a substrate. Bottom: Atom displacements in a 129-atom island for different systems adsorbate/substrate. The arrows represent the relaxation with respect to the (1 × 1) pseudomorphic configuration in Å. (a) Ag(111)/Ag; (b) Pd(111)/Ag; (c) Pt(111)/Ag; (d) Pt(111)/Ag. Colours also denote a displacement scale (Reprinted with permission from Ref. [60])
It is interesting to compare in the figure different behaviors: the homoepitaxy Ag (111) /Ag shows practically no relaxation at the center of the island, while some inwards relaxation at the borders becomes evident. On the other hand, the remaining systems present outwards relaxation.
With quantitative purposes, a misfit may be defined according to:
where a subs and a ads denote the lattice constants of substrate and adsorbate respectively. The values of ε mf Pd(111)/Ag , Pt (111) /Ag and Pt(111)/Au are −5.1, −4.3 and −4.1 respectively, something that is reflected by the qualitative behavior observed in the Fig. 5.20.
The surface stress changes calculated for the adsorption of monolayers is shown in Table 5.5. In the case of Ag /Pt (111) , the result of −4.9 N/m can be compared with −8.8 N/m, which is the value measured by Grossmann et al. [61]. For the systems Ag/Pd(111) and Au /Pt(111), large compressive stresses were also obtained (Table 5.8).
Rojas [62] extended the previous EAM Off-Lattice MC simulations to several systems, involving Ag , Au , Pt , Pd, and Cu . The results for stress changes are shown in Table 5.9. While the general trend is that a big adsorbate on a small substrate yields a compressive stress, and the opposite situation leads to tensile stress, there are also chemically specific effects. Comparison of these results with previous ones where relaxation of the adsorbate was not allowed [63], indicated that this effect is very important for the Cu(111)/Ag and the Cu(111)/Au systems, where misfits are very large.
Rojas also calculated underpotential shifts for all these systems, as reported in Table 5.10.
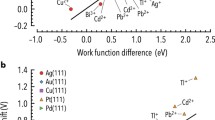
When the values in Table 5.10 are plotted as a function of surface energy difference, a linear relationship results, as shown in Fig. 5.21. This follows the predictions made by the jellium model , see discussion in Sect. 5.2.2, as well as those from first-principles calculations, see discussion in Sect. 5.2.3 and Fig. 5.8 therein.
Underpotential deposition shifts vs difference of average surface energies between substrate and adsorbate (Reprinted with permission from Ref. [62])
Oviedo et al. [64] used EAM Off-Lattice MC to study upd on low dimensional surface defects. They considered the energetics of the deposition of Ag , Cu and Pd atoms on a Pt (111) surface with vacancies, steps and holes, as compared with adsorption in monolayers, bilayers, etc. Some of the 0-D defects considered are illustrated in Fig. 5.22
Illustration of some of the 0-D defects considered to deposit atoms in a EAM Off-Lattice MC simulation. Left: terrace and vacancy sites. Right: Step and kink sites (Reprinted with permission from Ref. [64])
The main results for the binding energies obtained are summarized in Table 5.11.
From these results, it can be concluded that for adsorption of a single atom on defects, the absolute value of the binding energy (bond strength) increases with the increase of the coordination (U step(0D) < U kink(0D) < U vacancy(0D)). On the other hand, from the viewpoint of the dimensionality of the phase involved, the absolute value of binding energy decreases(bond strenght) with the dimensionality U step(1D) > U monolayer(2D) > U bulk(3D). Concerning upd, the present results indicate that, starting a negative potential sweep from a positive potential value where the substrate is naked, as the electrode potential is made more negative, the first sites to be filled with adsorbate should be the vacancies, followed by kink sites and steps. Then, monolayer formation would follow and finally the bulk deposit would appear. All these facts were found to be supported by experimental results, as discussed in Ref. [65] and shown schematically in Fig. 5.23.
Formation of low dimensional structures in upd systems at different substrate inhomogeneities in the undersaturation range, depending on electrode potential (Reprinted with permission from Ref. [65])
5.4.3 Lattice Monte Carlo
In the Lattice MC method, the particles constituting the system are located on the points of a lattice. This means that, in order to generate the chain of states implied by the Metropolis method, the displacement of atoms will take place between lattice points and, in the case of Grand Canonical simulations, atoms will be created or destroyed at these lattice points, as we discussed in Fig. 3.14. One of the advantages of these methods is that they allow dealing with a large number of particles at a relatively low computational cost.
These lattice models are of widespread use in studies of adsorption on surfaces. If the crystallographic misfit between the involved atoms is not important, it is a good approximation to assume that the adatoms adsorb on defined discrete sites on the surface, given by the positions of the substrate atoms. In principle, it must be kept in mind that continuum Hamiltonians should be much more realistic in those cases where epitaxial growth of an adsorbate leads to incommensurate adsorbed phases or to adsorbates with large coincidence cells. On the other hand, the use of fixed rigid lattices restricts enormously the number of possible configurations for the adsorbate and its use may be justified on the basis of experimental evidence or continuum computer simulations that predict a fixed lattice geometry.
5.4.3.1 Simulation of Relatively Simple Underpotential Deposition Systems
Pioneering application of lattice MC simulations to upd systems was undertaken by Van Der Eerden et al. [66]. These authors performed MC simulations using an Ising-type model (see Chap. 3), where the adsorbate atoms were assumed to have a diameter greater than the distance between two neighbouring adsorption sites on the substrate surface. Thus, each adatom is assumed to occupy only one adsorption site, but at the same time, due to exclusion effects, it blocks (first) neighbouring adsorption sites and prevents them from being occupied by other adatoms. This modeling has been denominated 1/n adsorption, where \( n=1/{\theta}_{\max } \). The cases considered were n = 2 for a square lattice and n = 4 for an hexagonal lattice. These authors investigated the occurrence of phase transitions as a function of the quantity \( \omega =\varsigma /{k}_{\mathrm{B}}T \), where ς is the interaction between two neighboring adsorbates, as defined in Chap. 3. Figure 5.24 shows the behavior of the isotherms for different values of ω for a square lattice with n = 2. A smooth behaviour is found for θ vs μ/k B T at low ω s, until \( \omega =1.4 \). Above this value, a hysteresis, characteristic for the occurrence of a phase transition becomes evident. We use this word to denote that the isotherms present separated upper and lower branches, yielding two coverages at the same chemical potential , one of which corresponds to a metastable state.
Simulation of adsorption isotherms for adsorption with exclusion effects on a square lattice. It is assumed that the adsorbate blocks two sites on the lattice substrate. (n = 2, see discussion in the text) (Reprinted with permission from Ref. [66])
Using this procedure, the authors determined critical ω values for the systems considered. In the case of the square lattice, the MC simulations yielded \( {\omega}_{\mathrm{critical}}=1.3 \). Comparison of the MC simulations with experimental results for the system Pb upd on Ag (100) are shown in Fig. 5.25, where it is found a good agreement for \( \omega =0.6 \), which is a value well below the critical one, so that according to this modelling a first-order phase transition should be excluded for this system.
Simulated isotherms for n = 2 adsorption on a square lattice with \( \omega =0.6 \) (○); experimental results for upd of Tl(●) and Pb (□) on Ag (100) (Reprinted with permission from Ref. [66])
As will be discussed in Sect. 5.4.4.2, the proper description of metallic binding requires the use of many-body potentials, where the embedded atom method has shown to be a reasonable alternative for many electrochemical applications. At first sight, this seems difficult to compute with a lattice model. To solve this problem in a computationally efficient way, the adsorption (desorption) of a particle may be considered at a site embedded in a certain environment surrounding it, as shown in Fig. 5.26 for a square lattice, which may be used to represent adsorption on a (100) fcc surface. The adsorption site for the particle is located in the central box, and the calculation of the interactions is limited to a circle of radius R. The adsorption energy for all the possible configurations of the environment of the central atom are calculated previous to the simulation, so that during the MC simulation the most expensive numerical operations are reduced to recover the index that characterizes the configuration surrounding the particle at the adsorption site.
Environment of 12 sites surrounding an adsorption site. These may be employed for the calculation of the adsorption/desorption energies of an adsorbate atom on a substrate for a cutoff radius corresponding to the distance between third-nearest neighbors. The particle is adsorbed on the central box (13) and the remaining sites may be occupied by adsorbate or substrate-like atoms. A total number of 311 configurations results
In the case of the electrochemical system, potentiostatic control is in many cases applied to fix the chemical potential of species at the metal/solution interface. Since the natural counterpart of potentiostatic experiments are Grand Canonical Monte Carlo (GCMC) simulation s, where the chemical potential μ is one of the parameters fixed in the simulations, this was the methodology chosen by Giménez and Leiva [67] to study the formation and growth of low dimensionality phases on surfaces with defects. This work is somehow a lattice model version of the Off-Lattice problem analyzed in Sect. 5.4.2. To simulate (100) surfaces, the system was represented by a square lattice with N adsorption sites, as that shown in Fig. 5.26. Different arrangements of the substrate atoms allowed for the simulation of various types of surface defects. Within the procedure described in Sect. 5.4.1 (Metropolis algorithm), thermodynamic properties were obtained after proper equilibration steps as average values of instantaneous magnitudes stored along a simulation run. A key result is the average coverage degree of the adsorbate atoms 〈θM〉 at a given chemical potential μ. To emulate different surface defects, substrate islands of various sizes and shapes were made by means of the MC-related technique denominated simulated annealing. Within this approach, a given number of substrate atoms is set on the surface, and a MC simulation is started at a very high initial temperature T 0, of the order of 104 K. The system is later cooled down according to a logarithmic law (\( {T}_{n+1}={T}_n{\alpha}_a \)), where α a is a positive constant lower than one and T n is the temperature at the nth iteration step. A given number of MC steps, say NMCS, are run at each temperature and the simulation is stopped when the desired T f is reached. By setting different N MCS, various kinds of structures may be obtained, as shown in Fig. 5.27.
Different island types obtained from simulated annealing simulations, used to obtain surfaces with different types of defects. The number of Monte Carlo steps N MCS increases from upper left to down right. \( {N}_{\mathrm{MCS}} = 20\times {2}^{m-1} \), where m is the ordinal number of the configuration in the figure (Reprinted with permission from Ref. [67])
The shape of the adsorption isotherms obtained with the different islands types turned out to be strongly sensitive to the structure of the surface, as shown on the left of Fig. 5.28. The isotherms obtained with more perfect surfaces (less steps) were steeper, becoming closer to the behavior expected for a first-order phase transition, which is shown on the right of the figure. We remind from the discussion performed in Chap. 3, that the voltammetric profiles are the derivatives of the isotherms, so that rounded isotherms lead to wider voltammetric peaks. Thus, we see that increasingly imperfect surfaces will lead to wider voltammograms. This is in rule with the theoretical modelling by Huckaby and Medved [48] that we presented at the end of Sect. 5.3.
Left: Adsorption isotherms for the decoration of monoatomic steps of Au defective surfaces with Ag upd. The Au surface structures considered were the final states of simulated annealing runs similar to those of Fig. 5.27 with m = 1, 5, 9, 13 and 16, resulting in the number of Monte Carlo Steps reported in the figure. The temperature was 300 K. Right: Adsorption isotherms for Ag upd on a perfect Au(111) surface, at different temperatures (Reprinted with permission from Ref. [67])
In a further contribution, Gimenez et al. [68] considered several systems involving Ag , Au , Pt and Pd. It was found that, taking into account some general trends, such systems can be classified into two large groups. The first one comprises Au(100)/Ag , Pt(100)/Ag , Pt(100)/Au and Pd(100)/Au , which have favorable binding energies as compared with the homoepitaxial growth of adsorbate-type atoms, as shown in Table 5.12. These are systems where underpotential deposition is expected, see Eq. (3.5) of Chap. 3.
For this type of systems, when the simulations are performed in the presence of substrate-type islands emulating surface defects, the islands remain almost unchanged, and the adsorbate atoms successively occupy kink sites, step sites and the complete monolayer. This is illustrated in Fig. 5.29 for the surface atomic arrangement of Ag on a Pt (100) surface with Pt islands. The corresponding adsorption isotherms are shown in Fig. 5.30.
Snapshots of the final state of the surface at three different chemical potentials (−4.27 eV, −3.44 eV, and −3.06 eV) for Ag decoration of a Pt(100) surface with Pt islands. The average island size is about 48 atoms. Note that the islands remain essentially unchanged (Reprinted with permission from Ref. [68])
The partial coverage degrees for step and kink sites in Fig. 5.30 were defined relative to the total number of step and kink sites available respectively. The sequential filling of kink sites, steps and the rest of the surface can be appreciated clearly in the partial isotherms.
The second group of systems, as considered by Gimenez et al. [68] is composed of Ag (100)/Au , Ag(100)/Pt , Au(100)/Pt, and Au(100)/Pd, for which monolayer adsorption is more favorable on substrates of the same nature than on the considered substrates (see Table 5.11) . When simulations are carried out in the presence of islands of substrate-type atoms, it is found that they tend to disintegrate, yielding 2D alloys with adsorbate atoms. This is illustrated in Fig. 5.31 for Pt deposition on Ag(100). For this second type of systems, the partial adsorption isotherms do not evidence any particular sequential filling, as can be observed in Fig. 5.32.
Snapshots of the final state of the surface at three different chemical potentials (−5.74, −5.32 and −5.21 eV) for Pt decoration of Ag islands on Ag(100). Average island size 53 atoms. Note the progressive disintegration of the Ag islands (Reprinted with permission from Ref. [68])
A detailed analysis of the environment of adatoms and substrate atoms at different adatom coverage degrees was found very helpful to understand the two types of behaviors described above.
More recently, Gimenez et al. [69] have shown that MC simulations with pair potential interactions between nearest neighbors may also yield the two types of behaviors described above, opening the way to a less demanding computational modeling. These authors have also extended this modeling to consider on-top adsorption of anions in upd systems [70].
5.4.3.2 Simulation of Cu Underpotential Deposition on Au (111) in Sulfate-Containing Electrolytes
We devote a special section to the analysis of Cu upd on Au (111) in the presence of sulfate ions, since the work developed by Zhang et al. [71] represents an interesting example of the application of the lattice MC technique to complex upd systems. As we have seen in Chap. 2, (Fig. 2.2) the voltammogram obtained for upd of Cu on Au(111) in the presence of sulfate anions presents two pairs of peaks, see also Fig. 5.35 below. From now on, the pair of peaks at more positive potentials will be labeled as #1 and the pair at more negative potentials as #2. According to experimental information [71–73], these correspond to transitions between a full monolayer (ML) of Cu at more negative potentials, an ordered \( \left(\sqrt{3}\times \sqrt{3}\right) \) mixed copper and sulfate phase at intermediate potentials, and a disordered low-coverage phase at more positive potentials. Inspired in the model proposed by Blum and Huckaby described in Sect. 5.3, these authors assumed that sulfate coordinates the (unreconstructed) triangular Au(111) surface through three of its oxygen atoms, with the fourth S–O bond pointing away from the surface. The Cu atoms were assumed to compete for the same adsorption sites as the sulfate. In order to obtain the configuration energies of the coadsorbed particles required for the MC simulation, the following three-state lattice-gas Hamiltonian was proposed:
where \( -{\tilde{\mu}}_{\mathrm{k}} \) denotes the change in the chemical potential of species k (k = S (sulfate) or C (copper)) when one i particle is removed from the bulk solution and adsorbed on the surface, c k i the occupation number (0 or 1) of site i by the species k, (n) indicates the rank of neighborhood between sites (first, second, etc), and \( -{\varPhi}_{\mathrm{km}}^{(n)} \) is the pairwise interaction energy between particles of type k and m that are first neighbors. The term Ĥ3 denotes three-particle interactions between sulfates, involving all second-neighbor equilateral triangles.
The lattice gas parameters were fitted by an iterative process, where they were finally fixed to yield reasonable agreement of the theoretical predictions with the shapes of the observed adsorption isotherms and voltammetric profiles, as well as with the dependences of the CV peak positions on the electrolyte composition in experiments. The interactions involved in Eq. (5.48) are shown in Fig. 5.33.
The relative positions of Cu (●) and sulfate (Δ) corresponding to the effective interactions in Eq. (5.48). Free adsorption sites are denoted by ○. The number underneath each bond representation is the corresponding effective interaction energy used in Ref. [71], given in kJ/mol. The interactions are invariant under symmetry operations on the lattice (Reprinted with permission from Ref. [71])
Part of the fitting involved the so-called ground-state configurations, which corresponded to the sets of most stable configurations at 0 K for given electrochemical potentials \( {\tilde{\mu}}_{\mathrm{C}} \) and \( {\tilde{\mu}}_{\mathrm{S}} \). This allowed the construction of phase diagrams as a function of \( {\tilde{\mu}}_{\mathrm{C}} \) and \( {\tilde{\mu}}_{\mathrm{S}} \), which are useful to interpreted the results of simulations, discussed below. Figure 5.34 shows such a diagram and their corresponding ground-state configurations.
The different phases in Fig. 5.34 are identified with the notation \( {\left(X\times Y\right)}_{\theta_{\mathrm{C}}}^{\theta_{\mathrm{S}}} \), where θ C and θ S denote the sulfate and copper coverages respectively. For example, \( {\left(1\times 1\right)}_0^0 \) denotes an empty surface, \( {\left(1\times 1\right)}_1^0 \) denotes a surface covered by a Cu monolayer, \( {\left(\sqrt{3}\times \sqrt{3}\right)}_{2/3}^{1/3} \) indicates a surface covered by a mixture of sulfate at \( {\theta}_{\mathrm{S}}=1/3 \) and Cu at \( {\theta}_{\mathrm{C}}=2/3 \), etc. It must be noted that the latter, which is the phase observed experimentally in the potential region between peaks #2 and #1, occupies a wide region in the ground-state diagram of Fig. 5.34. A detailed discussion of the occurrence of different phases in terms of the interactions of Eq. (5.48) is given in Ref. [71], we just point out here some general features to understand the idea behind the modeling.
The electrochemical potentials, which correspond to the axis on the right of Fig. 5.34 , are related to the bulk concentration of species k and electrode potential E according to:
where z S and z C are the effective electrovalences of sulfate and copper, respectively, und the superscript denote reference conditions. Thus, large \( {\tilde{\mu}}_{\mathrm{S}} \) positive values correspond to high sulfate concentrations or large positive potentials (z S is a negative quantity). On the other hand, large \( {\tilde{\mu}}_{\mathrm{C}} \) positive values correspond to high Cu2+ concentrations or large negative potentials (z C is a negative quantity). This is the reason why the pure Cu phase \( {\left(1\times 1\right)}_1^0 \) appears at large positive \( {\tilde{\upmu}}_{\mathrm{C}} \) values and rather negative \( {\tilde{\upmu}}_{\mathrm{S}} \). The converse situation (large positive \( {\tilde{\upmu}}_{\mathrm{S}} \) and negative \( {\tilde{\upmu}}_{\mathrm{C}} \)) leads the pure sulfate phase, \( {\left(\sqrt{3}\times \sqrt{3}\right)}_0^{1/3} \).
According to Eqs. (5.49) and (5.50) the electrochemical potentials \( {\tilde{\upmu}}_{\mathrm{S}} \) and \( {\tilde{\upmu}}_{\mathrm{C}} \) are linearly related, so that when a potential scan is applied to the system, this moves along a straight line in Fig. 5.34b. Three of these lines are depicted there. The equation describing this straight line has the form \( {\tilde{\mu}}_{\mathrm{C}}=\mathrm{constant}+{\tilde{\mu}}_{\mathrm{S}}{z}_{\mathrm{C}}/{z}_{\mathrm{S}} \). Let us consider for example a trajectory along the line labeled with 1, where the potential scan is initiated on the upper left side of the plot. The system starts with the pure Cu phase \( {\left(1\times 1\right)}_1^0 \) and ends up in the pure sulfate phase \( {\left(\sqrt{3}\times \sqrt{7}\right)}_0^{1/5} \), coming across two mixed Cu/sulfate phases. At the lines delimiting the phases, phase transitions are expected to take place, with drastic changes in the composition of the surface structure. These changes in the surface composition are due to the electrochemical adsorption/desorption of species, involving charge transfer and eventually leading to peaks in the cyclic voltammograms, as shown in the simulation below.
Since the adsorbed particles are restricted to adsorb on N well defined lattice sites, the coverage can be easily calculated from \( {\theta}_{\mathrm{k}}={\displaystyle \sum_i{c}_i^{\mathrm{k}}}/N \) and the charge flowing upon adsorption of the species of type k is \( {q}_{\mathrm{k}}=-{e}_0{z}_{\mathrm{k}}{\theta}_{\mathrm{k}} \). Sulfate coverage θ 2S adsorbed on top of the complete Cu monolayer in the negative-potential region was represented in terms of the Cu coverage θ C and the sulfate coverage in the first layer θ S by the equation:
where α was a fitting parameter, expected to be between zero and one. If the latter were the case, a full Cu monolayer would be covered by 1/3 of a monolayer of sulfate.
Considering a very low sweep rate so as to assume quasi-equilibrium conditions, the voltammetric current was calculated from the coverage degrees and their partial derivatives (obtained from coverage fluctuations [74] in the MC simulations) according to:
Figure 5.35 shows experimental and room-temperature simulated voltammograms. Given the complexity of the system, it can be stated that a good overall agreement is found.
Experimental (dot–dashed) and lattice MC simulated (solid) CV current densities. The left-hand vertical scale shows the current density for a scan rate of 2 mV/s, whereas the right-hand scale shows the current density normalized by the scan rate, in units of elementary charges per mV and Au(111) unit cell (Reprinted with permission from Ref. [71])
Besides the simulations devoted to comparison with the experimental data, Zhang et al. performed a finite-size scaling analysis. This is useful at the time of identifying the order of the phase transitions involved. On the basis of the equivalence of the lattice gas hamiltonian (Eq. 5.48) with the generalized triangular-lattice model of Blume–Emery–Griffiths [75], the authors concluded that the transition at peak #1 is a first-order phase transition, while the transition at peak #2 is a second-order one. These predictions were checked performing simulations with different system sizes (finite size scaling analysis).
5.4.4 Kinetic Monte Carlo Applications
5.4.4.1 Introduction
Although MC methods are often used to obtain static, or equilibrium properties of model systems as described above, this technique may also be utilized to study dynamical phenomena. This leads to the formulation currently denominated dynamic Monte Carlo or kinetic Monte Carlo (KMC).
The foundations of dynamical MC simulations have been discussed by Fichthorn and Weinberg [76] in terms of the theory of Poisson processes , and we give here a bird’s eye view on this methodology. There are many physical systems where the events of interest can be described at a coarse-grained, mesoscopic level, assuming that the complex microscopic behavior leads to various possible transitions that we can enumerate E = {el,e2, … ,en }, which can be characterized by average transition rates R = {r l,r 2, … ,r n }.
As an example, we chose the diffusional trajectories of an adatom on a (100) single crystal surface, as shown in Fig. 5.36. We assume that we monitor a number of trajectories where the adatom is initially trapped in the central adsorption site, ending at one of the four neighboring adsorption sites. At relatively low temperatures, the trajectories will look like those on the left plot, where the adatom spends a long time (in the atomic scale) at the central site and finally diffuses to some of its four neighboring sites through trajectories close to the minimum energy path. If the experiment (eventually the simulation) is made several times, the scape of the atom from the central site to each of its neighbors will be characterized by a set average times, say {τ 1, τ 2, τ 3, τ 4}. Due to the symmetry of the system chosen for this example, all these average scape times will be equal, but they may be generally different (for instance if the environments of the various sites are different). Thus, the fine grain problem on the left of the figure may be replaced by coarse grain problem on the right, where the adatom may undergo four different transitions, E={el,e2, … ,e4} , at four different average rates R = {1/τ 1, 1/τ 2, 1/τ 3, 1/τ 4}. These ideas may be generalized to more complex problems, as long as the kind of events involved fulfills some features. If each of these events satisfies the conditions necessary to be a Poisson event,Footnote 4 the probability density of times between successive events will have the following exponential form:
One interesting property of Poisson processes is that an ensemble of independent Poisson processes will behave as one, large Poisson processes. In the example of diffusion above, this means that if we have (simultaneously with diffusion) other phenomena occurring like adatom adsorption, adatom desorption, etc, that can be considered themselves as Poisson processes, the whole behavior of the system (diffusion + adsorption + desorption) may be treated as a single Poisson process. Thus, our vector of events will look like
where the upper indices have an obvious meaning: e diff1 is a diffusion event of type 1, e ad1 is an adsorption event, e des2 a desorption event, etc. Thus, the vector of events E contains all the events that may occur at a given instant (configuration) of the system.
Similarly, the rates vector will be:
Or alternatively:
where we have defined the average rates \( {v}_i=1/{\tau}_i \) A way to visualize the last equation is to draw a line, where the average rate of each process is represented by a segment on this line, as it is shown in Fig. 5.37 for three processes. Let us represent the event vector with \( \mathbf{E}=\left\{{\mathrm{e}}_1,{\mathrm{e}}_2,{\mathrm{e}}_3\right\} \) and the velocity vector with \( \mathbf{R}=\left\{{v}_1,{v}_2,{v}_3\right\} \).
Illustration of the way in which a given process is selected in a kinetic Monte Carlo simulation where only three processes may occur. The probability of each process to occur is represented on a straight line by a segment proportional to its rate v i . The sum of all the segments is normalized to unit length, so that the occurrence of a process can be selected by generating a random number v S between 0 and 1, and then choosing the process corresponding to the segment on which the random number is found to fall. Here v S falls in the segment corresponding to the rate v 3
Since no two Poisson events may occur simultaneously, we can make the status (configurations) of the system advance by choosing one of the events whose rates are shown in the figure. To do that, the whole velocity segment may be applied into the interval [0,1], and a random number η may be generated to select the event to happen. It is observed from the figure that the random number resulted in the occurrence of a process whose velocity is v 3.
Thus, what it must be done is to allow event e3 to happen. If the processes under consideration were \( {\mathrm{e}}_1:= \) diffusion of a particle, \( {\mathrm{e}}_2:= \) adsorption of a new particle, \( {\mathrm{e}}_3:= \) desorption of the particle, we would have to desorb the particle. The new configuration of the system would be an empty surface, and the new event vector would only contain a single element, corresponding to particle adsorption. Of course, in a real system we have many particles that may diffuse, desorb, adsorb, etc, and the event and rates vectors are very large, but this is the main idea. Upon updating the configuration of the system, we must update the time in the simulation, that is, we must add to the accumulated time a time increment representing the event that has just occurred. To do that, we appeal to an equation similar to Eq. (5.53), but taking into account that we are considering all the events of the system. Now, the overall rate is \( {v}_t={v}_1+{v}_2+{v}_3 \) and Eq. (5.53) turns into:
To generate time increments distributed according to the previous equation, we must use:
where v S is a uniform random number between 0 and 1. Note that random numbers close to zero lead to large time steps, while random numbers close to 1 yield short ones.
We see that according to the KMC method, the sampling of the system must involve transition probabilities based on a reasonable dynamic model of the physical phenomena involved. The transition probabilities should reflect a “dynamic hierarchy” related to the processes taking place in the system. With this aim, the rates v i are usually taken from some suited version of absolute rate theory, adapted to surface diffusion, electron transfer, etc.
Since in principle all the processes that may potentially occur must be included in the vector R, the application of KMC methods is restricted to lattice models of the system.
5.4.4.2 Electrochemical Phase Formation for an Ideal Frank-van der Merwe System
To illustrate the application of the KMC method, we discuss the system Au (hkl)/Ag . This is a typical example for M upd on a foreign substrate S, with strong M-S interaction but negligible M-S misfit (the lattice parameters are 4.09 Å and 4.08 Å for Ag and Au, respectively). Thus, the Frank-van der Merwe or layer by layer growth mechanism is expected to operate in this system, in contrast with the Stranksi-Krastanov growth mode, expected for systems with relatively large misfits [57], or the Volmer-Weber mechanism , expected for systems where the interaction with the substrate is relatively weak, as compared with the adsorbate-adsorbate interaction. As discussed in the literature [77] and in Chaps. 2 and 3 of the present book, these systems exhibit a number of complex features, like surface reconstruction, even in the absence of adsorbate, and different expanded phases. However, a simplified model as that we will discuss here, has been shown to be useful to understand some of the experimental observations, and may also be helpful to understand other upd related problems. Giménez et al. [77] have modeled nucleation and growth of Ag upd on Au(100) and Au(111) by KMC. We discuss their modeling in some detail, since it is illustrative of how this methodology may be implemented to study upd deposition phenomena.
5.4.4.2.1 Model for the Substrate
As stated above, the KMC methodology requires a finite number of processes taking place, so that a lattice model for the substrate appears as the best alternative. Thus, square and hexagonal lattices were selected to represent the Au (100) and Au(111) substrates respectively. Figure 5.38 shows the square lattice used to represent the former surface. There, the lattice consists of 1600 adsorption sites inserted between two Au steps, to simulate both island growth on a surface and at step borders. The image of the simulation cell is repeated periodically in the vertical direction (periodic boundary conditions).
Simulation box employed to study Ag nucleation and growth upon upd on a Au(100) surface. The system has periodic boundary conditions in the vertical direction (Reprinted with permission from Ref. [77])
5.4.4.2.2 Interactions Between the Particles of the System
The choice of proper interatomic potentials is a key issue in computer simulations. This is particularly the case in upd systems, which are characterized by metallic many-body interactions. Several methods are available to calculate the total energy of a many-particle metallic system, with a computational effort similar to that of a pair potential. Among them, it is worth mentioning the EAM [78], the N-body potentials of Finnis and Sinclair [79], the second-moment approximation [80] and the glue model [81]. The article here discussed used the EAM because it showed to reproduce important characteristics of the metallic binding. The EAM considers that the total energy U tot of a metallic system made of N particles may be calculated as the sum of energies U i corresponding to single particles according to:
U i is written as:
where F i is the so-called embedding function, which represents the energy resulting from embedding atom i in the electronic density ρ h,i at the position at which this atom is located. ρh,i is obtained from the superposition of the individual electronic densities ρ j (r ij );
while ρ j represents an attractive, many-body electronic contribution, the second term in Eq. (5.60) represents the repulsion between ion cores. The latter is described through a pair potential V ij (r ij ), which depends only on the distance between the cores r ij with the form:
where the Z i (r ij ) represent an effective charge, dependent on the nature of the atom i. The functions F i (ρ h,i ) and V ij (r ij ) have been parameterized to fit experimental data for the isolated metals like cohesive energies, elastic constants, bulk lattice constants and bimetallic properties like dissolution enthalpies of binary alloys.
5.4.4.2.3 Dynamic Hierarchy: Calculations of Rates for the Different Events
As stated in the introduction, KMC requires establishing a dynamic hierarchy, which allows the construction of the rate vector R (Eqs. 5.55 and 5.56). Thus, the rates of the events that may take place must be clearly determined. In the present case of study, surface phase formation, the following events may occur: (a) adatom formation (adsorption) (b) adatom oxidation (desorption) (c) adatom diffusion. If one is interested in the particular study of the formation/disappearance of the upd phase, processes (b) or (a) may alternatively be neglected with respect to the complementary one. For example, the study of Ref. [77] was focused on the deposition of Ag on Au (100) and Au(111), so that the dissolution rate was neglected and the deposition rate was used as a parameter. On the other hand, the diffusion rate was calculated using the EAM potentials. With this purpose, the diffusion of a Ag adatom on a Au surface was considered in different possible environments as illustrated in Fig. 5.39. The initial and the final positions of the diffusing atom are embedded in an environment of six neighboring sites, which may be free or occupied by Ag or Au atoms, thus yielding a total number of 36 = 729 configurations. Figure 5.39 shows three sample environments and the corresponding energy curves along the diffusion paths. The diffusion rates were calculated from these curves according to [82]:
where v is the attempt frequency and E a is the activation energy as calculated from a trajectory between the initial and the final state, using the EAM potentials.
(a)–(c) Sample environments considered for the diffusional motion of a Ag atom on a Au(100) surface. (d) Potential energy as a function of the distance along the diffusion path for the environments shown in (a)–(c) (Reprinted with permission from Ref. [77])
Details on the organization of the KMC procedure and a description of how the algorithm may be coded, including the storage and search algorithms that are used, are described for example in the Appendix of the manuscript by Drews et al. [83].
The steps of the KMC algorithm can then be summarized as:
-
1.
A random number, \( {v}_{{\mathrm{S}}_1} \), is chosen from a uniform distribution in the range (0,1).
-
2.
All the possible N t events are determined and their rates v i calculated.
-
3.
A transition event is selected from the event vector, by selecting the first index s for which \( {\displaystyle \sum_{j=1}^s{v}_i}/{\displaystyle \sum_{j=1}^{N_t}{v}_i}\ge {v}_{{\mathrm{S}}_1} \).
-
4.
The even selected is allowed to occur.
-
5.
All v i that have changed as a result of making the move are updated.
-
6.
The time in the simulations is advanced Δt where Δt is:
where \( {v}_{{\mathrm{S}}_2} \) is a second random number, also chosen from a uniform distribution in the range (0,1).
The previous modeling was used to analyze the different behavior of Ag nucleation and growth found on Au (100) and Au(111) faces. The KMC simulations indicated the nucleation and growth should take place with the characteristic time of tenths of seconds in the case of the Au(100) face and of the order of milliseconds in the case of the Au(111) face. Therefore, if Ag is deposited at intermediate rates on both surfaces, island growth is predicted to occur on Au(100) but not on Au(111), as found in experiment [84, 85]. These features are illustrated in Fig. 5.40.
Snapshots of Ag upd growth on Au(100) (left) and Au(111) surfaces (Right). Note the occurrence and the absence of islands in the first and the second case respectively (Reprinted with permission from Ref. [77])
Another valuable information that can be obtained with this simulation technique is the number of islands formed as a function of coverage degree at different adsorption rates, as illustrated in Fig. 5.41.
KMC results for the number of islands as a function of the coverage degree for Ag upd on Au(100) at different deposition rates v, as indicated in the figure. Each curve represents an average over six simulation runs (Reprinted with permission from Ref. [77])
The present methodology has been very recently extended by Treeratanaphitak et al. [86, 87] to account for collective surface diffusion processes, in addition to nearest-neighbor hopping, including atom exchange and step-edge atom exchange, allowing the study of polycrystalline metal electrodeposition. Thus, the combination of EAM potentials with KMC appears as a very promising tool for studying the present and other related phenomena, like for example the formation of surface alloys.
5.4.4.3 Other Simple Metal Deposition Systems Involving a Foreign Substrate
The previous formalism has also been used to tackle other upd-related deposition phenomena. Rather than simulating specific systems, a useful approach is sometimes to vary one or more of the parameters of the model applied and analyze how they affect the properties emerging from the simulation. The utility of this approach is twofold: on one side, it can be expected that if a simulation reflects the experiment results, its parameters may be close to those of the experimental system. This allows getting information that is not directly available from the experiment. On the other hand, the parameters of the simulation may be tuned to get a given result, like for example a uniform distribution of islands on a substrate. In this way, the simulation becomes a useful tool for system design.
Concerning the first type of application mentioned above, Giménez et al. [88] have used KMC to analyze three different situations for adatom deposition rates, as illustrated in Fig. 5.42: (a) a case where the deposition rate is the same on any adsorbate-free sites on the substrate (Model A); (b) a case where deposition is only allowed on sites characterized by adsorbate-free surroundings (Model B); (c) a more general case where deposition at edge sites and terraces is allowed at different rates (Model C). In the last two cases, the coverage vs time curves were fitted to a stretched exponential law \( \left(\theta =1- \exp \left[-{t}^{\alpha }/{k}_{\mathrm{B}}T\right]\right) \), with the finding that the parameter α can be used as a diagnose criterion to differentiate between the two cases. While in model B, α was found to be always smaller than 1, in model C, α was found to vary between 1.1 and 2.4, depending on the deposition rates assumed. This predictions may be contrasted with those of Avrami’s model [89], where the exponent α is 2 or 3, depending on whether the nucleation is progressive or instantaneous.
Scheme of the mechanisms for atom deposition considered in Ref. [88]: (a) Particle adsorption occurs on all unoccupied sites at the same rate k. (b) Particle adsorption occurs only at sites without neighboring adsorbates at the rate k. (c) Particles are considered to be discharged preferably at sites with neighboring adatoms at a rate k 2 and at a lowest rate, k 1, at those sites without neighboring adatoms (Reprinted with permission from Ref. [88])
Drews et al. [90] have also used KMC simulations to investigate nucleation and early stages of growth during metal electrodeposition on a foreign substrate. A negative overpotential was assumed (overpotential deposition). The authors also chose conditions where the kinetics of attachment of atoms to the electrode surface is rate-limiting, that is, low overpotentials. A negative overpotential was assumed (overpotential deposition). Adatom diffusion, characterized by a diffusion jump frequency w, was not only considered on the substrate, but also on a monolayer and on a bilayer of M. Adatom deposition was allowed on both the substrate or the metal M via a Tafel kinetics, at a deposition rate v dep. Some of the information obtained from the simulation was concerned with cluster density, average cluster size, and average cluster height. It was found that the energy barrier for metal-on-substrate surface diffusion had the strongest effect on the cluster density in the parameter regimes investigated, while the energy barrier for metal-on-metal surface diffusion had a weak effect.
In a subsequent article, Drews et al. [83] have used KMC to study the influence of the presence of metal seed clusters and other parameters on the cluster size distribution of deposits. According to these simulations, it was found that the best conditions for producing a uniform size distribution is an initial high number of seed clusters, a low applied potential and a low metal-surface diffusion energy barrier.
Although metal deposition on a foreign substrate was also assumed to occur under overpotential conditions as in the previous case, it is worth mentioning here the KMC work of Stephens and Alkire [91] concerning nucleation and growth at monatomic step edges. It was found that the propensity of the deposit to grow at step edges or to form islands on the surface may be measured by the adimensional quantity Λ, which was defined as:
where D is the diffusion coefficient, v dep is the deposition rate of adatoms and L is half the distance between steps. Since the denominator represents a diffusion length of the incoming atoms, it can be expected that if \( {\varLambda}_{\mathrm{d}}\gg 1 \), atoms being deposited will diffuse around the surface easily, with the result that most of the deposit would grow at the step edges. On the other hand, if \( {\varLambda}_{\mathrm{d}}\ll 1 \), the surface diffusion rate is small in comparison to the deposition rate, so that atoms will tend to stay near the site of deposition. The results of the simulation reflected this interpretation, as can be observed for example in Fig. 5.43, which was obtained from simulations for homoepitaxial growth. There, we can see the transition from regions of instantaneous nucleation \( \left({\varLambda}_{\mathrm{d}}>1\right) \) to progressive nucleation \( \left({\varLambda}_{\mathrm{d}}<1\right) \). In fact, in the first case we see little formation of clusters at large values of Λ d, since the simulations show very little formation of clusters other than the growth at the step edges. In the second case, for small values of Λ d, the cluster density shows an approximately linear relationship with respect to time, consistent with progressive nucleation.
Cluster density plotted as a function of Λ d and time. Time is represented by the amount of deposit on the surface (Reprinted with permission from Ref. [91])
Figure 5.44 shows snapshots of these simulations, for different Λ d, as well as for different jump frequencies w different heights of the diffusion energy barriers. There, it can be observed the transition from island formation to border decoration upon Λ d increase. On the other hand, the far left column of this figure shows results obtained with a low jump frequency and low surface diffusion energy barriers that may be contrasted with the results shown on the far right column, which shows results obtained with a high jump frequency and high energy barriers. It is apparent that in the former case large, facetted clusters are formed, while in the latter much less smooth and smaller clusters result.
Snapshots of simulation outputs after deposition of one-quarter equivalent monolayers of KMC simulated deposition, for several of the simulated parameter regimes. From top to bottom, the snapshots correspond to increasing Λ d values. From left to right, correspond to increasing jump frequencies and surface diffusion energy barriers (Reprinted with permission from Ref. [91])
Although the results we have shown above in Figs. 5.43 and 5.44 were for a homoepitaxial system, it was found that heteroepitaxial growth follows the same principles that govern the cluster density, step edge growth, and other deposit characteristics.
New advances in related KMC simulations, have been undertaken recently. As mentioned above, Treeratanaphitak et al. [86, 87] have extended the EAM-KMC methodology to include atom exchange and other phenomena. Another interesting improvement of KMC is the introduction of the first passage time algorithm [92] to replace the computationally demanding simulation of diffusion hops in KMC by larger jumps when particles are far away from step-edges or other particle. This innovation has allowed to analyze different categories of deposition systems: homoepitaxy , heteroepitaxy , multi-layer, step edge, and confined regions [93].
5.4.4.4 Kinetic Monte Carlo Analysis of Cu Underpotential Deposition on Au (111)
Similarly to the discussion done in Sect. 5.4.3.2 of this chapter, we discuss separately the work of Brown et al. [94] on the application of KMC techniques to complex upd systems. As we have seen in Sect. 5.4.3.2, an effective lattice-gas Hamiltonian was developed for the Au (111)/Cu system in the presence of sulfate anions. As pointed out above in Sect. 5.4.4.1 a dynamic hierarchy, involving the calculation of different transitions rates, is necessary for the implementation of the KMC procedure. It is illustrative to see how Eq. (5.48) can be used, along with some considerations, to construct such a hierarchy. At first, it is relevant to consider which processes are to be taken into account. In the present model these processes were, for both species, Cu and sulfate: (a) adsorption, (b) desorption, (c) one-step lateral diffusion. To proceed to assignation of rates, since these are related to processes involving single particles, it is more useful to consider the free energy associated with a single adsorbed particle of species X (X = S (Sulfate) or C (Copper)) occupying site i for a specific configuration of neighbors and to formulate the lattice-gas Hamiltonian:
where the symbols have the same meaning as in Sect. 5.4.3.2. The sum \( {\displaystyle {\sum}_{j(i)}^{(n)}} \) runs over all adsorption sites j that are that are nth neighbors of site X, the sum \( {\displaystyle {\sum}_{\Delta (i)}^{(n)}} \) runs over all second-neighbor equilateral triangles involving site i, the factor δ I,S is unity when X = S and zero otherwise, and the index Γ runs over all possible arrangements of neighboring adsorbate particles within the maximum interaction range from site i. The index X may also take the value 0 (unoccupied site), in which case \( {\widehat{\mathrm{H}}}_i\left(0,\varGamma \right)=0 \), regardless of the arrangement of the neighbors.
Let us now consider the desorption-adsorption process in terms of the hamiltonian (Eq. 5.66). With this purpose, we appeal to a representation of the free energy profile of the reaction in terms of the Butler-Volmer approximation [95], as depicted in Fig. 5.45. To analyze the adsorption of a particle, we move from right to left of the figure. Three different situations are considered for the ad-state. The most simple initial case, labeled with I, is an adsorbed particle without neighbors, in a condition where \( {\tilde{\mu}}_{\mathrm{X}}=0 \). Under this condition \( {\widehat{\mathrm{H}}}_i\left(\mathrm{X},\varGamma \right)=0 \), the free energy profile is completely symmetric, with a free energy barrier of magnitude Δ *0 (X). The next initial ad-case is labeled with II in the figure, and corresponds to an initial adsorbed particle without neighbors, but in the presence of an electrochemical potential \( {\tilde{\mu}}_I\ne 0 \). In this case \( {\widehat{\mathrm{H}}}_i\left(\mathrm{X},\Gamma \right)=-{\tilde{\mu}}_I \). The most general case is that denoted with III, where the single-particle Hamiltonian is Ĥ i (X, Γ). In this case, the free-energy barrier for adsorption is changed to:
where α a is the so-called symmetry factor, usually assumed to be close to 1/2. Thus, if the effective interactions of the ad-state are negative, the free energy activation barrier will be lowered by the amount given by the second term on the rhs of Eq. (5.67). Through this equation, we have solved a kinetic problem by using a thermodynamic expression, given by Eq. (5.66). A free parameter Δ *0 (X), which depends on the species being adsorbed, has emerged from the ansatz (Eq. 5.67).
Butler-Volmer-type free-energy barrier scheme for considering adsorption/desorption of particles. Three different cases are analyzed, as discussed in the text (Reprinted with permission of Ref. [94])
To get the activation energies for surface diffusion between neighboring sites i and j, the ansatz proposed was:
where the max[x, y] is a function that selects the maximum value between x and y and \( {\tilde{\varDelta}}_0^{*}\left(\mathrm{X}\right) \) is a new parameter to be chosen.
The parameters introduced in Eq. (5.66) to calculate Ĥ i (X, Γ) were not those presented in Sect. 5.4.3.2 but an improved version of them, which were also reported in Ref. [94]. The phase diagram obtained with this improved set of parameters is shown in Fig. 5.46, along with a cyclic voltammogram for Cu upd onto Au (111) surface.
(a) Improved ground-state phase diagram for the system Cu/Au(111) in the presence of sulfate anions, as presented in Ref. [94]. The structure of the different phases can be found in Fig. 5.35 of Sect. 5.3.2. The dotted line represents the isotherm used to simulate the potential-step experiments. It was chosen to match the transition potentials observed in experiments. (b) Cyclic voltammogram for Cu upd onto Au(111) surface, taken from Ref. [71]. Note the correlation between the peaks in the voltammograms (A/A′ and B/B′) in figure (b), with the crossings in the phase boundaries marked with arrows in figure (a) (Reprinted with permission from Refs. [94] and [71])
Rather than on voltammograms, the KMC simulations were focused on potentiostatic transients, motivated by experimental results that were discussed in Chap. 2 [96–98]. Hölzle et al. [97] measured current transients in potential-step experiments performed at both transitions marked with A/A′ and B/B′ in Fig. 5.46a, with both positive-going and negative-going steps. Figures 5.47 and 5.48 show simulated potential steps for the B/B′ and A/A′ transitions respectively. In the first case, it must be remarked that both transients reflect nucleation and growth mechanisms. As observed in the experimental data, the broad maximum becomes stronger and it shifts to shorter times as the size of the step is increased. In the second case, Fig. 5.48, it is remarkable that the transients are very different for positive and negative potential steps. While the positive step present current transients that are non-monotonic (left), the negative steps lead to monotonically decreasing transients, which do not present to a simple functional form. Snapshots of a simulation of this type of negative step shows that equilibration after the step occurs in a disordered phase with a relatively high sulfate coverage (see Fig. 5.49). The sulfate present collapses first with incoming copper atoms to form a domain of the phase \( {\left(\sqrt{3}\times \sqrt{3}\right)}_{1/3}^{1/3} \), metastable at the potential where the step was made (see Fig. 5.46a). This phase is filled later with Cu to yield finally the stable \( {\left(\sqrt{3}\times \sqrt{3}\right)}_{2/3}^{1/3} \) phase (see Fig. 5.49).
KMC simulation of potential steps across the transition between the \( {\left(1\times 1\right)}_1^0 \) and \( {\left(\sqrt{3}\times \sqrt{3}\right)}_{2/3}^{1/3} \) phases. Left: Potential step in the positive direction, as illustrated by the arrow B′ in Fig. 5.46a. Right: Potential step in the negative direction, as illustrated by the arrow B in Fig. 5.46b (Reprinted with permission from Ref. [94])
KMC simulation of potential steps across the transition between the \( {\left(\sqrt{3}\times \sqrt{3}\right)}_{2/3}^{1/3} \) and \( {\left(1\times 1\right)}_0^0 \) phases. Left: Potential step in the positive direction, as illustrated by arrow A′ in Fig. 5.46a. Right: Potential step in the negative direction, as illustrated by arrow A in Fig. 5.46b (Reprinted with permission from Ref. [94])
Series of snapshots after a negative-going potential step to 20 mV below the transition between the low coverage and mixed layers, see arrow A in Fig. 5.46a. Note the high concentration of sulfate species at 0 s, the predominance of phase \( {\left(\sqrt{3}\times \sqrt{3}\right)}_{1/3}^{1/3} \) at 0.25 s and the predominance of the \( {\left(\sqrt{3}\times \sqrt{3}\right)}_{2/3}^{1/3} \) at 1 s. The circles were drawn to focus on some compact, representative domains (Reprinted with permission from Ref. [94])
The authors pointed out that the fact that different dynamic paths can give current profiles qualitatively similar to those observed experimentally indicates that more study of the copper upd system is desirable. However, it must be recognized that these studies represented an important step forward in the understanding of this puzzling system.
5.5 Miscellaneous Models Applied to Underpotential Deposition
We devote this section to different models that have been applied to model upd, but which have not yet evolved to develop a wide branch of theoretical work.
5.5.1 Quantum Mechanical Semiempirical Calculations
Before the availability of DFT programs, much quantum mechanical work was based on semiempirical approximations. This was for example the case of the semi-empirical atom superposition and electron delocalization molecular orbital (ASED-MO) technique [99, 100]. This method became very popular at the end of the 1980s and the beginning of the 1990s, and found a number of applications to upd. Mehandru and Anderson [101] used this method to consider the behavior of quarter of a monolayer and a half-monolayer of Pb atoms adsorbed on Au (100) in relationship to the binding and orientation of the oxygen molecule on these surfaces. Lopez et al. calculated the stability of different Ni upd structures as a function of surface coverage and electric potential applied to the Pt (111) surface [102], and they also investigated the influence of different surface structures on coadsorbed water decomposition [103]. In the first case, the information obtained was related to the most favorable binding site and the growth mechanism of the metal deposit, which was accompanied by a molecular orbital analysis. Lopez et al. used the same methodology to consider the possible structures of copper electrodeposits on Pt(100) and Pt(111) clusters under different applied electric potentials [104].
5.5.2 Orientational Ordering of Adsorbed Monolayers
We have seen in Chaps. 2 and 3 that Tl and Pb monolayers adsorbed on Ag (111) surfaces form incommensurate, hexagonal monolayers that are compressed compared to the bulk metals by 0.1–3.2 % and rotated from the substrate [011] direction in several degrees. A similar observation has been made for Tl and Pb adsorbed on Au (111). To study these systems, Mola and Blum [105] and Mola et al. [106, 107] have set up a model for the adsorption energy of a hexagonal close packed monolayer deposited on a substrate surface of the same structure but different lattice constant as a function of the epitaxy angle between the principal axis. The underpotentially deposited Pb on the (111) surface of silver was the subject of these studies, but the model could easily be extended to other similar cases of different geometry. Figure 5.50 shows the geometrical arrangement that these authors employed to represent this system. The substrate S was considered to be described as a hexagonal lattice with lattice constant a, set equal to 1 for convenience, while the adsorbate defined a superimposed hexagonal arrangement of lattice constant b. Coordinate systems (x,y) and (x’,y’) were defined for A and S, respectively so that the vectors (m,n) and (r,s) with integer components define the positions of the point lattices A and S. Assuming a common origin for both coordinates, the angle θ defines the epitaxy angle.
The representation of a lattice point \( \mathbf{X}=\left(m,n\right) \) of the adsorbate lattice on the substrate system, say \( \mathbf{X}\hbox{'}=\left(x\hbox{'},y\hbox{'}\right) \) is given by:
where the matrix relating the components in the two systems, which are shown in Fig. 5.50, has a simple form:
The points at which the two lattices in Fig. 5.50 overlap define a coincidence lattice . These points, that we label within the adsorbate lattice with \( {\mathbf{R}}_{\mathrm{c}}=\left({x}_{\mathrm{c}},{y}_{\mathrm{c}}\right) \), fulfill the relationship:
where d(x c, s c) is the distance of the point R c to the center of the coordinates and h is an integer number. Using Eqs. (5.69), (5.70) and (5.71) we get:
which leads to the angle:
Considering the approximate experimental value of \( b=1.2010 \), Mola and Blum [105] calculated the values of h, x c and y c compatible with it, as well as the corresponding θ, finding the best agreement with experiment for h = 28, b = 1.2000 and \( \theta =\pm 4.43{}^{\circ} \).
Extensions of this model were developed by Mola et al. [106, 107], expanding the potential energy per surface atoms in a Fourier series:
where G denotes 2-dimensional reciprocal lattice vectors and R indicates the position of an adatom .
The binding energy per adatom was evaluated considering up to three or four harmonics in Eq. (5.74), finding a good agreement between the calculated θ values and the experimental ones.
5.5.3 Entropic Contribution to Underpotential Deposition Shift: Lattice Dynamics Analysis
Entropic contributions to underpotential shift (see definition in Chap. 1) have been seldom considered in the literature [108]. Pioneering work in the modeling of entropic contributions to underpotential shift was undertaken by Oviedo et al. [109] by means of lattice dynamics. In this approach, the Hamiltonian of the system, which takes into account potential and kinetic contributions to the energy of the system in normal coordinates ξ and momentum \( \dot{\upxi} \) is written as:
where U(0) is the energy of the system when all atoms are in their equilibrium positions, fi denotes an effective force constant and M i represents the effective mass of particle i. The energy of the system was calculated using the EAM , as discussed in Sect. 5.4.4.2, and the quasi-harmonic lattice dynamic method (EAMLD) developed by Barrera and co-workers [110]. Within this approximation, it is assumed that the Helmholtz energy of a crystal at a temperature T can be written as the sum of static and vibrational contributions:
where U stat is the potential energy of the static lattice in a given configuration and F vib is the sum of the harmonic vibrational contributions from all normal modes. For a periodic structure, the vibrational frequencies υ j (q) (q being a wave vector defined in the reciprocal lattice of the system) are obtained by diagonalization of the dynamic matrix, so that F vib is given by:
where the first term is the zero-point energy at T = 0 K. For a macroscopic crystal, the sum over q becomes an integral over a cell in reciprocal space, which can be evaluated by taking successively finer uniform grids until convergence is achieved. The normal mode frequencies υ j (q) depend on the interactions among the atoms in the solid, as described by the EAM.
The vibrational contribution to the entropy is in turn given by:
The specific heat at constant volume may be obtained from the previous equation considering the thermodynamic relationship \( {\left(\partial S/\partial T\right)}_{\mathrm{V}}={C}_{\mathrm{V}}/T \). Figure 5.51 shows the supercells used to perform the lattice dynamics analysis for several systems, including the (111), (100) and (110) faces of different substrate/adsorbate combinations containing Ag , Au , Pt , Pd and Cu . A 1 × 1 commensurate structure was assumed for all systems.
Diagram of the supercells employed to represent the substrate (single crystal face) + adsorbate system for the lattice dynamic analysis described in the text. It consists of a 14-layer basis (12 inner substrate layers plus two external adsorbate ones). (a) Slabs and their images in the z-direction. (b) Top view of the surface. Periodic boundary condition in x-, y- and z-directions were applied (Reprinted with permission from Ref. [109])
Figure 5.52 shows the entropic contribution to underpotential shifts for the systems analyzed, as function of the crystallographic misfit. The misfit was defined as in Eq. (5.47), but without the factor 100, so that the systems included in this figure are in the range \( 12\%<{\upvarepsilon}_{\mathrm{mf}}<14\% \). The first relevant information concerns the magnitude of the entropic contribution to upd shift, where it is found that this quantity is rarely largen than 20 meV, which translated into the electrochemical scale means changes at the most of the order of 20 mV. It can be observed that plots for all single crystal faces present a positive slope, so that negative and positive misfits roughly correspond to negative and positive entropic contributions, respectively. This has the following physical explanation: when an adsorbate is compressed to fit on a smaller substrate, its motion becomes more restricted delivering a negative contribution to upd shift. This general trend is modulated by specific chemical effects, but it seems to be valid in a first approximation. Experimental entropy shifts will very likely differ quantitatively from the values reported in Fig. 5.52, since the calculations assumed pseudomorphic structures, and real systems with a large misfit will relax this condition either by adopting incommensurate structures or via the occurrence of surface defects in the monolayer.
Entropic contribution to the underpotential shift as a function of the crystallographic misfit. The adsorption of M (M = Ag, Au, Pt, Pd, Cu) is considered on different substrates. (a) (111), (b) (100) and (c) (110) corresponding to the three single crystal surfaces studied. The inset shows the symbols employed to represent the different adsorbates on a given substrate. On each line representing a substrate, the adsorbates were, from left to right: Ag, Au, Pt, Pd and Cu (Reprinted with permission from Ref. [109])
5.5.4 Application of Molecular Dynamics and Related Techniques to Underpotential Deposition
Molecular Dynamics (MD) is a computer simulation technique that allows generating trajectories in the phase space of a given system. This procedure is performed by numerically solving the classical equations of motion (Eq. 5.6) and (Eq. 5.7), presented in the introduction of this chapter and can be summarized as:
In the quantum mechanical approach we took in the introduction of this chapter the set {R i } represented the position of nuclei or core ions, which were in principle treated separately from electrons. In a more approximate description often used, the {R i } represent the position of the atoms, viewed as a whole. Each atom is not viewed as composed of a nucleus and electrons, but considered as a whole entity, which interacts with other atoms via an effective potential. This is, for example, the case of the Lennard-Jones interaction potential , where the interaction between particles 1 and 2 is given by:
where ε LJ is the depth of the potential well, σ LJ is the finite distance at which the inter-particle potential is zero and \( {R}_{12}=\left|{\mathbf{R}}_2-{\mathbf{R}}_1\right| \). The potential energy for such a system can be written as \( U\left(\mathbf{R}\right)=\frac{1}{2}{\displaystyle \sum_{i\ne j}{v}_{ij}^{\mathrm{LJ}}}\left({R}_{ij}\right) \). In order to continue the discussion of the method, we introduce the atomic momenta \( \mathbf{p}=\left({\mathbf{p}}_1,{\mathbf{p}}_2,{\mathbf{p}}_3,\dots {\mathbf{p}}_N\right) \). Thus, the kinetic energy of the system (K) can be written as:
The total energy may then be written as a sum of kinetic and potential terms H = K + U. The time integration algorithm most commonly used in molecular dynamics is probably the so-called Verlet algorithm. The general idea behind this algorithm is to write third-order Taylor expansions for the positions \( {\mathbf{r}}_i\left(t\pm \Delta t\right) \), in different time directions. If we consider that, for particle i, v i is the velocity, a i is the acceleration, and b i is the third derivative of r i with respect to t, we can write:
By adding the two expressions, we obtain:
Since we are dealing with Newton’s equations of motion, a i (t) is just the force divided by the mass, and the force is, in turn, a function of the complete set of atomic coordinates {R i }, as established in Eq. (5.79).
Molecular or atom dynamics simulation as discussed above is a deterministic technique that allows the prediction of the “real” trajectories of motion at real time. However, to capture many relaxation processes, the integration time step must be very small, of the order of 10−15 s, and therefore the period of time explored cannot usually overcome the nanoseconds, something that makes the technique not suited for many physical problems involved in crystallization. Furthermore, in some cases not all the degrees of freedom considered are relevant for the process under study. Taking metal deposition as an example, in some cases the simulator may interested in the structure of the deposit being formed. While the coordinates of the discharged metal atoms are relevant for this purpose, not so the coordinates of the solvent molecules, since they rather participate as thermal bath where the depositing ions are immersed. One of the options to solve this situation was discussed in Sect. 5.4.4. Another, intermediate possibility is Langevin dynamics (LD), which was developed to follow the trajectories of ions or neutral atoms in a fluid at relatively low computational cost. The algorithm for LD is closely related to MD and is conceptually simple: the motion of the i-th atom with mass mi is governed by Langevin equation:
where the terms on the rhs of Eq. (5.85) denote: f i is the force as calculated in ordinary MD, the second term corresponds to an average frictional force with a macroscopic friction coefficient given by γ i , and f irand is a random Gaussian force obeying the fluctuation-dissipation theorem [111]. Ermak’s algorithm [112] provides a way to treat properly both the systematic dynamic and the stochastic elements of Langevin equation.
Schmickler et al. [113, 114] have developed a simulation method combining MD and LD to study systems of interest in upd. A scheme of this simulation method is shown in Fig. 5.53. The simulation system consists of three principal parts. The bottom part, labelled A, contains several layers of metal atoms arranged in an fcc lattice (or similar) containing 400 atoms per layer; the three bottom layers are kept fixed, the others are mobile and obey ordinary deterministic MD. The interaction between these metal atoms is calculated from the EAM [78]. In the electrolyte solution, only the metal ions are modeled explicitly as particles contained in the regions B and C. Their motion is described using LD. In region C, the concentration of the particles is kept constant by adding or removing particles, as required. In contrast, region B contains a variable number of particles and can thus represent a depletion layer for metal deposition. The particles in the solution do not interact with each other, but experience a constant background. Switching between LD and MD occurs at the interface B and A, allowing atom adsorption/desorption at rates that depend on the background chemical potential μ0.
Schmickler et al. [113] used the present methodology to study Ag upd on Au (111) surfaces and Ptopd on Au(111) surfaces. In a subsequent work, Mariscal et al. [114] used this methodology to analyze the decoration of Au islands on Au(111) surface by Ag atoms, and the deposition of Ni on Au(111) and Pt(111) surfaces. Snapshots of a simulation of the former system are shown in Fig. 5.54
Snapshots of a MD-LD simulation of Ag decoration of a Au island on a Au(111) surface (Reprinted with permission from Ref. [114])
Very recently, MD simulations have also been used along with the two-phase thermodynamic (2PT) method to study the entropic contribution to monolayer upd formation [115]. We explain briefly the idea behind this application. In the canonical thermodynamic ensemble, all thermodynamic functions can be calculated from the partition function Q. In the case of entropy, the relationship between entropy and the partition function is given by:
The thermodynamic properties of pure metals are in many cases calculated on the basis of a harmonic oscillator model using statistical mechanics [116]. Within the harmonic approximation, the partition function can obtained from the vibrational density of states DOS(v) of the system according to:
where v is the frequency of normal modes and W(v) corresponds to a weighting function given by \( W(v)=-hv/2{k}_{\mathrm{B}}T- \ln \left[1- \exp \left(-hv/2{k}_{\mathrm{B}}T\right)\right] \). The density of states (DOS) may be calculated from the Fourier transform of the velocity autocorrelation function [117]. The harmonic approximation may be a reasonable approach for bimetallic systems with negligible mobility and misfit [109]. However, in bimetallic upd systems like Pb /Au , characterized by a high adatom diffusivity and misfit, this approach may no longer be valid because of the significant anharmonic nature of the frequency modes. Furthermore, in very small bidimensional clusters the translational contribution may become important. This is the reason for the development of a more sophisticated approach including translational contributions, like the 2PT model. Within this model, the thermodynamic properties are determined from the sum of static, translational, and vibrational contributions. In the case of entropy:
This is possible by dividing the DOS distribution into solid-like and gas-like components:
The gas component is determined based on the DOS at zero frequency and ensures that all of the diffusive modes are included in this component. Once the gas-like component is determined, the solid-like component can be obtained from the difference between the total DOS and the gas-like DOS. So, the 2PT method allows the computation of anharmonic effects explicitly. The studies of Ref. [115] demonstrated that very small Pb clusters on Au (111) surfaces show an entropic contribution to their stability. This is expected from the observation of their DOS, as shown in Fig. 5.55, where the increasing translational contribution for smaller clusters is marked with arrows in the figure.
Density of states corresponding to Pb clusters of different sizes on a Au(111) surface at 300 K as is indicated in the legend. The curves have been normalized by dividing by the number of Pb atoms (Reprinted with permission from Ref. [115])
The entropic contribution of small clusters to underpotential shift, calculated using the 2PT method is shown in Table 5.13, together with the energetic and free energy contributions. It can be observed that the largest contribution to the upd shift stems from the vibrational part, being the translational practically negligible, even for the smallest clusters.
Notes
- 1.
A example of multicomponent is given in Chapter 6 in the case of upd on nanoparticles.
- 2.
\( {U}_{\mathrm{S}-{\mathrm{M}}_{\theta}}^{\mathrm{bind}} \) is calculated as: \( {U}_{\mathrm{S}-{\mathrm{M}}_{\theta}}^{\mathrm{bind}}=\left({U}_{\mathrm{S}+\mathrm{M}}-{U}_{\mathrm{S}}\right)/{N}_{\mathrm{M}}-{U}_{\mathrm{M}}^{\mathrm{vac}} \), where is \( {U}_{\mathrm{S}+\mathrm{M}} \) is the energy of substrate + adsorbate, U S is the energy of a nacked substrate, N M is the number of M atoms in the supercell, and U vacM is the energy of a single M atom in vacuum.
- 3.
Note that this quantity is different from the binding energy of an adsorbate atom, \( {U}_{{\mathrm{S}\hbox{-} \mathrm{M}}_{\uptheta}}^{\mathrm{bind}} \) used in Eq. (5.18), which is referred to isolated adsorbate atoms in vacuum. That is: \( {U}_{\mathrm{S}-\mathrm{M}}=\left({U}_{\mathrm{S}+\mathrm{M}}-{U}_{\mathrm{S}}-{U}_{\mathrm{adlayer}}^{\mathrm{vac}}\right)/{N}_{\mathrm{M}} \) where is \( {U}_{\mathrm{S}+\mathrm{M}} \) is the energy of substrate + adsorbate, U S is the energy of a nacked substrate, N M is the number of M atoms in the supercell, and U vacadlayer is the energy of a free standing adlayer in vacuum.
- 4.
Poisson processes in a nutshell: if N t (t) is a random variable characterizing the observation of a number of certain events during a time interval t, Poisson processes are characterized by: (a) \( {N}_t(0)=0 \), (b) N t (t 1) and N t (t 2) are independent if t 1 and t 2 are disjoint intervals. (c) The probability of observing a single event in the interval h increases linearly with h. (d) The probability of observing two or more events in the interval h increases with a power larger than one.
References
Oviedo OA, Negre CFA, Mariscal MM, Sánchez CG, Leiva EPM (2012) Electrochem Commun 16:1
Sánchez CG, Leiva EPM, Kohanoff J (2001) Langmuir 17:2219
Hill TL (1960) An introduction of statistical mechanics. Addison-Wesley Publishing Company Inc, Reading
Schmickler W (1979) J Electroanal Chem 100:533
Kornyshev A, Schmickler W (1985) J Electroanal Chem 185:253
Muscat JP, Newns DM (1978) Prog Surt Sci 9:1
Gadzuk JP (1975) Surface physics of materials, vol 2. Academic, New York
Schmickler W, Henderson D (1986) Prog Surf Sci 22:4
Schmickler W (1985) Chem Phys Lett 115:216
Kornyshev A, Schmickler W (1986) J Electroanal Chem 202:1
Newmark AR, Schmickler W (1992) J Electroanal Chem 329:159
Schmickler W (1995) Chem Phys Lett 237:152
Schmickler W (1996) Electrochim Acta 41:2329
Santos E, Quaino P, Schmickler W (2012) Phys Chem Chem Phys 14:11224
Leiva EPM, Schmickler W (1989) Chem Phys Lett 160:75
Schmickler W (1990) Chem Phys 141:95
Lehnert W, Schmickler W (1991) J Electroanal Chem 310:27
Lang ND, Kohn W (1970) Phys Rev B 1:4555
Ashcroft NW (1966) Phys Lett 23:38
Leiva EPM, Schmickler W (1994) Electrochim Acta 39:1015
Leiva EPM (1995) Surf Sci 335:83
Leiva EPM, Schmickler W (1995) Electrochim Acta 40:37
Kramar T, Podloucky R, Neckel A, Erschbaumer H, Freeman AJ (1991) Surf Sci 247:58
Sánchez CG, Leiva EPM (1998) J Electroanal Chem 458:183
Sánchez CG, Leiva EPM (1999) Electrochim Acta 45:691
Dietterle M, Will T, Kolb DM (1995) Surf Sci 342:2937
Ogaki K, Itaya K (1995) Electrochim Acta 40:1249
Kolb DM (1994) Ber Bunsenges Phys Chem 98:1421
Greeley J (2010) Electrochim Acta 55:5545
Hammer B, Hansen LB, Nørskov JK (1999) Phys Rev B 59:7413
Kittel C (2005) Introduction to solid state physics, 8th edn. Wiley, London
Mrozek P, Sung Y-E, Wieckowski A (1995) Surf Sci 335:44
Sánchez CG, Dassie SA, Leiva EPM (2002) Langmuir 18:6628
Soler JM, Artacho E, Gale J, García J, Junquera J, Ordejón J, Sánchez-Portal D (2002) J Phys Condens Matter 14:2745
Esplandiu MJ, Schneeweiss MA, Kolb MA (1999) Phys Chem Chem Phys 1:4847
Feibelman P (2001) Phys Rev B 64:125403
Pasti I, Mentus S (2010) J Alloys Compd 497:38
Giannozzi P, Baroni S, Bonini N, Calandra M, Car R, Cavazzoni C, Ceresoli D, Chiarotti GL, Cococcioni M, Dabo I, Dal Corso A, Fabris S, Fratesi G, de Gironcoli S, Gebauer R, Gerstmann U, Gougoussis C, Kokalj A, Lazzeri M, Martin-Samos L, Marzari N, Mauri F, Mazzarello R, Paolini S, Pasquarello A, Paulatto L, Sbraccia C, Scandolo S, Sclauzero G, Seitsonen AP, Smogunov A, Umari P, Wentzcovitch RM (2009) J Phys Condens Matter 21:395502
Perdev JP, Burke K, Ernzerhof M (1996) Phys Rev Lett 77:3865
Danilov AI, Nazmutdinov RR, Zinkicheva TT, Molodkina EB, Rudnev AV, Polukarov YM, Feliu JM (2008) Russ J Electrochem 44:697
Blum L, Huckaby DA (1990) J Chem Phys 92:2646
Blum L, Huckaby DA (1991) J Chem Phys 94:6887
Blum L, Huckaby DA, Legault M (1996) Electrochim Acta 41:2207
Huckaby DA, Blum L (1991) J Electroanal Chem 315:255
Huckaby DA, Blum L (1993) Proc Electrochem Soc 93:232
Blum L, Huckaby DA (1994) J EIectroanal Chem 375:69
Blum L, Legault M, Turq P (1994) J ELectroanal Chem 379:35
Huckaby DA, Medved I (2002) J Chem Phys 117:2914
Huckaby DA, Medved I (2006) Rom J Phys 51:603
Medved I, Huckaby DA (2010) Fluid Phase Equilib 290:21
Borgs C, Kotecky R (1990) J Stat Phys 61:79
Borgs C, Kotecky R (1995) J Stat Phys 79:43
White JH, Abruña HD (1990) J Phys Chem 94:894
Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E (1953) J Chem Phys 21:1087
Norman GE, Filinov VS (1969) High Temp 7:216
Del Popolo MG, Leiva EPM (1997) J Electroanal Chem 440:271
Budevski E, Staikov G, Lorenz WJ (1996) Electrochemical phase formation and growth. VCH, Weinheim
Dietterle M, Will T, Kolb DM (1995) Surf Sci 342:29
Rojas MI, Amilibia GE, Del Popolo MG, Leiva EPM (2002) Surf Sci Lett 499:L135
Rojas MI, Del Popolo MG, Leiva EPM (2004) Langmuir 20:4279
Grossmann A, Erley W, Hannon JB, Ibach H (1996) Phys Rev Lett 77:127
Rojas MI (2004) Surf Sci 569:76
Leiva EPM, Del Pópolo MG, Schmickler W (2000) Chem Phys Lett 320:393
Oviedo OA, Rojas MI, Leiva EPM (2005) Electrochem Commun 7:472
Lorenz W, Staikov G, Schindler W, Wiestbeck W (2002) J Electrochem Soc 149:K47
Van Der Eerden JP, Staikov G, Kashchiev D, Lorenz WJ, Budevski E (1979) Surf Sci 82:364
Giménez MC, Leiva EPM (1999) Electrochim Acta 45:699
Giménez MC, Leiva EPM (2003) Langmuir 19:10538
Giménez MC, Ramirez-Pastor AJ, Leiva EPM (2006) Surf Sci 600:4741
Giménez MC, Ramirez-Pastor AJ, Leiva EPM (2010) J Chem Phys 132:184703
Zhang J, Sung YE, Rikvold PA, Wieckowski A (1996) J Chem Phys 104:5699
Hachiya T, Honbo H, Itaya KJ (1991) Electroanal Chem 315:275
Magnussen OM, Hotlos J, Beitel G, Kolb DM, Behm RJ (1991) J Vac Sci Technol B 9:969
Binder K (1986) In: Binder K (ed) Monte Carlo methods in statistical physics, 2nd edn. Springer, Berlin
Blume M (1966) Phys Rev 141:517; Capel HW (1966) Physica 32:966; Blume M, Emery VJ, Griffiths RB (1971) Phys Rev A 4: 1071
Fichthorn KA, Weinberg WH (1991) J Chem Phys 95:1090
Giménez MC, Del Pópolo MG, Leiva EPM, García SG, Salinas DR, Mayer CE, Lorenz WJ (2002) J Electrochem Soc 149, E109
Foiles SM, Baskes MI, Daw MS (1986) Phys Rev B 33:7983
Finnis MW, Sinclair JE (1984) Philos Mag A 50:45
Carlsson AE (1990) In: Ehrenreich H, Seitz H, Turnbull D (eds) Solid state physics, vol 43. Academic, New York
Ercolessi F, Tosatti E, Parrinello M (1986) Phys Rev Lett 57:719
Hill TL (1960) An introduction to statistical thermodynamics. Addison-Wesley Publishing Company Inc., London
Drews TO, Braatz RD, Alkire RC (2007) Z Phys Chem 221:1287
García SG (1997) Ph.D. thesis. Universidad Nacional del Sur, Bahía Blanca, Argentina
Garcia S, Salinas D, Mayer C, Schmidt E, Staikov G, Lorenz WJ (1998) Electrochim Acta 43:3007
Treeratanaphitak T, Pritzker MD, Abukhdeir NM (2014) Electrochim Acta 121:407
Treeratanaphitak T, Pritzker MD, Abukhdeir NM (2014) Electrochem Commun 46:140
Giménez MC, Del Pópolo MG, Leiva EPM (2002) Langmuir 18:9087
Schmickler W (1996) Interfacial electrochemistry. Oxford University Press, New York
Drews TO, Radisik A, Erlenbacher J, Braatz RD, Searson PC, Alkire RC (2006) J Electrochem Soc 153:C434
Stephens RM, Alkire RC (2007) J Electrochem Soc 154:D418
Bezzola A, Bales BB, Alkire RC, Petzold LR (2014) J Comp Phys 256:183
Bezzola A, Bales BB, Petzold LR, Alkire RC (2014) J Electrochem Soc 161, E3001
Brown G, Rikvold PA, Novotny MA, Wieckowski A (1999) J Electrochem Soc 146:1035
Bard AJ, Faulkner LR (1980) Electrochemical methods: fundamentals and applications. Wiley, New York
Hölzle MH, Kolb DM (1994) Ber Bunsenges Phys Chem 98:330
Hölzle MH, Retter U, Kolb DM (1994) J Electroanal Chem 371:101
Hölzle MH, Zwing B, Kolb DM (1995) Electrochim Acta 40:1237
Anderson AB (1975) J Chem Phys 62:1187
Anderson AB, Grimes RW, Hong SY (1987) J Phys Chem 91:4245
Mehandru S, Anderson AB (1989) Surf Sci 216:105
Lopez MB, Estiu GL, Castro EA, Arvia AJ (1990) J Mol Struct (Theochem) 210:353
Lopez MB, Estiu GL, Castro EA, Arvia AJ (1990) J Mol Struct (Theochem) 210:365
Lopez MB, Estiu GL, Castro EA, Arvia AJ (1992) Surf Sci 277:184
Mola EE, Blum L (1989) Int J Quantum Chem Quantum Chem Symp 23:687
Mola EE, Vicente JL (1992) Blum L (1992) Int J Quantum Chem Quant Chem Symp (Proc Int Symp At Mol Condens Matter Theory. Comput Methods 26:621
Mola EE, Appignanessi G, Vicente JL, Blum L (1993) Proc Electrochem Soc 93–5:186
Conway BE, Chacha JC (2004) J New Mater Electrochem Syst 7:231
Oviedo OA, Leiva EPM, Rojas MI (2006) Electrochim Acta 51:3526
Isoardi EP, Allan NL, Barrera GD (2004) Phys Rev B 69:24303
Reif F (1965) Fundamentals of statistical and thermal physics. McGraw-Hill Kogakusha, Tokyo
Allen MP, Tildesley DJ (1987) Computer Simulation of Liquids. Oxford University Press, Oxford
Schmickler W, Mariscal MM, Pötting K (2006) Chem Phys 320:149
Mariscal MM, Leiva EPM, Pötting K, Schmickler W (2007) Appl Phys A 87:385
Farigliano LM, Villarreal MA, Oviedo OA, Leiva EPM (2014) ECS Trans 58:3
Kittel C (2004) Introduction to solid state physics, 8th edn. Wiley, New York
Haile JM (1992) Molecular dynamics simulation. Wiley, New York
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Oviedo, O.A., Reinaudi, L., García, S.G., Leiva, E.P.M. (2016). Modelling of Underpotential Deposition on Bulk Electrodes. In: Underpotential Deposition. Monographs in Electrochemistry. Springer, Cham. https://doi.org/10.1007/978-3-319-24394-8_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-24394-8_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-24392-4
Online ISBN: 978-3-319-24394-8
eBook Packages: Chemistry and Materials ScienceChemistry and Material Science (R0)