Parallel Algorithm for Solution-Adaptive Grid Movement in the Context of Fluid Structure Interaction

Abstract

We present a new grid movement strategy, tested for a generic fluid-structure interaction (FSI) test case. The test case describes a flat plate with a prescribed rotational movement in a turbulent channel flow. The transient turbulent flow field is calculated with a low-Re RANS model. To account for the deforming fluid domain two different grid movement methods are compared. Using transfinite interpolation with a grid-point distribution fitted to the stationary starting conditions as grid moving method leads to errors for the drag-coefficient. By employing a normalized wall distance adaptive method it is possible to fulfill the near-wall resolution requirements within every time step and, to thereby, get more accurate results. The parallelization is achieved by domain decomposition and is evaluated using a strong scaling experiment.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

For many engineering problems the interaction between a moving structure and a turbulent flow is of importance. Frequently, numerical models are used to predict the behavior of such systems. The overall solution fidelity strongly depends on the quality of the turbulent flow model used to calculate the forces acting on the structure.

We employ the finite volume method with an URANS (Unsteady Reynolds Averaged Navier Stokes) modeling approach. Here, the underlying spatial discretization is decisive for efficiency and accuracy. Furthermore, the grid resolution has to fulfill validity requirements implied by the turbulence model in the near wall regions. These are formulated in terms of a velocity normalized wall distance y ⁺ for the cells adjacent to the wall.

The need to change the grid that represents the deforming fluid domain induces a conflict of aims between geometrical cell quality and resolution requirements. Standard techniques for calculating the movement of grid points such as spring analogy methods or interpolation methods (see, for example [1–3]), are designed to keep the initial distribution constant relatively to the structure. These do not address the conflict of aims explicitly and may produce wrong flow solutions, if the resolution requirements change.

In this contribution we want show, that it is possible to meet the near wall resolution requirements of a RANS model in a generic test case by relocating grid-points according to the flow situation. The idea is, regarding that it is necessary to solve a grid movement problem for the deforming domain anyway, to incorporate solution information for a more suited fluid grid. We use the Target-Matrix-Paradigm (TMP) introduced in [4] to formulate the grid movement problem as an optimization problem. It offers the possibility to express different aspects of cell quality within a uniform principle.

First, we present the governing equations that are relevant for computing the turbulent flow fields and understanding why near wall resolution is of interest, then we describe the numerical methods used. Details about the parallelization of the grid movement strategy are given. After that, the test-case is described and evaluated for a reference grid movement method using transfinite interpolation and the y ⁺ adaptive movement method. The test-case is also used to evaluate the parallel efficiency of the presented algorithm.

2 Governing Equations

As we consider prescribed structure motion, only the fluid continuum has to be described. For an incompressible Newtonian fluid with constant properties, the following Reynolds-averaged equations in Einstein notation describe the turbulent mean flow field:

$$\displaystyle{ \frac{\partial u_{i}} {\partial x_{i}} = 0\quad, }$$

(1)

$$\displaystyle{ \rho \left [\frac{\partial u_{i}} {\partial t} + u_{j} \frac{\partial u_{i}} {\partial x_{j}}\right ] = -\frac{\partial p} {\partial x_{i}} + \frac{\partial } {\partial x_{j}}[\mu \frac{\partial u_{i}} {\partial x_{j}} -\rho \overline{u'_{i}u'_{j}}]\quad, }$$

(2)

where u _i represents the mean velocity, p is the mean static pressure, ρ is the density, μ is the dynamic viscosity, t is the time, and x _i are spatial coordinates. We close the system of equations with the Boussinesq eddy viscosity assumption

$$\displaystyle{ -\rho \overline{u'_{i}u'_{j}} =\mu _{t}\,\left (\frac{\partial u_{i}} {\partial x_{j}} + \frac{\partial u_{j}} {\partial x_{i}} \right ) -\frac{2} {3}\rho k\delta _{ij} }$$

(3)

and two additional transport equations for the turbulent kinetic energy k and the dissipation rate ε to model the turbulent viscosity μ _t (Chien [5]):

$$\displaystyle{ \frac{\partial } {\partial t}\left (\rho k\right ) + \frac{\partial } {\partial x_{j}}\left [\rho ku_{j} -\left (\mu + \frac{\mu _{t}} {\sigma _{k}}\right ) \frac{\partial k} {\partial x_{j}}\right ] = P -\rho \epsilon -\rho D\quad, }$$

(4)

$$\displaystyle{ \frac{\partial } {\partial t}\left (\rho \epsilon \right ) + \frac{\partial } {\partial x_{j}}\left [\rho \epsilon u_{j} -\left (\mu +\frac{\mu _{t}} {\sigma _{\epsilon }} \right ) \frac{\partial \epsilon } {\partial x_{j}}\right ] = \left (C_{\epsilon _{1}}P - C_{\epsilon _{2}}f_{1}\rho \epsilon \right ) \frac{\epsilon } {k} +\rho E\quad }$$

(5)

with

$$\displaystyle{ \mu _{t} = C_{\mu }f_{\mu }\rho \frac{k^{2}} {\epsilon } \quad, }$$

(6)

$$\displaystyle{ P =\tau _{ ij}^{turb} \frac{\partial u_{i}} {\partial x_{j}}\quad, }$$

(7)

$$\displaystyle{ D = 2\,\nu \, \frac{k} {y^{2}}\quad, }$$

(8)

$$\displaystyle{ E = -\frac{2\nu \epsilon } {y^{2}}\exp (-0.5y^{+})\quad, }$$

(9)

$$\displaystyle{ f_{\mu } = 1 -\exp (-0.0115y^{+})\quad, }$$

(10)

$$\displaystyle{ f_{1} = 1 - 0.22\exp (-\left (\frac{Re_{t}} {6} \right )^{2})\quad. }$$

(11)

$C_{\epsilon _{1}} = 1.35$, $C_{\epsilon _{2}} = 1.8$, C _μ  = 0. 09, $\sigma _{k} = 1$ and $\sigma _{\epsilon } = 1.3$ are model constants. The source terms (8), (9) as well as the damping functions (10), (11) introduce a dependency on the wall distance y ⁺, which is necessary to make the equation for k and ε valid down to the viscous sublayer.

3 Numerical Methods

Here we explain the main numerical methods involved when simulating the interaction of fluid and structure. As we only consider prescribed structure motion, methods to describe structure deformation are not outlined here.

3.1 Flow Solver

To solve the above system of partial differential equations, we use a finite volume scheme, implemented in our inhouse code FASTEST [6]. It is a boundary-fitted block-structured multigrid solver using hexahedral cells. The velocity-pressure coupling is achieved via the SIMPLE algorithm. For the time discretization, an implicit second order accurate backward differencing scheme is used. The convective fluxes are discretized with the upwind-scheme, whereas the central differencing scheme is used for the diffusive fluxes. The strongly implicit procedure is used to solve the systems of linear equations. The code is parallelized using domain decomposition methods. Each block of the grid is extended with a surface layer of halo cells to implement inter block communication. If blocks belong to different domains, MPI is used for the communication.

3.2 Grid Movement Strategy

For turbulent flows, the spatial discretization can be the source of two different kinds of errors. The obvious one is the discretization error which results from the fact that the continuous solution variables can not be perfectly represented with a finite number of unknowns. The other one is related to turbulence modeling, where the solved equations are only approximately describing the physical behavior. A special characteristic of many turbulence models is that the discretization is part of the model. In RANS models, the grid dependency is introduced with the near wall treatment approach, regardless of whether a wall function or a special near wall formulation is used. For this work it can be seen that in a finite-volume method equations (4) and (5) are associated to cell midpoints after discretization. In large eddy simulations, the filter width and the subgrid scale model are mesh width dependent. Hybrid models compare a turbulent length scale to the local mesh width for modeling turbulent viscosity. For the simulation of FSI problems, where the flow and the geometry are changing, the numerical method has to use a grid movement strategy, which is capable of limiting discretizaion and turbulence model errors. A new approach accomplishing this is explained first in this subsection. Afterwards, a method based on transfinite interpolation serving as reference in Sect. 4 is outlined.

3.2.1 Optimization Approach

3.2.1.1 Working Principle

To account for the deforming fluid domain, we use an optimization approach. In every new time step, the movement of the boundary grid points X _b is given by a prescribed motion. We want to find displacements for n inner grid points X _i such that an objective function f becomes minimal:

$$\displaystyle\begin{array}{rcl} \mathop{\mathop{\mathrm{minimize}}\nolimits }\limits_{X_{i}}\quad f(X_{i})& &{}\end{array}$$

(12)

$$\displaystyle\begin{array}{rcl} \mathop{\mathrm{where}}\nolimits f: \mathbb{R}^{n} \rightarrow \mathbb{R}.& &{}\end{array}$$

(13)

We use the target-matrix-paradigm introduced in [4] to formulate a relation q(X _i ) between grid points and the quality of the cells they belong to. Here, quality is defined in terms of deviation from an optimal cell. For detailed information see [4]. In the near wall region, we define the optimal cells as rectangular and scaled in wall normal direction according to the y+ requirements. In the rest of the field, optimal cells are chosen to be just rectangular with an arbitrary size.

The corresponding objective function for m cells can be defined as:

$$\displaystyle{ f\left (X_{i}\right ) =\sum _{ c=1}^{m}q_{ c}\left (X_{i}\right )\quad. }$$

(14)

In order to solve the optimization problem (13), we use the method of steepest descent.

To illustrate the working principle, Fig. 1a shows a simple square grid for which a displacement of it’s grid points for a given boundary deformation has to be found. After moving the boundary points to fit the new domain in Fig. 1b, the optimization problem can be formulated. Defining the optimal cell geometry to be square, one can obtain the valid discretization shown in Fig. 1d. Specifying an additional target size for every cell—as for example a linear distribution of cell heights along the vertical axis in Fig. 1c—can be used to adapt the grid to changing flow conditions. Figure 1e shows the resulting grid.

Fig. 1

Square grid example with a prescribed deformation at the bottom boundary. Sequence (a), (b), (d) shows the steps for finding a grid fitting into the new domain aiming for square cells and sequence (a), (c), (e) shows the steps if an additional cell size distribution is given. (a) Initial grid, (b) Grid after boundary deformation, (c) Linear target cell height distribution, (d) Optimization for square cells, (e) Optimization for target cell sizes

3.2.1.2 Parallelization

Simulating turbulent flow fields for technical applications can be computationally intensive. In this case, required computing resources can only be provided by parallel hardware. Therefore, the parallel software performance must scale with the number of compute units. According to Amdahl’s law [7], the speed-up is limited to the inverse of the serial portion of the software. So even if grid movement is only a small portion of the overall solution process it has to be suitably parallelized.

For an efficient parallelization, we use the same domain decomposition as for the flow solver. This avoids data transfer as the grid movement can be calculated on the processor on which it is needed. Also the grid movement code can directly work on the same grid representation in memory. Defining the optimization problem (13) for each subdomain, boundary points would be fixed as only inner points are optimized. Overlapping one vertex per dimension more than the subdomain boundary from one side, as depicted in Fig. 2, allows subdomain interfaces to be part of the solution. The overall solution is found by iteratively doing steepest descent iterations on each subdomain and updating the overlapping vertices at the boundaries. Figure 3 illustrates the exchange pattern. Convergence is measured by the relative change of the L ² norm over all displacements between two consecutive iterations.

Fig. 2

Two overlapping domains with one-sided ghost vertices

Fig. 3

Exchange pattern of overlapping domain decomposition for parallel grid movement

3.2.2 Blockwise Transfinite Interpolation

In this method the grid is regenerated in every deformation step. See [8] for detailed information. As we have a block structure it is sufficient to recreate the topological elements of the grid in hierarchical order. First, block edges are calculated with cubic splines between the given, new endpoints. By requesting constant angles at the endpoints with respect to the initial grid the splines are uniquely defined and orthogonality characteristics are preserved. The distribution of grid points along the length of the edges is also taken from the initial grid. Figure 4 illustrates this step. Transfinite interpolation [9] is then used to calculate new faces as illustrated in Fig. 5. Analogously, inner block points are calculated from the new faces.

Fig. 4

Cubic spline connection between moved endpoints as new edge

Fig. 5

Transfinite interpolation to calculate block faces

4 Results and Discussion

4.1 Description of the Test Case

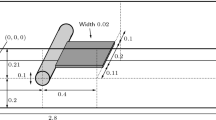
As test case, we use a two-dimensional flow in a channel with a length of 2 m and a height of 0. 45 m. In it’s center, a flat plate with a length of 0. 12 m, a height of 0. 006 m and rounded edges, which inclines with a constant angular velocity of 175 s⁻¹, serves as obstacle. At the inflow, a parabolic profile is chosen to avoid high gradients triggering the refinement mechanism at the edges. The Reynolds number based on the channel height and center inflow velocity $u_{max} = 4\,\text{ m/s}$ is Re = 2. 21 ⋅ 10⁵. Figure 6 illustrates the setup after 5 ms simulation time. The simulations are started from the stationary non-inclined solution.

Fig. 6

Velocity magnitude [m/s] at t = 5 ms

The starting grid shown in Fig. 7 is an O-Grid type mesh consisting of 274,880 control volumes. The treatment of turbulence in wall proximity, as introduced in Sect. 2, is based on the first control volume being located in the viscous sublayer. Thus y ⁺ should not exceed 5 and the initial grid has been chosen accordingly as shown in Fig. 8d.

Fig. 7

Starting grid

Fig. 8

Comparison of y ⁺ values on the purple marked lines in (a), (b), (c) for different simulation times between the reference grid movement method (d–f) and the y ⁺ adaptive method (g–i). (a) Flow field at t = 0 ms, (b) Flow field at t = 7 ms, (c) Flow field at t = 25 ms, (d) y ⁺ at t = 0 ms for reference grid movement method, (e) y ⁺ at t = 7 ms for reference grid movement method, (f) y ⁺ at t = 25 ms for reference grid movement method, (g) y ⁺ at t = 0 ms for adaptive grid movement, (h) y ⁺ at t = 7 ms for adaptive grid movement, (i) y ⁺ at t = 25 ms for adaptive grid movement

4.2 Evaluation and Discussion

In order to demonstrate that the near wall resolution can be controlled, Fig. 8 contains plots of y ⁺ on the plate’s top wall for both methods at different simulation times. The reference method does not change the near wall resolution. So in consequence of the accelerated flow towards the trailing edge, the y ⁺ values surpass the model limit of 5. For the y ⁺ adaptive method, we can not observe a raising tendency. A visual impression of the resulting grids after 25 ms is shown in Fig. 9.

Fig. 9

Comparison of grids for t = 25 ms. (a) Transfinite interpolation. (b) Adaptive grid movement

It has to be mentioned that the exceeding y ⁺ values could be avoided by choosing a finer initial mesh. But such a trial and error strategy might not be feasible for more complex FSI scenarios.

In order to determine the impact of under-resolved boundary layers on the quality of results, Fig. 10 shows both drag coefficients of the plate over time. Clearly, the solution obtained with transfinite interpolation as grid movement method produces lower drag forces as the velocity gradients on the wall are not represented correctly.

Fig. 10

Drag coefficients for adaptive grid movement (solid line) and for reference grid movement (dashed lined) over time

4.3 Parallel Performance

All performance measurements were carried out on the Lichtenberg high performance computer of TU Darmstadt with two Intel Xeon E5-2670 processors per node, each with 8 cores running at 2. 6 GHz base and 3. 3 GHz maximum turbo clock frequency per dual socket mainboard forming a network node. For inter node communication, FDR-10 InfiniBand is used. Four nodes were exclusively used to measure the strong scaling behavior. The MPI tasks are mapped to the cores in a sequential fashion, meaning that a minimum number of NUMA-levels is used. Figure 11 shows runtime results, taken for one time step on different numbers of cores. In order to avoid random effects, the measurements are repeated as many times as cores are used and then averaged. Solving the turbulent flow field takes the dominant portion of runtime for all numbers of cores. By looking at the corresponding speedup results in Fig. 12, it can be observed that the grid movement solver has a similar scaling behavior as the flow solver. The difference indicates higher losses in algorithmic efficiency for executing the steepest descent method on the decomposed domain. The intra-processor scaling up to 8 cores is afflicted by the turbo mode and shared memory bandwidth. The computational resources do not scale linearly in that region. Thus, in Fig. 13 the overall parallel efficiency is calculated based on the speedup towards the 8 core runtime.

Fig. 11

Runtime of one time step measured on the Lichtenberg cluster

Fig. 12

Runtime speedup of one time step measured on the Lichtenberg cluster

Fig. 13

Parallel efficiency scaling over number of processors

5 Conclusion

We have presented a turbulent test case with prescribed structural motion, for which we applied a y ⁺ adaptive and a non-solution-adaptive grid movement strategy. The conducted numerical experiments showed, that it is important to control the grid resolution for simulations with changing flow conditions as occurring for FSI scenarios. The grid moving strategy outlined in this work in principle is not restricted to just limiting y ⁺. Other solution dependent criteria are possible, as for example a posteriori error estimates aiming to reduce discretization errors.

We have also shown, that the solution adaptive grid movement can be calculated in an acceptable portion of total run time for serial as well as for parallel computation. The runtime results are of course test case dependent. Here the ratio of maximum displacement to a characteristic length of the computational domain is an important influence factor and has to be investigated in future work.