Abstract
We present a reflection principle of the form “If \(\ulcorner \varphi \urcorner \) is provable, then \(\varphi \)” implemented in the HOL4 theorem prover, assuming the existence of a large cardinal. We use the large-cardinal assumption to construct a model of HOL within HOL, and show how to ensure \(\varphi \) has the same meaning both inside and outside of this model. Soundness of HOL implies that if \(\ulcorner \varphi \urcorner \) is provable, then it is true in this model, and hence \(\varphi \) holds. We additionally show how this reflection principle can be extended, assuming an infinite hierarchy of large cardinals, to implement model polymorphism, a technique designed for verifying systems with self-replacement functionality.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Reflection Principle
- Polymorphism Model
- Large Cardinal Assumption
- HOL Theorem Prover
- Certificate Theorem
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Reflection principles of the formFootnote 1 “if \(\ulcorner \varphi \urcorner \) is provable, then \(\varphi \)” have long been of interest in logic and set theory (see, e.g., Franzén [5] and Jech [13]). In this paper, we show how to implement a reflection principle for HOL in the HOL4 theorem prover [21], using a novel approach for establishing a correspondence between the logic and an internal model. Such a reflection principle does not come for free, since by Gödel’s second incompleteness theorem, HOL cannot prove itself consistent [6]. We pay with an assumption about the existence of a “large enough” HOL type. But we endeavour to ensure that this assumption has the same content as the assumption, commonly studied in set theory [13], of the existence of a strongly inaccessible cardinal.
Reflection is about trying to fit a logic inside itself, so one has to keep two instances of the logic in mind separately. We use the term inner HOL to refer to the object logic (the HOL that is formalised) and outer HOL for the meta logic (the HOL in which inner HOL is formalised). We build upon Harrison’s formalisation of HOL in itself [11] that was extended in our previous work [15, 16] to support defined constants. The first reflection principle we implement uses a model of inner HOL provided by a large-cardinal assumption, together with the previously-proved soundness theorem, to show that provability of a proposition in inner HOL implies its truth in outer HOL.
This kind of reflection principle is asymmetric: the large-cardinal assumption used in outer HOL to justify reflection cannot be used again in inner HOL to justify further reflection. One setting in which it is useful to lessen this asymmetry is in constructing and verifying a system that can replace itself (including the replacement mechanism) by a new version while nevertheless always satisfying some safety property. We have extended the reflection principle above to an implementation of model polymorphism [3], which enables the use of reflective reasoning multiple times to verify such self-modifying systems.
Our specific contributions in this paper are as follows:
-
A simple approach to defining, in outer HOL, a partial embedding of outer HOL in inner HOL (Sect. 3). We re-use a single polymorphic constant, \(\mathsf{to\_inner }\), to embody the embedding at (almost) all outer HOL types.
-
An algorithm for producing theorems that relate the semantics of inner HOL terms to their outer HOL counterparts via the embedding (Sect. 4). The method applies to terms that include user-defined constants and types, and therefore supports construction of a semantic interpretation of constants based on replaying outer definitions in inner HOL (Sect. 5). Combined with the soundness theorem for inner HOL, this gives us a reflection principle for HOL (Sect. 7).
-
An extension of the reflection principle above to support model polymorphism [3] (Sect. 8).
-
A reduction of the unavoidable assumption on the proof (in previous work) of soundness and consistency of HOL within HOL to a traditionally-stated large-cardinal assumption (Sect. 6).
All the work we present has been implemented in the HOL4 theorem prover, and is available online at https://github.com/CakeML/hol-reflection.
Synopsis. Our reflection principle has two legs: (1) a soundness theorem for HOL (from previous work) asserting that a provable formula is true in all models, and (2) a formal correspondence between objects in a particular, reflective model (constructed assuming a large cardinal) and their counterparts outside. The reflection principle works as follows: if a formula \(\ulcorner \varphi \urcorner \) is provable, the soundness theorem asserts that \(\ulcorner \varphi \urcorner \) is true in the reflective model of HOL, and via the correspondence we may conclude that \(\varphi \) is true outside the model. The bulk of our work in this paper is in building the reflective model and establishing the correspondence, particularly in supporting user-defined constants.
2 Background: Inner HOL
The starting point for studying reflection principles is a formalisation of a logic inside itself. We use higher-order logic (HOL), the logic of the HOL Light theorem prover [12]. Our formalisation of HOL within itself is described carefully in previous work [15, 16], but we summarise it briefly in this section.
HOL has the syntax of the simply-typed lambda calculusFootnote 2 and a well-known semantics in Zermelo set theory. The judgements of the logic are sequents,

, where \({ {c}}\) is a formula (a term of Boolean type), \({ {hs}}\) is a set of formulas, and \({ {thy}}\) specifies the current set of axiom formulas and the current signature of constants and type operators. The semantics of each type is a non-empty set; the Boolean type is specified as a distinguished two-element set (\(\mathsf{Boolset }\), with elements \(\mathsf{True }\) and \(\mathsf{False }\)) and function types are specified as function spaces (a set of pairs forming a functional relation). The semantics of each term is an element of the semantics of its type. The semantics of each sequent is true, written \(({ {thy}}\mathsf{, }{ {hs}})\;\mathsf{\models }\;{ {c}}\), if the semantics of \({ {c}}\) is true whenever the semantics of all \({ {hs}}\) are true, in any model (an interpretation of constants satisfying the axioms) of \({ {thy}}\).
Since the semantic objects are sets, we need a model of set theory to define the semantics of inner HOL. Our semantics does not pin down a particular model of set theory. Instead, it is polymorphic: we use an outer HOL type variable, usually \(\mu \), for the universe of sets, and encode the axioms of set theory as a pair of assumptions, \(\mathsf{is\_set\_theory }\;{ {mem}}\) and \(\mathsf{\exists \,{} }{ {inf}}.\;\mathsf{is\_infinite }\;{ {mem}}\;{ {inf}}\), about a membership relation,  , on sets. All our semantic functions take the membership relation \({ {mem}}\) (and with it the universe \(\mu \)) as a parameter, and most theorems about the semantics assume the set-theory axioms hold. However, for brevity we usually hideFootnote 3 these parameters and assumptions when they are obvious in context. We write \({ {x}}\;\mathsf{\lessdot }\;{ {y}}\) for infix application of the \({ {mem}}\) relation (i.e., \({ {mem}}\;{ {x}}\;{ {y}}\)).
, on sets. All our semantic functions take the membership relation \({ {mem}}\) (and with it the universe \(\mu \)) as a parameter, and most theorems about the semantics assume the set-theory axioms hold. However, for brevity we usually hideFootnote 3 these parameters and assumptions when they are obvious in context. We write \({ {x}}\;\mathsf{\lessdot }\;{ {y}}\) for infix application of the \({ {mem}}\) relation (i.e., \({ {mem}}\;{ {x}}\;{ {y}}\)).
The important semantic function in this paper is the semantics of terms, that is, the function that assigns an element of \(\mu \) to each term of inner HOL. We illustrate how it works with an example, considering the semantics of the inner HOL version of the term \(\lambda \,{}{ {x}}.\;\mathsf{foo }\;{ {y}}\), where the constant \((\mathsf{foo } :\alpha \;\rightarrow \;\beta )\) is instantiated at the types  and
and  . The four parameters governing the semantics are: the membership relation \({ {mem}}\) (hidden), the signature (\({ {s}}\)) of constants and type operators in the theory, the interpretation (\({ {i}}\)) of constants and type operators, and the valuation (\({ {v}}\)) of free term and type variables. We denote the valuation of type variables by
. The four parameters governing the semantics are: the membership relation \({ {mem}}\) (hidden), the signature (\({ {s}}\)) of constants and type operators in the theory, the interpretation (\({ {i}}\)) of constants and type operators, and the valuation (\({ {v}}\)) of free term and type variables. We denote the valuation of type variables by

whereas for term variables we use

, and similar subscripts apply to the other semantic parameters. Our use of interpretations and valuations is intended to be conventional and unsurprising; we show the example here mainly to make our notation clear.Footnote 4

The semantics of the given lambda abstraction is a set-theoretic function (created with \(\mathsf{Abstract }\)) – in particular the set of two pairs, \(\mathsf{True }\mapsto { {sfoo}}\;\mathsf{' }\;{ {sy}}\) and \(\mathsf{False }\mapsto { {sfoo}}\;\mathsf{' }\;{ {sy}}\). The following equations show how we obtain the semantics of the applied type operator, the instantiated constant, and the free variable:

Inner HOL supports defined constants and type operators via the current theory, which is attached to each sequent. The inference system uses a concrete implementation of each theory as a list of updates. Such a list is called a context and every context can be viewed abstractly as a theory (written: \(\mathsf{thyof }\;{ {ctxt}}\)). Contexts are made from five kinds of update: new type operator, new constant, new axiom, new defined type operator, and new defined constant. The updates for defined type operators and constants have preconditions that require sequents proved in the previous context. If an update \({ {upd}}\) satisfies all the preconditions to be a valid update of the previous context \({ {ctxt}}\), we say \({ {upd}}\;\mathsf{updates }\;{ {ctxt}}\).
Both the within-theory inference rules and the theory-extending rules for making updates (except new axiom) have been proved sound with respect to the semantics. For the inference rules, the soundness theorem statesFootnote 5 that every provable sequent is true:

For the extension rules, the soundness theorem states that there exists an extended interpretation of the new theory that continues to be a model of the theory. Both theorems require the \(\mathsf{is\_set\_theory }\;{ {mem}}\) assumption.
3 An Inner Copy of Outer HOL
Given an outer HOL term, it is straightforward to write a function in ML—our function is called term_to_deep—that walks the structure of the term and builds the corresponding inner HOL term. For example, term_to_deep
This syntactic connection is straightforward. But what is the relationship between the semantics of an outer HOL term and its inner counterpart? Let

stand for \(\mathtt {term\_to\_deep}({ {tm}})\). Ideally, we would like a connection between \(\mathsf{Suc }\;{ {x}}\) and

. Such a connection would mean that the structure of outer HOL terms and types is replicated (indeed reflected) within the type denoted by \(\mu \). We cannot expect to reflect everything: in particular, we cannot reflect \(\mu \) within itself, nor anything depending on \(\mu \). But we can cover all other outer HOL types and terms generically.
Our solution is to define a polymorphic constant, \(\mathsf{to\_inner }\), which sends an outer HOL term to the element of \(\mu \) to which it is supposed to correspond. We show how to prove theorems of the form

. The type of \(\mathsf{to\_inner }\;{ {ty}}\) is \(\alpha \;\rightarrow \;\mu \).Footnote 6 (We explain the \({ {ty}}\) argument shortly.)
We do not want to have to specify exactly how \(\mathsf{to\_inner }\) creates its (partial) copy of outer HOL. What is important is that the copy is faithful, which means \(\mathsf{to\_inner }\) is injective. We formalise this injectivity property precisely by saying that \(\mathsf{to\_inner }\) at type \(\alpha \) should be a bijection between \(\mathcal {U}({:}\alpha )\) (everything of type \(\alpha \)) and the setFootnote 7 of elements of some set \({ {x}}\) in \(\mu \). Formally, we define a well-formedness condition:

Then we define \(\mathsf{to\_inner }\) as an arbitrary well-formed injection, using Hilbert choiceFootnote 8 as follows:
The \(\mathsf{tag }\;{ {ty}}\) part of the definition wraps the set produced by the well-formed injection with a tag for the given inner HOL type, \({ {ty}}\), thereby avoiding the possibility of inadvertently sending outer HOL terms with different types to the same element in \(\mu \). The need for this tagging is explained in Sect. 5.
Since Hilbert choice only picks a well-formed injection if one exists, the usefulness of \(\mathsf{to\_inner }\) at any particular outer HOL type depends on our assuming (or being able to prove) \(\mathsf{wf\_to\_inner }\;(\mathsf{to\_inner }\;{ {ty}})\). The automation we describe in Sect. 4 produces theorems that assume these well-formedness conditions, and the automation in Sect. 5 proves almost all of them.
Of course, since the well-formedness condition on \(\mathsf{to\_inner }\) says it is not just an injection but a bijection, we can also go in the other direction, from inner HOL terms to their outer counterparts. Given a well-formed injection \({ {ina}}\), we denote the set of terms of type \(\mu \) that are in its range—that is, the inner representation of the domain of \({ {ina}}\)—by \(\mathsf{range }\;{ {ina}}\). The faithfulness of the representation is summarised in the following two theorems exhibiting invertibility.

Usually, but not always, \({ {ina}}\) will be \(\mathsf{to\_inner }\;{ {ty}}\) for some \({ {ty}}\). We use \(\mathsf{to\_inner }\) to reflect outer HOL at all types except for those that depend on \(\mu \) and except for the two primitive types of HOL: Booleans and function types. The primitive types must be treated differently because the semantics of HOL requires them to be interpreted by a distinguished two-element set and by set-theoretic function spaces, respectively. We provide specialised constants that map these types to their intended interpretations instead of an arbitrary set:

We have now seen how we intend to reflect outer HOL terms into inner HOL, using \(\mathsf{to\_inner }\;{ {ty}}\) injections. We next describe an algorithm that produces a certificate theorem for (almost) any HOL term, asserting that the semantics of the inner version of the term matches the reflection of the outer version. We develop this algorithm in two stages: first (next section), we ignore the interpretation of constants and the valuation of variables in the semantics and simply make assumptions about them; then (Sect. 5), we build an interpretation and valuation that satisfies these assumptions.
4 Proof-Producing Reflection
Let us begin with an example of the kind of theorem produced by the first stage of our automation. Given as input the term \(\mathsf{Suc }\;{ {x}}\), we produce the following theorem that looks very long but whose components we will explain one by one. We call each such theorem a certificate theorem for the input term.

First, look at the conclusionFootnote 9 (the last line): we have produced an equality between the semantics of the inner version of our input term and its reflection created with \(\mathsf{to\_inner }\). Under what assumptions? The assumptions come in five categories:
-
1.
The assumption stated using \(\mathsf{good\_context }\), which represents the pervasive \(\mathsf{is\_set\_theory }\;{ {mem}}\) assumption as well as some basic well-formedness conditions on the signature and interpretation.
-
2.
\(\mathsf{wf\_to\_inner }\) assumptions on all base types appearing in the input term (in this case, just \(\mathsf{Num }\)). A base type is any type variable or any application of a non-primitive type operator. (For the primitives, Booleans and functions, we prove \(\mathsf{wf\_to\_inner }\) once and for all.)
-
3.
Signature (\({ {s}}\)) assumptions stating that all non-primitive constants and type operators in the input term (in this case \(\mathsf{Suc }\) and
 ) have the same type/arity in inner HOL as in outer HOL. (The only primitive constant, equality, is assumed to have the correct type as part of \(\mathsf{good\_context }\).)
) have the same type/arity in inner HOL as in outer HOL. (The only primitive constant, equality, is assumed to have the correct type as part of \(\mathsf{good\_context }\).) -
4.
Interpretation (\({ {i}}\)) assumptions stating that the inner versions of all the base types and constants of the input term are mapped to their reflections.
-
5.
Valuation (\({ {v}}\)) assumptions stating that the inner versions of all type and term variables in the input term are mapped to their reflections.
The algorithm for producing such a theorem works by recursively traversing the structure of the input term. We build a theorem like the one above, equating the semantics of an inner term to the reflection of its outer counterpart, for each subterm in the input term starting at the leaves and progressing bottom-up. When we encounter non-primitive type operators and constants we add signature and interpretation assumptions as required, and similarly add valuation assumptions for free variables. The substitution of type variables used to instantiate a polymorphic constant is easily reflected from outside to inside.
This algorithm works because the semantics itself is recursive. For example, shown below is a theorem about the semantics that our algorithm uses when it encounters a combination (function application) term. Notice that the theorem makes two assumptions of the same form as its conclusion – these correspond to recursive calls in the algorithm.

The analogous theorem for lambda abstractions requires us to prove connections between inner HOL types and their reflections (via \(\mathsf{range }\)). Therefore, we have a similar recursive algorithm for types as the one described above for terms.
So far, our certificate theorems leave the semantic parameters (\({ {s}}\), \({ {i}}\), and \({ {v}}\)) as free variables but make various assumptions about them. Our aim in the next section is to show how we can instantiate these parameters in such a way that most of the assumptions become provable. In other words, we show how to build a reflective model that satisfies the assumptions in each of the categories above.
5 Building a Reflective Interpretation and Valuation
Signature Assumptions. In outer HOL, types like  and constants like \(\mathsf{Suc }\) are all user-defined. Logically speaking, there is a context (typically not represented explicitly in the theorem prover) that lists the sequence of updates made to produce the current environment of defined constants. An appropriate signature (\({ {s}}\)) for a certificate theorem is one that corresponds to some context for the input term, which will naturally satisfy all the signature assumptions. We require the user of our automation to build an explicit representation of the desired context (although we provide tools to help with this), and with that information proceed to construct an interpretation and valuation to satisfy the assumptions of the certificate theorem.
and constants like \(\mathsf{Suc }\) are all user-defined. Logically speaking, there is a context (typically not represented explicitly in the theorem prover) that lists the sequence of updates made to produce the current environment of defined constants. An appropriate signature (\({ {s}}\)) for a certificate theorem is one that corresponds to some context for the input term, which will naturally satisfy all the signature assumptions. We require the user of our automation to build an explicit representation of the desired context (although we provide tools to help with this), and with that information proceed to construct an interpretation and valuation to satisfy the assumptions of the certificate theorem.
Algorithm for Building the Model. The idea is to reflect the updates from the outer context into the inner inference system, creating an inner context, and then, update by update, build an interpretation of the inner context. The interpretation we build must be reflective, which means it must satisfy the certificate theorem’s assumptions, namely: all the defined constants and types appearing in the input term are mapped to the reflections of their outer versions. We build the reflective interpretation by: (1) starting with the interpretation asserted to exist by the soundness theorem, and (2) making a finite number of modifications for each update in the context. We work recursively up the context applying the relevant modifications for the last-added update at each stage.
Interpretation Assumptions. Each update introduces some number of type operators, constants, and axiomsFootnote 10 to the theory. Each update thereby induces some constraints on an interpretation for the interpretation to be reflective. For example, the update that defines

has an associated constraint that this constant is interpreted as \(\mathsf{to\_inner }\;(\mathsf{Fun }\;\mathsf{Num }\;\mathsf{Num })\;\mathsf{Suc }\).
For polymorphic constants and type operators with arguments, the constraints are more involved. In general, a constraint is induced by each instance of the update and constrains the corresponding instance of the introduced constants. Importantly, we only consider instances of the update that correspond to the finitely many instances of the defined constants in the input term. We require \(\mathsf{to\_inner }\) to produce distinct reflections of distinct types, because otherwise we cannot reliably distinguish different instances of an update.
To show that an interpretation continues to be a model after being constrained, we require that at each constrained instance the axioms of the update are satisfied. We can prove this for the constraints we build (which map things to their reflections) because the axioms of the update being replayed are true in outer HOL. For each constrained instance of an axiom, we use the algorithm from the previous section to generate a certificate theorem with assumptions that are all easy to discharge because the constraint is reflective.
\(\mathsf{wf\_to\_inner }\)
Assumptions. To prove the \(\mathsf{wf\_to\_inner }\) assumptions (for defined type operators) on our certificate theorems, we use the fact that in outer HOL every defined type is represented by a predicate on a previously defined (or primitive) type. The same is true in inner HOL as we build up our interpretation, so the \(\mathsf{wf\_to\_inner }\) assumption on a defined type reduces to the \(\mathsf{wf\_to\_inner }\) assumption on its representing type. These assumptions propagate back recursively to the base case. The only \(\mathsf{wf\_to\_inner }\) assumptions left after this process are for type variables in the input term, and for the type of individuals ( ) – this last assumption may be introduced if not present.
) – this last assumption may be introduced if not present.
Base Case of the Algorithm. To finish describing how we build a constrained model that satisfies the assumptions of the certificate theorem, only the base case of the recursive algorithm remains. What model do we start with before replaying all the updates in the context? In our previous work [15, 16] on the soundness and consistency of HOL, we showed that there is a model for the base context of HOL (assuming the set-theory axioms, including infinity). We use this model in the base case of the algorithm for building a reflective interpretation, modulo some subtleties concerning the Hilbert choice operator.
The base context, \(\mathsf{hol\_ctxt }\), includes the primitive types and constants (Booleans, functions, equality) and the three axioms of HOL (extensionality, choice, and infinity). To state the axioms, the base context also includes some defined constants (conjunction, implication, etc.), and, importantly, the Hilbert choice constant, and the type of individuals. Although most constraints are dealt with before the base case, constraints on Hilbert choice remain. Therefore, we extend the proof that \(\mathsf{hol\_ctxt }\) has a model to show that in fact there is a model satisfying any finite number of constraints on the intepretation of Hilbert choice. We also modify the model to use \(\mathsf{range }\;(\mathsf{to\_inner }\;\mathsf{Ind })\) for the type of individuals.
Valuation Assumptions. So far we have described the algorithm for building an interpretation (\({ {i}}\)) to satisfy the interpretation assumptions on certificate theorems. To build a valuation (\({ {v}}\)) satisfying the valuation assumptions, we follow a similar approach based on constraining an arbitrary valuation so that it maps the free variables that occur in the input term to their reflections. We have not covered all the gory details of these algorithms, but hope to have shared the important insights. The ML code for our automation is around 1800 lines long, supported by around 1000 lines of proof script about constrained interpretations.
6 Set Theory from a Large-Cardinal Assumption
Up until now, we have been working under the assumption \(\mathsf{is\_set\_theory }\;{ {mem}}\), as used in previous work [15, 16], which consists of the set-theoretic axioms of extensionality, specification, pairing, union, and power sets. To produce models of \(\mathsf{hol\_ctxt }\) and all its extensions, we also require the set-theoretic axiom of infinity (which is implied by \(\mathsf{wf\_to\_inner }\;(\mathsf{to\_inner }\;\mathsf{Ind })\)). One of our contributions is to clarify that these assumptions are implied by a more traditionally-stated large-cardinal assumption.
Our large-cardinal assumption is strictly stronger than what is necessary for a model of HOL. We leave proving an equivalence between \(\mathsf{is\_set\_theory }\;{ {mem}}\) plus infinity and a large-cardinal assumption for future work, and here just prove implication from a strongly inaccessible cardinal. The point is to build confidence in our specification of set theory, by showing it is implied by a traditional specification (of a strong inaccessible).
We make use of Norrish and Huffman’s formalisation [20] of cardinals and ordinals in HOL4. We write \({ {s}}\;\mathsf{\prec }\;{ {t}}\) to mean the predicate \({ {s}}\) has smaller cardinality than the predicate \({ {t}}\), i.e., there is an injection from \({ {s}}\) to \({ {t}}\) but not vice versa. Remember that sets and predicates are usually identified in HOL; we use the usual notation for sets like \({ {x}}\;\mathsf{\in {} }\;{ {s}}\) (\({ {x}}\) is an element of \({ {s}}\)) and \({ {f}}\mathsf{\text {'}\!\text {'}\! }\;{ {s}}\) (the image of \({ {s}}\) under \({ {f}}\)) when \({ {s}}\) is a predicate.
The reduction theorem we have proved is that if some (outer HOL) type, say \(\mu \), is a strongly inaccessible cardinal, then there is a membership relation \({ {mem}}\) on that type that satisfies \(\mathsf{is\_set\_theory }\) and \(\mathsf{is\_infinite }\). Furthermore, according to this \({ {mem}}\), for every predicate \({ {s}}\) on the type \(\mu \) which is strictly smaller than \(\mathcal {U}({:}\mu )\), there is a Zermelo set \({ {x}}\) whose elements are exactly the extension of \({ {s}}\). In this section, we are explicit with all uses of the type variable \(\mu \) and the variable \({ {mem}}\). The formal statement of our reduction theorem is:

It is well known that the existence of a strongly inaccessible cardinal gives rise to a model of set theory [13, Lemma 12.13], and the proof of our reduction theorem contains no surprises. (The main lemma is that a strongly inaccessible cardinal is in bijection with its smaller subsets.) Our focus here is on the definition of \(\mathsf{strongly\_inaccessible }\), aiming to accurately capture traditional usage.
A cardinal is called “strongly inaccessible” if it is uncountable, a regular cardinal, and a strong limit cardinal [13]. Assuming the axiom of choice (which we do as we are working in HOL), a cardinal \({ {X}}\) is regular iff it cannot be expressed as the union of a set smaller than \({ {X}}\) all of whose elements are also smaller than \({ {X}}\) [13, Lemma 3.10]. Formally:
A cardinal is a strong limit if it is larger than the power set of any smaller cardinal. This is straightforward to formalise:

A cardinal is countable if it can be injected into the natural numbers (this is already defined in HOL4’s standard library). With these three ideas formalised, we define \(\mathsf{strongly\_inaccessible }\) as follows:
7 Proving Reflection Principles
We now have enough machinery in place to exhibit a reflection principle for HOL. In the examples that follow, we use a two-place predicate \(\mathsf{Safe }\;{ {t}}\;{ {v}}\) to construct our input propositions, to match the example in Sect. 8. However, \(\mathsf{Safe }\) can be considered as a placeholder for any two-place predicate. As a concrete, simple example, set \(\mathsf{Safe }\;{ {t}}\;{ {v}}\;\mathsf{\iff {} }\;{ {v}}\;\mathsf{\ne {} }\;\mathsf{Suc }\;{ {t}}\).
First, let us see how the reflection principle works on the input proposition \(\mathsf{\forall \,{} }{ {t}}.\;\mathsf{Safe }\;{ {t}}\;0\). Combining the automation from Sects. 4 and 5, we can construct a certificate theorem with almost all of the assumptions proved:

Here \(\mathsf{constrained\_model }\) and \(\mathsf{constrained\_valuation }\) are built as described in Sect. 5: they are a reflective model for the context (

) that defines

, and a reflective valuationFootnote 11 for the input proposition.
Next, consider the inner HOL sequent corresponding to provability of our input proposition:

The soundness theorem for inner HOL states that if this sequent is provable, then the semantics of its conclusion is true. Our certificate theorem above already tells us that the semantics of the conclusion is equal to the reflection of the input proposition. By definition of \(\mathsf{bool\_to\_inner }\), if the reflection of a proposition is true then that proposition holds, hence we obtain:

There would be additional \(\mathsf{wf\_to\_inner }\) assumptions for each additional type variable in the input term.
The final step is to replace the \(\mathsf{is\_set\_theory }\;{ {mem}}\) assumption with the large-cardinal assumption that provides us with a model of set theory. In this model, we can replace the \(\mathsf{wf\_to\_inner }\) assumption on  by a lower bound on the cardinality of \(\mu \). Similarly, any \(\mathsf{wf\_to\_inner }\) assumption on a type variable, say \(\alpha \), could be replaced by an assumption of the form \(\mathcal{{U}}({{:}}{\alpha })\;\mathsf{\prec }\;\mathcal{{U}}({{:}}{\mu })\). Such assumptions can be satisfied by large enough \(\mu \), except in the case \(\alpha = \mu \); hence, it is important that \(\mu \) not occur in the input proposition. The resulting theorem no longer contains any occurrences of \({ {mem}}\), not even hidden ones.
by a lower bound on the cardinality of \(\mu \). Similarly, any \(\mathsf{wf\_to\_inner }\) assumption on a type variable, say \(\alpha \), could be replaced by an assumption of the form \(\mathcal{{U}}({{:}}{\alpha })\;\mathsf{\prec }\;\mathcal{{U}}({{:}}{\mu })\). Such assumptions can be satisfied by large enough \(\mu \), except in the case \(\alpha = \mu \); hence, it is important that \(\mu \) not occur in the input proposition. The resulting theorem no longer contains any occurrences of \({ {mem}}\), not even hidden ones.

Thus we have shown that provability of our input proposition implies its truth, assuming the existence of a large cardinal that is larger than the type of individuals in outer HOL. We can prove a theorem like this for any input proposition (that does not mention \(\mu \)), including less obvious and even false propositions.
The reflection principle above can be generalised to a uniform reflection principle [4], which, for an input proposition with a free natural-number variable, requires an inner-HOL proof about only the relevant value of the variable. We write

for the inner HOL numeral corresponding to the value of the outer HOL variable \({ {v}}\); for example, if \({ {v}} = 1\) in outer HOL, then

denotes the term

. The uniform reflection principle for the predicate \(\mathsf{\forall \,{} }{ {t}}.\;\mathsf{Safe }\;{ {t}}\;{ {v}}\) is:

Since \({ {v}}\) is quantified in outer HOL, this theorem encapsulates infinitely many reflection theorems of the previous kind. To implement uniform reflection, we define an outer-HOL function  which can be spliced into the result of term_to_deep to provide terms of the form
which can be spliced into the result of term_to_deep to provide terms of the form

. It is straightforward to show that the semantics of

in a reflective valuation is equal to the reflection of \({ {v}}\), and uniform reflection follows.
8 An Implementation of Model Polymorphism
One application of reflection principles is in designing and verifying systems that include mechanisms for self-replacement. For concreteness, consider an operating system intended to satisfy a certain safety property (e.g., a certain file is never overwritten), but also with a mechanism for replacing itself by an arbitrary updated version. For this system to be safe, the replacement mechanism must be restricted to prevent replacement by an unsafe update. A simple restriction would be to require a proof that the updated version is safe until replacement is invoked, together with a syntactic check that the updated version’s replacement mechanism (including the proof checker) is unchanged (or that the replacement mechanism is removed altogether). To verify this system, we need to know that the system’s proof checker is sound (only admits valid proofs) and we need a reflection principle for its logic (the conclusions of valid proofs are true). But we only need to establish these properties once.
Things get more interesting if we want to allow updates that might change the replacement mechanism. A more general replacement mechanism simply requires a proof that the updated version (including any new replacement mechanisms) is safe. To verify this system, we need a reflection principle to conclude that any updated version is safe assuming only that it was proved safe before the update was made. Furthermore, if we want to leave open the possibility that later updated versions retain a general replacement mechanism, we need a reflection principle that can be iterated.
The reflection principles in the previous section do not iterate. Using the assumption that a strongly inaccessible cardinal exists and is larger than the type of individuals they let us prove results of the form “If \(\ulcorner \varphi \urcorner \) is provable, then \(\varphi \)” for every \(\varphi \) not containing type variables. However, the proof of \(\ulcorner \varphi \urcorner \) may only make use of the ordinary axioms of HOL: in particular, it cannot in turn assume that there is a strongly inaccessible cardinal. It is tempting to choose \(\varphi \) to be the formula \(\mathsf{strongly\_inaccessible }\;\mathcal {U}({:}\mu ) \Longrightarrow \psi \), for some formula \(\psi \). But this contains the type variable \(\mu \), leading our automation to produce the unsatisfiable assumption \(\mathcal{{U}}({{:}}{\mu })\;\mathsf{\prec }\;\mathcal{{U}}({{:}}{\mu })\). We could instead try to use a different type variable, as in \(\mathsf{strongly\_inaccessible }\;\mathcal {U}({:}\nu ) \Longrightarrow \psi \); this would lead to a theorem showing \(\psi \) under the assumptions that \(\mathsf{strongly\_inaccessible }\;\mathcal {U}({:}\mu )\), \(\mathsf{strongly\_inaccessible }\;\mathcal {U}({:}\nu )\), \(\mathcal{{U}}({{:}}{\nu })\;\mathsf{\prec }\;\mathcal{{U}}({{:}}{\mu })\), and the provability of \(\ulcorner \mathsf{strongly\_inaccessible }\;\mathcal {U}({:}\nu ) \Longrightarrow \psi \urcorner \). However, while the proof in inner HOL may now assume that there is one inaccessible (\(\nu \)), the theorem in outer HOL now assumes that there are two strongly inaccessible cardinals (\(\nu \) and \(\mu \)), one of which is larger than the other.
Indeed, there must always be a stronger assumption in outer HOL than in inner HOL, since by Gödel’s second incompleteness theorem, no consistent proof system as strong as Peano Arithmetic can prove the reflection principle for itself: Choosing \(\varphi \equiv \mathsf{F }\), the identically false proposition, the assertion “If \(\ulcorner \mathsf{F }\urcorner \) is provable, then \(\mathsf{F }\)” is equivalent to “\(\ulcorner \mathsf{F }\urcorner \) is not provable”, which asserts consistency of the proof system. But by the second incompleteness theorem, a sufficiently strong proof system which can show its own consistency is inconsistent.
Nevertheless, the construction outlined above can be repeated any finite number of times, showing that if there are \((n+1)\) nested strongly inaccessible cardinals, then a proposition \(\varphi \) holds if it is provable under the assumption that there are n inaccessibles. Formally, we can define a term \(\mathsf{LCA }\) of type  such that \(\mathsf{LCA }\;0\;\mathcal {U}({:}\mu )\) indicates that
such that \(\mathsf{LCA }\;0\;\mathcal {U}({:}\mu )\) indicates that  fits inside \(\mu \), and such that \(\mathsf{LCA }\;(\mathsf{Suc }\;{ {t}})\;\mathcal {U}({:}\mu )\) indicates that \(\mu \) is a strongly inaccessible cardinal and there is a strictly smaller subset \({ {Q}}\) of \(\mathcal {U}({:}\mu )\) which satisfies \(\mathsf{LCA }\;{ {t}}\;{ {Q}}\):
fits inside \(\mu \), and such that \(\mathsf{LCA }\;(\mathsf{Suc }\;{ {t}})\;\mathcal {U}({:}\mu )\) indicates that \(\mu \) is a strongly inaccessible cardinal and there is a strictly smaller subset \({ {Q}}\) of \(\mathcal {U}({:}\mu )\) which satisfies \(\mathsf{LCA }\;{ {t}}\;{ {Q}}\):

Then, we can show a reflection principle of the form “If  is provable, then \(\mathsf{LCA }\;(\mathsf{Suc }\;{ {t}})\; \mathcal {U}({:}\mu ) \Rightarrow {}\varphi \)”. This approach systematises the idea of allowing stronger systems to reflect the reasoning of weaker systems. As described below, we can strengthen this principle so that it requires proofs not about particular numerals
is provable, then \(\mathsf{LCA }\;(\mathsf{Suc }\;{ {t}})\; \mathcal {U}({:}\mu ) \Rightarrow {}\varphi \)”. This approach systematises the idea of allowing stronger systems to reflect the reasoning of weaker systems. As described below, we can strengthen this principle so that it requires proofs not about particular numerals

but about a universally quantified variable \({ {t}}\).
To see the relevance to problems like verifying the self-replacing operating system, consider interpreting \(\mathsf{Safe }\;{ {t}}\;{ {v}}\) as “candidate system \({ {v}}\), and any updated versions it permits, behave safely for \({ {t}}\) updates”, hence we want to show \(\mathsf{\forall \,{} }{ {t}}.\;\mathsf{Safe }\;{ {t}}\;{ {v_{\mathrm {0}}}}\) for the initial system \({ {v_{\mathrm {0}}}}\). Suppose we have proved \(\mathsf{Safe }\;0\;{ {v_{\mathrm {0}}}}\), that is, we have verified the initial system except for its replacement mechanism, and suppose the initial replacement mechanism requires a proof of the proposition

before installing update \({ {v}}\). We need, for all \({ {t}}\), to show \(\mathsf{Safe }\;(\mathsf{Suc }\;{ {t}})\;{ {v_{\mathrm {0}}}}\), but this is equivalent to showing \(\mathsf{Safe }\;{ {t}}\;{ {v}}\) for all \({ {v}}\) that satisfy the replacement mechanism’s proof requirement. The following reflection principle enables us to do just that, provided we assume \(\mathsf{LCA }\;(\mathsf{Suc }\;{ {t}})\;\mathcal {U}({:}\mu )\).

Furthermore, the same reflection principle can be used within the proof required by the replacement mechanism, because the increase in the value of \({ {t}}\) passed to \(\mathsf{LCA }\) is cancelled out by the decrease in the argument to \(\mathsf{Safe }\) when considering a new version.
To prove the theorem above (for any predicate \(\mathsf{Safe }\;{ {t}}\;{ {v}}\) not containing type variables), our automation shows that for every natural number t, \(\mathsf{LCA }\;(\mathsf{Suc }\;{ {t}})\;\mathcal {U}({:}\mu )\) implies the existence of a model of inner HOL in which \(\ulcorner \mathsf{LCA }\;{ {t}}\;\mathcal {U}({:}\mu )\urcorner \) is true (with the inner variable t being interpreted to equal its outer value). Thus, if the implication in the assumption of the theorem is provable, then  is true in this model as well, and by our link between inner and outer HOL, it follows that \(\mathsf{Safe }\;{ {t}}\;{ {v}}\). Footnote 12
is true in this model as well, and by our link between inner and outer HOL, it follows that \(\mathsf{Safe }\;{ {t}}\;{ {v}}\). Footnote 12
At the top level, we are still left with the assumption of \(\mathsf{LCA }\;(\mathsf{Suc }\;{ {t}})\;\mathcal {U}({:}\mu )\) for every t. A model of HOL in which this assumption is true can easily be constructed, for example, in ZFC extended with the much stronger assumption that there is a Mahlo cardinal [13, Chapter 8], a strongly inaccessible cardinal \(\kappa \) such that there are exactly \(\kappa \) strongly inaccessibles \(\preccurlyeq \kappa \). The assumption that a Mahlo cardinal exists is not uncommon in set-theoretical work, and has been used in studies of dependent type theory to justify inductive-recursive definitions [2].
9 Related Work
Reflection principles of the form “If \(\ulcorner \varphi \urcorner \) is provable, then \(\varphi \)”, as well as the uniform reflection principle “If \(\ulcorner \varphi (\overline{n})\urcorner \) is provable, then \(\varphi (n)\)”, have been studied by Turing [22] and Feferman [4]. These authors consider sequences of theories obtained by starting with a theory \(T_0\) (Peano Arithmetic, say), and repeatedly constructing theories \(T_{\alpha +1}\) by adding to \(T_\alpha \) the reflection principle for all theories \(T_\beta \), \(\beta \le \alpha \). One can extend these sequences transfinitely by letting \(T_\lambda := \bigcup _{\alpha <\lambda } T_\alpha \) at limit ordinals \(\lambda \). Turing and Feferman showed that, in a rather technical sense, sequences constructed in this way prove every true sentence of arithmetic (see Franzén [5] for an introduction, including an explanation why this statement is not as strong as it may appear). Set theorists have been interested in reflection principles, provable in ZF, which show that a sentence \(\varphi \) is true if it is provable from a fixed finite subset of ZF [13].
In the interactive theorem proving community, interest in reflection principles has mainly come from the perspective of computational reflection [10], which justifies the use of an efficient decision procedure by proving that if the decision procedure declares a sentence to be true, the sentence is in fact provable. For example, Allen et al. [1] extend Nuprl with a reflection rule, an inference rule to infer \(\varphi \) from “\(\ulcorner \varphi \urcorner \) is provable”. To avoid inconsistency, they stratify their rule in a manner similar to the transfinite progressions of Turing and Feferman: each invocation of the reflection rule is annotated with a level, \(\ell \), and an invocation at level \(\ell \) requires a proof that \(\ulcorner \varphi \urcorner \) is provable using the reflection rule only at levels \(<\ell \). Perhaps the most systematic use of reflection to justify more complex inference rules from simpler ones is in Milawa [18], which allows its entire proof checker to be replaced by a new version when given a proof that all sentences which are provable according to the new proof checker were also provable according to the old one.
Harrison [10], reviewing a large number of arguments and proposals for computational reflection, finds no evidence that it ever makes an otherwise infeasible proof technique feasible, though he concedes that in some cases, the speed-up can be significant. More recently, Coq’s ssreflect library [8] for computational reflection has been instrumental in the formal verification of the four-color theorem [7].
The algorithm in Sect. 4 bears a strong resemblance to the proof-producing translation (or code generation) algorithm presented by Myreen and Owens [19]. The input term in their algorithm is also an outer HOL term, but the target, instead of inner HOL, is the functional programming language CakeML. The semantics of CakeML is very different from the semantics of inner HOL, but the overall approach of producing certificate theorems bottom-up works similarly.
10 Conclusion
We have described automation for proving reflection principles of the form “If \(\ulcorner \varphi \urcorner \) is provable, then \(\varphi \)” from assumptions about the existence of large cardinals. Based on this work, we have discussed an implementation of model polymorphism [3], which allows reflective reasoning to be used in the verification of self-replacing systems.
In this paper, we have focused on the automation for proving reflection principles. In future work, we plan to apply this to an implementation of a self-modifying, self-verifying system. It would also be interesting to apply these techniques to create an extensible version of HOL, similar to Milawa [18]; in particular, where Milawa requires a proof that a new version of the proof checker is conservative (i.e., only accepts proofs of propositions that were also provable according to the old proof checker), our semantic approach would allow us to instead require a proof that the new version is sound (i.e., whenever it accepts a proof of a proposition, that proposition is semantically true). It would be interesting to explore how these syntactic and semantic extension principles compare in practice.
Notes
- 1.
\(\ulcorner \varphi \urcorner \) refers to \(\varphi \) as a syntactic object, represented e.g. by its Gödel number or by an abstract syntax tree.
- 2.
Including, as in Gordon [9], polymorphism (type variables and polymorphic constants) and defined constants and type operators.
- 3.
This is akin to working within an Isabelle [23] locale which fixes \(\mu \) and \({ {mem}}\) and assumes \(\mathsf{is\_set\_theory }\;{ {mem}}\). (We assume infinity only when necessary).
- 4.
The abstract syntax here is the inner HOL rendition of our example term. \(\mathsf{Bool }\) and \(\mathsf{Fun }\;{ {a}}\;{ {b}}\) are abbreviations for \(\mathsf{Tyapp }\;{\text {``bool''}}\;\mathsf{[\,] }\) and \(\mathsf{Tyapp }\;{\text {``fun''}}\;[{ {a}};\;{ {b}}]\).
- 5.
To understand the three turnstiles: \(\vdash \) denotes provability in outer HOL (and applies to the whole formula), infix |- denotes provability in inner HOL, and infix \(\models \) states that a sequent is valid according to the semantics of inner HOL.
- 6.
To be pedantic, \(\mathsf{to\_inner }\) also depends on the pervasive \({ {mem}}\) relation of the set theory.
- 7.
We follow the convention of treating predicates in outer HOL as sets. To be clear \(\mathcal {U}({:}\alpha )\) is a term of type
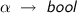 , and \(\left\{ \right. {}{ {a}}\;|{}\;{ {a}}\;\mathsf{\lessdot }\;{ {x}}\left. \right\} {}\) is a term of type
, and \(\left\{ \right. {}{ {a}}\;|{}\;{ {a}}\;\mathsf{\lessdot }\;{ {x}}\left. \right\} {}\) is a term of type  . These sets-as-predicates are distinct from the Zermelo sets, i.e., the terms of type \(\mu \).
. These sets-as-predicates are distinct from the Zermelo sets, i.e., the terms of type \(\mu \). - 8.
Also known as indefinite choice, the Hilbert choice principle in HOL provides a constant \((\mathsf{\varepsilon {} })\), usually written as a binder, together with the axiom \((\mathsf{\exists \,{} }{ {x}}.\;{ {P}}\;{ {x}})\;\mathsf{\Rightarrow {} }\;{ {P}}\;(\mathsf{\varepsilon {} }{ {x}}.\;{ {P}}\;{ {x}})\) which holds for any predicate \({ {P}}\).
- 9.
\(\mathsf{Num }\) is an abbreviation for \(\mathsf{Tyapp }\;{\text {``num''}}\;\mathsf{[\,] }\).
- 10.
When a new constant or type operator is defined, theorems produced by the definition are considered axioms of the resulting theory. The other source of axioms is new-axiom updates, which we do not support since they are not sound in general.
- 11.
Any valuation would do for this input since it has no free type or term variables.
- 12.
Our proof constructs a potentially slightly different model of inner HOL for each value of t; this is, roughly, the origin of the term model polymorphism.
References
Allen, S.F., Constable, R.L., Howe, D.J., Aitken, W.E.: The semantics of reflected proof. In: Proceedings of the LICS, pp. 95–105, IEEE Computer Society (1990)
Dybjer, P., Setzer, A.: A finite axiomatization of inductive-recursive definitions. In: Girard, J.-Y. (ed.) TLCA 1999. LNCS, vol. 1581, pp. 129–146. Springer, Heidelberg (1999)
Fallenstein, B., Soares, N.: Vingean reflection. Technical report, Machine Intelligence Research Institute, Berkeley, CA (2015)
Feferman, S.: Transfinite recursive progressions of axiomatic theories. J. Symb. Log. 27(3), 259–316 (1962)
Franzén, T.: Transfinite progressions: a second look at completeness. B. Symb. Log. 10(3), 367–389 (2004). http://www.math.ucla.edu/~asl/bsl/1003/1003-003.ps
Gödel, K.: Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. Monatshefte fr Mathematik und Physik 38(1), 173–198 (1931)
Gonthier, G.: The four colour theorem: engineering of a formal proof. In: Kapur, D. (ed.) ASCM 2007. LNCS (LNAI), vol. 5081, pp. 333–333. Springer, Heidelberg (2008)
Gonthier, G., Mahboubi, A.: An introduction to small scale reflection in Coq. J. Form. Reasoning 3(2), 95–152 (2010)
Gordon, M.: From LCF to HOL: a short history. In: Plotkin, G.D., Stirling, C., Tofte, M. (eds.) Proof, Language, and Interaction, Essays in Honour of Robin Milner, pp. 169–186. The MIT Press, Cambridge (2000)
Harrison, J.: Metatheory and reflection in theorem proving: A survey and critique. Technical report CRC-053, SRI, Cambridge, UK (1995). http://www.cl.cam.ac.uk/~jrh13/papers/reflect.dvi.gz
Harrison, J.: Towards self-verification of HOL Light. In: Furbach, U., Shankar, N. (eds.) IJCAR 2006. LNCS (LNAI), vol. 4130, pp. 177–191. Springer, Heidelberg (2006)
Harrison, J.: HOL Light: an overview. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 60–66. Springer, Heidelberg (2009)
Jech, T.: Set Theory. The Third Millenium Edition, Revised and Expanded. Springer Monographs in Mathematics. Springer, Heidelberg (2003)
Klein, G., Gamboa, R. (eds.): Interactive Theorem Proving. Springer, Heidelberg (2014)
Kumar, R., Arthan, R., Myreen, M.O., Owens, S.: HOL with definitions: semantics, soundness, and a verified implementation. In: Klein, G., Gamboa, R. (eds.) ITP 2014. LNCS, vol. 8558, pp. 308–324. Springer, Heidelberg (2014)
Kumar, R., Arthan, R., Myreen, M.O., Owens, S.: Self-formalisation of higher-order logic. J. Autom. Reasoning (2015), submitted. Preprint at https://cakeml.org
Mohamed, O.A., Muñoz, C.A., Tahar, S. (eds.): Theorem Proving in Higher Order Logics. Springer, Heidelberg (2008)
Myreen, M.O., Davis, J.: The reflective Milawa theorem prover is sound - (down to the machine code that runs it). In: Klein and Gamboa [14], pp. 421–436
Myreen, M.O., Owens, S.: Proof-producing translation of higher-order logic into pure and stateful ML. J. Funct. Program. 24(2–3), 284–315 (2014)
Norrish, M., Huffman, B.: Ordinals in HOL: transfinite arithmetic up to (and beyond) \(\omega _{1}\). In: Blazy, S., Paulin-Mohring, C., Pichardie, D. (eds.) ITP 2013. LNCS, vol. 7998, pp. 133–146. Springer, Heidelberg (2013)
Slind, K., Norrish, M.: A brief overview of HOL4. In: Mohamed et al. [17], pp. 28–32
Turing, A.M.: Systems of logic based on ordinals. Proc. LMS 2(1), 161–228 (1939)
Wenzel, M., Paulson, L.C., Nipkow, T.: The Isabelle framework. In: Mohamed et al. [17], pp. 33–38
Acknowledgements
We thank Magnus Myreen for feedback on a draft of this paper. We also thank the anonymous reviewers for their helpful criticism.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Fallenstein, B., Kumar, R. (2015). Proof-Producing Reflection for HOL. In: Urban, C., Zhang, X. (eds) Interactive Theorem Proving. ITP 2015. Lecture Notes in Computer Science(), vol 9236. Springer, Cham. https://doi.org/10.1007/978-3-319-22102-1_11
Download citation
DOI: https://doi.org/10.1007/978-3-319-22102-1_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-22101-4
Online ISBN: 978-3-319-22102-1
eBook Packages: Computer ScienceComputer Science (R0)





 ) have the same type/arity in inner HOL as in outer HOL. (The only primitive constant, equality, is assumed to have the correct type as part of
) have the same type/arity in inner HOL as in outer HOL. (The only primitive constant, equality, is assumed to have the correct type as part of 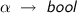 , and
, and  . These sets-as-predicates are distinct from the Zermelo sets, i.e., the terms of type
. These sets-as-predicates are distinct from the Zermelo sets, i.e., the terms of type