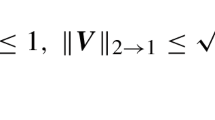Lower Bounds for Sparse Coding

Abstract

We give lower bounds on the reconstruction error for PCA , k-means clustering, and various sparse coding methods. It is shown that the two objectives of good data approximation and sparsity of the solution are incompatible if the data distribution is evasive in the sense that most of its mass lies away from any low dimensional subspace. We give closure properties and examples of evasive distributions and quantify the extent to which distributions of bounded support and bounded density are evasive.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Much recent work in machine learning and signal processing has concentrated on the problem of approximating high dimensional data $x\in \mathbb {R}^{N}$ by sparse linear combinations of the columns of a dictionary matrix ¹ $D=[d_{1},...,d_{K}]\in \mathbb {R}^{N\times K}$—see, for example, [3, 4, 6–12] and references therein. For a fixed dictionary D every such linear combination has the form

$$\begin{aligned} Dy=\sum _{i=1}^{K}y_{i}d_{i}, \end{aligned}$$

where the vector of coefficients y is chosen to be a solution of the optimisation problem

$$\begin{aligned} \min _{y\in \varLambda }\left\| x-Dy\right\| ^{2}. \end{aligned}$$

(24.1)

Here $\varLambda \subseteq \mathbb {R}^{K}$ is a fixed regularizing set, which implements constraints on the complexity of the chosen representations. We denote by y(x) such a solution, and it is one inherent objective that the vectors $y\left( x\right)$ obtained should be sparse, in that the number of their nonzero coefficients is much smaller than the ambient dimension N. If $y\left( x\right)$ is not sparse itself, it should at least have a close sparse approximation.

We assume that the data x are distributed at random according to a distribution $\mu$ on $\mathbb {R}^{N}$ corresponding to a random variable X taking values in $\mathbb {R}^{N}$. The reconstruction error $\left\| X-Dy\left( X\right) \right\| ^{2}$ is then a random variable and its expectation

$$\begin{aligned} R\left( D\right) =E\left\| X-Dy\left( X\right) \right\| ^{2} \end{aligned}$$

measures the failure of D to match the distribution $\mu$. Thus, given $\varLambda$, one wishes to choose D so as to minimize $R\left( D\right)$.

In this chapter we show that these methods are likely to produce poor results for a large class of seemingly well-behaved distributions on $\mathbb {R}^{N}$, because the two objectives are incompatible: With high probability the representing vector $y\left( X\right)$ is either not very sparse (or does not have a good sparse approximation), or the reconstruction error is large. Our negative results are independent of any problem of sample-based estimation and still hold if we have complete knowledge of the distribution $\mu$.

The “bad” distributions $\mu$ have the following property of evasiveness: For any low dimensional subspace M, the overwhelming majority of the mass of $\mu$ is bounded away from M. Below we use the notation $d\left( x,M\right) =\inf _{z\in M}\left\| x-z\right\|$.

Definition 24.1

Suppose $\alpha _{k}$ is a nonincreasing sequence of positive real numbers, $\beta$, $C>0$. A random variable X with values in $\mathbb {R}^{N}$ is said to be $\left( \alpha ,\beta ,C\right)$ -evasive if for every $k < N$, every k-dimensional subspace M of $\mathbb {R} ^{N}$ and every $t\in \left( 0,\alpha _{k}\right)$

$$\begin{aligned} \Pr \left\{ d\left( X,M\right) ^{2}\le \alpha _{k}-t\right\} \le Ce^{-N\beta t^{2}}. \end{aligned}$$

A probability measure $\mu$ on $\mathbb {R}^{N}$ is called $\left( \alpha ,\beta ,C\right)$-evasive if the corresponding random variable is.

We give two examples:

Example 24.1

(Noisy generative model) If Y is any random variable in $\mathbb {R}^{N}$ and Z is a centered isotropic Gaussian with variance $\sigma ^{2}$ and independent of Y, then the random variable $X=Y+Z$ is evasive with

$$\begin{aligned} \alpha _{k}=\sigma ^{2}\frac{N-k-\pi ^{2}-1}{N},\text { }\beta =\frac{1}{ 2\sigma ^{4}\pi ^{2}},\text { }C=2, \end{aligned}$$

as will be shown in Sect. 24.3.2. With Y taking values in a union of low dimensional subspaces generated by some potentially unknown dictionary, the random variable X can be viewed as a generative model contaminated by noise. Here we will prove lower bounds in the order of $\sigma ^{2}$.

Example 24.2

(Bounded support and bounded density) While the previous example is of a special form, this example is more generic. If a distribution $\mu$ has support in the unit ball $B_{N}$ of $\mathbb {R}^{N}$ and a bounded density $d\mu /d\rho$ with respect to the uniform measure $\rho$ on $B_{N}$, then $\mu$ is evasive with

$$\begin{aligned} \alpha _{k}=\left\| \frac{d\mu }{d\rho }\right\| _{\infty }^{\frac{-2}{ N-k}}\frac{N-k}{e^{3/2}N},\text { }\beta =1,\text { }C=1, \end{aligned}$$

where $\left\| .\right\| _{\infty }$ is the essential supremum norm w.r.t. $\rho$. This will be shown in Theorem 24.3 below.

We come to the announced negative results. Suppose first that in (24.1) a hard sparsity constraint is implemented by the regularizing set

$$\begin{aligned} \varLambda _{s}=\left\{ y\in \mathbb {R}^{K}:\left\| y\right\| _{0}\le s\right\} , \end{aligned}$$

(24.2)

where $\left\| y\right\| _{0}$ is the number of nonzero components of y and s is any integer $s\le K$. An easy union bound then gives the following result:

Theorem 24.1

Let $D=[d_{1},...,d_{K}]\in \mathbb {R}^{N\times K}$ be any dictionary and suppose that X is $\left( \alpha ,\beta ,C\right)$-evasive. Then for any integer $s\le K$ and $t\in \left( 0,\alpha _{s}\right)$

$$\begin{aligned} \Pr _{X\sim \mu }\left\{ \min _{y\in \varLambda _{s}}\left\| X-Dy\right\| ^{2}\le \alpha _{s}-t\right\} \le C\exp \left( -N\beta t^{2}+s\ln K\right) . \end{aligned}$$

(24.3)

If $s\ln K\ll N$ the reconstruction error is bounded away from zero with high probability.

We might hope to improve this situation by requiring the encoding vectors y to be sparse only in some approximate sense. The next result holds for all vectors $y\in \mathbb {R}^{K}$, sparse or not, and exhibits a tradeoff between the quality of two approximations: the approximation of the data by Dy and the $\ell _{1}$-approximation of y by its nearest vector of prescribed sparsity. For $y=(y_{1},\dots ,y_{K})\in \mathbb {R}^{K}$ and $s<K$ let $y^{s}$ denote the s-sparse approximation of y, obtained by setting all components $y_{i}$ equal to zero except for the s indices where $\left| y_{i}\right|$ is largest.

Theorem 24.2

Let D be any dictionary with $\left\| d_{i}\right\| =\left\| De_{i}\right\| \le B$ and suppose that X is $\left( \alpha ,\beta ,C\right)$-evasive. Then for every $\delta \in \left( 0,1\right)$ we have with probability at least $1-\delta$ for every $y\in \mathbb {R}^{K}$ and every $s\in \left\{ 1,...,K\right\}$ that

$$\begin{aligned} \left\| X-Dy\right\| ^{2}\ge \frac{\alpha _{s}}{2}-\frac{1}{2}\sqrt{ \frac{\left( 1+s\right) \ln K+\ln \frac{C}{\delta }}{N\beta }} -B^{2}\left\| y-y^{s}\right\| _{1}^{2}. \end{aligned}$$

In many applications we can assume $B=1$. So if $s\ln K\ll N$ and $\left\| y-y^{s}\right\| _{1}$ is small (so that y has a close s-sparse approximation) then the reconstruction error is of order $\alpha _{s}$.

Below we use these results on PCA, K-means clustering and sparse coding and delimit the class of distributions to which these methods of unsupervised learning can be successfully applied.

2 Applications and Examples

The framework described in the introduction is general enough to capture many approaches to unsupervised learning.

2.1 PCA

In problem (24.1), if $\varLambda$ is all of $\mathbb {R }^{K}$ with $K=s\ll N$, then an optimal D is found to be an isometry from $\mathbb {R}^{K}$ to a maximal K-dimensional subspace of the covariance of X. The resulting method is PCA, and trivially every representing vector is s-sparse, namely y(x) has at most $s=K$ nonzero components.

We could apply Theorem 24.1, but this would incur a superfluous term $K\ln K$ in the exponent of the bound. Instead, by directly appealing to the definition, we find that for $\left( \alpha ,\beta ,C\right)$-evasive X and any dictionary D

$$\begin{aligned} \Pr \left\{ \min _{y\in \mathbb {R} ^{K}}\left\| X-Dy\right\| ^{2}<\alpha _{K}-t\right\} \le Ce^{-\beta Nt^{2}}. \end{aligned}$$

An illustration of the evasiveness of bounded densities (Example 24.2 above) is the following: Suppose we do PCA in one thousand dimensions, and we know that the data distribution is contained in the unit ball. If we find a 100-dimensional subspace which achieves an expected reconstruction error of ${\approx }{0.1}$, then the supremum of the distribution density (if such exists, and relative to the uniform measure on the ball) must be at least in the order of $10^{45}$. The supremum relative to the Lebesgue measure must be at least $10^{45}/V_{1000}\approx 10^{1800}$, where $V_{N}$ is the volume of the unit ball in $\mathbb {R}^{N}$. To derive this we use $\left( \alpha _{K}-t\right) \left( 1-C\exp \left( -\beta Nt^{2}\right) \right)$ as a simple lower bound on the expected reconstruction error with $t=0.05$, $N=1000$, $K=100$, $\beta =1$, $C=1$, equate the bound to 0.1, and solve for the bound on the density.

2.2 K-means Clustering

At the other extreme from PCA, if $\varLambda =\left\{ e_{1},...,e_{K}\right\}$ is a basis for $\mathbb {R}^{K}$, then the method becomes K-means clustering or vector quantization, and the optimal dictionary atoms $d_{1},...,d_{K}$ are just the optimal centers. In this case the complexity constraint can be seen as a maximal sparsity requirement, as every member y of $\varLambda$ satisfies $\left\| y\right\| _{0}=1$, but we may now allow $K>N$.

With $\varLambda _{s}$ defined as in (24.2) we find $\left\{ e_{1},...,e_{K}\right\} \subseteq \varLambda _{1}$, so appealing to Theorem 24.1 we find for $\left( \alpha ,\beta ,C\right)$-evasive X and any dictionary D

$$\begin{aligned} \Pr \left\{ \min _{y\in \left\{ e_{1},...,e_{K}\right\} }\left\| X-Dy\right\| ^{2}<\alpha _{1}-t\right\}\le & {} \Pr \left\{ \min _{y\in \varLambda _{1}}\left\| X-Dy\right\| ^{2}<\alpha _{1}-t\right\} \\\le & {} C\exp \left( -N\beta t^{2}+\ln K\right) . \end{aligned}$$

Of course there is a slight giveaway here, because $\varLambda _{1}$ is somewhat more expressive than $\left\{ e_{1},...,e_{K}\right\}$.

2.3 Sparse Coding Methods

To make $\varLambda$ more expressive we can relax the extreme sparsity constraint, setting $\varLambda =\varLambda _{s}$ with $1\le s\ll N$. This is the situation directly addressed by Theorem 24.1, which immediately gives a lower error bound. The corresponding method is not very practical, however, because of the unwieldy nature of the $\ell _{0}$-function.

The alternative is to replace (24.1) with the following optimization problem

$$\begin{aligned} \min _{y\in \mathbb {R}^{K}}\left\| x-Dy\right\| ^{2}+\gamma \left\| y\right\| _{1}, \end{aligned}$$

(24.4)

where $\gamma$ is some positive constant, thus encouraging sparsity through the use of the $\ell _{1}$-norm regularizer. A large body of work has been dedicated to the study of this and related methods, the success of which depends on different coherence properties of D, see [1–3] and references therein. The search for an optimal D in this case corresponds to the sparse coding method proposed by Olshausen and Field [10], which was originally motivated by neurophysiological studies of the mammalian visual system.

A similar approach uses the initial formulation (24.1) and takes $\varLambda$ to be a multiple of the $\ell _{1}$-unit ball. It relates to (24.4) as Ivanov regularization relates to Tychonov regularization.

Another example in this suite of methods is nonnegative matrix factorization, as proposed by Lee and Seung [6], where the $d_{i}$ are required to be in the positive orthant of $\mathbb {R}^{N}$.

Theorem 24.2 immediately applies to all these cases and shows that for evasive distributions the requirements of good data approximation and approximate sparsity are incompatible.

3 Proofs

We review our notation and then prove the announced results.

For every vector $y\in \mathbb {R}^{K}$, we let $\Vert y\Vert _{0}$ denote the number of nonzero components of y. We say that y is s-sparse if $\Vert y\Vert _{0}=s$. We denote by $y^{s}$ an s-sparse vector which is nearest to y according to the $\ell _{1}$ norm. For every linear subspace M of $\mathbb {R}^{N}$, we let $P_{M}$ be the corresponding projection matrix and define $d(x,M)=\inf _{z\in M}\Vert x-z\Vert$, namely the distance of x to the linear subspace M. Note that $d(x,M)=\Vert P_{M^{\perp }}x\Vert$, where $M^{\perp }$ is the orthogonal complement of M. We denote by $\Vert \cdot \Vert$ the $\ell _{2}$ norm of a vector and by $|||\cdot |||$ the operator norm of a matrix. For every $n\in \mathbb {N}$, we let $B_{n}$ be the unit ball in $\mathbb {R}^{n}$ and let $V_{n}$ be its volume.

If $\nu$ and $\rho$ are measures on the same space and $\nu \left( A\right) =0$ for every A satisfying $\rho \left( A\right) =0$, then $\nu$ is called absolutely continuous w.r.t. $\rho$ and there exists a measurable density function $d\mu /d\rho$, called the Radon-Nykodym derivative, such that $d\nu =\left( d\nu /d\rho \right) d\rho$.

3.1 Limitations of Sparse Coding

We prove Theorems 24.1 and 24.2.

Proof

(Proof of Theorem 24.1) For $S\subseteq \left\{ 1,...,K\right\}$ let $M_{S}$ denote the subspace spanned by the $d_{i}$ with $i\in S$. In the event on the left-hand side of (24.3) there is some subset $S\subseteq \left\{ 1,...,K\right\}$ with cardinality $\left| S\right| \le s$ such that $d\left( X,M_{S}\right) ^{2}\le \alpha _{s}-t$. The dimension of $M_{S}$ is at most s, so we get from a union bound that

$$\begin{aligned}&\Pr \left\{ \min _{y:\left\| y\right\| _{0}\le s}\left\| X-Dy\right\| ^{2}\le \alpha _{s}-t\right\} \\\le & {} \Pr \left\{ \exists S\subseteq \left\{ 1,...,K\right\} ,\left| S\right| \le s,d\left( X,M_{S}\right) ^{2}\le \alpha _{s}-t\right\} \\\le & {} \left( {\begin{array}{c}K\\ s\end{array}}\right) Ce^{-N\beta t^{2}}\le C\exp \left( -N\beta t^{2}+s\ln K\right) . \end{aligned}$$

$\square$

Proof

(Proof of Theorem 24.2) Denote

$$ t_{s}\left( s\right) =\min \left\{ \alpha _{s},\sqrt{\left( \left( 1+s\right) \ln K+\ln \left( C/\delta \right) \right) /\left( N\beta \right) } \right\} . $$

For any $s\in \left\{ 1,...,K\right\}$, $x\in \mathbb {R}^{N}$ and $y\in \mathbb {R}^{K}$ we have the following sequence of implications:

$$\begin{aligned} \left\| x-Dy\right\| ^{2}< & {} \frac{\alpha _{s}-t\left( s\right) }{2} -B^{2}\left\| y-y^{s}\right\| _{1}^{2} \end{aligned}$$

(24.5)

$$\begin{aligned} \text {implies }\left\| x-Dy\right\| +B\left\| y-y^{s}\right\| _{1}< & {} \sqrt{\alpha _{s}-t\left( s\right) } \end{aligned}$$

(24.6)

$$\begin{aligned} \text { implies }\left\| x-Dy\right\| +\left\| D\left( y-y^{s}\right) \right\| _{1}< & {} \sqrt{\alpha _{s}-t\left( s\right) } \end{aligned}$$

(24.7)

$$\begin{aligned} \text {implies }\left\| x-Dy^{s}\right\| ^{2}< & {} \alpha _{s}-t\left( s\right) . \end{aligned}$$

(24.8)

(24.5)$\implies$(24.6) follows from $\left( a+b\right) ^{2}\le 2a^{2}+2b^{2}$, (24.6)$\implies$(24.7) from $\left\| Dy\right\| \le B\left\| y\right\| _{1}$, because of the bound on $\left\| d_{i}\right\|$, and (24.7)$\implies$(24.8) from the triangle inequality. Thus

$$\begin{aligned}&\Pr \left\{ \exists s\in \mathbb {N} ,\exists y\in \mathbb {R} ^{n},~\left\| X-Dy\right\| ^{2}\le \frac{\alpha _{s}-t\left( s\right) }{2}-B^{2}\left\| y-y^{s}\right\| _{1}^{2}\right\} \\\le & {} \Pr \left\{ \exists s\in \mathbb {N} ,\exists y\in \mathbb {R} ^{n},\left\| y\right\| _{0}\le s,\left\| X-Dy\right\| ^{2}\le \alpha _{s}-t\left( s\right) \right\} \\\le & {} \sum _{s=1}^{K}\Pr \left\{ \exists y\in \mathbb {R} ^{n},\left\| y\right\| _{0}\le s,\left\| X-Dy\right\| ^{2}\le \alpha _{s}-t\left( s\right) \right\} \\\le & {} \sum _{s=1}^{K}C\exp \left( -N\beta t_{s}^{2}+s\ln K\right) \text { by Theorem 24.1} \\\le & {} \delta \text { by definition of }t\left( s\right) \text {.} \end{aligned}$$

$\square$

3.2 Evasive Distributions

The parameters $\left( \alpha ,\beta ,C\right)$ of an evasive distribution transform under the operations of scaling, translation and convolution.

Proposition 24.1

Let X be $\left( \alpha ,\beta ,C\right)$-evasive with values in $\mathbb {R}^{N}$. Then

• (i) AX is $\left( |||A^{-1}|||^{-2}\alpha ,|||A^{-1}|||^{4}\beta ,C\right)$-evasive for every nonsingular $N\times N$ matrix A;

• (ii) cX is $\left( c^{2}\alpha ,c^{-4}\beta ,C\right)$-evasive for every $c\in \mathbb {R}$;

• (iii) $X+z$ is $\left( \alpha ^{\prime },\beta ,C\right)$-evasive with $\alpha _{k}^{\prime }=\alpha _{k+1}$, for every $z\in \mathbb {R}^{N}$;

• (iv) $X+Z$ is $\left( \alpha ^{\prime },\beta ,C\right)$-evasive with $\alpha _{k}^{\prime }=\alpha _{k+1}$, for every random variable Z independent of X.

Proof

If A is nonsingular and M is any k-dimensional subspace of $\mathbb {R}^{N}$ then for $z\in M$

$$\begin{aligned} \left\| X-A^{-1}z\right\| =\left\| A^{-1}\left( AX-z\right) \right\| \le |||A^{-1}|||\left\| AX-z\right\| , \end{aligned}$$

which shows that $d\left( AX,M\right) \ge |||A^{-1}|||^{-1}d\left( X,A^{-1}M\right)$. We therefore have for $t\in \left( 0,|||A^{-1}|||^{-2}\alpha \right)$ that

$$\begin{aligned} \Pr&\left\{ d\left( AX,M\right) ^{2}<|||A^{-1}|||^{-2}\alpha _{k}-t\right\} \\&\le \Pr \left\{ d\left( X,A^{-1}M\right) ^{2}<\alpha _{k}-|||A^{-1}|||^{2}t\right\} \\&\le \exp \left( -N\beta |||A^{-1}|||^{4}t^{2}\right) , \end{aligned}$$

since $A^{-1}M$ is also k-dimensional. (ii) is just (i) applied to $A=cI$. (iii) follows from

$$\begin{aligned} d\left( X+z,M\right) =d\left( X,M-z\right) \ge d\left( X,\text {Span}\left( M,z\right) \right) \end{aligned}$$

and the observation that the dimension of Span$\left( M,z\right)$ is at most $\dim M+1$. Finally (iv) follows from (iii) by first conditioning on Z:

$$\begin{aligned} \Pr \left\{ d\left( X+Z,M\right) ^{2}<\alpha _{k+1}-t\right\}= & {} E\left[ E \left[ 1_{\left\{ X:d\left( X+Z,M\right) ^{2}<\alpha _{k+1}-t\right\} }|Z \right] \right] \\\le & {} E\left[ Ce^{-N\beta t^{2}}\right] . \end{aligned}$$

$\square$

Next we show that the normalized isotropic Gaussian in $\mathbb {R}^{N}$ is evasive.

Proposition 24.2

Let X be an isotropic Gaussian random variable with values in $\mathbb {R}^{N}$ and $E\left\| X\right\| ^{2}=1$. Then for any k-dimensional subspace M we have

$$\begin{aligned} \Pr \left\{ d\left( X,M\right) ^{2}<\frac{N-k-\pi ^{2}}{N}-t\right\} \le 2e^{-Nt^{2}/\left( 2\pi ^{2}\right) }. \end{aligned}$$

Proof

For any k-dimensional subspace M we consider the Gaussian random variable $P_{M}X$ and find

$$\begin{aligned} E\left[ \left\| P_{M}X\right\| ^{2}\right] = k/N. \end{aligned}$$

(24.9)

We also note the Gaussian concentration property for the norm [5]

$$\begin{aligned} \Pr \left\{ \left| E\left\| P_{M}X\right\| -\left\| P_{M}X\right\| \right| >t\right\} \le 2\exp \left( -2Nt^{2}/\pi ^{2}\right) , \end{aligned}$$

(24.10)

which we will use repeatedly. For a bound on the variance of the norm we first use it together with integration by parts to get

$$\begin{aligned} E\left[ \left( \left\| P_{M}X\right\| -E\left\| P_{M}X\right\| \right) ^{2}\right] \le 4\int _{0}^{\infty }t\exp \left( -2Nt^{2}/\pi ^{2}\right) dt=\frac{\pi ^{2}}{N}. \end{aligned}$$

This implies that $E\left[ \left\| P_{M}X\right\| ^{2}\right] \le \left( E\left\| P_{M}X\right\| \right) ^{2}+\pi ^{2}/N$, and hence

$$\begin{aligned}&\Pr \left\{ E\left[ \left\| P_{M}X\right\| ^{2}\right] -\left\| P_{M}X\right\| ^{2}>t+\pi ^{2}/N\right\} \\\le & {} \Pr \left\{ \left( E\left\| P_{M}X\right\| \right) ^{2}-\left\| P_{M}X\right\| ^{2}>t\right\} \\= & {} \Pr \left\{ \left( E\left\| P_{M}X\right\| -\left\| P_{M}X\right\| \right) \left( E\left\| P_{M}X\right\| +\left\| P_{M}X\right\| \right) >t\right\} \text {.} \end{aligned}$$

Observe that the latter probability is nonzero only if $\left\| P_{M}X\right\| \le E\left\| P_{M}X\right\|$, and that by Jensen’s inequality and (24.9) $E\left\| P_{M}X\right\| \le \sqrt{k/N}\le 1$. Using (24.10) again we therefore obtain

$$\begin{aligned} \Pr \left\{ E\left[ \left\| P_{M}X\right\| ^{2}\right] -\left\| P_{M}X\right\| ^{2}>t\right\} \le \Pr \left\{ E\left\| P_{M}X\right\| -\left\| P_{M}X\right\| >\frac{t}{2}\right\} . \end{aligned}$$

From (24.9) and (24.10)

$$\begin{aligned} \Pr \left\{ \left\| P_{M}X\right\| ^{2}<\frac{k-\pi ^{2}}{N}-t\right\} \le 2e^{-Nt^{2}/\left( 2\pi ^{2}\right) }, \end{aligned}$$

and applying this inequality to the orthogonal complement $M^{\perp }$ instead of M gives the conclusion. $\square$

The isotropic Gaussian is thus evasive with $\alpha _{k}=\frac{N-k-\pi ^{2}}{ N},\beta =1/2\pi ^{2},C=2$. Using Proposition 24.1 (ii) and (iv) with $c=\sigma$ and addition of an appropriate independent random variable Y proves the claim about noisy generative models made in the introduction.

We now show that evasiveness is a generic behavior in high dimensions, if the distribution in question has a bounded support and a bounded density.

Theorem 24.3

Let the random variable X be distributed as $\mu$ in $\mathbb {R}^{N}$, where $\mu$ is absolutely continuous w.r.t. the uniform measure $\rho$ on the unit ball $B_{N}$ of $\mathbb {R}^{N}$. For every k let

$$\begin{aligned} \alpha _{k}=\left\| \frac{d\mu }{d\rho }\right\| _{\infty }^{\frac{-2}{ N-k}}\frac{N-k}{e^{3/2}N}. \end{aligned}$$

Then for every k-dimensional subspace M we have, for $t\in \left( 0,\alpha _{k}\right)$,

$$\begin{aligned} \Pr \left\{ d\left( X,M\right) ^{2}\le \alpha _{k}-t\right\} \le e^{-Nt^{2}}. \end{aligned}$$

(24.11)

For applications of the properties of evasive distributions it is crucial that the numbers $\alpha _{k}$ be reasonably large and decrease slowly. Figure 24.1 plots the decay of the $\alpha _{k}$ when $N=100$ and $\left\| d\mu /d\rho \right\| _{\infty }=1$ (corresponding to the uniform distribution on the ball $B_{100}$) or $\left\| d\mu /d\rho \right\| _{\infty }=10^{10}$ respectively.

Fig. 24.1

The sequence $\alpha _{k}$ for $\left\| d\rho /d \mu \right\| _{\infty }=1$ (dashed line) and $\left\| d\rho /d\mu \right\| _{\infty }=10^{10}$ (solid line) with $N=100$

To prove Theorem 24.3 we need the following technical lemma. Recall that we use $V_{n}$ to denote the volume of the unit ball in $\mathbb {R}^{n}$.

Lemma 24.1

For every $N,k\in \mathbb {N}$ and $1\le k<N$ we have

$$\begin{aligned} \frac{N-k}{Ne}\le \left( \frac{V_{N}}{V_{k}V_{N-k}}\right) ^{\frac{2}{N-k}}. \end{aligned}$$

Proof

For simplicity we only prove the case where k and N are even. The formula

$$\begin{aligned} V_{n}=\frac{\pi ^{n/2}}{\varGamma \left( n/2+1\right) } \end{aligned}$$

shows that

$$\begin{aligned} \frac{V_{k}V_{N-k}}{V_{N}}= & {} \frac{\varGamma \left( N/2+1\right) }{\varGamma \left( k/2+1\right) \varGamma \left( N/2-k/2+1\right) } \\= & {} \left( {\begin{array}{c}N/2\\ k/2\end{array}}\right) =\left( {\begin{array}{c}N/2\\ \left( N-k\right) /2\end{array}}\right) \\\le & {} \left( \frac{Ne}{N-k}\right) ^{\frac{N-k}{2}}, \end{aligned}$$

where the last inequality is a well-known bound on the binomial coefficients. The result follows. $\square$

Proof

(Proof of Theorem 24.3) First we work relative to Lebesgue measure $\lambda$. Let

$$\begin{aligned} a=\left\| \frac{d\mu }{d\lambda }\right\| _{\infty }=\left\| \frac{ d\mu }{d\rho }\right\| _{\infty }V_{N}^{-1}. \end{aligned}$$

Fix a k-dimensional subspace M. We prove the bound by considering the worst possible density which maximizes the probability in (24.11), subject to the constraint that $\left\| d\mu /d\lambda \right\| _{\infty }=a$ and that $\mu$ be supported in the unit ball. Relaxing the constraint on the support of $\mu$ from the unit ball to a larger set X will only increase the probability. We can therefore compute a bound on the probability by considering a distribution $\mu ^{\prime }$ which maximizes it, subject to the constraint that $\left\| d\mu ^{\prime }/d\lambda \right\| _{\infty }=a$ and that $\mu ^{\prime }$ is supported in the cylinder $\left( M\cap B_{N}\right) \times M^{\perp }$, which contains the unit ball $B_{N}$. Clearly a solution to this optimization problem is given by the density

$$\begin{aligned} \frac{d\mu ^{\prime }}{d\lambda }\left( x\right) =\left\{ \begin{array}{ccc} a &{} \text {if} &{} d\left( x,M\right) \le r_{\max } \\ 0 &{} \text {if} &{} d\left( x,M\right) >r_{\max } \end{array} \right. ,x\in \left( M\cap B_{N}\right) \times M^{\perp }\text {,} \end{aligned}$$

where $r_{\max }$ is determined from the normalization requirement on $\mu ^{\prime }$. This density $d\mu ^{\prime }/d\lambda$ has the maximal value a on a slab of thickness $2r_{\max }$, parallel and symmetric to $M\cap B_{N}$ and it is zero elsewhere. If $V_{n}$ denotes the volume of the unit ball in $\mathbb {R} ^{n}$ the volume of this slab is $V_{k}V_{N-k}r_{\max }^{N-k}$, from which we find

$$\begin{aligned} r_{\max }=\left( aV_{k}V_{N-k}\right) ^{-1/\left( N-k\right) }=\left( \left\| \frac{d\mu }{d\lambda }\right\| _{\infty }V_{k}V_{N-k}\right) ^{-1/\left( N-k\right) }. \end{aligned}$$

A similar computation for the volume of an analogous slab of thickness $2 \sqrt{a_{k}-t}$ gives

$$\begin{aligned} \Pr \left\{ d\left( X,M\right) ^{2}\le \alpha _{k}-t\right\} =\Pr \left\{ d\left( X,M\right) \le \sqrt{\alpha _{k}-t}\right\} =\left( \frac{\sqrt{ \alpha _{k}-t}}{r_{\max }}\right) ^{N-k}, \end{aligned}$$

(24.12)

where the probability is computed according to $\mu ^{\prime }$. Now we have to show that this is bounded by $e^{-Nt^{2}}$ for $t\in \left( 0,\alpha _{k}\right)$.

We get from the lemma that

$$\begin{aligned} \alpha _{k}= & {} \left\| \frac{d\mu }{d\rho }\right\| _{\infty }^{\frac{ -2}{N-k}}\left( \frac{N-k}{e^{3/2}N}\right) \\\le & {} e^{-1/2}\left\| \frac{d\mu }{d\rho }\right\| _{\infty }^{\frac{ -2}{N-k}}\left( \frac{V_{N}}{V_{k}V_{N-k}}\right) ^{\frac{2}{N-k}} \\= & {} e^{-1/2}\left( \left\| \frac{d\mu }{d\lambda }\right\| _{\infty }V_{k}V_{N-k}\right) ^{\frac{-2}{N-k}} \\= & {} r_{\max }^{2}e^{-1/2} \\\le & {} t+r_{\max }^{2}\exp \left( -\frac{2N}{N-k}t^{2}\right) . \end{aligned}$$

The last step follows from

$$ 0\le t\le \alpha _{k}=\left( N-k\right) /\left( e^{3/2}N\right) \le \sqrt{\left( N-k\right) /\left( 4N\right) }. $$

Thus

$$\begin{aligned} 0\le \alpha _{k}-t\le r_{\max }^{2}\exp \left( -\frac{2N}{N-k}t^{2}\right) , \end{aligned}$$

and substitution in (24.12) gives the conclusion. $\square$