Abstract
In nature, helical structures arise when identical structural subunits combine sequentially, the orientational and translational relation between each unit and its predecessor remaining constant. A helical structure is thus generated by the repeated action of a screw transformation acting on a subunit. A plane hexagonal lattice wrapped round a cylinder provides a useful starting point for describing the helical conformations of protein molecules, for investigating the geometrical properties of carbon nanotubes, and for certain types of dense packings of equal spheres.
Structural Chemistry 2002, 13(3/4):305–314.
This contribution is part of a collection titled Generalized Crystallography and dedicated to the 75th anniversary of Professor Alan L. Mackay, FRS.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
Introduction
An infinite strip of a tiling of the Euclidean plane by equilateral triangles, bounded by two parallel lines, can be wrapped around a circular cylinder so that the two strip edges meet. We shall refer to the resulting structure as a cylindrical hexagonal lattice or, briefly, a CHL. Alternatively, instead of rolling the strip around a cylinder, corresponding points on the edges may be brought into coincidence by folding along the fundamental lattice lines, keeping the triangular facets flat. We shall refer to the resulting structure as a triangulated helical polyhedron or, briefly, a THP. A THP is an “almost regular” polyhedron, in that its symmetry group, a rod group, acts transitively on the vertices and faces, although not on the edges.
The geometrical properties of the THPs are of relevance in structural chemistry for several reasons. As Sadoc and Rivier [1] have shown, the helical structures commonly occurring in proteins are metrically quite close to polygonal helices consisting of edges of THPs. The rodlike sphere packings investigated by Boerdijk [2] are derived from the Coxeter helix [3–5], which is the simplest THP. In a nanotube, the atomic positions correspond to a subset of the vertices of a THP.
The purpose of this work is twofold: to derive expressions for the metrical and topological parameters of the triangulated helical polyhedra and to indicate their importance by means of examples from the literature on protein helices, sphere packings, and nanotubes.
Nomenclature
A THP, or a CHL, is determined by the translation vector separating pairs of points on the strip boundaries that are to be identified. Let the components of this vector, referred to the underlying planar hexagonal coordinate system, be (m, n). The 6m symmetry of the plane hexagonal lattice implies that the integer pairs (m, n), (−l, m), (−n, −l), (−m, −n), (l, −m), and (n, l) all give rise to the same structure and (n, m), (l, n), (−m, l), (−n, −m), (−l, n), and (m, −l) refer to its mirror image (where l = n − m.) The redundancy in the notation is eliminated by the requirement
Thus each kind of THP (or CHL) may be denoted by a unique symbol (l, m, n). (See, for example, Sadoc and Rivier [1].)
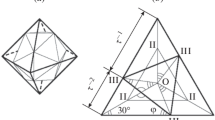
Except for the special cases (0, m, m) and (m, m 2m), the CHLs are chiral: (l, m, n)R has, by convention, right-handed {l} and {n} type helices and the {m} type is left-handed. The mirror image of (l, m, n)R is, of course, denoted by (l, m, n)L. Figure 1 illustrates the case (3, 5, 8). The direction of the strip edges can be arbitrary. Three special choices are indicated on the figure: strips with widths 3, 5, and 8 of the elementary equilateral triangles, along the directions [1, 1], [1, 0], and [0, 1], respectively. The corresponding lines of lattice points become helices on the cylinder: Three helices of type {3}, five of type {5}, and eight of type {8}. Figure 2 illustrates a portion of the THP of type (3, 5, 8)L.
Construction of the CHL (3, 5, 8).
The triangulated helical polyhedron (3, 5, 8)L.
Metrical Parameters of a CHL
A vertex of a plane hexagonal lattice can be identified by two integers (μ, ν)—its coordinates in terms of the hexagonal coordinates. In a CHL, the point (μ, ν) acquires a position on the cylinder, with three-dimensional (3-D) cylindrical coordinates (ρ, φ, z), which can be found as follows. On the plane hexagonal lattice the angle α between the directions (μ, ν) and (m, n) is given by
where λ = √(μ 2 + ν 2 − μν), k = √(m 2 + n 2 − mn). Then the coordinates of the point (μ, ν) in 3-D Euclidean space are
The {l}, {m}, and {n} type helices are, respectively, along [−1, −1], [0, 1], and [−1, 0], so that their rotational advances per edge are
and the translational advances are
Metrical Parameters of a THP
Sadoc and Rivier [1] have identified several wellknown helices occurring in protein structure with type {1} helices of THPs of the form (1, m, m + 1):
See, for example, Lehninger et al. [6] for the structure and nomenclature of the corresponding protein configurations. In these models, the type {1} polygonal helix represents the polypeptide chain. Other edges of the TPH correspond to the linking hydrogen bonds that are responsible for the helical configuration.
The method of Sadoc and Rivier for computing the metrical parameters of TPHs of the special kind (1, m, m + 1) is as follows. Let … A−2 A−1 A0 A1 A2 A3 … denote the sequence of successive vertices of the type {1} helix of the TPH (1, m, m + 1) and observe that A0A m A m+1 is a face—an equilateral triangle. Choose Cartesian coordinates so that A m has coordinates ρ (cos mφ, sin mφ, mc) and equate the three edge lengths A0A m , A0 A m+1 and A m A m+1 = A0A1. This gives
Eliminating c 2 and expressing cosmφ and cos(m + 1)φ as polynomials in χ = cosφ gives a polynomial in χ of degree m + 1. It can be shown that this polynomial has a factor (χ − 1)2, so we finally arrive at a polynomial in χ of order m − 1. Only one root (in fact, the largest root) is relevant; the other roots correspond to triangulated surfaces with self-intersections.
Consider now more general cases (l, m, n). For large vectors (m, n) it is obvious that the formulas for the parameters of a CHL will give reasonable approximations to those for the corresponding THP. For smaller values we resort to Fig. 3, which represents the projection of a THP on planes perpendicular and parallel to its axis, of the edges of a constituent equilateral triangle. To find the radius ρ, we start from the formula for the circumradius of a triangle with edges l 1, l 2, and l 3
From Fig. 3, we see that
and
so that l 2 and l 3 can be expressed as functions of l 1:
Thus, we get the radius ρ as a function of l 21 . Now observe that m steps of an {n} helix followed by n steps of an {m} helix brings one back to the starting vertex. The path has rotational advance 2π. From the figure, we see that the rotational advance per edge length is 2sin−1 (l 2 /2ρ) for the type {m} helices and 2sin−1 (l 3 /2ρ) for the type {n} helices. This gives
leading to a quite formidable transcendental equation in l 21 . The relevant root is the smallest root. A suitable starting value for finding this root by successive approximation can be taken to be the l 21 for the corresponding CHL, (m + n)2 /4(m 2 + n 2 − mn). Table 1 gives the metrical parameters obtained in this way, using Mathematica, for a few small values of (m, n). The final column is the radius ρ CHL of the corresponding CHL, for comparison:
The corresponding values for the rotational and translational advance per edge of the polygonal helices of types {l}, {m} and {n} are
Cases (0, m, m) and (m, m, 2m) have not been listed in the table because they are given, respectively, by the simple formulas
Projection of a triangular facet of a THP, along the axis, and perpendicular to the axis.
The Boerdijk–Coxeter Structure
The simplest nontrivial THP is (1, 2, 3) shown in Fig. 4. It is the surface of a stack of regular tetrahedra. We shall refer to it as the Boerdijk–Coxeter structure, or, simply, the “B-C structure.” The vertices, labeled … A−2 A−1 A0 A1 A2 A3 … consecutively along the type {1} helix are such that any four consecutive points are the vertices of a regular tetrahedron [3–5]. Buckminster Fuller [7] named this helical structure “the tetrahelix.” With unit edge length, five consecutive points on the type {1} polygonal helix can be taken to be
The action of a screw transformation x → Rx + a generates the whole structure, where
The axis direction n and the rotational advance per edge φ (of the type {1} polygonal helix) can be extracted from the formula for rotation through an angle φ about an axis along a unit vector n:
The translational advance d is the scalar product of n with a tetrahedron edge. The result is
The radius is got by substituting \( {l}_1=\sqrt{\left(9/{l}_0\right)} \), \( {l}_2=\sqrt{\left(6/{l}_0\right)} \), \( {l}_3=\sqrt{\left(1/{l}_0\right)} \) into the formula for ρ:
The Boerdijk–Coxeter structures (1, 2, 3) R and (1, 2, 3)L.
Sphere Packings
Boerdijk [2] investigated the Coxeter structure [the THP (1, 2, 3)] in connection with dense packings of equal spheres. The configuration of four spheres in a tetrahedral configuration, each touching other three, gives the Rogers upper bound for the upper limit of any possible packing fraction for equal spheres. The bound can never be achieved because regular tetrahedra will not pack together in Euclidean. However, sphere packings that fill only a portion of space can come much closer to the bound than hexagonal close packing—the densest lattice packing. Boerdijk considered the dense rod-shaped packing in which the sphere centers lie on the vertices of a (1, 2, 3) (Fig. 5).
The dense packing of spheres centered at the vertices of a B-C helix.
Extension of the Helical Sphere Packing
As pointed out by Boerdijk, the packing of spheres centred at the vertices of (1, 2, 3) can be extended by adding more spheres over the midpoints of edges of type {1} helices. Specifically, an extra vertex is placed over the midpoint of each edge of the type {1} helix, forming an equilateral triangle with the two vertices of that edge. This determines additional, only slightly irregular, tetrahedra, so that every edge of the type {1} helix is shared by five tetrahedra (Fig. 6)
Extension of the sphere packing. Sphere centers are at vertices of the tetrahedra. The additional tetrahedra are very nearly regular.
Further extensions of the Boerdijk–Coxeter structure are possible. The next stage of adding spheres gives a rodlike structure in which every vertex of the original (1, 2, 3) is surrounded by 12 others, configured as a somewhat distorted icosahedron, as shown in Fig. 7. Thus each tetrahedron of the initial (1, 2, 3) is now shared by four icosahedra. This 26-sphere cluster is a slightly distorted form of the 26-atom γ-brass cluster. Another interesting subset of the tetrahedra in this structure is the triplet of distorted B-C helices twisted around each other (Fig. 8). One could go on adding more spheres, but the deviation of the tetrahedra from regularity (corresponding to lower sphere packing fraction) becomes severe.
Further extension of Boerdijk’s sphere packing, represented by tetrahedra whose vertices are the sphere centers. Every sphere of the original configuration (Fig. 5) is now the center of a 13-sphere cluster.
Configuration of three helically coiled B-C structures.
Nanotubes
When m + n is divisible by three, the THP of type (l, m, n) can be converted to a model for a net of equilateral hexagons with all vertices lying on a cylinder, simply by omitting one in three of the vertices. Figure 9 illustrates this for the case (4, 7, 11). The algorithm described in the fourth section for determining the metrical properties of the THPs is thus applicable to the structure of carbon nanotubes.
Nanotubes [8, 9] can be classified by a pairs of integers [M, N], corresponding to the numbers of helices of edge-connected hexagons that wind around the nanotube to left and right. The relation between the (m, n) of a THP and the [M, N] describing this subset of its vertices that corresponds to the atoms of a nanotube is
For example, starting with a (4, 7, 11), the formulas give (7, 11) → [6, 5]. This corresponds to the standard triplet [1, 5, 6]. That is, the THP (4, 7, 11) gives rise to a metrical model for the nanotube [1, 5, 6]. More specifically, since a reflection is involved in the coordinate resetting of the final step, (4, 7, 11) L → [1, 5, 6] R.
The “chair” and “zigzag” type nanotubes (Fig. 10) are given by
The [0, 10, 10] “zigzag type” nanotube and the [5, 5, 10] “chair type”.
The density of a carbon nanotube of a given structural type (l, m, n) is readily calculated. The type {n} polygonal helices have a rise per edge of \( \sqrt{3}\left(n/k\right) \) (using the approximation given by the CHL formula). The number density of vertices per unit advance along the cylinder axis is, therefore, \( k/n\sqrt{3} \). There are n type {n} helices. In the carbon nanotube model, one-third of them are hexagon centers, so the number of carbon atoms per unit length of the nanotube is \( 2k/3\sqrt{3} \). The C—C bond length B is the unit of length. Denoting the mass of a carbon atom by M, we get, for the mass per unit length of the nanotube,
where R is the radius out to an atom center—the average of internal and external radius. For example, taking M = 10−3 gm and B = 1.42 Å (from graphite), gives 2.52 × 10−14 gm/cm for the case (4, 7, 11), corresponding to the [1, 5, 6] nanotube.
Collagen and the Polytope {3, 3, 5}
The regular four-dimensional polytope {3, 3, 5} has 120 vertices, 1200 edges, 720 equilateral triangle faces, and 600 regular tetrahedral cells. Five cells surround each edge and 20 surround each vertex—forming a regular icosahedron [4, 5, 10].
Circuits of 30 face-sharing tetrahedra occur in {3, 3, 5}. They are each metrically identical to the Boerdijk–Coxeter structure in 3-D Euclidean space. One can select four of them forming a configuration, which, when deformed to fit into 3-D Euclidean space, can give a fairly accurate structure of the collagen molecule. Collagen consists of three left-handed helical polypeptide chains twisted around each other with a right-handed helical twist [6]. In the model of Sadoc and Rivier [1], derived from the corresponding structure in the polytope {3, 3, 5}, a central B-C structure (1, 2, 3) R is surrounded by three somewhat distorted B-C structures (1, 2, 3) R each sharing a type {3} helix with it. The polypeptide chains correspond to the left-handed type {2} helices of the three outer structures. Other tetrahedron edges represent hydrogen bonds.
We have already noticed the geometrical structure in the extension of the Boerdijk’s sphere packing (Fig. 8). The pictures displayed in Fig. 11 was obtained by projecting from {3, 3, 5} [11]. Observe that the structures differ in pitch; in Fig. 8, the central core B-C structure is undistorted, whereas in Fig. 11, a slight untwisting has been applied to conform to give the pitch observed in the collagen structure.
General view of the three outer B-C structures of the collagen model proposed by Sadoc and Rivier. The polypeptide chains correspond to the type {2} helices of these structures. Other edges and edges of the central undeformed B-C structure (omitted for clarity) correspond to hydrogen bonds.
Defects in THPS and Nanotubes
If a net on a curved surfaces is adjusted so that all (straight) edge lengths are equal, it is obvious that the curvature properties of the surface and the connectivity properties of the net will be intimately related. Although no general theory exists, various fascinating structures have been explored, corresponding to the decoration of curved surfaces by graphite sheets containing defects; five-rings among the hexagons correspond to regions of positive Gaussian curvature, while seven- and eight-rings correspond to regions of negative Gaussian curvature [12–15]. Of special interest are the triply periodic minimal surfaces, tiled by hexagons and octagons.
A well-known topological relation satisfied by a triangulation of a surface of genus g (Euler characteristic χ) is
where n i is the number of i-connected vertices. The same relation is satisfied by the dual configuration: a tiling of the surface, with n i i-gonal tiles. This purely topological relation is linked to curvature properties of the surface through the Gauss–Bonnet theorem,
where K is Gaussian curvature.
Thus, for example, a tiling of the sphere (g = 0) by hexagons and pentagons must contain exactly 12 pentagons—a topological fact demonstrated in nature by the structure of the fullerenes. An equilateral net of hexagons, heptagons, and octagons may be associated with surfaces of negative Gaussian curvature. Mackay and Terrones [12] demonstrated the decoration of the triply periodic minimal surfaces P and D surfaces (g = 3, per unit cell) by graphite sheets that contain 12 octagons per unit cell. In the present work, we have chosen to restrict attention to the Euclidean geometry of various structures. Mention must be made at this point, however, of the geometry of the hyperbolic plane as a valuable tool in the study of networks on surfaces of negative Gaussian curvature. For recent important results, the interested reader is referred to the work of Hyde and co-workers [16–18].
Observe that in a plane (or cylindrical) hexagonal lattice, a composite “5–7 defect” consisting of a five-coordinated vertex and a seven-coordinated vertex does not affect the genus. It gives rise to a dislocation of the lattice. Defects of this kind may be classified in terms of a pair of integers (p, q), which specify, in a hexagonal coordinate system associated with the lattice, the displacement of the five-vertex from the seven-vertex. The Burger’s vector associated with a 5–7 defect of type (p, q) is (p − q, p). The dual of the above statements concern nanotubes, which can have analogous 5–7 defects consisting of a five-ring and a seven-ring. The Burger’s vectors of a pair of such composite defects may cancel. This kind of defect has been discussed by Stone and Wales [19] in the context of fullerene structure.
The incorporation of five-rings and seven-rings (in equal numbers) into a nanotube can cause it tube to be bent, by producing regions of positive and negative Gaussian curvature (helically coiled nanotubes have been observed). The exact relationship between the location of five-rings and seven-rings, and the resulting bending effect, is a difficult problem, which we shall not enter into here. The aim of this section will be simply to demonstrate how two TPHs of different types can be joined through a region containing a (p, q) defect. In particular, the radius of a nanotube may be varied along the length of the tube, by the introduction of five-rings and seven-rings (in equal numbers).
Figure 12 shows a net for constructing a THP with a (2, 2) defect. The net is to be folded along the grid lines to bring the edges marked with the same letter together, as in making card models of Platonic or Archimedean polyhedra. The three points indicated by the black circles becomes a single seven-connected vertex. The point indicated by the white circle becomes a five-connected vertex. Observe that the lower half of the THP will be a (3, 5, 8)L, while the upper half is a (1, 5, 6)L. We may write this in the form
Figure 13 demonstrates similarly the case
A CHL or a THP of type (m, n) can be joined to one of type (m′, n′), through a region containing a (p, q) defect. We find that
for example, (p, q) = (1, 2), (m, n) = (2, 3). Then (m′, n′) = (1, 3). Therefore
The handedness changes because converting (1, 3) to the three-index symbol (1, 2, 3) satisfying the inequalities (2.1) involves a reflection. This case corresponds simply to two mirror-twinned B-C structures; the situation is illustrated in Fig. 14.
Net for the construction of a TPH with a type (2, 2) defect. Observe that the lower half gives rise to a (3, 5, 8)L; the upper half produces a (1, 5, 6)L.
Net for the construction of a “mirror twin” (2, 4): (2, 4, 6)L → (2, 4, 6) R.
A mirror twin of two B-C structures and the net for constructing a model of it. Observe the 5–7 defect of type (1, 2).
Miscellany
Any Euclidean transformation
is uniquely determined if the four image points of four given nonplanar points are given. Writing the position vectors, referred to a cartesian coordinate system, of four given points as the columns of a 3 × 3 matrix A, and their four images as the corresponding columns of a matrix B, the transformation is given by
where j denotes the row 111. The Eq. (16), from which the metrical parameters of the B-C structure were deduced, are obtained from this prescription. The method is, clearly, readily applicable to the generation of more general structures from a given subunit once the position and orientation of a contiguous subunit is chosen. The tiling of three-space by face-sharing polyhedra is a concept fundamental to the understanding of many complex material structures. Structures built from identical face-sharing polyhedral subunits are readily deduced from the prescription (30). A transformation S can be computed from two chosen congruent faces of a polyhedron. Repeated application of S will then produce a structure with helical, zigzag, or ring form according to the nature of S (some possibilities lead to steric hindrance). The purpose of this final section is simply to illustrate this by means of a few curious examples.
Two examples of helical structures built from polyhedral subunits are the “octahelix” and the “icosahelix” of Pearce [20]. Figure 15 indicates that the vertices of the octahelix are the midpoints of the edges of a B-C structure and Fig. 16 indicates that the vertices of the icosahelix are at golden mean positions on the edges of an octahelix. Other helical towers of octahedra, or of icosahedra, with different pitches, can be generated by choosing different orientation relationships for the initial pair of subunits, giving rise to different screw transformations S. Figure 17, for example, is another “octahelix,” with a steeper pitch than the Pearce octahelix and Fig. 18 is a ring of 12 octahedra slightly distorted icosahedra generated by a roto-reflection. The helix of interpenetrating icosahedra in Fig. 19 is generated from a screw transformation S that relates two pentagonal sections of the icosahedral subunit.
Pearce’s octahelix inscribed in a B-C structure.
Pearce’s icosahelix inscribed in an octahelix.
An octahelix with steeper pitch.
A ring of 12 (slightly distorted) octahedra, generated by a roto-reflection; and the 12 “inscribed” icosahedra.
A helical structure of interpenetrating icosahedra. Observe that every pair of consecutive icosahedra is a “mirror twin” with the mirror perpendicular to the fivefold axis.
A polygonal subunit for the generation of helical structures can be chosen to be a portion of the B-C structure. This corresponds to the systematic introduction of defects along the length of the TPH (1, 2, 3). The remarkable ring structure (Fig. 20) consisting of 96 tetrahedra was discovered by Antoine Walter [21]. The subunit is a portion of the B-C structure consisting of six tetrahedra. The easiest way to understand the structure is to consider the smaller subunit of three tetrahedra (Fig. 21). The mirror symmetry of this subunit implies that the two face medians marked on the figure intersect. A simple calculation gives the angle θ between them, cos θ = 53/54, θ~11°. A twofold rotation about one of them produces a set of six tetrahedra of a B-C structure. The product of the two twofold rotations is a rotation through about 22°, whose repeated action gives a ring of 32 of the six tetrahedron units, which does not quite close. A slight deformation increasing the angle θ to 360°/32 = 11¼° produces the 96-tetrahedron ring.
The ring of 96 tetrahedra discovered by Antoine Walter. The subunit is a sequence of six of the tetrahedra of a B-C structure.
Three tetrahedra. The ring of 96 tetrahedra is generated by twofold rotations about the face medians marked in the figure. Very slight deformation of the tetrahedra is necessary for exact closure of the ring, as explained in the text.
Conclusions
Nanotubes, protein helices, and the sphere packings investigated by Boerdijk, have this in common: their structures are underpinned by the Euclidean geometry of triangulated helical polyhedra. The geometrical properties of the THPs provide a simple introduction to these important structures and methods of computing their metrical and topological properties can be employed in the production of graphic representations.
References
Sadoc J. F.; Rivier, N. Eur. Phys. J. 1999, B12, 309.
Boerdijk, A. H. Philips Res. Rept. 1952, 7, 303.
Coxeter, H. S. M. Introduction to Geometry 1st edn.; Wiley: New York, 1961.
Coxeter, H. S. M. Regular Polytopes; Macmillan: New York, 1948 (Dover: 1973).
Coxeter, H. S. M. Can. Math. Bull. 1985, 28, 385.
Lehninger, L.; Nelson D. L.; Cox, M. M. Principles of Biochemistry; Worth: New York, 1993.
Buckminster Fuller, R. Synergetics; Macmillan: New York, 1975.
Iijima, S. Nature (London) 1991, 354, 56.
Tanaka, K.; Yamabe, T.; Fukui K., Eds., The Science and Technology of Carbon Nanotubes; Elsevier: New York, 2000.
Sadoc, J. F.; Mosseri, R. Frustration Géometrique; Eyroles: Paris, 1997; Geometrical Frustration; Cambridge University Press: Cambridge, 1999.
Lord, E. A.; Ranganathan, S. Euro. Phys. J. 2002, 15, 335.
Mackay, A. L.; Terrones, H. Phil. Trans. Roy. Soc. London A 1993, 343, 113.
Terrones, H.; Mackay, A. L. Chem. Phys. Lett. 1993, 207, 45.
Terrones, H.; Terrones, M. Fullerene Sci. Technol. 1996, 4, 517.
Terrones, H.; Terrones, M. Phys. Rev. B 1997, 55, 9969.
Hyde, S. T.; Andersson, S.; Blum, Z.; Lidin, S.; Larsson, K.; Landt, T.; Ninham, B. W. The Language of Shape; Elsevier Science: Amsterdam, 1997.
Hyde S. T.; Ramsden, S. In Mathematical Chemistry D. Bonchev and D. Rouvray, Eds.; Gordon and Breach, New York, 2000; Vol. 6, Chap. 2.
Hyde, S. T.; Oguey, C. Eur. Phys. J. 2000, B16, 613.
Stone, A. J.; Wales, D. J. Chem. Phys. Lett. 1986, 128, 501.
Pearce, P. Structure in Nature is a Strategy for Design; MIT Press: Cambridge, MA, 1978.
Walter, A. Hyperspace 2000, 9, 22.
Brakke, K. A. Exp. Math. 1992, 1, 141.
Acknowledgments
The figures were produced using Surface Evolver [22], which I have found to be very convenient for the rapid production of pictures of polyhedra, quite apart from its intended use for the study of the kinematics and dynamics of curved surfaces. Alan Mackay introduced me to this software and we have enjoyed exploring minimal surfaces together. Alan’s enthusiasm for geometrical problems of all kinds is infectious; I have gained a great deal from my association with him. S. Ranganathan’s friendly interest, support, and encouragement have also been invaluable. I also thank Anandh Subramaniam for helping me with Mathematica.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Lord, E.A. (2015). Helical Structures: The Geometry of Protein Helices and Nanotubes. In: Hargittai, I., Hargittai, B. (eds) Science of Crystal Structures. Springer, Cham. https://doi.org/10.1007/978-3-319-19827-9_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-19827-9_8
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-19826-2
Online ISBN: 978-3-319-19827-9
eBook Packages: Chemistry and Materials ScienceChemistry and Material Science (R0)