Waterfall Traffic Identification: Optimizing Classification Cascades

Abstract

The Internet transports data generated by programs which cause various phenomena in IP flows. By means of machine learning techniques, we can automatically discern between flows generated by different traffic sources and gain a more informed view of the Internet.

In this paper, we optimize Waterfall, a promising architecture for cascade traffic classification. We present a new heuristic approach to optimal design of cascade classifiers. On the example of Waterfall, we show how to determine the order of modules in a cascade so that the classification speed is maximized, while keeping the number of errors and unlabeled flows at minimum. We validate our method experimentally on 4 real traffic datasets, showing significant improvements over random cascades.

1 Introduction

Internet traffic classification is a well-known problem in computer networks. Since introduction of Peer-to-Peer (P2P) networking and encrypted protocols we have seen a rapid growth of classification methods that apply statistical analysis and machine learning to various characteristics of IP traffic, e.g. [1–3]. Survey papers list many existing methods grouped in various categories [4, 5], yet each year still brings new publications in this field. Some authors suggested connecting several methods in multi-classifier systems as a future trend in traffic classification [6, 7]. For example, in [8], the authors showed that classifier fusion can increase the overall classification accuracy. In [9], we proposed to apply the alternative of classifier selection instead, showing that cascade classification can successfully be applied to traffic classification. This paper builds on top of that.

In principle, cascade traffic classification works by connecting many classifiers in a single system that evaluates feature vectors in a sequential manner. Our research showed that by using just 3 simple modules working in a cascade, it is possible to classify over 50 % of IP flows using the first packet of a network connection. We also showed that by adding more modules one can reduce the total amount of CPU time required for system operation. However, the problem still largely unsolved is how to choose from a possible large pool of modules, and how to order them properly so that the classification performance is maximized. In this paper, we propose a solution to this problem.

The contribution of our paper is as follows:

• 1. We propose a new solution to the cascade optimization problem, tailored to traffic classification (Sect. 3).

• 2. We give a quick method for estimating performance of a Waterfall system (Sect. 3).

• 3. We experimentally validate our proposal on 4 real traffic datasets, demonstrating that our algorithm works and can bring significant improvements to system performance (Sect. 4).

The rest of the paper is organized as follows. In Sect. 2, we give background on the Waterfall architecture and on existing methods for building optimal cascade classifiers. In Sect. 3, we describe our contribution, which is validated experimentally in Sect. 4. Section 5 concludes the paper.

2 Background

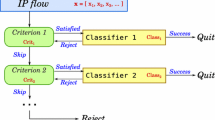
We introduced cascade traffic classification in [9]. Our Waterfall architecture integrates many different classifiers in a single “chain” of modules. The system sequentially evaluates module selection criteria and decides which modules to use for a given classification problem $\varvec{x}$. If a particular module is selected and provides a label for $\varvec{x}$, the algorithm finishes. Otherwise, the process advances to the next module. If there are no more modules, the flow is labeled as “Unknown”. The algorithm is illustrated in Fig. 1. We refer the reader to [9] for more details.

Fig. 1.

The Waterfall architecture. A flow enters the system and is sequentially examined by the modules. In case of no successful classification, it is rejected.

Cascade classification is a multi-classifier machine learning system, which follows the classifier selection approach [10]. Although presented in 1998 by Alpaydin and Kaynak [11], so far few authors considered the problem of optimal cascade configuration that would match the Waterfall architecture. In a 2006 paper [12], Chellapilla et al. propose a cascade optimization algorithm that only updates the rejection thresholds of the constituent classifiers. The authors apply an optimized depth first search to find the cascade that satisfies given constraints on time and accuracy. However, comparing with our work, the system does not optimize the module order. In another paper published in 2008 [13], Sherif proposes a greedy approach for building cascades: start with a generic solution and sequentially prepend a module that reduces CPU time. Comparing with our work, the approach does not evaluate all possible cascade configurations and thus can lead to suboptimal results.

In this paper, we propose a new solution to the cascade classification problem, which is better suited for traffic classification than [12, 13]. However, we assume no confidence levels on the classification outputs, thus we do not consider rejection thresholds as input values to the optimization problem. One can consider the same classifier parametrized with various thresholds as a set of separate modules available to build the cascade from.

3 Optimal Classification

Let us consider the problem of optimal cascade structure: we have n modules in set E that we want to use for cascade classification of IP flows in set F in an optimal way. In other words, we need to find a sequence of modules X that minimizes a cost function C:

$$\begin{aligned} E =&\; \lbrace 1, \dots \!, n \rbrace , \end{aligned}$$

(1)

$$\begin{aligned} X =&\; ( x_1, \dots \!, x_m ) \quad m \le n, \; x_i \in E, \; \forall _{i \ne j} \, x_i \ne x_j, \end{aligned}$$

(2)

$$\begin{aligned} C(X) =&\; f(t_X) + g(e_X) + h(u_X). \end{aligned}$$

(3)

The terms $t_X$, $e_X$, and $u_X$ respectively represent the total amount of CPU time used, the number of errors made, and the number of flows left unlabeled while classifying F with X. The terms f, g, and h are arbitrary real-valued functions. Because $m \le n$, some modules may be skipped in the optimal solution. Note that $u_X$ does not depend on the order of modules, because unrecognized flows always traverse till the end of the cascade.

3.1 Proposed Solution

To find the optimal cascade, we propose to quickly check all possible X. We propose an approximate method, because for an accurate method one would need to run the full classification process for each X, i.e. experimentally evaluate all permutations of all combinations in E. This would take S experiments, where

$$\begin{aligned} S = \sum _{i=1}^{n} \; \frac{n!}{(n - i)!}, \end{aligned}$$

(4)

which is impractical even for small n. On another hand, fully theoretical models of the cost function seem infeasible too, due to the complex nature of the cascade and module inter-dependencies.

Thus, we propose a heuristic solution to the cascade optimization problem. The algorithm has two evaluation stages:

• (A) Static: classify all flows in F using each module in E, and

• (B) Dynamic: find the X sequence that minimizes C(X).

A. Static Evaluation. In every step of stage A, we classify all flows in F using single module x, $x \in E$. We measure the average CPU time used for flow selection and classification: $t^{(x)}_s$ and $t^{(x)}_c$. We store each output flow in one of the three outcome sets, depending on the result: $F^{(x)}_S$, $F^{(x)}_O$, or $F^{(x)}_E$. These sets hold respectively the flows that were skipped, properly classified, and improperly classified. Let us also introduce $F^{(x)}_R$:

$$\begin{aligned} F^{(x)}_R = F \setminus \left( F^{(x)}_S \cup F^{(x)}_O \cup F^{(x)}_E\right) \!, \end{aligned}$$

(5)

the set of rejected flows. See Fig. 2 for an illustration of the module measurement procedure. As the result of every step, the performance of module x on F is fully characterized by a tuple of $P^{(x)}$:

$$\begin{aligned} P^{(x)} = \left( \,t^{(x)}_s, t^{(x)}_c, F^{(x)}_S, F^{(x)}_O, F^{(x)}_E\right) \!. \end{aligned}$$

(6)

Finally, after n steps of stage A, we obtain n tuples: the input to stage B.

Fig. 2.

Measuring performance of module $x \in E$

B. Dynamic Evaluation. Having all of the required experimental data, we can quickly estimate C(X) for arbitrary X. Because f, g, and h are used only for adjusting the cost function, we focus on their arguments: $t_X$, $e_X$, and $u_X$.

Let $X = (x_1, \dots \!, x_i, \dots \!, x_m)$ represent certain order and choice of modules, and $G_i$ represent the set of flows entering the module number i ($G_1 = F$). We estimate the cost factors using the following procedure:

$$\begin{aligned} t_X \approx&\; \sum _{i=1}^{m} \; |G_i| \cdot t^{(x_i)}_s + \left| G_i \setminus F^{(x_i)}_S\right| \cdot t^{(x_i)}_c, \end{aligned}$$

(7)

$$\begin{aligned} e_X =&\; \sum _{i=1}^{m} \; \left| G_i \cap F^{(x_i)}_E\right| \!, \end{aligned}$$

(8)

$$\begin{aligned} u_X =&\; |G_{m+1}|, \end{aligned}$$

(9)

where

$$\begin{aligned} G_{i+1} =&\; G_i{\setminus }\left( F^{(x_i)}_O \cup F^{(x_i)}_E\right) \quad i \le m. \end{aligned}$$

(10)

The difference operation in Eq. (10) is crucial, because we need to remove the flows that were classified in the previous step. In stage A, our algorithm evaluates static performance of every module, but in stage B we need to simulate cascade operation. The difference operator in Eq. (10) connects the static cost factors ($t_X, e_X, u_X$) with the dynamic effects of cascade classification.

Module performance depends on its position in the cascade because preceding modules alter the distribution of traffic classes in the flows conveyed onward. For example, a module designed for P2P traffic running before a port-based classifier can improve its accuracy, by removing the flows that run on non-standard ports or abuse the traditional port assignments.

3.2 Discussion

In our optimization algorithm we simplified the original problem to n experiments and several operations on flow sets. We can speed up the search for the best X because the algorithm is additive:

$$\begin{aligned} C(X + x_i) = C(X) + C(x_i). \end{aligned}$$

(11)

Thus, we can apply the branch and bound algorithm [14].

Note that the results depend on F: the optimal cascade depends on the protocols represented in the traffic dataset, and on the ground-truth labels. The presented method cannot provide the ultimate solution that would be optimal for every network, but it can optimize a specific cascade system working in a specific network. In other words, it can reduce the amount of required CPU power, the number of errors, and the number of unlabeled flows, given a set of modules and a set of flows. We evaluate this issue in Sect. 4 (Table 2).

We assume that the flows are independent of each other, i.e. labeling a particular flow does not require information on any other flow. In case such information is needed, e.g. DNS domain names for the dnsclass module, it should be extracted before the classification process starts. Thus, traffic analysis and flow classification must be separated to uphold this assumption. We successfully implemented such systems for our DNS-Class [15] and Mutrics [9] classifiers.

In the next section, we experimentally validate our method and show that it perfectly predicts $e_X$ and $u_X$, and approximates $t_X$ properly (see Fig. 3). The simulated cost accurately follows the real cost, hence we argue that our proposal is valid and can be used in practice. In the next section, we analyze the trade-offs between speed, accuracy, and ratio of labeled flows (Fig. 4), but the final choice of the cost function should depend on the purpose of the classification system.

4 Experimental Validation

In this section, we use real traffic datasets to demonstrate that our method is effective and gives valid results. We ran 4 experiments:

• 1. Comparing simulated $t_X$, $e_X$, and $u_X$ to real values, which proves validity of Eqs. (7)–(9);

• 2. Analyzing the effect of f, g, and h on the results, which proves that parameters influence the optimization process properly;

• 3. Optimizing the cascade on one dataset and testing it on another dataset, which verifies robustness in time and space;

• 4. Comparing optimized cascades to random configurations, which demonstrates that our work is meaningful.

We used 4 real traffic datasets, as presented in Table 1. Datasets Asnet1 and Asnet2 were collected at the same Polish ISP company serving ${<}500$ users, with an 8 month time gap. Dataset IITiS1 was collected at an academic network serving ${<}50$ users, at the same time as Asnet1. Dataset Unibs1 was also collected at an academic network (University of Brescia¹), but a few years earlier and without packet payloads. We established ground-truth using Deep Packet Inspection (DPI) and trained the modules using 60 % of flows chosen randomly – as described in our original work [9]. The remaining flows were used for evaluating our proposal. We used the following Waterfall modules: dstip, dnsclass [15], npkts, port, and portsize. We handled Unibs1 differently, because the dataset has no packet payloads and has all IP addresses anonimized: we used the stats module instead of dnsclass.

Table 1. Datasets used for experimental validation

Experiment 1. In the first experiment, we compare simulated cost factors with the reality. We randomly selected 100 000 flows from each dataset and ran the static evaluation on them. Next, we generated 100 random cascades, and for each cascade we ran real classification and the dynamic evaluation stage of our optimization algorithm. As a result, we obtained pairs of real and estimated values of $t_X$, $e_X$, and $u_X$ for same X values. The results for $t_X$ are presented in Fig. 3. For $e_X$ and $u_X$ we did not observe a single error, i.e. our method perfectly predicted the real values. For CPU time estimations, we see a high correlation of 0.95, with little under-estimation of the real value. For all datasets, the estimation error was below 20 % for majority of evaluated cascades (with respect to the real value). The error was above 50 % only for 5 % of evaluated cascades. We conclude that in general our method properly estimates the cost factors and we can use it to simulate different cascade configurations.

Fig. 3.

Experiment 1. Estimated classification time vs real classification time. Dashed line shows least-squares approximation, the correlation coefficient is 0.95.

Experiment 2. In our second experiment, we want to show the effect of tuning the cost function for different goals: minimizing the computation time, minimizing errors, and labeling as many flows as possible. We chose the following cost function:

$$\begin{aligned} C(X) = f(t_X) + g(e_X) + h(u_X) = t_X^{a} + e_X^{b} + u_X^{c} . \end{aligned}$$

(12)

Next, we separately varied the a, b, c exponents in range of 0–10, and observed the performance of the optimal cascade found by applying such cost function. We ran the experiment for Asnet1, Asnet2, and IITiS1. In Fig. 4, we present the results: dependence of CPU time, number of errors, number of unlabeled flows, and module count on $f(t_X)$, $g(e_X)$, and $h(u_X)$. As expected, higher f exponent leads to faster classification, with fewer number of modules in the cascade (more unclassified flows) and usually less errors. Optimizing for accuracy leads to reduction of errors and CPU time, at the cost of higher number of flows left without a label. Note that we observed more errors than in the case of time optimization – probably because the number of errors was low, thus the g exponent had less impact on such values. Finally, if we choose to classify as much traffic as possible, the system will use all available modules, at the cost of increasing the CPU time. We conclude that our proposal works, i.e. by varying the parameters we optimize the cascade for different goals.

Fig. 4.

Experiment 2. Optimizing the cascade for different goals: best classification time (a exponent), minimal number of errors (b exponent), and the lowest number of unlabeled flows (c exponent): the plot shows the averages for 3 datasets.

Experiment 3. In the third experiment, we verify if the result of optimization is stable in time and space, i.e. if the optimal cascade stays optimal with time and changes of the network. We ran optimization for 3 datasets (all flows in Asnet1, Asnet2, and IITiS1), obtaining different cascade configuration for each dataset. Next, we evaluated these configurations on the other datasets, i.e. Asnet1 on Asnet2 and IITiS1, etc. We measured the increase in the value of the cost function C(X) and compared it with the original value. Table 2 presents the results. We see that our proposal yielded results that are stable in time: the cascades found for Asnet1 and Asnet2, which are 8 months apart, are very similar and can be exchanged with little decrease in performance. However, the cascades found for Asnet1 and Asnet2 gave 7 % and 8 % decrease in performance compared with IITiS1. We conclude that optimization results are quite specific to the network, but also stable in time, for the evaluated datasets.

Table 2. Experiment 3. Optimization stability: increase in the cost C(X), depending on the reference dataset used for determining the optimal cascade.

Experiment 4. In our last experiment, we compare our proposal with random choice of the modules, i.e. a situation in which we have a possibly large number of “black box” modules to build the cascade from. For example, we could have a large number of npkts modules trained on different flow samples, and with different parameters. We used the data collected in Experiment 1 (100 000 flows and 100 random cascades for each of 4 datasets) and calculated the average $t_X$, $e_X$, and $u_X$ values. Next, we run our optimization algorithm on the same 100 000 flows for each dataset and measured the improvements with respect to the average performance of random cascades. We used the cost function given in Eq. (12), for $a=0.95$, $b=1.75$, and $c=1.20$. In Table 3, we present obtained results: in every case, our algorithm optimized the classification system to work better, significantly reducing the amount of CPU time required for operation. Thus, we conclude that our work is meaningful and can help a network administrator to configure a cascade classification system properly.

Table 3. Experiment 4. Average improvements compared to random cascade selection. We evaluated 100 random cascades on 100 000 random flows for each of 4 datasets.

5 Conclusions

In this paper, we presented a new method for optimizing cascade classifiers, on the example of the Waterfall traffic classification architecture. The method evaluates the constituent classifiers and quickly simulates cascade operation in every possible configuration. By searching for the cascade that minimizes a custom cost function, the method finds the best configuration for given parameters, which corresponds to minimizing required CPU time, number of errors, and number of unclassified IP flows. We experimentally validated our proposal on 4 real traffic datasets, demonstrating method validity, effectiveness, stability, and improvements with respect to random choices.

Not only does our proposal apply to traffic classification, but it can be also applied in the field of machine learning (for multi-classifier systems). However, our approach does not consider rejection thresholds of the classifiers, which is a certain limitation for application in other fields. We release an open source implementation of our proposal as an extension to the Mutrics classifier².