Flexible and Dynamic Modeling of Dependencies via Copulas

Abstract

In this chapter we first review recent developments in the use of copulas for studying dependence structures between variables. We discuss and illustrate the concepts of unconditional and conditional copulas and association measures, in a bivariate setting. Statistical inference for conditional and unconditional copulas is discussed, in various modeling settings. Modeling the dynamics in a dependence structure between time series is of particular interest. For this we present a semiparametric approach using local polynomial approximation for the dynamic time parameter function. Throughout the chapter we provide some illustrative examples. The use of the proposed dynamical modeling approach is demonstrated in the analysis and forecast of wind speed data.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

When the aim is to model the dependence structure between d random variables, denoted by $Y _{1},\ldots,Y _{d}$, we can distinguish between several approaches. In a regression approach, one is interested in how a variable of primary interest, say Y _d , and called the response variable, is influenced on average by $Y _{1},\ldots,Y _{d-1}$, the covariates. A general regression model is of the form

$$\displaystyle{Y _{d} = g(Y _{1},\ldots,Y _{d-1})+\varepsilon \;,}$$

where $g: \mathbb{R}^{d-1} \rightarrow \mathbb{R}$ is a (d − 1)-dimensional function of the covariates, and where the error term ɛ has conditional mean $E\left (\varepsilon \vert Y _{1},\ldots,Y _{d-1}\right )$ equal to zero. Consequently, the conditional mean function of Y _d given the covariates $Y _{1} = y_{1},\ldots,Y _{d-1} = y_{d-1}$, with $(y_{1},\ldots,y_{d-1}) \in \mathbb{R}^{d-1}$ equals $E\left (Y _{d}\vert Y _{1} = y_{1},\ldots,Y _{d-1} = y_{d-1}\right ) = g(y_{1},\ldots,y_{d-1})$. For the mean regression function g one can either assume some known parametric form, or leaving its form fully unspecified (and to be determined from the data), in respectively parametric and nonparametric regression. An alternative is a semiparametric modeling in which the influence of some covariates might be modeled parametrically, whereas the influence on average of other covariates on Y _d might be described via an unknown function (a nonparametric functional part). In a general approach, the dependencies between the various components in the random vector $(Y _{1},\ldots,Y _{d})$ are fully described by the joint distribution of $(Y _{1},\ldots,Y _{d})$, i.e. by the d-variate cumulative distribution function of $(Y _{1},\ldots,Y _{d})$ denoted by $P\{Y _{1} \leq y_{1},\ldots,Y _{d} \leq y_{d}\}$. From this one can calculate for example the conditional mean function $E\left (Y _{d}\vert Y _{1} = y_{1},\ldots,Y _{d-1} = y_{d-1}\right )$.

Denote the marginal cumulative distribution function of Y _j , by F _j , for $j = 1,\ldots,d$. According to Sklar’s Theorem [34] there exists a copula function C defined on [0, 1]^d such that

$$\displaystyle{P\{Y _{1} \leq y_{1},\ldots,Y _{d} \leq y_{d}\} = C\left (F_{1}(y_{1}),\ldots,F_{d}(y_{d})\right )\qquad \forall (y_{1},\ldots,y_{d}) \in \mathbb{R}^{d}\;.}$$

In case the marginal distribution functions, $F_{1},\ldots,F_{d}$, are continuous, the copula function C is unique. See [28]. The copula function couples the joint distribution function to its univariate margins $F_{1},\ldots,F_{d}$. The dependence structure between the components of $(Y _{1},\ldots,Y _{d})$ is fully characterized by the copula function C.

Note that a copula function is nothing but a joint distribution function on [0, 1]^d with uniform margins. Based on a joint distribution function, we can study conditional distribution functions derived from it, as well as characteristics of these (e.g. moments, medians, …). Translated into the copula context this leads to various concepts for describing dependence structures.

The aim of this chapter is to first provide a review of copula modeling concepts, and statistical inference for them in various settings (parametric, semiparametric and nonparametric). This is done in a setting of independent data in Sects. 2 and 3. For simplicity of presentation, we restrict throughout the chapter to the setting of bivariate copulas (the case d = 2). In Sect. 4 we turn to the dynamical modeling of the dependence between time series, extending existing approaches of local polynomial fitting to this setting. We conclude the chapter by an illustration of the use of the method in a practical forecasting application in Sect. 5.

2 Global Dependencies and Unconditional Copulas

2.1 Population Concepts

Consider two random variables Y ₁ and Y ₂, with joint distribution function H, and continuous marginal distributions functions F ₁ and F ₂ respectively. There then exists a (unique) bivariate copula function C, such that

$$\displaystyle{ H(y_{1},y_{2}) = P\{Y _{1} \leq y_{1},Y _{2} \leq y_{2}\} = C\left (F_{1}(y_{1}),F_{2}(y_{2})\right )\qquad (y_{1},y_{2}) \in \mathbb{R}^{2}\;. }$$

(1)

It is common practice to measure the strength of the relationship between Y ₁ and Y ₂ via a so-called association measure. There are various statistical association measures. Among the most well-known are: Pearson’s correlation coefficient, Kendall’s tau, Spearman’s rho, Gini’s coefficient, and Blomqvist’s beta. See [4, 16, 17, 27] and [25], among others. Pearson’s correlation coefficient, defined as $\mbox{ Cov}(Y _{1},Y _{2})/\sqrt{\mbox{ Var} (Y _{1 } )\,\mbox{ Var} (Y _{2 } )}$, only exists if the second order moments of both margins Y ₁ and Y ₂, exist, and equals ± 1 in case Y ₂ is a (prefect) linear transform of Y ₁. Gini’s coefficient and Blomqvist’s beta, are often used in economical sciences (for example, as a measure of inequality of income or wealth). Several well-known association measures can be expressed as functionals of the copula function. Denote by (Y ₁′, Y ₂′) and (Y ₁″, Y ₂″), two independent copies of (Y ₁, Y ₂). For the following association measures we give their definitions followed by an expression in terms of the copula function (for some measures alternative expressions in terms of C exist).

• Kendall’s tau:

  $$\displaystyle\begin{array}{rcl} \tau _{Y _{1},Y _{2}}& =& P\left \{(Y _{1} - Y _{1}')(Y _{2} - Y _{2}') > 0\right \} - P\left \{(Y _{1} - Y _{1}')(Y _{2} - Y _{2}') < 0\right \} \\ & =& 4\int \!\!\!\int _{[0,1]^{2}}C(u_{1},u_{2})dC(u_{1},u_{2}) - 1\;. {}\end{array}$$

  (2)

• Spearman’s rho:

  $$\displaystyle\begin{array}{rcl} \rho _{Y _{1},Y _{2}}& =& 3\left [P\left \{(Y _{1} - Y _{1}')(Y _{2} - Y _{2}'') > 0\right \} - P\left \{(Y _{1} - Y _{1}')(Y _{2} - Y _{2}'') < 0\right \}\right ] {}\\ & =& 12\int \!\!\!\int _{[0,1]^{2}}C(u_{1},u_{2})du_{1}du_{2} - 3. {}\\ \end{array}$$

• Gini’s coefficient:

  $$\displaystyle\begin{array}{rcl} \gamma _{Y _{1},Y _{2}}& =& 2E\left (\left \vert F_{1}(Y _{1}) + F_{2}(Y _{2}) - 1\right \vert -\left \vert F_{1}(Y _{1}) - F_{2}(Y _{2})\right \vert \right ) {}\\ & =& 2\int \!\!\!\int _{[0,1]^{2}}\left (\vert u_{1} + u_{2} - 1\vert -\vert u_{1} - u_{2}\vert \right )dC(u_{1},u_{2}). {}\\ \end{array}$$

• Blomqvist’s beta:

  $$\displaystyle{\beta _{Y _{1},Y _{2}} = 2P\left \{(Y _{1} - F_{1}^{-1}(0.5))(Y _{ 2} - F_{2}^{-1}(0.5)) > 0\right \} - 1 = 4C\left (\frac{1} {2}, \frac{1} {2}\right ) - 1\;,}$$

  where F _j ⁻¹(0. 5) is the median of the margin F _j , for j = 1, 2.

See [28] for an overview of association measures, their basic properties, and their interrelationships.

When talking about unraveling the dependence structure between Y ₁ and Y ₂, it is transparent from (1) that informations about the copula function C as well as about the two margins F ₁ and F ₂ are of importance. We illustrate the impact of these elements with some examples in Sect. 2.2.

2.2 Illustration: Examples

The copula function and the marginal distributions together determine the joint distribution function (see (1)), and consequently all of the population characteristics. This is reflected in, among others, the typical observed scatter plots and the different values for the association measures.

As an illustration we consider the following examples:

Example 1.

$$\displaystyle\begin{array}{rcl} & & Y _{1} \sim N(0,4),\qquad Y _{2} \sim \mbox{ Exp}(2) {}\\ & & C(u_{1},u_{2}) = \left (\max \left (u_{1}^{-\theta } + u_{ 2}^{-\theta }- 1,0\right )\right )^{-\frac{1} {\theta } },\qquad \theta = 1\;, {}\\ \end{array}$$

where the copula belongs to the Clayton copula family.

Example 2.

$$\displaystyle{Y _{1} \sim \mbox{ Exp}(2),\qquad Y _{2} \sim \mbox{ Beta}(1,4)}$$

and with the same copula as in Example 1.

Example 3.

$$\displaystyle\begin{array}{rcl} & & Y _{1} \sim \mbox{ Student}(5,3),\qquad Y _{2} \sim \mbox{ Ex}(0.2) {}\\ & & C(u_{1},u_{2}) =\exp \left (-\left ((-\log u_{1})^{\theta } + (-\log u_{2})^{\theta }\right )^{\frac{1} {\theta } }\right ),\qquad \theta = 3\;, {}\\ \end{array}$$

where Student(ν, μ) is a noncentral Student distribution with ν degrees of freedom and noncentrality parameter μ, and where the copula belongs to the Gumbel copula family.

Example 4.

$$\displaystyle{Y _{1} \sim \mbox{ Exp}(2),\qquad Y _{2} \sim \mbox{ Beta}(1,4)}$$

and the same copula as in Example 3.

In Fig. 1 we present a typical sample $((Y _{11},Y _{21}),\ldots,(Y _{1n},Y _{2n}))$ from (Y ₁, Y ₂) (with n the sample size) from the above models (left column of pictures) together with their pseudo-observations, defined as (F ₁(Y _1i ), F ₂(Y _2i )), for i = 1, …, n, (right column of pictures). Due to the probability integral transformation, the pseudo-observations F _j (Y _ji ) are uniformly distributed (for each j = 1, 2). For Examples 1 and 2 the marginal distribution functions are different, but the dependence structure (the copula) is the same. In the left panels of rows one and two of Fig. 1 we depict scatter plots based on random samples of sizes 700 and 400 from, respectively, Examples 1 and 2. The scatter plots look quite different for the samples from the two models, but notice the similarity between the plots for the pseudo-observations (right panels). We can observe a mild positive dependence everywhere with a higher concentration in the lower tails (the lower left corner of the plots). In Example 3, both the margins and the copula are different, and the scatter plots based on a sample of size n = 700 from that model looks very different from the previous examples. Here, there is clearly more positive dependence visible, and we also notice heavier right tail characteristics. When comparing the plots for samples from Examples 3 and 4 (rows three and four in Fig. 1) we can observe similarities in the scatter plots of the pseudo-observations (the right panels), due to the fact that these examples share the same underlying copula. Furthermore, looking at scatter plots of typical observations from Examples 2 and 4, we can see the impact of changing a copula while keeping the same marginal distributions.

Fig. 1

Typical samples for Examples 1–4 (top row to bottom row); left columns: scatter plot of the observations, right columns: scatter plots of the pseudo-observations

In Table 1 we present the values of some association measures for the four examples. Note the equality of the measures for Examples 1 and 2 on the one hand, and for Examples 3 and 4, on the other hand, since these examples share the same copula (i.e. have the same dependence structure). The values of the association measures only depend on the underlying copula function and not on the marginal distributions.

Table 1 Association measures for Examples 1–4

2.3 Statistical Inference

Suppose now that $((Y _{11},Y _{21}),\ldots,(Y _{1n},Y _{2n}))$ is a sample of size n of independent observations from (Y ₁, Y ₂), and the interest is in estimating the copula function in (1). Once an estimator for the copula function is available, the way is open to obtain estimates for association measures that can be expressed as functionals of the copula, as those for example listed in Sect. 2.1.

According to available information on either the copula and/or the margins we distinguish between different situations in the modeling aspects. In the fully parametric setting the copula function is assumed to be known, up to some parameters, and the same for the distribution of the margins. Other settings are listed in Table 2. We briefly review statistical inference under each of these settings.

Table 2 Situations for statistical inference

2.3.1 Fully Parametric Approach

In a fully parametric approach one starts by assuming a specific parametric model for the copula function as well as for the margins. More formally, suppose that the copula C(⋅ , ⋅ ) = C(⋅ , ⋅ ; θ _C ), and that F _j (⋅ ) = F(⋅ ; θ _j ), for $j = 1,2$, where $\boldsymbol{\theta }_{C}$, $\boldsymbol{\theta }_{j}$, for j = 1, 2 are the respective parameter vectors, taking values in parameter spaces $\boldsymbol{\varTheta }_{C}$, $\boldsymbol{\varTheta }_{1}$ and $\boldsymbol{\varTheta }_{2}$ respectively. These parameters spaces can have nonempty intersections, in other words, the parameter vectors $\boldsymbol{\theta }_{C}$ and $\boldsymbol{\theta }_{j}$ can have common elements.

Assume for simplicity that the density of the copula function exists, i.e. the second order partial derivative of the copula function exists

$$\displaystyle{c(u_{1},u_{2};\boldsymbol{\theta }_{C}) = \frac{\partial ^{2}C(u_{1},u_{2};\boldsymbol{\theta }_{C})} {\partial u_{1}\partial u_{2}} \qquad \forall (u_{1},u_{2}) \in [0,1]^{2}\;.}$$

If in addition the corresponding densities f _j of F _j , for j = 1, 2, exist, then the joint density of (Y ₁, Y ₂) is given by (see (1))

$$\displaystyle{h(y_{1},y_{2}) = c\left (F_{1}(y_{1}),F_{2}(y_{2})\right )\,f_{1}(y_{1})f_{2}(y_{2})\qquad \forall (y_{1},y_{2}) \in \mathbb{R}^{2}\;.}$$

Keeping this in mind, the logarithm of the likelihood function then equals

$$\displaystyle{ \ell_{n}(\boldsymbol{\theta }_{1},\boldsymbol{\theta }_{2},\boldsymbol{\theta }_{C}) =\sum _{ i=1}^{n}\log \left (c(F_{ 1}(Y _{1i};\boldsymbol{\theta }_{1}),F_{2}(Y _{2i};\boldsymbol{\theta }_{2});\boldsymbol{\theta }_{C})\,f_{1}(Y _{1i};\boldsymbol{\theta }_{1})f_{1}(Y _{2i};\boldsymbol{\theta }_{2})\right )\;, }$$

(3)

which needs to be maximized with respect to $(\boldsymbol{\theta }_{1},\boldsymbol{\theta }_{2},\boldsymbol{\theta }_{C})$. Denote this maximizer by $(\hat{\boldsymbol{\theta }}_{1},\hat{\boldsymbol{\theta }}_{2},\hat{\boldsymbol{\theta }}_{C})$.

An estimator for, for example, the associated Kendall’s tau is then obtained via (2)

$$\displaystyle{\hat{\tau }_{Y _{1},Y _{2}} = 4\int \!\!\!\int _{[0,1]^{2}}C(u_{1},u_{2};\hat{\boldsymbol{\theta }}_{C})dC(u_{1},u_{2};\hat{\boldsymbol{\theta }}_{C}) - 1\;.}$$

2.3.2 Semiparametric Approach

Suppose now that the margins F ₁ and F ₂ cannot be parametrized, but are fully unknown. For the copula function, on the contrary, we still believe that a parametric model $C(\cdot,\cdot;\boldsymbol{\theta }_{C})$ is a reasonable assumption. In this case, we thus need to estimate the margins from the available data. The log-likelihood in (3), where the margins F ₁ and F ₂ are unknown, is replaced by the pseudo log-likelihood

$$\displaystyle{ \ell_{n}(\theta _{C}) =\sum _{ i=1}^{n}\log \left (c(F_{ 1n}(Y _{1i}),F_{2n}(Y _{2i});\theta _{C})\right )\;, }$$

(4)

where the unknown margins F ₁ and F ₂ are replaced by the estimates

$$\displaystyle{F_{1n}(y_{1}) = \frac{1} {n + 1}\sum _{i=1}^{n}I\{Y _{ 1i} \leq y_{1}\}\qquad F_{2n}(y_{2}) = \frac{1} {n + 1}\sum _{i=1}^{n}I\{Y _{ 2i} \leq y_{2}\}\;,}$$

with I{y ∈ A} the indicator function on a set A, i.e. I{y ∈ A} = 1, if y ∈ A and I{y ∈ A} = 0, if $y\notin A$. In the empirical estimates, it is recommended to use the modified factor $(n + 1)^{-1}$ instead of the usual factor n ⁻¹, because by using $(n + 1)^{-1}$ the values F _jn (Y _ji ) are in the set $\{ \frac{1} {n+1},\ldots, \frac{n} {n+1}\}$ instead of in the set $\{ \frac{1} {n},\ldots, \frac{n-1} {n},1\}$, and hence by using this modified factor, one stays away from both boundary points, 0 as well as 1. Note that this modification has no effect on the (asymptotic) properties of the resulting estimates. See, for example, [15].

The pseudo log-likelihood estimate $\hat{\boldsymbol{\theta }}_{C}$ of θ _C is then obtained by maximizing the pseudo log-likelihood in (4) with respect to $\boldsymbol{\theta }_{C}$.

See [33] for a study on semiparametric efficient estimation in case of Gaussian copulas with unknown margins.

2.3.3 Fully Nonparametric Approach

We now turn to the fully nonparametric approach where one can neither for C nor for the margins (F ₁ and F ₂) propose an appropriate parametric model. Hence C, F ₁ and F ₂ are fully unknown.

Nonparametric estimation of a copula goes back to the early seventies. In the paper [10] the empirical copula estimator was introduced and studied. The basic idea behind this estimator is very simple. As can be seen from (1), C(⋅ , ⋅ ) is in fact nothing else but the joint cumulative distribution function after the margins have been transformed, via the probability integral transformation

$$\displaystyle{U_{1} = F_{1}(Y _{1})\qquad \mbox{ and}\qquad U_{2} = F_{2}(Y _{2})\;.}$$

In other words, C(⋅ , ⋅ ) is the joint cumulative distribution function of (U ₁, U ₂). If independent observations ((U ₁₁, U ₂₁), ⋯ , (U _1n , U _2n )) from (U ₁, U ₂) would be available, then the cumulative distribution function could be estimated via the usual bivariate empirical distribution function $\frac{1} {n}\sum _{i=1}^{n}I\left \{U_{ 1i} \leq u_{1},U_{2i} \leq u_{2}\right \}$. Since we have no observations from F ₁(Y ₁) and F ₂(Y ₂) we simply replace the unobserved U _ji  = F _j (Y _ji ) by a pseudo-observation, its ‘slightly modified’ rank F _nj (Y _ji ) in the original sample, and obtain the empirical copula estimator

$$\displaystyle{ C_{n}(u_{1},u_{2}) = \frac{1} {n}\sum _{i=1}^{n}I\left \{\tilde{U}_{ 1i} \leq u_{1},\tilde{U}_{2i} \leq u_{2}\right \}\qquad \quad \tilde{U}_{1i} = F_{1n}(Y _{1i})\quad \tilde{U}_{2i} = F_{2n}(Y _{2i})\;. }$$

(5)

This estimator was also studied further in [14] and [32], among others.

Obviously, the estimator in (5) is a step function, which might not be very desirable, when the function C(⋅ , ⋅ ) is continuous or even differentiable.

Nonparametric estimation methods that lead to smooth estimators for the copula C have been derived. Among these are kernel estimators. See, for example, [6, 18] and [29]. Kernel estimators of the copula C are essentially obtained by replacing the non-smooth indicator function $I\{\tilde{U}_{1i} \leq u_{1},\tilde{U}_{2i} \leq u_{2}\} = I\{\tilde{U}_{1i} \leq u_{1}\}\,I\{\tilde{U}_{2i} \leq u_{2}\}$ in (5) by a smooth kernel function. The non-smooth function $I\{\tilde{U}_{ji} \leq u_{j}\}$ is replaced by the smooth function $K\left (\frac{u_{j}-\tilde{U}_{ji}} {h_{n}} \right )$, where $K(y) =\int _{ -1}^{y}k(t)dt$ is the kernel distribution function associated with the kernel k, a symmetric density function, with support the interval [−1, 1], and h _n  > 0 is a bandwidth parameter. The bandwidth parameter determines the size of the neighbourhood in which the jump in the indicator function is ‘smoothed out’. An example of a kernel function k is the Epanechnikov kernel $k(x) = \frac{3} {4}(1 - x^{2})I\{\vert x\vert \leq 1\}$. As an illustration we depict in Fig. 2 the indicator function I{0. 6 ≤ u} as well as a smooth version of it, namely $K\left (\frac{u-0.6} {h_{n}} \right )$, with K based on the Epanechnikov kernel, for two different values of the bandwidth h _n . The larger the bandwidth, the larger the neighbourhood over which the jump is ‘smeared out’.

Fig. 2

The indicator function I{0. 6 ≤ u} and its smooth version $K\left (\frac{u-0.6} {h_{n}} \right )$, using the Epanechnikov kernel, and bandwidths h _n  = 0. 04 (dashed-dotted curve) and h _n  = 0. 20 (dashed curve)

Such a simple replacement of the indicator part by a smooth part, leads to the kernel estimator

$$\displaystyle{ \frac{1} {n}\sum _{i=1}^{n}K\left (\frac{u_{1} -\tilde{ U}_{1i}} {h_{n}} \right )\,K\left (\frac{u_{2} -\tilde{ U}_{2i}} {h_{n}} \right )\;.}$$

Since the copula C is defined on the interval [0, 1]² (a compact support) special attention however is needed to obtain a kernel estimator that shows the same nice asymptotic properties at the boundaries of [0, 1]² as in the interior of that support. The aim is to obtain kernel estimators for which the convergence rate is the same on the interior of the square [0, 1]² as well as on the edges of it. This can be done for example, by using a reflection type of method, which consists of reflecting each pseudo-observation $(\tilde{U}_{1i},\tilde{U}_{2i})$ with respect to all four corner points, and all four edges of the interval [0, 1]², resulting into an augmented data set of size 9n, from which the kernel estimator is defined. See Fig. 3 for an illustration of a data point and the eight points resulting from reflections of the given point with respect to all corners and edges of the unit square [0, 1]².

Fig. 3

A data point (indicated by a “•” in the unit square), and the reflected points (indicated by a “•”) with respect to all corners (see the dashed lines) and edges (see the dotted lines) of the unit square

This leads to the kernel Mirror-Reflection type estimator introduced and studied in [18]:

$$\displaystyle\begin{array}{rcl} \hat{C}_{n}^{\mbox{ MR}}(u_{ 1},u_{2})& =& \frac{1} {n}\sum _{i=1}^{n}\sum _{ \ell=1}^{9}\left [K\left (\frac{u_{1} -\tilde{ U}_{1i}^{(\ell)}} {h_{n}} \right ) - K\left (\frac{-\tilde{U}_{1i}^{(\ell)}} {h_{n}} \right )\right ] {}\\ & & \qquad \qquad \times \left [K\left (\frac{u_{2} -\tilde{ U}_{2i}^{(\ell)}} {h_{n}} \right ) - K\left (\frac{-\tilde{U}_{2i}^{(\ell)}} {h_{n}} \right )\right ], {}\\ \end{array}$$

where

$$\displaystyle\begin{array}{rcl} & & \{(\tilde{U}_{1i}^{(\ell)},\tilde{U}_{ 2i}^{(\ell)}),\;i = 1,\ldots,n,\;\ell= 1,\ldots,9\} {}\\ & & =\{ (\pm \tilde{U}_{1i},\pm \tilde{U}_{2i}),(\pm \tilde{U}_{1i},2 -\tilde{ U}_{2i}),(2 -\tilde{ U}_{1i},\pm \tilde{U}_{2i}),(2 -\tilde{ U}_{1i},2 -\tilde{ U}_{2i}),\;i = 1,\ldots,n\}.{}\\ \end{array}$$

and K is the integral of the considered kernel k, as mentioned above.

An alternative approach to deal with the boundary issue is by using local linear fitting, and its implicit boundary kernel. This was done by [6], and resulted in the kernel Local Linear estimator:

$$\displaystyle{\hat{C}_{n}^{\mbox{ LL}}(u_{ 1},u_{2}) = \frac{1} {n}\sum _{i=1}^{n}K_{ u_{1},h_{n}}\left (\frac{u_{1} -\tilde{ U}_{1i}} {h_{n}} \right )K_{u_{2},h_{n}}\left (\frac{u_{2} -\tilde{ U}_{2i}} {h_{n}} \right ),}$$

where $K_{u,h_{n}}$ is the integral of the modified boundary kernel

$$\displaystyle{k_{u,h}(x) = \frac{k(x)\left (a_{2}(u,h) - a_{1}(u,h)x\right )} {a_{0}(u,h)a_{2}(u,h) - a_{1}^{2}(u,h)}\,I\{\frac{u - 1} {h} < x < \frac{u} {h}\},}$$

where

$$\displaystyle{a_{\ell}(u,h) =\int _{ \frac{u-1} {h} }^{\frac{u} {h} }t^{\ell}k(t)dt\quad \mathrm{for}\ell = 0,1,2\;.}$$

Note that nonparametric methods such as the above kernel methods, involve the choice of a bandwidth parameter. This issue is not discussed here. See for example [29] (Section 3.2 in that paper), and references therein, for some discussion on bandwidth choice. One could also use other smoothing methods than the kernel method. We do not discuss these.

3 Local Dependencies and Conditional Copulas

3.1 Population Concepts

Suppose now that the interest is in the relationship between the random variables Y ₁ and Y ₂ but that both random variables are possibly influenced by another random variable, say X. A first interest is then in studying the conditional dependence between Y ₁ and Y ₂ given a specific value for X, say X = x. Instead of simply looking at the joint distribution between Y ₁ and Y ₂, as in Sect. 2, we now focus on the joint distribution of (Y ₁, Y ₂) conditionally upon X = x:

$$\displaystyle{H_{x}(y_{1},y_{2}) = P\{Y _{1} \leq y_{1},Y _{2} \leq y_{2}\left \vert X = x\right.\}\;.}$$

Applying Sklar’s theorem to this conditional joint distribution function results into

$$\displaystyle{ H_{x}(y_{1},y_{2}) = C_{x}\left (F_{1x}(y_{1}),F_{2x}(y_{2})\right )\qquad (y_{1},y_{2}) \in \mathbb{R}^{2}\;, }$$

(6)

where

$$\displaystyle{F_{1x}(y_{1}) = P\{Y _{1} \leq y_{1}\left \vert X = x\right.\}\qquad \mbox{ and}\qquad F_{2x}(y_{2}) = P\{Y _{2} \leq y_{2}\left \vert X = x\right.\}\;,}$$

denote the marginal cumulative distributions functions of Y ₁ and Y ₂, respectively, conditionally upon X = x. The main difference between (1) and (6) is that the copula function C _x changes with the fixed value of X (X = x), as well as the margins F _jx (for j = 1, 2). We refer to C _x as the conditional copula function. This notion was first considered by [30] in the specific context of modeling the dynamics of exchange rates, where the conditioning variable is related to time. See also Sect. 4.

Analogously to the case of the (unconditional) copula C in Sect. 2, the strength of the dependence relationship between Y ₁ and Y ₂, but now conditionally upon the given value of X = x, can be measured using an association measure. For simplicity of presentation, we just focus on the Kendall’s tau association measure. Denote by (Y ₁′, Y ₂′, X′) an independent copy of (Y ₁, Y ₂, X). Then the conditional Kendall’s tau function is defined as

$$\displaystyle\begin{array}{rcl} \tau (x)& =& P\left \{(Y _{1} - Y _{1}')(Y _{2} - Y _{2}') > 0\left \vert X = X' = x\right.\right \} \\ & & \qquad - P\left \{(Y _{1} - Y _{1}')(Y _{2} - Y _{2}') < 0\left \vert X = X' = x\right.\right \} \\ & =& 4\int \!\!\!\int _{[0,1]^{2}}C_{x}(u_{1},u_{2})dC_{x}(u_{1},u_{2}) - 1\;. {}\end{array}$$

(7)

For not making the notation too involved, we dropped the superscript {Y ₁, Y ₂} to indicate that we are interested in the dependence structure between Y ₁ and Y ₂ (conditionally upon X = x). See for example [20], for illustrations and examples of use of conditional association measures.

Note from (6) that the conditional dependence of Y ₁ and Y ₂ (conditionally given X = x) may be different for different values taken by X, i.e. the dependence structure, as well as its strength, may change with the value taken by the third variable X. This possible change in the strength of the relationship is reflected in the fact that Kendall’s tau is now a function of x.

It is often noticed that in applications, one uses the following simplification: the dependence structure itself, captured by the copula function, does not change with the specific value that X takes, and the dependence on x only comes in via the conditional margins, i.e.

$$\displaystyle{H_{x}(y_{1},y_{2}) = C\left (F_{1x}(y_{1}),F_{2x}(y_{2})\right )\qquad (y_{1},y_{2}) \in \mathbb{R}^{2}\;.}$$

In, for example, the literature on C-vine and D-vine copulas this assumption is inherently present. See [24] and [3], among others. See also the chapter (and its discussion) by [36], in which the dependence structure is assumed to stay constant in time.

3.2 Illustration: Examples

We now illustrate the concepts of Sect. 3.1 with some examples. A first example, Example 5, is an extension of Examples 1 and 2 of Sect. 2.2: instead of a bivariate Clayton copula we start from a three-variate Frank copula. In a second example, Example 6, we modify Example 3 of Sect. 2.2 by allowing the parameter of the copula and the marginal distribution of the second component to change with the random variable X. More precisely, the examples are as follows.

Example 5.

$$\displaystyle\begin{array}{rcl} & & Y _{1} \sim N(0,4),\qquad Y _{2} \sim \mbox{ Exp}(2),\qquad X \sim \mbox{ Beta}(1,4) {}\\ & & C(u_{1},u_{2},u_{3}) = -\frac{1} {\theta } \log \left (1 + \frac{\left (e^{-\theta u_{1}} - 1\right )\left (e^{-\theta u_{2}} - 1\right )\left (e^{-\theta u_{3}} - 1\right )} {\left (e^{-\theta }- 1\right )^{2}} \right )\;,\quad \ \ \theta = 3\;. {}\\ \end{array}$$

Example 6.

$$\displaystyle\begin{array}{rcl} & & Y _{1} \sim \mbox{ Student}(5,3),\qquad Y _{2}\vert X \sim \mbox{ Exp}(0.2(10\,X + 1)),\qquad X \sim \mbox{ U}(0,1) {}\\ & & C_{x}(u_{1},u_{2}) =\exp \left (-\left ((-\log u_{1})^{\theta (x)} + (-\log u_{ 2})^{\theta (x)}\right )^{ \frac{1} {\theta (x)} }\right ) {}\\ & & \theta (x) = 2\sin (2\varPi x) + 3\;, {}\\ \end{array}$$

with X independent from (Y ₁, Y ₂).

In Fig. 4 we present the pairwise scatter plots for a typical sample of size n = 800 from Example 6, revealing the independence between Y ₁ and X, but the dependence between Y ₂ and X. In the bottom right panel of Fig. 4 we plot $F_{1X_{i}}(Y _{1i})$ versus $F_{2X_{i}}(Y _{2i})$, for each i = 1, …, n. Each of these $F_{jX_{i}}(Y _{ji})$ should be (close to) uniformly distributed. In Fig. 5 we plot the conditional Kendall’s tau function for Examples 5 and 6. Note that in Example 5 there is a mild positive dependence between Y ₁ and Y ₂, conditionally upon X = x, but that the dependence increases with x. In Example 6 the dependence switches from very positive via independence back to strongly positive dependence.

Fig. 4

Scatter plots based on a typical sample of size n = 800 from Example 6

Fig. 5

Conditional Kendall’s tau function for Examples 5 (left panel) and 6 (right panel)

3.3 Statistical Inference

Suppose now that $((Y _{11},Y _{21},X_{1}),\ldots,(Y _{1n},Y _{2n},X_{n}))$ is a sample of size n of independent observations from (Y ₁, Y ₂, X). The interest is in estimating the conditional copula function C _x . As in Sect. 2, one can distinguish between different modeling settings, depending on what is known on possible appropriate parametric forms for C _x on the one hand and F _jx on the other hand. For convenience of the reader, we discuss similar modeling settings as in Sect. 2, but in a different order.

3.3.1 Fully Parametric Approach

In a fully parametric approach, we model C _x (⋅ , ⋅ ) via C(⋅ , ⋅ ; θ _C (x)) where θ _C (x) is a known parametric function of x, for example a polynomial of degree p: $\theta _{C}(x) =\theta _{C,1} +\theta _{C,2}x +\ldots \theta _{C,p}x^{p}$. We denote the corresponding parameter vector by $\boldsymbol{\theta }_{C} = (\theta _{C,1},\ldots,\theta _{C,p})$. Similarly, the conditional margins can be modeled via

$$\displaystyle{F_{jx}(\cdot ) = F_{j}(\cdot;\theta _{j}(x))\qquad \mbox{ with a parametric function }\theta _{j}(x)\;.}$$

For example, the functions $\theta _{j}(x)$ could be polynomial functions or any other given parametric functional form. Denote the resulting parameter vectors by $\boldsymbol{\theta }_{1}$ and $\boldsymbol{\theta }_{2}$ respectively. For example, if θ ₁(x) is a cubic function of x, then the dimension of $\boldsymbol{\theta }_{1}$ is 4.

With these parametrizations, we are again in a setting that is quite similar to that of Sect. 2.3.1. Indeed, considering the second order partial derivative of C _x (u ₁, u ₂) with respect to its arguments, we obtain

$$\displaystyle{c_{x}(u_{1},u_{2}) = \frac{\partial ^{2}C(u_{1},u_{2};\theta _{C}(x))} {\partial u_{1}\partial u_{2}} \qquad \forall (u_{1},u_{2}) \in [0,1]^{2}\;,}$$

which due to the structure can be written as c(u ₁, u ₂; θ _C (x)). Analogously denote the marginal densities by f ₁(⋅ ; θ ₁(x)) and f ₂(⋅ ; θ ₂(x)).

A data point (Y _1i , Y _2i , X _i ) contributes to the likelihood with the factor

$$\displaystyle{c\left (F_{1}(Y _{1i};\theta _{1}(X_{i})),F_{2}(Y _{2i};\theta _{2}(X_{i}));\theta _{C}(X_{i})\right )\,f_{1}(Y _{1i};\theta _{1}(X_{i}))f_{2}(Y _{2i};\theta _{2}(X_{i}))\;.}$$

Finally, we get to the logarithm of the likelihood function

$$\displaystyle\begin{array}{rcl} & & \tilde{\ell}_{n}(\boldsymbol{\theta }_{1},\boldsymbol{\theta }_{2},\boldsymbol{\theta }_{C}) \\ & & =\sum _{ i=1}^{n}\log \left (c\left (F_{ 1}(Y _{1i};\theta _{1}(X_{i})),F_{2}(Y _{2i};\theta _{2}(X_{i}));\theta _{C}(X_{i})\right )\,f_{1}(Y _{1i};\theta _{1}(X_{i}))f_{2}(Y _{2i};\theta _{2}(X_{i}))\right ) \\ & & =\sum _{ i=1}^{n}\log \left (c\left (F_{ 1}(Y _{1i};\theta _{1}(X_{i})),F_{2}(Y _{2i};\theta _{2}(X_{i}));\theta _{C}(X_{i})\right )\right ) \\ & & \qquad +\sum _{ i=1}^{n}\log \left (f_{ 1}(Y _{1i};\theta _{1}(X_{i}))f_{2}(Y _{2i};\theta _{2}(X_{i}))\right )\;, {}\end{array}$$

(8)

which needs to be maximized with respect to $(\boldsymbol{\theta }_{1},\boldsymbol{\theta }_{2},\boldsymbol{\theta }_{C})$. From that point on we proceed as in Sect. 2.3.1. Denote the maximizer of (8) by $(\hat{\boldsymbol{\theta }}_{1},\hat{\boldsymbol{\theta }}_{2},\hat{\boldsymbol{\theta }}_{C})$.

An estimator for, for example, the associated conditional Kendall’s tau function is then obtained by substituting $C_{x}(\cdot,\cdot ) = C(\cdot,\cdot;\theta _{C}(x))$ in (7) by its estimator $C(\cdot,\cdot;\hat{\theta }_{C}(x))$, where $\hat{\theta }_{C}(x)$ is obtained by replacing the parameter vector $\boldsymbol{\theta }_{C}$ in the parametric form of $\theta _{C}(x)$ by its maximum likelihood estimator $\hat{\theta }_{C}$. For example, in case $\theta _{C}(x) =\theta _{C,1} +\theta _{C,2}x +\ldots \theta _{C,p}x^{p}$, this is $\hat{\theta }_{C}(x) =\hat{\theta } _{C,1} +\hat{\theta } _{C,2}x +\ldots \hat{\theta } _{C,p}x^{p}$ based on $\hat{\boldsymbol{\theta }}_{C} = (\hat{\theta }_{C,1},\ldots,\hat{\theta }_{C,p})$. So, the estimator for the conditional Kendall’s tau is then

$$\displaystyle{\hat{\tau }(x) = 4\int \!\!\!\int _{[0,1]^{2}}C(u_{1},u_{2};\hat{\theta }_{C}(x))dC(u_{1},u_{2};\hat{\theta }_{C}(x)) - 1\;.}$$

3.3.2 Fully Nonparametric Approach

An alternative expression for (6) is

$$\displaystyle{ C_{x}(u_{1},u_{2}) = H_{x}\left (F_{1x}^{-1}(u_{ 1}),F_{2x}^{-1}(u_{ 2})\right )\qquad (u_{1},u_{2}) \in [0,1]^{2}\;, }$$

(9)

where F _jx ⁻¹(⋅ ) denotes the quantile function corresponding to F _jx (⋅ ), for j = 1, 2.

From (9) it is transparent that we need to find estimators for the conditional joint cumulative distribution function H _x (⋅ , ⋅ ) as well as for the (quantiles of the) conditional margins F _1x (⋅ ) and F _2x (⋅ ). Since these are conditional quantities, some smoothing in the domain of X is needed. Nonparametric estimation of a conditional distribution function using kernel methods has been well-studied in the literature. See for example [23] and [38], among others. A general estimator is obtained by ‘smearing out’ the mass n ⁻¹ that is in the expression for a bivariate (unconditional) empirical distribution function, in the covariate domain, using a weight function:

$$\displaystyle{ \hat{H}_{x}(y_{1},y_{2}) =\sum _{ i=1}^{n}w_{ ni}(x,b_{n})I\left \{Y _{1i} \leq y_{1},Y _{2i} \leq y_{2}\right \}\;, }$$

(10)

with w _ni (x, b _n ) ≥ 0, a sequence of weights that ‘smooths’ over the covariate space. Herein b _n  > 0 is a sequence of bandwidths. Since H _x (y ₁, y ₂) is a distribution function, the weights need to tend to 1 when y ₁ and y ₂ tend to infinity. This is achieved by ensuring that the weights are such that $\sum _{i=1}^{n}w_{ni}(x,b_{n}) = 1$ (either exactly or asymptotically, as n → ∞). There are many scenario’s of appropriate weight functions available in the literature. The simplest set of weights is given by the Nadaraya-Watson type of weights defined as

$$\displaystyle{w_{ni}(x,b_{n}) = \frac{k_{b_{n}}(X_{i} - x)} {\sum _{j=1}^{n}k_{b_{n}}(X_{j} - x)}\;,}$$

with $k_{b_{n}}(\cdot ) = \frac{1} {b_{n}}k(\cdot /b_{n})$ a rescaled version of k(⋅ ). Alternative scenario’s of weights are local linear weights, Gasser-Müller weights, etc.

From (10) we obtain estimators for the conditional marginal distribution functions F _jx (⋅ ) by simply letting the other argument in the estimated joint cumulative distribution function tend to infinity:

$$\displaystyle{ \hat{F}_{jx}(y) =\sum _{ i=1}^{n}w_{ ni}(x,b_{jn})I\left \{Y _{ji} \leq y\right \}\qquad \quad j = 1,2\;, }$$

(11)

where the bandwidth sequences b _1n  > 0 and b _2n  > 0 (for estimation of the conditional margins) do not need to be the same and/or do not need to be the same as this for the joint estimation. For practical simplicity one can take $b_{n} = b_{1n} = b_{2n}$.

Asymptotic properties for kernel type estimators of conditional distributions functions have been established in [35, 37] and [39], among others. For a recent contribution in the area, see [38].

Remark that in (10) and (11) one can again replace the indicator function by a smooth function, if differentiability properties of the resulting estimators are of importance.

From the estimators $\hat{F}_{jx}(\cdot )$ in (11), we obtain estimators for the quantile functions F _jx ⁻¹(⋅ ). From the estimators for H _x (⋅ , ⋅ ) and F _jx ⁻¹(⋅ ) one then derives an estimator for C _x (⋅ , ⋅ ) by replacing in (9) the former quantities by their estimators. In the literature these and improved estimators are studied, also in more complex frameworks (of multivariate or functional covariates). See, for example, [39] and [19].

3.3.3 Semiparametric Approach

There are at least a few semiparametric approaches, depending on the particular modeling setting. We just discuss some major approaches.

Firstly, assume that the conditional margins are fully known, i.e. F _jx (⋅ ), for j = 1, 2, are fully known for all x in the domain of X. Suppose that the conditional copula function C _x (⋅ , ⋅ ) depends on x through a parameter function θ _C (x), i.e. C _x (⋅ , ⋅ ) = C(⋅ , ⋅ ; θ _C (x)), but contrary to Sect. 3.3.1 the function θ _C (x) is fully unknown. This setting has been studied by [22] and [2], among others. In the sequel we drop the subscript C in θ _C and θ _C (x) for simplifying the notation.

The parametric copula family C(⋅ , ⋅ ; θ) that serves as a starting point here (and in fact also in Sect. 3.3.1, and before) of course has some restrictions on the parameter space Θ for θ. For example, for a Gaussian copula: θ ∈ (−1, 1); for a Clayton copula θ ∈ (0, ∞). Such restrictions on the parameter space of the parametric copula C(⋅ , ⋅ ; θ) should in fact not be ignored. The same holds when looking at a conditional copula modeled via C _x (u ₁, u ₂) = C(u ₁, u ₂; θ(x)), with corresponding copula density c(u ₁, u ₂; θ(x)).

Since the function θ(x) is fully unknown, we are going to approximate this function locally, i.e. in the neighbourhood of x by, for example, a polynomial of degree p say. But since a polynomial takes on values in $\mathbb{R}$, we need to take care of the restrictions on the parameter space Θ of the parametric copula family C(⋅ , ⋅ ; θ). One therefore transforms the function θ(x), which takes on values in Θ, via a given transformation ψ(⋅ ), into the function

$$\displaystyle{\eta (x) =\psi (\theta (x))\;,}$$

which takes on value in $\mathbb{R}$.

In the sequel, we assume that the inverse transformation ψ ⁻¹(⋅ ) exists, such that we can obtain θ(⋅ ) from η(⋅ ):

$$\displaystyle{ \theta (x) =\psi ^{-1}(\eta (x))\;, }$$

(12)

which takes values in Θ.

Consider now independent observations $((Y _{11},Y _{21},X_{1}),\ldots,(Y _{1n},Y _{2n},X_{n}))$ from (Y ₁, Y ₂, X). A data point (Y _1i , Y _2i , X _i ) then contributes to the (pseudo) log-likelihood with

$$\displaystyle{ \log c\left (F_{1X_{i}}(Y _{1i}),F_{2X_{i}}(Y _{2i});\theta (X_{i})\right ) =\log c\left (F_{1X_{i}}(Y _{1i}),F_{2X_{i}}(Y _{2i});\psi ^{-1}\left (\eta (X_{ i})\right )\right )\;. }$$

(13)

For a data point X _i in a neighbourhood of x, we then can approximate η(X _i ) using a Taylor expansion, by

$$\displaystyle\begin{array}{rcl} \eta (X_{i})& \approx & \eta (x) +\eta '(x)(X_{i} - x) + \cdots + \frac{\eta ^{(p)}(x)(X_{i} - x)^{p}} {p!} {}\\ & \equiv & \beta _{0} +\beta _{1}(X_{i} - x) + \cdots +\beta _{p}(X_{i} - x)^{p}\;, {}\\ \end{array}$$

where we denoted

$$\displaystyle{\beta _{r} =\beta _{r}(x) = \frac{\eta ^{(r)}(x)} {r!} \qquad r = 0,\ldots,p\;.}$$

If X _i is near x, then the contribution in (13) to the (pseudo) log-likelihood, can be approximated by

$$\displaystyle\begin{array}{rcl} & & \log c\left (F_{1X_{i}}(Y _{1i}),F_{2X_{i}}(Y _{2i});\theta (X_{i})\right ) {}\\ & & \quad \approx \log c\left (F_{1X_{i}}(Y _{1i}),F_{2X_{i}}(Y _{2i});\psi ^{-1}\left (\beta _{ 0} +\beta _{1}(X_{i} - x) + \cdots +\beta _{p}(X_{i} - x)^{p}\right )\right )\;. {}\\ \end{array}$$

This approximation is only valid for X _i near x, and this is taken care off by multiplying this contribution in the log-likelihood by a weight factor $k_{h_{n}}(\cdot ) = \frac{1} {h_{n}}k( \frac{\cdot } {h_{n}})$, with k(⋅ ) as before, and h _n  > 0 a bandwidth parameter.

This leads to the local log-likelihood

$$\displaystyle\begin{array}{rcl} \ell_{n}(\boldsymbol{\beta })& =& \sum _{i=1}^{n}\log c\left (F_{ 1X_{i}}(Y _{1i}),F_{2X_{i}}(Y _{2i});\psi ^{-1}\left \{\beta _{ 0} +\beta _{1}(X_{i} - x) + \cdots +\beta _{p}(X_{i} - x)^{p}\right \}\right ) \\ & & \phantom{\sum _{i=1}^{n}\log c\left (\right.F_{ 1X_{i}}(Y _{1i}),F_{2X_{i}}(Y _{2i});\psi ^{-1}\left \{\right.\beta _{ 0} +\beta _{1}(X_{i}} \times k_{h_{n}}(X_{i} - x)\;, {}\end{array}$$

(14)

which is a localized version of the (pseudo) log-likelihood function in the parametric setting. Maximization of this local log-likelihood with respect to $\boldsymbol{\beta }$ leads to the estimated vector $\hat{\boldsymbol{\beta }}= (\hat{\beta }_{0},\ldots,\hat{\beta }_{p})$, and hence, in particular, an estimator for η(x) is $\hat{\beta }_{0}$. From (12) an estimator for θ(x) is

$$\displaystyle{\hat{\theta }(x) =\psi ^{-1}(\hat{\beta }_{ 0})\;.}$$

By maximizing the local log-likelihood (14) in a grid of x-values, one obtains estimates of the unknown parameter function $\theta (\cdot )$ in a grid of points.

We next turn to the setting where also the conditional margins are fully unknown, i.e. F _jx (⋅ ), for j = 1, 2, are fully unknown for all x in the domain of X. For X _i in a neighbourhood of x, we then can replace the contribution

$$\displaystyle{\log c\left (F_{1X_{i}}(Y _{1i}),F_{2X_{i}}(Y _{2i});\psi ^{-1}\left \{\beta _{ 0} +\beta _{1}(X_{i} - x) + \cdots +\beta _{p}(X_{i} - x)^{p}\right \}\right )k_{ h_{n}}(X_{i} - x)}$$

in the log-likelihood function by

$$\displaystyle{\log c\left (F_{1x}(Y _{1i}),F_{2x}(Y _{2i});\psi ^{-1}\left \{\beta _{ 0} +\beta _{1}(X_{i} - x) + \cdots +\beta _{p}(X_{i} - x)^{p}\right \}\right )k_{ h_{n}}(X_{i} - x)\;,}$$

and next we substitute the unknown quantities F _1x (Y _1i ) and F _2x (Y _2i ) by nonparametric estimators, such as these provided in (11). This then leads to the local log-likelihood

$$\displaystyle\begin{array}{rcl} \tilde{\ell}_{n}(\boldsymbol{\beta })& =& \sum _{i=1}^{n}\log c\left (\hat{F}_{ 1x}(Y _{1i}),\hat{F}_{2x}(Y _{2i});\psi ^{-1}\left \{\beta _{ 0} +\beta _{1}(X_{i} - x) + \cdots +\beta _{p}(X_{i} - x)^{p}\right \}\right ) {}\\ & & \phantom{\sum _{i=1}^{n}\log c\left (\right.\hat{F}_{ 1x}(Y _{1i}),\hat{F}_{2x}(Y _{2i});\psi ^{-1}\{\beta _{ 0} +\beta _{1}(}\times k_{h_{n}}(X_{i} - x)\;, {}\\ \end{array}$$

which needs to be maximized with respect to $\boldsymbol{\beta }$.

This estimation method is called a local polynomial maximum pseudo log-likelihood estimation method. Properties of the resulting estimator have been studied in [1]. That paper also contains a brief discussion on some practical bandwidth selection methods, including a rule-of-thumb type of bandwidth selector and a cross-validation procedure. For a general treatment of the use of local polynomial modeling in a maximum likelihood framework, see for example [13]. For a general discussion on the choice of the degree of the polynomial approximation see [12].

4 Dynamics of a Dependence Structure and Copulas

When introducing copulas to the modeling of time series data different approaches are possible. Following, for example, [9] copulas can be used to model the inter-temporal dependence within one time series by specifying the transition probabilities in a Markov process. See [8] for recent developments and further references for such settings. In this section we focus on a different approach.

4.1 Dynamical Modeling of a Dependence Structure

Alternatively copulas can be used to model the spatial dependence of a bivariate stochastic process $\mathbf{Y}_{t} = (Y _{1,t},Y _{2,t})$, $t \in \mathbb{Z}$. As time series analysis is naturally formulated conditionally upon the history of the process we revert to the conditional copula concept, now enlarging the conditioning from one variable as in Sect. 3 to the entire past of the process. This is done in a mathematical rigorously way by conditioning upon the sigma-algebras generated by the past of the time series. We opted for a more layman’s term presentation here. As first introduced by [30] such a setting allows time dependent variation in the joint distribution of (Y _1, t , Y _2, t ) conditionally upon $\mathbf{W}_{t} = (\mathbf{Y}_{t-k})_{k>0}$ via

$$\displaystyle{ P\{Y _{1,t} \leq y_{1},Y _{2,t} \leq y_{2}\vert \mathbf{W}_{t} = \mathbf{w}_{t}\} = C_{t}(F_{1,t}(y_{1}),F_{2,t}(y_{2}))\;, }$$

(15)

where $F_{j,t}(y_{j}) = P\{Y _{j,t} \leq y_{j}\vert \mathbf{W}_{t} = \mathbf{w}_{t}\}$, j = 1, 2, and $C_{t}(\cdot,\cdot ) = C(\cdot,\cdot \vert \mathbf{W}_{t} = \mathbf{w}_{t})$ is the conditional copula implied by Sklar’s Theorem.

The conditional modeling in (15) can be readily combined with, for example, a GARCH(r, s) error structure for the two involved time series {Y _1, t } and {Y _2, t }. See [5], for example, for a standard reference to Generalized Autoregressive Conditional Heteroskedasticity (GARCH) type of modeling. More precisely, we model the marginal time series as

$$\displaystyle\begin{array}{rcl} Y _{j,t}& =& \mu _{j} +\varepsilon _{j,t},\qquad \mbox{ where }\qquad \varepsilon _{j,t} =\sigma _{j,t}\eta _{j,t}\;,{}\end{array}$$

(16)

$$\displaystyle\begin{array}{rcl} \sigma _{j,t}^{2}& =& \alpha _{ j} +\sum _{ \ell=1}^{r}\beta _{ j,\ell}\sigma _{j,t-\ell}^{2} +\sum _{ m=1}^{s}\gamma _{ j,m}\varepsilon _{j,t-m}^{2}\;,{}\end{array}$$

(17)

where α _j , β _j, ℓ , γ _j, m  ≥ 0, $\mu _{j} \in \mathbb{R}$, $r,s \in \mathbb{N}_{0}$ and $(\eta _{j,t})_{t\in \mathbb{Z}}$ is white noise with zero mean and unit variance. GARCH models are designed to account for the time varying and clustering volatility of shocks observed frequently, but not exclusively, in financial time series. This is accomplished by relating the time t variance of ɛ _j, t to the lagged r realized variances as well as to the lagged s realized shocks, where it is noteworthy that the dependence on the lagged shocks makes the variance itself stochastic (random). Combining (15) and (16) the marginal time series can now be fused into a joint model by specifying its conditional joint distribution

$$\displaystyle{\mathbf{Y}_{t}\vert \mathbf{W}_{t} = \mathbf{w}_{t} \sim C_{t}(F_{1,t},F_{2,t}),}$$

where the conditional mean and variance of F _j, t , for j = 1, 2, are only determined by information from the past (up to time point t − 1) and are given as μ _j and σ _j, t ². This framework combines autocorrelated shocks with a flexible modeling of the conditional joint distribution. A detailed review of copula models in economic time series can be found in [31]. For the purpose of this chapter, we focus on applying a semiparametric approach as discussed in Sect. 3.3.3 to the time series framework, with the difference that in the semiparametric approach described here, we model the marginal time series via parametric GARCH models. For simplicity, let $t \in \mathbb{N}_{0}$, and denote by (Y _1, t , Y _2, t ) _t = 1 ^T the available sample of size T ($T \in \mathbb{N}_{0}$). Furthermore, denote the observed (standardized) time points by t∕T, so that all observational points t∕T are in the interval [0, 1]. The conditional copula is chosen to be time dependent through an unknown parameter function θ _C (t ^∗) for t ^∗ ∈ [0, 1]. To obey restrictions in the parameter space we again consider a suitable one-to-one transformation ψ such that $\eta (t^{{\ast}}) =\psi (\theta _{C}(t^{{\ast}})) \in \mathbb{R}$ and recover θ _C via $\theta _{C}(t^{{\ast}}) =\psi ^{-1}(\eta (t^{{\ast}}))$. For a sample (Y _1, t , Y _2, t ) _t = 1 ^T we can write the log-likelihood of the overall joint density by successive conditioning in terms of the contributions of the bivariate densities $\mathbf{Y}_{t}\vert \mathbf{W}_{t} = \mathbf{w}_{t}$ to the log-likelihood as

$$\displaystyle\begin{array}{rcl} \ell_{T}& =& \sum _{t=1}^{T}\log \left (c\left (F_{ 1,t}(Y _{1,t}),F_{2,t}(Y _{2,t})\right );\theta _{C}(t/T)\right ) +\sum _{ j=1}^{2}\sum _{ t=1}^{T}\log \left (f_{ j,t}(Y _{j,t})\right ) {}\\ & =& \ell_{T,C} +\ell _{T,1} +\ell _{T,2}\;. {}\\ \end{array}$$

See also (8) in Sects. 3.3.1 and 3.3.3. Following the so-called inference of margins approach (a two-steps procedure), see [26], maximizing ℓ _T can be accomplished by first separately maximizing ℓ _T, 1 and ℓ _T, 2, under our semiparametric setting by a standard parametric maximum likelihood estimation method, and then maximizing ℓ _T, C taking estimates of the previous step into account by replacing the distribution functions F _j, t by their respective estimates $\hat{F}_{j,t}$ (for j = 1, 2). In order to maximize ℓ _T, C we extend the local constant fitting approach of [22] to the local polynomial approach discussed in Sect. 3.3.2. Asymptotic normality of the resulting estimator in case of local constant fitting can be found in [22]. The study of the asymptotic properties of the local polynomial dynamic copula estimator, presented in this section, is part of future research. Consider a fixed point t ^∗ ∈ [0, 1], and denote by $k_{h_{n}}(\cdot )$ a rescaled kernel with bandwidth h _n , as before. The local log-likelihood for the problem considered is then given by

$$\displaystyle\begin{array}{rcl} & & \ell_{T,C}(\boldsymbol{\beta }) \\ & & =\sum _{ t=1}^{T}\log c\left (\hat{F}_{ 1,t}(Y _{1,t}),\hat{F}_{2,t}(Y _{2,t});\psi ^{-1}\right. \\ & & \times \left.\left \{\beta _{0} +\beta _{1}\left ( \frac{t} {T} - t^{{\ast}}\right ) +\ldots +\beta _{ p}\left ( \frac{t} {T} - t^{{\ast}}\right )^{p}\right \}\right ) \times k_{ h_{n}}\left ( \frac{t} {T} - t^{{\ast}}\right )\;,{}\end{array}$$

(18)

which needs to be maximized with respect to $\boldsymbol{\beta } = (\beta _{0},\ldots,\beta _{p})$.

4.2 Illustrative Example

We illustrate the presented methodology by simulating from a bivariate GARCH(1,1) model, where the conditional marginal distributions are set to be Normal distributions, and the conditional copula is assumed to be a student t copula where the degrees of freedom are fixed to 4. The remaining free copula parameter is a time varying parameter function $\theta _{C}(t) = 2\sin (0.95\pi (2B(t;2,3) - 1)/6)$, with B(t; a, b) the cumulative distribution function of the Beta distribution. See [11] for a reference on (student) t copulas. The remaining parameters are set to $\mu _{1} =\mu _{2} = 0$, $\alpha _{1} =\alpha _{2} = 0.1$ $\beta _{1,1} =\beta _{2,1} = 0.4$ and $\gamma _{1,1} =\gamma _{2,1} = 0.4$.

Figure 6 show the first and second marginal time series for a simulated trajectory of the process, highlighting the volatility clustering inherent in the process. In Fig. 7 we show simulated scatter plots of the unconditional distribution at three different time points. As expected the time varying conditional dependence structure carries over to the distribution of (Y _1, t , Y _2, t ), displaying a negative dependence at early time stages, and gradually switching to a positive dependence later on (moving from the left panel to the right panel).

Fig. 6

Marginal time series Y _1, t (left) and Y _2, t (right) of a simulated bivariate copula-GARCH(1,1) model, t = 1, …, 500

Fig. 7

Simulated scatter plot of (Y _1, 50, Y _2, 50) (left panel); (Y _1, 250, Y _2, 250) (middle panel) and (Y _1, 450, Y _2, 450) (right panel). The scatter plots are based on 250 independently simulated trajectories

To illustrate the local log-likelihood estimation of θ(⋅ ) we first obtain estimates $\hat{\mu }_{1}$, $\hat{\mu }_{2}$, $\hat{\alpha }_{1}$, $\hat{\alpha }_{2}$, $\hat{\beta }_{1,1}$, $\hat{\beta }_{2,1}$, $\hat{\gamma }_{1,1}$ and $\hat{\gamma }_{2,1}$ by fitting a GARCH(1,1) model to each of the marginal time series individually. From the estimates we can then recover, for j = 1, 2, the conditional variances $\hat{\sigma }_{j,t}^{2}$ to find $\hat{F}_{j,t}(Y _{j,t}) =\varPhi ((Y _{j,t} -\hat{\mu }_{j})/\hat{\sigma }_{j,t})$, where Φ denotes the standard normal distribution function. To perform the local log-likelihood estimation in (18) we settle for a local approximation with a polynomial of degree p = 1, i.e. performing local linear fitting. For a fixed point t ^∗ ∈ [0, 1] we then maximize ℓ _T, C (β ₀, β ₁) as given in (18), where we choose $\psi ^{-1}: \mathbb{R} \rightarrow (-1,1)$, with $\psi ^{-1}(x) =\tanh (x)$.

In the left panel of Fig. 8 we show the true and estimated θ(t ^∗) when using different bandwidths h _n in the estimation procedure. In the right panel of Fig. 8 we also plot the true and estimated conditional Blomqvist’s beta as a function of time, using the same bandwidths as for the estimation of θ(⋅ ).

Fig. 8

True (solid curve) and estimated curve using bandwidths h _n  = 0. 01 (dashed) and h _n  = 0. 02 (dotted). Left panel: true and estimated θ(t ^∗). Right panel: true and estimated conditional Blomqvist’s beta. Calculations are based on a simulated sample of size T = 500

5 Dynamic Modeling via Copulas: Application in Forecasting

We consider wind speed data obtained by weather stations in Kennewick (southern Washington) and Vansycle/Butler Grade (north-eastern Oregon), in the USA. The raw data¹ consist of average wind speeds (in miles per hour = mph) for intervals of 5 min. For the analysis here we restrict to the period between April 1 and July 1, 2013. A more detailed description and analysis of these data can be found in [21]. In this section, we illustrate how the discussed methods can be used for estimation and for forecasting of wind speeds.

To fit the time series data we extend the model described in (16) and (17) to include an autoregressive component, leading to an AR(q)-GARCH(r, s) model, where (16) is replaced by (for j = 1, 2)

$$\displaystyle{ Y _{j,t} =\mu _{j} +\sum _{ \ell=1}^{q}\phi _{ j,\ell}Y _{j,t-\ell} +\varepsilon _{j,t}\;,\qquad \mbox{ where }\qquad \varepsilon _{j,t} =\sigma _{j,t}\eta _{j,t}\;, }$$

(19)

and (17) is kept. Herein $\phi _{j,\ell} \in \mathbb{R}$, $q \in \mathbb{N}_{0}$. As in Sect. 4 the conditional marginal distributions are Normal, and the marginal time series are coupled by a time dependent copula to form a bivariate model.

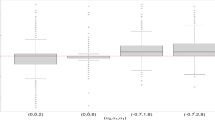
As wind speed forecasts with a two-hour forecast horizon are needed to meet practical demands (see [21]), we transform the raw data into the hourly averages, shown in Fig. 9, and denote the sample by (Y _1, t , Y _2, t ) _t = 1 ^2, 184. In the next step we fit an AR(1)-GARCH(1, 1) model, described by (19) and (17), to the marginal time series in an one hour rolling window type fashion as follows. The first estimates $(\hat{\mu }_{j},\hat{\phi }_{j,1},\hat{\alpha }_{j},\hat{\beta }_{j,1},\hat{\gamma }_{j,1})$, j = 1, 2, are obtained by fitting the AR-GARCH model to $(Y _{j,t})_{t=1}^{744}$. The second estimates are then based on the shifted data (Y _j, t ) _t = 2 ⁷⁴⁵ and so forth. We repeat this process 240 times, yielding estimates covering a span of 10 days. By keeping the number of observations fixed at 744 all estimates are effectively based on data of the last respective 31 days. The so obtained estimates are plotted against the window shift in Figs. 10 and 11. While the mean and AR coefficients (Fig. 10) are very comparable between both sites, the GARCH parameters show a differing pattern: while the baseline variance and lagged realized shock coefficients are generally higher in Kennewick than in Butler Grade (left and right panels of Fig. 11), the situation is reversed considering the dependence on lagged realized variances. See the middle panel of Fig. 11. The two weather stations are on different altitudes, the difference being around 130 m. This could may be explain the differences noticed.

Fig. 9

Hourly averages of wind speed (mph) at Kennewick (left) and at Butler Grade (right) from April 1 to July 1, 2013

Fig. 10

Estimates of μ _j (left panel) and of ϕ _j, 1 (right panel), for j = 1, 2, for the 240 rolling windows, based on 744 observations each

Fig. 11

Estimates of α _j, 1 (left panel), of β _j, 1 (middle panel) and of γ _j, 1 (right panel), for j = 1, 2, for the 240 rolling windows, based on 744 observations each

The conditional dependence structure between the marginal time series is modeled by a student t copula with 4 fixed degrees of freedom, where the remaining parameter θ is allowed to vary as a smooth function of time, as explained in Sect. 4. In Fig. 12 (left panel) we show the estimated conditional copula parameter function for observations (Y _j, t ) _t = 1 ⁷⁴⁴ (the solid curve) using the previously estimated AR-GARCH parameters, and applying local linear fitting with bandwidth h = 0. 2 (see Sect. 4). We repeat the procedure also based on the very last 744 observations (Y _j, t ) _{t = 1, 441} ^2, 184 (i.e. the June period) and show the results in the left panel of Fig. 12 (the dotted curve). We also present the corresponding results for the estimated conditional Blomqvist’s beta in the right panel of Fig. 12. As can be seen, the dependence structure (between the observations from the two stations) varies within the periods (April and June), but also seems to be different for the two periods examined (early spring and summer period).

Fig. 12

Estimates of θ(t ^∗) (left) and the conditional Blomqvist’s beta (right), by local-linear fitting with h = 0. 2, for a student t copula with 4 degrees of freedom based on the observations (Y _1, t , Y _2, t ) _t = 1 ⁷⁴⁴ (for the April period) and on the observations (Y _1, t , Y _2, t ) _{t = 1, 441} ^2, 184 (for the June period). Solid line: April period; Dotted line: June period

Turning towards forecasting we compute for each set of rolling window estimates the conditional copula parameter at t ^∗ = 1, i.e. $\hat{\theta }(744)$ for the first window, $\hat{\theta }(745)$ for the second and so on. This yields successive estimates $(\hat{\beta }_{0},\hat{\beta }_{1})$ that we use to predict the one hour ahead forecast and, respectively, the two hours ahead forecast of $\theta (t)$ by $\tilde{\theta }(T + k) =\psi ^{-1}(\hat{\beta }_{0} + k\hat{\beta }_{1}/744)$, with k = 1, respectively k = 2, where ψ ⁻¹ is the link function as in Sect. 4 and T denotes the last time point of the respective rolling window sample. The obtained 2 h ahead forecast of θ is shown in the left panel of Fig. 13.

Fig. 13

Left: Two hours ahead prediction of θ(⋅ ) for the rolling windows, based on 744 observations. Right: Realized minus two hours ahead predicted wind speeds in Kennewick for the rolling windows

Concerning the marginal time series we use the point estimates of the parameters as one and two hours ahead forecasts of the parameters. This allows to compute point forecasts of the wind speed by (see (19))

$$\displaystyle\begin{array}{rcl} & & \tilde{Y }_{j,T+1} = \mbox{ E}\left [Y _{j,T+1}\vert Y _{j,T-\ell},\ell\geq 0\right ] =\mu _{j} +\phi _{j,1}\,Y _{j,T} {}\\ & & \tilde{Y }_{j,T+2} = \mbox{ E}\left [Y _{j,T+2}\vert Y _{j,T-\ell},\ell\geq 0\right ] =\mu _{j} +\phi _{j,1}\,\left (\mu _{j} +\phi _{j,1}Y _{j,T}\right ) {}\\ \end{array}$$

for j = 1, 2.

To assess the forecast quality we compute the square root of the mean squared error of the predicted to the realized values for the 240 forecasts, denoted by RMSE. For one hours ahead forecasts we obtain: RMSE = 2. 9485 for the Kennewick station, and RMSE = 3. 0026 for the Butler Grade station. For the two hours ahead forecasts these are: RMSE = 4. 4725 for Kennewick and RMSE = 4. 8190 for Butler Grade. The right panel of Fig. 13 depicts the differences of realized to predicted two hours ahead forecasts at Kennewick.

Having predictions of the marginal time series, as well as the conditional dependence between them allows to go beyond point forecasting and to predict their joint behaviour. In Fig. 14 we show contours of the predicted two hours ahead joint distribution for the first rolling window, and then 5.5 days later, in respectively the left and right side panels. As shown by the figure, not only the mean of the distribution, represented by the wind speed point forecasts, but also the shape changes as implied by the prediction of θ(⋅ ).

Fig. 14

Two hours ahead prediction of the conditional joint density of (Y _1, 746, Y _2, 746) (left) and the conditional joint density of (Y _1, 877, Y _2, 877) (right) based on the first rolling window, respectively on rolling window 132

To further visualize the impact of the time varying association we forecast the probability of Y _1, T+2 and Y _2, T+2 staying jointly below their conditional α × 100 % quantiles. Within a copula framework this probability equals C(α, α; θ(T + 2)). See [7] for an application in economics. For example based on the first rolling window we compute the conditional two hours ahead 40 % quantiles as 10. 1487 (for Kennewick) and 6. 1633 (for Butler Grade). This yields a prediction of P{Y _1, 746 ≤ 10. 1487, Y _2, 746 ≤ 6. 1633} = 0. 1777. Figure 15 shows the obtained predictions for different values of α.

Fig. 15

Two hours ahead prediction of C(α, α; θ(T + 2)) for the rolling windows, based on 744 observations