Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The general setting of hierarchical time series (HTS) forecasting has been extensively studied because of its applications to, among others, inventory management for companies [7], euro-area macroeconomic studies [13], forecasting Australian domestic tourism [11], and balancing the national budget of states [4, 16]. As a consequence of the recent deployment of smart grids and autodispatchable sources, HTS have also been introduced in electricity demand forecasting [3], which is essential for electricity companies to reduce electricity production cost and take advantage of market opportunities.

A Motivating Example: Electricity Forecasting

The electrical grid induces a hierarchy in which customer demand is viewed at increasing levels of aggregation. One may organize this hierarchy in different ways, but in any case the demand of individual customers is at the bottom, and the top level represents the total demand for the whole system. Depending on the modelling purpose, intermediate levels of aggregation may represent groups of clients that are tied together by geographical proximity, tariff contracts, similar consumption structure or other criteria.

Whereas demand data were previously available only for the whole system, they are now also available at regional (intermediate) levels or even at the individual level, which makes it possible to forecast electricity demand at different levels of aggregation. To this end, it is not only necessary to extend existing prediction models to lower levels of the customer hierarchy, but also to deal with the new possibilities and constraints that are introduced by the hierarchical organization of the predictions. In particular, it may be required that the sum of lower-level forecasts is equal to the prediction for the whole system. This was demanded, for example, in the Global Energy Forecasting Competition 2012 [10], and it also makes intuitive sense that the forecasts should sum in the same way as the real data. Moreover, we show in Theorems 1 and 2 below that this requirement, if enforced using a general method that we will introduce, can only improve the forecasts.

Hierarchical Time Series

Electricity demand data that are organized in a customer hierarchy, are a special case of what is known in the literature as contemporaneous HTS: each node in the hierarchy corresponds to a time series, and, at any given time, the value of a time series higher up is equal to the sum of its constituent time series. In contrast, there also exist temporal HTS, in which time series are aggregated over periods of time, but we will not consider those in this work. For both types of HTS, the question of whether it is better to predict an aggregate time series directly or to derive forecasts from predictions for its constituent series has received a lot of attention, although the consensus appears to be that there is no clear-cut answer. (See [7, 13] for surveys.) A significant theoretical effort has also been made to understand the probability structure of contemporaneous HTS when the constituent series are auto-regressive moving average (ARMA) models [8].

HTS Forecasting

The most common methods used for hierarchical time series forecasting are bottom-up, top-down and middle-out [3, 7]. The first of these concentrates on the prediction of all the components and uses the sum of these predictions as a forecast of the whole. The second one predicts the top level aggregate and then splits up the prediction into the components according to proportions that may be estimated, for instance, from historical proportions in the time series. The middle out strategy is a combination of the first two: one first obtains predictions at some level of the hierarchy; then one uses the bottom-up strategy to forecast the upper levels and top-down to forecast the lower levels.

As observed by Hyndman et al. [11], all three methods can be viewed as linear mappings from a set of initial forecasts for the time series to reconciled estimates that are aggregate consistent, which means that the sum of the forecasts of the components of an hierarchical time series is equal to the forecast of the whole. A more sophisticated linear mapping may be obtained by setting up a linear regression problem in which the initial forecasts are viewed as noisy observations of the expected values of the time series [4] (see Sect. 2.3). In this approach, which goes back to Stone et al. [16], it is then inescapable to assume that the initial forecasts are unbiased estimates, so that the noise has mean zero. Assuming furthermore that the covariance matrix Σ of the noise can be accurately estimated for each time step, the outcomes for the time series can be estimated using a generalized least-squares (GLS) method, which solves the linear regression problem with aggregate consistency constraints on the solution.

Although the assumption of unbiased initial forecasts rules out using any type of regularized estimator (like, for instance, the LASSO [17] which we consider in Sect. 3.1), it might still be manageable in practice. The difficulty with GLS, however, is estimating Σ, which might be possible on accounting data by laboriously tracing back all the sources of variance in the estimates [6], but does not seem feasible in our motivating example of electricity demand forecasting. (Standard estimators like those of White [18] or MacKinnon and White [14] do not apply, because they estimate an average of Σ over time instead of its value at the current time step.) Alternatively, it has therefore been proposed to make an additional assumption about the covariances of the initial forecasts that allows estimation of Σ to be sidestepped [11], but it is not clear when we can expect this assumption to hold (see Sect. 2.3).

Our Contribution

Considering the practical difficulties in applying GLS, and the limited modelling power of bottom-up, top-down, middle-out methods, we try to approach HTS forecasting in a slightly different way. All these previous approaches have been restricted by combining the requirement of aggregate consistency with the goal of sharing information between hierarchical levels. Instead, we propose to separate these steps, which leads to an easier way of thinking about the problem. As our main contribution, we will introduce a Game-Theoretically OPtimal (GTOP) reconciliation method to map any given set of forecasts, which need not be aggregate consistent, to new aggregate consistent forecasts that are guaranteed to be at least as good. As the GTOP method requires no assumptions about the probability structure of the time series or the nature of the given set of forecasts, it leaves a forecaster completely free to use the prediction method of their choice at all levels of the hierarchy without worrying about aggregate consistency or theoretical restrictions like unbiasedness of their forecasts. As illustrated in Sect. 3.2, taking aggregate consistency out of the equation allows one to go beyond simple bottom-up, top-down or middle-out estimators, and consider estimators that use more complicated regression structures, in the same spirit as those considered by Lütkepohl [13, Section 5.3].

Outline

In the next section, we present the GTOP method and formally relate it to the GLS approach. Then, in Sect. 3, we demonstrate how GTOP may be applied with forecasts that do not satisfy the traditional unbiasedness assumption, first on simulated data, and then on real electricity demand data. Finally, Sect. 4 provides an extensive discussion.

2 Game-Theoretically Optimal Reconciliation

We will now introduce the GTOP method, which takes as input a set of forecasts, which need not be aggregate consistent, and produces as output new aggregate consistent forecasts that are guaranteed to be at least as good. In Sect. 2.1, we first present the method for the simplest possible hierarchies, which are composed of two levels only, and then, in Sect. 2.2, we explain how the procedure generalizes in a straightforward way to arbitrary hierarchies. Proofs and computational details are postponed until the end of Sect. 2.2. Finally, in Sect. 2.3, we show how GTOP reconciliation may formally be interpreted as a special case of GLS, although the quantities involved have different interpretations.

2.1 Two-Level Hierarchies

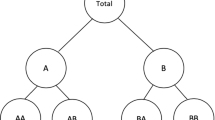
For two-level hierarchies, we will refer to the lower levels as regions, in reference to our motivating application of electricity demand forecasting, even though for other applications the lower levels might correspond to something else. Suppose there are K such regions, and we are not only interested in forecasting the values of a time series \((Y _{k}[t])_{t=1,2,\ldots }\) for each individual region k = 1, …, K, but also in forecasting the sum of the regions \((Y _{\mathrm{tot}}[t])_{t=1,2,\ldots }\), where

$$\displaystyle{ Y _{\mathrm{tot}}[t] =\sum _{ k=1}^{K}Y _{ k}[t]\qquad \mbox{ for all $t$}, }$$
(1)

as illustrated by Fig. 1.

Fig. 1
figure 1

A two-level hierarchical time series structure

Full size image

Having observed the time series for times 1, …, t, together with possible independent variables, we will be concerned with making predictions for their values at time τ > t, but to avoid clutter, we will drop the time index [τ] from our notation whenever it is sufficiently clear from context. Thus, for any region k, let \(\hat{Y }_{k} \equiv \hat{ Y }_{k}[\tau ]\) be the prediction for \(Y _{k} \equiv Y _{k}[\tau ]\), and let \(\hat{Y }_{\mathrm{tot}} \equiv \hat{ Y }_{\mathrm{tot}}[\tau ]\) be the prediction for \(Y _{\mathrm{tot}} \equiv Y _{\mathrm{tot}}[\tau ]\). Then we evaluate the quality of our prediction for region k by the squared loss

$$\displaystyle{ \ell_{k}(Y _{k},\hat{Y }_{k}) = a_{k}(Y _{k} -\hat{ Y }_{k})^{2}, }$$

where a k  > 0 is a weighting factor that is determined by the operational costs associated with prediction errors in region k. (We give some guidelines for the choice of these weighting factors in Sect. 4.1.) Similarly, our loss in predicting the sum of the regions is

$$\displaystyle{ \ell_{\mathrm{tot}}(Y _{\mathrm{tot}},\hat{Y }_{\mathrm{tot}}) = a_{\mathrm{tot}}(Y _{\mathrm{tot}} -\hat{ Y }_{\mathrm{tot}})^{2}, }$$

with a tot > 0. Let Y = (Y 1, …, \(Y _{K},Y _{\mathrm{tot}})\) and \(\hat{\mathbf{Y}} = (\hat{Y }_{1},\ldots,\hat{Y }_{K},\hat{Y }_{\mathrm{tot}})\). Then, all together, our loss at time τ is

$$\displaystyle{ \ell(\mathbf{Y},\hat{\mathbf{Y}}) =\sum _{ k=1}^{K}\ell_{ k}(Y _{k},\hat{Y }_{k}) +\ell _{\mathrm{tot}}(Y _{\mathrm{tot}},\hat{Y }_{\mathrm{tot}}). }$$

Aggregate Inconsistency

In predicting the total Y tot, we might be able to take advantage of covariates that are only available at the aggregate level or there might be noise that cancels out between regions, so that we have to anticipate that \(\hat{Y }_{\mathrm{tot}}\) may be a better prediction of Y tot than simply the sum of the regional predictions \(\sum _{k=1}^{K}\hat{Y }_{k}\), and generally we may have \(\hat{Y }_{\mathrm{tot}}\neq \sum _{k=1}^{K}\hat{Y }_{k}\).Footnote 1 In light of (1), allowing such an aggregate inconsistency between the regional predictions and the prediction for the total would intuitively seem suboptimal. More importantly, for operational reasons it is sometimes not even allowed. For example, in the Global Energy Forecasting Competition 2012 [10], it was required that the sum of the regional predictions \(\hat{Y }_{1},\ldots,\hat{Y }_{K}\) were always equal to the prediction for the total \(\hat{Y }_{\mathrm{tot}}\). Or, if the time series represent next year’s budgets for different departments, then the budget for the whole organization must typically be equal to the sum of the budgets for the departments.

We are therefore faced with a choice between two options. The first is that we might try to adjust our prediction methods to avoid aggregate inconsistency. But this would introduce complicated dependencies between our prediction methods for the different regions and for the total, and as a consequence it might make our predictions worse. So, alternatively, we might opt to remedy the problem in a post-processing step: first we come up with the best possible predictions \(\hat{\mathbf{Y}}\) without worrying about any potential aggregate inconsistency, and then we map these predictions to new predictions \(\tilde{\mathbf{Y}} = (\tilde{Y }_{1},\ldots,\tilde{Y }_{K},\tilde{Y }_{\mathrm{tot}})\), which are aggregate consistent:

$$\displaystyle{ \tilde{Y }_{\mathrm{tot}} =\sum _{ k=1}^{K}\tilde{Y }_{ k}. }$$

This is the route we will take in this paper. In fact, it turns out that, for the right mapping, the loss of \(\tilde{\mathbf{Y}}\) will always be smaller than the loss of \(\hat{\mathbf{Y}}\), no matter what the actual data Y turn out to be, which provides a formal justification for the intuition that aggregate inconsistent predictions should be avoided.

Mapping to Aggregate Consistent Predictions

To map any given predictions \(\hat{\mathbf{Y}}\) to aggregate consistent predictions \(\tilde{\mathbf{Y}}\), we will use a game-theoretic set-up that is reminiscent of the game-theoretic approach to online learning [5]. In this formulation, we will choose our predictions \(\tilde{\mathbf{Y}}\) to achieve the minimum in the following minimax optimization problem:

$$\displaystyle{ V =\min _{\tilde{\mathbf{Y}}\in \mathcal{A}}\max _{\mathbf{Y}\in \mathcal{A}\cap \mathcal{B}}\Big\{\ell(\mathbf{Y},\tilde{\mathbf{Y}}) -\ell (\mathbf{Y},\hat{\mathbf{Y}})\Big\}. }$$
(2)

(The sets \(\mathcal{A}\) and \(\mathcal{B}\) will be defined below.) This may be interpreted as the Game-Theoretically OPtimal (GTOP) move in a zero-sum game in which we first choose \(\tilde{\mathbf{Y}}\), then the data Y are chosen by an adversary, and finally the pay-off is measured by the difference in loss between \(\tilde{\mathbf{Y}}\) and the given predictions \(\hat{\mathbf{Y}}\). The result is that we will choose \(\tilde{\mathbf{Y}}\) to guarantee that \(\ell(\mathbf{Y},\tilde{\mathbf{Y}}) -\ell (\mathbf{Y},\hat{\mathbf{Y}})\) is at most V no matter what the data Y are. Satisfyingly, we shall see below that V ≤ 0, so that the new predictions \(\tilde{\mathbf{Y}}\) are always at least as good as the original predictions \(\hat{\mathbf{Y}}\).

We have left open the definitions of the sets \(\mathcal{A}\) and \(\mathcal{B}\), which represent the domains for our predictions and the data. The former of these will represent the set of vectors that are aggregate consistent:

$$\displaystyle{ \mathcal{A} =\Big\{ (X_{1},\ldots,X_{K},X_{\mathrm{tot}}) \in \mathbb{R}^{K+1}\mid X_{\mathrm{ tot}} =\sum _{ k=1}^{K}X_{ k}\Big\}. }$$

By definition, both our predictions \(\tilde{\mathbf{Y}}\) and the data Y must be aggregate consistent, so they are restricted to lie in \(\mathcal{A}\). In addition, we introduce the set \(\mathcal{B}\), which allows us to specify any other information we might have about the data. In the simplest case, we may let \(\mathcal{B} = \mathbb{R}^{K+1}\) so that \(\mathcal{B}\) imposes no constraints, but if, for example, prediction intervals \([\hat{Y }_{k} - B_{k},\hat{Y }_{k} + B_{k}]\) are available for the given predictions, then we may take advantage of that knowledge and define

$$\displaystyle{ \mathcal{B} =\Big\{ (X_{1},\ldots,X_{K},X_{\mathrm{tot}}) \in \mathbb{R}^{K+1}\mid X_{ k} \in [\hat{Y }_{k} - B_{k},\hat{Y }_{k} + B_{k}]\mbox{ for $k = 1,\ldots,K$}\Big\}. }$$
(3)

We could also add a prediction interval for \(\hat{Y }_{\mathrm{tot}}\) as long as we take care that all our prediction intervals together do not contradict aggregate consistency of the data. In general, we will require that \(\mathcal{B}\subseteq \mathbb{R}^{K+1}\) is a closed and convex set, and \(\mathcal{A}\cap \mathcal{B}\) must be non-empty so that \(\mathcal{B}\) does not contradict aggregate consistency.

GTOP Predictions as a Projection

Let \(\|\mathbf{X}\| = (\sum _{i=1}^{d}X_{i}^{2})^{1/2}\) denote the L2-norm of a vector \(\mathbf{X} \in \mathbb{R}^{d}\) for any dimension d. Then the total loss may succinctly be written as

$$\displaystyle{ \ell(\mathbf{Y},\hat{\mathbf{Y}}) =\| A\mathbf{Y} - A\hat{\mathbf{Y}}\|^{2}, }$$
(4)

where \(A =\mathop{ \mathrm{diag}}\nolimits (\sqrt{a_{1}},\ldots,\sqrt{a_{K}},\sqrt{a_{\mathrm{tot }}})\) is a diagonal \((K + 1) \times (K + 1)\) matrix that accounts for the weighting factors. In view of the loss, it is quite natural that the GTOP predictions turn out to be equal to the L2-projection

$$\displaystyle{ \tilde{\mathbf{Y}}_{\mathrm{proj}} =\mathop{ \mathrm{arg\,min}}\limits _{\tilde{\mathbf{Y}}\in \mathcal{A}\cap \mathcal{B}}\|A\hat{\mathbf{Y}} - A\tilde{\mathbf{Y}}\|^{2} }$$
(5)

of \(\hat{\mathbf{Y}}\) unto \(\mathcal{A}\cap \mathcal{B}\) after scaling all dimensions according to A.

Theorem 1 (GTOP: Two-level Hierarchies)

Suppose that \(\mathcal{B}\) is a closed, convex set and that \(\mathcal{A}\cap \mathcal{B}\) is not empty. Then the projection \(\tilde{\mathbf{Y}}_{\mathrm{proj}}\) uniquely exists, the value of (2) is

$$\displaystyle{ V = -\|A\tilde{\mathbf{Y}}_{\mathrm{proj}} - A\hat{\mathbf{Y}}\|^{2} \leq 0, }$$

and the GTOP predictions are \(\tilde{\mathbf{Y}} =\tilde{ \mathbf{Y}}_{\mathrm{proj}}\) .

Thus, in a metric that depends on the loss, GTOP makes the minimal possible adjustment of the given predictions \(\hat{\mathbf{Y}}\) to make them consistent with what we know about the data. Moreover, the fact that V ≤ 0 implies that the GTOP predictions are at least as good as the given predictions:

$$\displaystyle{ \ell(\mathbf{Y},\tilde{\mathbf{Y}}_{\mathrm{proj}}) \leq \ell (\mathbf{Y},\hat{\mathbf{Y}})\qquad \mbox{ for any data $\mathbf{Y} \in \mathcal{A}\cap \mathcal{B}$}. }$$

Theorem 1 will be proved as a special case of Theorem 2 in the next section.

Example 1

If \(\mathcal{B} = \mathbb{R}^{K+1}\) does not impose any constraints, then the GTOP predictions are

$$\displaystyle\begin{array}{rcl} \tilde{Y }_{\mathrm{proj},k}& =& \hat{Y }_{k}\ \ + \frac{ \frac{1} {a_{k}}} {\sum _{i=1}^{K} \frac{1} {a_{i}} + \frac{1} {a_{\mathrm{tot}}} } \varDelta \quad \mbox{ for $k = 1,\ldots,K$}, {}\\ \tilde{Y }_{\mathrm{proj},\mathrm{tot}}& =& \hat{Y }_{\mathrm{tot}} - \frac{ \frac{1} {a_{\mathrm{tot}}} } {\sum _{i=1}^{K} \frac{1} {a_{i}} + \frac{1} {a_{\mathrm{tot}}} } \varDelta, {}\\ \end{array}$$

where \(\varDelta =\hat{ Y }_{\mathrm{tot}} -\sum _{k=1}^{K}\hat{Y }_{k}\) measures by how much \(\hat{\mathbf{Y}}\) violates aggregate consistency. In particular, if the given predictions \(\hat{\mathbf{Y}}\) are already aggregate consistent, i.e. \(\hat{Y }_{\mathrm{tot}} =\sum _{ k=1}^{K}\hat{Y }_{k}\), then the GTOP predictions are the same as the given predictions: \(\tilde{\mathbf{Y}}_{\mathrm{proj}} =\hat{ \mathbf{Y}}\).

Example 2

If \(\mathcal{B}\) consists of the prediction intervals specified in (3), then the extreme values \(B_{1} =\ldots = B_{K} = 0\) make the GTOP predictions exactly equal to those of the bottom-up forecaster.

Example 3

If \(\mathcal{B}\) defines prediction intervals as in (3) and \(a_{1} = \cdots = a_{K} = a\) and \(B_{1} = \cdots = B_{K} = B\), then the GTOP predictions are

$$\displaystyle\begin{array}{rcl} \tilde{Y }_{\mathrm{proj},k}& =& \hat{Y }_{k} +\Big [ \frac{\frac{1} {a}} {\frac{K} {a} + \frac{1} {a_{\mathrm{tot}}} } \varDelta \Big]_{B}\quad \mbox{ for $k = 1,\ldots,K$}, {}\\ \tilde{Y }_{\mathrm{proj},\mathrm{tot}}& =& \sum _{k=1}^{K}\tilde{Y }_{\mathrm{ proj},k}, {}\\ \end{array}$$

where \([x]_{B} =\max \big\{ -B,\min \{B,x\}\big\}\) denotes clipping x to the interval [−B, B] and \(\varDelta =\hat{ Y }_{\mathrm{tot}} -\sum _{k=1}^{K}\hat{Y }_{k}\).

In general the GTOP predictions \(\tilde{\mathbf{Y}}_{\mathrm{proj}}\) do not have a closed-form solution, but, as long as \(\mathcal{B}\) can be described by a finite set of inequality constraints, they can be computed using quadratic programming. The details will be discussed at the end of the next section, which generalizes the two-level hierarchies introduced so far to arbitrary summation constraints.

2.2 General Summation Constraints

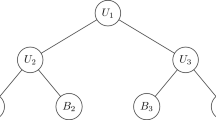
One might view (1) as forecasting K + 1 time series, which are ordered in a hierarchy with two levels, in which the time series (Y 1[t]), …, (Y K [t]) for the regions are at the bottom, and their total (Y tot[t]) is at the top (see Fig. 1). More generally, one might imagine having a multi-level hierarchy of any finite number of time series \((Y _{1}[t]),\ldots,(Y _{M}[t])\), which are organised in a tree T that represents the hierarchy of aggregation consistency requirements. For example, in Fig. 2 the time series (Y 1[t]) might be the expenditure of an entire organisation, the time series \((Y _{2}[t]),(Y _{3}[t])\), and (Y 4[t]) might be the expenditures in different subdivisions within the organization, time series \((Y _{5}[t]),(Y _{6}[t])\) and (Y 7[t]) might represent the expenditures in departments within subdivision (Y 2[t]), and similarly (Y 8[t]) and (Y 9[t]) would be the expenditures in departments within (Y 3[t]).

Fig. 2
figure 2

Example of a multi-level hierarchical time series structure

Full size image

The discussion from the previous section directly extends to multi-level hierarchies as follows. For each time series m = 1, …, M, let c(m) ⊂ { 1, …, M} denote the set of its children in T. Then aggregate consistency generalizes to the constraint

$$\displaystyle{ \mathcal{A} =\Big\{ (X_{1},\ldots,X_{M}) \in \mathbb{R}^{M}\mid X_{ m} =\sum _{i\in c(m)}\!\!\!X_{i}\mbox{ for all $m$ such that $c(m)$ is non-empty}\Big\}. }$$

Remark 1

We note that all the constraints \(X_{m} =\sum _{i\in c(m)}X_{i}\) in \(\mathcal{A}\) are linear equality constraints. In fact, in all the subsequent developments, including Theorem 2, we can allow \(\mathcal{A}\) to be any set of linear equality constraints, as long as they are internally consistent, so that \(\mathcal{A}\) is not empty. In particular, we could even allow two (or more) predictions for the same time series by regarding the first prediction as a prediction for a time series (Y m [t]) and the second as a prediction for a separate time series (Y m′[t]) with the constraint that Y m [t] = Y m′[t]. To keep the exposition focussed, however, we will not explore these possibilities in this paper.

Having defined the structure of the hierarchical time series through \(\mathcal{A}\), any additional information we may have about the data can again be represented by choosing a convex, closed set \(\mathcal{B}\subseteq \mathbb{R}^{M}\) which is such that \(\mathcal{A}\cap \mathcal{B}\) is non-empty. In particular, \(\mathcal{B} = \mathbb{R}^{M}\) represents having no further information, and prediction intervals can be represented analogously to (3) if they are available.

As in the two-level hierarchy, let \(\hat{\mathbf{Y}} = (\hat{Y }_{1},\ldots,\hat{Y }_{M})\) be the original (potentially aggregate inconsistent) predictions for the time series \(\mathbf{Y} = (Y _{1},\ldots,Y _{M})\) at a given time τ. We assign weighting factors a m  > 0 to each of the time series m = 1, …, M, and we redefine the diagonal matrix \(A =\mathop{ \mathrm{diag}}\nolimits (\sqrt{a_{1}},\ldots,\sqrt{a_{M}})\), so that we may write the total loss as in (4). Then the GTOP predictions \(\tilde{\mathbf{Y}} = (\tilde{Y }_{1},\ldots,\tilde{Y }_{M})\) are still defined as those achieving the minimum in (2), and the L2-projection \(\tilde{\mathbf{Y}}_{\mathrm{proj}}\) is as defined in (5).

Theorem 2 (GTOP: Multi-level Hierarchies)

The exact statement of Theorem  1 still holds for the more general definitions for multi-level hierarchies in this section.

The proof of Theorems 1 and 2 fundamentally rests on the Pythagorean inequality, which is illustrated by Fig. 3. In fact, this inequality is not restricted to the squared loss we use in this paper, but holds for any loss that is based on a Bregman divergence [5, Section 11.2], so the proof would go through in exactly the same way for such other losses. For example, the Kullback-Leibler divergence, which measures the difference between two probability distributions, is also a Bregman divergence.

Fig. 3
figure 3

Illustration of the Pythagorean inequality P 2 + Q 2 ≤ R 2, where \(P =\| A\mathbf{Y} - A\tilde{\mathbf{Y}}_{\mathrm{proj}}\|\), \(Q =\| A\tilde{\mathbf{Y}}_{\mathrm{proj}} - A\hat{\mathbf{Y}}\|\) and \(R =\| A\mathbf{Y} - A\hat{\mathbf{Y}}\|\). Convexity of \(\mathcal{A}\cap \mathcal{B}\) ensures that γ ≥ 90∘

Full size image

Lemma 1 (Pythagorean Inequality)

Suppose that \(\mathcal{B}\) is a closed, convex set and that \(\mathcal{A}\cap \mathcal{B}\) is non-empty. Then the projection \(\tilde{\mathbf{Y}}_{\mathrm{proj}}\) exists and is unique, and

$$\displaystyle{ \|A\mathbf{Y} - A\tilde{\mathbf{Y}}_{\mathrm{proj}}\|^{2} +\| A\tilde{\mathbf{Y}}_{\mathrm{ proj}} - A\hat{\mathbf{Y}}\|^{2} \leq \| A\mathbf{Y} - A\hat{\mathbf{Y}}\|^{2}\qquad \mbox{ for all $\mathbf{Y} \in \mathcal{A}\cap \mathcal{B}$.} }$$

Proof

The lemma is an instance of the generalized Pythagorean inequality [5, Section 11.2] for the Bregman divergence corresponding to the Legendre function \(F(\mathbf{X}) =\| A\mathbf{X}\|^{2}\), which is strictly convex (as required) because all entries of the matrix A are strictly positive. (The set \(\mathcal{A}\) is a hyperplane, so it is closed and convex by construction. The assumptions of the lemma therefore ensure that \(\mathcal{A}\cap \mathcal{B}\) is closed, convex and non-empty.) ⊓⊔

Proof (Theorem 2)

Let \(f(\mathbf{Y},\tilde{\mathbf{Y}}) =\ell (\mathbf{Y},\tilde{\mathbf{Y}}) -\ell (\mathbf{Y},\hat{\mathbf{Y}})\). We will show that \((\tilde{\mathbf{Y}}_{\mathrm{proj}},\tilde{\mathbf{Y}}_{\mathrm{proj}})\) is a saddle-point for f, which implies that playing \(\tilde{\mathbf{Y}}_{\mathrm{proj}}\) is the optimal strategy for both players in the zero-sum game and that

$$\displaystyle{ V =\min _{\tilde{\mathbf{Y}}\in \mathcal{A}}\max _{\mathbf{Y}\in \mathcal{A}\cap \mathcal{B}}f(\mathbf{Y},\tilde{\mathbf{Y}}) =\max _{\mathbf{Y}\in \mathcal{A}\cap \mathcal{B}}\min _{\tilde{\mathbf{Y}}\in \mathcal{A}}f(\mathbf{Y},\tilde{\mathbf{Y}}) = f(\tilde{\mathbf{Y}}_{\mathrm{proj}},\tilde{\mathbf{Y}}_{\mathrm{proj}}) = -\|A\tilde{\mathbf{Y}}_{\mathrm{proj}}-A\hat{\mathbf{Y}}\|^{2} }$$

[15, Lemma 36.2], which is to be shown.

To prove that \((\tilde{\mathbf{Y}}_{\mathrm{proj}},\tilde{\mathbf{Y}}_{\mathrm{proj}})\) is a saddle-point, we need to show that neither player can improve their pay-off by changing their move. To this end, we first observe that, by the Pythagorean inequality (Lemma 1),

$$\displaystyle\begin{array}{rcl} f(\mathbf{Y},\tilde{\mathbf{Y}}_{\mathrm{proj}}) =\| A\mathbf{Y} - A\tilde{\mathbf{Y}}_{\mathrm{proj}}\|^{2} -\| A\mathbf{Y} - A\hat{\mathbf{Y}}\|^{2} \leq -\|A\tilde{\mathbf{Y}}_{\mathrm{ proj}} - A\hat{\mathbf{Y}}\|^{2} = f(\tilde{\mathbf{Y}}_{\mathrm{ proj}},\tilde{\mathbf{Y}}_{\mathrm{proj}})& & {}\\ \end{array}$$

for all \(\mathbf{Y} \in \mathcal{B}\cap \mathcal{A}\). It follows that the maximum is achieved by \(\mathbf{Y} =\tilde{ \mathbf{Y}}_{\mathrm{proj}}\). Next, we also have

$$\displaystyle{ \mathop{\mathrm{arg\,min}}\limits _{\tilde{\mathbf{Y}}\in \mathcal{A}}f(\tilde{\mathbf{Y}}_{\mathrm{proj}},\tilde{\mathbf{Y}}) =\mathop{ \mathrm{arg\,min}}\limits _{\tilde{\mathbf{Y}}\in \mathcal{A}}\|A\tilde{\mathbf{Y}}_{\mathrm{proj}} - A\tilde{\mathbf{Y}}\|^{2} =\tilde{ \mathbf{Y}}_{\mathrm{ proj}}, }$$

which completes the proof. □ 

Efficient Computation

For special cases, like the examples in the previous section, the GTOP projection \(\tilde{\mathbf{Y}}_{\mathrm{proj}}\) sometimes has a closed form. In general, no closed-form solution may be available, but \(\tilde{\mathbf{Y}}_{\mathrm{proj}}\) can still be computed by finding the solution to the quadratic program

$$\displaystyle{\begin{array}{rl} \min _{\tilde{\mathbf{Y}}}\qquad \quad &\|A\hat{\mathbf{Y}} - A\tilde{\mathbf{Y}}\|^{2} \\ \text{subject to}\qquad \quad &\tilde{\mathbf{Y}} \in \mathcal{A}\cap \mathcal{B}.\end{array} }$$

Since \(\mathcal{A}\) imposes only equality constraints, this quadratic program can be solved efficiently as long as the further constraints imposed by \(\mathcal{B}\) are manageable. In particular, if \(\mathcal{B}\) imposes only linear inequality constraints, like, for example, in (3), then the solution can be found efficiently using interior point methods [12] or using any of the alternatives suggested by Hazan et al. [9, Section 4]. The experiments in Sect. 3 were all implemented using the quadprog package for the R programming language, which turned out to be fast enough.

2.3 Formal Relation to Generalized Least-Squares

As discussed in the introduction, HTS has been modelled as a problem of linear regression in the economics literature [4]. It is interesting to compare this approach to GTOP, because the two turn out to be very similar, except that the quantities involved have different interpretations. The linear regression approach models the predictions as functions of the means of the real data

$$\displaystyle{ \hat{\mathbf{Y}}[\tau ] = \mathbb{E}\big\{\mathbf{Y}[\tau ]\big\} +\varepsilon [\tau ] }$$

that are perturbed by a noise vector \(\varepsilon [\tau ] = (\varepsilon _{1}[\tau ],\ldots,\varepsilon _{M}[\tau ])\), where all distributions and expectations are conditional on all previously observed values of the time series. Then it is assumed that the predictions are unbiased estimates, so that the noise variables all have mean zero, and the true means \(\mathbb{E}\{\mathbf{Y}[\tau ]\}\) can be estimated using the generalized least-squares (GLS) estimate

$$\displaystyle{ \begin{array}{rl} \min _{\tilde{\mathbf{Y}}}\qquad \quad &(\hat{\mathbf{Y}} -\tilde{\mathbf{Y}})^{\top }\varSigma ^{-1}(\hat{\mathbf{Y}} -\tilde{\mathbf{Y}}) \\ \text{subject to}\qquad \quad &\tilde{\mathbf{Y}} \in \mathcal{A},\end{array} }$$
(6)

where \(\varSigma \equiv \varSigma [\tau ]\) is the M × M covariance matrix for the noise \(\varepsilon [\tau ]\) [4]. This reveals an interesting superficial relation between the GTOP forecasts and the GLS estimates: if

$$\displaystyle{ \varSigma ^{-1} = A^{\top }A\qquad \mbox{ and }\qquad \mathcal{B} = \mathbb{R}^{M}, }$$
(7)

then the two coincide! However, the interpretation of A and Σ −1 is completely different, and the two procedures serve different purposes: whereas GLS tries to address both reconciliation and the goal of sharing information between hierarchical levels at the same time, the GTOP method is only intended to do reconciliation and requires a separate procedure to share information. The case where the two methods coincide is therefore only a formal coincidence, and one should not assume that the choice \(\varSigma ^{-1} = A^{\top }A\) will adequately take care of sharing information between hierarchical levels!

Ordinary Least-squares

Given the difficulty of estimating Σ, Hyndman et al. [11] propose an assumption that allows them to sidestep estimation of Σ altogether: they show that, under their assumption, the GLS estimate reduces to the Ordinary Least-squares (OLS) estimate obtained from (6) by the choice

$$\displaystyle{ \varSigma = I, }$$

where I is the identity matrix. Via (7) it then follows that the OLS and GTOP forecasts formally coincide when we take all the weighting factors in the definition of the loss to be equal: \(a_{1} =\ldots = a_{M}\), and let \(\mathcal{B} = \mathbb{R}^{M}\). Consequently, for two-level hierarchies, OLS can be computed as in Example 1.

The assumption proposed by Hyndman et al. [11] is that, at time τ, the covariance \(\mathop{\mathrm{Cov}}\nolimits (\hat{Y }_{m},\hat{Y }_{m'})\) of the predictions for any two time series decomposes as

$$\displaystyle{ \mathop{\mathrm{Cov}}\nolimits (\hat{Y }_{m},\hat{Y }_{m'}) =\sum _{\begin{array}{c}i\in S(m) \\ j\in S(m')\end{array}}\mathop{ \mathrm{Cov}}\nolimits (\hat{Y }_{i},\hat{Y }_{j})\quad \mbox{ for all $m,m'$,} }$$
(8)

where S(m) ⊆ { 1, …, M} denotes the set of bottom-level time series out of which Y m is composed. That is, \(Y _{m} =\sum _{i\in S(m)}Y _{i}\) with Y i childless (i.e. \(c(i) =\emptyset\)) for all i ∈ S(m).

Although the OLS approach appears to work well in practice (see Sect. 3.2), it is not obvious when we can expect (8) to hold. Hyndman et al. [11] motivate it by pointing out that (8) would hold exactly if the forecasts would be exactly aggregate consistent (i.e. \(\hat{\mathbf{Y}} \in \mathcal{A}\)). Since it is reasonable to assume that the forecasts will be approximately aggregate consistent, it then also seems plausible that (8) will hold approximately. However, this motivation seems insufficient, because reasoning as if the forecasts are aggregate consistent leads to conclusions that are too strong: if \(\hat{\mathbf{Y}} \in \mathcal{A}\), then any instance of GLS would give the same answer, so it would not matter which Σ we used, and in the experiments in Sect. 3 we see that this clearly does matter.

We therefore prefer to view OLS rather as a special case of GTOP, which will work well when all the weighting factors in the loss are equal and the constraints in \(\mathcal{B}\) are vacuous.

3 Experiments

As discussed above, the GTOP method only solves the reconciliation part of HTS forecasting; it does not prescribe how to construct the original predictions \(\hat{\mathbf{Y}}\). We will now illustrate how GTOP might be used in practice, taking advantage of the fact that it does not require the original predictions \(\hat{\mathbf{Y}}\) to be unbiased. First, in Sect. 3.1, we present a toy example with simulated data, which nevertheless illustrates many of the difficulties one might encounter on real data. Then, in Sect. 3.2, we apply GTOP to real electricity demand data, which motivated its development.

3.1 Simulation Study

We use GTOP with prediction intervals as in (3). We will compare to bottom-up forecasting, and also to the OLS method described in Sect. 2.3, because it appears to work well in practice (see Sect. 3.2) and it is one of the few methods available that does not require estimating any parameters. We do not compare to top-down forecasting, because estimating proportions in top-down forecasting is troublesome in the presence of independent variables (see Sect. 4.2).

Data

We consider a two-level hierarchy with two regions, and simulate data according to

$$\displaystyle\begin{array}{rcl} Y _{1}[t] =\beta _{1,0} +\beta _{1,1}X[t] +\epsilon _{1}[t]\qquad \ \ Y _{2}[t] =\beta _{2,0} +\beta _{2,1}X[t] +\epsilon _{2}[t]& & {}\\ \end{array}$$

where (X[t]) is an independent variable, \(\beta _{1} = (\beta _{1,0},\beta _{1,1})\) and \(\beta _{2} = (\beta _{2,0},\beta _{2,1})\) are coefficients to be estimated, and (ε 1[t]) and (ε 2[t]) are noise variables. We will take \(\beta _{1} =\beta _{2} = (1,5)\), and let

$$\displaystyle\begin{array}{rcl} \epsilon _{1}[t] =\tau \vartheta _{1}[t] +\sigma \upsilon [t]\qquad \ \ \epsilon _{2}[t] =\tau \vartheta _{2}[t] -\sigma \upsilon [t]\qquad \mbox{ for all $t$,}& & {}\\ \end{array}$$

where \(\vartheta _{1}[t],\vartheta _{2}[t]\) and \(\upsilon [t]\) are uniformly distributed on [−1, 1], independently over t and independently of each other, and τ and σ are scale parameters, for which we will consider different values. Notice that the noise that depends on \(\upsilon [t]\) cancels from the total \(Y _{\mathrm{tot}}[t] = Y _{1}[t] + Y _{2}[t]\), which makes the total easier to predict than the individual regions. We sample a train set of size 100 for the fixed design \((X[t])_{t=1,\ldots,100} = (1/100,2/100,\ldots,1)\) and a test set of the same size for \((X[t])_{t=101,\ldots,200} = (1 + 1/100,\ldots,2)\).

Fitting Models on the Train Set

Based on the train set, we find estimates \(\hat{\beta }_{1}\) and \(\hat{\beta }_{2}\) of the coefficients β 1 and β 2 by applying the LASSO [17] separately for each of the two regions, using cross-validation to calibrate the amount of penalization. Then we predict Y 1[τ] and Y 2[τ] by

$$\displaystyle\begin{array}{rcl} \hat{Y }_{1}[\tau ] =\hat{\beta } _{1,0} +\hat{\beta } _{1,1}X[\tau ]\qquad \quad \hat{Y }_{2}[\tau ] =\hat{\beta } _{2,0} +\hat{\beta } _{2,1}X[\tau ].& & {}\\ \end{array}$$

Remark 2

In general, it is not guaranteed that forecasting the total Y tot[τ] directly will give better predictions than the bottom-up forecast [13]. Consequently, if the bottom-up forecast is the best we can come up with, then that is how we should define our prediction for the total, and no further reconciliation is necessary!

If we would use the LASSO directly to predict the total Y tot[τ], then, in light of Remark 2, it might not do better than simply using the bottom-up forecast \(\hat{Y }_{1}[\tau ] +\hat{ Y }_{2}[\tau ]\). We can be sure to do better than the bottom-up forecaster, however, by adding our regional forecasts \(\hat{Y }_{1}[\tau ]\) and \(\hat{Y }_{2}[\tau ]\) as covariates, such that we fit Y tot[τ] by

$$\displaystyle{ \beta _{\mathrm{tot},0} +\beta _{\mathrm{tot},1}X[\tau ] +\beta _{\mathrm{tot},2}\hat{Y }_{1}[\tau ] +\beta _{\mathrm{tot},3}\hat{Y }_{2}[\tau ], }$$
(9)

where \(\beta _{\mathrm{tot}} = (\beta _{\mathrm{tot},0},\beta _{\mathrm{tot},1},\beta _{\mathrm{tot},2},\beta _{\mathrm{tot},3})\) are coefficients to be estimated. For β tot = (0, 0, 1, 1) this would exactly give the bottom-up forecast, but now we can also obtain different estimates if the data tell us to use different coefficients. However, to be conservative and take advantage of the prior knowledge that the bottom-up forecast is often quite good, we introduce prior knowledge into the LASSO by regularizing by

$$\displaystyle{ \vert \beta _{\mathrm{tot},0}\vert + \vert \beta _{\mathrm{tot},1}\vert + \vert \beta _{\mathrm{tot},2} - 1\vert + \vert \beta _{\mathrm{tot},3} - 1\vert }$$
(10)

instead of its standard regularization by \(\vert \beta _{\mathrm{tot},0}\vert + \vert \beta _{\mathrm{tot},1}\vert + \vert \beta _{\mathrm{tot},2}\vert + \vert \beta _{\mathrm{tot},3}\vert\), which gives it a preference for coefficients that are close to those of the bottom-up forecast. Thus, from the train set, we obtain estimates \(\hat{\beta }_{\mathrm{tot}} = (\hat{\beta }_{\mathrm{tot},0},\hat{\beta }_{\mathrm{tot},1},\hat{\beta }_{\mathrm{tot},2},\hat{\beta }_{\mathrm{tot},3})\) for β tot, and we predict Y tot[τ] by

$$\displaystyle{ \hat{Y }_{\mathrm{tot}}[\tau ] =\hat{\beta } _{\mathrm{tot},0} +\hat{\beta } _{\mathrm{tot},1}X[\tau ] +\hat{\beta } _{\mathrm{tot},2}\hat{Y }_{1}[\tau ] +\hat{\beta } _{\mathrm{tot},3}\hat{Y }_{2}[\tau ]. }$$

Remark 3

The regularization in (10) can be implemented using standard LASSO software by reparametrizing in terms of \(\beta '_{\mathrm{tot}} = (\beta _{\mathrm{tot},0},\beta _{\mathrm{tot},1},\beta _{\mathrm{tot},2} - 1,\beta _{\mathrm{tot}_{3}} - 1)\) and subtracting \(\hat{Y }_{1}[t]\) and \(\hat{Y }_{2}[t]\) from the observation of Y tot[t] before fitting the model. This gives estimates \(\hat{\beta }'_{\mathrm{tot}} = (\hat{\beta }'_{\mathrm{tot},0},\hat{\beta }'_{\mathrm{tot},1},\hat{\beta }'_{\mathrm{tot},2},\hat{\beta }'_{\mathrm{tot},3})\) for β′tot, which we turn back into estimates \(\hat{\beta }_{\mathrm{tot}} = (\hat{\beta }'_{\mathrm{tot},0},\hat{\beta }'_{\mathrm{tot},1},\hat{\beta }'_{\mathrm{tot},2} + 1,\hat{\beta }'_{\mathrm{tot},3} + 1)\) for β tot.

Reconciliation

The procedure outlined above gives us a set of forecasts \(\hat{\mathbf{Y}} = (\hat{Y }_{1},\hat{Y }_{2},\hat{Y }_{\mathrm{tot}})\) for any time τ, but these forecasts need not be aggregate consistent. It therefore remains to reconcile them. We will compare GTOP reconciliation to the bottom-up forecaster and to the OLS method. To apply GTOP, we have to choose the set \(\mathcal{B}\), which specifies any prior knowledge we may have about the data. The easiest would be to specify no prior knowledge (by taking \(\mathcal{B} = \mathbb{R}^{3}\)), but instead we will opt to define prediction intervals for the two regional predictions as in (3). We will use the same prediction bounds B 1 and B 2 for the entire test set, which are estimated (somewhat simplistically) by the 95 % quantile of the absolute value of the residuals in the corresponding region in the train set.

Results on the Test Set

We evaluate the three reconciliation procedures bottom-up, OLS and GTOP by summing up their losses (4) on the test set, giving the totals L BU, L OLS and L GTOP, which we compare to the sum of the losses \(\hat{L}\) for the unreconciled forecasts by computing the percentage of improvement \((\hat{L} - L)/\hat{L} \times 100\,\%\) for \(L \in \{ L_{\mbox{ BU}},L_{\mbox{ OLS}},L_{\mbox{ GTOP}}\}\). It remains to define the weighting factors a 1, a 2 and a tot in the loss, and the scales σ and τ for the noise variables. We consider five different sets of weighting factors, where the first three treat the two regions symmetrically (by assigning them both weight 1), which seems the most realistic, and the other two respectively introduce a slight and a very large asymmetry between regions, which is perhaps less realistic, but was necessary to find a case where OLS would beat GTOP. Finally, we always let \(\sigma +\tau = 2\), so that the scale of the noise is (somewhat) comparable between experiments. Table 1 shows the median over 100 repetitions of the experiment of the percentages of improvement.

Table 1 Percentage of improvement over unreconciled forecasts for simulated data
Full size table

First, we remark that, in all but one of the cases, GTOP reconciliation performs at least as good as or better than OLS and bottom-up, and GTOP is the only of the three methods that always improves on the unreconciled forecasts, as was already guaranteed by Theorems 1 and 2. Moreover, the only instance where OLS performs better than GTOP (\(a_{1} = 1,a_{2} = a_{\mathrm{tot}} = 20\)), appears to be the least realistic, because the regions are treated very asymmetrically. For all cases where the weights are equal (\(a_{1} = a_{2} = a_{\mathrm{tot}} = 1\)), we see that GTOP and OLS perform exactly the same, which, in light of the equivalence discussed in Sect. 2.3, suggest that the prediction intervals that make up \(\mathcal{B}\) do not have a large effect in this case.

Secondly, we note that the unreconciled predictions are much better than the bottom-up forecasts. Because bottom-up and the unreconciled forecasts make the same predictions \(\hat{Y }_{1}\) and \(\hat{Y }_{2}\) for the two regions, this means that the difference must be in the prediction \(\hat{Y }_{\mathrm{tot}}\) for the sum of the regions, and so, indeed, the method described in (9) and (10) makes significantly better forecasts than the simple bottom-up forecast \(\hat{Y }_{1} +\hat{ Y }_{2}\). We also see an overall trend that the scale of the percentages becomes larger as σ increases (or τ decreases), which may be explained by the fact that forecasting Y tot becomes relatively easier, so that the difference between \(\hat{Y }_{\mathrm{tot}}\) and \(\hat{Y }_{1} +\hat{ Y }_{2}\) gets bigger, and the effect of reconciliation gets larger.

3.2 EDF Data

To illustrate how GTOP reconciliation works on real data, we use electricity demand data provided by Électricité de France (EDF). The data are historical demand records ranging from 1 July 2004 to 31 December 2009, and are sampled each 30 min. The total demand is split up into K = 17 series, each representing a different electricity tariff. The series are divided into a calibration set (from 1 July 2004 to 31 December 2008) needed by the prediction models, and a validation set (from 1 January 2009 to the end) on which we will measure the performance of GTOP.

Every night at midnight, forecasts are required for the whole next day, i.e. for the next 48 time points. We use a non-parametric function-valued forecasting model by Antoniadis et al. [1], which treats every day as a 48-dimensional vector. The model uses all past data on the calibration and validation sets. For every past day d, it considers day d + 1 as a candidate prediction and then it outputs a weighted combination of these candidates in which the weight of day d depends on its similarity to the current day. This forecasting model is used independently on each of the 17 individual series and also on the aggregate series (their total).

We now use bottom-up, OLS and GTOP to reconcile the individual forecasts. Similarly to the simulations in the previous section, the prediction intervals \(B_{1},\ldots,B_{K}\) for GTOP are computed as quantiles of the absolute values of the residuals, except that now we only use the past 2 weeks of data from the validation set, and we use the q-th quantile, where q is a parameter. We note that, for the special case q = 0 %, we would expect B k to be close to 0, which makes GTOP very similar to the bottom-up forecaster. (See Example 2.)

For each of the three methods, the percentages of improvement on the validation set are computed in the same way as in the simulations in the previous section. Table 2 shows their values for different choices of realistic weighting factors, using q = 10 % for GTOP, which was found by optimizing for the weights a tot = 17 and a k  = 1 (k = 1, …, 17), as will be discussed below.

Table 2 Percentage of improvement over unreconciled forecasts for EDF data, using q = 10 % for GTOP
Full size table

We see that GTOP consistently outperforms both the bottom-up and the OLS predictor, with gains that increase with a tot. Unlike in the simulations, however, the bottom-up forecaster is comparable to or even better than the unreconciled forecasts in terms of its percentage of improvement. In light of Remark 2, we have therefore considered simply replacing our prediction for the total by the bottom-up predictor, which would make reconciliation unnecessary. However, when, instead of looking at the percentage of improvement, we count the times when the unreconciled forecaster gives a better prediction for the total than the bottom-up forecaster, we see that this is 56 %, so the unreconciled forecaster does predict better than bottom-up slightly more than half of the time, and consequently there is something to gain by using it. As will be discussed next, this does make it necessary to use a small quantile q with GTOP.

Choosing the Quantile

To determine which quantile q to choose for GTOP, we plot its percentage of improvement as a function of q for the case a tot = 17 and a k  = 1 (see Fig. 4). We see that all values below 60 % improve on the bottom-up forecaster, and that any value below 30 % improves on OLS. The quantile q ≈ 10 % gives the best results, and, for ease of comparison, we use this same value in all the experiments reported in Table 2. In light of the interpretation of the prediction intervals, it might appear surprising that the optimal value for q would be so small. This can be explained by the fact that the unreconciled forecasts are only better than bottom-up 56 % of the time, so that a small value of q is beneficial, because it keeps the GTOP forecasts close to the bottom-up ones.

Fig. 4
figure 4

Percentages of improvement as a function of q for GTOP, OLS and bottom-up, using a tot = 17 and a k  = 1 (k = 1, …, 17)

Full size image

4 Discussion

We now turn to several subjects that we have not been able to treat in full detail in the previous parts of the paper. First, in Sect. 4.1, we discuss appropriate choices for the weighting factors that determine the loss. Then, in Sect. 4.2, we discuss how estimating proportions in top-down forecasting is complicated by the presence of independent variables, and, finally, in Sect. 4.3, we conclude with a summary of the paper and directions for future work.

4.1 How to Choose the Weighting Factors in the Loss

In the General Forecasting Competition 2012 [10], a two-level hierarchy was considered with weights chosen as a k  = 1 for k = 1, …, K and a tot = K, so that the forecast for the total receives the same weight as all the regional forecasts taken together. At first sight this appears to make sense, because predicting the total is more important than predicting any single region. However, one should also take into account the fact that the errors in the predictions for the total are on a much larger scale than the errors in the predictions for the regions, so that the total is already a dominant factor in the loss without assigning it a larger weight.

To make this argument more precise, let us consider a simplified setting in which we can compute expected losses. To this end, define random variables \(\epsilon _{k} = Y _{k} -\hat{ Y }_{k}\) for the regional prediction errors at time τ and assume that, conditionally on all prior observations, (1) \(\epsilon _{1},\ldots,\epsilon _{K}\) are uncorrelated; and (2) the regional predictions are unbiased, so that \(\mathbb{E}\{\epsilon _{k}\} = 0\). Then the expected losses for the regions and the total are

$$\displaystyle\begin{array}{rcl} \mathbb{E}\ell_{k}(Y _{k},\hat{Y }_{k})& =& a_{k}\mathbb{E}\big\{(Y _{k} -\hat{ Y }_{k})^{2}\big\} = a_{ k}\mathop{ \mathrm{Var}}\nolimits (\epsilon _{k})\qquad (k = 1,\ldots,K) {}\\ \mathbb{E}\ell_{\mathrm{tot}}(Y _{\mathrm{tot}},\hat{Y }_{\mathrm{tot}})& =& a_{\mathrm{tot}}\mathbb{E}\big\{(\sum _{k}Y _{k} -\sum _{k}\hat{Y }_{k})^{2}\big\} = a_{\mathrm{ tot}}\mathop{ \mathrm{Var}}\nolimits \Big(\sum _{k=1}^{K}\epsilon _{ k}\Big) = a_{\mathrm{tot}}\sum _{k=1}^{K}\mathop{ \mathrm{Var}}\nolimits (\epsilon _{ k}), {}\\ \end{array}$$

where \(\mathop{\mathrm{Var}}\nolimits (Z)\) denotes the variance of a random variable Z.

We see that, even without assigning a larger weight to the total, \(\mathbb{E}\ell_{\mathrm{tot}}(Y _{\mathrm{tot}},\hat{Y }_{\mathrm{tot}})\) is already of the same order as the sum of all \(\mathbb{E}\ell_{k}(Y _{k},\hat{Y }_{k})\) together, which suggests that choosing a tot to be 1 or 2 (instead of K) might already be enough to assign sufficient importance to the prediction of the total.

4.2 The Limits of Top-Down Forecasting

As a thought experiment, think of a noiseless situation in which

$$\displaystyle\begin{array}{rcl} Y _{1}[t] = X[t],\qquad Y _{2}[t] = X[t] + 1,\qquad Y _{\mathrm{tot}}[t] = Y _{1}[t] + Y _{2}[t] = 2X[t] + 1& & {}\\ \end{array}$$

for some independent variable (X[t]). Suppose we use the following top-down approach: first we estimate Y tot[τ] by \(\hat{Y }_{\mathrm{tot}}[\tau ]\) and then we make regional forecasts as \(\hat{Y }_{1}[\tau ] =\lambda \hat{ Y }_{\mathrm{tot}}[\tau ]\) and \(\hat{Y }_{2}[\tau ] = (1-\lambda )\hat{Y }_{\mathrm{tot}}[\tau ]\) according to a constant λ that we will estimate. Because we are in a noise-free situation, let us assume that estimation is easy, and that we can predict Y tot[τ] exactly: \(\hat{Y }_{\mathrm{tot}}[\tau ] = Y _{\mathrm{tot}}[\tau ]\). Moreover, we will assume we can choose λ optimally as well. Then how should λ be chosen? We want to fit:

$$\displaystyle\begin{array}{rcl} \lambda = \frac{Y _{1}[t]} {Y _{\mathrm{tot}}[t]} = \frac{1} {2} - \frac{1} {4X[t] + 2},\qquad 1-\lambda = \frac{Y _{2}[t]} {Y _{\mathrm{tot}}[t]} = \frac{1} {2} + \frac{1} {4X[t] + 2}.& & {}\\ \end{array}$$

But now we see that the optimal value for λ depends on X[t], which is not a constant over time! So estimating λ based on historical proportions will not work in the presence of independent variables.

4.3 Summary and Future Work

Unlike previous approaches, like bottom-up, top-down and generalized least-squares forecasting, we propose to split the problem of hierarchical time series forecasting into two parts: first one constructs the best possible forecasts for the time series without worrying about aggregate consistency or theoretical restrictions like unbiasedness, and then one uses the GTOP reconciliation method proposed in Sect. 2 to turn these forecasts into aggregate consistent ones. As shown by Theorems 1 and 2, GTOP reconciliation can only make any given set of forecasts better, and the less consistent the given forecasts are, the larger the improvement guaranteed by GTOP reconciliation.

Our treatment is for the squared loss only, but, as pointed out in Sect. 2, Theorems 1 and 2 readily generalize to any other loss that is based on a Bregman divergence, like for example the Kullback-Leibler divergence. It would be useful to work out this generalization in detail, including the appropriate choice of optimization algorithm to compute the resulting Bregman projection.

In the experiments in Sect. 3, we have proposed some new methods for coming up with the initial forecasts, but although they demonstrate the benefits of GTOP reconciliation, these approaches are still rather simple. In future work, it would therefore be useful to investigate more advanced ways of coming up with initial forecasts, which allow for even more information to be shared between different time series. For example, it would be natural to use a Bayesian approach to model regions that are geographically close as random instances of the same distribution on regions.

Finally, there seems room to do more with the prediction intervals for the GTOP reconciled predictions as defined in (3). It would be interesting to explore data-driven approaches to constructing these intervals, like for example those proposed by Antoniadis et al.[2].