Multi-view Point Cloud Registration Using Affine Shape Distributions

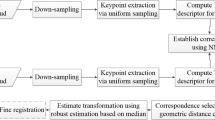
Abstract

Registration is crucial for the reconstruction of multi-view single plane illumination microscopy. By using fluorescent beads as fiduciary markers, this registration problem can be reduced to the problem of point clouds registration. We present a novel method for registering point clouds across views. This is based on a new local geometric descriptor - affine shape distribution - to represent the random spatial pattern of each point and its neighbourhood. To enhance its robustness and discriminative power against the missing data and outliers, a permutation and voting scheme based on affine shape distributions is developed to establish putative correspondence pairs across views. The underlying affine transformations are estimated based on the putative correspondence pairs via the random sample consensus. The proposed method is evaluated on three types of datasets including 3D random points, benchmark datasets and datasets from multi-view microscopy. Experiments show that the proposed method outperforms the state-of-the-arts when both point sets are contaminated by extremely large amount of outliers. Its robustness against the anisotropic z-stretching is also demonstrated in the registration of multi-view microscopy data.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

With recent advances in multi-view single plane illumination microscopy (multi-view SPIM) [1–5], high resolution in vivo volume images for relatively large biological specimens can be obtained by fusing the volume images from multiple views into a single volume. Registration is an essential step to align the volume images across views into one common coordinate system before information fusion. The state-of-the-arts, the bead-based registration [3, 6], use fluorescent beads embedded in the mounting medium around the sample, which allows for accurate and sample-independent reconstruction. By considering the beads as fiduciary markers, the registration for multi-view SPIM can be reduced to the problem of point cloud registration.

Fig. 1.

Point cloud registration for multi-view SPIM. For the point clouds from two views, there exists a common but unknown spatial point patterns (the contour of a fish) as shown in Panels (a) and (b). The underlying spatial transformation between views is affine. As shown in Panel (c), the proposed method aims to detect the points of correspondence and solve for the underlying transformation in the present of an extremely large amount of outliers and missing data in both point clouds.

The bead-based registration for multi-view SPIM brings new challenges to the field of point cloud registration. We use a simple example to illustrate the main challenges of this ill-posed problem, as shown in Fig. 1. Firstly, no presuming geometries or distinctive image features can be used to establish the correspondence pairs of points between views since beads are randomly distributed in the medium without texture information. In addition, there exist optical distortions such as the anisotropic $z$-stretching of each view introduced by the differential refraction index mismatch between water and the mounting medium [3]. Thus, the underlying spatial transformation between views is affine, rather than rigid. Most importantly, the common point patterns across views are contaminated by an extremely large amount of outliers (up to $90\,\%$ of thousands of points) due to the imaging setting of the SPIM: beads can be observed only in the illuminated region under each view, and the overlaps between illuminated regions across views are small. The opacity of samples and light scattering also give rise to missing correspondence in the overlapping region.

Our method tries to overcome the above challenges. We first propose a local geometric descriptor: affine shape distribution. The descriptor represents the affine invariant shapes for local point patterns between views and also takes into account the positional uncertainty of each point. To address the outliers or missing data within the local constellation of each point, a permutation and voting scheme based on affine shape distributions is introduced to enhance its robustness and discriminative power against the missing data and outliers. The common patterns preserved across views are identified by matching the entries of affine shape distribution among all possible combinations of neighbouring points. Next, the difference between affine shape distributions is measured by the Fréchet distance, which allows us to represent each distribution as a high-dimensional vector in Euclidean space. Therefore, a hierarchical tree-based algorithm with logarithmic complexity is used to efficiently search for the putative matching pairs across views among hundreds of thousands of entries due to the highly combinatorial nature of this problem. The underlying affine transformation is estimated based on the putative correspondence pairs via the random sample consensus [7]. Finally, the proposed method is evaluated under different parameter settings and compared against the state-of-the-arts on both the benchmark datasets for point cloud matching and real datasets from multi-view SPIM.

2 Related Works

Point cloud registration is a fundamental yet challenging task in many areas such as computer vision, robotics and autonomous systems and medical image analysis to name but a few (see e.g., [8–10] for comprehensive reviews). Based on the optimization strategies, they can be separated into two main categories.

The methods in the first category employ an objective function, a closed form expression to measure the dissimilarity between the aligned point sets under the tentative transformation. The correspondence detection and transformation estimation is conducted iteratively during the minimization of the objective function. The iterative closest point (ICP) [11] method is one of most well-known algorithm to iteratively find point correspondence based on the nearest neighbour relationship and update the transformations. However, ICP is prone to being trapped in local minima, especially under bad initial alignments. To address this problem, the robust point matching (RPM) [12] relaxes point correspondence to be continuously valued and employs deterministic annealing for optimization. The coherent point draft (CPD) [13] method uses one point set to represent the Gaussian mixture model and converts point matching into the problem of fitting the model to another point set. Similarly, the robust point set matching uses Gaussian mixture model (RPM-GMM) [14] to minimize the distance between two mixtures of Gaussian representing two point sets. Despite their success in many applications, those approaches tend to degrade badly if the proportion of outliers in the point sets become large [15].

Another popular strategy is to use a two-stage process. In the first stage, a set of putative correspondences are computed by using a feature-descriptor distance to reduce the set of possible matches. The second stage is designed to remove the outliers in the correspondence set and estimate the transformation, where a standard procedure to enforce the global geometric consistency of the correspondence is RANSAC [7]. Notably, the first stage is crucial to the success of those methods. If discriminative features (e.g., SIFT [16]) are used, the correspondence detection problem can be greatly alleviated. For problems where the features are non-discriminative, it is pairwise geometric information that helps in finding the right correspondence. The 4-points congruent sets method (4PCs) [17] matches the pairs of widely separated 4 points within the same plane. Spin images [18] compute 2D histograms of points falling within a cylindrical volume by means of a plane spins around the normal of its underlying surface. 3D shape context [19] generalizes the basic idea of spin images by accumulating 3D histograms of points within a sphere centered at the feature point. However, the needs to find the particular geometry such as coplanar four points for 4PCs or the normal of their underlying surface for 3D shape context make them unsuitable for our problem. The most related to our work is the bead-based registration in Fiji-Plugin [3], where the author introduces a translation and rotation invariant local geometric descriptor by representing each point as a vector in the six-dimensional descriptor space. The vector was determined by the unique constellation of its four neighbouring points and similar descriptors in different views had a small Euclidean distance. The drawback of this descriptor is its sensitivity to selection of the neighbourhood of individual points under different local spatial density of the points. To address this problem, a rotation invariant local feature is proposed using group integration [6]. However, neither descriptors takes into account outliers or missing data within the local constellation of individual constituent points and their descriptors are not affine-invariant.

Belonging to the second category, our approach addresses the limitations of the state-of-the-arts, the bead-based registration in Fiji-Plugin [3] and can achieve good results in difficult data. The contributions of the proposed method include:

• 1. a novel local geometric descriptor, i.e., affine shape distribution, which represents the affine invariant shape for local point patterns together with its positional uncertainty;

• 2. a permutation and voting scheme, which enhances robustness and discriminative power of affine shape distributions against the outliers or missing data within the local constellation of each point;

• 3. an efficient search scheme for the putative matching pairs using a hierarchical tree-based algorithm allowing for fast and precise point cloud registration.

3 Methodology

In this section, we first define an representation for the local spatial pattern of one point together with its neighbours, named as affine shape. Next, the probability distributions of the affine shape are derived from their positional uncertainty. Finally, we introduce a complete algorithm to establish the putative correspondence based on affine shape distributions and estimate the underlying spatial transformation between the random point sets of two views.

3.1 Affine Shape for Local Point Patterns

Let’s have one point $\mathbf {p}\in \mathbb {R}^d$ and its $k$ neighbours, $\mathbf {p}_1,\mathbf {p}_2,...,\mathbf {p}_k$, where $k$ is the minimum number of points required to define a canonical frame that is invariant to affine transformations. In other word, $k$ points form a simplex to define an affine basis. (e.g., $k=3$ in two dimensional case and $k=4$ in three dimensional case).

Given a point $\mathbf {p}$ and its $k$ neighbours with an arbitrary order, an affine invariant labelling for its $k$ neighbours can first be performed based on their affine invariant coefficients. Assume $\mathbf {p}_1,\mathbf {p}_2,...,\mathbf {p}_k$ is not degenerate, point $\mathbf {p}$ can be represented by a weighted linear combination of its $k$ neighbours. Here $\mathbf {p}=\sum ^{k}_{i=1} w_i \mathbf {p}_i=[\mathbf {p}_1,\mathbf {p}_2,...,\mathbf {p}_k ]\mathbf {w}$, with $\sum ^{k}_{i=1} w_i=1$. The coefficients, $w_i$, are known to be invariant to any affine transformation applied to the point set. We can rearrange the order of those points by sorting their corresponding $\left| w_i\right|$ in ascending order. Given any selected point $\mathbf {p}$, this rearrangement allows for an affine invariant labelling for its neighbours and thus avoids the need for the calculation of all the possible permutations of its $k$ neighbours. In the rest of this paper, we consider the points $\mathbf {p}_1,\mathbf {p}_2,...,\mathbf {p}_k$ arranged in such a way, with $\mathbf {p}_k$ according to the point with the largest $\left| w_i\right|$.

Given one point $\mathbf {p}$ with its $k$ neighbours, $\mathbf {p}_1,\mathbf {p}_2,...,\mathbf {p}_k$, as labelled above, we show that the shape of the $k+1$ points can be represented as a point at standardized Euclidean shape space [20], $\varOmega$, which is a subspace of $\mathbb {R}^d$. Let’s take the three dimensional case ($k=4$) for instance. We first choose one point, say $\mathbf {p}_4$, as the local frame origin. Then, a matrix, $A=[\mathbf {p}_1-\mathbf {p}_4,\mathbf {p}_2-\mathbf {p}_4,\mathbf {p}_3-\mathbf {p}_4]$, can be defined by subtracting the origin, $\mathbf {p}_4$, from the other points. Similarly, we subtract the selected point, $\mathbf {p}$, by the origin and denote $\mathbf {p}_t=\mathbf {p}-\mathbf {p}_4$. We now consider the inverse mapping of $A$, $A^{-1}$, which transforms the three points, $\mathbf {p}_1$, $\mathbf {p}_2$, $\mathbf {p}_3$, to the points with unit length on $x$, $y$ and $z$ axes respectively. By applying the mapping to the selected point in the local frame, $\mathbf {p}_t$, we get a vector, $\mathbf {q}\in \varOmega$, at standardized Euclidean shape space as

$$\begin{aligned} \mathbf {q}=[\mathbf {p}_1-\mathbf {p}_4,\mathbf {p}_2-\mathbf {p}_4,\mathbf {p}_3-\mathbf {p}_4]^{-1}\cdot (\mathbf {p}-\mathbf {p}_4) = A^{-1}\mathbf {p}_t. \end{aligned}$$

(1)

Note that the vector, $\mathbf {q}$, encodes the affine invariant spatial patterns of those five points ($\mathbf {p}$ and $\mathbf {p}_{1,2,3,4}$) and serves as a descriptor for the local point pattern. Thus, we refer to $\mathbf {q}$ as the affine shape of these $(k+1)$ points.

3.2 Affine Shape Distribution

We now address the problem of inherent uncertainty of observed points. There are two sources of uncertainty in the resulting affine shape representations. One comes from the uncertainty of the observed point $\mathbf {p}$ itself, while another stems from the variability of the affine basis.

Let’s consider that the position of each point $\mathbf {p}$ is a random variable following a Gaussian distribution function with mean $\bar{\mathbf {p}}$ and covariance matrix $\varSigma _{\mathbf {p}} \in \mathbb {R}^{ d\times d}$. If we assume the affine basis have no variability, the affine shape, $\mathbf {q}$, also follows a Gaussian distribution function with mean $\bar{\mathbf {q}}=A^{-1}\bar{\mathbf {p}}$ and covariance matrix $\varSigma _{\mathbf {q}}=A^{-1}\varSigma _{\mathbf {p}} A^{-\top }$.

To consider the uncertainty of the points used to define the affine basis, we make use of the following classic theorem [21].

Proposition 1

(Uncertainty Propagation). Let $v$ be a random vector in $\mathbb {R}^d$ with mean $\bar{v}$ and covariance matrix $\varSigma$, and $f: \mathbb {R}^d\rightarrow \mathbb {R}^{d'}$ be an affine map. Then $f(v)$ is a random vector in $\mathbb {R}^{d'}$ with mean $f(\bar{v})$ and covariance matrix $J\varSigma J^{\top }$, where $J$ is the Jocabian matrix of $f$ at point $\bar{v}$.

For the three dimensional case, given $4$ points as a simplex, we can calculate its affine matrix, $A$, from Eq. (1). The Jacobian matrix of $A$ for each entry of the $4$ points is equal to

$$\begin{aligned} \frac{\partial \textit{vec}(A)}{\partial \textit{vec}(\mathbf {p}_{1,2,3,4})}= \left[ \begin{array}{cccc} \mathbf {I}_3 &{} \mathbf {0} &{} \mathbf {0} &{} -\mathbf {I}_3\\ \mathbf {0} &{} \mathbf {I}_3 &{} \mathbf {0} &{} -\mathbf {I}_3\\ \mathbf {0} &{} \mathbf {0} &{} \mathbf {I}_3 &{} -\mathbf {I}_3\end{array} \right] , \end{aligned}$$

(2)

where $\mathbf {0}$ is a $3\times 3$ all-zero matrix and $\mathbf {I}_3$ is a $3\times 3$ identity matrix. Differentiating $AA^{-1}=\mathbf {I}_3$, we obtain that $d(A^{-1})=-A^{-1} dA A^{-1}$. Using the Kronecker product $\otimes$, it can be rewritten as $\textit{vec}(d(A^{-1}))=-(A^{-\top }\otimes A^{-1})\textit{vec}(dA)$. Thus, we can calculate the Jacobian of $A^{-1}$ at $A$ with respect to the $4$ points, as follows

$$\begin{aligned} J=\frac{\partial \textit{vec}(A^{-1})}{\partial \textit{vec}(\mathbf {p}_{1,2,3,4})}=-(A^{-\top }\otimes A^{-1})\frac{\partial \textit{vec}(A)}{\partial \textit{vec}(\mathbf {p}_{1,2,3,4})}. \end{aligned}$$

(3)

Following the Proposition 1, we get

$$\begin{aligned} \varSigma _{A^{-1}}=J\cdot \text {diag}\left( \varSigma _{\mathbf {p}_1},\varSigma _{\mathbf {p}_2},\varSigma _{\mathbf {p}_3},\varSigma _{\mathbf {p}_{4}}\right) \cdot J^{\top }, \end{aligned}$$

(4)

where $\text {diag}\left( \varSigma _{\mathbf {p}_1},\varSigma _{\mathbf {p}_2},\varSigma _{\mathbf {p}_3},\varSigma _{\mathbf {p}_{4}}\right)$ denotes the block-diagonal matrix of size $12\times 12$ with block matrices $\varSigma _{\mathbf {p}_1},\varSigma _{\mathbf {p}_2},\varSigma _{\mathbf {p}_3},\varSigma _{\mathbf {p}_4}$ on its diagonal. Note that we consider the position variation of each point is independent on each other.

Based on Eq. (1), we can naturally get $\varSigma _{\mathbf {p}_t}=\varSigma _{\mathbf {p}} + \varSigma _{\mathbf {p}_4}$ for $\mathbf {p}_t$. Again, by using the Proposition 1, the complete $\varSigma _{\mathbf {q}}$ considering the variation in all the points can be given as

$$\begin{aligned} \varSigma _{\mathbf {q}}=L \varSigma _{A^{-1}} L^{\top }+A^{-1}\varSigma _{\mathbf {p}_t}A^{-\top }, \end{aligned}$$

(5)

where $L=\left[ \text {diag}(\mathbf {p}_t) \ \text {diag}(\mathbf {p}_t) \ \text {diag}(\mathbf {p}_t)\right]$ is a $3\times 9$ block matrix with $3$ identical $3\times 3$ blocks.

It is worth noting that the probabilistic distribution of affine shape is invariant to rotation and translation. In addition, its mean, $\bar{\mathbf {q}}$, is equal to the affine invariant coefficients, while its covariance matrix, $\varSigma _{\mathbf {q}}$, encodes the information related to the affine bases and uncertainties of the points. In the rest of this paper, we refer this probabilistic distribution of affine shape as affine shape distribution.

3.3 Fréchet Distance for Affine Shape Distributions

To measure the difference between two affine shape distributions, we adopt Fréchet distance between multivariate normal distributions [22] as

$$\begin{aligned} \text {dist}\left( \mathcal {N}(\bar{\mathbf {q}}_1,\varSigma _{\mathbf {q}_1}), \mathcal {N}(\bar{\mathbf {q}}_2,\varSigma _{\mathbf {q}_2})\right) = \left| \bar{\mathbf {q}}_1 - \bar{\mathbf {q}}_2\right| ^2+\mathrm {tr}\left[ \varSigma _{\mathbf {q}_1}+\varSigma _{\mathbf {q}_2}-2(\varSigma _{\mathbf {q}_1}\varSigma _{\mathbf {q}_2})^{\frac{1}{2}}\right] , \end{aligned}$$

(6)

where $\mathrm {tr}(\cdot )$ stands for the trace of a matrix and $|\cdot |$ is $L^2$ norm in vector space. Noting that the first term measures the Euclidean distance between two affine-invariant coefficients in the space of $\varOmega$. The second term accounts for the difference between the non-rigid parts (skewing and anisotropic scaling) of two underlying affine transformations and the positional uncertainties of all the points.

3.4 Point Cloud Matching Using Affine Shape Distributions

A robust point matching has to satisfy two requirements: the stability and the discrimination power. The stability means, given the constellation of a point and its $m$ neighbours in one view, the corresponding pattern of one point together with its $m$ neighbours can also be found in another view. However, it is not easy to find such correspondent pairs of patterns. Affine transformation may change the Euclidean distance between points, and thus changes the members of neighbourhood of one point selected by nearest neighbours searching. The constellation of local point patterns can also be contaminated by the unexpected occlusion and outliers occurred in the local neighbourhood for the given point. Therefore, given any point, we need to consider a larger neighbourhood by including its nearest $n$ neighbours, where $n>m$. Then, all possible combinations of $m$ points from $n$ nearest points should be examined. As long as at least one combination of $m$ points is common, a stable feature for matching of point patterns can be established.

The discrimination power ensures that different point patterns in one view should match their respective patterns in another view. However, it is often not the case since similar affine shape distributions can be obtained from other different spatial pattern of points. To increase the discrimination power, we have to consider the case when $m>k$ and assume there exist at least $\left( {\begin{array}{c}m\\ k\end{array}}\right)$ common combinations of $k$ points out of $\left( {\begin{array}{c}n\\ k\end{array}}\right)$ possible combinations from the $n$ nearest points. To enforce this constraint, a voting system is introduced to establish a matching between two point patterns in different views only when there exist at least $\left( {\begin{array}{c}m\\ k\end{array}}\right)$ pairs of similar entries of affine shape distributions between their corresponding local neighbourhoods.

Given a random point set, all the entries of its affine shape distributions can be calculated as detailed in Algorithm 1. The next step is to establish the putative correspondence pairs between those entries of two point sets. Due to the highly combinatorial nature of this problem, there is a need for speeding up the search for potential matching pairs among the huge amount of entries for affine shape distributions. Inspired by the ideas in [22], we transform the covariance matrix of each affine shape distributions into a diagonal matrix. As discussed in the work [23], under the commutative case, the calculation of the Fréchet distance between two affine shape distributions in Eq. (6) can be simplified as

$$\begin{aligned} \text {dist}\left( \mathcal {N}(\bar{\mathbf {q}}_1,\varSigma _{\mathbf {q}_1}), \mathcal {N}(\bar{\mathbf {q}}_2,\varSigma _{\mathbf {q}_2})\right) = \left| \bar{\mathbf {q}}_1 - \bar{\mathbf {q}}_2\right| ^2+\left| \textit{vec}{(\varSigma ^{\frac{1}{2}}_{\mathbf {q}_1})}-\textit{vec}{(\varSigma ^{\frac{1}{2}}_{\mathbf {q}_2})}\right| ^2. \end{aligned}$$

(7)

Note that each affine shape distribution can be represented by a vector in a feature space with $L^2$ norm. Therefore, for each entry of affine shape distribution, we employ a KD-tree to search for its nearest neighbours as potential matching pairs in this high dimensional vector space. The complete algorithm for random point matching based on affine shape distributions is summarized in Algorithm 2.

4 Results

4.1 Experiments on Synthetic 3D Random Points

In this experiment, we evaluate the performance of the proposed method under different parameter settings. To generate data sets of 3D random points, we first generate $100$ points randomly distributed in a $100 \times 100 \times 100$ space as inliers of one view. We obtain the corresponding inliers in another view by transforming those points using an random affine transformation and independently adding Gaussian positional jitter, $\mathcal {N}(0,\sigma ^2\mathbf {I}_3)$, to each point. Next, we add outliers randomly into the surrendering regions of the inliers for both views. For each trial, we compare the ground truth with the putative correspondences detected by the proposed method before further refinement via RANSAC. Their precision and recall ratios are recorded for 100 random trials. Three types of experiments are conducted under different parameter settings.

For the first type of experiment, we fix the number of nearest neighbours, $n=8$, and vary the number of common neighbours, $m$, under different amounts of outliers with $\sigma =0.1$. As shown in Fig. 2(a), when $m=5$, it achieves a good balance between the discriminative power and robustness against outliers. Similarly, given $m=5$ as fixed, the second type of experiments varies $n$ under the different number of outliers with $\sigma =0.1$. According to Fig. 2(b), a trade-off between precision and recall ratios for the choice of $n$ is obtained when $n=8$. Therefore, we can fix the parameters ($m=5,n=8$) for the rest of experiments. Finally, to investigate the influence of positional jitter for the proposed method, we evaluate its performance under four levels of Gaussian positional jitter ($\sigma =0.01, 0.1, 0.5, 1$) respectively. Theoretically, the expected relative distance between points, $r$, is equal to $1/\rho ^{1/3}$, where $\rho$ is the density of the point cloud. In our case, the range of $r$ are from 15 to 22 depending on total number of points including both inliers and outliers. Compared to the relative distance between local neighbors, the registration problem under the high levels of Gaussian positional jitter ($\sigma \ge 0.5$) is considered quite challenging. As shown in Fig. 2(c), when the level is high ($\sigma \ge 0.5$), both precision and recall ratios for true correspondent pairs drop rapidly. Similar results were also reported in [6]. It is a well-known limitation that such descriptors derived from local point pattern are relatively sensitive to the positional jitter due to their dependence on local spatial constellation of points [24]. Despite their limitations, this type of local descriptors are widely used in many applications such as camera-based document image retrieval [25] and pose estimation using a projected dense dot pattern [26], for its robustness against large number of outliers.

Fig. 2.

The mean and standard deviation of precision and recall ratios over $100$ random trials under different parameter settings against different numbers of outliers.

4.2 Experiments on Benchmark Datasets

In this experiment, we focus on investigating the robustness of the proposed methods against the large number of outlier. Two types of point patterns (’fish’ and ’character’) from the benchmark synthesized datasets [12] are used to evaluate the performance of our method against the state-of-the-arts. Those methods include iterative closest point (ICP) [11], coherent point drift (CPD) [13] and robust point set matching using Gaussian mixture model (RPM-GMM) [14], whose source codes are publicly available. We also compare our method with the algorithm described in [3] noted as Fiji. We implement our method using Matlab and all the methods are run on a laptop with 2.2GHz CPU and 8G RAM. Rigid transformation between two point sets is applied for a fair comparison since the available version of RPM-GMM only supports the estimation of rigid transformation.

In each trial, we generate a random rigid transformation and apply it to the prototype patterns to obtain a pair of point patterns related by the transformation. Both patterns are located within an area of size $10 \times 10$. We also add a Gaussian positional jitter with $\sigma =0.001$ to each point of the transformed prototype patterns. To evaluate the performances of the methods under heavy outliers or occlusions, two types of tests are designed: (1) Outlier test. Random outliers following an uniform spatial distribution are added to both sides of the point patterns respectively; (2) Occlusion test. We remove a portion of true correspondence from both point patterns and add same numbers of random outliers as those of the removed inliers to both sides of the point patterns. The examples of the synthesized point sets of both types are shown in Fig. 3. One point set is considered as the moving point set while the other is taken as the fixed point set. The matching error is defined as the mean of Euclidean distances between the inliers in the fixed point set and their correspondences in the transformed moving point set obtained by each method. The average matching errors over $100$ random trials by all the methods for two types of tests are shown in Fig. 4. Obviously, the performances of our method are much better than others especially under heavy outliers and occlusions. For ICP, the large mean and standard deviation of registration error arise under all the cases due to local minima and bad initial alignments. CPD, RPM-GMM and Fiji perform well in the cases with a few outliers or occlusions, but they yield far less robust alignments than our method under the cases with large amount of outliers or occlusions. The average running times of different methods are listed in Table 1. Our method is slower than others as we need to consider combinatorial optimizations.

Table 1. Average running times of different methods against the total number of points $N$ (in seconds).

Fig. 3.

Left column shows the prototype shapes for fish and character. The middle column shows an example of character case with outliers, where the points in one view are plotted as blue circles while those in another view are red crosses. The right column shows an example of fish case with occlusion.

Fig. 4.

The mean and standard deviation of matching errors over 100 random trials by different methods for the two types of tests.

4.3 Experiments on Dataset from Multiview SPIM

The data set of multi-view SPIM is obtained from [27] associated with [3]. A live Drosophila egg was recorded from seven views with angles of $45^{\circ }$. Each view contains approximately two thousands of fluorescent beads of $0.5\,\mu m$ diameter. The resulting images have a size of ($1040 \times 1388 \times 90$) with voxels of size ($0.731\,\mu m \times 0.731\,\mu m \times 2\,\mu m$).

The beads of all the views are first extracted with subpixel accuracy using a difference of Gaussian filter [28]. We set $\sigma =1$ for this experiments. An example of the result by the proposed method is shown in Fig. 5. To conduct quantitative comparisons against the state-of-the-arts (CPD and the bead-based registration in Fiji-Plugin [3]), the ground truth of corresponding beads across views is required. Since the Fiji-Plugin is a well-established method in this field, we first register each image to the image of first view using the Fiji-Plugin and consider the detected corresponding beads as ground truth. Then, we apply all the methods to estimate the underlying transformations across views. The registration error is defined by the average Euclidean distance between beads of ground truth in the first view and their correspondences of another view warped by the estimated transformations using each method. As listed in Table 2, the proposed method achieves comparable registration accuracies for all the views as the Fiji-Plugin, while the CPD yields large registration errors. The average execution times for the CPD, Fiji-Plugin and our method are around $35$, $37$ and $76$ seconds respectively.

Fig. 5.

Illustration of the bead-based registration result between two views using the proposed method. Panel (a) shows the extracted bead from two views. Noting that the contours of samples in both views are mistakenly identified as beads. Later, they are automatically treated as outliers by the proposed method. The result of registration between two views with a rotation around $45^\circ$ are illustrated in Panel (b). The yellow circles indict the correspondence pairs detected by the proposed method.

Table 2. Comparison of the average registration errors between the reference beads in view 1 and those in the rest of views.

Table 3. Comparison of the average registration errors and the number of true correspondent pairs under different levels of anisotropic scaling in $z$-axis ($s_z$). Note that the total number of pairs of true correspondence as inliers is $219$ and the total number of extracted beads in two views are $2736$ and $2538$ respectively.

It is well-known that there exists the anisotropic $z$-stretching of each view introduced by the differential refraction index mismatch between water and agarose since the sample is never perfectly centered in the agarose column [3]. To evaluate the effect of anisotropic $z$-stretching on registration accuracy, an affine transformation, $\text {diag}(1,1,s_z)$, is created, where $s_z$ is a scaling factor on $z$-axis. We apply those additional affine transformations to the images of the first two views to simulate anisotropic $z$-stretching. We simulate four levels of anisotropic scaling with $s_z=0.6, 0.7, 0.8, 0.9$, where the level with $s_z=0.6$ is the one with the largest anisotropic scaling among all of the levels. Table 3 shows the average registration error and the numbers of true correspondence pairs detected by each method under different scaling factors $s_z$. Note that the local descriptor used by the Fiji-Plugin is not affine-invariant as we discussed in the related work section. Therefore, for the case with large anisotropic scaling ($s_z=0.6,0.7$), the proposed method can register well, while the Fiji-Plugin fails due to the inadequate number of true correspondence pairs detected by its local descriptor.

5 Conclusion

We have presented a point cloud registration using affine shape distributions for multi-view SPIM. The proposed method detects the points of correspondence and solves for the underlying transformation in the presence of an extremely large amount of outliers and missing data in both point clouds. Experiments show this method is more reliable against the large amount of outliers and the anisotropic scaling of the underlying affine transformation, even in cases when the well-established methods fail. However, our method is sensitive to positional jitter. Hence, our future work is to explore descriptors which are robust to potential positional jitter and non-linear deformations.