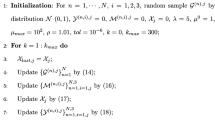A Two-Step Image Inpainting Algorithm Using Tensor SVD

Abstract

In this paper, we present a novel exemplar-based image inpainting algorithm using the higher order singular value decomposition (HOSVD). The proposed method performs inpainting of the target image in two steps. At the first step, the target region is inpainted using HOSVD-based filtering of the candidate patches selected from the source region. It helps to propagate the structure and color smoothly in the target region and restrict to appear unwanted artifacts. But a smoothing effect may be visible in the texture regions due to the filtering. In the second step, we recover the texture by an efficient heuristic approach using the already inpainted image. The experimental results show the superiority of the proposed method compared to the state of the art methods.

This work is partially supported by Department of Science and Technology, Government of India (NRDMS/11/1586/09/Phase-I/Project No. 9).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Inpainting is the process of generating information into a region(s) marked by the user of an image or video in such a way that the filled region(s) is visually plausible [1, 2]. Recently, this system becomes popular and widely used in various field of image processing and computer vision liker restoration (scratch removal of old photograph) and image editing (text or object removal). Previous approaches of image inpainting can be divided roughly into two categories: (i) partial differential equation (PDE) based approach for structure propagation and (ii) exemplar-based approach for texture synthesis. Here our main concern is about the second category.

The PDE-based image inpainting technique propagates information smoothly inward the target region from the surrounding source region along the isophote directions [1]. In [3] the total variation is minimized in the processed image maintaining the fidelity with the input image. The base line idea of these types of methods is to transmit the contours smoothly into the region being inpainted. The second type of approaches is exemplar-based where the selected patch (target patch) from the target region is replaced by the most similar candidate patch from the source region. This concept is first introduced by Efors et al. for texture synthesis [4]. Criminisi et al. [2] proposed similar method where the structure completion is emphasized over the texture synthesis. For this, they proposed an ordering of the target patches from the boundary of the target region depending on the structure strength. A synthesized patch is estimated to fill the missing pixels of the target patch. Recently, sparse representation is applied in image inpainting like the other fields of image processing and computer vision because of it’s robustness [5–7]. Komodakis et al. [8] proposed coherence in the image inpainting formulation by favoring the similarity with the overlapping region of patches. Liu et al. [9] introduced multiscale graph cuts algorithm in image inpainting as a energy minimization problem. Meur et al. [10, 11] proposed image inpainting based on hierarchical single frame super-resolution combining different inpaint versions of the target image for different settings of the input parameters. But still these methods have several limitations related to structure and texture completion. In this paper we adopt exemplar-based inpainting algorithm proposed in [2] as our base-line method.

1.1 Motivation

To overcome the above mentioned problems, we suggest to inpaint the target region several times sequentially in a multiresolution framework. In a particular resolution, first the candidate patches similar to the target patch are filtered using transform domain approach and combine them using loopy belief propagation to infer the target patch. When the target region is totally inpainted, it is re-inpainted because a smoothing effect may appear in the texture region due to the transformation. We have two main motivation in the step of transformation based inpainting. First, it removes the artifacts from the candidate patches if appear in some of the patches. The artifacts in the set of candidate patches corresponds to the pixels which are different from most of the patches at a particular position (see supplementary). Second it is easy to inpaint with the smooth candidate patches so that information propagates smoothly in the target region. For this, we build a 3D array of candidate patches to apply the higher order singular value decomposition (HOSVD) with hard thresholding. The advantage of this transformation is that it performs not only across the height and width of the patches but also along the third dimension, that is, along different candidate patches. It reduces the variation among the candidate patches which ultimately restricts artifacts to appear in the target region and helps to propagate structure correctly inwards the target region. Several authors suggested to combine the candidate patches in different ways, the most popular and the robust one is sparse representation. But the representation depends only the known pixels of the target patch and the corresponding pixels of the candidate patches. This may create artifacts in the unknown region. The hard thresholding in HOSVD transformation remove these artifacts if present in any of the candidate patches. Also, we suggest to apply loopy belief propagation to combine the patches and obtain an approximate solution for a global optimization problem. Due to the transformation, it may produce a smoothing effect in the texture region. To avoid this, traditional texture synthesis approach is applied on the smoothly inpainted image which is obtained from the first step. The above two steps are executed in a multiresolution framework since it is easy to inpaint in the coarser resolution of the target image. The idea of the HOSVD transformation has been applied earlier for dynamic texture synthesis [12] and denoising [13].

Fig. 1.

Steps of HOSVD-based inpainting. (a) This step illustrates the estimation of the target patch $\varPsi _p$ using HOSVD. (b) Inpainted image after all target patch completion. (c) Image after texture recovery.

2 Overview of the Proposed Method

Image inpainting is a challenging task for large blob type target region with complex background and random textures. In literature, different types of exemplar-based techniques have been proposed to solve the inpainting problem. The common steps of these algorithms are patch priority computation and inferring the selected target patch combining the most similar candidate patches [7, 14, 15]. In this paper, we propose a new approach to combine these candidate patches using HOSVD in a multiresolution framework. We briefly describe the main steps of the proposed algorithm in the next paragraph.

The proposed method have two main steps. The first step is to inpaint the target image using HOSVD-based patch filtering. For this, a target patch is selected from the boundary of the missing region and find the candidate patches similar to the target patch. For HOSVD transformation, three 3D array (for color image) of candidate patches is built-up. Then coefficient matrix of singular values is computed applying HOSVD on the 3D array for each color channel. The singular values below some threshold in the coefficient matrix represent the variation among the patches and artifacts. These coefficients are modified by hard thresholding and the patches are reconstructed by inverse transformation [13]. Then we combine these filtered patches using loopy belief propagation to determine the unknown pixels of the target patch. This technique gives more robustness in inpainting by smoothly propagating structure and color into the unknown region. The candidate patches are selected from local as well as global source region and a histogram based similarity measure is taken to approximate the unknown part of the target patch. For local patch selection, we take relatively large neighborhood surrounding the target patch so that local as well as global consistency in the inpainted region is maintained. Beside the advantage of this transform domain technique, the hard thresholding of the HOSVD may produce smoothness effect in fine texture region. To avoid it, in the second step, we recover the texture from the neighborhood of the target region in the already inpainted image. Figure 1 shows different steps of the proposed inpainting algorithm.

3 HOSVD-Based Inpainting

The proposed exemplar-based method have two core steps: $(i)$ To select target patch on the boundary of the missing region based on some priority computation and to fill-in the target patch using HOSVD of candidate patches iteratively until the whole missing region is inpainted, and $(ii)$ to recover appropriate texture in the smooth region reconstructed in the previous step. It is observed that the structure or edge preservation is more important than the texture synthesis since former carries major information and gives meaning to the regions in the image. Several authors [7, 10, 14] introduced different priority terms to choose the target patch from the structure region. Though many priority terms are available in the literature, here we employ the simplest priority measure proposed by Criminisi et al. [2]. For a candidate target patch $\varPsi _p$ at $p$, the priority term $Pr(p)$ is defined as $Pr(p) = K(p)V(p)$ where $K(p)$ is the $knowledge$ term which measures the fraction of patch surrounding the pixel $p$ is known already, and $V(p)$ is $local$ $variation$ term, which in a sense gives an idea of local structure. The proposed method with this simple priority term can produce structure better compared to the more complicated method.

3.1 HOSVD-Based Patch Completion

The main goal of the proposed method is to infer the unknown pixels of the target patch $\varPsi _p$ selected from the previous step. The very first task of this step is to select some patches similar to $\varPsi _p$ from the source region $\varOmega ^c$. Then we apply patch filtering based on the HOSVD transformation to preserve the color and structure consistency in the target region. The robustness of this technique shows it’s superiority to eliminate unwanted artifacts if present in some of these candidate patches. Here we also incorporate the local as well as global patch consistency.

Fig. 2.

(a) Target image with red marked target region. (b) Inpainted image using only local patches. (c) Inpainted image using only global patches. (d) Inpainted image using both local and global patches (Color figure online).

Patch Similarity and Patch Selection: In this work our objective is to select the candidate patches in such a way that fill-in the target patch $\varPsi _p$ following the local as well as global consistency. That means after target patch completion, unwanted artifacts do not appear in the filled-in region. We consider a neighborhood window $N_p$ centered at $p$ and find $m$ similar patches from $N_p$. But fixed $m$ may give some patches with larger dissimilarity. Hence we find the similar patches $\varPsi _{q_j}$ of $\varPsi _{p}$ from $N_p$ as

$$\begin{aligned} \mathcal {X}_p = {\Big \{} \varPsi _{q_j} \in N_p : d_{SSD}(\varPsi ^{k}_{p},\varPsi ^{k}_{q_j}) < \epsilon \; \text{ and } \; d_{H}(\varPsi ^{k}_{p},\varPsi _{q_j}) < \delta {\Big \}} \end{aligned}$$

(1)

where $\varPsi ^{k}_{p}$ and $\varPsi ^{k}_{q_j}$ are the known part of $\varPsi _p$ and corresponding part of $\varPsi _{q_j}$, $d_{SSD}$ is the sum of square difference among the patches and $\epsilon ,\delta$ are the threshold parameters. The histogram based dissimilarity measure $d_{H}$ is defined by euclidean distance as

$$\begin{aligned} d_{H}(\varPsi ^{k}_{p},\varPsi _{q_j}) = \sqrt{\sum _{i=1}^{b}|h_{p}(i) - h_{q_j}(i)|^2} \end{aligned}$$

(2)

where $h_{p}$ and $h_{q_j}$ denotes the normalized histogram of the known part of the patch $\varPsi _p$ and full part of the neighbor patch $\varPsi _{q_j}$, and $b$ is the number of histogram bins. This measure approximates the unknown pixels of the target patch by of it’s known pixels so that both the parts look similar. The histogram is computed on the intensity channel of color space.

Also some candidate patches $\mathcal {Y}_p =\{\varPsi _{p_i}\}$ are obtained in the similar way as described in (1), but here the search range is the source region $\varOmega ^c$ instead of $N_p$. These candidate patches are also added to $\mathcal {X}_p$ to get a list $\mathcal {P}_p$ of local and global patches for HOSVD transformation. This idea behind the selection of candidate patches is to approximate the estimated target patch consistent with the local as well as global texture and structure. Top row of Fig. 2, shows inpainting using only local patches produce wrong texture in the target region, but when we take both the local and global patches, it works well. Similar thing happens in the bottom row also, but here local patches almost correctly recover the target region whereas global patches fail to generate proper texture. Local and global patches together, however, consistently recover the texture in the target region. Here we define $\epsilon = \lambda * n_{ch}*|\varPsi _{p}^{k}|$ where $\lambda$ is the factor determining the error tolerance of SSD-based dissimilarity measure, $n_{ch}$ is the number of channel of the input image and $|\varPsi _{p}^{k}|$ is the count of known pixels in $\varPsi _p$. $\lambda$ is set to $3\delta$ where $\delta$ is the threshold of histogram-based dissimilarity measure. Since $\delta$ is a fixed parameter we may obtain an empty set of both $\mathcal {X}_p$ and $\mathcal {Y}_p$. In such a case, we decreases the priority of the current target patch $\varPsi _p$ to say half of its original priority and select a new patch based on priority. However if no such candidate patch is found we increase the value error tolerance $\delta$ by 0.1. This assumption also helps to restrict selection of target patch with large dissimilarity to both the local and the global patches.

HOSVD for Inpainting: Due to the unknown pixels of the target patch, the candidate patches selected from the local and global source region may not be similar in the unknown region. They may differ slightly from each other or some artifacts may appear in the unknown part. But here the main goal is to process the candidate patches in such a way that the unknown part of the patches looks similar to the known part. HOSVD provides the solution because it filters the candidate patches as well as takes into account the similarity among the pixels of at all locations. In the next section, we discuss about the standard SVD and it’s higher order generalization HOSVD. Lastly, HOSVD is introduced in image inpainting with mentioning it’s different steps.

Background: Given a matrix $A$ of size $m \times n$, the singular value decomposition (SVD) is of the from $A = USV^{T}$ where $U$ is a $m\times m$ orthonormal matrix, $S$ is a $m \times n$ diagonal matrix of positive singular values in the descending order and $V$ is a $n \times n$ orthonormal matrix. The columns of $U$ and $V$ are the eigen vectors of $AA^{T}$ and $A^{T}A$ respectively. The square of the singular values in $S$ are the eigen values of $AA^{T}$ (or $A^{T}A$). The HOSVD is an extension of the matrix SVD for higher order matrices [16]. Usually, matrices of order higher than 2, is called tensor. Suppose $\mathcal {A} \in R^{ I_{1}\times I_{2} \times ... \times I_{r}}$ is a tensor of order $r$ where $I_1,I_2,...,I_r$ denotes the number of elements for each dimension. The r-order tensor $\mathcal {A}$ may be decomposed as

$$\begin{aligned} \mathcal {A} = \mathcal {S} \, \times _{1} \, U^{(1)} \, \times _{2} \, U^{(2)} ...\times _{r} \, U^{(r)} \end{aligned}$$

(3)

where $U^{(1)}$, $U^{(2)},...,U^{(r)}$ are orthogonal matrices containing the orthonormal vectors spanning the column space of the matrix unfolding $A_{(p)}$ with $p=1,2,...,r$ and $\mathcal {S}$ is the core tensor analogous to the diagonal matrix $S$ in the standard SVD. Note that, generally $\mathcal {S}$ is a full tensor that means it is not a diagonal matrix like $S$. The $s$-th mode tensor product $\times _{s}$ for a tensor $\mathcal {X} \in R^{ I_{1}\times I_{2} \times ... \times I_{s}... \times I_{r}}$ and a matrix $\mathcal {Y} \in J_{s}\times I_{s}$ may be denoted by $\mathcal {X} \times _{s} \mathcal {Y}$ and is a tensor $\mathcal {Z} \in R^{I_{1}\times I_{2} \times ... \times {J_{s}}... \times I_{r}}$. Therefore

$$\begin{aligned} z_{i_{1} i_{2}...i_{s-1} j_{s} i_{s+1}...i_{r}} = \sum _{i_{s}} x_{i_1 i_2... i_s...i_r} y_{j_s i_s}. \end{aligned}$$

(4)

The core tensor $\mathcal {S}$ is obtained by

$$\begin{aligned} \mathcal {S} = \mathcal {A} \times _{1} U^{(1)^H} \times _{2}U^{(2)^H} ...\times _{r} U^{(r)^H} \end{aligned}$$

(5)

where $H$ denotes the Hermitian matrix transpose operator.

There is an equivalent matrix formulation of the tensor decomposition. For this, we first define the $p$-mode matrix unfolding (also called matricization) $A_{(p)} \in R^{I_p \times (I_{p+1} \times ... \times I_r \times I_1 \times ... \times I_{p-1})}$ consists of the tensor element $a_{i_1,i_2,...,i_r}$ at $(i_p,j)$ where

$$\begin{aligned} j = 1+ \sum _{l=1,l \ne p}^{r} (i_l-1)\prod _{m=1,m\ne p}^{r}I_m \end{aligned}$$

(6)

The Eq. (3) can be expressed in matrix format as

$$\begin{aligned} A_{(p)} = U^{(p)} S_{(p)} ( U^{(p+1)} \otimes U^{(p+2)} ... U^{(r)} \otimes U^{(1)} \otimes U^{(2)} ... U^{(p-1)} )^H \end{aligned}$$

(7)

where $U^{(p)}$ is obtained from SVD of $A_{(p)}$ by

$$\begin{aligned} A_{(p)} = U^{(p)} \varSigma ^{(p)} V^{(p)^H} \end{aligned}$$

(8)

and the symbol $\otimes$ denotes the Kronecker product. The diagonal matrix $\varSigma ^{(p)}$ is defined as

$$\begin{aligned} \varSigma ^{(p)} = diag(\sigma _{1}^{(p)}, \sigma _{2}^{(p)}, ..., \sigma _{I_p}^{(p)} ) \end{aligned}$$

(9)

where $\sigma _{1}^{(p)}, \sigma _{2}^{(p)}, ..., \sigma _{I_p}^{(p)}$ are the Fobenius-norms of $S_{(p)}$.

The matrix formulation of Eq. (5) is

$$\begin{aligned} S_{(p)} = U^{(p)} A_{(p)} ( U^{(p+1)} \otimes U^{(p+2)} ... U^{(r)} \otimes U^{(1)} \otimes U^{(2)} ... U^{(p-1)} ) \end{aligned}$$

(10)

Patch fill-in using HOSVD: Now we will discuss how HOSVD is applied in the proposed inpainting method. Given a target patch $\varPsi _p$ of size $m \times n$, we find $K$ number of candidate patches $\mathcal {P}_p$ (see the previous section). So the size of the tensor is defined by $I1=m$, $I2=n$ and $I3=K$. We first build a 3D array $\mathcal {A}$ using the candidate patches. Since we deal with color images, actually one 3D array is taken for each individual channel and same scheme is followed for each of the arrays. The HOSVD-based patch synthesis method consists of following steps: (1) Unfolding of $\mathcal {A}$ to $A_{(1)}, A_{(2)},A_{(3)}$ and decomposition of $A_{(p)}$ using standard SVD to obtain $U^{(p)},S_{(p)}$ for $p=1,2,3$ using Eqs. (8) and (10), (ii) manipulation of singular values in $S_{(p)}$ and reconstruct the array $\mathcal {A}$ by inverse transformation using (7), and (iii) averaging the filtered candidate patches for obtaining an estimated target patch. Usually the coefficients are manipulated (typically by hard thresholding) to obtain the filtered patch in the HOSVD-based transform domain. Here the main purpose of patch filtering is to remove unwanted artifacts from a collection of almost similar patches and obtain a smooth version of the patches preserving the edges. The basic idea behind this approach is that it is easy to inpaint the target region surrounded by smooth patches. The random textures and structure surrounding the target region may mislead in estimating the target patch since it’s some part is unknown. The singular values in the coefficient matrix represent the variation among the candidate patches. To suppress these variation, we nullify the coefficients which are below the hard threshold $\sigma \sqrt{2\log (mnK)}$. The 3D array $\mathcal {\hat{A}}$ is then reconstructed by inverting the transformed candidate patches. Since the target patch have unknown pixels and approximating them by a set of candidate patches, some unwanted artifacts may appear in the unknown region of the target patch. The artifacts in a set of candidate patches corresponds to the pixels of patches which are very much different from most of the patches in the set. The singular values below some threshold in the coefficient matrix corresponds to the variation among the patches and also the artifacts. The HOSVD-based filtering try to remove those artifacts from the candidate patches. In Fig. 3, we show the results of inpainting for different values of $\sigma$ and it is clear that higher value of $\sigma$ can efficiently remove the unwanted artifacts better from the target region. In the second figure of supplementary material, we have shown the effect of patch filtering for different set of candidate patches and in some cases artifacts are removed in the filtered patches.

Fig. 3.

Left column shows the target image and other columns show the inpainted images for different values of $\sigma$.

Finally, we estimate the target patch by combining the filtered candidate patches. In literature, $K$ candidate patches are combined by different approaches like sparse representation [7], comprehensive framework [14]. Some authors also consider weighted averaging [10, 15] because of it’s computational simplicity, defined as

$$\begin{aligned} \hat{\varPsi }_{p} = \sum _{\varPsi _q \in \mathcal {P}_p} \lambda _{p,q}\varPsi _q \end{aligned}$$

(11)

where $\varPsi _q$ is the candidate patch after HOSVD-based filtering and

$$\begin{aligned} \lambda _{p,q} = \frac{1}{N} \exp {\Big (} -\frac{d_{SSD}(\varPsi ^{k}_{p},\varPsi ^{k}_{q})}{2\eta ^2} {\Big )} . \end{aligned}$$

(12)

Here $d_{SSD}$ denotes the sum of square differences, $N$ is the normalization constant such that $\sum _{\varPsi _q \in \mathcal {P}_p} \lambda _{p,q} = 1$ and $\eta$ is a scaling parameter set to 10.0. This procedure of combining several candidate patches can estimate the unknown pixels in the target image. But it does not ensure to give the global optimization solution for inpainting. Also it may introduce blur ring effect on the fine texture regions (see Fig. 4(b)). To overcome these problems we incorporate loopy belief propagation which is able to produce an approximation solution of a global optimization problem.

3.2 Loppy Belief Propagation

The problem in belief propagation is to assign a label to each unknown patch $\varPsi _p$ in the target region $\varOmega$. For the large number of labels, the algorithm suffers from the high time complexity. Komodakis et al. [8] introduced priority belief propagation (PBP) where each patch in the source region is assigned by a label. In [11] the authors used loopy belief propagation (LBP) to combine multiple inpainted images. The multiple images are obtained by inpainting the target image with different patch size and rotation. But in our case the approach is somewhere difference. We assign a lable ($z \in \mathcal {Z}$) to the target patch $\varPsi _p$ from the set of already filtered candidate patches $\mathcal {P}_p$. That means each candidate patch have a label and number of labels may vary for different target patches. Markov Random Field (MRF) formalization of the objective function can be represented by a graph $G = (\nu , \varepsilon )$. The MRF nodes $\nu$ are the lattice consisting of the target patches in the unknown region $\varOmega$ and the edges $\varepsilon$ of the MRF are the 4-neighborhood system $\mathcal {N}_4$ on the lattice. Now the problem of label assigning is to assign a label $z \in \mathcal {Z}$ to each node/patch $\varPsi _p \in \varOmega$ so that the total energy $\mathcal {E}$ of the MRF is minimized, where

$$\begin{aligned} \mathcal {E}(z) = \sum _{p \in \nu } V_\mathbf{{s}}(z_p) + \sum _{(p,q) \in \mathcal {N}_4} V_\mathbf{{p}}(z_p,z_q) \end{aligned}$$

(13)

The single node potential (also called the label cost) $V_\mathbf{{l}}(z_p)$ represents the cost of placing $\varPsi ^{*}_{z_p} \in \mathcal {P}_p$ over the target patch $\varPsi _p$. The formula of the above cost may be written as

$$\begin{aligned} V_\mathbf{{s}}(z_p) = \sum _{x\in \varPsi _p \cap \varOmega ^c} \{ \varPsi ^{*}_{z_p}(x) - \varPsi _p(x) \}^{2} \end{aligned}$$

(14)

The pairwise potential cost $V_\mathbf{{p}}(z_p,z_q)$ represents the cost of placing the patches $\varPsi ^{*}_{z_p} \in \mathcal {P}_p$ and $\varPsi ^{*}_{z_q} \in \mathcal {P}_q$ over the neighbors $p,q$ is given by

$$\begin{aligned} V_\mathbf{{p}}(z_p,z_q) = \sum _{x\in \varPsi ^{*}_{z_p}} \{ \varPsi ^{*}_{z_p}(x) - \varPsi ^{*}_{z_q}(x) \}^{2} \end{aligned}$$

(15)

The minimization of the above objective function $\mathcal {E}$ can be estimated using loopy belief propagation [17].

Fig. 4.

(a) Target image with red marked target region, (b) image inpainted by HOSVD, (c) image inpainted by texture recovery (Color figure online).

3.3 Texture Recovery

In the previous step, we obtain an inpainted image with a smooth target region preserving all the structure and color details. Textures are smoothed out due to HOSVD-based patch filtering. In this section our aim is to recover the texture sharpness using neighborhood texture information of the target region in the inpainted image obtained from the previous step. This step is similar to as the basic of inpainting by priority computation and patch completion, but here the target region is fully known by the previous step. Since a real scene image may contain texture, structure and smooth regions, we want to recover only those regions which are smoothed, but surrounded by texture regions. The constraint is defined in terms of edge map of the inpainted image using HOSVD. For this, we take the window $N_{p}$ at the pixel $p$ in the edge image. If $N_{p} \cap \varOmega$ does not contain any edge pixels and $N_{p} \cap \varOmega ^{c}$ contains sufficient edge pixels, we consider $\varPsi _p$ as a patch in the smooth target region and must have to recover the texture of this patch. Accordingly, the final estimated target patch $\hat{\varPsi }_p$ is recovered by

$$\begin{aligned} \hat{\varPsi }_p = \arg \max _{\varPsi _{q} \in N_{p} \cap \varOmega ^{c}} {\Big \{} d_{SSD}(\varPsi _{p},\varPsi _{q}) < \epsilon {\Big \}} \end{aligned}$$

(16)

We take $\epsilon = \lambda * n_{ch}*|\varPsi _{p}|$ as similar to the patch selection step. Note that, here $\varPsi _p$ and $\varPsi _q$ both are fully known. Figure 4 illustrates the efficiency and necessity of this step. The inpainted image (b) using HOSVD is smooth in the snow region. The result of the texture recovery in Fig. 4(c) shows, our proposed method is robust to recover the texture.

3.4 Multiresolution Approach

Several authors incorporate multiresolution scheme in the proposed inpainting algorithm. There are a few reasons behind this consideration. It permits to capture various details like structure in different scales. It enforces to reduce time complexity and it is also easy to inpaint on the coarse version of the image [10, 14, 15]. The multiresolution scheme follows an recursive process in multiple scales using spatial pyramid. First, inpainting algorithm runs at the coarsest level of the pyramid and the result of this level is considered as an initialization for the finer level for further modification. Here we use 3–5 pyramid level with resolution factor 1.5.

Fig. 5.

(a) Target image with red marked target region. Inpainted image using (b) KSVD [18]. (c) BM3D [19]. (d) HOSVD (Color figure online).

Fig. 6.

(a) Target image. (b) Criminisi’s [2]. (c) Komodakis’s [8]. (d) Pritch’s [20]. (e) He’s [21]. (f) Proposed method.

3.5 HOSVD vs. KSVD and BM3D in Inpainting

The main advantage in choosing HOSVD is it’s simplicity compare to KSVD [18] and BM3D [19]. The KSVD algorithm learns an overcomplete dictionary and represent data samples by pursuit algorithm. It need some parameters which are not easy to tune, such as the number of dictionary elements, the stopping criterion for the pursuit algorithm and the trade off between data fidelity and sparsity terms. Our main aim is to jointly filter the candidate patches which is not possible by KSVD. The idea of jointly filtering multiple patches is introduced earlier in BM3D for denoising. But the algorithm is complex in some sense. The filtering of similar patches go through the 2D followed by 1D transformation in BM3D. But in HOSVD 3D filtering is not combination of such 2D and 1D filtering. BM3D have many parameters such as the choice of 2D and 1D filtering, the maximum number of similar patches, the choice of patch size depending on the noise variance, the choice of pre-filter for patch similarity in the first stage, and also the set of parameters used in Wiener filtering in the second stage. HOSVD learns spatially adaptive bases whereas BM3D uses fixed bases. HOSVD has only two parameters, the number of candidate patches and the value of sigma in the hard threshold which are common to BM3D. In [13] it is shown that HOSVD outperforms KSVD and with Wiener filtering produce better result compare to BM3D for some examples. In Fig. 5, it is shown that our HOSVD-based inpainting approach outperforms over KSVD and better than BM3D.

Fig. 7.

(a) Target image. (b) Criminisi’s [2]. (c) Komodakis’s [8]. (d) Pritch’s [20]. (e) He’s [21]. (f) Liu’s [9]. (g) Proposed method.

Fig. 8.

(a) Image with mask. (b) Criminisi’s exemplar-based method [2]. (c) Liu’s graph cuts approach [9]. (d) Proposed method.

4 Experimental Results and Discussions

In this section, we first set the parameters used in our experiments and then test the proposed method on different types of natural images. We also compare our algorithm with the existing state-of-the-art methods based on exemplar by Criminisi [2], priority belief propagation by Komodakis [8], shift-map by Pritch [20], patch-offsets by He [21], graph cuts by Liu [9] and super-resolution by Meur [11]. We set the size of the patch to $9\times 9$, the value of $\delta =1.0$ and the value of $\sigma = 30.0$ in HOSVD. For local consistency, we select some candidate patches from a restricted search window $N_p$ (neighborhood) centering the target patch. We set the window size to $\kappa \tau$ where $\kappa$ is the level of spatial pyramid ($\kappa =1$ for the coarsest level) and $\tau$ is a fixed parameter set to 30. The MATLAB implementation of the proposed method on Intel 3.07 GHz CPU takes 65 s for the last example of Fig. 8.

Fig. 9.

(a) Image with mask. (b) Criminisi’s exemplar-based method [2]. (c) Meur’s super-resolution based algorithm [11]. (d) Proposed method.

Fig. 10.

Some failure cases. (a, c) Target images. (b, d) Images inpaited of (a) and (c) respectively by our proposed method.

Figure 6 shows that the proposed method visually outperforms Criminisi’s exemplar-based [2] and Komadakis’s belief propagation based [8] method, and provides comparable result to the methods proposed by Pritch et al. [20] based on shift-map and He et al. [21] based on statistics of patch offsets.

Figure 7 shows an popular example of bungee jump. The methods compared in the previous example produce wrong texture in the structure area and both graph cuts proposed by Liu et al. [9] and our proposed method produce visually plausible interpolation.

In Fig. 8, we give more comparisons with Criminisi’s approach and recently proposed method [9] for several natural images. From the results, it is clear that the proposed method produce better texture (second example) and structure (third example) completion compare to the other techniques.

Figure 9 illustrates the performance of the proposed method and the comparison with super-resolution based inpainting proposed by Meur et al. [11]. The results show that the proposed method perfectly recover the target region whereas the other methods fails in many cases to generate proper texture and structure. Note that, with simplest priority term, the proposed method produce better structure than [11] in most of the examples (zoom to see the difference).

In Fig. 10 we show some examples where our method fails to recover both texture and structure.

5 Conclusions

In this paper, we have proposed a novel inpainting algorithm using higher order singular value decomposition of candidate patches. The novelty in choosing HOSVD is that it measures the similarity among the candidate patches which robustly recover the target region with structure and color. Texture recovery step reconstruct the texture which is smoothed due to the filtering step. Experiments and comparisons show that our proposed exemplar-based algorithm can produce better results in most of the cases. In future, we plan to employ this algorithm, combined with de-blurring techniques and hue correction, to digital restoration of old heritage murals and paintings.